VI-DGP: A Variational Inference Method with Deep Generative Prior for Solving High-Dimensional Inverse Problems

Abstract

Solving high-dimensional Bayesian inverse problems (BIPs) with the variational inference (VI) method is promising but still challenging. The main difficulties arise from two aspects. First, VI methods approximate the posterior distribution using a simple and analytic variational distribution, which makes it difficult to estimate complex spatially-varying parameters in practice. Second, VI methods typically rely on gradient-based optimization, which can be computationally expensive or intractable when applied to BIPs involving partial differential equations (PDEs). To address these challenges, we propose a novel approximation method for estimating the high-dimensional posterior distribution. This approach leverages a deep generative model to learn a prior model capable of generating spatially-varying parameters. This enables posterior approximation over the latent variable instead of the complex parameters, thus improving estimation accuracy. Moreover, to accelerate gradient computation, we employ a differentiable physics-constrained surrogate model to replace the adjoint method. The proposed method can be fully implemented in an automatic differentiation manner. Numerical examples demonstrate two types of log-permeability estimation for flow in heterogeneous media. The results show the validity, accuracy, and high efficiency of the proposed method.

Appendices

Appendix A: The Derivation of VAE and the Reparameterization Trick

Note that Maximizing ${\mathcal {L}}({\varvec{\theta },\varvec{\phi }};\varvec{k})$ in Eq. (8) will maximize the marginal log-likelihood and also make approximation $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ close to the true posterior $p_{\varvec{\theta }}(\varvec{z}|\varvec{k})$. So we can maximize ${\mathcal {L}}({\varvec{\theta },\varvec{\phi }};\varvec{k})$ rather than the marginal log-likelihood for computational convenience [22]. For the given training dataset ${\textbf{K}}$, we can write the ELBO for any given $\varvec{k}^{(i)}$ as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}({\varvec{\theta },\varvec{\phi }};\varvec{k}^{(i)})&= {\mathbb {E}}_{q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)})} [\log p_{\varvec{\theta }}(\varvec{k}^{(i)},\varvec{z}) - \log q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)})] \\&= {\mathbb {E}}_{q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)})} [\log p_{\varvec{\theta }}(\varvec{k}^{(i)}|\varvec{z}) ] - D_{KL}\left( q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)}) || p_{\varvec{\theta }}(\varvec{z})\right) . \end{aligned} \end{aligned}$$

(25)

Obviously, these two terms play different roles in optimization. The first term is the expected log-likelihood $\log p_{\varvec{\theta }}(\varvec{k}|\varvec{z})$, where $\varvec{z}$ is sampled from the probabilistic encoder $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$. Maximizing this term enforces $p_{\varvec{\theta }}(\varvec{k}|\varvec{z})$ to assign most of the probability density close to the original $\varvec{k}$. The second term aims to minimize the KL divergence between $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ and $p_{\varvec{\theta }}(\varvec{z})$, which regularizes the probabilistic encoder $q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)})$ to resemble the prior distribution $p_{\varvec{\theta }}(\varvec{z})$. These two terms are the reconstruction term and the regularization term, respectively. For loss computation and parameters $\varvec{\phi }$ and $\varvec{\theta }$ optimization, we still need to specify the distributions for $p_{\varvec{\theta }}(\varvec{k}|\varvec{z})$, $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$, and $p_{\varvec{\theta }}(\varvec{z})$ in Eq. (25). Typically, one can assign a simple isotropic Gaussian distribution as the prior distribution, e.g.,

$$\begin{aligned} \begin{aligned} p_{\varvec{\theta }}(\varvec{z})={\mathcal {N}}\left( \varvec{z}; {\textbf{0}}, {\varvec{I}}\right) . \end{aligned} \end{aligned}$$

(26)

Ideally, an appropriate probabilistic encoder $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ should be able to approximate the target distribution $p_{\varvec{\theta }}(\varvec{z})$ well. Additionally, a Gaussian distribution with a diagonal covariance can be selected as the variational distribution:

$$\begin{aligned} \begin{aligned} q_{\varvec{\phi }}(\varvec{z}|\varvec{k}) = {\mathcal {N}}\left( \varvec{z}; \varvec{\mu }_{\phi }(\varvec{k}), {\text {diag}}(\varvec{\sigma }_{\varvec{\phi }}(\varvec{k})^2)\right) , \end{aligned} \end{aligned}$$

(27)

where $\varvec{\mu }_{\phi }(\varvec{k})$ and $\varvec{\sigma }_{\phi }(\varvec{k})$ are computed by the encoder neural networks. The KL divergence term in Eq. (25) has an analytic form [22] since both $p_{\varvec{\theta }}(\varvec{z})$ and $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ are the factorized Gaussian distribution. The distribution $p_{\varvec{\theta }}(\varvec{k}|\varvec{z})$ usually depends on the training data. In this paper, we select the Gaussian distribution ${\mathcal {N}}\left( \varvec{k}; {\mathcal {G}}_{\varvec{\theta }}(\varvec{z}), {\varvec{I}}\right)$ for the probabilistic decoder, where ${\mathcal {G}}_{\varvec{\theta }}(\varvec{z})$ is the output of the decoder neural networks. The stochastic gradient-based method is applied for large-scale training data to realize the joint optimization for $\{\varvec{\theta }, \varvec{\phi }\}$ using the objective function ${\mathcal {L}}({\varvec{\theta },\varvec{\phi }};\varvec{k})$. The reconstruction term in Eq. (25) involves the expectation computation, which is tackled by Monte Carlo estimation. The gradient $\nabla _{\varvec{\theta }}{\mathbb {E}}_{q_{\varvec{\phi }}(\varvec{z}|\varvec{k})} [\log p_{\varvec{\theta }}(\varvec{k}|\varvec{z})]$ can be estimated directly, where the latent variable $\varvec{z}$ is randomly sampled from $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ for expectation approximation. However, the gradient $\nabla _{\varvec{\phi }}{\mathbb {E}}_{q_{\varvec{\phi }}(\varvec{z}|\varvec{k})} [\log p_{\varvec{\theta }}(\varvec{k}|\varvec{z})]$ is difficult to obtain. One cannot swap the gradient and the expectation since the expectation with respect to the distribution $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ is a function of $\varvec{\phi }$. The score function estimator [3, 39] can be applied for gradient estimation, but its high variance leads to a slow optimization process. An alternative differentiable estimator with low variance is the reparameterization trick [22, 40], where the latent variable $\varvec{z}$ is represented by a deterministic transformation $\varvec{z}= \varvec{g}_{\varvec{\phi }} (\varvec{\epsilon };\varvec{k})$.

The differentiable transformation $\varvec{g}_{\varvec{\phi }} (\varvec{\epsilon };\varvec{k})$ maps the auxiliary random noise to the Gaussian distribution in Eq. (27) by the following procedure:

$$\begin{aligned} \begin{aligned} \varvec{z}\sim q_{\varvec{\phi }}(\varvec{z}\mid \varvec{k}) \quad \Leftrightarrow \quad \varvec{g}_{\varvec{\phi }} (\varvec{\epsilon };\varvec{k})=\varvec{\mu }_{\varvec{\phi }}(\varvec{k})+\varvec{\sigma }_{\varvec{\phi }}(\varvec{k}) \odot \varvec{\epsilon }, \quad \varvec{\epsilon }\sim \pi (\varvec{\epsilon }), \end{aligned} \end{aligned}$$

(28)

where $\odot$ denotes the element-wise product and $\pi (\varvec{\epsilon }) = {\mathcal {N}}({\textbf{0}}, {\textbf{I}})$. Then the random variable $\varvec{z}$ only depends on two deterministic outputs of the encoder neural networks by introducing an auxiliary random variable $\varvec{\epsilon }$. Since the operators $+$ and $\odot$ are differentiable, the gradient $\nabla _{\varvec{\phi }}{\mathbb {E}}_{q_{\varvec{\phi }}(\varvec{z}|\varvec{k})} [\log p_{\varvec{\theta }}(\varvec{k}|\varvec{z})]$ is available. It can be written as

$$\begin{aligned} \begin{aligned} \nabla _{\varvec{\phi }}{\mathbb {E}}_{q_{\varvec{\phi }}(\varvec{z}|\varvec{k})} [\log p_{\varvec{\theta }}(\varvec{k}|\varvec{z})]&= {\mathbb {E}}_{\pi (\varvec{\epsilon })}(\nabla _{\varvec{\phi }}\log p_{\varvec{\theta }}(\varvec{k}| \varvec{z})))\\&={\mathbb {E}}_{\pi (\varvec{\epsilon })}\left[ \frac{\partial \log p_{\varvec{\theta }}(\varvec{k}| \varvec{z})}{\partial \varvec{z}} \frac{ \partial \varvec{g}_{\varvec{\phi }} (\varvec{\epsilon };\varvec{k})}{\partial \varvec{\phi }}\right] _{\varvec{z}=\varvec{g}_{\varvec{\phi }} (\varvec{\epsilon };\varvec{k})}, \end{aligned} \end{aligned}$$

(29)

which can be directly estimated by the Monte Carlo method with L samples drawn from $\pi (\varvec{\epsilon })$. Then the ELBO in Eq. (25) can be rewritten as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}({\varvec{\theta },\varvec{\phi }};\varvec{k}^{(i)}) = \frac{1}{L}\sum _{l=1}^{L} \log p_{\varvec{\theta }} (\varvec{k}^{(i)}|\varvec{z}^{(i,l)}) - D_{KL}\left( q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)}) || p_{\varvec{\theta }}(\varvec{z})\right) , \end{aligned} \end{aligned}$$

(30)

where $\varvec{z}^{(i,l)}$ is the $l-$th sample drawn from $q_{\varvec{\phi }}(\varvec{z}|\varvec{k}^{(i)})$. To improve computational efficiency, the training of neural networks usually adopts the minibatch stochastic gradient-based method, where the training dataset is divided into many subsets. Each subset contains n data points for each iteration. The optimization objective function in each iteration can be written as

$$\begin{aligned} \begin{aligned} \tilde{{\mathcal {L}}}({\varvec{\theta },\varvec{\phi }};\varvec{k}^n) = \frac{1}{n}\sum _{i=1}^{n} {\mathcal {L}}({\varvec{\theta },\varvec{\phi }};\varvec{k}^{(i)}). \end{aligned} \end{aligned}$$

(31)

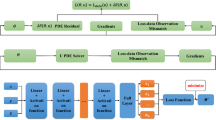
One can apply the stochastic gradient-based method, such as Adam [21], to optimize the probabilistic encoder $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$ and the probabilistic decoder $p_{\varvec{\theta }}(\varvec{k}|\varvec{z})$ using the above objective function. Figure 16 depicts a schematic illustration of the VAE model and the reparameterization trick.

Fig. 16

The schematic illustration of the VAE model and the reparameterization trick. The spatially-varying parameter $\varvec{k}$ is mapped to a latent variable $\varvec{z}$ by the probabilistic encoder $q_{\varvec{\phi }}(\varvec{z}|\varvec{k})$. In turn, the latent variable $\varvec{z}$ is mapped to the parameter $\varvec{k}$ by the probabilistic decoder $p_{\varvec{\theta }}(\varvec{k}|\varvec{z})$

Appendix B: The Network Architectures for the Encoder and Decoder in VAE

In this work, we use fully-connected neural networks as the encoder and decoder for both Gaussian and channel cases. Table 3 illustrates the implemented neural networks for the encoder and decoder. For the decoder, we use ReLU and Sigmoid as the activation function for the Gaussian and channel cases, respectively. Additionally, for the channel case, we apply an extra Sigmoid activation function for the last layer of the decoder model, which ensures that the output values are within the interval [0, 1]. h denotes the number of neurons in the encoder’s hidden layer, which will also define the dimensionality of the latent variable $\varvec{z}$. We set h to 256 and 512 for the Gaussian and channel cases, respectively.

Appendix C: The Network Architectures for the Physics-Constrained Surrogate Model

We can rewrite the loss function in discretization form for the given PDEs in Eq. (21) and Eq. (22). The PDEs loss and boundary loss in Eq. (19) can be written as

$$\begin{aligned} \begin{aligned} J_{\text {pde}}(u(\varvec{x}, \varvec{k}; \varTheta )) =&\frac{1}{n_s n_p}\sum _{j=1}^{n_s}\sum _{i=1}^{n_p} ( \Vert \nabla \cdot \varvec{v}(\varvec{x}_{{\mathcal {D}}}^{(i)}) - f(\varvec{x}_{{\mathcal {D}}}^{(i)}) \Vert ^2\\ +&\Vert \varvec{v}(\varvec{x}_{{\mathcal {D}}}^{(i)}) + \exp (\varvec{k}^{(j)}(\varvec{x}_{{\mathcal {D}}}^{(i)})) \odot \nabla p(\varvec{x}_{{\mathcal {D}}}^{(i)})\Vert ^2 ),\\ J_{\text {b}}(u(\varvec{x}, \varvec{k}; \varTheta )) =&\frac{1}{n_{bl}}\sum _{i=1}^{n_{bl}}\Vert p(\varvec{x}_{{\mathcal {D}}_l}^{(i)}) -1\Vert ^2 +\frac{1}{n_{br}}\sum _{i=1}^{n_{br}}\Vert p(\varvec{x}_{{\mathcal {D}}_r}^{(i)}) \Vert ^2\\ +&\frac{1}{n_{bt}}\sum _{i=1}^{n_{bt}}\Vert \varvec{v}(\varvec{x}_{{\mathcal {D}}_t}^{(i)}) \Vert ^2 +\frac{1}{n_{bb}}\sum _{i=1}^{n_{bb}}\Vert \varvec{v}(\varvec{x}_{{\mathcal {D}}_b}^{(i)}) \Vert ^2,\\ \end{aligned} \end{aligned}$$

(32)

respectively, where $n_b$ boundary samples include $n_{bl}$ samples of left boundary ${\mathcal {D}}_l$, $n_{br}$ samples of right boundary ${\mathcal {D}}_r$, $n_{bt}$ samples of top boundary ${\mathcal {D}}_t$, and $n_{bb}$ samples of bottom boundary ${\mathcal {D}}_b$.

Table 3 The employed network architectures of the VAE model. $\text {Linear} (H_{in}, H_{out})$ denotes the linear operator, where $H_{in}$ and $H_{out}$ are the parameter size of the input and output, respectively

The network architectures applied in this paper are based on previous works [60, 61]. These works perform greatly in uncertainty quantification tasks for the flow in heterogeneous media. The main architectures are shown in Table 4. The number of dense layers in the three dense blocks is 6, 8, 6, with a growth rate of 16. Each dense layer contains a Conv block (Batch-ReLU-Conv). Encoding 1, Decoding 1, and Decoding 2 have 2, 2, 3 Conv blocks, respectively. The nearest mode is used for the upsampling operator in the decoding layers.

Table 4 The network architectures for the physics-constrained surrogate in this paper

Appendix D: The pCN Algorithm for MCMC Simulation

We employ the pCN algorithm to explore the posterior distribution, which is the reference method for the proposed approach. The details are shown in the Algorithm 4, where the forward model ${\mathcal {F}}(\cdot )$ can be either the learned neural network surrogate or the finite element method. These correspond to MCMC-NN and MCMC-FEM in the experiments, respectively.

Algorithm 4

pCN algorithm with the DGP