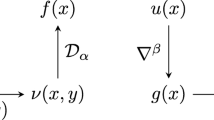Abstract
We present a finite element discretization scheme for multidimensional fractional diffusion problems with spatially varying diffusivity and fractional order. We consider the symmetric integral form of these nonlocal equations defined on general geometries and in arbitrary bounded domains. A number of challenges are encountered when discretizing these equations. The first comes from the heterogeneous kernel singularity in the fractional integral operator. The second comes from the formally dense discrete operator with its quadratic growth in memory footprint and arithmetic operations. An additional challenge comes from the need to handle volume conditions—the generalization of classical local boundary conditions to the nonlocal setting. Satisfying these conditions requires that the effect of the whole domain, including both the interior and exterior regions, be computed on every interior point in the discretization. Performed directly, this would result in quadratic complexity. In order to address these challenges, we propose a strategy that decomposes the stiffness matrix into three components. The first is a sparse matrix that handles the singular near-field separately, and is computed by adapting singular quadrature techniques available for the homogeneous case to the case of spatially variable order. The second component handles the remaining smooth part of the near-field as well as the far-field, and is approximated by a hierarchical \({\mathcal {H}}^2\) matrix that maintains linear complexity in storage and operations. The third component handles the effect of the global mesh at every node, and is written as a weighted mass matrix whose density is computed by a fast-multipole type method. The resulting algorithm has therefore overall linear space and time complexity. Analysis of the consistency of the stiffness matrix is provided and numerical experiments are conducted to illustrate the convergence and performance of the proposed algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fractional diffusion equations are becoming increasingly important in modeling phenomena where nonlocal effects are significant, including fractured media in material science [46, 48], transport in complex media [47, 51], stable Lévy processes in finance [16, 37], Gaussian random fields in spatial statistics [40, 41], image denoising [28], among many others. In addition to physics-based modeling, fractional operators have also been used in controlling the smoothness of priors in Bayesian inverse problems involving distributed parameters [15]. While there has been much work devoted to the formulation and discretization of fractional diffusion in the homogenous case with constant fractional order and material properties (diffusivity, permeability, etc.), there has been comparatively little work that addresses the practically useful heterogenous case with variable coefficients, particularly in multiple spatial dimensions. Our motivation in this work is to develop methods for the efficient discretization of the fractional diffusion operator with variable fractional order and properties.
A standard formulation of fractional diffusion involves the integral representation of the fractional Laplacian \((-\varDelta )^s\) of order \(s\in (0,1)\), where the fractional order characterizes the global smoothness of the solution [11, 27, 31]. The model may be extended to the variable order and diffusivity case by defining these quantities as functions in a physical domain; see e.g. [17, 19, 29, 48]. The specific form of the variable-order fractional diffusion operator we consider here is defined in a bounded domain \(\varOmega \subset {\mathbb {R}}^d\) with \(d=1,2,3\) as:
where \(a(x,y): \varOmega \times \varOmega \rightarrow {\mathbb {R}}^+\) denotes the diffusion coefficient and \(s(x): {\mathbb {R}}^d\rightarrow (0,1)\) is the variable-order function. Formal settings for the above operator with appropriate volume constraints to insure well-posedness are described in Sect. 2 below.
The operator (1) becomes the classical integral fractional Laplacian operator (or the Riesz potential) when s(x) and a(x, y) are constant functions and \(\varOmega ={\mathbb {R}}^d\). The numerical approximation and analysis of this integral fractional Laplacian have been extensively studied in the literature. We refer to [24, 25, 33, 34, 44] for finite difference methods, [53] for a collocation approach, and [12, 30, 42, 57] for particle methods as well as random walk approaches. In terms of finite element methods, we refer to [2, 3] for a classical conforming scheme, [20] based on volume constraints, [9] for a non-conforming approach by the Dunford-Taylor integral formulation, [39, 49] for Petrov–Galerkin approaches, and [36] based on the well-known Caffarelli–Silvestre extension (cf. [14]).
In contrast, the numerical study for the variable-order fractional operator (1) has just started in recent years. For one dimensional problems, we refer to [6, 35, 58, 60] for the numerical approximations of different formulations of variable-order fractional diffusion operators. In multiple spatial dimensions, finite difference schemes were presented in [5] for discretizing the operator (1) in Cartesian geometries. A finite element approach is presented in [19] for domains where the variability consists of uniform inclusions in an otherwise homogeneous medium. There is still however no complete treatment of general variable order and properties for arbitrary geometries in the multidimensional setting. In this work, we extend the considerations from the finite-difference method on cartesian grids developed in [5] to the quasi-uniform meshes for general polytopes, and approximate variable-order fractional diffusion problems involving (1) using a linear finite element discretization scheme.
A primary challenge in the finite element discretization of (1) is that the non-local fractional kernel results in a dense stiffness matrix with a prohibitive \(O(N^2)\) quadratic growth in memory footprint and arithmetic operations, where N denotes the number of degrees of freedom. In [3], the stiffness matrix is decomposed into the near-field and the far-field based on interactions between element pairs and an \({\mathcal {H}}^2\) approximation is constructed from a kernel interpolation [32]. The corresponding near-field matrix is sparse while the far-field matrix can be compressed as a hierarchically low-rank matrix, thus reducing the complexity of the assembly process to O(N), with constants depending on the order of the quadrature and polynomial approximation of the kernel. We also refer to [8, 12, 36, 38, 59] for related hierarchical low-rank approximations, also all in the context of constant-order fractional problems. The variable coefficient case, however, requires additional considerations that are not present in the constant coefficient setting. For example, the work in [3, 4] takes the advantage of the constant-order property to evaluate the integral fractional Laplacian locally; see [3, Lemma 4], a procedure that cannot be readily extended to the variable-order case.
In our approach, the non-singular far-field matrix is expressed as the sum of two terms, where the first is a matrix that fits the structure for the \({\mathcal {H}}^2\) approximation,
where U and V are finite element functions and \(\gamma _{{\mathcal {T}}}\) is a de-singularized kernel depending on the subdivision \({\mathcal {T}}\) of \(\varOmega \). The second term is a sparse weighted mass matrix with the density function \(\rho _{{\mathcal {T}}}(x) = \int _\varOmega \gamma _{{\mathcal {T}}}(x,y)\,{{\textrm{d}}}y\). We compute this weighted mass matrix by quadrature on each element. The bottleneck of this procedure is that a direct evaluation of the density function at each quadrature point is O(N), resulting in a quadratic overall complexity. To remedy this growth, we propose a fast multipole method to obtain the values at all the quadrature points in linear time complexity.
Another challenge of (1) is that the singularity of the kernel requires special quadrature rules in order not to slow down the rate of convergence as the discretization is refined. To address this challenge, we adapt techniques from boundary element computations (see e.g. [45]) to resolve the singularities of the integrand when computing the entries in element stiffness matrices. Thus, we extend the techniques developed for the constant-order problem [1, 2] and achieve a treatment similar to that in [5] which relied on a singularity subtraction technique that is particularly convenient to express on a cartesian finite difference grid.
The main contributions of this work are:
-
We propose a decomposition of the stiffness matrix for the finite element approximation of (1) into three sub-matrices. All three sub-matrices can be computed in O(N), with construction criteria depending on the distance between shape function pairs and element pairs in the subdivision. This strategy allows the handling of general domains with spatially-variable order and coefficients as well as bounded exterior regions.
-
We generalize the variable-order setting discussed in [19] from element-wise constant functions to element-wise analytic functions. The numerical integration techniques for singular integral kernels developed by [1, 2] are generalized as well. The quadrature error is shown to converge at rates controllable simply by the order of the quadrature used. We also note that the proposed computation techniques can be applied to more general nonlocal kernels introduced by [22].
-
We propose an \({\mathcal {H}}^2\) representation to approximate the form (2) and a variable-kernel fast multipole method for computing the density \(\rho _{{\mathcal {T}}}(x)\) at quadrature points. The variable-kernel fast multipole computation is cast as a matrix vector product, where the matrix is constructed as an \({\mathcal {H}}^2\) matrix via a collocation method and the vector consists of quadrature weights. The errors in these approximations are shown to converge at rates readily controllable by the order of the polynomial used in the kernel approximation.
The rest of this paper is organized as follows. Section 2 presents a weak formulation of the problem and its finite-element discretization. Section 3 describes the decomposition of the stiffness matrix into three sub-matrices that handle different aspects of the problem. Sections 4 to 6 discuss the numerical approximation of these individual sub-matrices and analyze the resulting discretization errors. Specifically, Sect. 4 introduces a tensor-product quadrature rule to directly compute the singular near-field interactions. Section 5 presents an \(\mathcal{H}^2\) representation of the sub-matrix that approximates the non-singular part of the near-field as well as the far-field. Section 6 describes the fast multipole machinery to efficiently account for global interactions at quadrature points. Section 7 presents numerical experiments to illustrate the convergence of the finite element approximation as well as the linear-complexity of the proposed assembly process. Section 8 concludes with directions for future work.
Notation. In the following, we set \(a\lesssim b\) if \(a\le Cb\) with C denoting a positive constant independent of a, b, and the discretization parameters (e.g. the mesh size h, the number of degrees of freedom N, the quadrature order n, and the polynomial degree p). We set \(a\sim b\) when \(a\lesssim b\) and \(b\lesssim a\).
2 Weak Formulation and Finite Element Discretization
Our weak formulation for the nonlocal symmetric operator (1) starts from the definition of a generalized nonlocal divergence operator, \({\mathcal {D}}\), introduced in [23]. For a vector field \(v: {\mathbb {R}}^d\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}\),
Here the vector field \(\alpha (x,y): {\mathbb {R}}^d \times {\mathbb {R}}^d \rightarrow {\mathbb {R}}^d\) satisfies the antisymmetric property \(\alpha (x,y) = -\alpha (y,x)\). An adjoint operator \({\mathcal {D}}^*\) corresponding to \({\mathcal {D}}\) under the \(L^2({\mathbb {R}}^d)\) inner product may be written as
with \(-{\mathcal {D}}^*\) interpreted as a nonlocal gradient.
Similarly to the classical diffusion operator which is defined with a second-order diffusion coefficient a (a symmetric tensor representing diffusivity, permeability, or related material properties), the nonlocal diffusion operator can be defined as
with
In order to simplify our discussion, we set a to be diagonal, and assume that there exists an analytic function \(\kappa (x)\) so that \(\kappa (x)\ge \delta >0\) for some positive constant \(\delta \), and that \(a(x,y) = \sqrt{\kappa (x)\kappa (y)} I\) with \(I\in {\mathbb {R}}^{d\times d}\) denoting the identity matrix.Footnote 1 We are interested in the numerical approximation of the diffusion operator \({\mathcal {L}}\) with \(\alpha \) defined by
where s(x) is an analytic function satisfying that
Plugging the above definition of \(\alpha \) into (3) yields
a spatially variable-order generalization of the integral fractional Laplacian.
2.1 Volume-Constrained Problems
We shall apply the operator \({\mathcal {L}}\) in a bounded domain \(\varOmega :={{\overline{{\varOmega ^{\text {int}}}}}}\cup {\varOmega ^{\text {ext}}}\subset {\mathbb {R}}^d\) with \({\varOmega ^{\text {int}}}\cap {\varOmega ^{\text {ext}}}= \emptyset \). Here the domain \({\varOmega ^{\text {int}}}\) has Lipschitz boundary and \({\varOmega ^{\text {ext}}}\) is an enclosing region of \({\varOmega ^{\text {int}}}\) satisfying that \(0< |{\varOmega ^{\text {ext}}}|<\infty \) or \({\varOmega ^{\text {ext}}}= {\mathbb {R}}^d \setminus {\varOmega ^{\text {int}}}\). Unlike classical, second-order elliptic problems, where imposing boundary conditions on \(\partial {\varOmega ^{\text {int}}}\) is sufficient to guarantee well-posedness, a general non-local fractional operator requires that volume constraints be imposed on \({\varOmega ^{\text {ext}}}\) [23].Footnote 2 These conditions are in a sense the equivalent of the boundary conditions of the local operator. Here we focus on the Dirichlet volume-constrained problem which can be stated as: given a data function f supported in \({\varOmega ^{\text {int}}}\), we seek \(u \in \varOmega \) satisfying
with the operator
2.2 Weak Formulation
Define the energy space
where the energy norm \(\Vert .\Vert _{{\mathbb {V}}}\) is given by \(\Vert v\Vert _{{\mathbb {V}}}^2:= \Vert v\Vert _{L^2(\varOmega )}^2 + |v|_{{\mathbb {V}}}^2\) with
Clearly, the energy space \({\mathbb {V}}\) is a Hilbert space. By utilizing a standard argument (e.g., Proposition 2.2 and 2.4 in [2]), we can show the following Poincaré inequality
Multiplying the first equation of (5) with a test function \(v\in {\mathbb {V}}\), and integrating the resulting equation over \(\varOmega \), we have
To obtain the second equality we switched the order of the double integral and used the fact that \(\gamma (x,y) = \gamma (y,x)\). Summing up the two double integrals on the right hand side leads to the definition of the bilinear form
So our weak formulation reads: find \(u\in {\mathbb {V}}\) satisfying that
Clearly, \({\mathcal {A}}(u,v)\le \Vert u\Vert _{{\mathbb {V}}}\Vert v\Vert _{{\mathbb {V}}}\) by the Cauchy–Schwarz inequality. So \({\mathcal {A}}(.,.)\) is bounded in \({\mathbb {V}}\). Thanks to (6), we obtain the coercivity of the bilinear form. Thus, the Lax-Milgram lemma guarantees that the weak formulation (8) admits a unique solution \(u\in {\mathbb {V}}\).
2.3 Finite Element Discretization
We consider a simplicial finite element mesh that subdivides the interior and exterior polytope regions \({\varOmega ^{\text {int}}}\) and \({\varOmega ^{\text {ext}}}\). We denote by \({\mathcal {T}}:={\mathcal {T}}(\varOmega )\) the resulting subdivision of \(\varOmega \), and assume that \({\mathcal {T}}(\varOmega )\) matches the boundary of \({\varOmega ^{\text {int}}}\), i.e., \({{\overline{{\varOmega ^{\text {int}}}}}}\cap {{\overline{{\varOmega ^{\text {ext}}}}}}\) consists of faces from \({\mathcal {T}}\), allowing us to identify \({\mathcal {T}}^\text {int}\) and \({\mathcal {T}}^\text {ext}\) as the subdivisions of the interior and exterior regions. Let \({\mathcal {N}}:= \{{{\textbf{x}}}_i\}_{i=1}^M\) be the set of vertices associated with the subdivision \({\mathcal {T}}\). In particular, we set the first N (\(N<M\)) nodes to be the interior nodes in \({\varOmega ^{\text {int}}}\) and denote the collection of them to be \({\mathcal {N}}^\circ \). Also, we let \({\mathcal {N}}^c:={\mathcal {N}}\backslash {\mathcal {N}}^\circ \). Let \({\mathbb {V}}({\mathcal {T}})\subset {\mathbb {V}}\) be the conforming continuous piecewise linear finite element space associated with \({\mathcal {T}}\). For each node \({{\textbf{x}}}_i\in {\mathcal {N}}\), we set \(\psi _i \in {\mathbb {V}}({\mathcal {T}})\) to be the corresponding linear shape function. The above notations allow us to write the discrete solution as \(U= \sum _{j=1}^N u_j \psi _j\) with \({\underline{U}} = (u_1,u_2,\ldots , u_N)^T\in {\mathbb {R}}^N\) and express the test function as \(V = \sum _{i=1}^N v_i\psi _i\) with the coefficient vector \({\underline{V}} = (v_1,v_2,\ldots , v_N)^T\in {\mathbb {R}}^N\). We also denote the support of \(\psi _i\) by \({\mathcal {S}}_i\), and the patch of each cell \(\tau \in {\mathcal {T}}\) by \({\mathcal {S}}_\tau \), namely (see Fig. 1)
A finite element discretization with respect to (7) seeks \(U\in {\mathbb {V}}({\mathcal {T}})\) so that \(U = 0\) in \({\varOmega ^{\text {ext}}}\) and
Because the above numerical scheme is conforming, namely \({\mathbb {V}}({\mathcal {T}})\subset {\mathbb {V}}\), the well-posedness follows from the continuous formulation (7). Using the finite element mesh, we can rewrite the discrete bilinear form in (8) as
where
The stiffness matrix assembly, i.e., the construction of the matrix \({\underline{A}} \in {\mathbb {R}}^{N\times N}\) with entries \({\underline{A}}_{ij} = {\mathcal {A}}(\psi _j,\psi _i)\), is based on contributions of element pairs (\(\tau , \tau '\)) from (9), with each such contribution involving interactions (9) between shape functions that are supported on either \(\tau \) or \(\tau '\). In other words, if we let \({\mathcal {I}}(\tau ,\tau ')\subset \{1,\ldots ,N\}\) be the union of the global index sets of the vertices of elements \(\tau \) and \(\tau '\) so that for \(i \in {\mathcal {I}}(\tau ,\tau ')\), we have \(\tau \subset {\mathcal {S}}_i\) or \(\tau ' \subset {\mathcal {S}}_i\). Then we can define the local stiffness matrix of an element pair as
and assemble these elemental contributions into a global stiffness matrix \({\underline{A}}\).
3 Decomposition of the Stiffness Matrix
A direct assembly of the elemental stiffness matrices \({\underline{A}}^{\tau ,\tau '}\) of (10) into a global stiffness matrix \({\underline{A}}\) will obviously result in a scheme with quadratic complexity in both storage and operations. In this section, we outline a splitting scheme that decomposes the stiffness matrix into three components, in order to obtain a linear complexity algorithm. The splitting reflects distinct computational characteristics of the problem, and the resulting decomposition is primarily motivated by the different linear-complexity construction algorithms for the three matrix components. We describe the details of these matrices for the two-dimensional case in Sects. 4, 5, and 6, respectively.
Our consideration for the decomposition of \({\underline{A}}\) starts with the relation between two elements \(\tau ,\tau '\in {\mathcal {T}}\). Our goal is to write the bilinear form in (8) as the sum:
The first term of the sum handles the singular integrals that arises when \(\tau \) and \(\tau '\) are not separated. When \(\tau \) and \(\tau '\) are separated, the bilinear form \({\mathcal {A}}_{\tau ,\tau '}(.,.)\), which is now non-singular, can be split into two components: \({\mathcal {K}}_{\tau ,\tau '}(.,.)\) which represents effects of \(\tau \) on all non-neighboring elements of the mesh, and \({\mathcal {M}}_{\tau ,\tau '}(.,.)\) which represents effects from all non-neighboring elements of the mesh (including elements in \({\mathcal {T}}^\text {ext}\)) on \(\tau \). Formal definitions for these two forms will be given later in (13). We will show that under a suitable mesh setting the matrix associated with the first term turns out to be sparse, whereas hierarchical matrix algorithms and fast multipole methods allow us to construct the last two terms of (11) in linear complexity.
3.1 Case \(\tau \cap \tau ' \ne \emptyset \)
When \(\tau \) and \(\tau '\) are direct neighbors or \(\tau = \tau '\), we define the corresponding near-field bilinear form as
Here we note that the elements \(\tau \) in the above form are restricted to those in \({\varOmega ^{\text {int}}}\) since both U and V vanish in \({\varOmega ^{\text {ext}}}\). Denoting the near-field matrix \({\underline{B}} \in {\mathbb {R}}^{N\times N}\) with entries \({\underline{B}}_{ij} = {\mathcal {B}}(\psi _j,\psi _i)\), we assemble it directly from element-pair local stiffness matrices \({\underline{A}}^{\tau , \tau '}\) and call this process \(\texttt {DirectEval}(\tau ,\tau ')\). The primary challenge here is the accurate evaluation of these local stiffness matrices which involves singular integrands with spatially-varying fractional order. As we describe in detail in Sect. 4, we generalize ideas from boundary element methods for transferring the singular integrands in (9) to analytical integrands (cf. [1]) to handle the case of variable order.
We further assume that the triangulation \({\mathcal {T}}\) is shape-regular and quasi-uniform, i.e., there exist two positive constants \(c_{\texttt {sr}}\) and \(c_{\texttt {u}}\) so that for all \(\tau \in {\mathcal {T}}\) and \(\tau \subset \varOmega \), there holds that
with \(h_\tau \) and \(\rho _\tau \) denoting the size of \(\tau \) and the maximum size of the inscribed ball in \(\tau \). Thus \({\underline{B}}\) is a sparse matrix and the maximum number of the nonzero column entries, namely
is uniformly bounded and only depends on \(c_{\texttt {sr}}\), insuring linear complexity.
3.2 Case \(\tau \cap \tau ' = \emptyset \)
When the elements \(\tau \) and \(\tau '\) are separated, \(|x - y| > 0\) for all \(x \in \tau \) and \(y \in \tau '\), the singularity of the integrand is avoided but another difficulty is introduced because of the quadratic number of the element pairs that have to be considered. A different strategy is hence needed for constructing this contribution to the stiffness matrix.
We start by observing that if both \(\tau ,\tau '\in {\varOmega ^{\text {ext}}}\), we immediately get \({\mathcal {A}}_{\tau ,\tau '}(\psi _j,\psi _i)=0\). We can therefore fix \(\tau \in {\mathcal {T}}^{\text {int}}\) and further consider this case by whether \(\tau '\) is located in \({\varOmega ^{\text {int}}}\) or in \({\varOmega ^{\text {ext}}}\).
3.2.1 Subcase \(\tau , \tau ' \in {\mathcal {T}}^\text {int}\)
Since the \({\mathcal {A}}_{\tau ,\tau '}(.,.)\) is not singular, we can rewrite it as
We sum \({\mathcal {K}}_{\tau ,\tau '}\) for all elements \(\tau ,\tau '\) in \({\varOmega ^{\text {int}}}\). By the symmetry of choosing between \(\tau \) and \(\tau '\), we can derive that
where \(\gamma _{{\mathcal {T}}}\) is a mesh-dependent kernel
This mesh-dependent kernel evaluates to zero precisely in the integration regions that have already been handled by the first case above, i.e., when \(\tau \cap \tau ' \ne \emptyset \).
Following a similar argument, we sum \({\mathcal {M}}_{\tau ,\tau '}\) for all \(\tau ,\tau '\subset {\varOmega ^{\text {int}}}\) to define
3.2.2 Subcase \(\tau \in {\mathcal {T}}^\text {int}\), \(\tau ' \in {\mathcal {T}}^\text {ext}\)
In this case, we can simplify the form \({\mathcal {A}}_{\tau ,\tau '}(.,.)\) knowing that \(U(y)=V(y)=0\) for \(y\in \tau '\) due to \(U,V\in {\mathbb {V}}({\mathcal {T}})\). The second term in (13) vanishes and \({\mathcal {A}}_{\tau ,\tau '}(.,.)\) is simply \({\mathcal {M}}_{\tau ,\tau '}(U,V)\), which we sum for all \(\tau \in {\mathcal {T}}^\text {int}\) and \(\tau '\in {\mathcal {T}}^\text {ext}\) to obtain
Here we also have the factor 2 in the above equation because we accounted for the symmetric case \(\tau '\in {\mathcal {T}}^\text {int}\) and \(\tau \in {\mathcal {T}}^\text {ext}\).
Gathering (16) and (17), we can define the form
where
recalling that \(\gamma _{{\mathcal {T}}}\) is defined in (15). In this form, it is easy to see that a matrix \({\underline{M}}\) with entries \({\underline{M}}_{i,j}={\mathcal {M}}(\psi _j,\psi _i)\) for \(i,j=1,\ldots , N\) has the footprint of a mass matrix and may be assembled from element contributions. If i and j are the indices for the shape functions defined on \(\tau \), an element stiffness matrix is written as:
\({\underline{M}}\) is in fact a weighted mass matrix with \(\rho _{{\mathcal {T}}}(x)\) playing the role of a density function. The evaluation of \(\rho _{{\mathcal {T}}}(x)\) is required at all quadrature points, with each evaluation requiring a global integration. This appears to demand quadratic complexity in arithmetic operations. However, a method akin to a fast multipole method for spatially-varying kernels can evaluate \(\rho _{{\mathcal {T}}}(x)\) at all quadrature points in linear complexity as we show in Sect. 6.
3.3 Assembly of Complete Stiffness Matrix
The bilinear forms in (12), (14), (18) provide the three components, \({\underline{B}}\), \({\underline{K}}\), and \({\underline{M}}\) of the stiffness matrix \({\underline{A}}\) of the problem, where \({\underline{K}}_{i,j} = {\mathcal {K}}(\psi _j,\psi _i)\) for \(i,j=1,\ldots ,N\). The matrices \({\underline{B}}\) and \({\underline{M}}\) are sparse and can be stored directly. The matrix \({\underline{K}}\) however is formally dense. We take advantage of the structure of the bilinear form \({\mathcal {K}}(.,.)\) with its de-singularized kernel to store \({\underline{K}}\) in linear complexity using \({\mathcal {H}}^2\)-matrix compression techniques [32]. We also use construction algorithms that approximate the smooth kernel using piecewise polynomial interpolants and build the compressed matrix in linear complexity. We call this procedure \({\texttt {HMATRIX}}({\mathcal {T}})\) and describe it in Sect. 5.
The overall algorithm can then be summarized as shown in Algorithm 1.
4 Direct computation of the singular near-field integrals
In this section, we describe our 2d implementation for computing the singular integrals \({\mathcal {A}}_{\tau ,\tau '}(\psi _j,\psi _i)\) when two triangles \(\tau ,\tau '\) are touching each other. The implementation is based on techniques popularized in boundary element methods; see e.g. [45, Chapter 5]. We refer to [1, 3, 4] for constant-order problems and to [21] for a more general class of nonlocal problems.
Let \({{\hat{\tau }}}\) be the reference triangle with vertices \((0,0)^T\), \((1,0)^T\) and \((1,1)^T\). For each triangle \(\tau \in {\mathcal {T}}\), we denote by \(\chi _\tau : {{\hat{\tau }}}\rightarrow \tau \) an affine transformation from the reference triangle to \(\tau \). When mapping a touching element pair \((\tau , \tau ')\) to \({\hat{\tau }}\) we distinguish three cases depending on the number of shared vertices (see Fig. 2):
-
If \(\tau \) and \(\tau '\) share only one vertex, the affine mappings \(\chi _\tau \) and \(\chi _{\tau '}\) satisfy \(\chi _\tau ((0,0)^T) = {\chi _{\tau '}} ((0,0)^T)\);
-
if \(\tau \) and \(\tau '\) share a common edge, we assume that \(\chi _\tau (({{\hat{x}}}_1,0)^T) = {\chi _{\tau '}} (({{\hat{x}}}_1,0)^T)\) for \({{\hat{x}}}_1\in [0,1]\);
-
if \(\tau = \tau '\), we set \(\chi _\tau = \chi _{\tau '}\).
Under the above assumptions, we set \((x,y) = \chi _{\tau ,\tau '}({{\hat{x}}},{{\hat{y}}}):= (\chi _\tau ({{\hat{x}}}),\chi _{\tau '}({{\hat{y}}}))\).
Suppose that the supports of basis functions \(\psi _i\) and \(\psi _j\) contain either \(\tau \) or \(\tau '\), we shall compute \({\mathcal {A}}_{\tau ,\tau '}(\psi _j,\psi _i)\) on the reference elements, namely
where \(J_\tau \) and \(J_{\tau '}\) denote the Jacobian of \(\chi _\tau \) and \(\chi _{\tau '}\) respectively and \(|J_\tau |\) and \(|J_{\tau '}|\) are the absolute values of the corresponding determinants. The difficulties in the evaluation of the above integral are primarily due to the singularities at \(\chi _{\tau }({{\hat{x}}}) = \chi _{\tau '}({{\hat{y}}})\). The strategy for accurate evaluation is to split the integration domain \({{\hat{\tau }}}\times {{\hat{\tau }}}\) into several subregions (depending on the relation between \(\tau \) and \(\tau '\)) so that the integrand in each subregion can be transformed into \([0,1]^4\) and is analytic. We then compute the resulting integrals with tensor-product Gaussian quadrature schemes.
4.1 Vertex-Sharing Case
When \(\tau \) and \(\tau '\) share only one vertex, we use the transformations \(({{\hat{x}}},{{\hat{y}}}) = {\mathfrak {T}}_V^{(i)}(\xi ,\varvec{\eta })\) with \(\xi \in (0,1)\) and \(\varvec{\eta }\in (0,1)^3 \subset {\mathbb {R}}^3\), satisfying
So we can decompose \({{\hat{\tau }}}\times {{\hat{\tau }}}\) into two regions and write
Here we recall that \((x,y) = \chi _{\tau ,\tau '}\circ {\mathfrak {T}}_V^{(k)}(\xi ,\varvec{\eta })\) for \(k=1,2\). \(\varPsi _{V,i}^{(k)}\) provides the difference between \(\psi _i(x)-\psi _i(y)\) for all the five associated shape functions and rescaled by \(\xi ^{-1}\), namely
The denominator \(d_V^{(k)}\) comes from the difference \(x-y\) but is rescaled by extracting the factor \(\xi \) to give
The integrand in (23) is now non-singular and can thus be approximated by the tensorized Gaussian quadrature rule with order n. Here we apply an extra transformation for the variable \(\xi \) with \(\xi = \zeta ^{1/(4-2{{\overline{s}}})}\) and rewrite (23) as
where \((x,y) = \chi _{\tau ,\tau '}\circ {\mathfrak {T}}_V^{(k)}(\zeta ^{1/(4-2{{\overline{s}}})},\varvec{\eta })\). We shall apply the tensorized Gaussian quadrature rule to the above integral and denote the corresponding approximation of \({\mathcal {A}}_{\tau ,\tau '}(\psi _j,\psi _i)\) by \(Q^n_{V}(\psi _j,\psi _i)\). The reason to compute \({\mathcal {A}}_{\tau ,\tau '}(\psi _j,\psi _i)\) by (25) rather than (23) is to improve the quadrature approximation rates for a more general setting of s(x) and a(x, y); see Remark 3 below for details.
To analyze the quadrature error, we follow the argument from Section 5.3.2 in [45], which is based on the derivative-free quadrature error estimates [18]. The error estimate for \(\int _{(0,1)^4}f(x_1,\ldots ,x_4)\,{{\textrm{d}}}{\textbf{x}}\) requires that for each direction \(x_i\), the integrand f can be analytically extended from [0, 1] to \({\mathcal {E}}_{\rho _i}\subset {\mathbb {C}}\), where \({\mathcal {E}}_{\rho _i}\) is a closed ellipse with the focus points 0 and 1, and where \(\rho _i>\tfrac{1}{2}\) denotes the sum of semimajor and semiminor axes. Then, the error between the exact integral and its n-th order tensor product Gaussian quadrature, denoted by \(Q^n f\), can be estimated by (cf. [45, Theorem 5.3.15])
To verify that the above estimate can by applied to (23), we shall check that the integrand in (25) (or (23)) can be analytically extended to \({\mathcal {E}}_\rho \) for each component with \(\rho >\tfrac{1}{2}\). To this end, we first note that the mappings \({\mathfrak {T}}_V^{(k)}\) in (22) are component-wise analytic in \({\mathbb {C}}\). Thus, the analyticity also holds for the mapping \(\chi _{\tau ,\tau '}\circ {\mathfrak {T}}_V^{(k)}\) as well as the diffusion coefficient a(x, y) and \(s(x)+s(y)\) due to the analyticity assumption for a(., .) and s(.). So \(\zeta ^{(2{{\overline{s}}}-s(x)-s(y))/(4-2{{\overline{s}}})}\) (or \(\xi ^{3-s(x)-s(y)}\)) and \(|d_V^{(k)}(\varvec{\eta })|^{2+s(x)+s(y)}\) are analytic. Noting that the product \((\varPhi ^{(k)}_{V,j}(\varvec{\eta })\varPhi ^{(k)}_{V,i}(\varvec{\eta }))\) is a polynomial with degree no more than four, there exists an analytic extension of it in the complex space.
Now we estimate the maximum of the integrand for each component in \((\zeta ,\varvec{\eta })\). For the numerator, we choose \(\rho \in (\tfrac{1}{2}, 1)\) so that
and
For the denominator, we further assume that h is sufficiently small so that \(|d_V^{(k)}(\varvec{\eta })| \le 1\) (since \(|d_V^{(k)}(\varvec{\eta })|\sim h\)). So there holds
This implies that
Gathering the above estimates and invoking (26) for the approximation (25) (or (23)) one sees that when h is sufficiently small, there holds
4.2 Edge-Sharing Case
When \(\tau \) and \(\tau '\) share a common edge, we shall use the the following transformations \(({\hat{x}},{{\hat{y}}}) = {\mathfrak {T}}_E^{(k)}(\xi ,\varvec{\eta })\) for \(k=1,\ldots ,5\) and \((\xi ,\varvec{\eta })\in [0,1]^4\):
We again use the change of variable \(\xi = \zeta ^{1/(4-2{{\overline{s}}})}\) to write (21) as
Here \((x,y) = \chi _{\tau ,\tau '}\circ {\mathfrak {T}}_E^{(k)}(\zeta ^{1/(4-2{{\overline{s}}})},\varvec{\eta })\) for \(k=1,\ldots ,5\). In the numerator above, \(J_E^{(1)} = \eta _1^2\) and \(J_E^{(k)} = \eta _1^2\eta _2\) for \(k=2, \ldots , 5\) are Jacobians. The functions \(\varPsi _{E,i}^{(k)}\) are the transformations (rescaled by \(\xi ^{-1}\)) of \(\psi _i(x)-\psi _i(y)\) for all four associated shape functions (defined on the corresponding four vertices of \(\tau \cup \tau '\)):
In the denominator, the rescaled distances \(d_E^{(k)}(\varvec{\eta })\) are
Following a similar argument as in the previous case, we can show that the function in the above integral can be analytically extended to \({\mathcal {E}}_\rho \) with some \(\rho \in (\tfrac{1}{2},1)\) for each component of \((\xi ,\varvec{\eta })\). The detailed proof is omitted for brevity. So we can apply the n-th order tensorized Gaussian quadrature rule, denoted by \(Q_E^n(\psi _j,\psi _i)\), to approximate the integral. Assuming that the mesh size h is small enough so that \(d_E^{(k)}(\varvec{\eta }) < 1\) for \(k=1,\ldots , 5\), the quadrature error can be estimated with
4.3 Identical Case
When \(\tau =\tau '\) we use the following transformations \(({{\hat{x}}},{{\hat{y}}}) = {\mathfrak {T}}_I^{(k)}(\xi ,\varvec{\eta })\) for \(k=1,\ldots ,6\) and \((\xi ,\varvec{\eta })\in [0,1]^4\):
with \({\mathfrak {S}}({{\hat{x}}},{{\hat{y}}}) = ({{\hat{y}}},{{\hat{x}}})\). Thanks to the symmetry property between the mappings \({\mathfrak {T}}_I^{(k)}\) and \({\mathfrak {T}}_I^{(k+3)}\) for \(k=1,2,3\) (i.e., the operator \({\mathfrak {S}}\)) as well as the symmetry property for the kernel function, we arrive at
where \((x,y) = \chi _{\tau ,\tau '}\circ {\mathfrak {T}}_I^{(k)}(\xi ,\varvec{\eta })\) with \(\xi = \zeta ^{1/(4-2{{\overline{s}}})}\), \(\varPsi _{I,i}^{(k)}(\eta _3)\) are the three rescaled shape functions (\(\psi _i(x)-\psi _j(y)\)) defined on \(\tau \) provided by
and
are the rescaled distances between x and y. Notice that the integrand in (32) could be singular at \(\eta _2 = 0\) due to the term \(\eta _2^{1-s(x)-s(y)}\) when \(s(x)+s(y)>1\). To resolve this, we use the change of variable \(\eta _2 = t^{1/(2-2{{\overline{s}}})}\) to write
where we recall that \((x,y) = \chi _{\tau ,\tau '}\circ {\mathfrak {T}}_I^{(k)}(\zeta ^{1/(4-2{{\overline{s}}})},\eta _1, t^{1/(2-2{{\overline{s}}})},\eta _3)\). We then apply the tensorized Gaussian quadrature to (33). If \({{\overline{s}}}<\tfrac{1}{2}\), we can also simply apply the same quadrature rule to (32). Denoting \(Q_I^n(\psi _j,\psi _i)\) the resulting quadrature approximation with order n based on (32) or (33). Following the arguments above, we obtain that when h is small enough, there holds
for some \(\rho \in (\tfrac{1}{2},1]\).
4.4 Quadrature Error for the Singular Near-Field Formulation
The quadrature schemes provided by the proceeding subsections for all \(\tau \in {\varOmega ^{\text {int}}}\) and \(\tau '\in {\mathcal {S}}_\tau \) form an approximation of the bilinear form \({\mathcal {B}}(U,V)\) for \(U,V\in {\mathbb {V}}({\mathcal {T}})\). We denote this approximation by \(Q^n_{{\mathcal {B}}}(U,V)\). The following proposition shows the corresponding consistency error. The proof follows the standard arguments for the quadrature approximation for bilinear forms (see e.g. [3, Theorem 10] and [45, Theorem 5.3.29]). Here we provide a proof for completeness.
Proposition 1
(quadature error for near-field approximations) For \(U,V\in {\mathbb {V}}({\mathcal {T}})\), let \(Q^n_{{\mathcal {B}}}(U,V)\) be the approximation of \({\mathcal {B}}(U,V)\) by replacing \({\mathcal {A}}_{\tau ,\tau '}(U,V)\) with \({\mathcal {Q}}^n_V\), \({\mathcal {Q}}^n_E\) or \({\mathcal {Q}}^n_I\) defined in Sects. 4.1 to 4.3 depending on the relations between \(\tau \) and \(\tau '\). When the mesh size h is small enough, there exists \(\rho \in (\tfrac{1}{2},1)\) such that
Proof
Denote \(e^{ij}_{\tau ,\tau '} = {\mathcal {A}}_{\tau ,\tau '}(\psi _j,\psi _i) - Q^n(\psi _j,\psi _i)\), where \(Q^n\) is the tensor product Gaussian quadrature form \(Q_V^n\), \(Q_E^n\), or \(Q_I^n\). According to the quadrature error estimates Eqs. (29), (31), and (34), there holds that for h sufficiently small,
Now we set \(U=\sum _{j=1}^Nu_j\psi _j\) and \(V=\sum _{i=1}^N v_i\psi _i\). To estimate the target error, we use the definition (12) and write
Here, we recall that \({\mathcal {I}}(\tau ,\tau ')\subset \{1,\ldots , N\}\) is the index set whose associated global shape functions are non-zero on \(\tau \cup \tau '\). Utilizing the Cauchy–Schwarz inequality, we have
where \(\#{\mathcal {I}}(\tau ,\tau ')\) denotes the cardinality of \({\mathcal {I}}(\tau ,\tau ')\) and where for the last inequality we used the fact that \(\#{\mathcal {I}}(\tau ,\tau ')\lesssim 1\) and that
We note that due to the shape-regularity property for \({\mathcal {T}}\), the number of cells in \({\mathcal {S}}_\tau \) is uniformly bounded for all \(\tau \in {\varOmega ^{\text {int}}}\). So we insert (36) into (35) and continue to bound the summation in (35) by the Cauchy–Schwarz inequality. This leads to
Together with (35), we arrive at
as desired. \(\square \)
We end the section with the following remarks.
Remark 1
(order of the quadrature rule) In order to get the convergence rate \(h^{\beta }\) with \(\beta >0\) for the consistency error in Proposition 1, we need to set
with some positive constant \(C>1\). This implies that the quadrature order should be chosen to satisfy that
Remark 2
(near-field consistency) Note that by the fact that \(\tau '\in {\mathcal {S}}_\tau \) and that \({\mathcal {S}}_\tau \) is quasi-uniform, the error estimate we obtained in Proposition 1 improves the results from [3, Theorem 10] by removing the factor N (the number of degrees of freedom).
Remark 3
(a general setting for s(x) and a(x, y)) The above implementation for the matrix \({\underline{B}}\) can be also extended when s(x) has jumps across the edges. Here we assume that for each triangle \(\tau \in {\mathcal {T}}\), \(s(\chi _\tau ({{\hat{x}}}))\) can be analytically extended to a complex neighborhood of the reference triangle \({{\hat{\tau }}}\), denoted by \({{\hat{\tau }}}^*\). Similar assumptions can be also applied to a(., y) and a(x, .). Following the argument in [45, Lemma 5.3.19], we can show that \(s(\chi _\tau \circ {\mathfrak {T}}_V^{(k)}(\zeta ,\varvec{\eta }))\) is analytic for \(\zeta \in {\mathcal {E}}_{\rho _1/h}\) with \(\rho _1>0\) sufficiently small and is analytic for \(\eta _\ell \in {\mathcal {E}}_{\rho _2}\) for some \(\rho _2\in (\tfrac{1}{2}, 1)\) with \(\ell =1,2,3\). Under the above restriction for \(\zeta \), we shall update the estimate (27) with
This implies the new error estimate for approximating (25)
On the other hand, if we approximate (25), we have
Here we note that for the first term on the right-hand side above, the convergence rate is lower than the previous approach and could even be negative when \(n=1\). We can analogously analyze the quadrature for Eqs. (30) and (33) and follow the argument in Proposition 1 to obtain that
Hence, when choosing the quadrature order according to Remark 1 to achieve the rate \(O(h^\beta )\), a sufficient condition is to set
In our numerical simulations in Sect. 7, we set \(n=1\) when assembling \({\underline{B}}\).
5 \({\mathcal {H}}^2\)-Matrix Approximation of the Non-singular Interactions
We now consider the construction of a hierarchical matrix approximation of the second term in (11) so as to avoid the quadratic complexity that a direct computation would entail. The construction here is now dealing with a de-singularized kernel, since the singularities due to element-pairs that are touching have been resolved by the integrations of the previous section.
5.1 Construction of the \({\mathcal {H}}^2\) Matrix Structure
One of the key approximations in hierarchical matrix representations involves clustering neighboring vertices and representing their net effect on other, sufficiently far-away, clusters by appropriate 2-dimensional polynomials. Therefore the first step of the construction is to generate a hierarchy of spatial clusters for the mesh vertices. We do this by partitioning the interior vertices using a KD-tree, with repeated plane splits along coordinate directions. The construction is recursive starting from the whole point set as the topmost cluster. The points within each cluster are first sorted by projecting along the largest dimension of their bounding box. The sorted point clusters are then split along their median into two children clusters, with the recursion stopping when the cardinality of leaf clusters reaches a specified parameter m. This procedure produces a complete binary cluster tree \({\mathscr {T}}\) that has \(L = 1 + \log (N/m)\) levels with leaves of size no larger than m.
The resulting cluster tree \({\mathscr {T}}\) together with an admissibility condition provides the structure and the starting point for constructing the \({\mathcal {H}}\)-matrix approximation \(\widetilde{{\underline{K}}}\) of \({\underline{K}}\). Specifically, let \(\sigma \) and \(\sigma '\) be the vertex index sets for two clusters at the same level \(\ell \) in \({\mathscr {T}}\) and \(\omega _{\sigma }\) and \(\omega _{\sigma '}\) their corresponding bounding boxes, respectively. The matrix block \(\widetilde{{\underline{K}}}_{\sigma ,\sigma '}\) with rows \(\sigma \) and columns \(\sigma '\) may be represented as a single low rank approximation if the corresponding bounding boxes satisfy the admissibility condition
for some \(\lambda _1 > 0\). Here \(\omega _{\sigma }^e\) and \(\omega _{\sigma '}^e\) are the bounding-box extensions containing all elements in the support of the basis functions of nodes in \(\sigma \) and \(\sigma '\). This extends the elements in the clusters whose bounding boxes are \(\omega _{\sigma }\) and \(\omega _{\sigma '}\) by a band that is one-element wide (see Fig. 3a), and therefore insures that no element pair (\(\tau \), \(\tau '\)) from the two bounding boxes \(\omega _{\sigma }^e\) and \(\omega _{\sigma '}^e\) satisfying (37) involves singular integrals, and that the kernel \(\gamma _{{\mathcal {T}}}(x, y) = \gamma (x, y)\) in this cluster pair. We denote by \({P^{\text {far}}}\) the collection of the cluster pairs \((\sigma ,\sigma ')\in {\mathscr {T}}\times {\mathscr {T}}\) that satisfy the admissibility condition and describe the computation of their low rank approximation in Sect. 5.3 below.
When the admissibility condition is not satisfied for clusters at the leaf level L, the entries in the blocks \(\widetilde{{\underline{K}}}_{\sigma ,\sigma '}\) are computed by direct numerical quadrature. Since we have already accounted for the singular integrals involving element pairs \((\tau , \tau ')\) with \(\tau \cap \tau ' \ne 0\) directly in Sect. 4, the integrals here involve only smooth integrands and we describe their computation in Sect. 5.2 below. We will denote by \({P^{\text {near}}}\) the set of leaf-level cluster pairs that violate the admissibility condition and are computed directly. They represent the non-singular smooth part of the near field. Hence, \({P^{\text {far}}}\cup {P^{\text {near}}}\) covers all the cluster pairs.
The construction of the hierarchical structure of the matrix is recursive and starts from the root of the matrix quadtree \({\mathscr {T}}\times {\mathscr {T}}\). At every level l, the pairs \((\sigma ,\sigma ')\) with \(\sigma \) in the first (row) tree and \(\sigma '\) in the second (column) tree are considered. If a pair satisfies the admissibility condition, a low rank approximation of it is constructed from a suitable polynomial approximation of the kernel, and the corresponding matrix block is no longer subdivided. If the admissibility condition is violated, the children of \(\sigma \) and \(\sigma '\) at level \(l+1\) are considered. The recursion terminates when the leaf level L is reached. The blocks at that level with clusters that do not satisfy the admissibility condition are computed directly as described next; this includes the diagonal blocks with \(\sigma = \sigma '\).
\({\mathcal {H}}^2\) computations. a \(\omega _{\sigma }^e\) extends the bounding box \(\omega _{\sigma }\) of the shaded cluster \(\sigma \) to include a band that is one-element wide. b Near-field entries: entry \(A_{ik}\) sums contributions from the 36 elements pairs in \({\mathcal {S}}_i\) and \({\mathcal {S}}_k\), but entry \(A_{ij}\) ignores the four vertex-touching pairs
5.2 Direct Computation of the Smooth Near-Field
Let us first consider the (non singular) near-field entries. For the entry \(\widetilde{{\underline{K}}}_{ij}\) for \(i,j=1,\ldots ,N\) with \(i\in \sigma \), \(j\in \sigma '\), and \((\sigma ,\sigma ')\in {P^{\text {near}}}\), we have
where \({{\hat{\psi }}}_i\) are the corresponding shape functions defined on \({{\hat{\tau }}}\). The sum is over non-touching element pairs in the support of \(\psi _i\) and \(\psi _j\) (see Fig. 3b). The computation for every such element pair (the integral on the right-hand side above) is based on a strategy similar to the one introduced in Sect. 4. Here we apply the Duffy coordinates \({\mathfrak {T}}: [0,1]^4\rightarrow {{\hat{\tau }}}\times {{\hat{\tau }}}\) satisfying that
We then again apply the tensor-product Gaussian quadrature scheme with order n to the transformed integral and denote by \(\widetilde{{\underline{K}}}_{ij}\) the resulting approximation of \({\underline{K}}_{ij}\).
5.3 Approximation of the Far-Field
Let’s consider a matrix block \(\widetilde{{\underline{K}}}_{\sigma ,\sigma '}\) with \((\sigma ,\sigma ')\in {P^{\text {far}}}\), which is represented as a low rank block. The ij-th entry of that block, \((\widetilde{{\underline{K}}}_{\sigma ,\sigma '})_{ij}\) for \(i\in \sigma \) and \(j\in \sigma '\) may be written as:
where \(I^{p}_{\sigma ,\sigma '}\) is the nodal interpolant on the domain \(\omega _{\sigma }^e\times \omega _{\sigma '}^e\) using a tensor-product Chebyshev polynomial of order p,
where \(\{\xi _{\sigma ,\alpha },\xi _{\sigma ',\beta }\}\) are Chebyshev nodes and \(\{\ell _{\sigma ,\alpha }, \ell _{\sigma ',\beta }\}\) are the corresponding d-dimensional Lagrange basis polynomials in \(\omega ^e_\sigma \) and \(\omega ^e_{\sigma '}\), respectively. This allows us to write the ij-th entry of \(\widetilde{{\underline{K}}}_{\sigma ,\sigma '}\) as
which in factored form is given by
The representation \({\underline{U}}_\sigma \, {\underline{S}}_{\sigma , \sigma '} \, {\underline{V}}_{\sigma '}^T\) is a rank-p factorization of the \(\widetilde{{\underline{K}}}_{\sigma ,\sigma '}\) block. It is written in the bases \({\underline{U}}_\sigma \) and \({\underline{V}}_{\sigma '}\). These bases are of size (\(\#\sigma \times p\)) and (\(\#\sigma ' \times p\)) and are common to all block rows \(\sigma \) and block columns \(\sigma '\) in \(\widetilde{{\underline{K}}}\), respectively. Individual matrix blocks have their own small \({\underline{S}}_{\sigma , \sigma '}\) (\(p \times p\)) factors. Evaluation of the bases can be done exactly using \(\lceil \tfrac{p+1}{2}\rceil \)-order Gaussian quadrature schemes since the integrands involved in their entries are polynomials of order no more than \(p+1\).
There is one final step needed to achieve linear overall complexity, since the approximation of the admissible blocks by the low rank approximation \({\underline{U}}_\sigma \, {\underline{S}}_{\sigma , \sigma '} \, {\underline{V}}_{\sigma '}^T\) above would result in \(O(N \log N)\) complexity. In order to remove the \(\log N\) factor we can build nested bases to avoid generating and storing \({\underline{U}}_\sigma \) and \({\underline{V}}_{\sigma '}\) explicitly for all levels of the hierarchy. This can be done by expressing the p polynomial bases used in the approximation over a region \(\omega ^e_\sigma \) at level l in terms of the approximating polynomials over the subregions of its children clusters in the cluster tree \({\mathscr {T}}\). In practice, this allows us to generate and store the bases \({\underline{U}}_\sigma \) and \({\underline{V}}_{\sigma '}\) explicitly at the leaf level only, with small inter-level transfer matrices that allow the implicit generation of the bases at coarser levels, recursively. This hierarchical (nested) basis of the hierarchically partitioned matrix is called the \({\mathcal {H}}^2\) representation and attains the optimal complexity [10]. While asymptotically optimal, the thus constructed matrix does not generally have optimal constants, as it uses a generic polynomial basis for the construction. As a result, we are able to further compress the matrix algebraically and reduce the ranks of the matrix blocks and the overall memory footprint of the matrix. The details of this algebraic compression process and a demonstration of its effectiveness are described in [12, 56].
5.4 Consistency
There are two approximation errors that need to be analyzed: (i) the local quadrature error for \({\mathcal {K}}_{\tau ,\tau '}(\psi _j,\psi _i)\) when \((\sigma ,\sigma ')\in {P^{\text {near}}}\), and (ii) the local interpolation error for \(I_{\sigma ,\sigma '}^p\) when \((\sigma ,\sigma ')\in {P^{\text {far}}}\). For \(U,V\in {\mathbb {V}}({\mathcal {T}})\), we denote by \(\widetilde{{\mathcal {K}}}^{\text {near}}(U,V)\) the bilinear form associated with the near-field part, i.e., the non-zero entries in (38), and \(\widetilde{{\mathcal {K}}}^{\text {far}}(U,V)\) the far-field part defined in (39). So \({\mathcal {K}}(U,V)\) is approximated by
We can also similarly decompose \({\mathcal {K}}(.,.)\) to the near-field part \({\mathcal {K}}^{\text {near}}(.,.)\) and the far-field part \({\mathcal {K}}^{\text {far}}(.,.)\) and we shall estimate their errors separately.
5.4.1 Near-Field
In order to bound the error from the near-field part, we first note that the cardinality of \({P^{\text {near}}}\) is uniformly bounded. Hence, the near-field entries in \(\widetilde{{\underline{K}}}\) form a sparse matrix. In order to show this, we first note that thanks to the quasi-uniformity assumption on \({\mathcal {T}}\), for each leaf cluster \(\sigma \in {\mathscr {T}}\), \(\omega _\sigma \) is regular and satisfies that \(|\omega _\sigma |\sim 2^{-l_{\max }}|{\varOmega ^{\text {int}}}|\). For \((\sigma ,\sigma ')\in {P^{\text {near}}}\) and \(x\in \omega _{\sigma }^e\) and \(y\in \omega _{\sigma '}^e\), there holds
where for the second inequality above we used the fact that \((\sigma ,\sigma ')\) is non-admissible and where for the last inequality we applied the setting for the partition of the cluster tree so that for each leaf \(\sigma \in {\mathscr {T}}\) there holds
The estimate (43) implies that given an index i and a cluster \(\sigma \) so that \({\mathcal {S}}_i\subset \omega _{\sigma }^e\), the union of the near-field leaves \(\sigma \), namely \((\sigma ,\sigma ')\in {P^{\text {near}}}\), is covered by \(\varSigma = \cup _{x\in \omega _{\sigma }^e}B_r(x)\). Since \(|\varSigma |\lesssim r^2 + |\omega _{\sigma }^e|\lesssim 2^{-l_{\max }} + h^2\), we then utilize (44) to derive that
where we note that the above hidden constant depends on \(|{\varOmega ^{\text {int}}}|\), \(\lambda _1\) as well as the quasi-uniformity constant.
Let \(Q^n_K(\psi _j,\psi _i)\) denote the approximation of \(K_{\tau ,\tau '}(\psi _j,\psi _i)\) in Sect. 5.2. Following the argument from Sect. 4.1 (see also [45, Lemma 5.3.20 & Theorem 5.3.24]), we have that when h is sufficiently small,
for some \(\rho \in (\tfrac{1}{2}, 1)\). Using the argument from Proposition 1 and applying the local error estimate (45), we can show the consistency of the near-field part by
5.4.2 Far-Field
For the consistency error from the far-field part, we first note that the error estimate for the kernel interpolation \(I^p_{\sigma ,\sigma '}\) [10, Theorem 4.22 & Remark 4.23] (see also [32, Lemma 5.1])
where \(c_1=\min \{\tfrac{c_0\lambda _1}{c_0\lambda _1+1},\tfrac{c_0\lambda _1}{2}\}\) for some \(c_0>0\) and where the hidden constant depends only on p and d. We follow the proof of [45, Theorem 7.3.18] to obtain that
5.4.3 Overall Error
Gathering (45) and (47) gives the consistency error for the \({\mathcal {H}}\)-matrix approximation.
Proposition 2
(consistency for the \({\mathcal {H}}^2\)-approximation) For \(U,V\in {\mathbb {V}}({\mathcal {T}})\), let \({{\widetilde{K}}}(U,V)\) be the approximation of \({\mathcal {K}}(U,V)\) by the \({\mathcal {H}}^2\)-approximation using Chebyshev polynomials with order p together with the admissibility condition (37). A tensor-product Gaussian quadrature rule with order n is used to compute the near-field part of the \({\mathcal {H}}\)-matrix; see (39). Then there exist constants \(\rho \in (\tfrac{1}{2}, 1]\) and \(c_1\in (0,1)\) so that
Remark 4
(general settings for s(x) and a(x, y)) The consistency result above relies on the analyticity of s(x). For the case where there are jumps across element edges, the strategy for showing exponential convergence for the \({\mathcal {H}}^2\)-approximation versus polynomial degree will no longer hold since the \(I_{\sigma ,\sigma '}^p\) is not well-defined. A more refined argument, following the approach in [10, Section 9.2 and Theorem 9.5], is needed to establish that the low rank approximation indeed allows the operator and solution errors to retain an exponential convergence with the rank/degree. The technical details are, however, beyond the scope of the present work.
6 Fast Multipole Acceleration for Computing the Weighted Mass Matrix
We finally consider the construction of the matrix approximation \({\underline{M}}\) of the third term in (11). \({\underline{M}}\) has the footprint of a mass matrix but is weighted by a global density function whose direct computation would require an expensive \(O(N^2)\) computation.
6.1 Element Computations
For each cell \(\tau \in {\mathcal {T}}^{\text {int}}\), we shall first compute the local contributions \({\underline{M}}^\tau \) defined in (20) by the n-th order tensor-product quadrature scheme used in (38) but only for x. We use this scheme primarily for the convenience of having the same code and analysis as the previous sections. Letting \(i,j=1,2,3\) be the indices of the local shape functions in \(\tau \), the quadrature scheme leads to
with \(N_\tau \) denoting the number of quadrature points and \({\mathcal {Q}}_\tau := \{q_\ell \}_{\ell =1}^{N_\tau }\) and \({\mathcal {W}}_\tau := \{w_\ell \}_{\ell =1}^{N_\tau }\) are the quadrature points and weights. Denote the collection of all the quadrature points for \(\tau \in {\mathcal {T}}^{\text {int}}\) by \({\mathcal {Q}}^{\text {int}}\), i.e.,
We similarly define \({\mathcal {W}}^{\text {int}}\) for the quadrature weights. We first show that evaluation of \(\rho _{{\mathcal {T}}}(q)\) for every \(q\in {\mathcal {Q}}^{\text {int}}\) requires O(N) operations. Recalling the definition of \(\rho _{{\mathcal {T}}}(x)\) from (18), we write the computation for \(q_i\in {\mathcal {Q}}^{\text {int}}\) as
We shall again approximate the right-hand side above by quadrature. Denoting \({\mathcal {Q}}^{\text {ext}}\) and \({\mathcal {W}}^{\text {ext}}\) the set of quadrature points and weights for \(\int _{{\varOmega ^{\text {ext}}}}\gamma (q_i,y)\,{{\textrm{d}}}y\), we set \({\mathcal {Q}} = {\mathcal {Q}}^{\text {int}}\cup {\mathcal {Q}}^{\text {ext}}\) and \({\mathcal {W}} = {\mathcal {W}}^{\text {int}}\cup {\mathcal {W}}^{\text {ext}}\). Using the quadrature scheme generated by \({\mathcal {Q}}\) and \({\mathcal {W}}\), we have
Assuming a suitable subdivision of \({\mathcal {T}}\) so that the cardinality \(\#({\mathcal {Q}})\) is O(N), the computation of the right-hand side above obviously requires O(N) operations.
In principle, we can use the kernel-independent fast multipole method [54] to accelerate the evaluations of \(\rho _{{\mathcal {T}}}(q_i)\) for all \(q_i\in {\mathcal {Q}}^{\text {int}}\). Here we consider (49) as a N-body problem by treating \({\mathcal {Q}}\), \({\mathcal {Q}}^{\text {int}}\) and \({\mathcal {W}}\) as source points, target points and source densities, respectively. For the numerical simulation, one could use available fast multipole open source libraries such as exafmm [52], PVFMM [43], or PBBFMM3D [50]. Unfortunately, these libraries only support a kernel with constant order and constant diffusion coefficients. Our alternative solution is to interpret the general fast multipole method as a hierarchical matrix–vector product in the \({\mathcal {H}}^2\) format [55] and again use an \({\mathcal {H}}^2\)-approximation as we describe below.
6.2 An \({\mathcal {H}}^2\)-Approximation for Density Evaluation
We introduce a collocation approach using an \({\mathcal {H}}^2\)-matrix to compute \(\rho _{{\mathcal {T}}}(q_i)\) for all \(q_i\in {\mathcal {Q}}^{\text {int}}\). To this end, denote the space \({\mathbb {V}}_s\) the span of Dirac delta distributions for the source points \({\mathcal {Q}}\), namely
Here \(\delta _q\) denotes the Dirac delta distribution at q. We similarly define the space \({\mathbb {V}}_t\) for the target points \({\mathcal {Q}}^{\text {int}}\). We first consider the following rectangular matrix
Letting \({{\underline{\rho }}} = (\rho _{{\mathcal {T}}}(q_i))_{q_i\in {\mathcal {Q}}^{\text {int}}}^T\) and \({\underline{w}}:= (w_j)_{q_j\in {\mathcal {Q}}}^T\), we have
Therefore, in order to generate the necessary density values at all quadrature points we need to generate an \({\mathcal {H}}^2\)-approximation of \({\underline{K}}_\rho \) and perform the multiplication in (50) efficiently. The \({\mathcal {H}}^2\)-approximation algorithm for \({\underline{K}}_\rho \) is similar to the one presented in Sect. 5 for \({\underline{K}}\) and starts by constructing two cluster trees \({\mathscr {T}}_t\) and \({\mathscr {T}}_s\) for the row index set for \({\mathbb {V}}_t\) and the column index set for \({\mathbb {V}}_s\), respectively. When building the \({\mathcal {H}}^2\)-matrix, we do not need to extend the bounding boxes for the clusters \(\sigma \in {\mathscr {T}}_t\) and \(\sigma ' \in {\mathscr {T}}_s\); consequently, we may define the interpolation operator \(I_{\sigma ,\sigma '}^p\) for \(\gamma (x,y)\) in \(\omega _{\sigma }\times \omega _{\sigma '}\). The admissibility condition is given by
for some fixed \(\lambda _2 >0\). We similarly define \({P^{\text {far}}}\) to be the collection of all the admissible blocks \((\sigma ,\sigma ')\) and define \({P^{\text {near}}}\) to be the rest of the blocks. We shall further assume that \(\lambda _2\) is small enough to guarantee that \({{\,\textrm{dist}\,}}(\omega _{\sigma },\omega _{\sigma '}) \ge 3h \) so that \(\gamma _{{\mathcal {T}}}(x,y) = \gamma (x,y)\), and is therefore smooth. Hence, the interpolation \(I_{\sigma ,\sigma '}^p \gamma _{{\mathcal {T}}}\) makes sense for \((\sigma ,\sigma ')\in {P^{\text {far}}}\) and satisfies that
where \(c_2 = \min \{\tfrac{c_0\lambda _2}{c_0\lambda _2+1},\tfrac{c_0\lambda _2}{2}\}\).
Once the matrix \({\underline{K}}_\rho \) is constructed, the matrix–vector multiplication in (50) can be performed via standard multilevel methods for \({\mathcal {H}}^2\) matrices which involve a pair of upward and downward passes over the basis trees and multiplication by the small low rank blocks at all levels of the hierarchy. The operation can be done in O(N) (cf. [13]).
6.3 Consistency
Given \(U,V\in {\mathbb {V}}({\mathcal {T}})\), let us first denote the quadrature approximation of \({\mathcal {M}}(U,V)\) by \({\mathcal {Q}}_{{\mathcal {M}}}^n(U,V)\). We also denote by \({\mathcal {Q}}_{{\mathcal {M}}}^{n,p}(U,V)\) the resulting bilinear form when \(\{\rho _{{\mathcal {T}}}(q_i)\}_{q_i\in {\mathcal {Q}}^{\text {int}}}\) are approximated using the \({\mathcal {H}}^2\) matrix–vector product. Here we recall that p is the degree of the Chebyshev polynomials. By the triangle inequality, the consistency error between \({\mathcal {M}}(U,V)\) and \({\mathcal {Q}}_{{\mathcal {M}}}^{n,p}(U,V)\) can be bounded with
We first estimate the quadrature error, namely the first error on the right-hand side above. Set \(e^{ij}_\tau \) to be the error of the quadrature approximation in (48), following the argument in Sect. 4.1, we have that there exists a constant \(\rho \in (\tfrac{1}{2}, 1]\) so that
Here we note for the last inequality we used the fact that
where \(B_{r}(0)\) is a ball entered at origin with radius r and where \(\varepsilon >0\) is sufficiently small. Using the above local error estimate, we again follow the same argument in Proposition 1 to derive that
In order to estimate the error from the \({\mathcal {H}}^2\)-approximation for \(\rho _{{\mathcal {T}}}\), we let \(\sigma \in {\mathscr {T}}_t\) and \(\sigma '\in {\mathscr {T}}_s\). For \(q_i\in {\mathcal {Q}}^{\text {int}}\), let \({{\widetilde{\rho }}}_{{\mathcal {T}}}(q_i)\) be the resulting approximation of \(\rho _{{\mathcal {T}}}(q_i)\). We invoke the interpolation error estimate (52) as well as \(w_j\sim h^2\) to bound the error
where for the last inequality we used the fact the number of far-field indices j is bounded by \(N\sim h^{-2}\). This means that the \({\mathcal {H}}^2\)-approximation for \(\rho _{{\mathcal {T}}}(q_\ell )\) leads to the quadrature formula in (48) perturbed by the error \(Cc_2^p h^{-2{{\overline{s}}}}\). Thus we again apply the argument in Proposition 1 to obtain that
Gathering the errors (54) and (55) into (53), we conclude that
Proposition 3
(consistency for \({\mathcal {M}}(U,V)\)) For \(U,V\in {\mathbb {V}}({\mathcal {T}})\), let \({\mathcal {Q}}_{{\mathcal {M}}}^{n,p}(U,V)\) be the resulting approximation of \({\mathcal {M}}(U,V)\) by quadrature with order n as well as \({\mathcal {H}}^2\)-approximation for the quadrature points. Then there exists a constant \(\rho \in (\tfrac{1}{2},1]\) and \(c_2\in (0,1)\) so that
6.4 Overall Consistency
We conclude this section with the following theorem by combining the consistency error estimates from Propositions 1 to 3. For simplicity, we will use the same n-th order tensor-product Gaussian quadrature to approximate the integral and the same polynomial degree p for the \({\mathcal {H}}\)-matrices in Sects. 5 and 6.
Theorem 1
(total error) For \(U,V\in {\mathbb {V}}({\mathcal {T}})\), define the final approximation of \({\mathcal {A}}(U,V)\) by
where the bilinear forms on right-hand side are defined in Propositions 1 to 3, respectively. Then there holds that
7 Numerical Illustrations
In this section, we present numerical examples to illustrate the performance of our proposed finite element algorithm. In particular, we report the decay of \(L^2({\varOmega ^{\text {int}}})\) errors with respect to a sequence of the quasi-uniform meshes as the mesh size h is systematically reduced, and the increase in computational cost as N increases to verify the linear complexity of the algorithm. Our numerical implementation is based on the Deal.II (version 9.4) finite element library [7] which supports simplex meshes and the H2Opus library [56] for hierarchical matrices. We use the TimerOutput class in deal.II to record the computation time. Solutions are obtained by a conjugate gradient solver. No attempt was made to fine tune algorithmic parameters, nor to parallelize or optimize the code, which was executed on a single core of a standard-issue laptop computer.
In the construction of the hierarchical matrix approximations for constructing \({\underline{K}}\) and \({\underline{M}}\), we use the slightly more convenient geometric admissibility condition \(\lambda \Vert C_\sigma - C_{\sigma '} \Vert \ge (D_{\sigma } + D_{\sigma '})/2\) where C and D refer to the center and diameter of the bounding box (\(\omega \) or \(\omega ^e\)) used for a cluster. We use \(\lambda =0.75\), leaf size \(m=128\), and approximate the kernel function \(\gamma _{{\mathcal {T}}}\) using degree 10 Legendre polynomials. This guarantees that the \({\mathcal {H}}\)-matrix approximation does not dominate the total approximation error. We use 3-point Gaussian quadrature (namely the quadrature order \(n=1\)) to compute element integrals when assembling \({\underline{K}}\) and \({\underline{M}}\). We also point out that since H2Opus currently supports square matrices only, we expand the target space \({\mathbb {V}}_t\) to \({\mathbb {V}}_s\) for the quadrature evaluations by the \({\mathcal {H}}^2\)-approximation mentioned in Sect. 6.2, but only use the subset of values of the matrix–vector product that correspond to interior quadrature points.
7.1 Tests for the Integral Fractional Laplacian
We first consider a classical fractional diffusion problem involving the integral fractional Laplacian, namely \(a(x,y)\equiv 1\), the order function \(s(x) \equiv s\) is a constant in (0, 1), and the exterior domain \({\varOmega ^{\text {ext}}}={\mathbb {R}}^2\backslash {\varOmega ^{\text {int}}}\). So the solution u satisfies \(u\in {{\widetilde{H}}}^s({\varOmega ^{\text {int}}})\) and
where \(\widetilde{.}\) denotes the zero extension from \({\varOmega ^{\text {int}}}\) to \({\mathbb {R}}^2\) and the fractional Sobolev space
7.1.1 An Extra Step
One bottleneck in generating a linear finite approximation for the above problem is to deal with the integral on the unbounded domain \({\mathbb {R}}^2\backslash {\varOmega ^{\text {int}}}\). Here we borrow the assembling strategy from [1] and briefly introduce the implementation below. We set an auxiliary triangulation \({\mathcal {T}}_B\) for a ball \(\varOmega _B\) centered at the origin with radius R and containing the triangulation of \({\varOmega ^{\text {int}}}\). We set R large enough so that the distance between \({\varOmega ^{\text {int}}}\) and \(\partial \varOmega _B\) is strictly positive. This guarantees that the patch \({\mathcal {S}}_\tau \) for each cell \(\tau \) in \({\varOmega ^{\text {int}}}\) is contained in B. Whence, we follow Sects. 4 and 5 exactly to assemble \({\underline{B}}\) and \({\underline{K}}\). To compute \({\underline{M}}\), according to (18), we can split the discrete bilinear form \({\mathcal {M}}(.,.)\) as
Denote \({\underline{M}}^\text {in}\) and \({\underline{M}}^{\text {out}}\) the associated weighted mass matrices for the two bilinear forms on the right-hand side of the equation above. We apply the fast multipole approximation technique of Sect. 6 to \({\underline{M}}^{\text {in}}\). For \({\underline{M}}^{\text {out}}\), we use the fact that \(\rho _B\) is radial in \({\mathbb {R}}^2\backslash \varOmega _B\) and thus rewrite \(\rho _B\) in polar coordinates with (cf. [1, Section A.5])
where
Thus when assembling \({\underline{M}}^{\text {out}}\) by using quadrature formulas for each \(\tau \in {\varOmega ^{\text {int}}}\), we evaluate \(\rho _B\) at each quadrature point by approximating the integral in (57) by numerical integration. Here we use a 9-point Gaussian quadrature formula. The stiffness matrix corresponding to the weak problem (56) is now decomposed into four sub-matrices, i.e.,
7.1.2 Simulation and Results
We set \({\varOmega ^{\text {int}}}\) to be the unit ball. For the auxiliary ball \(\varOmega _B\), we set its radius \(R=1.1\). We shall test the convergence of the finite element approximation by using the well-known analytic solution
so that \(f=1\) in \({\varOmega ^{\text {int}}}\). Starting from a coarse grid \({\mathcal {T}}_1\) for \(\varOmega _B\), we generate a sequence for meshes \(\{{\mathcal {T}}_j\}_{j=1}^6\) by refining the mesh globally. We set \({{\overline{s}}} = 0.9\) for the computation of the sub-matrix \({\underline{B}}\).
The left panel of Fig. 4 reports the \(L^2({\varOmega ^{\text {int}}})\)-error between u and its finite element approximation \(U_j\) against the number of degrees of freedom when \(s=0.7\). The slope of the log-log error plot implies that \(U_j\) converges to u in the first order, which is the optimal rate that can be reached and is limited only by the reduced regularity of the solution itself, which has singular derivatives at the boundary. The right panel of Fig. 4 reports the CPU time for assembling the sub-matrices \({\underline{B}}\), \({\underline{K}}\) and \({\underline{M}}^{\text {in}}\), respectively. As the number of degrees of freedom increases, we observe a linear complexity for all three assembly routines.
Figure 5 depicts the tree structure of the \({\mathcal {H}}\)-matrix for \({\underline{K}}\) (left panel). Here the blocks in red are computed directly while the blocks in green are approximated by the low-rank matrices based on the Lagrange interpolation. The right plot of Fig. 5 illustrates the tree structure of the \({\mathcal {H}}\)-matrix that is used to compute the density function \(\rho _{{\mathcal {T}}}\); see Sect. 6 for details. Note that the matrix on the right is larger than the one on the left because it includes all interior and exterior degrees of freedom and we are using a 3-point Gaussian quadrature for the density function \(\rho _{{\mathcal {T}}}\) in (18).
Integral fractional Laplacian test: (left) \({\mathcal {H}}^2\)-matrix structure of \({\underline{K}}\) for the mesh \({\mathcal {T}}_4\) and (right) the corresponding \({\mathcal {H}}^2\)-matrix structure for the quadrature evaluations for \(\rho _{{\mathcal {T}}}\). Matrix blocks in red are computed directly while the blocks in green are approximated by low-rank factorizations based on polynomial Lagrange interpolation of the kernel (Color figure online)
7.2 Tests for Variable Order
Next we test our algorithm with variable-order FDEs. We let constant \(s^*\in (\tfrac{1}{2},1)\) be the so-called background order in \(\varOmega \). This means that the variable order function \(s(x) = s^*\) in \({\varOmega ^{\text {ext}}}\). In \({\varOmega ^{\text {int}}}\), we consider a tensor product bump function that is supported on a square in \({\varOmega ^{\text {int}}}\) and centered at the point \((x^c_1,x^c_2)\) with the size \(\ell \). Specifically, we let
where
and \(\eta \) is a fixed constant satisfying that \(s(x)\in [\tfrac{1}{2},1)\). For simplicity, we fix the diffusion coefficient \(a(x,y)\equiv 1\).
(Left) the coarsest uniform grid for the domain \(\varOmega = (-2,2)^2\). The grid for the interior domain \({\varOmega ^{\text {int}}}= (-1,1)^2\) is marked in red. (Right) variable order function in \({\varOmega ^{\text {int}}}\) with \(s^* =0.7\), \(\eta =0.2\), \(\ell = 1.0\) and \(x^c=(-0.4,0.4)\) (Color figure online)
Our computational domain \(\varOmega \) is set to be a square \((-2,2)^2\) and the interior domain \({\varOmega ^{\text {int}}}\) is set to be \((-1,1)^2\). We construct a sequence of uniform grids \(\{{\mathcal {T}}_j\}_{j=1}^6\) with the mesh size \(h_j = \sqrt{2}/j^{j+1}\) generated by globally refining the coarse grid \({\mathcal {T}}_1\); see the coarsest grid \({\mathcal {T}}_1\) in Fig. 6.
Remark 5
We note that the subdivision in \({\varOmega ^{\text {ext}}}\) mainly contributes to the assembly of matrix \({\underline{M}}\) by computing the density function \(\rho _{{\mathcal {T}}}(x)\) as in (18). By utilizing the decay property of \(\gamma (x,y)\), graded meshes in \({\varOmega ^{\text {ext}}}\) can be used in order to reduce the computational cost. This strategy will be explored in future work. Here we rely on quasi-uniform meshes in \({\varOmega ^{\text {ext}}}\) to guarantee that the error from \(\rho _{{\mathcal {T}}}\) does not affect the total error.
For spatially varying fractional order, we do not have analytic solutions to examine the rate of convergence of our numerical scheme. As an alternative, we perform a comparison test by computing the difference between the finite element solution \(U_j\) on \({\mathcal {T}}_j\) and a finite difference approximation \({{\widetilde{U}}}_j\) developed in [5] using a cartesian grid \(\widetilde{{\mathcal {T}}}_j\) with the same node locations. We also perform self-convergence tests.
Variable-order comparison test: (left) \(L^2\)-error between u and \(U_j\) against degrees of freedoms \(\#\text {DoFs}\) and the self-convergence of \(U_j\) in \(L^2\) and \(L^\infty \) norms; (right) CPU times for assembling routines versus degrees of freedoms \(\#\text {DoFs}\). Linear complexity in time is confirmed
The left plot of Fig. 7 reports the \(L^2({\varOmega ^{\text {int}}})\)-error decay between \(U_j\) and \({{\widetilde{U}}}_j\) for \(f\equiv 20\) and for the variable order function s(x) in (58) with \(s^* = 0.7\), \(\eta = 0.2\), \(\ell =1.0\), and \((x_c,y_c) = (-0.4,0.4)\); see Fig. 6. We also report the self-convergence of \(U_j\), namely the error \(e_{u,j} = U_{j+1}-U_j\), in both \(L^2({\varOmega ^{\text {int}}})\) and \(L^\infty ({\varOmega ^{\text {int}}})\) norms, by estimating the error on each grid by using the next finer grid as the reference solution. It is seen that all three errors exhibit a first order decay. Such error behavior is similar to the constant-order integral fractional Laplacian case when \(s \ge 1/2\), and might be expected here since \({\underline{s}} \ge 1/2\). We also observe the singular behavior of the solution at \(\partial {\varOmega ^{\text {int}}}\); see the approximate solution along \(x_1=-0.4\) in the right plot of Fig. 8. The right panel of Fig. 7 shows the performance of the assembly routines for matrices \({\underline{B}}\), \({\underline{K}}\) and \({\underline{M}}\). We again observe a linear complexity in time for each assembly procedure, though the time for \({\underline{M}}\) is relatively large due the quasi-uniform triangulation of \(\varOmega \) as mentioned in Remark 5.
Figure 8 shows the finite element approximation \(U_6\) with 16,129 degrees of freedom in \({\varOmega ^{\text {int}}}\) (131,072 cells total in \(\varOmega \)). In the left panel we see a faster diffusion rate in the variable-order region \([-0.9,0.1]\times [-0.1,0.9]\). This diffusive behavior of the solution can also be observed along \(x_1=-0.4\) shown in the right panel of Fig. 8.
In Fig. 9, we test the same problem using the same parameters except that the coefficient bump function is negative, namely \(\eta =-0.2\). As shown in the left panel, we again obtain first-order convergence in \(L^2({\varOmega ^{\text {int}}})\) when comparing against the solution obtained from the finite difference method. In the right panel, we instead observe a less diffusive behavior of the solution in the bump region. Figure 10 displays the estimated condition number of the system (computed from the CG iterates) against the number of degrees of freedom. We observe that the condition number is nearly \(O(h^{-2\,s^*})\), where \(s^*\) denotes the background order.
The first-order convergence rate O(h) observed in the examples above is primarily due to the lack of regularity of the solution itself and is essentially the best that can be obtained for these solutions because of the singular derivatives at the boundary. One may wonder whether the proposed linear finite element discretization can produce second-order convergence when the solution has sufficient regularity.
To verify higher-order convergence, and since we cannot readily manufacture a solution analytically for variable order problems, we consider the following numerical alternative. We start from a given smooth solution and apply the forward operator discretized by a finite difference scheme to obtain a right-hand side. We then use this right-hand side in the finite element solver to recover the given solution.
Variable-order test with smooth solutions: (left) \(L^2\)-error between u and \(U_j\) against the number of degrees of freedom \(\#\text {DoFs}\) and the self-convergence of \(U_j\) in \(L^2\) and \(L^\infty \) norms. (right) self-convergence of the right-hand side approximation using a finite difference method
Specifically, we seek the solution u with right-hand side data \(F_j = I_j A_{\text {FD},j}u\), where \(A_{\text {FD},j}u\) is the discrete right hand side data produced by the finite difference method [5] using the cartesian grid \(\widetilde{{\mathcal {T}}}_j\) and \(I_j\) is the Lagrange nodal interplant on \({\mathbb {V}}({\mathcal {T}}_j)\). We fix u to be the smooth function \(u(x,y) = (1-x^2)^{15}(1-y^2)^{15}\) and set the same variable order function s(x) in the previous variable order test. Here we note that we choose the power 15 so that u is smooth enough to mitigate the effect of consistency errors in the right-hand side introduced by the finite difference discretization (i.e., the approximation error of \(I_j A_{\text {FD}, j}\)). Figure 11 shows the results of this test. The right panel of Fig. 11 shows the convergence of the right hand side data as the mesh is refined. While in general only a first-order rate of convergence for \(r_j:=F_{j+1}-F_j\) in \(L^2({\varOmega ^{\text {int}}})\)-norm is expected due to the singularity at the boundary, we obtain here second-order convergence since the solution is sufficiently smooth. The left plot of Fig. 11 shows that the proposed finite element approximation can indeed obtain second-order convergence when solution regularity allows it.
8 Conclusions
We presented an asymptotically optimal finite element methodology for modeling non-local fractional diffusion operators with spatial variation in fractional order and material coefficients and in general geometries. In the finite-element formulation, triangle pairs in the spatial mesh are the basic units that generate elemental stiffness matrices to be assembled into a global stiffness matrix. We address the singularities in evaluating touching triangle pairs through specialized mapping and quadrature schemes designed to handle the variable-order case. The computational complexity due to the quadratic number of interacting triangle pairs is overcome through (i) the construction of the hierarchical matrix approximations for representing the effect of every interior node on all other ones, and (ii) a generalized variable-order fast multipole method that computes the cumulative effect of all triangles on every interior node. The overall complexity for building the complete discrete operator is optimal, O(N), both in memory and in operations. We show the consistency of the method and the ability to control its accuracy through the number of quadrature points in the direct integrations and the degree of the polynomial interpolant of the kernel in the far field. Numerical experiments verify the accuracy and complexity of the methods proposed. The techniques are general and should apply to a broader class of nonlocal kernels.
There are a number of directions we are pursing in further work. First, the current work focused on the construction and application of the discrete operator. We are developing scalable preconditioners to allow the iterative solution of general fractional diffusion problems and are pursuing a geometric multilevel strategy that would allow end-to-end solutions in linear complexity. Second, the computations involved in building and applying the operator have high arithmetic intensity and substantial concurrency. We are developing performant implementations that are GPU-accelerated and can take advantage of multiple cores in a node and multiple distributed-memory nodes. This should produce dramatic improvements in absolute efficiency and make it quite practical to work with fractional operators in various application domains. We are also interested in extending the present finite element development to the case of anisotropic variability in fractional order and coefficients as well to three-dimensional geometry, a setting that has not yet been addressed sufficiently in the literature and where graded meshes will be particularly important. Finally, we are working on incorporating the forward solver in the inner loop of an inverse problem that seeks to recover the spatial distribution of fractional order and coefficients. In this context, the flexibility and linear complexity in memory and operations of the forward solver are essential from a practical point of view. We plan to report on these developments elsewhere.
Data Availability
The datasets generated and analyzed during the current study are available from the authors on reasonable request.
Notes
Even though we consider globally defined kernels here, our treatment also applies to finite horizon problems where a vanishes when \(|x-y|\) exceeds an interaction distance threshold.
We limit our discussion to \(|{\varOmega ^{\text {ext}}}| > 0\) as this guarantees well-posedness of the Dirichlet problem. If \(\varOmega = {\varOmega ^{\text {int}}}\), then the problem may not be well-posed when \({\underline{s}} \le 1/2\) (cf. [26]).
References
Acosta, G., Bersetche, F.M., Borthagaray, J.P.: A short FE implementation for a 2d homogeneous Dirichlet problem of a fractional Laplacian. Comput. Math. Appl. 74(4), 784–816 (2017). https://doi.org/10.1016/j.camwa.2017.05.026
Acosta, G., Borthagaray, J.P.: A fractional Laplace equation: regularity of solutions and finite element approximations. SIAM J. Numer. Anal. 55(2), 472–495 (2017). https://doi.org/10.1137/15M1033952
Ainsworth, M., Glusa, C.: Aspects of an adaptive finite element method for the fractional Laplacian: a priori and a posteriori error estimates, efficient implementation and multigrid solver. Comput. Methods Appl. Mech. Eng. 327, 4–35 (2017). https://doi.org/10.1016/j.cma.2017.08.019
Ainsworth, M., Glusa, C.: Towards an efficient finite element method for the integral fractional Laplacian on polygonal domains. In: Contemporary computational mathematics—a celebration of the 80th birthday of Ian Sloan. vol. 1, 2, pp. 17–57. Springer, Cham (2018)
Alzahrani, H., Turkiyyah, G., Knio, O., Keyes, D.: Space-fractional diffusion with variable order and diffusivity: discretization and direct solution strategies. Commun. Appl. Math. Comput. 4(4), 1416–1440 (2022). https://doi.org/10.1007/s42967-021-00184-9
Alzahrani, H.H., Lucchesi, M., Mustapha, K., Maître, O.P.L., Knio, O.M.: Bayesian calibration of order and diffusivity parameters in a fractional diffusion equation. J. Phys. Commun. 5(8), 085014 (2021). https://doi.org/10.1088/2399-6528/ac1507
Arndt, D., Bangerth, W., Feder, M., Fehling, M., Gassmöller, R., Heister, T., Heltai, L., Kronbichler, M., Maier, M., Munch, P., et al.: The deal. II library, version 9.4. J. Numer. Math. 30(3), 231–246 (2022)
Bauer, M., Bebendorf, M., Feist, B.: Kernel-independent adaptive construction of \({\cal{H} }^{2}\)-matrix approximations. Numer. Math. 150(1), 1–32 (2022). https://doi.org/10.1007/s00211-021-01255-y
Bonito, A., Lei, W., Pasciak, J.E.: Numerical approximation of the integral fractional Laplacian. Numer. Math. 142(2), 235–278 (2019). https://doi.org/10.1007/s00211-019-01025-x
Börm, S.: Efficient Numerical Methods for Non-local Operators: \({\cal{H} }^{2}\)-Matrix Compression, Algorithms and Analysis, vol. 14. European Mathematical Society (2010)
Borthagaray, J.P., Nochetto, R.H.: Besov regularity for the Dirichlet integral fractional Laplacian in Lipschitz domains. J. Funct. Anal. 284(6), 109829 (2023). https://doi.org/10.1016/j.jfa.2022.109829
Boukaram, W., Lucchesi, M., Turkiyyah, G., Le Maître, O., Knio, O., Keyes, D.: Hierarchical matrix approximations for space-fractional diffusion equations. Comput. Methods Appl. Mech. Eng. 369, 113191, 22 (2020). https://doi.org/10.1016/j.cma.2020.113191
Boukaram, W., Turkiyyah, G., Keyes, D.: Hierarchical matrix operations on GPUs: matrix-vector multiplication and compression. ACM Trans. Math. Softw. 45(1), 3:1-3:28 (2019). https://doi.org/10.1145/3232850
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32(7–9), 1245–1260 (2007). https://doi.org/10.1080/03605300600987306
Chen, P., Villa, U., Ghattas, O.: Hessian-based adaptive sparse quadrature for infinite-dimensional Bayesian inverse problems. Comput. Methods Appl. Mech. Eng. 327, 147–172 (2017). https://doi.org/10.1016/j.cma.2017.08.016. (Advances in Computational Mechanics and Scientific Computation—the Cutting Edge)
Cont, R., Tankov, P.: Financial Modelling with Jump Processes. Chapman & Hall/CRC Financial Mathematics Series. Chapman & Hall/CRC, Boca Raton (2004)
Contreras, A.A., Le Maître, O.P., Aquino, W., Knio, O.M.: Multi-model polynomial chaos surrogate dictionary for Bayesian inference in elasticity problems. Probab. Eng. Mech. 46, 107–119 (2016). https://doi.org/10.1016/j.probengmech.2016.08.004
Davis, P.J.: Interpolation and Approximation. Dover Publications Inc, New York (1975). (Republication, with minor corrections, of the 1963 original, with a new preface and bibliography)
D’Elia, M., Glusa, C.: A fractional model for anomalous diffusion with increased variability: analysis, algorithms and applications to interface problems. Numer. Methods Partial Differ. Equ. 38(6), 2084–2103 (2022)
D’Elia, M., Gunzburger, M.: The fractional Laplacian operator on bounded domains as a special case of the nonlocal diffusion operator. Comput. Math. Appl. 66(7), 1245–1260 (2013). https://doi.org/10.1016/j.camwa.2013.07.022
D’Elia, M., Gunzburger, M., Vollmann, C.: A cookbook for approximating Euclidean balls and for quadrature rules in finite element methods for nonlocal problems. Math. Models Methods Appl. Sci. 31(8), 1505–1567 (2021). https://doi.org/10.1142/S0218202521500317
Du, Q., Gunzburger, M., Lehoucq, R.B., Zhou, K.: Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev. 54(4), 667–696 (2012). https://doi.org/10.1137/110833294
Du, Q., Gunzburger, M., Lehoucq, R.B., Zhou, K.: A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws. Math. Models Methods Appl. Sci. 23(3), 493–540 (2013). https://doi.org/10.1142/S0218202512500546
Duo, S., van Wyk, H.W., Zhang, Y.: A novel and accurate finite difference method for the fractional Laplacian and the fractional Poisson problem. J. Comput. Phys. 355, 233–252 (2018). https://doi.org/10.1016/j.jcp.2017.11.011
Duo, S., Zhang, Y.: Accurate numerical methods for two and three dimensional integral fractional Laplacian with applications. Comput. Methods Appl. Mech. Eng. 355, 639–662 (2019). https://doi.org/10.1016/j.cma.2019.06.016
Fall, M.M.: Regional fractional Laplacians: boundary regularity. J. Differ. Equ. 320, 598–658 (2022)
Faustmann, M., Marcati, C., Melenk, J.M., Schwab, C.: Weighted analytic regularity for the integral fractional Laplacian in polygons. SIAM J. Math. Anal. 54(6), 6323–6357 (2022). https://doi.org/10.1137/21M146569X
Gatto, P., Hesthaven, J.S.: Numerical approximation of the fractional Laplacian via hp-finite elements, with an application to image denoising. J. Sci. Comput. 65(1), 249–270 (2015). https://doi.org/10.1007/s10915-014-9959-1
Glusa, C., D’Elia, M., Capodaglio, G., Gunzburger, M., Bochev, P.B.: An asymptotically compatible coupling formulation for nonlocal interface problems with jumps (2022). arXiv preprint arXiv:2203.07565
Gorenflo, R., Mainardi, F., Vivoli, A.: Continuous-time random walk and parametric subordination in fractional diffusion. Chaos Solitons Fractals 34(1), 87–103 (2007). https://doi.org/10.1016/j.chaos.2007.01.052
Grubb, G.: Fractional Laplacians on domains, a development of Hörmander’s theory of \(\mu \)-transmission pseudodifferential operators. Adv. Math. 268, 478–528 (2015). https://doi.org/10.1016/j.aim.2014.09.018
Hackbusch, W., Börm, S.: \({{\mathscr {H}}}^{2}\)-matrix approximation of integral operators by interpolation. Appl. Numer. Math. 43(1–2), 129–143 (2002). https://doi.org/10.1016/S0168-9274(02)00121-6. (19th Dundee Biennial Conference on Numerical Analysis (2001))
Hao, Z., Zhang, Z., Du, R.: Fractional centered difference scheme for high-dimensional integral fractional Laplacian. J. Comput. Phys. 424, 109851 (2021). https://doi.org/10.1016/j.jcp.2020.109851
Huang, Y., Oberman, A.: Numerical methods for the fractional Laplacian: a finite difference-quadrature approach. SIAM J. Numer. Anal. 52(6), 3056–3084 (2014). https://doi.org/10.1137/140954040
Jia, J., Wang, H., Zheng, X.: A fast collocation approximation to a two-sided variable-order space-fractional diffusion equation and its analysis. J. Comput. Appl. Math. 388, 113234 (2021). https://doi.org/10.1016/j.cam.2020.113234
Karkulik, M., Melenk, J.M.: \({\cal{H} }\)-matrix approximability of inverses of discretizations of the fractional Laplacian. Adv. Comput. Math. 45(5–6), 2893–2919 (2019). https://doi.org/10.1007/s10444-019-09718-5
Levendorskiĭ, S.Z.: Pricing of the American put under Lévy processes. Int. J. Theor. Appl. Finance 7(3), 303–335 (2004). https://doi.org/10.1142/S0219024904002463
Li, X., Mao, Z., Wang, N., Song, F., Wang, H., Karniadakis, G.E.: A fast solver for spectral elements applied to fractional differential equations using hierarchical matrix approximation. Comput. Methods Appl. Mech. Eng. 366, 113053 (2020). https://doi.org/10.1016/j.cma.2020.113053
Lian, Y., Ying, Y., Tang, S., Lin, S., Wagner, G.J., Liu, W.K.: A Petrov–Galerkin finite element method for the fractional advection-diffusion equation. Comput. Methods Appl. Mech. Eng. 309, 388–410 (2016). https://doi.org/10.1016/j.cma.2016.06.013
Lindgren, F., Bolin, D., Rue, H.V.: The SPDE approach for Gaussian and non-Gaussian fields: 10 years and still running. Spat. Stat. 50, 100599 (2022). https://doi.org/10.1016/j.spasta.2022.100599
Lindgren, F., Rue, H.V., Lindström, J.: An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 73(4), 423–498 (2011). https://doi.org/10.1111/j.1467-9868.2011.00777.x
Luchko, Y.: A new fractional calculus model for the two-dimensional anomalous diffusion and its analysis. Math. Model. Nat. Phenom. 11(3), 1–17 (2016). https://doi.org/10.1051/mmnp/201611301
Malhotra, D., Biros, G.: PVFMM: a parallel kernel independent FMM for particle and volume potentials. Commun. Comput. Phys. 18(3), 808–830 (2015). https://doi.org/10.4208/cicp.020215.150515sw
Minden, V., Ying, L.: A simple solver for the fractional Laplacian in multiple dimensions. SIAM J. Sci. Comput. 42(2), A878–A900 (2020). https://doi.org/10.1137/18M1170406
Sauter, S.A., Schwab, C.: Boundary Element Methods, Springer Series in Computational Mathematics, vol. 39. Springer-Verlag, Berlin (2011). https://doi.org/10.1007/978-3-540-68093-2
Silling, S.A.: Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 48(1), 175–209 (2000). https://doi.org/10.1016/S0022-5096(99)00029-0
Song, F., Xu, C., Karniadakis, G.E.: A fractional phase-field model for two-phase flows with tunable sharpness: algorithms and simulations. Comput. Methods Appl. Mech. Eng. 305, 376–404 (2016). https://doi.org/10.1016/j.cma.2016.03.018
Suzuki, J.L., Gulian, M., Zayernouri, M., D’Elia, M.: Fractional modeling in action: a survey of nonlocal models for subsurface transport, turbulent flows, and anomalous materials. J. Peridyn. Nonlocal Model. (2022). https://doi.org/10.1007/s42102-022-00085-2
Wang, H., Yang, D., Zhu, S.: A Petrov–Galerkin finite element method for variable-coefficient fractional diffusion equations. Comput. Methods Appl. Mech. Eng. 290, 45–56 (2015). https://doi.org/10.1016/j.cma.2015.02.027
Wang, R., Chen, C., Lee, J., Darve, E.: PBBFMM3D: a parallel black-box algorithm for kernel matrix-vector multiplication. J. Parallel Distrib. Comput. 154, 64–73 (2021). https://doi.org/10.1016/j.jpdc.2021.04.005
Wang, T., Song, F., Wang, H., Karniadakis, G.E.: Fractional Gray–Scott model: well-posedness, discretization, and simulations. Comput. Methods Appl. Mech. Eng. 347, 1030–1049 (2019). https://doi.org/10.1016/j.cma.2019.01.002
Wang, T., Yokota, R., Barba, L.A.: ExaFMM: a high-performance fast multipole method library with C++ and Python interfaces. J. Open Source Softw. 6(61), 3145 (2021)
Xu, K., Darve, E.: Isogeometric collocation method for the fractional Laplacian in the 2d bounded domain. Comput. Methods Appl. Mech. Eng. 364, 112936 (2020). https://doi.org/10.1016/j.cma.2020.112936
Ying, L., Biros, G., Zorin, D.: A kernel-independent adaptive fast multipole algorithm in two and three dimensions. J. Comput. Phys. 196(2), 591–626 (2004). https://doi.org/10.1016/j.jcp.2003.11.021
Yokota, R., Turkiyyah, G., Keyes, D.: Communication complexity of the fast multipole method and its algebraic variants. Supercomput. Front. Innov. Int. J. 1(1), 63–84 (2014). https://doi.org/10.14529/jsfi140104
Zampini, S., Boukaram, W., Turkiyyah, G., Knio, O., Keyes, D.: H2Opus: a distributed-memory multi-GPU software package for non-local operators. Adv. Comput. Math. 48(3), 31 (2022). https://doi.org/10.1007/s10444-022-09942-6
Zhang, H., Liu, F., Anh, V.: Numerical approximation of Lévy–Feller diffusion equation and its probability interpretation. J. Comput. Appl. Math. 206(2), 1098–1115 (2007). https://doi.org/10.1016/j.cam.2006.09.017
Zhao, T., Mao, Z., Karniadakis, G.E.: Multi-domain spectral collocation method for variable-order nonlinear fractional differential equations. Comput. Methods Appl. Mech. Eng. 348, 377–395 (2019). https://doi.org/10.1016/j.cma.2019.01.040
Zhao, X., Hu, X., Cai, W., Karniadakis, G.E.: Adaptive finite element method for fractional differential equations using hierarchical matrices. Comput. Methods Appl. Mech. Eng. 325, 56–76 (2017). https://doi.org/10.1016/j.cma.2017.06.017
Zheng, X., Wang, H.: An optimal-order numerical approximation to variable-order space-fractional diffusion equations on uniform or graded meshes. SIAM J. Numer. Anal. 58(1), 330–352 (2020). https://doi.org/10.1137/19M1245621
Acknowledgements
The authors are grateful to anonymous referees for comments and suggestions that have significantly improved the quality of this paper.
Funding
This work is funded by the Extreme Computing Research Center at KAUST.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lei, W., Turkiyyah, G. & Knio, O. Finite Element Discretizations for Variable-Order Fractional Diffusion Problems. J Sci Comput 97, 5 (2023). https://doi.org/10.1007/s10915-023-02318-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02318-y
Keywords
- Fractional diffusion
- Variable order
- Finite element approximation
- Hierarchical low-rank approximations
- Fast multipole method