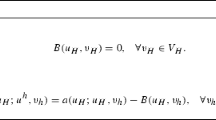Appendix A: Proof of Lemma 3.3
For the sake of presentation, throughout the proof, we shall write \(u_p\) instead of \({\mathcal {P}}_p^1u\).
We set \(u_p''\) as the Legendre expansion of \(u''\) truncated at order \(p-2\). In other words, expanding \(u''\) as a series of Legendre polynomials \(L_j(\xi )\), \(j \in {\mathbb {N}}_0\),
$$\begin{aligned} u''(\xi ) = \sum _{i=0}^{+\infty } b_j L_j(\xi ), \end{aligned}$$
(46)
we define
$$\begin{aligned} u_p''(\xi ):= \sum _{i=0}^{p-2} b_j L_j(\xi ). \end{aligned}$$
(47)
Standard properties of Legendre polynomials, see, e.g., [32, Appendix C], imply
$$\begin{aligned} {b_j = \frac{2j+1}{2} \int _{-1}^1 u''(\xi ) L_j(\xi ) d\xi .} \end{aligned}$$
(48)
For \(k\ge 0\), we recall [32, Lemma 3.10] that
$$\begin{aligned} \sum _{i=k}^{+\infty } \frac{2}{2i+1} \frac{(i+k)!}{(i-k)!} \vert b_i \vert ^2 = \int _{{\widehat{I}}} (1-\xi ^2)^k {\vert u^{({k+2})}(\xi ) \vert ^2} d\xi {\le {\left\| {u^{({k+2})}} \right\| }_{0,{\widehat{I}}}^2}. \end{aligned}$$
(49)
Using the orthogonality properties of Legendre polynomials [32, eq. (C.24)], the fact that \(s \le p-2\), and (49), we obtain
$$\begin{aligned} \begin{aligned} {\left\| {u''-u_p''} \right\| }_{0,{\widehat{I}}}^2&= \sum _{i=p-1}^{+\infty } \frac{2}{2i+1} \vert b_i \vert ^2 = \sum _{i=p-1}^{+\infty } \frac{2}{2i+1} \frac{(i+s)!}{(i-s)!} \vert b_i \vert ^2 \frac{(i-s)!}{(i+s)!}\\&\le \frac{(p-s-1)!}{(p+s-1)!} \sum _{i=s}^{+\infty } \frac{2}{2i+1} \frac{(i+s)!}{(i-s)!} \vert b_i \vert ^2 {\le \frac{(p-s-1)!}{(p+s-1)!} {\left\| {u^{({s+2})}} \right\| }_{0,{\widehat{I}}}^2}. \end{aligned} \end{aligned}$$
The two above equations yield the first bound in (12).
Next, we introduce
$$\begin{aligned} u_p'(\xi ) = \int _{-1}^\xi u_p''(t) dt + u'(-1). \end{aligned}$$
(50)
We have \(u_p'(-1) = u'(-1)\). Moreover, recalling that \(u_p''\) and \(u''\) have the same average over \({\widehat{I}}\), we also have
$$\begin{aligned} u_p'(1) = \int _{-1}^1 u_p''(t) dt + u'(-1) = \int _{-1}^1 u''(t) dt + u'(-1) = u'(1), \end{aligned}$$
which proves (11) for the derivative of \(u_p\) at the endpoints of \({\widehat{I}}\).
At this point, we observe
$$\begin{aligned} u'(\xi ) - u_p'(\xi ) = \int _{-1}^\xi (u''(t) - u_p''(t)) dt = \sum _{i=p-1}^{+\infty } b_i \int _{-1}^{\xi } L_i(t) dt =: \sum _{i=p-1}^{+\infty } b_i \phi _i(\xi ). \end{aligned}$$
(51)
Recall the Legendre differential equation [32, eq. (C.2.3)]
$$\begin{aligned} ((1-\xi ^2)L_i'(\xi ))' + i(i+1)L_i(\xi )=0 \qquad \forall i \in {\mathbb {N}}_0. \end{aligned}$$
Integrating the above identity over \((-1,\xi )\), \(\xi \in (-1,1)\), yields
$$\begin{aligned} \phi _i (\xi ) = -\frac{1}{i(i+1)} (1-\xi ^2) L_i'(\xi ). \end{aligned}$$
(52)
Recall the orthogonality property of the derivatives of Legendre polynomials [32, eq. (3.39)]:
$$\begin{aligned} \int _{-1}^1 (1-\xi ^2) L_i'(\xi ) L_j'(\xi ) d\xi = \frac{2\delta _{i,j}}{2i+1} \frac{(i+1)!}{(i-1)!}. \end{aligned}$$
(53)
Combining (52) and (53), for all i, \(j \in {\mathbb {N}}_0\), we deduce
$$\begin{aligned} \begin{aligned} \int _{-1}^1 (1-\xi ^2)^{-1} \phi _i(\xi ) \phi _j(\xi ) d\xi&= \frac{1}{i(i+1)j(j+1)} \int _{-1}^1 (1-\xi ^2) L_i'(\xi ) L_j'(\xi ) d\xi \\&= \frac{1}{i^2(i+1)^2} \frac{2\delta _{i,j}}{2i+1} \frac{(i+1)!}{(i-1)!} = \frac{2\delta _{i,j}}{i(i+1)(2i+1)}. \end{aligned} \end{aligned}$$
(54)
Using \(s \le p-2\), we write
$$\begin{aligned} \begin{aligned}&\int _{-1}^1 \vert u'(\xi ) -u_p'(\xi ) \vert ^2 d\xi = \int _{-1}^1 \vert \!\!\!\sum _{i=p-1}^{+\infty } b_i \phi _i(\xi ) \vert ^2 d\xi \le \int _{-1}^1 (1-\xi ^2)^{-1} \vert \!\!\! \sum _{i=p-1}^{+\infty } b_i \phi _i(\xi ) \vert ^2 d\xi \\&\overset{(54)}{\le } \sum _{i=p-1}^{+\infty } \frac{2\vert b_i \vert ^2}{i(i+1)(2i+1)} = \sum _{i=p-1}^{+\infty } \left( \frac{2\vert b_i \vert ^2}{2i+1} \frac{(i+s)!}{(i-s)!} \right) \frac{(i-s)!}{(i+s)!} \frac{1}{i(i+1)}\\&\le \frac{(p-s-1)!}{(p+s-1)!} \frac{1}{(p-1)p} \left( \sum _{i=s}^{+\infty } \frac{2\vert b_i \vert ^2}{2i+1} \frac{(i+s)!}{(i-s)!} \right) \overset{(49)}{\le } \frac{(p-s-1)!}{(p+s-1)!} \frac{1}{(p-1)p} {\left\| {u^{(s+2)}} \right\| }_{0,{\widehat{I}}}^2, \end{aligned} \end{aligned}$$
which is the second bound in (12).
Finally, we introduce
$$\begin{aligned} u_p(\xi ) = \int _{-1}^\xi u_p'(t) dt + u(-1). \end{aligned}$$
(55)
We observe that \(u_p(-1) = u(-1)\). Since \(L_1'(t)=1=L_0(t)\), standard manipulations imply
$$\begin{aligned} \begin{aligned} u_p(1)-u_p(-1)&= \int _{-1}^1 u_p'(t)dt \overset{(50)}{=} 2 u'(-1) + \int _{-1}^1 \left( \int _{-1}^t u_p''(x)dx \right) dt \\&\overset{(46),(51)}{=} 2 u'(-1) + \int _{-1}^1 \sum _{i=0}^{p-2} b_i \phi _i(t) dt = 2 u'(-1) + \sum _{i=0}^{p-2} b_i \int _{-1}^1 \phi _i(t) dt \\&\overset{(52)}{=} 2 u'(-1) - \sum _{i=0}^{p-1} b_i \int _{-1}^1 \frac{1}{i(i+1)} (1-t^2) L_i'(t) L_1'(t) dt\\&\overset{(53)}{=} 2 u'(-1) - \sum _{i=0}^{+\infty } b_i \int _{-1}^1 \frac{1}{i(i+1)} (1-t^2) L_i'(t) L_1'(t) dt\\&\overset{(52),(46)}{=} 2 u'(-1) + \int _{-1}^1 \left( \int _{-1}^t u''(x)dx \right) dt = \int _{-1}^1 u'(t) dt = u(1)-u(-1). \end{aligned} \end{aligned}$$
Using that \(u_p(-1) = u(-1)\), we deduce \(u_p(1)=u(1)\).
We are left with proving error estimates in the \(L^2\) norm. To this aim, observe that
$$\begin{aligned} u(\xi )-u_p(\xi ) = \int _{-1}^\xi (u'(t) - u_p'(t)) dt. \end{aligned}$$
We arrive at
$$\begin{aligned} u(\xi )-u_p(\xi ) \overset{(51)}{=} \sum _{i=p-1}^{+\infty } b_i \int _{-1}^{\xi } \phi _i(x) \ dx \ dt =: \sum _{i=p-1}^{+\infty } b_i \psi _i(\xi ). \end{aligned}$$
(56)
We prove certain orthogonality properties of the \(\psi _i\) functions. Recall the identity [32, eq. (C.2.5)]:
$$\begin{aligned} L_i(\xi ) = \frac{L'_{i+1}(\xi ) - L'_{i-1}(\xi )}{2i+1} \qquad \forall i\ge 2, \qquad \qquad L_0(\xi )=L_1'(\xi ). \end{aligned}$$
Integrating over \((-1,t)\), \(t\in (-1,1)\), and using \(L_{i+1}(-1)=L_{i-1}(-1)\), see [32, eq. (C.2.6)], we deduce
$$\begin{aligned} \phi _i(t)= \frac{L_{i+1}(\xi ) - L_{i-1}(\xi )}{2i+1}. \end{aligned}$$
Upon integrating the above identity over \((-1,\xi )\), \(\xi \in (-1,1)\), we arrive at
$$\begin{aligned} \psi _i(\xi ) = \frac{\int _{-1}^\xi L_{i+1}(t)\ dt - \int _{-1}^\xi L_{i-1}(t) \ dt}{2i+1} \overset{(51)}{=} \frac{\phi _{i+1}(\xi ) - \phi _{i-1}(t)}{2i+1}. \end{aligned}$$
With the notation \(\phi _{-1}(\xi )=0\), we get
$$\begin{aligned} \begin{aligned}&\psi _i(\xi ) \psi _j(\xi )\\&= \frac{1}{(2i+1)(2j+1)} \left( \phi _{i+1}(\xi ) \phi _{j+1}(\xi ) + \phi _{i-1}(\xi ) \phi _{j-1}(\xi ) - \phi _{i+1}(\xi ) \phi _{j-1}(\xi ) - \phi _{i-1}(\xi ) \phi _{j+1}(\xi ) \right) . \end{aligned} \end{aligned}$$
In (54), we proved that the \(\phi _i\) functions are orthogonal with respect to the \((1-\xi ^2)\)-weighted \(L^2\) inner product. Therefore, testing the above identity by \((1-\xi ^2)^{-1}\) and integrating over \((-1,1)\) we arrive at
$$\begin{aligned}{} & {} \int _{-1}^1 (1-\xi ^2)^{-1} \psi _i(\xi ) \psi _j(\xi ) \ d\xi \nonumber \\ {}{} & {} \quad = \frac{1}{(2i+1)(2j+1)} \left( \aleph _{i+1,j+1} + \aleph _{i-1,j-1} - \aleph _{i+1,j-1} - \aleph _{i-1,j+1} \right) , \end{aligned}$$
(57)
where, from (54),
$$\begin{aligned} \aleph _{\ell , k} = {\left\{ \begin{array}{ll} 0 &{} \quad \text {if } \ell \le 0 \text { or } k\le 0,\\ \frac{2\delta _{\ell ,k}}{\ell (\ell +1)(2\ell +1)} &{} \quad \text {if } \ell , \ k>0. \end{array}\right. } \end{aligned}$$
We provide explicit values for the expression in (57). If \(j \in \{ i-2, i, i+2 \}\), then
$$\begin{aligned} \int _{-1}^1 (1-\xi ^2)^{-1} \psi _i(\xi ) \psi _j(\xi ) \ d\xi = 0. \end{aligned}$$
If \(j=i\), then
$$\begin{aligned} \int _{-1}^1 (1-\xi ^2)^{-1} \psi _i(\xi ) \psi _i(\xi ) \ d\xi = \beth ^i_1 + \beth ^i_2, \end{aligned}$$
where
$$\begin{aligned} \beth _1^i:= \frac{1}{(2i+1)^2} \frac{2}{(i+1)(i+2)(2i+3)} \quad \forall i \in {\mathbb {N}}; \qquad \beth _2^i:= {\left\{ \begin{array}{ll} 0 &{}\quad \text {if } i=1, \\ \frac{1}{(2i+1)^2} \frac{2}{(i-1) i (2i-1)} &{} \quad \text {if } i\ge 2. \end{array}\right. } \end{aligned}$$
(58)
If \(j=i+2\), then
$$\begin{aligned} \int _{-1}^1 (1-\xi ^2)^{-1} \psi _i(\xi ) \psi _{i+2}(\xi ) \ d\xi = - \frac{1}{(2i+1)(2i+5)} \cdot \frac{2}{(i+1)(i+2)(2i+3)} =: -\beth ^i_3. \end{aligned}$$
(59)
If \(j=i-2\), then
$$\begin{aligned} \int _{-1}^1 (1-\xi ^2)^{-1} \psi _i(\xi ) \psi _{i-2}(\xi ) \ d\xi = - \beth ^i_4:= {\left\{ \begin{array}{ll} - \frac{1}{(2i+1)(2i-3)}\cdot \frac{2}{(i-1) i (2i-1)} &{}\quad \text {if } i\ge 3,\\ 0 &{} \quad \text {if } i\le 2. \end{array}\right. } \end{aligned}$$
(60)
In light of the above orthogonality properties, we can estimate the \(L^2\) approximation error as follows:
$$\begin{aligned} \begin{aligned} {\left\| {u-u_p} \right\| }^2_{0,{\widehat{I}}}&\overset{(56)}{=} {\left\| {\sum _{i=p-1}^{{+\infty }} b_i \psi _i} \right\| }^2_{0,{\widehat{I}}} \le \sum _{i,j=p-1}^{+\infty } {\left| {b_i \ b_j \int _{-1}^1 (1-\xi ^2)^{-1} \psi _i(\xi ) \psi _j(\xi ) d\xi } \right| }\\&\overset{(58), (59), (60)}{\le } \sum _{i=p-1}^{+\infty } \vert b_i \vert ^2 \left( \beth ^i_1 + \beth ^i_2 + \beth ^i_3 + \beth ^i_4 \right) . \end{aligned} \end{aligned}$$
We cope with the four terms on the right-hand side separately. We begin with \(\beth ^i_1\):
$$\begin{aligned} \begin{aligned} \sum _{i=p-1}^{+\infty } \vert b_i \vert ^2 \beth ^i_1&\overset{(58)}{=} \sum _{i=p-1}^{+\infty } \vert b_i \vert ^2 \frac{1}{(2i+1)^2} \cdot \frac{2}{(i+1)(i+2)(2i+3)}\\&= \sum _{i=p-1}^{+\infty } \left( \frac{2}{2i+1} \vert b_i \vert ^2 \frac{(i+s)!}{(i-s)!} \right) \left( \frac{(i-s)!}{(i+s)!} \frac{1}{(i+1)(i+2)(2i+1)(2i+3)} \right) \\&\overset{(49)}{\le } \frac{(p-s-1)!}{(p+s-1)!} \frac{1}{p(p+1)(2p-1)(2p+1)} {\left\| {u^{(s+2)}} \right\| }_{0,{\widehat{I}}}^2. \end{aligned} \end{aligned}$$
Next, we focus on \(\beth ^i_2\), \(i\ge 2\):
$$\begin{aligned} \begin{aligned} \sum _{i=\max (2,p-1)}^{+\infty } \vert b_i \vert ^2 \beth ^i_2&\overset{(58)}{=} \sum _{i=\max (2,p-1)}^{+\infty } \vert b_i \vert ^2 \frac{1}{(2i+1)^2} \cdot \frac{2}{(i-1) i (2i-1)}\\&= \sum _{i=\max (2,p-1)}^{+\infty } \left( \frac{2}{2i+1} \vert b_i \vert ^2 \frac{(i+s)!}{(i-s)!} \right) \left( \frac{(i-s)!}{(i+s)!} \frac{1}{(i-1) i (2i-1)(2i+1)} \right) \\&\overset{(49)}{\le } \frac{(p-s-1)!}{(p+s-1)!} \frac{1}{(p-2)(p-1)(2p-3)(2p-1)} {\left\| {u^{(s+2)}} \right\| }_{0,{\widehat{I}}}^2. \end{aligned} \end{aligned}$$
As for the term \(\beth ^i_3\), we proceed as follows:
$$\begin{aligned} \begin{aligned} \sum _{i=p-1}^{+\infty } \vert b_i \vert ^2 \beth ^i_3&\overset{(59)}{=} \sum _{i=p-1}^{+\infty } \vert b_i \vert ^2 \frac{1}{(2i+1)(2i+5)} \cdot \frac{2}{(i+1)(i+2)(2i+3)}\\&= \sum _{i=p-1}^{+\infty } \left( \frac{2}{2i+1} \vert b_i \vert ^2 \frac{(i+s)!}{(i-s)!} \right) \left( \frac{(i-s)!}{(i+s)!} \frac{1}{(i+1)(i+2)(2i+3)(2i+5)} \right) \\&\overset{(49)}{\le } \frac{(p-s-1)!}{(p+s-1)!} \frac{1}{p(p+2)(2p+1)(2p+3)} {\left\| {u^{(s+2)}} \right\| }_{0,{\widehat{I}}}^2. \end{aligned} \end{aligned}$$
Eventually, we cope with the term \(\beth ^i_4\), \(i\ge 3\):
$$\begin{aligned} \begin{aligned} \sum _{i=\max (3,p-1)}^{+\infty } \vert b_i \vert ^2 \beth ^i_4&\overset{(60)}{=} \sum _{i=\max (3,p-1)}^{+\infty } \vert b_i \vert ^2 \frac{1}{(2i+1)(2i-3)} \cdot \frac{2}{(i-1) i (2i-1)}\\&= \sum _{i=p-1}^{+\infty } \left( \frac{2}{2i+1} \vert b_i \vert ^2 \frac{(i+s)!}{(i-s)!} \right) \left( \frac{(i-s)!}{(i+s)!} \frac{1}{(i-1) i (2i-3)(2i-1)} \right) \\&\le \frac{(p-s-1)!}{(p+s-1)!} \frac{1}{(p-2)(p-1)(2p-5)(2p-3)} {\left\| {u^{(s+2)}} \right\| }_{0,{\widehat{I}}}^2. \end{aligned} \end{aligned}$$
Collecting the five bounds above concludes the proof.
Appendix B: Proof of Theorem 3.6 (2D Case)
The continuity properties (15) follow from the definition of the operator \({\mathcal {P}}_p\cdot \). Therefore, we only focus on the error estimates. We split the proof into several steps. Recall that \({\mathcal {P}}_p^x\) and \({\mathcal {P}}_p^y\) are the projections in Lemma 3.3 along the x and y directions, respectively.
Some identities The following identities are valid:
$$\begin{aligned} \partial _y{\mathcal {P}}_p^xu = {\mathcal {P}}_p^x(\partial _yu), \qquad \partial _x{\mathcal {P}}_p^yu = {\mathcal {P}}_p^y(\partial _xu). \end{aligned}$$
(61)
We only show the first one as the second can be proven analogously. For all \(y \in (-1,1)\), after writing \({\mathcal {P}}_p^xu (x,y)\) in integral form with respect to the x variable, we have
$$\begin{aligned} \begin{aligned}&{\mathcal {P}}_p^xu ( x,y ) = \int _{-1}^x \left[ \left( \int _{-1}^t \partial _x^2 {\mathcal {P}}_p^xu (x,y) dx \right) + \partial _xu(-1,y) \right] dt + u(-1,y)\\&\overset{(11)}{=} \int _{-1}^x \left[ \left( \int _{-1}^t \partial _x^2 {\mathcal {P}}_p^xu (x,y) dx \right) + \partial _xu(-1,y) \right] dt + u(-1,y)\\&\overset{(47),(48)}{=} \int _{-1}^x \left[ \left( \int _{-1}^t \partial _x^2 \left( \sum _{i=0}^{p-2} \frac{2i+1}{2} \int _{-1}^1 u(s,y) L_i(s) ds \right) L_i(x) dx \right) + \partial _xu(-1,y) \right] dt \\ {}&\quad + u(-1,y). \end{aligned} \end{aligned}$$
Taking the partial derivative with respect to y on both sides yields
$$\begin{aligned} \begin{aligned}&\partial _y{\mathcal {P}}_p^xu ( x,y )\\&= \int _{-1}^x \left[ \left( \int _{-1}^t \partial _x^2 \left( \sum _{i=0}^{p-2} \frac{2i+1}{2} \int _{-1}^1 \partial _yu(s,y) L_i(s) ds \right) L_i(x) dx \right) + \partial _x\partial _yu(-1,y) \right] dt\\ {}&\quad + \partial _yu(-1,y)\\&\overset{(47),(50),(55)}{=} {\mathcal {P}}_p^x\partial _yu ( x,y ). \end{aligned} \end{aligned}$$
\(L^2\) estimates Using the definition of \({\mathcal {P}}_p\), the triangle inequality, the one dimensional approximation properties (13), the third stability property in (14), and the identities (61) we write
$$\begin{aligned} \begin{aligned} {\left\| {u-{\mathcal {P}}_pu} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {u-{\mathcal {P}}_p^xu} \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^x(u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s-2} {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {u-{\mathcal {P}}_p^yu} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 (u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}\\&= p^{-s-2} {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {u-{\mathcal {P}}_p^yu} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 u-{\mathcal {P}}_p^y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
The assertion follows using again the one dimensional approximation properties (13).
\(H^1\) estimates First, we cope with the bound on the derivative with respect to x. Adding and subtracting \({\mathcal {P}}_p^xu\), and using the triangle inequality yield
$$\begin{aligned} \begin{aligned} {\left\| {\partial _x(u-{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {\partial _x(u-{\mathcal {P}}_p^xu)} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x{\mathcal {P}}_p^x(u- {\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}} =: T_1 + T_2. \end{aligned} \end{aligned}$$
(62)
As for the term \(T_1\), we use the one dimensional approximation properties (13) and get
$$\begin{aligned} T_1 \lesssim p^{-s-1} {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}}. \end{aligned}$$
(63)
As for the term \(T_2\), we use the second stability estimate in (14) and get
$$\begin{aligned} T_2 \lesssim {\left\| {\partial _x(u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _x^2 (u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}. \end{aligned}$$
Thanks to the identities (61) and the one dimensional approximation properties (13), we can estimate the term \(T_2\) from above as follows:
$$\begin{aligned} T_2&\lesssim p^{-1} {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}\nonumber \\\lesssim & {} p^{-s-1} \left( {\left\| {\partial _x\partial _y^{s+1} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^{s} u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned}$$
(64)
Collecting the estimates (63) and (64) in (62), we arrive at
$$\begin{aligned} {\left\| {\partial _x(u-{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}} \lesssim p^{-s-1} \left( {\left\| {\partial _x^{s+2}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y^{s+1}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^{s}u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned}$$
With similar arguments for the y derivative term, we deduce (17).
\(H^2\) estimates We begin by showing an upper bound on the second derivative with respect to x. Using the triangle inequality, the one dimensional approximation properties (13), the stability properties (14), and the identities (61), we obtain
$$\begin{aligned} \begin{aligned} {\left\| {\partial _x^2 (u-{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {\partial _x^2 (u-{\mathcal {P}}_p^xu)} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 {\mathcal {P}}_p^x(u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 (u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}\\ {}&= p^{-s} {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 u-{\mathcal {P}}_p^y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} \left( {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^{s} u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
Analogously, we can prove
$$\begin{aligned} {\left\| {\partial _y^2 (u-{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}} \lesssim p^{-s} \left( {\left\| {\partial _y^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^{s} \partial _y^2 u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned}$$
Eventually, we cope with the mixed derivative term. Using the triangle inequality and the identities (61), we get
$$\begin{aligned} \begin{aligned} {\left\| {\partial _x\partial _y(u-{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {\partial _x\partial _y(u-{\mathcal {P}}_p^xu)} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y{\mathcal {P}}_p^x(u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}\\&= {\left\| {\partial _x(\partial _yu-{\mathcal {P}}_p^x\partial _yu)} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x{\mathcal {P}}_p^x\partial _y(u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}} =: S_1 + S_2. \end{aligned} \end{aligned}$$
(65)
We estimate the two terms \(S_1\) and \(S_2\) separately. Using the one dimensional approximation properties (13), we can write
$$\begin{aligned} \begin{aligned} S_1&\lesssim p^{-s} {\left\| {\partial _x^{s+1} \partial _yu} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
(66)
On the other hand, using the one dimensional approximation properties (13) and the stability properties (14), we get
$$\begin{aligned} \begin{aligned} S_2&\lesssim {\left\| {\partial _x\partial _y(u-{\mathcal {P}}_p^yy)} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _x^2 \partial _y(u-{\mathcal {P}}_p^yu)} \right\| }_{0,{\widehat{Q}}}\\&= {\left\| {\partial _y(\partial _xu-{\mathcal {P}}_p^y\partial _xy)} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _y(\partial _x^2 u-{\mathcal {P}}_p^y\partial _x^2 u)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} \left( {\left\| {\partial _x\partial _y^{s+1}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^{s} u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
(67)
Collecting the estimates (66) and (67) in (65), we arrive at
$$\begin{aligned} {\left\| {\partial _x\partial _y(u-{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}} \lesssim p^{-s} \left( {\left\| {\partial _x^{s+1} \partial _yu} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y^{s+1}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^{s} u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned}$$
Combining the estimates on all second derivatives terms, we obtain (18).
Appendix C: Proof of Theorem 3.6 (3D Case)
The continuity properties follow exactly as in the two dimensional case. Thus, we only show the details for the approximation properties. We split the proof in several steps. Recall that \({\mathcal {P}}_p^x\), \({\mathcal {P}}_p^y\), and \({\mathcal {P}}_p^z\) are the projections in Lemma 3.3 along the x, y, and z directions, respectively.
Some identities Analogous to their two dimensional counterparts in (61), we have the following identities:
$$\begin{aligned} \begin{aligned}&\partial _y{\mathcal {P}}_p^xu = {\mathcal {P}}_p^x(\partial _yu), \qquad \partial _x{\mathcal {P}}_p^yu = {\mathcal {P}}_p^y(\partial _xu), \qquad \partial _y{\mathcal {P}}_p^zu = {\mathcal {P}}_p^z(\partial _yu),\\&\partial _z{\mathcal {P}}_p^yu = {\mathcal {P}}_p^y(\partial _zu), \qquad \partial _x{\mathcal {P}}_p^zu = {\mathcal {P}}_p^z(\partial _xu), \qquad \partial _z{\mathcal {P}}_p^xu = {\mathcal {P}}_p^x(\partial _zu). \end{aligned} \end{aligned}$$
(68)
\(L^2\) estimates The triangle inequality and the one dimensional approximation properties (13) imply
$$\begin{aligned} \begin{aligned} {\left\| {u-{\mathcal {P}}_pu} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {u-{\mathcal {P}}_p^xu} \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^x(u-{\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}}\\ {}&\lesssim p^{-s-2}{\left\| {\partial _x^{s+2}u} \right\| }_{0,{\widehat{Q}}} \!\!\!+ {\left\| {{\mathcal {P}}_p^x(u-{\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
We focus on the second term. To this aim, we use the stability properties (14), the triangle inequality, the one dimensional approximation properties (13), and the identities (68), and deduce
$$\begin{aligned} \begin{aligned}&{\left\| {{\mathcal {P}}_p^x(u-{\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}} \le {\left\| {u - {\mathcal {P}}_p^y{\mathcal {P}}_p^zu} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}\\&\lesssim {\left\| {u - {\mathcal {P}}_p^yu} \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^y(u - {\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {{\mathcal {P}}_p^y(\partial _x^2 u - {\mathcal {P}}_p^z\partial _x^2 u)} \right\| }_{0,{\widehat{Q}}} \\&\lesssim p^{-s -2} {\left\| {\partial _y^{s+2}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {u-{\mathcal {P}}_p^zu} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _y^2 u - {\mathcal {P}}_p^z\partial _y^2 u} \right\| }_{0,{\widehat{Q}}} + p^{-s-4} {\left\| {\partial _x^2\partial _y^2\partial _z^{s-2}u} \right\| }_{0,{\widehat{Q}}}\\&\quad +p^{-2} {\left\| {\partial _x^2u-{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} + p^{-4} {\left\| {\partial _x^2 \partial _y^2 u - {\mathcal {P}}_p^z\partial _x^2 \partial _y^2 u} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
The \(L^2\) estimates eventually follow from the one dimensional approximation properties (13).
\(H^1\) estimates We show the details for the x derivative, as the other two cases can be dealt with analogously. The triangle inequality and the one dimensional approximation properties (13) imply
$$\begin{aligned} \begin{aligned} {\left\| {\partial _x(u -{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}}&\lesssim {\left\| {\partial _x(u -{\mathcal {P}}_p^xu)} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x{\mathcal {P}}_p^x(u -{\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s-1} {\left\| {\partial _x^{s+2}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x{\mathcal {P}}_p^x(u -{\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
We focus on the second term on the right-hand side. The stability properties (14) and the identities (68) entail
$$\begin{aligned} {\left\| {\partial _x{\mathcal {P}}_p^x(u -{\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}} \lesssim {\left\| {\partial _xu - {\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _xu} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} =: T_1+T_2. \end{aligned}$$
As for the term \(T_1\), the triangle inequality, the identities (68), and the one dimensional approximation properties (13) imply
$$\begin{aligned} \begin{aligned} T_1&\!\lesssim \! {\left\| {\partial _xu \!-\! {\mathcal {P}}_p^y\partial _xu} \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^y(\partial _xu \!-\! {\mathcal {P}}_p^z\partial _xu)} \right\| }_{0,{\widehat{Q}}}\\ {}&\lesssim \! p^{-s-1} {\left\| {\partial _x\partial _y^{s+1} u } \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^y(\partial _xu \!-\! {\mathcal {P}}_p^z\partial _xu)} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
The second term on the right-hand side can be estimated using the stability properties (14), the identities (68), and the one dimensional approximation properties (13):
$$\begin{aligned} \begin{aligned}&{\left\| {{\mathcal {P}}_p^y(\partial _xu \!-\! {\mathcal {P}}_p^z\partial _xu)} \right\| }_{0,{\widehat{Q}}} \lesssim {\left\| {\partial _xu \!-\! {\mathcal {P}}_p^z\partial _xu} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x\partial _y^2 u \!-\! {\mathcal {P}}_p^z\partial _x\partial _y^2 u)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s-1} \left( {\left\| {\partial _x\partial _z^{s+1}u} \right\| }_{0,{\widehat{Q}}} +{\left\| {\partial _x\partial _y^2 \partial _x^{s-1}u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
With similar arguments based on substituting \(\partial _xu\) by \(\partial _x^2 u\), we find an upper bound for \(T_2\):
$$\begin{aligned} T_2 \lesssim p^{-s-1} \left( {\left\| {\partial _x^2 \partial _y^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _z^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2\partial _y^2 \partial _z^{s-2}u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned}$$
Collecting the above estimates, we arrive at
$$\begin{aligned} \begin{aligned}&{\left\| {\partial _x(u -{\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}} \lesssim p^{-s-1} \Big ( {\left\| {\partial _x^{s+2} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y^{s+1} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _z^{s+1} u} \right\| }_{0,{\widehat{Q}}} \\&\quad + {\left\| {\partial _x\partial _y^2 \partial _z^{s-1} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^s u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _z^{s} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^2 \partial _z^{s-2} u} \right\| }_{0,{\widehat{Q}}} \Big ). \end{aligned} \end{aligned}$$
By similar arguments on the y and x partial derivatives, we deduce (20).
\(H^2\) estimates First, we show the details for the second x derivative, since the second y and z derivatives can be dealt with analogously. The triangle inequality, the one dimensional approximation properties (13), and the identities (68) imply
$$\begin{aligned} \begin{aligned} {\left\| {\partial _x^2 (u - {\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {\partial _x^2 (u - {\mathcal {P}}_p^xu)} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 {\mathcal {P}}_p^x(u - {\mathcal {P}}_p^y{\mathcal {P}}_p^zu)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} {\left\| {\partial _x^{s+2}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}. \end{aligned} \end{aligned}$$
We are left with estimating the second term on the right-hand side. Applying a further triangle inequality, the one dimensional approximation properties (13), and the stability properties (14), we arrive at
$$\begin{aligned} \begin{aligned} {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}&\le {\left\| {\partial _x^2 u - {\mathcal {P}}_p^y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^y(\partial _x^2 u - {\mathcal {P}}_p^z\partial _x^2 u)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} {\left\| {\partial _x^2 \partial _y^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 u - {\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 \partial _y^2 u - {\mathcal {P}}_p^z\partial _x^2\partial _y^2 u} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} \left( {\left\| {\partial _x^2 \partial _y^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _z^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^2 \partial _z^{s-2}u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
Collecting the two above estimate above gives
$$\begin{aligned} {\left\| {\partial _x^2 (u - {\mathcal {P}}_pu)} \right\| }_{0,{\widehat{Q}}} \lesssim p^{-s} \left( {\left\| {\partial _x^{s+2}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _z^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^2 \partial _z^{s-2}u} \right\| }_{0,{\widehat{Q}}} \right) .\nonumber \\ \end{aligned}$$
(69)
Next, we focus on the mixed xy derivative and observe that the yz and xz counterparts are dealt with analogously. Using the triangle inequality, the one dimensional approximation properties (13), the identities (68), and the stability properties (14) leads us to
$$\begin{aligned} \begin{aligned}&{\left\| {\partial _x\partial _yu - {\mathcal {P}}_p\partial _x\partial _yu} \right\| }_{0,{\widehat{Q}}} \le {\left\| {\partial _x\partial _yu - {\mathcal {P}}_p^x\partial _x\partial _yu} \right\| }_{0,{\widehat{Q}}} + {\left\| {{\mathcal {P}}_p^x(\partial _x\partial _yu - {\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x\partial _yu)} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} {\left\| {\partial _x^{s+1}\partial _yu} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _y\partial _xu - \partial _y{\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _xu} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _y\partial _x^2 u - \partial _y{\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}\\&= p^{-s} {\left\| {\partial _x^{s+1}\partial _yu} \right\| }_{0,{\widehat{Q}}} + T_3+T_4. \end{aligned} \end{aligned}$$
We estimate the terms A and B separately. First, we focus on A. Using the triangle inequality, the one dimensional approximation properties (13), the identities (68), and the stability properties (14), entail
$$\begin{aligned} \begin{aligned} T_3&\le {\left\| {\partial _y\partial _xu - \partial _y{\mathcal {P}}_p^y\partial _xu} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _y{\mathcal {P}}_p^y\partial _xu - \partial _y{\mathcal {P}}_p^y\partial _xu} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} {\left\| {\partial _x\partial _y^{s+1}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _y\partial _xu - {\mathcal {P}}_p^z\partial _y\partial _xu} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _y^2\partial _xu - {\mathcal {P}}_p^z\partial _y^2\partial _xu} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} \left( {\left\| {\partial _x\partial _y^{s+1}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y\partial _z^{s}u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y^2 \partial _z^{s-1}u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
Next, we focus on the term B. Using the triangle inequality, the one dimensional approximation properties (13), the identities (68), and the stability properties (14), leads to
$$\begin{aligned} \begin{aligned} T_4&\le p^{-1} {\left\| {\partial _y\partial _x^2 u - \partial _y{\mathcal {P}}_p^y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _y{\mathcal {P}}_p^y\partial _x^2 u - \partial _y{\mathcal {P}}_p^y{\mathcal {P}}_p^z\partial _x^2 u} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} {\left\| {\partial _x^2\partial _y^{s}} \right\| }_{0,{\widehat{Q}}} + p^{-1} {\left\| {\partial _y\partial _x^2 u - {\mathcal {P}}_p^z\partial _y\partial _x^2 u} \right\| }_{0,{\widehat{Q}}} + p^{-2} {\left\| {\partial _x^2 \partial _y^2 u - {\mathcal {P}}_p^z\partial _x^2 \partial _y^2 u} \right\| }_{0,{\widehat{Q}}}\\&\lesssim p^{-s} \left( {\left\| {\partial _x^2\partial _y^{s}} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2\partial _y\partial _z^{s}} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2\partial _y^2 \partial _z^{s-2}} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
Collecting the above estimates gives
$$\begin{aligned} \begin{aligned}&{\left\| {\partial _x\partial _yu - {\mathcal {P}}_p\partial _x\partial _yu} \right\| }_{0,{\widehat{Q}}}\\&\quad \lesssim p^{-s} \left( {\left\| {\partial _x^{s+1}\partial _yu} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y^{s+1} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x\partial _y\partial _z^{s} u} \right\| }_{0,{\widehat{Q}}} {\left\| {\partial _x\partial _y^2 \partial _z^{s-1} u} \right\| }_{0,{\widehat{Q}}} \right. \\&\quad \left. + {\left\| {\partial _x^2 \partial _y^{s} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y\partial _z^{s-1} u} \right\| }_{0,{\widehat{Q}}} + {\left\| {\partial _x^2 \partial _y^2 \partial _z^{s-2} u} \right\| }_{0,{\widehat{Q}}} \right) . \end{aligned} \end{aligned}$$
(70)
Bound (21) follows combining the estimates on the second derivative term (69), the mixed derivative term (70), and the corresponding estimates for similar derivative terms.