Singly TASE Operators for the Numerical Solution of Stiff Differential Equations by Explicit Runge–Kutta Schemes

Abstract

In this paper new explicit integrators for numerical solution of stiff evolution equations are proposed. As shown by Bassenne, Fu and Mani in (J Comput Phys 424:109847, 2021), the action on the original vector field of the stiff equations of an appropriate time-accurate and highly-stable explicit (TASE) linear operator, allows us to use explicit Runge–Kutta (RK) schemes with these modified equations so that the resulting algorithm becomes stable for the original stiff equations. Here a new family of TASE operators is considered. The new operators, called Singly TASE, have the advantage over the TASE operators of Bassenne et al. that the action on the vector field depends on the powers of the inverse of only one matrix, which can be computationally more simple, without loosing stability properties. A complete study of the linear stability properties of k–stage, kth–order explicit RK schemes under the action of Singly TASE operators of the same order is carried out for $k \le 4$. For orders two, three and four, particular schemes that are nearly strongly A–stable and therefore suitable for stiff problems are devised. Further, explicit RK schemes with orders three and four that can be implemented with only two storage locations under the action of Singly TASE operators of the same order are discussed. A particular implementation of the classical four–stage fourth–order RK scheme with two Singly TASE operators is presented. A set of numerical experiments has been conducted to demonstrate the performance of the new schemes by comparing with previous RKTASE and other established methods. The main conclusion is that the new integrators provide a very simple solver for stiff systems with good stability properties and avoids the difficulties of using implicit algorithms.

1 Introduction

Numerical methods for the solution of stiff Initial Value Problems must have adequate stability properties. Unfortunately, for general problems such properties imply that the method must be implicit, which makes the implementation of the integrators complicated and the computational cost can be large for high dimensional problems. However, for particular classes of stiff problems, explicit Runge–Kutta (RK) schemes with suitable stability properties can be constructed. For example, in the semidiscretization of parabolic PDEs, that are known to have large negative real spectrum, the so called (damped) Chebyshev Runge–Kutta methods [1,2,3] can be adequate. These methods are explicit, and with s stages and order less or equal than two they have a stability interval $\left[ -\alpha , 0\right]$ with $\alpha \le 2\,s^2$ (see e.g. [1]), and a thin stability region around the real axis and they have given raise to an integration code [4]. This class of schemes can solve stiff problems with eigenvalues located near the real axis, but at the price of having probably a large number of (explicit) stages.

In [5, 6], a family of explicit Runge–Kutta schemes, referred to as Paired Explicit Runge–Kutta schemes, that are suitable for the solution of stiff systems of equations, is proposed. The P-ERK approach allows Runge–Kutta schemes to have a (bounded) large stability region at the price of having a large number of stages, and this make the schemes suitable for midly stiff problems. Highly stiff problems would require a very large number of (explicit) stages.

For stiff problems for which the eigenvalues of the Jacobian matrix are separated into two clusters, one containing the “stiff” or fast components, and the other containing the slow components, Bocher et al. [7] proposed a family of explicit Runge–Kutta schemes that use exponential fitting techniques. The stability region of these methods contains two regions, one close to the origin and the other one fitting the large eigenvalues.

In this paper we are considering a different approach to solve stiff problems by means of explicit RK methods. This approach was proposed by Bassenne, Fu and Mani in a recent paper [8], where, together the differential system associated to the step from $(t_n, Y_n)$ to $(t_n+\Delta t, Y_{n+1})$

$$\begin{aligned} \dfrac{d}{dt} Y(t) = F ( t, Y(t)), \quad Y(t_n)=Y_n \in \mathbb {R}^N \end{aligned}$$

(1)

the authors consider a second IVP that here will be called the stabilized IVP

$$\begin{aligned} \dfrac{d}{dt} U(t) = T \; F ( t, U(t)), \quad U(t_n)=U_n \equiv Y_n \in \mathbb {R}^N, \end{aligned}$$

(2)

where $T = T( \Delta t \; L)$ is a linear operator, referred to as the TASE operator, that depends on the product of the time step size $\Delta t$ and a d-dimensional linear operator L that approximates the Jacobian $F_u ( t_n, U_n)$ at the initial values at each time-step. The TASE operator is choosen so that the numerical solution of Eq. (2) $U_{RK}(t_n + \Delta t)$ obtained with an explicit RK of order p approximates the exact solution of (1), $Y(t_n+ \Delta t)$ at $t_n+ \Delta t$ with order p i.e.

$$\begin{aligned} U_{RK}(t_n + \Delta t) - Y(t_n + \Delta t) = \mathcal {O}(\Delta t ^{p+1}), \quad ( \Delta t \rightarrow 0), \end{aligned}$$

and also $U_{RK}(t_n + \Delta t)$ satisfies some stability requirements, such as A- or L- stability, that are necessary for solving stiff systems. Thus the introduction of the TASE operator into the original governing equation allows us to overcome the numerical stability restrictions of explicit RK time-advancing schemes for solving stiff systems.

In the simplest case of a linear system, i.e., $F(t,Y)= L \; Y$, by defining the TASE operator as $T = ( I - \Delta t \; L )^{-1}$ and solving Eq. (2) with the explicit Euler with the time step size $\Delta t$, we get the approximation $U_{n+1}=U_{RK}(t_n+\Delta t) \approx U(t_{n+1})$ given by

$$\begin{aligned} U_{n+1} = U_n + \Delta t \; T \; L \; U_n = Y_n + \Delta t (I- \Delta t L)^{-1} L \; Y_n = ( I - \Delta t \; L)^{-1} \; Y_n, \end{aligned}$$

which is equivalent to apply the first order BDF method to the original problem (1) and as shown in [9] is L-stable and therefore does not have stability restrictions on the step size $\Delta t$ for diffusion problems and other stiff systems with strongly damped components in the solution. On the other hand by choosing $T = \left( I - ( \Delta t/2) L \right) ^{-1}$ and solving again the stabilized IVP by explicit Euler’s scheme we get

$$\begin{aligned} U_{n+1} = Y_n + \Delta t \; \left( I - ( \Delta t/2) L \right) ^{-1} \; L \; Y_n = \left( I + ( \Delta t/2) L \right) \; \left( I - ( \Delta t/2) L \right) ^{-1} \; Y_n, \end{aligned}$$

that is the implicit midpoint rule (see [10], p. 204) that is suitable for convective problems.

Observe that according to the nonlinear variation-of-constants formula [10, p. 96], assuming that F is sufficiently smooth the solutions of (1) and (2) satisfy

$$\begin{aligned} U(t_n+ & {} \Delta t)- Y(t_n+ \Delta t) = \nonumber \\= & {} \int _{t_n}^{t_n+ \Delta t} \dfrac{\partial Y }{\partial Y_n } (t_n + \Delta t; s, U(s) ) \left[ T \; F ( s, U(s)) - F(s, U(s)) \right] \; ds\\= & {} \int _{t_n}^{t_n+ \Delta t} \dfrac{\partial Y }{\partial Y_n } ( t_n + \Delta t; s, U(s) ) \left( T - I \right) \; F(s, U(s)) \; ds, \nonumber \end{aligned}$$

(3)

where $Y(t) \equiv Y( t; t_n, Y_n)$ is the solution of (1). Hence if the TASE operator $T = T( \Delta t \; L)$ satisfies

$$\begin{aligned} T ( \Delta t \; L ) = I + \mathcal {O} ( \Delta t^q), \quad (\Delta t \rightarrow 0), \end{aligned}$$

(4)

for some integer $q\ge 1$ (the order of approximation of the operator to the identity), it follows from (3) that

$$\begin{aligned} \Vert U(t_n + \Delta t) - Y(t_n + \Delta t) \Vert \le \mathcal {O} ( \Delta t^{q+1}), \quad (\Delta t \rightarrow 0). \end{aligned}$$

(5)

Moreover if the explicit RK scheme applied to the stabilized equation (2) has order p, then

$$\begin{aligned} \Vert U(t_n + \Delta t) - U_{RK} (t_n + \Delta t) \Vert = \mathcal {O} ( \Delta t^{p+1}), \quad (\Delta t \rightarrow 0), \end{aligned}$$

(6)

and from Eqs. (5) and (6) it follows that

$$\begin{aligned} \Vert Y(t_n + \Delta t) - U_{RK} (t_n + \Delta t) \Vert = \mathcal {O} ( \Delta t^{\min (p,q)+1}). \quad (\Delta t \rightarrow 0). \end{aligned}$$

(7)

That is, the numerical solution of the stabilized system Eq. (2), $U_{RK}(t_n)$ has at least order $\min (p,q)$.

A crucial point in the above approach is the construction of TASE operators that satisfy (5) together with the A–stability and/or L–stability requirements. In [8], the authors propose the TASE operator $T = T_p( \alpha \; \Delta t)$ defined recursively by

$$\begin{aligned} T_p( \alpha \Delta t ) = \left\{ \begin{array}{lcl} ( I - \alpha \; \Delta t \; L )^{-1}, &{} \hbox {if} &{} p=1, \\ \left( \dfrac{2^{p-1}}{2^{p-1} -1}\right) T_{p-1}\left( \dfrac{\alpha }{2} \; \Delta t\right) -\left( \dfrac{1}{2^{p-1} -1}\right) T_{p-1}( \alpha \; \Delta t), &{} \hbox {if} &{} p>1, \end{array} \right. \end{aligned}$$

(8)

Here $T_p (\alpha \Delta t)$ has an accuracy of order p and $\alpha >0$ is a real parameter to be chosen by the stability requirements. By choosing $\alpha \ge \alpha _{\min } = ( 2^p-1) \; C_p^{-1},$ where $C_p$ is the stability abscissae of the explicit RK scheme of order p, some specific schemes that combine explicit p–stage RK schemes with orders $p \le 4$ and TASE operators with the same orders have been derived in [8], and their linear stability properties have been studied as well. Moreover applications to some benchmark equations showed that this approach leads to time marching algorithms that can be easily implemented and do not suffer from the stability restrictions on the step size.

More recently, Calvo et al. [11] have considered a more general family of TASE operators with the form

$$\begin{aligned} T= T_p= \sum _{j=1}^p \beta _j \; (I-\alpha _j \; \Delta t L)^{-1}, \end{aligned}$$

(9)

where $\beta _j$ and $\alpha _j >0$, $j=1, \ldots ,p$, are free real parameters with $\alpha _j$ distinct between them, and $\beta _j$ uniquely determined by the condition $T_p = I + \mathcal {O} ( \Delta t^p)$. Here the free parameters $\alpha _j$ have been selected to improve the linear stability properties of an explicit RK scheme with order p for the scaled equation Eq. (2).

Even though TASE operators are very recent, they have already been considered in a number of related papers ([12,13,14]) which encourages us to advance in this research.

Note that, in the TASE operators of types described by Eqs. (8) and (9), each $T_p$ evaluation involves the inversion of the p linear operators $( I - \Delta t \; \alpha _j \; L)$, $j=1, \ldots ,p$, for given positive $\alpha _j$. In fact, for an s–stage explicit RK scheme defined by the Butcher tableau [15]

$$\begin{aligned} \begin{array}{c|ccccc} 0 &{} &{} &{} &{} &{} \\ c_2 &{} a_{21} &{} &{} &{} &{} \\ \vdots &{} &{} &{} &{} &{} \\ c_s &{} \quad a_{s1} &{} \quad a_{s2} &{} \quad \ldots &{} \quad a_{s,s-1} &{} \\ \hline &{} b_1 &{} \quad b_2 &{} \quad \ldots &{} \quad b_{s-1} &{} \quad b_s \end{array} \qquad c_i = \sum _{j=1}^{i-1} a_{ij}, \quad i= 2, \ldots , s, \end{aligned}$$

the numerical solution of Eq. (2) is advanced from $(t_n, U_n) \rightarrow (t_{n+1}= t_n + \Delta t, U_{n+1})$ by the formulas

$$\begin{aligned} U_{n+1} = U_n + \Delta t \left[ b_1 \; K_1 + \cdots + b_s \; K_s \right] , \end{aligned}$$

(10)

where $K_j$, $j=1, \ldots ,s$ are computed recursively from the formulas

$$\begin{aligned} \begin{array}{l} F_1= F(t_n, U_n),\\ K_1 = T \; F_1 = \sum _{j=1}^p \beta _j \; ( I - \alpha _j \; \Delta t \; L)^{-1} \; F_1,\\ F_2 = F \left( t_n+ c_2 \Delta t, U_n+ \Delta t \; a_{21} K_1 \right) , \\ K_2 = T \; F_2 = \sum _{j=1}^p \beta _j \; ( I - \alpha _j \; \Delta t \; L)^{-1} \; F_2, \\ \qquad \vdots \\ F_s = F \left( t_n+ c_s \Delta t, U_n+ \Delta t \; \sum _{k=1}^{s-1} a_{s k} K_k \right) , \\ K_s = T \; F_s = \sum _{j=1}^p \beta _j \; ( I - \alpha _j \; \Delta t \; L)^{-1} \; F_s. \end{array} \end{aligned}$$

(11)

The explicit scheme defined by the Eqs. (10), (11), will be called a RKTASE scheme with s stages and order p. Now the computational cost is the s evaluations of the vector field in Eq. (11) and the computation of the $p \times s$ matrix operations

$$\begin{aligned} ( I - \alpha _j \; \Delta t \; L )^{-1} \; F_k, \quad j=1, \ldots , p, \quad k=1, \ldots , s. \end{aligned}$$

Note that these operations do not require the computation of the inverse of the matrices, because as usual they can be done by solving the associated linear systems.

The aim of this paper is to study a new family of RK TASE schemes associated to TASE operators given by

$$\begin{aligned} T = ST_p( \Delta t \; L) = \sum _{j=1}^p \beta _{pj} \; ( I - \Delta t \; \alpha \; L)^{-j}, \quad \alpha >0, \end{aligned}$$

(12)

where $\alpha >0$ and $\beta _{p,j}$, $j=1, \ldots ,p$ are real parameters. It will be seen that $\beta _{pj}$, $j=1, \ldots ,p$ are uniquely determined as functions of $\alpha$ by the condition that $ST_p( \Delta t \; L ) = I + \mathcal {O} ( \Delta t^p)$. Note that this family is not a subclass of the family (9) because that family dependes on the operator $(I - \Delta t \; \alpha _j \; L)^{-1}$ with the power $-1$ whereas in the proposed family the operator $(I-\Delta t \; \alpha \; L)^{-j}$, with power $-j$ is used.

The reason of the choice (12) is that the calculation of the stabilized stages $ST_p \; F_k$ requires a matrix operation with only the powers of the inverse of one matrix $( I - \Delta t \; \alpha \; L)$. Moreover it will be seen that with a suitable choice of the free parameter $\alpha >0$ the linear stability properties are similar to the RK TASE schemes with the TASE operator (9). Clearly, these operators require the solution of s linear systems all of them with the same matrix $(I-\Delta t \;\alpha \; L)$, similarly to the case of Singly Implicit RK methods [16, 17] and the Singly Diagonally RK methods [18, 19] when simplified Newton is used to solve the implicit stage equations. For this reason, the TASE operators (12) will be called Singly–TASE operators hereafter. Moreover, for high dimensional ODEs that arise in the spatial semidiscretization of some PDEs, the techniques used in their numerical solution must take into account not only the accuracy and stability properties and it may be convenient to use low–storage RK schemes [20, 21]. Then we will consider the use of the schemes that combine 2N–storage RK schemes where N is the dimension of the system of ODEs, with Singly TASE operators.

The outline of this paper is as follows. In Sect. 2, we propose a new family of TASE operators of order p that requires the computation of p linear systems with the same matrix of coefficients. They depend on one free parameter $d=\alpha ^{-1}$ that can be optimized to adjust the stability properties of the resulting Singly–RKTASE scheme. In Sect. 3, the stability of two-stage Singly–RKTASE schemes with order two is studied, and the necessary and sufficient conditions on the free parameter d for A-stability and strong A-stability are obtained; In Sect. 4, the stability of three-stage Singly–RKTASE schemes with order three is considered. It is observed that there are no A-stable schemes, but there exist $A(\theta )$-stable schemes with $\theta = 89.05$ degrees and also strongly $A(\theta )$-stable schemes with $\theta = 88.99$ degrees; Sect. 5 deals with the case of four-stage schemes with order four. It is noticed that no scheme of this class can be A-stable, but there are $A(\theta )$-stable and strongly $A(\theta )$-stable schemes with $\theta = 87.18$ and $\theta = 87.17$ degrees, respectively. Finally, in Sect. 5, we present the results of some numerical experiments with selected stiff benchmark problems, comparing the new schemes with previous RKTASE schemes and also with Rosenbrock and Singly Diagonally Implicit RK (SDIRK) methods.

2 Singly–RKTASE Schemes

To simplify some expressions, Eq. (12) will be written in the equivalent form

$$\begin{aligned} T = ST_p ( \Delta t \; L ) = \sum _{j=1}^p b_{pj} \; \left( d \; I - \Delta t \; L \right) ^{-j}, \end{aligned}$$

(13)

where $d = \alpha ^{-1} >0$, and $b_{pj} = \beta _{pj} \; \alpha ^{-j}$, $j=1, \ldots ,p$.

First of all, we determine the coefficients $b_{pj}$ of Eq. (13) so that $ST_p$ has order $( \Delta t)^p$, i.e.,

$$\begin{aligned} ST_p(\Delta t L) = I + Q_p \; ( \Delta t)^p \; L^p + \mathcal {O}( \Delta t^{p+1}). \end{aligned}$$

This is equivalent to say that the scalar function $ST_p (z)$, defined as

$$\begin{aligned} ST_p (z) = \sum _{j=1}^p b_{pj} \; ( d- z)^{-j}, \end{aligned}$$

(14)

should be of order $z^p$, i.e.,

$$\begin{aligned} ST_p (z) = 1 + Q_p z^p + \mathcal {O} ( z^{p+1}), \qquad z \rightarrow 0. \end{aligned}$$

Then such a requirement leads to the non-singular linear system of p equations with regard to p unknowns $b_{pj}$, $j=1, \ldots ,p$, that are

$$\begin{aligned} \sum _{j=1}^p b_{pj} d^{-j}=1, \quad \sum _{j=1}^p b_{pj} d^{-j} \left( {\begin{array}{c}j+k-1\\ k\end{array}}\right) =0, \quad k=1,\ldots ,p-1. \end{aligned}$$

It has the unique solution

$$\begin{aligned} b_{p,j} = \left( \begin{array}{c} p \\ p-j \end{array} \right) \; d^j \; (-1)^{-1+j}, \quad j=1, \ldots ,p. \end{aligned}$$

(15)

Furthermore, the error coefficient $Q_p$ of the Singly–TASE operator Eq. (14) with the coefficients Eq. (15) satisfies

$$\begin{aligned} Q_p = \dfrac{(-1)^{p+1}}{d^p \; p!}. \end{aligned}$$

Also in view of Eq. (15), the function Eq. (14) can be written in the compact form

$$\begin{aligned} ST_p (z) = \dfrac{(z-d)^p - z^p}{(z-d)^p }. \end{aligned}$$

(16)

In particular for $p=2,3,4$, the coefficients $b_{pj}$ have the values

$$\begin{aligned} \begin{array}{llll} b_{21}= 2 d, &{} b_{22} = - d^2, \\ b_{31}= 3 d, &{} b_{32} = - 3 d^2, &{} b_{33} = d^3, \\ b_{41}= 4 d, &{} b_{42} = - 6 d^2, &{} b_{43} = 4 d^3, &{} b_{44} = - d^4. \end{array} \end{aligned}$$

Next, we study the linear stability properties of an explicit s–stage RK scheme of order p combined with a singly TASE operator of the same order. When applied to the scalar test equation $y' = \lambda y$ with $\lambda \in \mathbb {C}$, the modified equation becomes

$$\begin{aligned} u' = ST_p ( \Delta t \; \lambda ) \; \lambda \; u, \end{aligned}$$

and therefore if

$$\begin{aligned} R_s(z) = 1 + z + \cdots +\dfrac{z^p}{p!}+ a_{p+1} \; \dfrac{z^{p+1}}{(p+1)!} + \cdots + a_s \; \dfrac{z^s}{s!} \end{aligned}$$

is the stability function of the explicit s–stage RK scheme with some real coefficients $a_j$, the stability function of the stabilized scheme RST(z) will be

$$\begin{aligned} RST (z; d ) = R_s \left( z \; ST_p(z) \right) =\sum _{j=1}^p \dfrac{1}{j!} \; \left[ z \; ST_p(z) \right] ^j + \sum _{j=p+1}^s \dfrac{a_j}{j!}\; \left[ z \; ST_p(z) \right] ^j. \end{aligned}$$

Recall the following stability properties:

• A method is called A-stable if $\vert RST( z)\vert \le 1$ for all Re $z\le 0$;

• A method is said to be L–stable if it is A–stable and $\vert RST(\infty )\vert =0$;

• A method is called Strongly A–stable if it is A–stable and $\vert RST(\infty )\vert = \mu <1$;

• A method is called A$(\theta )$–stable if $\vert RST(z)\vert <1$ for all z such that $\arg (-z) \le \theta$, that is, its stability region contains the left hand region of the complex plane with angle $\theta$. If in addition $RST(\infty )=0$ (resp. $\vert RST(\infty )\vert < 1$), it is called L$(\theta )$–stable (resp. Strongly A$(\theta )$–stable).

We first derive a necessary condition for A–stability. Since

$$\begin{aligned} \lim _{z \rightarrow \infty } z \; ST_p (z) = b_{p1} = - p \; d, \end{aligned}$$

then

$$\begin{aligned} RST_s ( \infty ; d ) = \lim _{z \rightarrow \infty } RST_s (z) = R_s ( -p \; d), \end{aligned}$$

and therefore for given values of $s \ge p$, a necessary condition for A–stability is that the available positive parameter d satisfies

$$\begin{aligned} \vert R_s ( - p \; d ) \vert \le 1. \end{aligned}$$

(17)

A sufficient condition for A–stability can be derived from the application of the modulus maximum theorem to $RST_s (z)$ along the imaginary axis $z = i \; y$. In fact, it follows from Eq. (16) that $RST_s(z)$ has the form

$$\begin{aligned} RST_s (z; d ) = R_s(zT_s)=\dfrac{\pi _{2s}(z)}{(z-d)^{2s}}, \end{aligned}$$

where the numerator $\pi _{2s}(z)$ is a polynomial in z of degree $\le 2\,s$ with coefficients depending polynomially on d. Now,

$$\begin{aligned} \left| RST_s ( i \; y; d ) \right| ^2 = \dfrac{\vert \pi _{2s} ( i \; y)^2 \vert }{(y^2+ d^2)^{2s}} \end{aligned}$$

is an even function of y and taking into account that the scheme has order p

$$\begin{aligned} \left| RST_s ( i \; y ) \right| ^2 - 1 = \dfrac{\mu _{2p} \; y^{2p} + \mu _{2p+2} \; y^{2p+2} + \cdots + \mu _{4s} \; y^{4s}}{(y^2 + d^2 )^{2s}}, \end{aligned}$$

(18)

with $\mu _j$ polynomial functions of d.

Clearly, a necessary and sufficient condition for A–stability is that the numerator of Eq. (18) should be $\le 0$ for all $y^2 >0$, or else that the polynomial

$$\begin{aligned} P_s (u) = \mu _{2p} + \mu _{2p+2} \; u + \cdots + \mu _{4s} \; u^{2s-p-1} \le 0, \end{aligned}$$

(19)

for all $u >0$. In general, this condition becomes too complicated to be checked, but there is a necessary condition that can be easily checked, for example that $\mu _{2p} \le 0$.

3 Second Order Singly–RKTASE Schemes

We need at least a two–stage RK scheme with order two combined with a second-order Singly–TASE operator. Next we study the linear stability properties of this scheme.

The stability function of a two–stage RK scheme with order two is

$$\begin{aligned} R_2 (z) = 1 + z + \dfrac{z^2}{2}, \end{aligned}$$

and it can be seen that $\vert R_2 (z) \vert \le 1$ if and only if $z \in [-2,0]$. Further the minimum value of $R_2(z)$ in the interval $[-2,0]$ is attained at $z= -1$ with $R_2(-1) = 1/2$. The first necessary condition for A–stability (17) holds if and only if $d \in (0,1].$

Next, we investigate whether or not this condition is also sufficient. We consider the polynomial Eq. (19) with $s=p=2$ that is

$$\begin{aligned} P_2 (u) = \mu _4 + \mu _6 u + \mu _8 u^2, \end{aligned}$$

with

$$\begin{aligned} \mu _4 = d^5 (d^3-16), \ \mu _6 =8 d^6 - 8 d^5-32 d^3, \ \mu _8 = 16 d^4- 32 d^3+ 32 d^2 -16 d. \end{aligned}$$

Since $\mu _4 < 0$, $\mu _6 <0$ and $\mu _8 \le 0$ for all $d \in (0,1]$, for all $d \in (0,1]$ all second order Singly RK schemes with $s=2$ are A–stable. Moreover for all $d \in (0,1)$, $\vert RST_2 ( \infty ) \vert < 1$ and the schemes are strongly A–stable. In particular $\min \vert RST_2 ( \infty ) \vert =1/2$ is attained for $d=1/2$ and therefore there are no L–stable second order Singly RK schemes with two stages.

If we want to have L–stable second order Singly RK schemes we must consider second order RK schemes with $s=3$ three stages. Now the stability polynomial will be

$$\begin{aligned} R_3(z)= 1 + z + \dfrac{z^2 }{2!} + a_3 \; \dfrac{z^3}{3!}, \end{aligned}$$

(20)

and the condition

$$\begin{aligned} \lim _{z \rightarrow \infty } R_3 ( ST_2 (z) \; z ) = 0 \end{aligned}$$

is satisfied if and only if

$$\begin{aligned} a_3 = \dfrac{3(1- 2 d + 2 d^2)}{4 d^3}. \end{aligned}$$

(21)

A numerical study of the conditions (18) and (19) leads to conclude that $\vert T ST_2 (i y) \vert \le 1$ for all $y \in \mathbb {R}$ iff $d \in (0.2625\ldots ,1.915\ldots )$. In conclusion we may state the following

Theorem 1

• (1) A Singly–RKTASE scheme of order two with two stages is A–stable if and only if the parameter d satisfies $d \in (0,1] \ (\alpha \ge 1).$

• (2) For all $d \in (0,1)$ the Singly–RKTASE schemes are strongly A–stable. The $\min \vert RST ( \infty )\vert =1/2$ is attained for $d=1/2$.

• (3) There exist L–stable Singly –RKTASE schemes of second order and three stages with stability function given by (20) with (21) for all $d \in ( 0.2625\ldots ,1.915\ldots )$.

In the right plot of Fig. 1, we display (solid line) the boundary of the stability region of the Singly–RKTASE $RT_2$ for $d=1$ as well as (dashed line) that of the Singly–RKTASE scheme with $d=1/2$. A remarkable fact is that the stability regions are not connected. In fact, apart from the component that includes the negative complex plane, they have a small component in the positive complex semi–plane. For comparison purposes, we plot also in the left plot of Fig. 1 the boundary of the stability regions of the RKTASE schemes proposed in [8, 11].

In addition to the plots, we include in the Figure two tables with the error coefficient $Q_2$ and the stability angle $\theta$ that, since all the schemes are A–stable, is 90 degrees.

Fig. 1

Boundary of the stability region of A–stable second-order TASE schemes Left: RKTASE, Right: Singly–RKTASE. Solid lines correspond to the schemes for which $RT_2(\infty )=1$ and dashed lines to the schemes for which $RT_2(\infty )=1/2$ is minimum

In view of the Tables displayed in Fig. 1 it can be seen that the RKTASE schemes, in spite of having been selected within a family with two free parameters $\alpha _1$ and $\alpha _2$, have larger error constants than those of the Singly–RKTASE schemes, for which there is only one free parameter $\alpha =1/d$. Finally, it is worth to remark that (see [10]) there exist a one–parameter family of two–stage RK schemes with order two, and each scheme of this family supplemented with Singly TASE $ST_2$ leads to Singly–RKTASE with the same linear stability properties.

4 Third Order Singly–RKTASE Schemes

We will consider three–stage third order RK schemes. The third-order Singly TASE operator is defined by

$$\begin{aligned} ST_3 (z)= \dfrac{3 d}{(d-z)}+ \dfrac{- 3 d^2}{(d-z)^2}+ \dfrac{d^3}{(d-z)^3}= \dfrac{(z-d)^3 - z^3}{(z-d)^3} \end{aligned}$$

and taking into account that the stability function of a three-stage RK scheme with order three is

$$\begin{aligned} R_3 (z) = 1 + z + \dfrac{z^2}{2!}+ \dfrac{z^3}{3!}, \end{aligned}$$

(22)

the stability function of the third-order RKTASE is

$$\begin{aligned} RST_3 (z; d) = 1 + (z\; T_3(z)) + \dfrac{(z\; T_3(z))^2}{2!}+ \dfrac{(z\; T_3(z))^3}{3!}. \end{aligned}$$

Recalling that $R_3(z)$ given by Eq. (22) satisfies $\vert R_3(z) \vert \le 1$ if and only if $z \in \left[ z_{sol},0 \right]$ with

$$\begin{aligned} z_{sol} = -1 - \left( -4 + \sqrt{17} \right) ^{-1/3} + \left( -4 + \sqrt{17} \right) ^{1/3} \simeq -2.51275, \end{aligned}$$

the first necessary condition for A–stability (17) holds iff

$$\begin{aligned} d \in (0, - z_{sol}/3=d_A ]. \end{aligned}$$

(23)

Moreover, since

$$\begin{aligned} \left| RST_3 ( i \; y ) \right| ^2 - 1 = \left( -\dfrac{1}{12} + \dfrac{2}{d^3} \right) y^4 + \mathcal {O}( y^6), \end{aligned}$$

(24)

and for all d that satisfies Eq. (23) the coefficient of $y^4$ in Eq. (24) is positive, all the schemes that satisfy Eq. (23) cannot be A–stable. In fact, the stability region does not contain the imaginary axis around the origin and is nearly A–stable.

On the other hand, since $R_3 (u_L) =0$ for

$$\begin{aligned} u_L = -1 - \left( -1 + \sqrt{2} \right) ^{-1/3} + \left( -1 + \sqrt{2} \right) ^{1/3} \simeq -1.59607, \end{aligned}$$

with $d =d_L = - u_L/3$, $RST_3 ( \infty ; -3 \; d_L )=0$, then $RST_3 ( - 3 d_L) =0$ for $d_L = -u_L/3$ and consequently the corresponding scheme is $L(\theta )$–stable. Hence we conclude:

Theorem 2

• (1) A Singly–RKTASE scheme of order three with three stages cannot be A–stable.

• (2) For $d= d_A$ the three stage Singly–RKTASE is $A(\theta )$– stable with $\theta = 89.05^{\circ }$.

• (3) For $d=d_L$ the three stage Singly–RKTASE is $L(\theta )$ stable with $\theta = 88.99^{\circ }$.

In the right plot of Fig. 2, we display (solid line) the boundary of the stability region of the third-order Singly–RKTASE scheme with $d=d_A$ together with (dashed line) that of the Singly–RKTASE scheme with $d=d_L$ that is nearly L–stable. In the left plot of the Fig. 2 we also display the boundary of the stability regions of the RKTASE schemes of order three proposed in [8, 11]. In addition to the plots, we include in the Fig. 2 two tables with the error coefficient $Q_3$ and the stability angle $\theta$ in degrees.

Fig. 2

Boundary of the stability region of third-order schemes. Left: RKTASE, Right: Singly–RKTASE. Solid lines correspond to the schemes for which $RT_3(\infty )=1$ and dashed lines to the schemes for which $RT_3(\infty )=0$ is minimum

For the third-order schemes, the error coefficients of the Singly–RKTASE schemes are smaller than those of the RKTASE schemes. However, the stability angle (none of them is A-stable) is slightly smaller for the Singly–RKTASE schemes.

To show the behavior of the boundaries around the origin, we present here a zoomed-in view around this point of the boundaries in Fig. 3.

Fig. 3

Zoom of the boundary of the stability region of Singly–RKTASE nearly A–stable third-order schemes. Solid line corresponds to $d=d_A$ for which $RT_3(\infty )=1$ and dashed line to $d=d_L$ for which $RT_3(\infty )=0$

Remark 1

We must remark that (see [10]) there exist a two–parameter family of three–stage RK schemes with order three. All of these schemes possess the same linear stability function R(z). Therefore all the associated Singly RKTASE scheme of order three have the same stability properties that depend only on the parameter d in the $ST_3$ operator. Hence we may select the RK scheme taking into account some additional criteria as accuracy or low storage requirements.

As an example of 2N–storage implementation of a third order RK scheme with three stages supplemented with a Singly TASE $ST_3$, we may consider the RK scheme proposed by Williamson [20] and Carpenter and Kennedy [21] with the Butcher array

where the coefficients have been selected so that they minimize the local truncation error among the three stage RK schemes with order three that can be cast in the 2N–storage implementation of Williamson. Recall that in this implementation the two 2N–storage are $U_j$ and $dU_j$ that are computed by (see [20])

$$\begin{aligned} \left. \begin{array}{ccc} d U_j &{} = A_j \; dU_{j-1} + \Delta t \; ( ST_3) \; F(U_{j-1}) &{} \\ U_j &{} = U_{j-1} + B_j \; dU_j &{} \end{array} \right\} (j=1,2,\ldots ,p) \end{aligned}$$

(25)

with $p=3$, $U_0 = Y_0$, $U_3 = Y_1$ and $A_j$ and $B_j$ given by

$$\begin{aligned} \begin{array}{|c||c|c|c|} \hline A_j &{} 0 &{} -5/9 &{} - 153/128 \\ \hline B_j&{} 1/3 &{} 15/16 &{} 8/15\\ \hline \end{array} \end{aligned}$$

Each successive stage is written onto the same register without zeroing the previous value.

5 Fourth–Order Singly RKTASE

First of all we consider explicit four-stage fourth–order RK schemes supplemented with Singly TASE operators of order four. Following the notations of the previous sections, we have

$$\begin{aligned} ST_4(z)=\dfrac{(z-d)^4 - z^4}{(z-d)^4}, \ R_4(z) = \sum _{j=0}^4 \dfrac{z^j}{j!}, \ RST_4(z; d ) =\sum _{j=0}^4 \dfrac{( z T_4(z))^j}{j!}. \end{aligned}$$

(26)

Taking into account that

$$\begin{aligned} \vert R_4 (z) \vert \le 1 \quad \Leftrightarrow \quad z \in [ \gamma _4, 0], \end{aligned}$$

where $\gamma$ is the real stability abscissae of $R_4(z)$, given by

$$\begin{aligned} \gamma _4 = \dfrac{1}{3} \left[ -4 - 10 \; 2^{1/3} \; ( -43 + 9 \sqrt{29})^{-1/3} + 2^{2/3} \; ( -43 + 9 \sqrt{29})^{1/3} \right] \simeq - 2.78529, \end{aligned}$$

the necessary condition of A–stability derived from $\vert \ RST_4 ( \infty ; d ) \vert \le 1$ is $d \in (0, d_A = - \gamma _4/4].$

On the other hand, since

$$\begin{aligned} \min \left\{ RST_4 (\infty ; d) ; \; d \in (0, - \gamma _4/4] \right\} = 0.270395, \end{aligned}$$

that is attained at

$$\begin{aligned} z = z_{min} = -1 - ( -1 + \sqrt{2})^{-1/3} + ( -1 + \sqrt{2})^{1/3} \simeq - 1.59607. \end{aligned}$$

The optimal strong A–stability scheme will be for

$$\begin{aligned} d = d_L = - \dfrac{z_{min}}{4}. \end{aligned}$$

Concerning the second necessary condition for A–stability, we have

$$\begin{aligned} \left| RST_4 ( i \; y; d ) \right| ^2 - 1 = \left( - \dfrac{1}{72} + \dfrac{8}{d^5} \right) y^6 + \mathcal {O} ( y^8 ), \end{aligned}$$

(27)

and taking into account that the coefficient of $y^6$ in Eq. (27) is non negative for all $d \in (0, - \gamma _4/4]$, all schemes that satisfy this condition are not A–stable. In fact, small values of $z= i y$ near the origin in the imaginary axis are not contained in the stability region of the scheme, and we conclude:

Theorem 3

• (1) A Singly–RKTASE scheme of order four with four stages can not be A–stable.

• (2) For $d \in (0, - \gamma _4/4]$ the Singly–RKTASE is $A( \theta )$ stable. In particular for $d = - \gamma /4$ is $A ( 87.8^\circ )$–stable.

• (3) For $d \in (0, - \gamma _4/4)$ the Singly-RKTASE is strongly stable. The $\min \vert RST_4( \infty ; d )\vert = 0.270395$ is attained for $d=d_L$.

In the right plot of Fig. 4, we display (solid line) the boundary of the stability region of the fourth-order Singly–RKTASE for $d=d_A = - \gamma _4/4$ together with (dashed line) that of the Singly–RKTASE scheme with $d=d_L$ that is nearly strongly A–stable. In the left plot of the Fig.  4, we display the boundary of the stability regions of the schemes of order four proposed in [8, 11].

In addition to the plots, we include in the Fig. 4 two Tables with the error coefficients $Q_4$ and the stability angles $\theta$ in degrees. It can be seen in the Tables that the properties of Singly–RKTASE schemes are very similar to those of RKTASE schemes.

Fig. 4

Boundary of the stability region of RKTASE (left plot) and Singly–RKTASE (right plot) fourth-order schemes. Solid lines correspond to the schemes for which $RT_4(\infty )=1$ and dashed lines to the schemes for which $RT_4(\infty )=0.270395$ is minimum

To show the behavior of the boundaries around the origin, we present here a zoomed-in view around this point of the boundaries in Fig. 5.

Fig. 5

Zoom of the boundary of the stability region of Singly–RKTASE nearly A–stable fourth-order schemes. Solid line corresponds to $d=d_A$ for which $RT_4(\infty )=1$ and dashed line to $d=d_L$ for which $RT_4(\infty )=0.270395$

One may wonder whether or not the consideration of RK schemes with five stages and order four would make possible to have L–stable schemes. For a five–stage fourth–order RK scheme the stability function is

$$\begin{aligned} R_5 (z) = \sum _{j=0}^{4} \dfrac{z^j}{j!}+ \nu \dfrac{z^5}{5!}, \end{aligned}$$

with some constant $\nu \ne 0$. Then a necessary condition for L–stability is

$$\begin{aligned} \lim _{z \rightarrow \infty } R_5 \Big ( z \; ST_4(z) \Big ) = \dfrac{1}{120} (120 - 480 d + 960 d^2 - 1280 d^3 + 1280 d^4 - 1024 d^5 \nu ) =0 \end{aligned}$$

and a numerical study shows that this condition is not compatible with

$$\begin{aligned} \left| R_5 \Big ( i y \; ST_4(i y ) \Big ) \right| \le \quad \hbox {for all} \quad y \in \mathbb {R}. \end{aligned}$$

Remark 2

It can be seen (see [10], page 135) that there exist several families of four–stage fourth–order RK schemes depending on one or two parameters. All these schemes have the same linear stability function R(z). Clearly each of these schemes combined with the Singly TASE $ST_4$ gives a Singly RKTASE with order four whose stability properties depend only on the parameter d. Hence we may select the RK scheme taking into account some additional criteria as accuracy or low storage requirements. We can for example take a four stages fourth order low-storage Runge Kutta scheme (see e.g. [22]) or else the classical RK of order four and combine it with the Singly TASE operator $ST_4$ and apply it to stiff problems.

6 The Implementation of Singly RKTASE Schemes

In this section we examine the main issues in the implementation of a Singly RKTASE scheme for the numerical solution of stiff IVPs (1). We will consider the case of four stages, $s=4$, but the generalization to any other s is straightforward. For the Singly TASE operator $ST_4= ST_4( \Delta t \; L)$ (26) we will take either $d = -\gamma _4/4$ ($A(\theta = 87.18^\circ )$–stable) with $RST_4 ( \infty ; d_A) = 1$ or else $d= d_L$ ( strongly $A( \theta = 87.17^\circ )$–stable) with $RST_4 ( \infty ; d_L) = 0.270395$.

A first point is the choice of the linear operator L in $ST_4$. If the original IVP (1) is linear $F(t,Y) = M(t) \; Y + g(t)$, the safest option is to take at the step from $t_n$ to $t_n+\Delta t$, $L = M(t_n)$. In the non linear case we could take $L = \partial _Y F(t_n, Y_n)$. However, the order of the scheme is not reduced if L is not the exact Jacobian, so we can take an approximation instead whenever the stability of the numerical solution is maintained. Something similar happens with implicit Runge–Kutta methods, where the Jacobian matrix is often frizzed for several steps unless the iterative scheme used has som problems to converge. Thus, to reduce the computational effort, we can freeze the Jacobian for several steps (even the whole integration), or even take an approximation to it that makes the solution of the linear systems cheaper.

A second point is the computation of the scaled stages (11)

$$\begin{aligned} K_k = ( ST_4) \; F_k, \quad k=1, \ldots ,4. \end{aligned}$$

(28)

Taking into account that

$$\begin{aligned} ST_4 = \sum _{j=1}^4 \beta _{4j} \; ( d \; I - \; \Delta t \; L)^{-j} \equiv \sum _{j=1}^4 \beta _{4j} \; W^{-j}, \end{aligned}$$

(29)

with

$$\begin{aligned} \beta _{41}=4, \quad \beta _{42}= -6, \quad \beta _{43}= 4, \quad \beta _{44}=-1, \quad W= ( d I - \Delta t \; L) \end{aligned}$$

(30)

we compute (28) by using a Horner type algorithm because due to (29), $K_k$ can be written in the form

$$\begin{aligned} \left( \left( \left( - W^{-1} + 4 \right) W^{-1} -6 \right) W^{-1} + 4 \right) W^{-1} \; F_k. \end{aligned}$$

And therefore given $F_k$ computed by (11) and $W = dI-\; \Delta t \; L$, the scaled stage $K_k$ of (28) can be computed by the recurrence

The implementation of the complete RKTASE integrator is very simple. We can take the implementation of the explicit Runge–Kutta scheme (of order four in this case) and add the above algorithm just after each evaluation of the vector field. With this, the integrator can be used to solve stiff problems.

7 Numerical Experiments

In this section, some numerical experiments are presented to confirm the theoretical analyses in the above sections and to compare the performance of our proposed Singly–RKTASE methods with that of the methods in [8] and [11]. Specifically, we will consider the following fourth-order RKTASE and Singly–RKTASE methods based on the classical RK scheme of fourth-order given by the Butcher array

$$\begin{aligned} \begin{array}{c|cccc} 0 &{} &{} &{} &{} \\ 1/2 &{} 1/2 &{} &{} &{} \\ 1/2 &{} 0 &{} 1/2 &{} &{} \\ 1 &{} 0 &{} 0 &{} 1 &{} \\ \hline &{} 1/6 &{} 1/3 &{} 1/3 &{} 1/6 \end{array} \end{aligned}$$

and the following TASE operators:

TASE-A:

(not strongly) A$(\theta )$–stable, $\theta =88.36$, for which $\vert RT_4(\infty )\vert =1$ [8] and the parameters are given as

$$\begin{aligned} \begin{array}{ll} \alpha = 5.38542873795360379398, &{} b_1=-1/21, \\ \alpha _2= \alpha _1/2, &{} b_2= 2/3, \\ \alpha _3= \alpha _1/4, &{} b_3= -8/3, \\ \alpha _4= \alpha _1/8, &{} b_4= 64/21. \end{array} \end{aligned}$$

TASE-S:

Strongly A$(\theta )$–stable, with minimum value $\vert RT_4(\infty )\vert =0.270395$ [11] and the parameters are given as

$$\begin{aligned} \begin{array}{ll} \alpha _1 = 3.939556, &{} b_1 = -2.3487740262789467740, \\ \alpha _2 = 2.450558, &{} b_2 = 139.59763724183703275, \\ \alpha _3 = 2.227083, &{} b_3 = -313.52837746665272729, \\ \alpha _4 = 2.061235, &{} b_4 = 177.27951425109464132. \\ \end{array} \end{aligned}$$

STASE-A:

(not strongly) A$(\theta )$–stable Singly–RKTASE, $\theta =87.18$, for which $\vert RT_4(\infty )\vert =1$ and the parameters are given as

$$\begin{aligned} \begin{array}{l} \gamma _4=-2.7852935634052827,\\ \alpha = -4/\gamma _4=1.4361143301209602, \\ b_1=4, \quad b_2=-6, \quad b_3=4, \quad b_4= -1. \end{array} \end{aligned}$$

STASE-S:

Strongly A$(\theta )$–stable, with minimum value $\vert RT_4(\infty )\vert =0.270395$ and the parameters are given as

$$\begin{aligned} \begin{array}{l} z_{min}=-1.5960716379833215, \\ \alpha = -4/z_{min}=2.5061531730831987, \\ b_1=4, \quad b_2=-6, \quad b_3=4, \quad b_4= -1. \end{array} \end{aligned}$$

We want also to compare the proposed methods with some Rosenbrock methods [23], which have a structure similar to RKTASE schemes, and with the SDIRK methods [18, 19]. More specifically, the following methods will be used.

SDIRK-A:

Fourth-order, three-stage, SDIRK A-stable scheme (see Hairer et al. [9]) defined by the Butcher array

SDIRK-L:

Fourth-order, five-stage, SDIRK L-stable scheme (see Hairer et al. [9]) defined by the Butcher array

ROS-L:

Fourth-order, four-stage, L-stable Rosenbrock method (see Hairer et al. [9]) defined by the equations

$$\begin{aligned} \begin{array}{ll} \left( \dfrac{1}{h\gamma }I - f_y(t_0,y_0)\right) ^{-1} u_i \\ \qquad \qquad = f\left( t_0+\alpha _i h, y_0 +\displaystyle \sum _{j=1}^{i-1} a_{ij} u_j\right) + \displaystyle \sum _{j=1}^{i-1} \dfrac{c_{ij}}{h} u_j + h \gamma _i f_t(t_0,y_0), \quad i=1, \ldots , 5, \\ y_1= y_0 + \sum _{j=1}^{s} m_j u_j. \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} a_{21}= 2 &{} c_{21}=-7.13761503641231, \\ a_{31}= 1.867943637803922 &{} c_{31}= 2.580708087951457,\\ a_{32}= 0.2344449711399156 &{} c_{32}= 0.6515950076447975,\\ \alpha _2=1.14564 &{} c_{41}=-2.137148994382534,\\ \alpha _3=0.655216863815590 &{} c_{42}=-0.3214669691237626,\\ \gamma = 0.57282 &{} c_{43}=-0.6949742501781779,\\ \gamma _1=\gamma &{} m_1= 2.255570073418735,\\ \gamma _2=-1.769193891319234 &{} m_2= 0.2870493262186792,\\ \gamma _3=0.759263343792048 &{} m_3= 0.4353179431840180,\\ \gamma _4=-0.104902108710045 &{} m_4= 1.093502252409163.\\ \end{array} \end{aligned}$$

With these methods, we will integrate the following four stiff differential problems, with which two of them are linear while the other two are non-linear.

• Problem 1 (linear) The 1D diffusion of a scalar function $y=y(x, t)$, with a time dependent source term (taken from [8] and [11])

  $$\begin{aligned} \dfrac{\partial y}{\partial t}=\dfrac{\partial ^2 y}{\partial x^2} + A \sin (t/\tau _s), \qquad \tau _s=50, \quad A=1/10. \end{aligned}$$

  The solution $y=y(x,t)$ is assumed to be $2\pi$-periodic in x. As the initial condition, we have taken

  $$\begin{aligned} y(x,0)= 1 -\cos (x)^{101}. \end{aligned}$$

  For the spatial discretization, we have used fourth-order centered difference schemes with a grid resolution of $N=512$ ($\Delta x = 2\pi /512$) and periodic conditions are assumed at the two domain boundaries. The real part of the eigenvalues of the Jacobian matrix of the semi-discrete problem ranges from $-3.5\times 10^{4}$ to $2.79\times 10^{-5}$.

• Problem 2 (linear) The two-species advection–diffusion–reaction problem in the bounded domain of $0\le x \le 1$ is taken from [8] as

  $$\begin{aligned} \begin{array}{l} \dfrac{\partial y_1}{\partial t} + U\dfrac{\partial y_1}{\partial x}=\dfrac{\partial ^2 y_1}{\partial x^2} + K (y_2 - y_1), \\ \dfrac{\partial y_2}{\partial t} + U\dfrac{\partial y_2}{\partial x}=\dfrac{\partial ^2 y_2}{\partial x^2} - K (y_2 - y_1), \end{array} \end{aligned}$$

  with $K= 10^4$, $D= 10^2$, and $U=10^2$. Two different initial and boundary conditions have been considered as

  • (i)
    $$\begin{aligned} \begin{array}{l} y_1(x,0)= x, \quad y_2(x,0)= x^2, \\ y_1(0,t)=y_2(0,t)=0,\\ y_1(1,t)=y_2(1,t)=1. \end{array} \end{aligned}$$
  • (ii)
    $$\begin{aligned} \begin{array}{l} y_1(x,0)= x, \quad y_2(x,0)= 0.1 x^2, \\ y_1(0,t)=y_2(0,t)=0, \\ y_1(1,t)=1, \quad y_2(1,t)=1/10. \end{array} \end{aligned}$$

  Dirichlet condition is assumed at the two boundaries, and for the spatial discretization, we used fourth-order centered difference schemes in $x\in [0,1]$, with a grid resolution of $N=256$ ($\Delta x = 1/256$). The real part of the eigenvalues of the Jacobian matrix of the semi-discrete problem ranges from $-3.5\times 10^{7}$ to $1.4\times 10^{-9}$ in both cases, suggesting that the problem is highly stiff.

• Problem 3 (non-linear) The 1D Burgers’ equation can be written in the conservative form as

  $$\begin{aligned} \dfrac{\partial y}{\partial t}=\varepsilon \dfrac{\partial ^2 y}{\partial x^2} - \dfrac{\partial }{\partial x}\left( \dfrac{y}{2} \right) ^2, \end{aligned}$$

  where $\varepsilon >0$ denotes the constant viscosity coefficient. The initial condition y(x, 0) is given as

  $$\begin{aligned} y(x,0)= 1 -\cos (x)^{101}. \end{aligned}$$

  The solution is $2\pi$-periodic, and we have solved this problem on a spatial grid of $0 \le x \le 2\pi$ using fourth-order centered difference schemes with a grid resolution of $N=512$ ($\Delta x = 2\pi /512$). Periodic conditions will be used for both boundaries. The real part of the eigenvalues of the Jacobian matrix of the semi-discrete problem ranges from $-3.5\times 10^{3}$ to $2.6\times 10^{-6}$, indicating that the problem is mildly stiff.

• Problem 4 (non-linear) This non-linear problem is taken from [8] with the governing equation as

  $$\begin{aligned} \dfrac{\partial y}{\partial t}=\dfrac{\partial }{\partial x} \left( \Big (\dfrac{y }{2}\Big )^\beta \dfrac{\partial y}{\partial x}\right) ,\qquad y(x,0)=1+e^{-x^2/4}, \qquad x\in [-5,5], \end{aligned}$$

  where $\beta$ is a positive constant. For the spatial discretization, we have used fourth-order centered difference schemes with a grid resolution of $N=512$ ($\Delta x = 2\pi /512$). Neumann conditions, i.e., $\partial y/\partial x \vert _{x=-5}=2.5 e^{-25/4}$ and $\partial y/\partial x \vert _{x=5}=-2.5 e^{-25/4}$, are assumed at the left and right domain boundaries, respectively. The real part of the eigenvalues of the Jacobian matrix of the semi-discrete problem ranges from $-1.38\times 10^{4}$ to $6.41\times 10^{-6}$.

With respect to the implementation of TASE operators, for the linear problems 1 and 2 we have taken as operator L the Jacobian matrix of the vector field F(t, Y). Since in both cases this matrix is constant it was computed just once at the first time-step.

For the nonlinear problem 4 we have taken as operator L the Jacobian matrix of the vector field F(t, Y), computed by standard finite difference schemes and it has been re-evaluated at each time-step.

For problem 3 we have taken as operator L the Jacobian matrix of only the diffusion term, which is not the Jacobian matrix of the full vector field at any point $(t_n, Y_n)$. In this way, the matrix L is constant and need to be computed only at the first step of the integration. This has been also used in the implementation of Rosenbrock and SDIRK methods to save computational effort.

In all the cases, the corresponding linear systems were solved by factorizing the matrix in the LU form.

For the solution of the non-linear systems that appear in SDIRK methods, we used a simplified Newton method, iterated until the norm of the difference between two consecutive approximations was smaller than the threshold of $10^{-9}$.

7.1 Results

Regarding the comparison between Singly–RKTASE and previous RKTASE schemes, in all the cases, all the considered methods behave very similarly with respect to accuracy as well as stability. The only relevant difference is that the new Singly–RKTASE schemes required, as expected, a lower computational cost than the standard RKTASE methods.

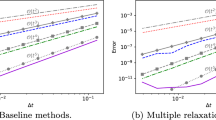
For the highly stiff problems (i.e., problems 1 and 2), strongly $A(\theta )$-stable methods present a better convergence behavior for large time step sizes (see Figs. 6, 7 8, 9). For mildly stiff problems (problems 3 and 4), the Singly–RKTASE and RKTASE methods with $\vert R(\infty )\vert =1$ present a slightly better convergence behavior (smaller global error), due to their smaller error coefficients (see Figs. 11, 12, 13 and 14).

Concerning the computational efficiency, the Singly–RKTASE schemes are clearly more efficient than the standard RKTASE methods, and, moreover, the strongly $A(\theta )$-stable methods are more efficient for highly stiff problems.

Fig. 6

Problem 1. Left plot: approximation to $y(x,t=6)$ given by the methods with time step size $\Delta t = 0.2$. Right plot: approximation to $y(x=0,t)$

Fig. 7

Problem 1. Efficiency plot. Maximum error at $t=6$ (logarithmic scale) versus CPU time in seconds

Fig. 8

Problem 2. Left plot: approximations to $y_1(x,t=0.1)$ with time step size $\Delta t = 0.01$ and initial condition $y_2(x,0)= x^2$. Right plot: approximations to $y_1(x,t=0.1)$ with initial condition $y_2(x,0)=0.1 \, x^2$

Fig. 9

Problem 2. Left plot: approximations to $y_1(x=1/2,t)$ with time step size $\Delta t = 0.01$ and initial condition $y_2(x,0)= x^2$. Right plot: approximation to $y_1(x=1/2,t)$ with initial condition $y_2(x,0)= 0.1 x^2$

Fig. 10

Problem 2. Efficiency plot. Maximum error at $t=0.1$ (logarithmic scale) versus CPU time

Fig. 11

Problem 3. Left plot: approximation to $y(x,t=6)$ given by the methods with time step size $\Delta t = 0.2$. Right plot: approximation to $y(x=0,t)$

Fig. 12

Problem 3. Efficiency plot. Maximum error at $t=6$ (logarithmic scale) versus CPU time in seconds

Fig. 13

Problem 4 ($\beta =4$). Left plot: approximation to $y(x,t=0.6)$ given by the methods with time step size $\Delta t = 0.15$. Right plot: approximation to $y(x=1/2,t)$

Fig. 14

Problem 4 ($\beta =4$). Efficiency plot. Maximum error at $t=0.6$ (logarithmic scale) versus CPU time in seconds

Regarding the comparison with the classical SDIRK and Rosenbrock methods, for the highly stiff problems the strongly stable Singly–RKTASE and RKTASE schemes present efficiency plots (see Fig. 10) comparable to the other methods.

For problem 3, the efficiency of Singly-RKTASE schemes is similar to that of SDIRK methods for large time step sizes. Rosenbrock scheme (see Fig. 12) looses efficiency because it does not use the exact Jacobian matrix and this makes the method to lose order of accuracy. Moreover, for the largest time step size $\Delta t=0.4$, Rosenbrock, TASE-A and STASE-A are not stable enough and the numerical solution becomes very large (Fig. 13).

Rosenbrock and SDIRK methods present better efficiency plots than Singly–RKTASE methods for problems 1 and 4 (see Figs. 7, and 14). The reason is not the lower computational cost of these methods (indeed, the cost is similar for all the methods), but the lower global error given by the integrators. Note that the selected SDIRK and Rosenbrock methods are among the most efficient ones in their families. This encourages us to undertake a further research to find the most efficient combination of the RK schemes and the TASE operators.

Also note that SDIRK schemes require, at each time step, the solution of several non-linear systems by means of some iterative method. It runs the risk that, for a specific problem, the iterative method fails to converge. In general, any implicit method requires at each step the solution of one (or more) non-linear implicit system of equations, and therefore the overall efficiency of the integrator depends strongly on the non-linear solver used. On the other hand, the Rosenbrock and TASE methods do not involve any non-linear equation and therefore do not have this possible problem.

An advantage of the Singly–RKTASE methods with respect to the Rosenbrock schemes is that the order of accuracy does not change if we take an approximation to the Jacobian matrix [24], which further allows to save Jacobian matrix evaluations and LU matrix factorizations, as was the case for example with problem 3.

8 Conclusions

In this work, a new family of STASE operators for the solution of stiff differential equations has been proposed. The advantage over previous TASE operators [8, 11] is that they require the solution of linear systems with the same coefficient matrix, whereas in the previous cases there are different coefficient matrices. As a consequence, the new STASE method only relies on the inverse of a single matrix. The new schemes are computationally comparable to the classical Rosenbrock methods. A detailed study of the accuracy and the linear stability properties up to fourth-order methods has been carried out, resulting in nearly A–stable and strongly A–stable Singly–RKTASE schemes. The results of several numerical experiments have been presented by comparing two new Singly–RKTASE fourth-order schemes with the standard RKTASE methods of the same order in [8, 11]. The new methods are also compared with the classical SDIRK and Rosenbrock methods.

The main conclusions derived from the numerical experiments are as follows.

• Singly–RKTASE schemes are more efficient than their corresponding RKTASE methods.

• For highly stiff problems, strong stability is an essential feature.

• In most problems, Singly–RKTASE schemes introduce larger global errors than the SDIRK and Rosenbrock methods. Further research needs to be done to find an efficient and optimal combination of the RK schemes and the STASE operators.