Gradient Robust Mixed Methods for Nearly Incompressible Elasticity

Abstract

Within the last years pressure robust methods for the discretization of incompressible fluids have been developed. These methods allow the use of standard finite elements for the solution of the problem while simultaneously removing a spurious pressure influence in the approximation error of the velocity of the fluid, or the displacement of an incompressible solid. To this end, reconstruction operators are utilized mapping discretely divergence free functions to divergence free functions. This work shows that the modifications proposed for Stokes equation by Linke (Comput Methods Appl Mech Eng 268:782–800, 2014) also yield gradient robust methods for nearly incompressible elastic materials without the need to resort to discontinuous finite elements methods as proposed in Fu et al. (J Sci Comput 86(3):39–30, 2021).

1 Introduction

The Stokes equation for steady flow of an incompressible fluid is given as

$$\begin{aligned} \begin{aligned} -\nu \Delta {\textbf{u}} - \nabla p&= {\textbf{f}}{} & {} \text {in }\Omega , \\ \nabla \cdot {\textbf{u}}&= 0{} & {} \text {in }\Omega , \\ u&= 0{} & {} \text {on }\Omega , \end{aligned} \end{aligned}$$

(1)

in a, polygonal, domain $\Omega \subset {\mathbb {R}}^d; d = 2,3$ for given data ${\textbf{f}} \in L^2(\Omega )$ and $\nu > 0$, where ${\textbf{u}}$ denotes the fluid velocity and p denotes the pressure. Under the famous inf-sup condition for the finite element spaces ${\textbf{V}}_h$ and $Q_h$, the use of mixed finite elements allows to obtain discrete approximations ${\textbf{u}}_h \in {\textbf{V}}_h$ and $p_h \in Q_h$ satisfying an error estimate of the form

$$\begin{aligned} \Vert {\textbf{u}}-{\textbf{u}}_h\Vert _1 \le \frac{c}{\beta } \inf _{{\textbf{v}}_h \in {\textbf{V}}_h} \Vert {\textbf{u}}-{\textbf{v}}_h\Vert _1 + \frac{c}{\nu }\inf _{q_h \in Q_h}\Vert p-q_h\Vert _0, \end{aligned}$$

see, e.g., [3] Here $\beta$ is the inf-sup constant associated to the choice of ${\textbf{V}}_h$ and $Q_h$, $\Vert \,\cdot \,\Vert _1$ and $\Vert \,\cdot \,\Vert _0$ denote the $H^1$ and $L^2$ norm on $\Omega$, respectively. Further, here and throughout the paper c denotes a generic constant which is independent of all relevant quantities of the estimate but may take a different value at each appearance.

While the estimate can yield asymptotically optimal orders, provided suitable finite element spaces are taken, without the need to utilize exactly divergence free finite element functions for the approximation of ${\textbf{u}}_h$ the right hand side of the estimate hints towards an undesirable influence of the pressure on the approximation error of the velocity. In fact, it has been observed, e.g., in [1] that indeed complicated pressures can give rise to a large error in the velocity approximation, even in situations where the true velocity can be represented in the discrete space ${\textbf{V}}_h$.

A potential remedy, allowing for arbitrary inf-sup stable element pairs while providing pressure independent velocity has been proposed by [1]. He proposed the use of reconstruction operators on the right hand side of the equation to map discretely divergence free functions to divergence free functions. This proposed method has been implemented to a range of problems and a variety of finite element pairs for the discretization of Stokes equation, such as non-conforming Crouzeix–Raviart element [4], Taylor-Hood and MINI elements with continuous pressure spaces [5], on rectangular elements [6], for embedded discontinuous Galerkin methods (EDG) [7]. For 3-d polyhedral domains with concave edges a pressure robust reconstruction is given in [8]. While the obtained convergence orders are optimal, the price to pay, for these methods is a loss of quasi optimality of the method due to Strang’s first lemma. Recently, [9] showed that a more involved construction of the reconstruction operator allows for a quasi-optimal discretization.

In this paper, we consider the extension of these results to nearly incompressible linear elasticity, e.g.,

$$\begin{aligned} \begin{aligned} -2\mu \nabla \cdot \varepsilon ({\textbf{u}}) - \lambda \nabla (\nabla \cdot {\textbf{u}})&= {\textbf{f}}{} & {} \text {in }\Omega ,\\ u&= 0{} & {} \text {on }\partial \Omega , \end{aligned} \end{aligned}$$

where $\varepsilon ({\textbf{u}})$ denotes the symmetric gradient, and $\mu , \lambda > 0$ are the Lamé parameters. To avoid the locking phenomenon, e.g., [10, Chapter VI.3], typically a mixed form

$$\begin{aligned} \begin{aligned} -2\mu \, \nabla \cdot \varepsilon ({\textbf{u}}) - \nabla p&= {\textbf{f}}{} & {} \text { in } \Omega , \\ \nabla \cdot {\textbf{u}} - \frac{1}{\lambda } p&= 0{} & {} \text { in } \Omega , \\ {\textbf{u}}&= 0{} & {} \text { on } \partial \Omega , \end{aligned} \end{aligned}$$

(2)

is considered. Here the incompressible case, i.e., $\lambda =\infty$, can easily be included by dropping the term $-\frac{1}{\lambda }p$ in the second line. It is clear conceptually that the same difficulties as for the Stokes problem will occur in the incompressible limit. However, the treatment of the nearly incompressible case requires additional care. To this end, [2] defined a discretization to be “gradient robust”, if the influence of gradient forces ${\textbf{f}} = \nabla \phi$ in the discrete solution vanishes sufficiently fast as $\lambda \rightarrow \infty$. [2] showed that a standard mixed discretization of (2) is not gradient robust and provided a gradient robust hybrid discontinuous Galerkin (HDG) scheme. Within this article, we will show that mixed methods can be made gradient robust using the approach proposed by [1] for the mixed discretization of (2).

The rest of the paper is structured as follows. In Sect. 2, we introduce the notion of gradient robustness and discuss the discretization of (2). Next, in Sect. 3, we show that the proposed discretization is indeed gradient robust and provide error estimates. We conclude the paper with a series of examples highlighting the derived results in Sect. 4.

2 Gradient Robustness and Discretization

2.1 Gradient Robustness

We define the spaces ${\textbf{V}}^0$ of divergence free function and its orthogonal complement ${\textbf{V}}^\bot$ as

$$\begin{aligned} {\textbf{V}}^{0}&= \left\{ {\textbf{u}} \in H^1_0(\Omega ;{\mathbb {R}}^d) : \nabla \cdot {\textbf{u}} = 0\right\} , \\ {\textbf{V}}^\bot&= \left\{ {\textbf{u}} \in H^1_0(\Omega ;{\mathbb {R}}^d) : a({\textbf{u}}, {\textbf{v}}) = 0 , \forall \, {\textbf{v}} \in {\textbf{V}}^{0} \right\} , \end{aligned}$$

where for ${\textbf{u}}, {\textbf{v}}\in {\textbf{V}} = H^1_0(\Omega ;{\mathbb {R}}^d)$, we define the bilinear form (scalar product) $a :{\textbf{V}} \times {\textbf{V}} \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} a({\textbf{u}}, {\textbf{v}}) = 2\mu (\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{v}})), \end{aligned}$$

(3)

with the $L^2(\Omega )$-scalar product $(\,\cdot ,\,\cdot \,)$. Now, any function ${\textbf{u}} \in {\textbf{V}}$ can be uniquely written as ${\textbf{u}} = {\textbf{u}}^0 + {\textbf{u}}^\bot \in {\textbf{V}}^0 \oplus {\textbf{V}}^\bot$.

Using Helmholtz decomposition, ${\textbf{f}} \in L^2(\Omega ; {\mathbb {R}}^d)$ can be uniquely decomposed as

$$\begin{aligned} {\textbf{f}} = \nabla \phi + {\textbf{w}}, \end{aligned}$$

(4)

where $\phi \in H^1(\Omega )/ {\mathbb {R}}$ is irrotational, ${\textbf{w}}$ is divergence free and both are orthogonal with respect to the $L^2(\Omega )$-scalar product, i.e.,

$$\begin{aligned} ({\textbf{w}},\nabla \, \phi ) = 0. \end{aligned}$$

(5)

With these definitions, the decay of the influence of gradient forces, i.e., ${\textbf{w}} = 0$, onto the solutions ${\textbf{u}}$ of (2) can be quantified as the following result from [2, Theorem 1] shows:

Lemma 1

If ${\textbf{f}} \in H^{-1}(\Omega )$ is a gradient, i.e., ${\textbf{f}} = \nabla \phi ,$ for some $\phi \in L^2(\Omega )$. Then for the solution ${\textbf{u}} = {\textbf{u}}^0 + {\textbf{u}}^\bot$ of (2) it holds ${\textbf{u}}^0 = 0$ and

$$\begin{aligned} \Vert {\textbf{u}}\Vert _1 = \Vert {\textbf{u}}^\bot \Vert _1 \le \frac{c}{\mu + \lambda }\Vert \phi \Vert _0. \end{aligned}$$

In particular, $\Vert {\textbf{u}}\Vert _1 = O(\lambda ^{-1})$ as $\lambda \rightarrow \infty$.

Since this bound need not hold for arbitrary, inf-sup stable, discretizations, [2, Definition 2] introduced the following notion:

Definition 1

A discretization of (2) is called gradient robust, if for any fixed ${\textbf{f}} = \nabla \phi$ with $\phi \in L^2(\Omega )$, $\mu > 0$ and any discretization parameter h there is a constant $c_h$ such that the approximate solution ${\textbf{u}}_h \in {\textbf{V}}_h^\bot$ and satisfies

$$\begin{aligned} \Vert {\textbf{u}}_h\Vert _1 \le \frac{c_h}{\lambda }\Vert \phi \Vert _0. \end{aligned}$$

2.2 Abstract Discretization

In order to discretize (2), we define a second bilinear form $b:Q \times {\textbf{V}} \rightarrow {\mathbb {R}}$, with $Q=L^2_0(\Omega )$, by

$$\begin{aligned} b(q,{\textbf{v}}) = (p,\nabla \cdot {\textbf{v}}). \end{aligned}$$

(6)

Now we select subspaces ${\textbf{V}}_h \subset {\textbf{V}}$ and $Q_h \subset Q$ such that there is a positive constant $\beta$ satisfying the inf-sup condition

$$\begin{aligned} \inf _{q_h \in Q_h} \sup _{{\textbf{v}}_h \in {\textbf{V}}_h} \frac{\left( q_h, \nabla \cdot {\textbf{v}}_h\right) }{\Vert q_h\Vert _0 \Vert {\textbf{v}}_h\Vert _1} \ge \beta . \end{aligned}$$

(7)

Now, the standard, in general not gradient robust, weak formulation is given as follows: Find $({\textbf{u}}_h, p_h) \in {\textbf{V}}_h \times Q_h$ such that

$$\begin{aligned} \begin{aligned} a({\textbf{u}}_h,{\textbf{v}}_h) + b(p_h, {\textbf{v}}_h)&= ({\textbf{f}},{\textbf{v}}_h)&\forall&{\textbf{v}}_h \in {\textbf{V}}_h, \\ b(q_h,{\textbf{u}}_h) - \frac{1}{\lambda } (p_h,q_h)&= 0&\forall&q_h \in Q_h. \end{aligned} \end{aligned}$$

(8)

Under the well known inf-sup condition (7) on ${\textbf{V}}_h$ and $Q_h$, the system (8) is uniquely solvable [11, Theorem 5.5.2]. Following [11, Proposition 5.5.3] the displacement error is thus bounded as follows:

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{u}}_h\Vert _1 \le \frac{c}{\beta }\inf _{{\textbf{v}}_h \in {\textbf{V}}_h} \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 + \frac{1}{\mu }\left( \frac{1}{\lambda } + 1\right) \inf _{q_h \in Q_h}\Vert p - q_h\Vert _0. \end{aligned}$$

(9)

Following [1], we assume that there exists a reconstruction operator

$$\begin{aligned} \varvec{\pi }^{\mathrm{{div}}} :{\textbf{V}}_h \rightarrow H^{\mathrm{{div}}}(\Omega ; {\mathbb {R}}^d) = \left\{ {\textbf{v}} \in L^2(\Omega ; {\mathbb {R}}^d) :\, \nabla \cdot {\textbf{v}} \in L^2(\Omega )\right\} , \end{aligned}$$

to be specified later in Sect. 2.3, mapping discretely divergence free functions to divergence free functions. Then the modified problem is given as:

$$\begin{aligned} \begin{aligned} a({\textbf{u}}_h,{\textbf{v}}_h) + b(p_h, {\textbf{v}}_h)&= ({\textbf{f}},\varvec{\pi }^{\mathrm{{div}}}{\textbf{v}}_h)&\forall&{\textbf{v}}_h \in {\textbf{V}}_h, \\ b(q_h,{\textbf{u}}_h) - \frac{1}{\lambda } (p_h,q_h)&= 0&\forall&q_h \in Q_h. \end{aligned} \end{aligned}$$

(10)

Clearly, by construction, the modified problem (10) admits a solution under the same conditions as (8), since only the right hand side has been modified. In Theorem 4, we will see that the discretization (10) is gradient robust, under appropriate assumptions on $\varvec{\pi }^{\mathrm{{div}}}$. Further, in Theorem 5, we show the gradient robust displacement error estimate

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{u}}_h\Vert _1 \le ch^k \left( 1 + \sqrt{\frac{\mu }{\lambda }}\right) \Vert {\textbf{u}}\Vert _{k+1} + c\frac{h^k}{\lambda }\Vert p\Vert _k, \end{aligned}$$

(11)

where $\Vert \,\cdot \,\Vert _k$ denotes the norm on $H^{k}(\Omega )$ or $H^{k}(\Omega ;{\mathbb {R}}^d)$; of course assuming sufficient regularity of ${\textbf{u}}$ and p and approximation order of ${\textbf{V}}_h$ and $Q_h$. While the introduction of a variational crime in (10) means that instead of a quasi-best approximation error we only provide an estimate of optimal convergence order the estimate (11) is clearly better than (9) in view of the asymptotics as $\lambda \rightarrow \infty$ and $\mu \rightarrow 0$.

2.3 Reconstruction Operator and Assumptions

The construction of the reconstruction operator $\varvec{\pi }^{\mathrm{{div}}}$ proposed by [1] is based on the choice of a suitable subspace ${\mathcal {M}}_h \subset H^{\mathrm{{div}}}(\Omega ; \!\!{\mathbb {R}}^d)$ satisfying the commuting diagram in Fig. 1 where $\pi ^{L^2}$ denotes the $L^2$-projection onto $Q_h$.

Fig. 1

Commutative diagram for the reconstruction operator $\varvec{\pi }^{\mathrm{{div}}}$

The commuting diagram is equivalently expressed by the equation

$$\begin{aligned} b(q_h,\varvec{\pi }^{\mathrm{{div}}}{\textbf{v}}_h) = b(q_h,{\textbf{v}}_h) \qquad \forall {\textbf{v}}_h \in {\textbf{V}}_h, q_h \in Q_h, \end{aligned}$$

(12)

holds assuming that $\nabla \cdot {\mathcal {M}}_h \subseteq Q_h$. Further, we define

$$\begin{aligned} {\textbf{V}}_h^0&= \{ {\textbf{v}}_h \in {\textbf{V}}_h\,:\, b(q_h,{\textbf{v}}_h) = 0 \; \forall q_h \in Q_h\} ,\end{aligned}$$

(13)

$$\begin{aligned} H^{\mathrm{{div}}}_0(\Omega ; {\mathbb {R}}^d)&= \{{\textbf{v}}\in H^{\mathrm{{div}}}(\Omega ; {\mathbb {R}}^d)\,:\, \nabla \cdot v = 0\}. \end{aligned}$$

(14)

Then clearly, by (12) we have that the restriction of $\varvec{\pi }^{\mathrm{{div}}}$ to discretely divergence free functions maps into divergence free functions, i.e.,

$$\begin{aligned} \varvec{\pi }^{\mathrm{{div}}}:{\textbf{V}}_h^0 \rightarrow H^{\mathrm{{div}}}_0(\Omega ;{\mathbb {R}}^d) \end{aligned}$$

(15)

and further for any ${\textbf{v}}_h \in {\textbf{V}}_h$ it holds

$$\begin{aligned} \varvec{\pi }^{\mathrm{{div}}}{\textbf{v}}_h \cdot {\textbf{n}} = 0 \quad \text {on }\partial \Omega \end{aligned}$$

(16)

where, ${\textbf{n}}$ is the unit outward normal vector. Analogously to the continuous setting, we can define the orthogonal complement ${\textbf{V}}_h^\bot$ by

$$\begin{aligned} {\textbf{V}}_h^\bot = \left\{ {\textbf{u}}_h \in {\textbf{V}}_h: a({\textbf{u}}_h, {\textbf{v}}_h) = 0, \forall \, {\textbf{v}}_h \in {\textbf{V}}_h^{0} \right\} , \end{aligned}$$

and the corresponding discrete decomposition ${\textbf{u}}_h = {\textbf{u}}_h^0 + {\textbf{u}}_h^\bot \in {\textbf{V}}_h^0 \oplus {\textbf{V}}_h^\bot$.

Before we continue, let us make some, generic assumptions on the considered spaces ${\textbf{V}}_h$ and $Q_h$ defined on a shape regular family ${\mathcal {T}}_h$ of decompositions of $\Omega$.

Assumption 1

Following [6, Assumptions A1,A2, and A3], we assume, that for some $k \ge 2$ and $i = 0,1$ the finite element space ${\textbf{V}}_h$ is equipped with an interpolation operator $I_h :H^{k+1}(\Omega ;{\mathbb {R}}^d) \rightarrow {\textbf{V}}_h$ satisfying

$$\begin{aligned} h_T^i\Vert I_h {\textbf{v}} - {\textbf{v}}\Vert _{i,T} \le ch_T^{k+1}\Vert {\textbf{v}}\Vert _{k+1,T} \qquad \forall {\textbf{v}}\in H^{k+1}(\Omega ;{\mathbb {R}}^d), T \in {\mathcal {T}}_h \end{aligned}$$

where $\Vert \,\cdot \,\Vert _{i,T}$ denotes the respective norm on the element T, and $h_T$ is the element diameter. For the space $Q_h$, we assume that the $L^2$-projection $\pi ^{L^2} :H^{k}(\Omega ) \rightarrow Q_h$ satisfies

$$\begin{aligned} h_T^i\Vert \pi ^{L^2} q - q\Vert _{i,T} \le ch_T^{k}\Vert q\Vert _{k,T} \qquad \forall q\in H^{k}(\Omega ), T \in {\mathcal {T}}_h. \end{aligned}$$

Further, it is assumed that ${\textbf{V}}_h$ and $Q_h$ satisfy the inf-sup inequality (7). Finally, we assume that there exists a subspace $\widetilde{{\textbf{Q}}}_h \subset L^2(\Omega ; {\mathbb {R}}^d)$ such that the respective $L^2$-projection $\widetilde{\varvec{\pi }}^{L^2}$ satisfies

$$\begin{aligned} h_T^i\Vert \widetilde{\varvec{\pi }}^{L^2} {\textbf{q}} - {\textbf{q}}\Vert _{i,T} \le ch_T^{k-1}\Vert {\textbf{q}}\Vert _{k-1,T} \qquad \forall {\textbf{q}}\in H^{k}(\Omega ;{\mathbb {R}}^d), T \in {\mathcal {T}}_h. \end{aligned}$$

Further requirements on $\widetilde{{\textbf{Q}}}_h$ will be made in Assumption 2.

With these preparations, we can now state the additional assumptions on the reconstruction operator.

Assumption 2

Following [6, Assumption A4], we first assume, that the reconstruction operator satisfies the following orthogonality relation

$$\begin{aligned} \left( {\textbf{v}}_h - \varvec{\pi }^{\mathrm{{div}}} {\textbf{v}}_h, {\textbf{q}}\right) = 0\qquad \forall {\textbf{v}}_h \in {\textbf{V}}_h, {\textbf{q}}\in \widetilde{{\textbf{Q}}}_h, \end{aligned}$$

(17)

where $\widetilde{{\textbf{Q}}}_h \subset L^2(\Omega ;{\mathbb {R}}^d)$ is given in Assumption 1. Second, we assume the following local approximation property to hold

$$\begin{aligned} \Vert \varvec{\pi }^{\mathrm{{div}}} {\textbf{v}}_h - {\textbf{v}}_h\Vert _{0,T} \le ch^m_T|{\textbf{v}}_h|_{m,T} \qquad \forall \; {\textbf{v}}_h \in {\textbf{V}}_h, T \in {\mathcal {T}}_h, m = 0, 1. \end{aligned}$$

(18)

Before concluding the assumption, let us note that the assumptions can indeed be satisfied. To this end, we give an example which we will also use for the numerical results in Sect. 4.

Example 1

Let us assume that the domain can be decomposed into a family ${\mathcal {T}}_h$ of shape regular rectangular ($d=2$) or brick ($d=3$) elements. For the space ${\textbf{V}}_h = {\textbf{V}}_h^k$, we consider, parametric, piecewise ${\mathcal {Q}}_k$ and globally continuous finite elements with $k \ge 2$. For the discretization of $Q_h = Q_h^{k-1}$, we select the space of discontinuous piecewise $P_{k-1}$ functions. Indeed theses pairs satisfy the inf-sup condition (7), see, e.g., [11, Sec. 8.6.3 & 8.7.2] for $k=2$, for arbitrary k [3, Sec. 3.2] or [12] for mapped pressure spaces. Moreover, [6, Sec. 4.2.1] showed, that the choice ${\mathcal {M}}_h = \mathcal {{\text {BDM}}}_k$ as space of Brezzi-Douglas-Marini elements yield the desired commuting diagram property (12) together with the canonical interpolation $\varvec{\pi }^{\mathrm{{div}}}$. Further, they showed [6, Lemma 2.1], that the restriction of $\varvec{\pi }^{\mathrm{{div}}}$ to discretely divergence free functions maps into divergence free functions, i.e.,

$$\begin{aligned} \varvec{\pi }^{\mathrm{{div}}}:\left\{ {\textbf{v}}_h \in {\textbf{V}}_h:\, b(q_h,{\textbf{v}}_h)\; \forall q_h \in Q_h\} \rightarrow \{{\textbf{v}}\in H^{\mathrm{{div}}}(\Omega ; {\mathbb {R}}^d):\, \nabla \cdot v = 0\right\} \end{aligned}$$

and further for any ${\textbf{v}}_h \in {\textbf{V}}_h$ it holds

$$\begin{aligned} \varvec{\pi }^{\mathrm{{div}}}{\textbf{v}}_h \cdot {\textbf{n}} = 0 \quad \text {on }\partial \Omega . \end{aligned}$$

Further, [6, Sect. 4.2.1] shows the validity of Assumption 2 where $\widetilde{{\textbf{Q}}}_h$ is the space of discontinuous piecewise $P_{k-2}^d$ functions.

Remark 1

Infact, [6] showed that (12) follow from a set of assumed orthogonality properties and surjectivity of divergence and normal traces from which suitable choices of ${\mathcal {M}}_h$ and constructions of $\varvec{\pi }^{\mathrm{{div}}}$ can be obtained.

3 Error Analysis

In this section, we proceed with error analysis of the modified weak form (10). We split the analysis in two parts for incompressible materials $(\lambda = \infty )$ and nearly incompressible materials $(\lambda \ne \infty )$.

3.1 Incompressible Materials

We proceed to the error analysis of incompressible materials, where $\lambda = \infty$ and the term involving $\frac{1}{\lambda }$ is dropped in (10). The analysis follows, at large, the arguments in [4] with some minor adjustments to the elasticity case.

Theorem 2

Let Assumptions 1 and 2 be satisfied and $\lambda = \infty$. Then the solution $({\textbf{u}}, p) \in H^{k+1}(\Omega ;{\mathbb {R}}^d) \times H^k(\Omega )$ of the continuous problem (2) and the solution $({\textbf{u}}_h, p_h) \in {\textbf{V}}_h\times Q_h$ of (10) satisfy the error estimate

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{u}}_h\Vert _{1}^2 \le c\sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T|{\textbf{u}}|^2_{k+1,T} \le c h^{2k}\Vert {\textbf{u}}\Vert _{k+1}, \end{aligned}$$

where $|\,\cdot \, |_k$ denotes the $H^k$-semi-norm, where $k \ge 2$ is given by Assumption 1.

Before proving the above theorem, we would like to prove an important lemma which is need to prove the theorem.

Lemma 3

Let Assumptions 1 and 2 be satisfied and $\lambda = \infty$. Then for any functions ${\textbf{u}} \in H^{k+1}(\Omega ;{\mathbb {R}}^d)$ and ${\textbf{w}}_h\in {\textbf{V}}_h$ it is

$$\begin{aligned} \bigl |(\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h) + (\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h))\bigr |\le c \sum \limits _{T \in {\mathcal {T}}_h} h_T^k|{\textbf{u}}|_{k+1,T} \Vert {\textbf{w}}_h\Vert _{1,T} , \end{aligned}$$

(19)

where $|\,\cdot \, |_{k,T}$ denotes the $H^k$-semi-norm on T, where $k \ge 2$ is given by Assumption 1.

Proof

We add and subtract $\left( \nabla \cdot \varepsilon ({\textbf{u}}), {\textbf{w}}_h\right)$ on the left to obtain

$$\begin{aligned} \begin{aligned} (\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h) + (\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h)) =&\; (\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h)\\&\;+(\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h)) + (\nabla \cdot \varepsilon ({\textbf{u}}), {\textbf{w}}_h). \end{aligned} \end{aligned}$$

(20)

Since $\nabla \cdot \varepsilon ({\textbf{u}}) \in L^2(\Omega ;{\mathbb {R}}^d)$, we can apply the projection $\widetilde{\varvec{\pi }}^{L^2}$, from Assumption 1, to get $\widetilde{\varvec{\pi }}^{L^2} \nabla \cdot \varepsilon ({\textbf{u}}) \in \widetilde{{\textbf{Q}}}_h$. By the assumed orthogonality in (17), we have

$$\begin{aligned}\left( \widetilde{\varvec{\pi }}^{L^2} \nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h\right) = 0, \qquad \forall \; {\textbf{w}}_h \in {\textbf{V}}_h. \end{aligned}$$

Using Assumption 1 and (18), we obtain, for the first summand on the right of (20),

$$\begin{aligned} \begin{aligned}&\Bigl ( \nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h - {\textbf{w}}_h\Bigr ) = \left( \nabla \cdot \varepsilon ({\textbf{u}}) - \widetilde{\varvec{\pi }}^{L^2} \nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h - {\textbf{w}}_h\right) \\&\quad \le \sum \limits _{T \in {\mathcal {T}}_h} \Vert \nabla \cdot \varepsilon ({\textbf{u}}) - \widetilde{\varvec{\pi }}^{L^2} \nabla \cdot \varepsilon ({\textbf{u}})\Vert _{0, T} \Vert \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h\Vert _{0, T} \\&\quad \le \sum \limits _{T\in {\mathcal {T}}_h} c h_T^{k-1}|\nabla \cdot \varepsilon ({\textbf{u}})|_{k-1,T} h_T\Vert {\textbf{w}}_h\Vert _{1,T} \\&\quad \le \sum \limits _{T\in {\mathcal {T}}_h} ch_T^k|{\textbf{u}}|_{k+1,T}\Vert {\textbf{w}}_h\Vert _{1,T}. \end{aligned} \end{aligned}$$

(21)

For the last two summands of (20), we apply Gauss divergence theorem to get

$$\begin{aligned} (\nabla \cdot \varepsilon ({\textbf{u}}), {\textbf{w}}_h) + (\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h)) = \int \limits _{\partial \Omega } \varepsilon ({\textbf{u}})\cdot {\textbf{n}} \; {\textbf{w}}_h \,\textrm{d}s = 0 \end{aligned}$$

(22)

since ${\textbf{w}}_h = 0$ on $\partial \Omega$. Combining (20) with the bounds (21) and (22) the assertion is shown. $\square$

Now, we continue to prove Theorem 2

proof of Theorem 2

Let ${\textbf{u}}_h$ be the solution of (10), with $\lambda = \infty$, and let ${\textbf{v}}_h \in {\textbf{V}}_h^0$ be arbitrary. Defining ${\textbf{w}}_h = {\textbf{u}}_h - {\textbf{v}}_h \in {\textbf{V}}_h^0$ and applying the triangle inequality gives

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{u}}_h\Vert _1 = \Vert {\textbf{u}} - {\textbf{w}}_h -{\textbf{v}}_h\Vert _{1} \le \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 + \Vert {\textbf{w}}_h\Vert _1. \end{aligned}$$

(23)

In view of the interpolation estimate in Assumption 1, we are left to estimate $\Vert {\textbf{w}}_h\Vert _1$. From Korn’s inequality, we have

$$\begin{aligned} c\Vert {\textbf{w}}_h\Vert ^2_1 \le \Vert \varepsilon ({\textbf{w}}_h)\Vert ^2_0. \end{aligned}$$

From this, we conclude

$$\begin{aligned} \begin{aligned} 2\mu c\Vert {\textbf{w}}_h\Vert ^2_1&\le a({\textbf{w}}_h, {\textbf{w}}_h) \\&= a({\textbf{u}}_h - {\textbf{v}}_h, {\textbf{w}}_h) \\&= a({\textbf{u}}_h -{\textbf{v}}_h + {\textbf{u}}- {\textbf{u}}, {\textbf{w}}_h) \\&\le |a({\textbf{u}} -{\textbf{v}}_h, {\textbf{w}}_h)|+ |a({\textbf{u}}_h - {\textbf{u}}, {\textbf{w}}_h)|. \end{aligned} \end{aligned}$$

(24)

For the first summand on the right of (24) we use Cauchy-Schwartz inequality to get

$$\begin{aligned} |a({\textbf{u}} - {\textbf{v}}_h, {\textbf{w}}_h)|\le 2 \mu \Vert \varepsilon ({\textbf{u}} - {\textbf{v}}_h)\Vert _0\Vert \varepsilon ({\textbf{w}}_h)\Vert _0 \le 2 \mu \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 \Vert {\textbf{w}}_h\Vert _1. \end{aligned}$$

(25)

Before we come to the bound of the second summand in (24), we make some preliminary calculations. Since ${\textbf{u}}_h$ is the solution of (10), choosing ${\textbf{v}}_h = {\textbf{w}}_h \in {\textbf{V}}_h^0$ gives

$$\begin{aligned} a({\textbf{u}}_h,{\textbf{w}}_h) = a({\textbf{u}}_h,{\textbf{w}}_h) + b(p_h,{\textbf{w}}_h) = ({\textbf{f}}, \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h). \end{aligned}$$

(26)

Further, since ${\textbf{u}}$ is the solution to the equation (2) multiplication with $\varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h$ and integration yields

$$\begin{aligned} -2\mu \int \limits _\Omega \nabla \cdot \varepsilon ({\textbf{u}}) \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h \,\textrm{d}x - \int \limits _\Omega \nabla p \;\varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h \,\textrm{d}x = \int \limits _\Omega {\textbf{f}} \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h \,\textrm{d}x \end{aligned}$$

by the compatibility of the reconstruction with the kernel of the divergence, i.e., (15) and (16), this gives

$$\begin{aligned} -2\mu ( \nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h) = ({\textbf{f}}, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h) \end{aligned}$$

Combining this with (26), we get

$$\begin{aligned} a({\textbf{u}}_h, {\textbf{w}}_h) = -2\mu (\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h). \end{aligned}$$

(27)

Now, we can bound the second summand on the right of (24), using (27) we get

$$\begin{aligned} \begin{aligned} |a({\textbf{u}}_h - {\textbf{u}}, {\textbf{w}}_h)|&= \Bigl |-2\mu (\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h) - 2 \mu (\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h))\Bigr |\\&\le 2 \mu \Bigl |(\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h) + (\varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h))\Bigr |. \end{aligned} \end{aligned}$$

By the previously shown lemma, i.e., (19), we can bound the right hand side to get

$$\begin{aligned} \begin{aligned} |a({\textbf{u}}_h - {\textbf{u}}, {\textbf{w}}_h)|&\le 2\mu c \sum \limits _{T \in {\mathcal {T}}_h} \left( h^k_T|{\textbf{u}}|_{k+1,T}\Vert {\textbf{w}}_h\Vert _{1,T} \right) \\&\le 2\mu c \left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T|{\textbf{u}}|^2_{k+1,T}\right) ^{\frac{1}{2}}\Vert {\textbf{w}}_h\Vert _1. \end{aligned} \end{aligned}$$

(28)

Now combining (24) with the two bounds (25) and (28), we get

$$\begin{aligned} \Vert {\textbf{w}}_h\Vert _1 \le c\Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 + c\left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T |{\textbf{u}}|^2_{k+1, T}\right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting this in (23) yields

$$\begin{aligned} \Vert {\textbf{u}}- {\textbf{u}}_h\Vert _1 \le c\Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 + c \left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T |{\textbf{u}}|^2_{k+1, T}\right) ^{\frac{1}{2}}. \end{aligned}$$

(29)

To bound the best approximation error on ${\textbf{V}}_h^0$ in this inequality, we proceed using inf-sup condition as in [3, Chapter 2, (1.16)] and the assumed interpolation estimate on ${\textbf{V}}_h$ in Assumption 1, to get the estimate

$$\begin{aligned} \inf \limits _{{\textbf{v}}_h \in {\textbf{V}}_h^0} \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 \le c \inf \limits _{{\textbf{v}}_h \in {\textbf{V}}_h} \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 \le c\left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T |{\textbf{u}}|^2_{k+1, T}\right) ^{\frac{1}{2}}. \end{aligned}$$

Using this in (29) gives the desired estimate. $\square$

3.2 Nearly Incompressible Materials

For the nearly incompressible case, i.e., $(\lambda \ne \infty )$, we start by assuming a gradient force ${\textbf{f}} = \nabla \phi$, for some $\phi \in L^2(\Omega )$. From Lemma 1, we have that the solution of (2) for such an ${\textbf{f}}$ is ${\textbf{u}} = {\textbf{u}}^\bot$. The following result shows, that our mixed discretization (10) is gradient robust in the sense of Definition 1.

Theorem 4

Let Assumptions 1 and 2 be satisfied. If the right hand side ${\textbf{f}} \in H^{-1}(\Omega ;{\mathbb {R}}^d)$ of equation (10) is a gradient field, i.e., ${\textbf{f}} = \nabla \phi$, for some $\phi \in L^2(\Omega )$, then the solution $({\textbf{u}}_h, p_h) \in {\textbf{V}}_h \times Q_h$ of (10) with $\lambda \ne \infty$ satisfies ${\textbf{u}}_h \in {\textbf{V}}_h^\bot$ and the gradient robust bound

$$\begin{aligned} \Vert {\textbf{u}}_h\Vert _1\le c\frac{1}{\lambda + \mu } \Vert \phi \Vert _0. \end{aligned}$$

(30)

with a constant c independent of h.

Proof

Consider ${\textbf{v}}_h = {\textbf{u}}_h$ in equation (10) with ${\textbf{f}} = \nabla \phi$. Then integration by parts for the right hand side, using the zero trace from (16), we get

$$\begin{aligned} a({\textbf{u}}_h, {\textbf{u}}_h) + b(p_h, {\textbf{u}}_h) = - ( \phi , \nabla \cdot \varvec{\pi }^{\mathrm{{div}}} {\textbf{u}}_h ). \end{aligned}$$

(31)

Since $\nabla \cdot \varvec{\pi }^{\mathrm{{div}}} {\textbf{u}}_h \in Q_h$ we can rewrite the right hand side as

$$\begin{aligned} (\phi , \nabla \cdot \varvec{\pi }^{\mathrm{{div}}} {\textbf{u}}_h) = (\pi ^{L^2} \phi , \nabla \cdot \varvec{\pi }^{\mathrm{{div}}} {\textbf{u}}_h). \end{aligned}$$

(32)

Since $\pi ^{L^2} \nabla \cdot {\textbf{u}}_h \in Q_h$, we can use it to test the second line in (10) giving

$$\begin{aligned} \begin{aligned} (\pi ^{L^2} \nabla \cdot {\textbf{u}}_h, \pi ^{L^2} \nabla \cdot {\textbf{u}}_h)&= (\pi ^{L^2} \nabla \cdot {\textbf{u}}_h, \nabla \cdot {\textbf{u}}_h ) \\&=\frac{1}{\lambda } (p_h, \pi ^{L^2}\nabla \cdot {\textbf{u}}_h)\\&=\frac{1}{\lambda } (p_h, \nabla \cdot {\textbf{u}}_h)\\&=\frac{1}{\lambda } b(p_h,{\textbf{u}}_h). \end{aligned} \end{aligned}$$

(33)

Substituting (32) and (33) in (31), we get

$$\begin{aligned} a({\textbf{u}}_h, {\textbf{u}}_h) + \lambda (\pi ^{L^2} \nabla \cdot {\textbf{u}}_h, \pi ^{L^2} \nabla \cdot {\textbf{u}}_h ) = -(\pi ^{L^2} \phi , \nabla \cdot \varvec{\pi }^{\mathrm{{div}}} {\textbf{u}}_h). \end{aligned}$$

(34)

Now $\pi ^{L^2} \phi \in Q_h$ and ${\textbf{u}}_h \in {\textbf{V}}_h$ hence, by (12), it holds

$$\begin{aligned} (\pi ^{L^2} \phi , \nabla \cdot \varvec{\pi }^{\mathrm{{div}}} {\textbf{u}}_h) = ( \pi ^{L^2} \phi , \nabla \cdot {\textbf{u}}_h). \end{aligned}$$

Filling this into (34) gives

$$\begin{aligned} \begin{aligned} 2 \mu \left( \varepsilon ({\textbf{u}}_h), \varepsilon ({\textbf{u}}_h)\right) + \lambda \left( \pi ^{L^2} \nabla \cdot {\textbf{u}}_h, \pi ^{L^2} \nabla \cdot {\textbf{u}}_h \right)&= - \left( \pi ^{L^2}\phi ,\pi ^{L^2} \nabla \cdot {\textbf{u}}_h\right) . \end{aligned} \end{aligned}$$

(35)

Using Cauchy-Schwartz inequality, we get

$$\begin{aligned} 2\mu \Vert \varepsilon ({\textbf{u}}_h)\Vert ^2_0 + \lambda \Vert \pi ^{L^2} \nabla \cdot {\textbf{u}}_h\Vert _0^2 \le \Vert \pi ^{L^2} \phi \Vert _0 \Vert \pi ^{L^2}\nabla \cdot {\textbf{u}}_h\Vert _0 \le \Vert \phi \Vert _0\Vert \pi ^{L^2}\nabla \cdot {\textbf{u}}_h\Vert _0. \end{aligned}$$

(36)

Now, to estimate the $H^1$-norm of ${\textbf{u}}_h$, we notice that by the choice of ${\textbf{f}}$ and (15), testing the first equation in (10) with a function ${\textbf{v}}_h \in {\textbf{V}}_h^0$ yields

$$\begin{aligned} a({\textbf{u}}_h,\mathbf {v_h}) = -b(p_h,{\textbf{v}}_h)-(\phi ,\nabla \cdot \varvec{\pi }^{\mathrm{{div}}}{\textbf{v}}_h) = 0 \end{aligned}$$

and thus ${\textbf{u}}_h \in {\textbf{V}}_h^\bot$. Hence by, e.g., [13, Lemma 3.58] it holds

$$\begin{aligned} \Vert {\textbf{u}}_h\Vert _1 \le c\Vert \pi ^{L^2}\nabla \cdot {\textbf{u}}_h\Vert _0 \end{aligned}$$

(37)

with a constant c depending on the inf-sup constant $\beta$ from (7), since $\pi ^{L^2}\nabla \cdot {\textbf{u}}_h \in Q_h$.

Using Korn’s inequality, (36), and (37), we get

$$\begin{aligned} \begin{aligned} (\mu +\lambda ) \Vert {\textbf{u}}_h\Vert ^2_1&\le c\mu \Vert \varepsilon ({\textbf{u}}_h)\Vert _0^2 + \lambda c\Vert \pi ^{L^2}\nabla \cdot {\textbf{u}}_h\Vert _1^2 \\&\le c\Vert \phi \Vert _0\Vert {\textbf{u}}_h\Vert _1, \end{aligned} \end{aligned}$$

(38)

and thus the assertion is shown. $\square$

Theorem 5

Let Assumptions 1 and 2 be satisfied. Then the solutions $({\textbf{u}}, p) \in {\textbf{V}} \times Q$, of the problem (2) and $({\textbf{u}}_h, p_h) \in {\textbf{V}}_h \times Q_h$ of (10) satisfy the error estimate

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{u}}_h\Vert _1 \le c\, h^k \left( 1 + \sqrt{\frac{\mu }{\lambda }}\right) \Vert {\textbf{u}}\Vert _{k+1} + c\frac{h^k}{\lambda }\Vert p\Vert _k, \end{aligned}$$

(39)

provided the regularity $({\textbf{u}}, p) \in H^{k+1}(\Omega ;{\mathbb {R}}^d)\times H^k(\Omega )$ is given, where $k \ge 2$ is given by Assumption 1.

Proof

As in the proof of Theorem 2, we could split the error

$$\begin{aligned} ({\textbf{u}}-{\textbf{u}}_h,p-p_h) = ({\textbf{u}}-{\textbf{v}}_h,p-q_h) + ({\textbf{v}}_h-{\textbf{u}}_h,q_h-p_h) \end{aligned}$$

with arbitrary ${\textbf{v}}_h \in {\textbf{V}}_h$ and $q_h \in Q_h$. However, as it will turn out to be useful, we will select $q_h = \pi ^{L^2} p$ and ${\textbf{v}}_h$ as a particular Fortin operator applied to ${\textbf{u}}$, i.e., satisfying the following equation

$$\begin{aligned} \left( \varepsilon ({\textbf{v}}_h), \varepsilon (\varvec{\varphi }_h)\right) + b({\tilde{p}}_h, \varvec{\varphi }_h)&= \left( \varepsilon ({\textbf{u}}), \varepsilon (\varvec{\varphi }_h)\right){} & {} \forall \varvec{\varphi }_h \in {\textbf{V}}_h, \nonumber \\ b(s_h,{\textbf{v}}_h)&= b(s_h, {\textbf{u}}){} & {} \forall s_h \in Q_h. \end{aligned}$$

(40)

Clearly, the solution to the continuous counterpart is $({\textbf{v}},{\tilde{p}}) = ({\textbf{u}},0)$. Since the above equation is uniquely solvable, see, e.g. [11, Theorem 4.2.3], we have the orthogonality $b(\pi ^{L^2} p - p_h, {\textbf{u}} - {\textbf{v}}_h) = 0$ and the approximation error satisfies, e.g., [11, Theorem 5.2.2].

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 + \Vert {\tilde{p}} - {\tilde{p}}_h\Vert _0 \le c\inf \limits _{\varvec{\varphi }_h \in {\textbf{V}}_h} \Vert {\textbf{u}} - \varvec{\varphi }_h\Vert _1 + c\inf \limits _{s_h \in Q_h}\Vert 0- s_h\Vert _0, \end{aligned}$$

(41)

which gives

$$\begin{aligned} \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 \le c\inf \limits _{\varvec{\varphi }_h \in {\textbf{V}}_h } \Vert {\textbf{u}} - \varvec{\varphi }_h\Vert _1 \end{aligned}$$

(42)

Due to the interpolation estimates in Assumption 1, we are left with bounding ${\textbf{w}}_h = {\textbf{u}}_h - {\textbf{v}}_h \in {\textbf{V}}_h$ and $r_h = p_h - q_h \in Q_h$. We split ${\textbf{w}}_h = {\textbf{w}}_h^0 + {\textbf{w}}_h^\bot \in {\textbf{V}}_h^0 \oplus {\textbf{V}}_h^\bot$. By definition of the bilinear forms a and b, i.e., (3) and (6), and the first line in (10) and (2), the remainder ${\textbf{w}}_h$ and $r_h$ satisfy, for any discrete function $\varvec{\varphi }_h \in {\textbf{V}}_h$,

$$\begin{aligned} \begin{aligned} a({\textbf{w}}_h, \varvec{\varphi }_h)&+ b(r_h,\varvec{\varphi }_h) = a({\textbf{u}}_h - {\textbf{v}}_h, \varvec{\varphi }_h) + b(p_h - q_h,\varvec{\varphi }_h) \\&= ({\textbf{f}}, \varvec{\pi }^{\mathrm{{div}}}\varvec{\varphi }_h - \varvec{\varphi }_h) + a({\textbf{u}} - {\textbf{v}}_h, \varvec{\varphi }_h) + b(p - q_h, \varvec{\varphi }_h). \end{aligned} \end{aligned}$$

(43)

Analogously, from the second line in (10) and (2), we get for arbitrary $s_h \in Q_h$

$$\begin{aligned} \begin{aligned} b(s_h,{\textbf{w}}_h) - \frac{1}{\lambda } ( r_h, s_h)&= b(s_h,{\textbf{u}}_h - {\textbf{v}}_h) - \frac{1}{\lambda }(p_h - q_h, s_h) \\&= b(s_h,{\textbf{u}}_h) - \frac{1}{\lambda }(p_h, s_h) - \bigl (b(s_h,{\textbf{v}}_h) - \frac{1}{\lambda }(q_h, s_h)\bigr ) \\&= b(s_h,{\textbf{u}} - {\textbf{v}}_h) - \frac{1}{\lambda }(p - q_h, s_h). \end{aligned} \end{aligned}$$

(44)

Testing (43) and (44) with $\mathbf {\varphi }_h=\mathbf {w_h}$ and $s_h=r_h$ we get

$$\begin{aligned} \begin{aligned} c\mu \Vert {\textbf{w}}_h\Vert ^2_1 + \frac{1}{\lambda } \Vert r_h\Vert ^2_0&\le a({\textbf{w}}_h, {\textbf{w}}_h) + \frac{1}{\lambda } (r_h, r_h)\\&= a({\textbf{w}}_h, {\textbf{w}}_h) + b(r_h,{\textbf{w}}_h) - b(r_h,{\textbf{w}}_h) + \frac{1}{\lambda }(r_h, r_h) \\&= ({\textbf{f}}, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) + a({\textbf{u}} - {\textbf{v}}_h, {\textbf{w}}_h) \\&\;\;\;\; +b(p - q_h,{\textbf{w}}_h) - b(r_h,{\textbf{u}} - {\textbf{v}}_h) + \frac{1}{\lambda }(p - q_h, r_h). \end{aligned} \end{aligned}$$

(45)

Using (19) and (2), we obtain a bound on $({\textbf{f}}, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h)$ as follows

$$\begin{aligned} \begin{aligned}&({\textbf{f}}, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) = -2\mu (\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h -{\textbf{w}}_h) - (\nabla p, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) \\&\quad = -2\mu (\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h) - 2\mu \left( \varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h)\right) + b(p,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) \\&\quad \le c\mu \sum \limits _{T \in {\mathcal {T}}_h} h_T^k|{\textbf{u}}|_{k+1,T} \Vert {\textbf{w}}_h\Vert _{1,T} + b(p,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) \\&\quad \le 2\mu c \left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T|{\textbf{u}}|^2_{k+1,T}\right) ^{\frac{1}{2}}\Vert {\textbf{w}}_h\Vert _1 + b(p,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h). \end{aligned} \end{aligned}$$

Substituting this in (45), we get

$$\begin{aligned} \begin{aligned}&c\mu \Vert {\textbf{w}}_h\Vert ^2_1 + \frac{1}{\lambda } \Vert r_h\Vert ^2_0 \le 2\mu c \left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T|{\textbf{u}}|^2_{k+1,T}\right) ^{\frac{1}{2}}\Vert {\textbf{w}}_h\Vert _1 \\&\quad + \Bigl (b(p,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) + b(p - q_h,{\textbf{w}}_h) - b(r_h,{\textbf{u}} - {\textbf{v}}_h)\Bigr ) \\&\quad +\Bigl (a({\textbf{u}}- {\textbf{v}}_h, {\textbf{w}}_h) + \frac{1}{\lambda }(p - q_h, r_h)\Bigr ). \end{aligned} \end{aligned}$$

(46)

The last line can be estimated as

$$\begin{aligned} a({\textbf{u}}- {\textbf{v}}_h, {\textbf{w}}_h) + \frac{1}{\lambda }(p - q_h, r_h) \le \frac{c\mu }{2}\Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1^2 + \frac{c\mu }{2} \Vert {\textbf{w}}_h\Vert ^2_1 + \frac{1}{2\lambda }\Vert p - q_h\Vert ^2_0 + \frac{1}{2\lambda } \Vert r_h\Vert ^2_0. \end{aligned}$$

From (12), we have that $b(q_h,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) = 0$. Hence the second line in (46) becomes

$$\begin{aligned} b(p,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) +&\, b(p - q_h,{\textbf{w}}_h) - b(r_h,{\textbf{u}} - {\textbf{v}}_h) \\&\quad = b(p - q_h,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) + b(p-q_h,{\textbf{w}}_h) - b(r_h,{\textbf{u}} - {\textbf{v}}_h) \\&\quad = b(p - q_h,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h) - b(p_h - q_h,{\textbf{u}} - {\textbf{v}}_h)\\&\quad = b(\pi ^{L^2}p - q_h,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h) - b(p_h - q_h,{\textbf{u}} - {\textbf{v}}_h)\\&\quad = b(\pi ^{L^2}p - q_h,{\textbf{w}}_h) - b(p_h - q_h,{\textbf{u}} - {\textbf{v}}_h)\\ \end{aligned}$$

where we used the properties of the $L^2$ projection $\pi ^{L^2}$, the commutative diagram (12) and $\nabla \cdot {\mathcal {M}}_h \subset Q_h$. Now, we utilize the choice $q_h = \pi ^{L^2} p$ to further simplify the representation of the second line in (46) to be

$$\begin{aligned} b(p,\varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h - {\textbf{w}}_h) +&\, b(p - q_h,{\textbf{w}}_h) - b(r_h,{\textbf{u}} - {\textbf{v}}_h) \\&= b(\pi ^{L^2}p - q_h,{\textbf{w}}_h) - b(p_h - q_h,{\textbf{u}}-{\textbf{v}}_h) \\&= b(\pi ^{L^2} p - p_h,{\textbf{u}} - {\textbf{v}}_h)\\&= 0 \end{aligned}$$

by our choice of ${\textbf{v}}_h$. This provides the bound

$$\begin{aligned} \begin{aligned} \frac{c\mu }{2}\Vert {\textbf{w}}_h\Vert ^2_1&+ \frac{1}{2\lambda } \Vert r_h\Vert ^2_0 \le 2\mu c \left( \sum \limits _{T \in {\mathcal {T}}_h} h^{2k}_T|{\textbf{u}}|^2_{k+1,T}\right) ^{\frac{1}{2}}\Vert {\textbf{w}}_h\Vert _1 \\&+ \frac{c\mu }{2}\Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1^2 + \frac{1}{2\lambda }\Vert p - q_h\Vert ^2_0. \end{aligned} \end{aligned}$$

(47)

Of course (47) provides a bound on ${\textbf{w}}_h$ but as it is suboptimal, in view of the $\lambda$ dependence, we continue by splitting ${\textbf{w}}_h = {\textbf{w}}_h^0+{\textbf{w}}_h^{\bot }$.

We first bound $\Vert {\textbf{w}}_h^0\Vert _1$. Consider $c\mu \Vert {\textbf{w}}_h^0\Vert _1$ and using that $a({\textbf{w}}_h^\bot , {\textbf{w}}_h^0) = 0$, we have, using (13), (43), and the choice of ${\textbf{v}}_h$ by (40) that

$$\begin{aligned} \begin{aligned} c\mu \Vert {\textbf{w}}_h^0\Vert _1^2&\le a({\textbf{w}}_h^0, {\textbf{w}}_h^0) = a({\textbf{w}}_h, {\textbf{w}}_h^0) = a({\textbf{w}}_h, {\textbf{w}}_h^0) + b(r_h, {\textbf{w}}_h^0) \\&= (f, \varvec{\pi }^{\mathrm{{div}}}{\varvec{w}}_h^0 - {\varvec{w}}_h^0) \\&\le \left( -2\mu \nabla \cdot \varepsilon ({\textbf{u}}) + \nabla p, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h^0 - {\textbf{w}}_h^0 \right) \\&\le \left( -2\mu \nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h^0 - {\textbf{w}}_h^0 \right) + \left( \nabla p, \varvec{\pi }^{\mathrm{{div}}}{\textbf{w}}_h^0 - {\textbf{w}}_h^0 \right) \\&\le \left( -2\mu \nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h^0\right) - \mu \left( \varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h^0)\right) \\&\le \mu \left( -2\nabla \cdot \varepsilon ({\textbf{u}}), \varvec{\pi }^{\mathrm{{div}}} {\textbf{w}}_h^0\right) - \mu \left( \varepsilon ({\textbf{u}}), \varepsilon ({\textbf{w}}_h^0)\right) . \\ \end{aligned} \end{aligned}$$

Thus, by Lemma 3, we conclude

$$\begin{aligned} c\mu \Vert {\textbf{w}}_h^0\Vert _1^2 \le \mu c \sum \limits _{T \in {\mathcal {T}}_h} h_T^k\Vert {\textbf{u}}\Vert _{k+1,T} \Vert {\textbf{w}}_h^0\Vert _{1,T} \le c\mu h^k \Vert {\textbf{u}}\Vert _{k+1} \Vert {\textbf{w}}_h^0\Vert _1 \\ \end{aligned}$$

and hence

$$\begin{aligned} \Vert {\textbf{w}}_h^0\Vert _1 \le ch^k \Vert {\textbf{u}}\Vert _{k+1}. \end{aligned}$$

(48)

For $\Vert {\textbf{w}}_h^\bot \Vert _1$, we utilize ${\textbf{w}}_h^\bot \in {\textbf{V}}_h^\bot$, i.e.,

$$\begin{aligned} \left( \nabla \cdot {\textbf{w}}_h, q_h\right) = \left( \nabla \cdot {\textbf{w}}_h^\bot , q_h\right) \qquad \forall q_h \in Q_h \end{aligned}$$

meaning

$$\begin{aligned} \pi ^{L^2} \nabla \cdot {\textbf{w}}_h = \pi ^{L^2}\nabla \cdot {\textbf{w}}_h^\bot . \end{aligned}$$

Using [13, Lemma 3.58], we get with a constant c depending on the inf-sup constant

$$\begin{aligned} \begin{aligned} \Vert {\textbf{w}}_h^\bot \Vert _1&\le c \Vert \pi ^{L^2} \left( \nabla \cdot {\textbf{w}}_h \right) \Vert _0 \\&\le c \Vert \pi ^{L^2} \nabla \cdot {\textbf{u}}_h - \pi ^{L^2}\nabla \cdot {\textbf{v}}_h\Vert _0 \\&\le c\Bigl \Vert \frac{p_h}{\lambda } - \pi ^{L^2}\nabla \cdot {\textbf{u}}\Bigr \Vert _0 \end{aligned} \end{aligned}$$

from the definition of ${\textbf{v}}_h$ in (40). Hence, noting that $\nabla \cdot u = \frac{1}{\lambda } p$, we obtain

$$\begin{aligned} \Vert {\textbf{w}}_h^\bot \Vert _1 \le \frac{c}{\lambda }\Vert p_h - q_h\Vert _0 = \frac{c}{\lambda } \Vert r_h\Vert _0. \end{aligned}$$

We conclude from (47)

$$\begin{aligned} \begin{aligned} \Vert r_h\Vert _0^2&\le c\mu \lambda h^{2k}\Vert {\textbf{u}}\Vert ^2_{k+1} + c\Vert p - q_h\Vert _0^2 \end{aligned} \end{aligned}$$

and thus we obtain the final bound on ${\textbf{w}}_h^\bot$

$$\begin{aligned} \begin{aligned} \Vert {\textbf{w}}_h^\bot \Vert _1&\le \frac{c}{\lambda } \Vert r_h\Vert _0\\&\le c\sqrt{\frac{\mu }{\lambda }}h^k\Vert {\textbf{u}}\Vert _{k+1} + \frac{c}{\lambda }\Vert p - q_h\Vert _0. \end{aligned} \end{aligned}$$

(49)

Now, we can bound $\Vert {\textbf{w}}_h\Vert _1$ using (48) and (49)

$$\begin{aligned} \begin{aligned} \Vert {\textbf{w}}_h\Vert _1&\le \Vert {\textbf{w}}_h^0\Vert _1 + \Vert {\textbf{w}}_h^\bot \Vert _1 \\&\le ch^k\Vert {\textbf{u}}\Vert _{k+1} + \frac{c}{\lambda }\Vert r_h\Vert _0 \\&\le ch^k\Vert {\textbf{u}}\Vert _{k+1} + c\sqrt{\frac{\mu }{\lambda }}h^k\Vert {\textbf{u}}\Vert _{k+1} + \frac{c}{\lambda }\Vert p -q_h\Vert _0\\&\le c\left( 1 + \sqrt{\frac{\mu }{\lambda }}\right) h^k\Vert {\textbf{u}}\Vert _{k+1} + \frac{c}{\lambda }\Vert p - q_h\Vert _0. \end{aligned} \end{aligned}$$

(50)

Finally, we arrive at the desired bound

$$\begin{aligned} \begin{aligned} \Vert {\textbf{u}} - {\textbf{u}}_h\Vert _1&\le \Vert {\textbf{u}} - {\textbf{v}}_h\Vert _1 + \Vert {\textbf{w}}_h\Vert _1 \\&\le c\left( 1 + \sqrt{\frac{\mu }{\lambda }}\right) h^k\Vert {\textbf{u}}\Vert _{k+1} + \frac{c}{\lambda }h^k\Vert p\Vert _k \end{aligned} \end{aligned}$$

(51)

by definition of $q_h$ and Assumption 1. $\square$

4 Numerical Results

For our computation, we use DOpElib [14] based on the deal.II [15] finite element library with rectangular meshes. All examples are posed on square domains and the meshes are obtained by bisection.

For the computation we considered the inf-sup stable Taylor-Hood element (${\mathcal {Q}}_2\times {\mathcal {Q}}_1$), for comparison of our results with [2]. Further, we utilized the inf-sup stable discretization ${\mathcal {Q}}_2\times {\text {DGP}}_1$ (discontinuous $P_1$ pressure) and its gradient robust modification by interpolation into $\mathcal {{\text {BDM}}}_2$ as discussed in Example 1.

First, we present an example for incompressible materials.

Example 2

For the first numerical example, we consider a small variation of Example 5.1 in [1], where the displacement and pressure on the domain $\Omega = (0,1)^2$ is given as

$$\begin{aligned}{} & {} {\textbf{u}}(x, y) = \begin{bmatrix} 200 x^2y (1-x)^2(1-y)(1-2y) \\ -200 y^2x(1-y)^2(1-x)(1-2x) \end{bmatrix} \end{aligned}$$

(52)

$$\begin{aligned}{} & {} p(x,y) = -10\left( \left( x - \frac{1}{2}\right) ^3y^2 + (1-x)^3\left( y-\frac{1}{2}\right) ^3 + \frac{1}{8}\right) . \end{aligned}$$

(53)

for the incompressible linear elasticity equation

$$\begin{aligned} \begin{aligned} -2\mu \nabla \cdot \varepsilon ({\textbf{u}}) + \nabla p = {\textbf{f}}, \\ \nabla \cdot {\textbf{u}} = 0 \end{aligned} \end{aligned}$$

(54)

with homogeneous boundary conditions on ${\textbf{u}}$ and thus define ${\textbf{f}}$, of course the pressure is defined up to a constant only.

Fig. 2

Comparing displacement error in $H^1$ norm vs. $\frac{1}{\mu }$ for Example 2 with and without gradient robust modification for 64 square elements

Comparing (9) with Fig. 2, we notice that the $H^1$-norm displacement error without interpolation asymptotically grows linearly w.r.t $\frac{1}{\mu }$ as predicted due to the appearance of the pressure term $\frac{1}{\mu } \inf \limits _{q_h \in Q_h} \Vert p - q_h\Vert _0$ in (9). The error is independent of $\mu$, highlighting the prediction of Theorem 2.

For future examples, we consider nearly incompressible materials given by equation (2).

Example 3

For the second numerical example, we set the right hand side $f = \nabla \phi ; \phi = x^6 + y^6$ on the domain $\Omega = (0,1)^2$ and consider nearly incompressible elasticity, i.e.,

$$\begin{aligned} \begin{aligned} -2\mu \, \nabla \cdot \varepsilon ({\textbf{u}}) - \nabla p&= {\textbf{f}}, \\ \nabla \cdot {\textbf{u}} - \frac{1}{\lambda } p&= 0 \end{aligned} \end{aligned}$$

with homogeneous boundary conditions on ${\textbf{u}}$ as in [2, Example 2].

Fig. 3

Comparing displacement error in $H^1$ norm for Example 3 with and without gradient robust modification for 64 square elements

From Lemma 1, the solution for Example 3 in the limiting case $(\lambda = \infty )$ is given as ${\textbf{u}}^\infty = 0$ and $p^\infty = x^6 + y^6$. From equation (30), we have the bound for the solution ${\textbf{u}}_h^\lambda$ as

$$\begin{aligned} \Vert {\textbf{u}}^\infty - {\textbf{u}}_h^\lambda \Vert _1 = \Vert {\textbf{u}}_h^\lambda \Vert _1 \le \frac{c}{\lambda + \mu } \Vert \phi \Vert _0 \end{aligned}$$

on the discrete function for a gradient robust discretization. For $\mu = 10^{-5}$, we have $\lambda + \mu \approx \lambda , \forall \lambda \ge 1$. Hence, we see a green line with positive slope in Fig. 3a for the gradient robust method, while the non robust method shows an almost constant $\Vert {\textbf{u}}^\lambda _h\Vert _1 \ne 0$. However, for $\lambda = 10^{5}$ we have $\frac{1}{\lambda + \mu } \approx c$(constant) $\forall 0 < \mu \le 1$, which is seen in the flat green line in Fig. 3b.

For non-gradient robust methods, we have

$$\begin{aligned} \Vert {\textbf{u}}^\lambda _h\Vert _1 \le \frac{c}{\mu }\left( \frac{1}{\lambda } + 1\right) \Vert \phi \Vert _0 \end{aligned}$$

from equation (9). For $\mu = 10^{-5}$, the term $\left( \frac{1}{\lambda } + 1\right) \rightarrow 1$ as $\lambda \rightarrow \infty$. The same is shown by the flat red line in Fig. 3a. However, for $\lambda = 10^{-5}$, we have $\Vert {\textbf{u}}^\lambda _h\Vert _1 \le \frac{c}{\mu }\Vert \phi \Vert _0$. Which is shown by the red line with negative slope in Fig. 3b.

It should be noted in this example, that the (blue with triangles) line for the non-gradient robust ${\mathcal {Q}}_2\times {\text {DGP}}_1$ method coincides with the (green with dots) line for the gradient robust modification. However, this appears to be due to the particular problem data hiding the non-gradient robustness of the ${\mathcal {Q}}_2\times {\text {DGP}}_1$ discretization. That indeed, the standard ${\mathcal {Q}}_2\times {\text {DGP}}_1$ method is not gradient robust is shown in the following example.

Example 4

For the third numerical example, we consider the right hand side $f = \nabla \phi ; \phi = -\left( 10(x-0.5)^3y^2 + (1-x)^3(y-0.5)^3 + 1/8\right)$ in Example 3 while keeping the homogeneous boundary values, and the equation, for ${\textbf{u}}$.

Figure 4 shows our previous statement, that Example 3 failed to show the missing gradient robustness of the standard ${\mathcal {Q}}_2 \times {\text {DGP}}_1$ discretization. Indeed, in this example, both ${\mathcal {Q}}_2\times {\mathcal {Q}}_1$ and ${\mathcal {Q}}_2 \times {\text {DGP}}_1$ discretization show the undesirable blowup for $\mu \rightarrow 0$ and the constant value as $\lambda \rightarrow \infty$, while the gradient robust modification shows the desired convergence.

Fig. 4

Comparing displacement error in $H^1$ norm for Example 4 with and without gradient robust modification for 64 square elements

Example 5

For the fourth numerical example, we consider, again, the nearly incompressible case with homogeneous boundary conditions on ${\textbf{u}}$, the values of ${\textbf{u}}^\infty$ and thus f are given as in Example 2 and the domain $\Omega = (0,1)^2$.

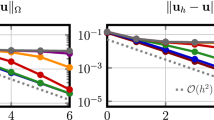
In this example, for $\lambda = \infty$, the solution ${\textbf{u}}^{\infty }$ is known, i.e., it is given in (52). We denote the solution, for $\lambda \ne \infty$, as $\left( {\textbf{u}}^\lambda , p^\lambda \right)$. We compute the error $\Vert {\textbf{u}}^\infty - {\textbf{u}}_h^\lambda \Vert _1$ in our numerical results, where ${\textbf{u}}_h^\lambda$ is the discrete approximated solution for a given value of $\lambda$. Since, Theorem 5 provides an estimate, for $\Vert {\textbf{u}}^\lambda - {\textbf{u}}^\lambda _h\Vert _1$, we use the triangle inequality to get

$$\begin{aligned} \begin{aligned} \Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda _h\Vert _1&\le \Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda \Vert _1 + \Vert {\textbf{u}}^\lambda - {\textbf{u}}^\lambda _h\Vert _1, \\&\le \Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda \Vert _1 + c\left( 1+\sqrt{\frac{\mu }{\lambda }}\right) h^2\Vert {\textbf{u}}^\lambda \Vert _3 + \frac{ch^2}{\lambda }\Vert p^\lambda \Vert _2. \end{aligned} \end{aligned}$$

(55)

Fig. 5

Comparing displacement error in $H^1$ norm for Example 5 with and without gradient robust modification for 64 square elements

Figure 5b follows the same pattern as Fig. 4b. However, there is a slight difference between Figs. 4a and 5a, which can be explained by (55). In the limit $\lambda \rightarrow \infty$ and fixed $\mu = 10^{-5}$, we have $\left( 1 + \sqrt{\frac{\mu }{\lambda }}\right) \rightarrow 1$ and $\Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda \Vert _1 \rightarrow 0$, and we observe

$$\begin{aligned} \Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda _h\Vert _1 \rightarrow \Vert {\textbf{u}}^\infty - {\textbf{u}}^\infty _h\Vert _1 \le ch^2\Vert {\textbf{u}}^\infty \Vert _3 \end{aligned}$$

(56)

for fixed refinement as it is shown in Fig. 5a. Figure 5a further confirms (56) as we can see the order ${\mathcal {O}}(h^2)$ for $\Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda _h\Vert _1$ for large values of $\lambda$. In Fig. 5b, we observe the convergence $\Vert {\textbf{u}}^\infty - {\textbf{u}}^\lambda _h\Vert _1 \rightarrow \Vert {\textbf{u}}^\infty -{\textbf{u}}^\lambda \Vert$ as $h \rightarrow 0$ and the decay of the error $\Vert {\textbf{u}}^\infty -{\textbf{u}}^\lambda \Vert \rightarrow 0$ as $\lambda \rightarrow 0$

Fig. 6

Comparing displacement error in $H^1$ norm for the robust modification of Example 5 for $\mu = 10^{-5}$

Fig. 7

Displacement vector for different number of elements with ${\mathcal {Q}}_2 \times {\text {DGP}}_1\times {\mathcal {Q}}_2$ with ${\text {BDM}}$ Interpolation

Example 6

Finally, we would like to compare our results with the thermo-elastic solids example given in [2, Sect. 6]. The gradient force ${\textbf{f}}$ is given by a temperature $\theta$ as

$$\begin{aligned} {\textbf{f}} = -\left( 2\mu + 3\lambda \right) \alpha \nabla \theta . \end{aligned}$$

The material used is a nearly incompressible hard rubber with Young’s Modulus $E = 5 \times 10^7[{\textrm{Pa}}]$, Poisson ratio $\nu = 0.4999$ and the thermal expansion coefficient $\alpha = 8 \times 10^{-5}[\mathrm {1/K}]$. Hence the Lamé parameters are $\lambda = 8.332 \times 10^{10}[{\textrm{Pa}}]$ and $\mu = 1.6667 \times 10^7[{\textrm{Pa}}]$. We take the domain $\Omega = (0, L)^2$ with $L = 0.1[\textrm{m}]$. The temperature field is obtained as the solution to the stationary heat equation:

$$\begin{aligned}-\nabla \cdot \gamma \nabla \theta = f,\end{aligned}$$

where $\gamma = 0.2[\mathrm {W/(m K)}]$ is the thermal conductivity coefficient and $f = 4 \times \textrm{exp}(-40r^2)[\mathrm {W/m^3}]$ is the heat source, with $r^2 = (x-0.5L)^2 + (y-0.5L)^2$. Homogeneous Dirichlet boundary conditions are applied on both temperature and displacement. It is important to note that $\theta \in H^1(\Omega )$ and thus ${\textbf{f}} \in L^2(\Omega ;{\mathbb {R}}^2)$. For numerical computation, we additionally solve the temperature equation by a standard $H^1$-conforming finite element discretization. Hence, the finite element spaces now consist of three components, the first two denote the displacement and pressure discretization as before. The third element, always ${\mathcal {Q}}_2$, is used to solve the equation for the temperature $\theta$.

In Fig. 7, we can see that we achieve a well represented solution for the displacement with only 64 elements using a gradient robust method, and the magnitude is already captured with only 16 elements. In comparison, the non gradient robust methods require 256 and 1024 elements, respectively, to get a solution of similar shape and magnitude, see Figs. 8 and 9.

Fig. 8

Displacement vector for different number of elements with ${\mathcal {Q}}_2 \times {\mathcal {Q}}_1\times {\mathcal {Q}}_2$

Fig. 9

Displacement vector for different number of elements with ${\mathcal {Q}}_2 \times {\text {DGP}}_1\times {\mathcal {Q}}_2$

5 Conclusion

In this paper, we have shown that a gradient robust modification of nearly incompressible elasticity is possible by the same techniques proposed for incompressible flows. For this gradient robust methods, we have shown convergence estimates of optimal order w.r.t the mesh size and optimal dependence on the Lamé-constants. Several numerical examples highlighted the proven convergence rates.