1 Introduction

Mesh adaptive methods exhibit an efficient tool for the numerical solution of partial differential equations (PDEs) since they are able to significantly reduce the computational cost necessary to achieve a given error tolerance [3, 5, 11, 32, 45]. The mesh adaptive methodology is well established for time-independent problems, where the current mesh is adapted based on suitable error estimates of the available approximate solution. This process is repeated several times until the required accuracy is achieved. If any inaccuracy appears during the computational process, it can be compensated by the computations on next adaptive levels, i.e., the error does not propagate. On the other hand, the numerical solution of time-dependent problems is more complicated since the computation is performed step-by-step and any inaccuracy propagates in the physical time.

Among the most efficient adaptive techniques belong the hp-methods which admit refinement (and coarsening) of the mesh elements and variation of the local polynomial approximation degrees. Under some assumptions, an exponential rate of convergence of the computational error with respect to the number of degrees of freedom can be achieved [4, 12, 32, 38, 40].

Moreover, the so-called anisotropic mesh adaptation techniques exhibit an efficient tool for the solution of problems containing interior or boundary layer and/or line discontinuities, see, e.g., [1, 8, 29,30,31, 44, 48] and the references mentioned therein. For a review, we refer to [34, 46]. In contrast to the standard mesh refinement method, where the mesh elements are merely split (isotropically and/or anisotropically), the current grid is completely re-meshed.

In recent years, we have developed the anisotropic hp-mesh adaptation method for the numerical solution of time-independent boundary value problems, which combines both aforementioned approaches [14, 19, 20]. This technique offers sufficient flexibility in the minimization of the number of degrees of freedom (and reduction of the computational time) necessary to achieve a given error tolerance. In particular, we derived interpolation error estimates employing the geometry of mesh elements which are used for the local optimization of the element shape and the polynomial approximation degrees. Further, using the so-called continuous mesh and error models (cf. [19, 29, 30]) the size of mesh elements is optimized, and the corresponding metric field, used for the mesh construction, is defined. For further details, see the references given above.

The extension of the anisotropic hp-mesh adaptation technique to the solution of time-dependent problems is not straightforward. The use of non-matching and non-nested, possibly anisotropic meshes at different time levels can produce inaccuracies, which propagate in time and can degrade the accuracy of the approximate solution. An adaptive finite element method employing isotropic but non-nested grids was proposed in [35] for a linear parabolic problem. In [27], a piecewise linear finite element approximation with anisotropic mesh adaptation controlling the error in \({L}^\infty (0,T;L^q(\varOmega ))\)-norm was proposed for the simulation of an unsteady bi-fluid model. Further, these techniques were developed and applied mostly to unsteady flow simulation, see, e.g., [2, 6, 26]. Finally, additional aspects of the adaptive methods for time-dependent problems on unstructured grids were developed, e.g., [9, 10, 37]. For theoretical aspects, we refer [7] and the references cited therein.

In this paper, we develop an anisotropic hp-mesh adaptive method for the numerical solution of the time-dependent partial differential equation written the form

$$\begin{aligned} \partial _t {\vartheta ({\varvec{w}})} + {\mathscr {L}}{\varvec{w}}= f \qquad \text{ in } \varOmega \times (0,T), \end{aligned}$$
(1)

where \(\varOmega \subset {\mathbb R}^2\) is the computational domain, \(T>0\) is the time to be reached and \({\varvec{w}}:\varOmega \times (0,T) \rightarrow {\mathbb R}^n\), \(n\ge 1\) is the sought unknown function. Moreover, \(\partial _t {}\) denotes the partial derivative with respect to \(t\in (0,T)\), \({\mathscr {L}}\) is a (possibly nonlinear) differential operator acting on \({\varvec{w}}\) and \(f:\varOmega \times (0,T)\rightarrow {\mathbb R}^n\) is a source term. Finally, \(\vartheta :{\mathbb R}^n\rightarrow {\mathbb R}^n\) is a function given by the physical model. In many cases it is an identity (i.e., \(\vartheta ({\varvec{w}})= {\varvec{w}}\)), but one of the numerical examples presented below addresses the simulation of variably saturated flow through a porous medium, where \(\vartheta \) is a nonlinear function of \({\varvec{w}}\). We assume that \(\varOmega \) is polygonal, for simplicity. Equation (1) is accompanied by the initial condition \( {\varvec{w}}(x, 0) = {\varvec{w}}_0(x)\), \(x\in \varOmega \), where \({\varvec{w}}_0:\varOmega \rightarrow {\mathbb R}^n\) is a prescribed function. Moreover, (1) has to be equipped with suitable boundary conditions depending on the properties of \({\mathscr {L}}\).

We discretize (1) by the space-time discontinuous Galerkin method, which treats different meshes at different time levels in a natural way. We adopt the aforementioned anisotropic hp-mesh adaptation technique to the solution of (1). The resulting space-time adaptive scheme admits hp-adaptation in space, as well as the adaptive choice of the size of the time step, but the time polynomial approximation degree is kept fixed. However, an adaptive choice of the time polynomial degree is possible in principle. We demonstrate the potential of the proposed scheme by a set of numerical experiments. In particular, we show that the use of non-matching, non-nested anisotropic hp-meshes at different time instances does not negatively affect the accuracy of numerical solution.

The content of the paper is the following. In Sect. 2 we describe the mesh optimization process for a given sufficiently regular function defined on a space domain \(\varOmega \). We present a theoretical framework leading to the hp-variant of the error equi-distribution, which is directly used in the adaptive algorithm. This is the first novelty of the paper. In Sect. 3 we briefly recall the discontinuous Galerkin discretization of problem (1). The main novelty is given in Sect. 4, where we extend our mesh adaptation technique to the numerical solution of (1). Several implementation aspects are presented and discussed. The performance of the proposed algorithm is demonstrated by several experiments in Sect. 5. A summary of the results is given in Sect 6.

2 Anisotropic hp-mesh Optimization Process for a Given Function

Let \(\varOmega \subset {\mathbb R}^2\) be the computational domain. In this section, we briefly describe the mesh optimization process for a given, sufficiently regular function \(w:\varOmega \rightarrow {\mathbb R}\). In this discussion, time dependence plays no role. The proposed method draws from our previous work on mesh optimization methods, based on interpolation error control using continuous mesh models. More details on this theoretical framework, including the possible extension to the 3D case, can be found in our recent monograph [18].

By \({\mathscr {T}}_{h{{\pmb {p}}}}=\{{{\mathscr {T}}_h},{\pmb {p}}\}\), we denote an hp-mesh of \(\varOmega \), where \({{\mathscr {T}}_h}=\{K\}\) is a conforming grid of \(\varOmega \) consisting of triangles K with mutually disjoint interiors, and the set of integers \({\pmb {p}}=\{{p_K}\in \mathbb {I},\ K\in {{\mathscr {T}}_h}\}\) represents the polynomial approximation degrees for each \(K\in {{\mathscr {T}}_h}\). In general, elements \(K\in {{\mathscr {T}}_h}\) are anisotropic but hanging nodes are not admitted.

To each hp-mesh \({\mathscr {T}}_{h{{\pmb {p}}}}\) there exists the unique space of discontinuous piecewise polynomial functions

$$\begin{aligned} S_{\!h{\pmb {p}}}:=\left\{ {{\varphi }_h}: \varOmega \rightarrow {\mathbb R};\ {{\varphi }_h}|_K\in P_{{p_K}}(K),\ K\in {{\mathscr {T}}_h}\right\} , \end{aligned}$$
(2)

where \( P_{{p_K}}(K) \) is the space of polynomial functions over \(K\in {\mathscr {T}}_{h{{\pmb {p}}}}\) with total degree at most \({p_K}\). The dimension of \(S_{\!h{\pmb {p}}}\) is given by \(\dim S_{\!h{\pmb {p}}}= \sum _{K\in {{\mathscr {T}}_h}}({p_K}+1)({p_K}+2)/2\). This value is called the number of degrees of freedom (\({\textrm{DoF}}\)).

Let \({C^{\infty }(\varOmega )}\) denote the space of infinitely differentiable functions. We introduce a projection \(\varPi _{h{{\pmb {p}}}}:{C^{\infty }(\varOmega )}\rightarrow S_{\!h{\pmb {p}}}\) such that

$$\begin{aligned} \textrm{D}^\alpha \varPi _{h{{\pmb {p}}}}w(x_K) =\textrm{D}^\alpha w(x_K)\quad \forall \alpha ,0\le |\alpha |\le p_K,\ K\in {{\mathscr {T}}_h}, \end{aligned}$$
(3)

where \(\alpha =(\alpha _1,\alpha _2)\) is a multi-index, \(\textrm{D}^\alpha \) denotes the partial derivative of degree \(|\alpha |=\alpha _1+\alpha _2\) and \(x_K\) is the barycenter of \(x_K,\ K\in {{\mathscr {T}}_h}\).

The projection \(\varPi _{h{{\pmb {p}}}}w\) is easy to construct element-wise and the difference \(w-\varPi _{h{{\pmb {p}}}}w\) is called the interpolation error. We are ready to formulate the main problem of this section.

Problem 1

Let \(w\in {C^{\infty }(\varOmega )}\) be a given function and let \({{\omega }}>0\) be a given tolerance. We seek an hp-mesh such that

  1. (i)

    \({\left\| {w-\varPi _{h{{\pmb {p}}}}w}\right\| _{}^{}} \le {{\omega }}\),

  2. (ii)

    \(\dim S_{\!h{\pmb {p}}}(={\textrm{DoF}})\) is minimal,

where \({\left\| {\cdot }\right\| _{}^{}} \) denotes the Lebesgue norm for some \(q\in [1,\infty ]\).

The existence (but not the uniqueness) of the solution of Problem 1 is guaranteed by Zorn’s lemma [28]: Since the set of hp-meshes satisfying (i) is nonempty and \(\dim S_{\!h{\pmb {p}}}>0\), this set has a minimal element. However, the practical search of an (approximate) solution of Problem 1 is not an easy task. One possible solution is the local setting of an optimal shape of mesh elements and the determination of the element size distribution using the continuous mesh and error models. These steps are briefly described in the rest of this section.

2.1 Interpolation Error Function and its Anisotropic Bound

We approximate the interpolation error \(w-\varPi _{h{{\pmb {p}}}}w\) on \(K\in {{\mathscr {T}}_h}\) by the Taylor polynomial of degree \({p_K}+1\) evaluated at the barycenter \(x_K=(x_{K,1}, x_{K,2})\). Hence, we define the interpolation error function at \(x_K\) by

$$\begin{aligned} {{e}_{x_K,p_K}^{w}}(x):= \sum _{|\alpha | = {p_K}+1} \frac{(|\alpha |-1)!}{\alpha _1!\,\alpha _2!} \frac{\partial ^{|\alpha |} w(x_K)}{\partial x_1^{\alpha _1} \partial x_2^{\alpha _2}} (x_1 - x_{K,1})^{\alpha _1} (x_2 - x_{K,2})^{\alpha _2} \end{aligned}$$
(4)

for \(x=(x_1,x_2)\in \varOmega \). Obviously, \({{e}_{x_K,p_K}^{w}}\) approximates \( w-\varPi _{h{{\pmb {p}}}}w\) on \(K\in {{\mathscr {T}}_h}\) and also on its neighbourhood (including the whole domain \(\varOmega \)). According to [14, Lemma 3.12], we have the following result: There exist \({ A_{w} }>0\), \({ \rho _{w} }\ge 1\) and \({\varphi _{w}}\in [0,2\pi ]\) such that

$$\begin{aligned} |{{e}_{x_K,p_K}^{w}}(x)| \le { A_{w} }\left( (x-x_K)^{{\textsf{T}}}\mathbb {Q}_{{\varphi _{w}}} \mathbb {D}_{{ \rho _{w} }} \mathbb {Q}_{\varphi _{w}}^{{\textsf{T}}}(x-x_K)\right) ^{({p_K}+1)/2}, \quad x\in \varOmega , \end{aligned}$$
(5)

where \(\mathbb {D}_{{ \rho _{w} }} = \textrm{diag}(1, { \rho _{w}^{-{2}/(p_K+1)} })\) is a \(2\times 2\) diagonal matrix and \(\mathbb {Q}_{{\varphi _{w}}}\) is a rotation matrix through the angle \({\varphi _{w}}\). The triple \(\{{ A_{w} },\,{ \rho _{w} },\,{\varphi _{w}}\}\) is called the anisotropic bound of the interpolation error \({{e}_{x_K,p_K}^{w}}\) at \(x_K\), and it depends on the partial derivatives of \(w\) at \(x_K\) appearing in (4). This triple can be determined by the procedure described in [14, Section 3.2].

Remark 1

The values \({ A_{w} }\), \({ \rho _{w} }\) and \({\varphi _{w}}\) depend only on the derivatives of degree \({p_K}+1\) of \(w\) at \(x_K\). Therefore, it is possible to evaluate them at any \(x\in \varOmega \) and for any integer \({p_K}\), hence we write

$$\begin{aligned} { A_{w} }={ A_{w} }(x,{p_K}),\ \ { \rho _{w} }={ \rho _{w} }(x,{p_K}),\ \ {\varphi _{w}}={\varphi _{w}}(x,{p_K}),\ \ x\in \varOmega ,\ {p_K}\in \mathbb {I}\end{aligned}$$
(6)

and call them the anisotropic bound functions.

They are employed in Sect. 2.5 in the framework of the continuous error model.

2.2 Geometry of Mesh Element

Let \( {\hat{K}}\) denote an equilateral reference triangle having the barycenter at the origin of the coordinate system and let \( {\hat{K}}\) be circumscribed by a unit circle. For each \(K\in {{\mathscr {T}}_h}\) there exists an affine mapping \(F_K\) which maps \( {\hat{K}}\) on K and can be written as \( F_K {\hat{x}}= \mathbb {F}_K {\hat{x}}+ x_K\), where \(\mathbb {F}_K\) is a \(2\times 2\) matrix. The singular value decomposition of \(\mathbb {F}_K\) gives

$$\begin{aligned} \mathbb {F}_K = \mathbb {Q}_{{\phi _K}} \mathbb {L}_K \mathbb {Q}_{\psi _K}^{\textsf{T}}, \end{aligned}$$
(7)

where \(\mathbb {Q}_{\phi _K}\) and \(\mathbb {Q}_{\psi _K}\) are rotation matrices through the angles \({\phi _K}\) and \(\psi _K\), respectively, and \(\mathbb {L}_K =\textrm{diag}(\ell _{K,1}, \ell _{K,2})\) is a diagonal matrix with the singular values \(\ell _{K,1}\ge \ell _{K,2}>0\). We define the geometry of triangle K by the triplet

$$\begin{aligned} \{{{\mu }}_K,\ {\sigma _K},\ \phi _K\},\qquad \text{ where } \quad {{\mu }}_K:=\sqrt{\ell _{K,1} \ell _{K,2}}, \quad {\sigma _K}:=\sqrt{\ell _{K,1}/\ell _{K,2}}, \end{aligned}$$
(8)

and \({\phi _K}\) is the angle of rotation from (7). We note that \({{\mu }}_K\sim |K|^{1/2}\) where |K| is the area of \(K\in {{\mathscr {T}}_h}\).

2.3 Interpolation Error Estimates Employing the Geometry of Mesh Elements

We formulate the estimate of the interpolation error function which takes into account the geometry of mesh elements. For brevity, we consider the case \( 1\le q< \infty \), the case \(q=\infty \) is easier to treat and we refer to [18, Chapter 3].

Lemma 1

Let \( q \in [1,\infty )\), \(K\in {{\mathscr {T}}_h}\) with the geometry \(\{{{\mu }}_K,\, {\sigma _K},\,{\phi _K}\}\) (cf. (8)), \(w\in P^{{p_K}}(K)\) and \({{e}_{x_K,p_K}^{w}}\) be the corresponding interpolation error function (4) with the anisotropic bound \(\{{ A_{w} },\, { \rho _{w} },\, {\varphi _{w}}\}\) at the barycenter \(x_K\) satisfying (5). Then

$$\begin{aligned} {\left\| {{{e}_{x_K,p_K}^{w}}}\right\| _{L^q(K)}^{q}} \le \frac{ { A_{w}^{q}}\, {{\mu }}_K^{q({p_K}+1)+2} }{q({p_K}+1)+2} \ G(q({p_K}+1)/2,{p_K}+1,{ \rho _{w} },{\varphi _{w}};{\sigma _K},{\phi _K}) \end{aligned}$$
(9)

where

$$\begin{aligned} G(s_1,s_2,\rho ,{\varphi };\sigma ,\phi )&= \! \int _0^{2\pi } \Big ( \sigma ^{2} [\cos ^2(\phi -{\varphi }) + { \rho ^{-{2}/{s_2}} }\sin ^2(\phi -{\varphi })] \cos ^2t \nonumber \\&\quad - 2 \sin (\phi -{\varphi }) \cos (\phi -{\varphi }) (1-{ \rho ^{-{2}/{s_2}} }) \sin t \cos t\nonumber \\&\quad + \sigma ^{-2} [\sin ^2(\phi -{\varphi }) + { \rho ^{-{2}/{s_2}} }\cos ^2(\phi -{\varphi })]\sin ^2t\Big )^{s_1} \,\textrm{d}t. \end{aligned}$$
(10)

Proof

For the proof we refer to [18, Lemma 3.21] or [20, Lemma 5.6], where the case \(q=2\) is treated. The idea is to integrate the q-power of (5) over K, transform the integral to the reference \( {\hat{K}}\) and bound the integral over \( {\hat{K}}\) by the integral over the circumscribed unit ball. By a direct computation, we obtain (9). \(\square \)

The minimization of function \(G\) from (10) with respect to \({\sigma _K}\) and \({\phi _K}\) allows us to find the optimal shape of triangle K with fixed area which minimizes the interpolation error bound in the \(L^q\)-norm. In particular, we have the following result:

Lemma 2

[18, Theorem 5.4] Let \(1\le q < \infty \), K be a triangle with size \({{\mu }}_K\) and barycenter \(x_K\). Let \(w\in P^{{p_K}}\) and \({{e}_{x_K,p_K}^{w}}\) be the corresponding interpolation error function (4) with the anisotropic bound \(\{{ A_{w} },\, { \rho _{w} },\, {\varphi _{w}}\}\) at \(x_K\) satisfying (5). Then triangle K, having the size \({{\mu }}_K\) and minimizing the upper bound of the interpolation error from Lemma 1, has the geometry

$$\begin{aligned} {\sigma _K}= { \rho _{w}^{{1}/{(2p_K+2)}} },\qquad {\phi _K}= \pi /2 + {\varphi _{w}}. \end{aligned}$$
(11)

Moreover, the corresponding interpolation error bound is

$$\begin{aligned} {\left\| {{{e}_{x_K,p_K}^{w}}}\right\| _{L^q(K)}^{q}}&\le \frac{2 \pi }{q ({p_K}+1)+2} { A_{w}^{q}}\,{ \rho _{w}^{-{q}/{2}} }\,{{\mu }}_K^{q ({p_K}+1) + 2},\qquad 1\le q< \infty . \end{aligned}$$
(12)

2.4 Continuous Mesh Model

The idea of the continuous mesh model was first introduced in [29, 30] for the h-variant of anisotropic mesh adaptation for piecewise linear approximation. It was extended to higher order piecewise polynomial approximation in [36] and to the hp-version in [19] . Let \({\mathscr {T}}_{h{{\pmb {p}}}}\) be an hp-mesh characterized by the values \(\{{{\mu }}_K,\ {\sigma _K},\ {\phi _K},\, {p_K}\}\), \(K\in {{\mathscr {T}}_h}\), cf. (8). The idea of the continuous mesh model is to define a continuous analogue of \({\mathscr {T}}_{h{{\pmb {p}}}}\) by the functions

$$\begin{aligned} \mu :\varOmega \rightarrow (0,\infty ),\quad {\sigma }:\varOmega \rightarrow [1,\infty ),\quad {\phi }:\varOmega \rightarrow [0,2\pi ),\quad {p}:\varOmega \rightarrow [1,\infty ) \end{aligned}$$
(13)

such that

$$\begin{aligned} \mu |_K \approx {{\mu }}_K,\quad {\sigma }|_K \approx {\sigma _K},\quad {\phi }|_K \approx {\phi _K},\quad {p}|_K \approx {p_K}. \end{aligned}$$
(14)

We call the function \(\mu \) the element size distribution and \({p}\) the polynomial degree distribution. Further, we define the complexity of the continuous mesh by

$$\begin{aligned} \mathcal N(\mu ,{p}) := \int _{\varOmega } {d}(x) \mu (x)^{-2}\,\textrm{d}x, \quad \text{ where } \ {d}(x):= \frac{({p}(x)+1)({p}(x)+2)}{2}, \end{aligned}$$
(15)

the integrand of the previous integral exhibits the density of \({\textrm{DoF}}\).

Remark 2

Using (14), we have from (15)

$$\begin{aligned} \mathcal N&= \frac{1}{2}\sum _{K\in {{\mathscr {T}}_h}} \int _{K} ({p}(x)+1)({p}(x)+2) \mu (x)^{-2}\,\textrm{d}x\nonumber \\&\approx \frac{1}{2}\sum _{K\in {{\mathscr {T}}_h}} \int _K ({p_K}+1)({p_K}+2){{\mu }}_K^{-2}\,\textrm{d}x\approx \frac{1}{2}\sum _{K\in {{\mathscr {T}}_h}} ({p_K}+1)({p_K}+2), \end{aligned}$$
(16)

where we have used the fact that that \(|K|\sim {{\mu }}_K^2\). The value on the right-hand side of (15) is equal to the dimension of the space \(S_{\!h{\pmb {p}}}\) corresponding to \({\mathscr {T}}_{h{{\pmb {p}}}}\).

2.5 Continuous Error Model

In the same spirit we introduce the continuous error model related to the interpolation error estimate (12). Let \({p}:\varOmega \rightarrow [1,\infty )\) be the polynomial degree distribution function from (13). In virtue of Remark 1, for \(w\in {C^{\infty }(\varOmega )}\), we set functions \({ A_{w} }(x) = { A_{w} }(x,\left[ {p}(x)\right] )\) and \({ \rho _{w} }(x) = { \rho _{w} }(x,\left[ {p}(x)\right] )\), \(x\in \varOmega \), cf. (6), where the symbol \(\left[ \cdot \right] \) denotes the nearest integer of its argument. In particular, for \(x\in \varOmega \), the values \({ A_{w} }(x)\) and \({ \rho _{w} }(x)\) are computed by the same procedure as the values in estimate (5) for \(x_K:=x\) and \({p_K}:=\left[ {p}(x)\right] \).

Then, we define the total continuous interpolation error estimate by

$$\begin{aligned} {\mathcal E}(\mu ,{p})&:= \int _{\varOmega } ({e}(x))^q\,\textrm{d}x, \end{aligned}$$
(17)

where

$$\begin{aligned} {e}(x) := {B}(x)\,\mu (x)^{({p}(x)+1) },\quad {B}(x) :=\left( \tfrac{2 \pi }{q ({p}(x)+1)+2}\right) ^{\frac{1}{q}} { A_{w} }(x)\,{ \rho _{w} }(x)^{-\frac{1}{2}} \end{aligned}$$
(18)

and \(\mu :\varOmega \rightarrow (0,\infty )\) is the element size distribution function, cf. (14).

Remark 3

Employing (14), we have from (17), (18) and (12) the relations

$$\begin{aligned} {\mathcal E}&= \sum _{K\in {{\mathscr {T}}_h}}\int _{K} ({e}(x))^q\,\textrm{d}x\approx \sum _{K\in {{\mathscr {T}}_h}}\int _{K} \tfrac{2 \pi }{q ({p_K}+1)+2} \left( { A_{w} }\,{ \rho _{w}^{-{1}/{2}} }\right) ^q\,{{\mu }}_K^{q({p_K}+1) }\,\textrm{d}x\nonumber \\&\approx \sum _{K\in {{\mathscr {T}}_h}} \tfrac{2 \pi }{q ({p_K}+1)+2} \left( { A_{w} }\,{ \rho _{w}^{-{1}/{2}} }\right) ^q\,{{\mu }}_K^{q({p_K}+1)+2 } \ge \sum _{K\in {{\mathscr {T}}_h}} {\left\| {{{e}_{x_K,p_K}^{w}}}\right\| _{L^q(K)}^{q}} , \end{aligned}$$
(19)

where we have used again that \(|K|\sim {{\mu }}_K^2\). Hence, relation (19) gives an analogue between the (discrete) interpolation error estimate (12) and its continuous variant (17).

2.6 hp-mesh Optimization Problem and its Solution

The continuous interpolation error estimate (17) depends on the element size and polynomial degree distributions \(\mu \) and \({p}\), respectively. We recall that the estimate (12) (and therefore (17)) makes sense if the mesh is locally optimized, i.e., (11) is valid. Now, we formulate the continuous analogue of the mesh-optimization Problem 1.

Problem 2

Let \({{\omega }}>0\) and \(w\in {C^{\infty }(\varOmega )}\) be given.

We seek functions \(\mu :\varOmega \rightarrow (0,\infty )\) and \({p}: \varOmega \rightarrow [1,\infty )\) such that

  1. (P1)

    \({\mathcal E}(\mu ,{p}) \le {{\omega }}\), where \({\mathcal E}\) is given by (17),

  2. (P2)

    \(\mathcal N(\mu ,{p}) \) given by (15) is minimal.

In principle, Problem 2 can be solved by the tools of constrained optimization. However, the presence of the unknown function \({p}\) in the exponent of \({\mathcal E}\) (cf. (18)) prevents us from finding an analytical solution, see Appendix. Therefore, in [19], we proposed a semi-analytical solution of Problem 2, which consists of two steps that can be repeated until a (pseudo-)convergence is achieved:

  1. (S1)

    fix the polynomial distribution function \({p}\) and, by the tools of variational calculus, find an optimal distribution of the element size distribution \(\mu \);

  2. (S2)

    having function \(\mu \), modify locally the polynomial approximation degree \(p_K\) for each \(K\in {{\mathscr {T}}_h}\) by selecting the degree giving the minimal error estimate for fixed density of \({\textrm{DoF}}\), cf. Sect. 2.6.2.

The step (S1) is resolved by the following Lemmas.

Lemma 3

Let \({{\omega }}>0\) and \(w\in {C^{\infty }(\varOmega )}\) be given.

Further, let \({p}:\varOmega \rightarrow [1,\infty )\) be the polynomial distribution function. Then element size distribution function \(\mu \), which fulfils conditions (P1) –(P2) of Problem 2, satisfies the relation

$$\begin{aligned} {q {B}(x)^q } ({p}(x)+2)^{-1}\big (\mu (x)\big )^{q({p}(x)+1)+2} = \text{ const } =:Z, \qquad \forall x\in \varOmega , \end{aligned}$$
(20)

where \({B}(x)={B}(x,{p}(x))\) is defined by (18).

Proof

We set the Lagrangian corresponding to (P2) with constraint (P1) as

$$\begin{aligned} {\mathscr {L}}(\mu , \lambda )&:= \mathcal N- \lambda ({{\omega }}- {\mathcal E}) \nonumber \\&=\int _{\varOmega } {d}(x) \mu (x)^{-2}\,\textrm{d}x- \lambda \left( {{\omega }}- \int _{\varOmega } \left( {B}(x)\,\mu (x)^{({p}(x)+1)} \right) ^q\,\textrm{d}x\right) , \end{aligned}$$
(21)

where \(0\not =\lambda \in {\mathbb R}\) is the Lagrange multiplier. Function \(\mu \) is the solution of Problem 2 (with fixed \({p}\)) if

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}{\mathscr {L}}(\mu +t \tilde{\mu }, \lambda )|_{t=0} = 0\quad \text{ for } \text{ any } \text{ perturbation } \tilde{\mu }. \end{aligned}$$
(22)

Then, from (21) – (22), we obtain by differentiation

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}t}{\mathscr {L}}(\mu +t \tilde{\mu }, \lambda )|_{t=0} \nonumber \\&\quad = \int _{\varOmega }\left( -2 {d}(x) \big (\mu (x)\big )^{-3} +\lambda q({p}(x)+1) {B}(x)^q\,\big (\mu (x)\big )^{q({p}(x)+1)-1} \right) \tilde{\mu }(x) \,\textrm{d}x. \end{aligned}$$
(23)

The right-hand side of (23) is equal to 0 for all perturbations \(\tilde{\mu }\) if

$$\begin{aligned}&0 = -2 {d}(x) \big (\mu (x)\big )^{-3} + \lambda q({p}(x)+1) {B}(x)^q\,\big (\mu (x)\big )^{q({p}(x)+1)-1} \nonumber \\&\quad \Longleftrightarrow \frac{1}{\lambda } = \frac{q({p}(x)+1) {B}(x)^q }{2 {d}(x) } \big (\mu (x)\big )^{q({p}(x)+1)+2}, \end{aligned}$$
(24)

which together with (15) implies (20) since \(\lambda \) is a constant. \(\square \)

A consequence of Lemma 3 is the following result, which can be employed in practical realization:

Lemma 4

Let \({p}\) be the polynomial distribution function and \(\mu \) be the element size distribution function satisfying (20). Then the interpolation error is equi-distributed over \(\varOmega \) in the sense

$$\begin{aligned} (p_K+2)^{-1}{{\left\| {u - \varPi _{h{{\pmb {p}}}}u}\right\| _{L^q(K)}^{q}} }{} \approx \text{ const } \qquad \forall K\in {{\mathscr {T}}_h}\end{aligned}$$
(25)

where \(p_K\approx {p}|_K\).

Proof

In virtue of (20), we have the identity related to the continuous mesh model

$$\begin{aligned}&\int _{K} ({e}(x))^q\,\textrm{d}x= \int _{K} {B}(x)^q\,\mu (x)^{q({p}(x)+1) }\,\textrm{d}x\nonumber \\&\quad = \int _{K} \underbrace{\frac{q {B}(x)^q }{{p}(x)+2} \big (\mu (x)\big )^{q({p}(x)+1)+2} }_{= Z \text{ due } \text{ to } (20)} \frac{ {p}(x)+2}{q \mu (x)^2} \,\textrm{d}x= \frac{Z}{q} \int _K \frac{ {p}(x)+2}{q \mu (x)^2} \,\textrm{d}x. \end{aligned}$$
(26)

The “transformation” of identity (26) to its discrete form by \({p}(x)|_K \approx p_K\), \(\mu (x)^2\sim |K|\) and \({\left\| {w- \varPi _{h{{\pmb {p}}}}w}\right\| _{L^q(K)}^{q}} \lesssim \int _{K} ({e}(x))^q\,\textrm{d}x\) (due to (19)) gives (25). \(\square \)

2.6.1 Setting the Size of the Mesh Elements (Step (S1))

We employ the error equi-distribution (25) for the optimization of the size of mesh elements. Obviously, we have to set \(\mu _K\), \(K\in {{\mathscr {T}}_h}\) such that the corresponding interpolation error estimates satisfy

$$\begin{aligned} \sum _{K\in {\mathscr {T}}_{h{{\pmb {p}}}}} e_K^q= {{\omega }}^q, \quad \text{ where } e_K:={\left\| {w- \varPi _{h{{\pmb {p}}}}w}\right\| _{L^q(K)}^{}} . \end{aligned}$$
(27)

From (25) we deduce that \({e_K^q}({p_K + 2})^{-1} \approx C\) for some \(C>0\) and consequently \(e_K^q\approx C (p_K + 2)\), \(K\in {{\mathscr {T}}_h}\). This relation together with (27) implies

$$\begin{aligned} {{\omega }}^q = \sum _{K\in {{\mathscr {T}}_h}} e_K^q= C \sum _{K}(p_K + 2) \qquad \Rightarrow \qquad C = \frac{{{\omega }}^q}{\sum _{K}(p_K + 2)}. \end{aligned}$$
(28)

Hence, we define the local tolerances

$$\begin{aligned} {{\omega }}_K := {{\omega }}\left( \frac{{p_K}+2}{\sum _{K\in {{\mathscr {T}}_h}}(p_K + 2)}\right) ^{1/q}, \qquad K\in {{\mathscr {T}}_h}, \end{aligned}$$
(29)

and the aim is to modify the element size \({{\mu }}_K\) such that \(e_K\approx {{\omega }}_K\) \(\forall K\in {{\mathscr {T}}_h}\).

Therefore, we set the new size of mesh elements \({\mu _K^\star }\) by the relation

$$\begin{aligned} {\mu _K^\star }= {{\mu }}_K\, \kappa (e_K/{{\omega }}_K), \qquad K\in {{\mathscr {T}}_h}, \end{aligned}$$
(30)

where \(\kappa >0\) is a scaling function continuously depending on \(e_K/{{\omega }}_K\) such that \(\kappa (e_K/{{\omega }}_K) > 1 \) for \(e_K< {{\omega }}_K\) and \(\kappa (e_K/{{\omega }}_K) < 1 \) for \(e_K> {{\omega }}_K\). A suitable choice is shown in Fig. 1, where \(\kappa \) attains the minimum 0.25 for large values \(e_K/{{\omega }}_K\) (= the maximal reduction of an element size in one level of mesh adaptation) and \(\kappa \) attains its maximum 2.5 for small values \(e_K/{{\omega }}_K\) (= the maximal increase of an element size in one level of mesh adaptation). The function \(\kappa \) is almost constant for \(e_K/{{\omega }}_K\approx 1\), which makes the algorithm more stable.

Fig. 1
figure 1

Example of function \(\kappa =\kappa (e_K/{{\omega }}_K)\)

Full size image

2.6.2 Setting of the Polynomial Approximation Degrees (Step (S2))

The polynomial approximation degrees are adapted locally for each \(K\in {{\mathscr {T}}_h}\). From the set \(Q_K:=\{p_K-1,\, p_K,\, p_K+1\}\), we select the new degree \({p_K^\star }\) which gives the smallest interpolation error bound for the same density of \({\textrm{DoF}}\) (cf. (15)). In particular, for each \(\ell \in Q_K\), we evaluate the anisotropic bound functions \({ A_{w,\ell } }\), \({ \rho _{w,\ell } }\) and \({\varphi _{w,\ell }}\), cf. (5) (depending on the \(\ell +1\)-th derivatives of \(w\)). In order to fix the density of \({\textrm{DoF}}\), we set the element sizes \({\mu }_{K,\ell }\), \(\ell \in Q_K\)

$$\begin{aligned} {\mu }_{K,\ell }:= {\mu _K^\star }\left( \frac{(\ell +1)(\ell +2)}{({p_K}+1)({p_K}+2)} \right) ^{1/2}, \qquad \ell \in Q_K. \end{aligned}$$
(31)

Then we evaluate the corresponding right-hand side of (12) as

$$\begin{aligned} E_K^{(\ell )}(w):= \frac{2 \pi }{q (\ell +1)+2} { A_{w,\ell } }\,({ \rho _{w,\ell } })^{-q/2} \,({\mu }_{K,\ell })^{q (\ell +1) + 2}, \quad \ell \in Q_K, \end{aligned}$$
(32)

and chose \(\ell \in Q_K\) minimizing this interpolation error bound, i.e.,

$$\begin{aligned} {p_K^\star }= \arg \min _{\ell \in Q_K} E_K^{(\ell )}, \qquad K\in {{\mathscr {T}}_h}. \end{aligned}$$
(33)

2.7 Mesh Adaptive Algorithm

Employing the setting of optimal shape (Lemma 2), optimal size (Sect. 2.6.1), and polynomial degree (Sect. 2.6.2) of mesh elements, we define Algorithm 1, which exhibits one iteration of a modification of the given hp-mesh \({\mathscr {T}}_{h{{\pmb {p}}}}\) to produce a new (better) hp-mesh \({\mathscr {T}}_{h{{\pmb {p}}}}^\star \).

figure a

The technique of the construction of \({\mathscr {T}}_{h{{\pmb {p}}}}^\star \) from \(\{{\mu _K^\star },{\sigma _K^\star },{\phi _K^\star },{p_K^\star };\ K\in {{\mathscr {T}}_h}\}\) (Step 9 of Algorithm 1) is carried out by a definition of a metric field over \(\varOmega \) and performing a sequence of local operations in order to construct an uniform triangulation under this metric.

Remark 4

The aforementioned metric is usually represented by a set of ellipses centered at barycentres of triangles of the mesh to be optimized. Each ellipse is defined as the smallest circumscribed ellipse of the triangle with geometry \(\{{\mu _K^\star },{\sigma _K^\star },{\phi _K^\star }\}\). For more detail, see, e.g., [18]. We use the in-house code Angener [13] to generate meshes from a prescribed metric.

Problem 1 can be solved approximately by performing several loops of Algorithm 1, see Algorithm 2. We note that sometimes it is necessary to carry out a high number of loops in Algorithm 2 in order to fulfil condition (i) of Problem 1. The number of loops can be reduced by calling subroutine \(hp\textrm{AMA}\) with a smaller tolerance \({{\omega }}\). Typically we choose one half or one quarter of the prescribed tolerance. Then condition (i) of Problem 1 is achieved earlier but the corresponding number of \({\textrm{DoF}}\) is naturally larger.

figure b

3 Space-Time Discontinuous Galerkin Method

In this section, we formulate the approximate solution of problem (1) by the time-discontinuous Galerkin method. By \(\left( {\cdot },{\cdot }\right) _{\!0}\), we denote the \(L^2(\varOmega )\)-scalar product.

3.1 Weak Solution

First, we formally introduce a weak formulation of (1). For simplicity, we assume that \(\vartheta \) is continuously differentiable. Let \({W}\) and \({V}\) be suitable spaces of the trial and test functions, respectively, related to the operator \({\mathscr {L}}\). We denote by \({\varvec{w}}(t)(x):= {\varvec{w}}(x,t)\) a function on \(\varOmega \) for any \(t\in (0,T)\). We say that function \({\varvec{w}}\) is the weak solution of (1) if \({\varvec{w}}(t)\in {W}\) for almost all \( t\in {W}\) and

$$\begin{aligned} \left( {\partial _t {\vartheta ({\varvec{w}})}},{{\varvec{v}}}\right) _{\!0} + a({\varvec{w}},{\varvec{v}})&= 0\qquad \forall {\varvec{v}}\in {V}, \text{ a.e. } t\in (0,T), \nonumber \\ \left( {{\varvec{w}}(\cdot , 0)},{{\varvec{v}}}\right) _{\!0}&= \left( {{\varvec{w}}_0},{{\varvec{v}}}\right) _{\!0}\qquad \forall {\varvec{v}}\in L^2(\varOmega ), \end{aligned}$$
(34)

where \(a(\cdot ,\cdot )\) represents the weak form of the operator \({\mathscr {L}}\). The right-hand side of (1) is included in a, which is nonlinear with respect its first argument, in general. We assume that there exists a unique weak solution of (34).

3.2 Space-Time Discretization

We approximate the solution of (34) by a space-time piecewise polynomial function defined on varying meshes for different time levels. Let \(0=t_0< t_1< t_2 <\dots t_r = T\) be a partition of [0, T], and we set the size of the time steps \(\tau _m:=t_m - t_{m-1}\) and the intervals \(I_m:=(t_{m-1}, t_m)\) for \(m=1,\dots ,r\). Obviously, this partition is not known a priori, but the time steps are chosen adaptively.

For each \(m=0,\dots ,r\), we consider a conforming triangular mesh \({{\mathscr {T}}_{h,m}}\) of \(\varOmega \) and hp-mesh \({{\mathscr {T}}_{h{{\pmb {p}}},m}}=\{{{\mathscr {T}}_{h,m}},{\pmb {p}}\}\), where \({\pmb {p}}=\{{p_K}\in \mathbb {I},\ K\in {{\mathscr {T}}_{h,m}}\}\), and \({p_K}\) denotes again the polynomial approximation degree assigned to \(K\in {{\mathscr {T}}_{h,m}}\). Then, for each \(m=0,\dots ,r\), we define the space

$$\begin{aligned} \pmb {S}_{h,{\pmb {p}},m}:=\left\{ {\pmb {{\varphi }}_h}: \varOmega \rightarrow {\mathbb R}^n;\ {\pmb {{\varphi }}_h}|_K\in [P_{\!{p_K}}(K)]^n,\ K\in {{\mathscr {T}}_{h,m}}\right\} , \end{aligned}$$
(35)

where \( [P_{{p_K}}(K)]^n \) denotes the space of vector-valued polynomial functions over \(K\in {{\mathscr {T}}_{h,m}}\) whose total degree is at most \({p_K}\) in each component of \({\pmb {{\varphi }}_h}=({\varphi }_1,\dots ,{\varphi }_n)^{\textsf{T}}\). We recall that \(n\ge 1\) denotes the number of equations in (1).

Whereas we consider a varying polynomial approximation degree \({p_K}\) with respect to space, the polynomial approximation degree \(q\ge 0\) is kept fixed. Hence, for any space-time element \({K\!\times \! I_m}\), \(K\in {{\mathscr {T}}_{h,m}},\ m=1,\dots , r\), we introduce the spaces of space-time polynomial functions

$$\begin{aligned} {P}_{\!{p_K}}^q({K\!\times \! I_m}):= \left\{ {{\varvec{v}}_h}(x,t)=\sum \nolimits _{j=0}^q t^j\, \pmb {\psi }_j(x),\ \pmb {\psi }_j\in [P_{\!{p_K}}(K)]^n,\, t\in I_m \right\} . \end{aligned}$$
(36)

Further, we define the space of piecewise polynomial functions over the space-time layer \(\varOmega \times I_m\) by

$$\begin{aligned} \pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}}:=\left\{ {{\varvec{v}}_h}:\varOmega \times I_m\rightarrow {\mathbb R}^n;\ {{\varvec{v}}_h}|_{{K\!\times \! I_m}} \in {P}_{\!{p_K}}^q({K\!\times \! I_m}),\ K\in {{\mathscr {T}}_{h,m}}\right\} , \end{aligned}$$
(37)

which consists of polynomials of degree \(q\ge 0 \) with respect to time. Later, we will employ the functional spaces \(\pmb {S}_{h,{\pmb {p}}+\pmb {1},m}^{\tau ,{q}}\), \(\pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}+1}\) and \(\pmb {S}_{h,{\pmb {p}}+\pmb {1},m}^{\tau ,{q}+1}\) defined as (37) by the increase of polynomial approximation degrees \({p_K},\ K\in {{\mathscr {T}}_{h,m}}\) and/or q by one. Finally, we define the space of polynomial functions over the whole space-time cylinder \(\varOmega \times (0,T)\) by

$$\begin{aligned} \pmb {S}_{h,{\pmb {p}}}^{\tau ,{q}}:=\left\{ {{\varvec{v}}_h}:\varOmega \times (0,T)\rightarrow {\mathbb R}^n;\ {{\varvec{v}}_h}|_{\varOmega \times I_m} \in \pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}}\quad \forall m=1,\dots , r\right\} . \end{aligned}$$
(38)

Obviously, functions from \(\pmb {S}_{h,{\pmb {p}}}^{\tau ,{q}}\) are discontinuous with respect to space as well as time coordinates.

Let \({{\varvec{w}}_{h\tau }}\in \pmb {S}_{h,{\pmb {p}}}^{\tau ,{q}}\). For each \(m=0,\dots ,r-1\), we define the traces of \({{\varvec{w}}_{h\tau }}\) at \(t_m\) and the jumps of \({{\varvec{w}}_{h\tau }}\) on \(t_m\) by

$$\begin{aligned} {{\varvec{w}}_{h\tau }}(x)|_{m}^\pm := \lim _{t\rightarrow t_{m}^\pm } {{\varvec{w}}_{h\tau }}(x,t), \quad \{\!\!\{{{{\varvec{w}}_{h\tau }}(x)}\}\!\!\}_{m}&:= {{\varvec{w}}_{h\tau }}(x)|_{m}^+ - {{\varvec{w}}_{h\tau }}(x)|_{m}^- \end{aligned}$$
(39)

for \(x\in \varOmega \). Hence, \( \{\!\!\{{{{\varvec{w}}_{h\tau }}}\}\!\!\}_{m-1}\) is a piecewise polynomial function on the “intersection” of meshes \({{\mathscr {T}}_{h{{\pmb {p}}},m-1}}\) and \({{\mathscr {T}}_{h{{\pmb {p}}},m}}\), \(m=1,\dots ,r\).

For \(m=1,\dots ,r\), we define the form \(A_{h,m}:\pmb {S}_{h,{\pmb {p}}}^{\tau ,{q}}\times \pmb {S}_{h,{\pmb {p}}}^{\tau ,{q}}\rightarrow {\mathbb R}\) by

$$\begin{aligned}&A_{h,m}({{\varvec{w}}_{h\tau }}, {{\varvec{v}}}) \nonumber \\&\quad := \int _{I_m} \Big ( \left( {\partial _t {\vartheta ({{\varvec{w}}_{h\tau }})}},{{{\varvec{v}}}}\right) _{\!0} + {a_h}({{\varvec{w}}_{h\tau }},{{\varvec{v}}})\Big ) \,\textrm{d}t+\left( {\{\!\!\{{\vartheta ({{\varvec{w}}_{h\tau }})}\}\!\!\}_{m-1}},{{{\varvec{v}}}|_{m-1}^+}\right) _{\!0}, \end{aligned}$$
(40)

where the form \({a_h}\) represents the discretization of the form a from (34). For more detail see, e.g., [16, Chapters 2-4]. Then the space-time discontinuous approximate solution reads:

Definition 1

We say that \({{\varvec{w}}_{h\tau }}\in \pmb {S}_{h,{\pmb {p}}}^{\tau ,{q}}\) is the approximate solution of (34) if

$$\begin{aligned} A_{h,m}({{\varvec{w}}_{h\tau }}, {{\varvec{v}}})&= 0\qquad \forall {{\varvec{v}}}\in \pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}},\quad m=1,\dots ,r, \end{aligned}$$
(41a)
$$\begin{aligned} \left( {{{\varvec{w}}_{h\tau }}|_{0}^-},{{{\varvec{v}}_h}}\right) _{\!0}&= \left( {{\varvec{w}}_0},{{{\varvec{v}}_h}}\right) _{\!0}\qquad \forall {{\varvec{v}}_h}\in \pmb {S}_{h,{\pmb {p}},0}. \end{aligned}$$
(41b)

Relations (1) represent systems of nonlinear algebraic equations of the size equal to the dimension of the space \(\pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}}\) for each time level \(m=1,\dots ,r\). We assume that there exists a unique approximate solution \({{\varvec{w}}_{h\tau }}\). We refer to [16, Chapter 6] for some theoretical results related to the existence and a priori error analysis for a convection-diffusion equation. In particular, for fixed polynomial approximation degree \({p_K}=p,\ K\in {{\mathscr {T}}_{h,m}},\ m=1,\dots ,r\), \(\tau := \max _{m=1,\dots ,r} \tau _m\) and \(h := \max _{m=1,\dots ,r} \max _{K\in {{\mathscr {T}}_{h,m}}} \textrm{diam}(K)\), we have

$$\begin{aligned} \max _{t\in (0,T)} {\left\| {{\varvec{w}}(t) - {{\varvec{w}}_{h\tau }}(t)}\right\| _{L^2(\varOmega )}^{}} \le C\left( h^{p+1} + \tau ^{q+1}\right) , \end{aligned}$$
(42)

provided that the exact weak solution \({\varvec{w}}\) is sufficiently regular.

3.3 Recomputation Between Meshes on Two Consecutive Time Levels

As mentioned above, the approximate solution is discontinuous with respect to time. The solution on two successive time intervals \(I_{m-1}\) and \(I_m\) is joined together in the weak sense by the last term on the left-hand side of (40), i.e.,

$$\begin{aligned} \left( {\{\!\!\{{\vartheta ({{\varvec{w}}_{h\tau }})}\}\!\!\}_{m-1}},{{{\varvec{v}}}|_{m-1}^+}\right) _{\!0} = \left( {\ \vartheta ({{\varvec{w}}_{h\tau }})|_{m-1}^+},{{{\varvec{v}}}|_{m-1}^+}\right) _{\!0} - \left( {\ \vartheta ({{\varvec{w}}_{h\tau }})|_{m-1}^-},{{{\varvec{v}}}|_{m-1}^+}\right) _{\!0}. \end{aligned}$$
(43)

Obviously, \({{\varvec{w}}_{h\tau }}|_{m-1}^+, {{\varvec{v}}}|_{m-1}^+\in \pmb {S}_{h,{\pmb {p}},m}\) but \({{\varvec{w}}_{h\tau }}|_{m-1}^-\in \pmb {S}_{h,{\pmb {p}},m-1}\). Therefore, the first term on the right-hand side of (43) is easy to evaluate by a numerical quadrature, but the evaluation of the second term is rather delicate since its arguments \({{\varvec{w}}_{h\tau }}|_{m-1}^-\) and \({{\varvec{v}}}|_{m-1}^+\) are given element-wise on different meshes \({{\mathscr {T}}_{h,m-1}}\) and \({{\mathscr {T}}_{h,m}}\), respectively. See Fig. 2, left, for an illustration. If the test function \({{\varvec{v}}}|_{m-1}^+\in \pmb {S}_{h,{\pmb {p}},m}\) has support on one element \(K\in {{\mathscr {T}}_{h,m}}\) (the blue triangle outlined in bold in Fig. 2, left), then it intersects several triangles \(K'\in {{\mathscr {T}}_{h,m-1}}\).

One possibility how to evaluate the last integral in (43) is to determine all intersections of any \(K\in {{\mathscr {T}}_{h,m}}\) with \(K'\in {{\mathscr {T}}_{h,m-1}}\), split the arising polygons onto triangles, and perform the integration over them. Although this approach is mathematically rigorous, its numerical implementation is rather complicated. Moreover, if the intersection of \(K\cap K'\) for some \(K'\in {{\mathscr {T}}_{h,m-1}}\) is very small and it has an obtuse shape then the numerical evaluation is ill-conditioned, see Fig. 2, center.

Fig. 2
figure 2

Example of the non-nested triangular meshes \({{\mathscr {T}}_{h,m-1}}\) (red) and \({{\mathscr {T}}_{h,m}}\) (blue) (left), “ill-conditioned” intersection of \(K\cap K',\ K\in {{\mathscr {T}}_{h,m}}\), \(K'\in {{\mathscr {T}}_{h,m-1}}\) (center), and inter-element splitting of \(K\in {{\mathscr {T}}_{h,m}}\) onto \(k\in D(K)\) (right)

Full size image

A more robust (and less accurate) approach is the evaluation of the last integral in (43) by a composite quadrature rule. In particular, let \({{\varvec{v}}}\) be a basis function of \(\pmb {S}_{h,{\pmb {p}},m}\) having a support on \(K\in {{\mathscr {T}}_{h,m}}\). Then

$$\begin{aligned} \left( {\ \vartheta ({{\varvec{w}}_{h\tau }})|_{m-1}^-},{{{\varvec{v}}}|_{m-1}^+}\right) _{\!0}&\approx \sum _{k\in D(K)} \sum _{i=1}^N \gamma _i \vartheta ({{\varvec{w}}_{h\tau }}(x_{k,i}))|_{m-1}^- {{\varvec{v}}}(x_{k,i})|_{m-1}^+, \end{aligned}$$
(44)

where D(K) denotes a non-overlapping partition of K onto simplexes k (cf. Figure 2, right), and the integrals over \(k\in D(K)\) are approximated by a quadrature with weights \(\gamma _i\) and nodes \(x_{k,i}\), \(i=1,\dots ,N\). In practice, K is split on 4, 9, or 16 self-similar sub-elements k and the Dunavant quadratures [22] are employed. In the experiments presented in this paper, the splitting on 9 sub-elements is employed, the use of more sub-elements has only a slight influence on the solution. Obviously, the quadrature nodes can belong to different \(K'\in {{\mathscr {T}}_{h,m-1}}\), and the order of any quadrature is low since the restriction of \(\vartheta ({{\varvec{w}}_{h\tau }})|_{m-1}^-\) is discontinuous on \(K\in {{\mathscr {T}}_{h,m}}\). However, we demonstrate in Sect. 5 that this approach is sufficiently accurate, namely that there is not an essential difference between the matching and non-matching grids.

4 Anisotropic hp-mesh Adaptation for Time-Dependent PDEs

In this section, we extend the mesh adaptive algorithm from Sect. 2 to the numerical solution of time-dependent problems. In Sect. 4.1, we introduce an analogue of Problem 1 and in Sect. 4.2, we describe the whole space-time adaptive procedure including several implementation issues.

4.1 Problem Formulation

Let \({\varvec{w}}(t)\in {W}\), \(t\in (0,T)\) be the weak solution of (34) and \(\{I_m\}_{m=1}^r\) be the partition of (0, T) introduced in Section 3.2. Let \(\varPi _{m}{\varvec{w}}(t)\in \pmb {S}_{h,{\pmb {p}},m}\) be the projections of \({\varvec{w}}(t)\), \(t\in I_m,\ m=1,\dots ,r\), cf. (35). In virtue of (42), we introduce the following problem:

Problem 3

Let \({{\omega }}>0\) be a given tolerance and \(\{I_m\}_{m=1}^r\) be the given partition of (0, T). We seek the finite sequence of spaces \(\pmb {S}_{h,{\pmb {p}},m}\), \(m=1,\dots ,r\) (i.e., meshes \({{\mathscr {T}}_{h,m}},\ m=1,\dots , r\) with the polynomial approximation degrees \({p_K},\ K\in {{\mathscr {T}}_{h,m}}\)) such that

  1. (i)

    \(\max _{m=1,\dots ,r}\max _{t\in I_m} {\left\| {{\varvec{w}}(t) - \varPi _{m}{\varvec{w}}(t)}\right\| _{L^q(\varOmega )}^{}} \le {{\omega }}\),

  2. (ii)

    \(\sum _{m=1}^r N_m\) is minimal, where \(N_m := \dim \pmb {S}_{h,{\pmb {p}},m}\).

Problem 3 means that we control the interpolation error \({\varvec{w}}-\varPi _{m}{\varvec{w}}\) for any time \(t\in (0,T)\). However, for practical reasons, it makes sense to consider the interpolation error only for a finite set of time levels, typically at the integration nodes used for the evaluation of the time integral over \(I_m\) in (41a) and at the endpoints of each \(I_m\). We denote such sets by \(J_m\), \(m=1,\dots ,r\). Therefore, we replace Problem 3 by

Problem 4

Let \({{\omega }}>0\) be a given tolerance and \(\{I_m\}_{m=1}^r\) be the given partition of (0, T). We seek the spaces \(\pmb {S}_{h,{\pmb {p}},m}\), \(m=1,\dots ,r\) such that

  1. (i)

    \(\max _{m=1,\dots ,r} \max _{t\in J_m} \Vert {\varvec{w}}(t) - \varPi _{m}{\varvec{w}}(t) \Vert \le {{\omega }}\),

  2. (ii)

    \(N_{h{{\pmb {p}}}}:=\sum _{m=1}^r N_m\) is minimal, where \(N_m := \dim \pmb {S}_{h,{\pmb {p}},m}\).

Similar to Problem 1, the space-time problem Problem 4 has a (possibly non-unique) solution. However, the practical solution of Problem 4 is rather difficult and we solve it approximately by the adopting the technique introduced in Sect. 2, which is described in the following section.

4.2 Full Space-Time Adaptive Method

4.2.1 Higher-Order Reconstruction

Condition 4 in Problem 4 contains the exact solution \({\varvec{w}}(t)\), \(t\in J_m\), which is not available in practice. Therefore, we replace \({\varvec{w}}\) in this condition by a higher-order reconstruction \({\widehat{{\varvec{w}}}_{h\tau }}\), computable from the approximate solution \({{\varvec{w}}_{h\tau }}\).

In [14, 19, 20], we developed a higher-order reconstruction technique based on the least squares approximation. Here, we present its space-time variant. Let \(I_m\), \(m=1,\dots ,r\) be an interval and \({{\varvec{w}}_{h\tau }}|_{\varOmega \times I_m}\in \pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}}\) be the space-time piecewise polynomial function satisfying (41a) for all \({{\varvec{v}}}\in \pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}}\). Let \(N(K),\ K\in {{\mathscr {T}}_{h,m}}\) be a set of \(K'\in {{\mathscr {T}}_{h,m}}\) sharing at least a vertex with K. We define the function \({\widehat{{\varvec{w}}}_{K,m}}\in {P}_{\!{p_K}+1}^{q+1}(N(K)\!\times \! I_m)\) (cf. (36)) such that

$$\begin{aligned} {\widehat{{\varvec{w}}}_{K,m}}= \arg \min _{{\varvec{u}}\in {P}_{\!{p_K}+1}^{q+1}(N(K)\!\times \! I_m)}\sum _{K'\in N(K)} \delta _{K'} {\left\| {{\varvec{u}}- {{\varvec{w}}_{h\tau }}}\right\| _{L^2(I_m, H^1(K'))}^{2}} , \end{aligned}$$
(45)

where \({\left\| {\cdot }\right\| _{L^2(I_m, H^1(K'))}^{}} \) is the Bochner norm over the space-time element \(K'\times I_m,\ K'\in N(K)\) and \(\delta _{K'} \ge 0\) are the weights. We set \(\delta _{K'} = 1\) for \(K'\) sharing a face with K, and \(\delta _{K'} = \epsilon \) for \(K'\in N(K)\) sharing only a vertex with K. A typical value is \(\epsilon = 0.25\). The reconstruction (45) is local, and \({\widehat{{\varvec{w}}}_{K,m}}\) approximates \({{\varvec{w}}_{h\tau }}\) in the weighted least-square sense. Having the local reconstructions \({\widehat{{\varvec{w}}}_{K,m}}\), \(K\in {{\mathscr {T}}_{h,m}}\), we set the global one \({\widehat{{\varvec{w}}}_{h\tau }}\in \pmb {S}_{h,{\pmb {p}}+\pmb {1},m}^{\tau ,{q}+1}\) by gluing them together, i.e.,

$$\begin{aligned} {\widehat{{\varvec{w}}}_{h\tau }}\in \pmb {S}_{h,{\pmb {p}}+\pmb {1},m}^{\tau ,{q}+1},\quad {\widehat{{\varvec{w}}}_{h\tau }}|_{{K\!\times \! I_m}} := {\widehat{{\varvec{w}}}_{K,m}}|_{{K\!\times \! I_m}} \quad \forall K\in {{\mathscr {T}}_{h,m}}. \end{aligned}$$
(46)

4.2.2 Adaptive Choice of the Time Step

In Problem 4 we considered an a priori given partition of the time interval (0, T). In practical computations, the choice of the size of time steps \(\tau _m:=t_m - t_{m-1}\), \(m=1,\dots \), has to be done adaptively based on the available approximate solution. It is necessary to balance the accuracy (too large time steps cause increase of the computational error) and the efficiency (too small time steps increase the number of time steps and can prolongate the computational time). A reasonable strategy is to choose the time step in such a way that the errors arising from the spatial and temporal discretizations are comparable. We employ the approach proposed in [21], where the space and time errors are estimated by residual-based estimators \(\eta _\textrm{S}^m\) and \(\eta _\textrm{T}^m\), respectively. The numerical examples in [21] show that, whereas \(\eta _\textrm{S}^m\) is (almost) independent on \(\tau _m\), \(m=1,\dots ,r\), the time estimator fulfills \(\eta _\textrm{T}^m= O(\tau _m^{q+1})\). Then \(\tau _m\) is chosen such that

$$\begin{aligned} \eta _\textrm{T}^m\approx c_T \eta _\textrm{S}^m,\qquad m=1,\dots ,r, \end{aligned}$$
(47)

where \(0< c_T \le 1\) is the chosen safety factor. Typically we put \(c_T=0.1\). The aforementioned estimators are defined for each \(m=1,\dots ,r\), using (37), by

$$\begin{aligned} \eta _\textrm{S}^m({u_{h\tau }}) := \max _{{{\varvec{v}}_h}\in \pmb {S}_{h,{\pmb {p}}+\pmb {1},m}^{\tau ,{q}}} \frac{A_{h,m}({{\varvec{w}}_{h\tau }}, {{\varvec{v}}})}{{\left\| {{{\varvec{v}}}}\right\| _{S}^{}} },\quad \eta _\textrm{T}^m({u_{h\tau }}) = \max _{{{\varvec{v}}_h}\in \pmb {S}_{h,{\pmb {p}},m}^{\tau ,{q}+1}} \frac{A_{h,m}({{\varvec{w}}_{h\tau }}, {{\varvec{v}}})}{{\left\| {{{\varvec{v}}}}\right\| _{S}^{}} }, \end{aligned}$$
(48)

where the norm is chosen element-wise as

$$\begin{aligned} {\left\| {{{\varvec{v}}}}\right\| _{S}^{2}} := \sum _{K\in {{\mathscr {T}}_{h,m}}}\big ({\left\| {{{\varvec{v}}}}\right\| _{L^2({K\!\times \! I_m})}^{2}} + {\left\| {\nabla {{\varvec{v}}}}\right\| _{L^2({K\!\times \! I_m})}^{2}} + {\left\| {\partial _t {{{\varvec{v}}}}}\right\| _{L^2({K\!\times \! I_m})}^{2}} \big ). \end{aligned}$$
(49)

Due to the choice (49), both estimators in (48) are computable element-wise and therefore their setting is cheap.

In order to fulfill (47), we have developed in [21] the adaptive choice of the time step by the relation \(\eta _\textrm{T}^m= O(\tau _m^{q+1})\), cf. (42). However, this technique is not sufficiently efficient, e. g., for porous media flow problems, probably by the lack of regularity of the weak solution.

Therefore, we present here a more robust and efficient technique. We set the parameter \(\xi _m := \log ({\eta _\textrm{T}^m}/({c_T \eta _\textrm{S}^m}))\) for \(m=1,\dots ,r\). Obviously, the optimal size of the time step gives \(\xi _m \approx 0\). Moreover, if \(\xi _m > 0\) the time step should be decreased, and if \(\xi _m < 0\) the time step should be increased. The new size of the time step is set according to the following empirical formula

$$\begin{aligned} \tau _m^{\textrm{new}} = \beta \tau _m, \end{aligned}$$
(50)

where

$$\begin{aligned} \beta =\beta (\xi _m) := {\left\{ \begin{array}{ll} s_{\max } &{} \text{ if } {\xi _m} \le -S, \\ \frac{s_{\max }-s_{\min }}{2} \left( \cos (\pi \frac{\xi _m+S}{2S}) + 1\right) + s_{\min } &{} \text{ if } -S< {\xi _m} < S, \\ s_{\min }&{} \text{ if } S \le {\xi _m}, \\ \end{array}\right. } \end{aligned}$$

and S, \(s_{\max }\) and \(s_{\min }\) are user-defined parameters. Obviously, \(\beta (\xi _m)\) is continuously differentiable with respect to \(\xi _m\). The values \(s_{\max } > 1\) and \(s_{\min }>0\) describe the maximal relative increase and the maximal relative decrease of the time step, respectively, and \(S>0\) is the threshold. We use the values \(S=1\), \(s_{\max }=1.25\), and \(s_{\min }=0.5\).

The idea of the adaptive choice of the time step during the computational procedure is the following: We perform the m-th step by the solution of (41a) and evaluate \(\eta _\textrm{S}^m\) and \(\eta _\textrm{T}^m\). If condition \(\eta _\textrm{T}^m> c_T \eta _\textrm{S}^m\) (cf. (47)), the current time step is refused and we repeat it with a new time step size \(\tau ^{\textrm{new}}\) given by (50). Otherwise, we proceed to the next time step, again using \(\tau ^{\textrm{new}}\) from (50). Alternatively, although not considered here, it would be possible to increase the time polynomial degree or repeat several last time steps.

Finally, let us note that based on numerical experience, we automatically reduce the size of the time step by a factor \(\beta = s_{\min }\) after each re-meshing. This typically helps us to avoid several time steps which are rejected. The whole adaptive algorithm is explained in the next section.

4.2.3 Adaptive Algorithm

The whole adaptive procedure for the solution of time-dependent PDEs is summarized in Algorithm 3. At each time step, we check if the error estimator \(\eta _m\) is under the given tolerance (cf. step 14 of Algorithm 3). If this condition is satisfied, we use the hp-mesh from the previous time step(s). Otherwise, we perform a re-meshing. We employ the anisotropic hp-mesh adaptation technique from Sect. 2, namely we call the subroutine \(hp\textrm{AMA}\) (cf. Algorithm 1) for the solution at \(t|_{m-1}^+\) and \(t|_{m}^-\) in each time step \(m=1,\dots ,r\), see steps 17 and 18 of Algorithm 3. Then we obtain two hp-meshes, denoted as \({\mathscr {T}}_{h{{\pmb {p}}}}^{(\textrm{L})}\) and \({\mathscr {T}}_{h{{\pmb {p}}}}^{(\textrm{R})}\), and then we apply the so-called intersection of metrics \({\mathscr {T}}_{h{{\pmb {p}}}}^{(\textrm{L})}\cap {\mathscr {T}}_{h{{\pmb {p}}}}^{(\textrm{R})}\) (Step 19 of Algorithm 3). For the relation between a metric and a mesh, see Remark 4.

The intersection of two metrics are defined through the geometrical intersection of two corresponding ellipses having the same barycenter as the ellipse which is a subset of both ellipses and having the maximal possible area. Moreover, concerning the choice of the polynomial approximation degree, we adopt technique (31)–(33) in such a way that in step (32), we take the maximal value from \(E_K^{(\ell )}({\widehat{{\varvec{w}}}_{h\tau }}|_{m-1}^+)\) and \(E_K^{(\ell )}({\widehat{{\varvec{w}}}_{h\tau }}|_{m}^-)\) for each \(\ell \in Q_K\), \(K\in {{\mathscr {T}}_{h,m}}\).

figure c

Finally, we note that it is possible to reduce the number of re-meshing operations by using a smaller input tolerance in the calls of Algorithm 1, cf. steps 17-18 of Algorithm 3. However, the resulting hp-grids have naturally higher number of \({\textrm{DoF}}\), and then the reduction of computational cost is questionable.

5 Numerical Verification

In this section, we present several numerical experiments demonstrating the ability of the proposed anisotropic hp-mesh method to solve various problems of type (1). First, we consider a scalar nonlinear convection-diffusion equation with known analytical solution where the exact error and its estimate can be compared. Moreover, we consider several more complicated test examples, namely the isentropic vortex propagation (inviscid compressible flow), the Kelvin-Helmholtz instability (viscous compressible flow) and the simulation of a flow though a variably saturated porous media described by the Richards equation. In all cases, we employ the space-time discontinuous Galerkin method. For the description of the method together with the implementation detail, we refer to [16] and for the porous media problem to [17].

5.1 Moving Interior Layer

We solve the viscous Burgers equation written as

$$\begin{aligned} \partial _t {w} + w \frac{\partial {w}}{\partial {x_1}} + w \frac{\partial {w}}{\partial {x_2}} - \varepsilon \Delta {w} = 0 \qquad \text{ in } \varOmega \times (0,T), \end{aligned}$$
(51)

where \(\varOmega = (-1,1)\times (-1,1)\), \(T=1\) and \(\varepsilon > 0\) is the diffusion coefficient. We prescribe the Dirichlet boundary condition on \({\varGamma }:=\partial \varOmega \) and the initial condition such that the exact solution reads

$$\begin{aligned} w(x_1,x_2,t) =\left( 1+\exp \left( (x_1+ x_2 +1 - t)/2\varepsilon \right) \right) ^{-1},\quad (x_1,x_2)\in \varOmega ,\ t\in (0,T). \end{aligned}$$
(52)

This problem exhibits a propagation of an interior layer in the diagonal direction (1, 1). The width of the layer is proportional to \(\varepsilon \). We consider the values \(\varepsilon =10^{-2}\) and \(\varepsilon =10^{-3}\).

Since the exact solution is available, we are able to evaluate the exact error and compare it to the proposed error estimate. To produce reference data, we carried out the computation on fixed uniform triangular grids consisting of rectangular triangles with element size \(h=1/6\), \(h=1/12\), and \(h=1/24\). We employ the polynomial approximations \(p=1,2,3\) with respect to space and \(q=1,2\) with respect to time. The time step was fixed at \(\tau =10^{-2}\).

The computations on the fixed grids are compared to the anisotropic hp-mesh adaptation, Algorithm 3, with several tolerances \({{\omega }}\). The initial mesh was a coarse uniform (\(h=1/6\)) and the initial polynomial degree was set to \(p_K=2\), \(K\in {{\mathscr {T}}_h}\). The corresponding results are shown in Tables 1–4, where

  • \({\textrm{DoF}}\) is the average number of degrees of freedom per time step,

  • \(\#\tau _m \) is the number of time steps needed to reach the final time T,

  • \( e_h:={\left\| {w-{w_{h\tau }}}\right\| _{L^\infty (0,T; L^2(\varOmega ))}^{}} \) is the error of the approximate solution \({w_{h\tau }}\),

  • \( E_h:={\left\| {\widehat{w}_{h\tau }-{w_{h\tau }}}\right\| _{L^\infty (0,T; L^2(\varOmega ))}^{}} \) is the corresponding error estimate obtained by the higher-order reconstruction,

  • the quantities

    $$\begin{aligned} J^{\textrm{aver}}= \frac{1}{r}\sum _{m=1}^r \Vert \{{w_{h\tau }}\}_{m} \Vert _{L^2(\varOmega )}, \quad J^{\textrm{max}} = \max _{m=1,\dots ,r} \Vert \{{w_{h\tau }}\}_{m} \Vert _{L^2(\varOmega )} \end{aligned}$$
    (53)

    measure the jumps with respect to time (the “time-inconsistency”) due to the time discontinuous approximation,

  • \( i_N\) is the total number of nonlinear iteration for all time levels,

  • \(i_L\) is the total number of linear (GMRES) iteration for all nonlinear iterations and all time levels,

  • “time” is the total computational time in seconds. It depends on the implementation so it has only an informative character.

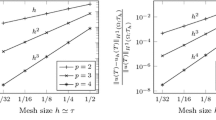
Some outputs from these tables are also shown for \(q=2\) in Fig. 3, namely the convergence of the error \(e_h\) and its estimate \(E_h\) with respect to \({\textrm{DoF}}\) and computational time.

Table 1 Moving interior layer (51)–(52) with \(\varepsilon =10^{-2}\), computations without adaptation and with fixed time step
Full size table
Table 2 Moving interior layer (51)–(52) with \(\varepsilon =10^{-2}\), computations using anisotropic hp-mesh adaptation
Full size table
Table 3 Moving interior layer (51)–(52) with \(\varepsilon =10^{-3}\), computations without adaptation and with fixed time step
Full size table
Table 4 Moving interior layer (51)–(52) with \(\varepsilon =10^{-3}\), computations using anisotropic hp-mesh adaptation
Full size table

As one might expect, we observe that higher polynomial approximation degree on fixed meshes leads to faster decay of the errors and higher efficiency in terms of \({\textrm{DoF}}\) as well as computational time. The use of mesh adaptation significantly reduces the computational cost required to achieve the given error tolerance. Moreover, the error estimate using the higher order reconstruction does not provide an upper bound of the error, but the approximation is reasonable, as the rates of \(e_h\) and \(E_h\) are quite similar. Finally, comparing the values \( J^{\textrm{aver}}\) and \(J^{\textrm{max}} \), we arrive at the conclusion that the use of non-nested meshes with the recomputation from Sect. 3.3 does not bring any essential increase of the inaccuracies. These values depend on the polynomial approximation degree with respect to time (for \(q=2\) they are much smaller than for \(q=1\)), but there are minor differences between the computation with and without mesh adaptation.

Fig. 3
figure 3

Moving interior layer (51)–(52) with \(\varepsilon =10^{-2}\), the convergence of the error \(e_h\) (full lines) and its estimate \(E_h\) (dashed lines) with respect to \({\textrm{DoF}}\) (left) and computational time (right), comparison of the computations without mesh adaptation using \(P_p,\ p=1,2,3\) and the computation with hp-mesh adaptation

Full size image

Moreover, Fig. 4 demonstrates the performance of Algorithm 3. The left-hand-side figure shows the error estimate \(\eta _m\) of all computed time steps (blue square boxes). The time steps having \(\eta _m> {{\omega }}\) are refused, while the accepted time steps are marked by black crosses. The right-hand side figure shows the comparison of the error \({\left\| {w-{w_{h\tau }}}\right\| _{L^{\infty }(I_m,L^2(\varOmega ))}^{}} \) and its estimate \(\eta _m\) for all (accepted as well as refused) time steps \(m=1,\dots ,r\). We observe a reasonable approximation of the error locally in time.

Fig. 4
figure 4

Moving interior layer (51)–(52) with \(\varepsilon =10^{-2}\), performance of Algorithm 3, error estimate for all and the accepted time steps (left) and the comparison of the error and its estimate (right) with respect to the physical time

Full size image

Finally, Figs. 5 and 6 show the achieved hp-meshes and the corresponding isolines of the solution at time instants \(t=0.2\), \(t=0.6\), and \(t=1.0\). We observe a strong anisotropic refinement along the interior layers, the refinement is stronger for the case with \(\varepsilon =10^{-3}\). Outside of the layer, the mesh consists of large elements with the lowest polynomial approximation degree. The isolines show a perfect capturing without any oscillations.

Fig. 5
figure 5

Moving interior layer (51)–(52) with \(\varepsilon =10^{-2}\), hp-meshes obtained by Algorithm 3 with \({{\omega }}=2.5\cdot 10^{-4}\) (top) and the corresponding isolines of the solution (right) at \(t=0.2\), \(t=0.6\) and \(t=1.0\) (from left to right)

Full size image
Fig. 6
figure 6

Moving interior layer (51)–(52) with \(\varepsilon =10^{-3}\), hp-meshes obtained by Algorithm 3 with \({{\omega }}=5\cdot 10^{-4}\) (top) and the corresponding isolines of the solution (right) at \(t=0.2\), \(t=0.6\) and \(t=1.0\) (from left to right)

Full size image

5.2 Isentropic Vortex Propagation

The propagation of an isentropic vortex through the periodic domain is a classical benchmark proposed in [39]. This problem is described by the compressible Euler equations where the sought solution vector is \({\varvec{w}}=(\rho ,{\varvec{v}},e)^{{\textsf{T}}}\in {\mathbb R}^4\): \(\rho \) is the density, \({\varvec{v}}\) is the velocity vector, and e is the energy. This system is accompanied by the state equation defining the relation between the energy and pressure \(\textrm{p}\), namely \(e = \textrm{p}/(\gamma -1) + \tfrac{1}{2}\rho |{\varvec{v}}|^2\), where \(\gamma =1.4\) is the adiabatic Poisson constant. For details, we refer to, e.g., [25, 47].

We consider the computational domain \(\varOmega :=[0,10]\times [0,10]\) which is extended periodically in both directions. The mean flow is defined by \(\bar{\rho }=1\), \(\bar{{\varvec{v}}}=(1,1)^{{\textsf{T}}}\) and \(\bar{\textrm{p}}=1\). An isentropic vortex is added to the mean flow, i.e., there is a perturbation in \({\varvec{v}}\) and the temperature \(\theta =\textrm{p}/\rho \), but no perturbation in the entropy \(S=\textrm{p}/\rho ^{\gamma }\), where \(\gamma \) is the Poisson constant. For analytical relations we refer to [39] or [16, Chapter 8].

The aforementioned problem setting leads to the passive convection of the vortex with the mean velocity, hence the analytical solution is available and the error can be evaluated. In particular, the flow is time-periodic with the period \(\bar{t}=10\), i.e., we have \({\varvec{w}}(x,t) = {\varvec{w}}(x,t+10)\) for all \(x\in \varOmega \) and \(t>0\). We carried out the computation till \(T=30\), hence 3 time-periods have been computed.

We applied Algorithm 3 with several tolerances. The corresponding results are shown in Table 5. The symbols are the same as in the previous example. Obviously, for decreasing tolerances, the error as well as its estimates are decreasing. Similar to the scalar example from Sect. 5.1, we observe a reasonable approximation of the error by the interpolation error in the \(L^\infty (0,T; L^2(\varOmega ))\)-norm. The time inconsistency quantities \(J^{\textrm{aver}}\) and \(J^{\textrm{max}} \) are decreasing for decreasing tolerances.

Figure 7 shows the error and its estimates for all time steps (including the refused time steps). We observe that although the error approximation during the first period (\(t\in (0,10)\)) is reasonable, the error starts to increase during the second period, whereas the error estimate is under the tolerance \({{\omega }}\). This is caused by the fact that the computational error is accumulated for the long time interval, whereas the higher-order reconstruction is local in time.

Moreover, Fig. 8 shows the hp-meshes and the isolines of the Mach number \(M:=|{\varvec{v}}|/\sqrt{\gamma \textrm{p}/\rho }\) at the time levels \(t=10\), \(t=20\) and \(t=30\). As mentioned above, the exact solution fulfills \({\varvec{w}}(\cdot , 10) = {\varvec{w}}(\cdot , 20) = {\varvec{w}}(\cdot , 30)\), and we observe that the graphs of isolines are very similar. This effect is also demonstrated by Fig. 9 where the distribution of the density and the Mach number along the diagonal cut through the vortex at \(t=10\), \(t=20\), and \(t=30\) are shown. We observe almost identical results. Hence the use of non-nested anisotropic hp-meshes in combination with space-time DGM does not cause any essential lost of accuracy.

Table 5 Isentropic vortex propagation, computations using Algorithm 3
Full size table
Fig. 7
figure 7

Isentropic vortex propagation, performance of Algorithm 3, error estimate for all time steps with respect to the physical time (left) and the comparison of the error and its estimate (right)

Full size image
Fig. 8
figure 8

Isentropic vortex propagation, hp-meshes obtained by Algorithm 3 with \({{\omega }}=5\cdot 10^{-4}\) (top) and the corresponding isolines of the solution (bottom) at \(t=10\), \(t=20\) and \(t=30\) (from left to right)

Full size image
Fig. 9
figure 9

Isentropic vortex propagation, diagonal cuts of the density (top) and the Mach number (bottom) at \(t=10\), \(t=20\) and \(t=30\) (from left to right)

Full size image

5.3 Kelvin-Helmholtz Instability

The next example exhibits the simulation of the Kelvin-Helmholtz instability, which appears when a velocity difference across the interface between two fluids is presented. Then there appear the typical Kelvin-Helmholtz roll-ups, which are challenging to simulate numerically. The problem is described by the compressible Navier-Stokes equation having the same sought vector \({\varvec{w}}= (\rho , v_1, v_2, e)\) as in Sect. 5.2. For details, we refer again to [25, 47].

We consider exactly the same setting as in [42]. The computational domain \(\varOmega =(0,1)^2\) is extended periodically in both directions and the final time is \(T=2\). The initial conditions are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho = 2,\ v_1 = - 0.5 + \varepsilon ,\ v_2 = \varepsilon ,\ \textrm{p}= 2.5 &{} \text{ if } 0.25< x_2 < 0.75, \\ \rho = 1,\ v_1 = 0.5 + \varepsilon ,\quad v_2 = \varepsilon ,\ \textrm{p}= 2.5 &{} \text{ if } 0.25 \ge x_2 \text{ or } x_2 \ge 0.75, \\ \end{array}\right. } \end{aligned}$$
(54)

where we set \(\varepsilon = 0.01\sin (4\pi x_1)\) to trip the instability. We consider the fluid viscosity \(\mu = 2\cdot 10^{-4}\), the heat capacity at constant pressure \(c_p = 1005\), the adiabatic Poisson constant \(\gamma =1.4\), and the Prandtl number \(Pr = 0.72\).

Figure 10 shows the hp-meshes and the density distribution obtained by Algorithm 3 at several time instants. We observe the development of the roll-ups and the expectable hp-mesh adaptation. High polynomial degrees are generated within the roll-ups, the shapes of elements follow their directions. The lowest polynomial degrees (\(p=1\)) are outside the interfaces where the solution is almost constant.

Fig. 10
figure 10

Kelvin-Helmholtz instabilities arising from the initial condition (54), hp-meshes obtained by Algorithm 3 and the corresponding density distribution at \(t=0\), 0.4, 0.8, 1.2, 1.6 and \(t=2\) (from left to right and from top to bottom)

Full size image

5.4 Simulation of the Single Ring Infiltration

The last example exhibits a simulation of the flow through a variably saturated medium described by the Richards equation, written in the form

$$\begin{aligned} \partial _t {(}\vartheta ({\psi })) - \nabla \cdot ({\textbf{K}}({\psi }) \nabla {\varPsi }) = 0\qquad \text{ in } \varOmega \times (0,T), \end{aligned}$$
(55)

where \({\psi }\) and \({\varPsi }\) denote the pressure and hydraulic heads, respectively, related by \({\varPsi }= {\psi }+ x_2\), and \(x_2\) is the vertical coordinate. Moreover, \({\textbf{K}}({\psi })\) is the unsaturated hydraulic conductivity given by \( {\textbf{K}}({\psi }) = K_r({\psi }) {\textbf{K}}_s\), where \(K_r({\psi })\) is the relative hydraulic conductivity, and \({\textbf{K}}_s\) is the saturated hydraulic conductivity tensor. Furthermore, \(\vartheta ({\psi })\) denotes the active pore volume given by \( \vartheta ({\psi }) := \theta ({\psi }) + \frac{S_s}{\theta _S} \int _{-\infty }^{{\psi }} \theta (\xi )\,\textrm{d}\xi \), where \(\theta ({\psi })\) is the water content function, \(\theta _S\) is the limited saturated water content, and \(S_s\) is the specific storativity. The function \(\theta ({\psi })\) is given by the van Genuchten’s law [43], and the relative conductivity \(K_r({\psi })\) is given by the Mualem function [33]. For a more detailed description we refer to, e.g., [17, 41]. Both functions, \(\vartheta \) and \({\textbf{K}}\), depend nonlinearly on their arguments, and they are not continuously-differentiable at \({\psi }=0\), which causes difficulties in the convergence of the solvers.

We consider the simulation of the single-ring infiltration. The computational domain is shown in Fig. 11. At the time \(t=0\), a dry medium with \({\varPsi }= -2\) is prescribed. On the boundary part \(\varGamma _D\) we set the Dirichlet boundary condition \({\varPsi }= 1.05\), and on \(\partial \varOmega \setminus \varGamma _D\) we consider the homogeneous Neumann boundary condition. We note that the smaller “magenta” vertical lines starting at \(\varGamma _D\) also belong to the boundary and they are impermeable. The inconsistency of the initial and boundary condition on \(\varGamma _D\) makes the computation rather difficult for \(t\approx 0\).

Fig. 11
figure 11

Single ring infiltration, the computational domain with the input (Dirichlet) boundary \(\varGamma _D\) and the rest of the boundary (red and magenta), where the homogeneous Neumann boundary condition is used

Full size image

We carried out the computation until the physical time \(T=2\) hours, and we are interested in the water flux through the boundary \(\varGamma _D\). Hence, we consider two quantities, the actual flux and the total (accumulated) flux given by

$$\begin{aligned}&F(t) := -\int _{\varGamma _2} {\textbf{K}}({\psi }) \nabla {\varPsi }(x,t)\cdot {\varvec{n}}\,\textrm{d}S, \quad t\in [0,T], \nonumber \\ \text{ and }\qquad&{\overline{F}}(t) := -\int _0^t \int _{\varGamma _2} {\textbf{K}}({\psi }) \nabla {\varPsi }(x,t')\cdot {\varvec{n}}\,\textrm{d}S\textrm{d} t', \quad t\in [0,T], \end{aligned}$$
(56)

respectively. The results obtained by Algorithm 3 for several tolerances are shown in Table 6. Besides the quantities measuring the jumps with respect to the time, the number of algebraic iterations, and computational time, we present the accumulated flux \({\overline{F}}(T)\) and also the quantity \(\delta (T)\) indicating the conservativity of the numerical method. Namely, \(\delta (t)\) is the relative difference between the increase of the water contents \(\int _{\varOmega } (\vartheta (x, t) - \vartheta (x, 0))\,\textrm{d}x\) and the total flux \(-\int _0^t \int _{\partial \varOmega } {\textbf{K}}({\psi }) \nabla {\varPsi }(x,t')\cdot {\varvec{n}}\,\textrm{d}S\textrm{d} t'\) (\(\approx {\overline{F}}(t)\) due to the prescribed boundary conditions). Table 6 shows that \(\delta (T)\) is about 1% which is an acceptable inaccuracy.

Furthermore, Fig. 12 presents the dependence of the actual flux F(t) on \(t\in (0,T)\) for the treated tolerance. The left figure shows the global view and the other ones the details close \(t=0\) and \(t=T\). We observe that the computations with lower tolerances do not capture the behavior well. On the other hand, this inaccuracy affects the total flux only slightly.

Table 6 Single ring infiltration, computations using anisotropic hp-mesh adaptation
Full size table
Fig. 12
figure 12

Single ring infiltration, dependence of the actual flux F(t) on \(t\in (0,T)\) for the treated tolerance, total view (left), the details near \(t=0\) (center) and \(t=T\) (right)

Full size image

Moreover, Fig. 13 shows the hp-meshes and the distribution of the hydraulic head at selected time levels obtained from Algorithm 3 with \({{\omega }}=\)5E-03. Finally, we note that computational times observed for this example (last column in Table 6) are very large, which is caused by the high number of linear and nonlinear iterations. This is caused in turn by the non-regularity of the constitutive relations for \(\vartheta \) and \({\textbf{K}}\) in (55). Hence, the use of an efficient adaptation method, which significantly reduces the number of \({\textrm{DoF}}\), is an essential tool which can accelerate the computational process.

Fig. 13
figure 13

Single ring infiltration, hp-meshes obtained by Algorithm 3 with \({{\omega }}=5\cdot 10^{-4}\) (top) and the corresponding hydraulic head distribution (right) at \(t=0.4\), \(t=0.8\) and \(t=2\) hours (from left to right)

Full size image

6 Summary

We proposed an adaptive space-time discontinuous Galerkin method for the numerical solution of time-dependent PDEs based on the control of the interpolation error, which is estimated by the space-time variant of a higher-order reconstruction. If the interpolation error estimate is over the prescribed tolerance in the particular time step, the computational grid is completely re-meshed including the shape of elements and the polynomial approximation degrees, and the time step is repeated. Thus the anisotropic methodology reliably aligns the grid with dominant solution features leading to significant error reduction. Although the grids employed at the different time steps are non-nested and non-matching, a simple recomputation technique among them does not lead to any essential decrease of accuracy. This effect was demonstrated by the presented numerical examples.

One downside of the current approach is that the interpolation error estimates employed do not provide an upper bound of the error. One possibility is to use the approach developed, e.g., in [23, 24]. However, from a practical point of view, a better option seems to be the development of goal-oriented error estimates. We dealt with this technique in [15, 20] for time-independent problems. Nevertheless, the goal-oriented anisotropic hp-mesh adaptation method for time dependent problems is currently completely open.

Finally, the presented approach is based on the minimization of the number of degrees of freedom. However, the reduction of \({\textrm{DoF}}\) does not imply the reduction of the computational cost at the same rate. The presence of anisotropic elements, as well as the varying polynomial approximation degrees, typically increase the difficulty in the solution of the arising algebraic systems. The effect requires a deeper numerical analysis which will be the subject of further research.