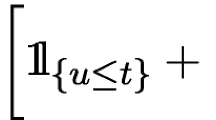Computation of Conditional Expectations with Guarantees

Abstract

Theoretically, the conditional expectation of a square-integrable random variable Y given a d-dimensional random vector X can be obtained by minimizing the mean squared distance between Y and f(X) over all Borel measurable functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$. However, in many applications this minimization problem cannot be solved exactly, and instead, a numerical method which computes an approximate minimum over a suitable subfamily of Borel functions has to be used. The quality of the result depends on the adequacy of the subfamily and the performance of the numerical method. In this paper, we derive an expected value representation of the minimal mean squared distance which in many applications can efficiently be approximated with a standard Monte Carlo average. This enables us to provide guarantees for the accuracy of any numerical approximation of a given conditional expectation. We illustrate the method by assessing the quality of approximate conditional expectations obtained by linear, polynomial and neural network regression in different concrete examples.

1 Introduction

The goal of this paper is to compute the conditional expectation $\mathbb {E}[Y \mid X]$ of a square-integrable random variable Y given a d-dimensional random vector X, both defined on a common probability space $(\Omega , \mathcal {F}, \mathbb {P})$. The accurate estimation of conditional expectations is an important problem arising in different branches of science and engineering as well as finance, economics and various business applications. In particular, it plays a central role in regression analysis, which tries to model the relationship between a response variable Y and a number of explanatory variables $X_1, \dots , X_d$ [see, e.g., [17, 20, 29, 36]]. But it also appears in different computational problems, such as the numerical approximation of partial differential equations and backward stochastic differential equations [see, e.g., [4, 7, 10, 19, 21, 25, 26]], stochastic partial differential equations [see, e.g., [6]], stochastic control problems [see, e.g., [2, 3]], stochastic filtering [see, e.g., [31]], complex financial valuation problems [see, e.g. [8, 11, 12, 16, 35, 37]] as well as financial risk management [see, e.g. [5, 13, 18, 28, 34]]. In addition, conditional expectations are closely related to squared loss minimization problems arising in various machine learning applications [see, e.g., [27, 29]].

If it is possible to simulate from the conditional distribution of Y given X, the conditional expectation $\mathbb {E}[Y \mid X]$ can be approximated with nested Monte Carlo simulation; see, e.g., [5, 13, 14]]. While the approach can be shown to converge for increasing sample sizes, it often is too time-consuming to be useful in practical applications. On the other hand, it is well known that $\mathbb {E}[Y \mid X]$ is of the form $\bar{f}(X)$ for a regression function $\bar{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ which can be characterized as a minimizer¹ of the mean squared distance

$$\begin{aligned} \mathbb {E} \! \left[ (Y - f(X))^2 \right] \end{aligned}$$

(1.1)

over all Borel functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$ [see, e.g., [15]]. However, in many applications, the minimization problem (1.1) cannot be solved exactly. For instance, the joint distribution of X and Y might not be known precisely, or the problem might be too complicated to admit a closed-form solution. In such cases, it can be approximated with a least squares regression, consisting in minimizing an empirical mean squared distance

$$\begin{aligned} \frac{1}{M} \sum _{m=1}^M \left( \mathcal {Y}^m - f(\mathcal {X}^m) \right) ^2 \end{aligned}$$

(1.2)

based on realizations $(\mathcal {X}^m,\mathcal {Y}^m)$ of (X, Y) over a suitable family $\mathcal{S}$ of Borel functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$. This typically entails the following three types of approximation errors:

• (i) a function approximation error if the true regression function $\bar{f}$ does not belong to the function family $\mathcal{S}$;

• (ii) a statistical error stemming from estimating the expected value (1.1) with (1.2);

• (iii) a numerical error if the minimization of (1.2) over $\mathcal {S}$ has to be solved numerically.

Instead of analyzing the errors (i)–(iii), we here derive an alternative representation of the minimal mean squared distance $\mathbb {E}[(Y - \bar{f}(X))^2]$, which does not involve a minimization problem or require knowledge of the true regression function $\bar{f}$. This enables us to provide quantitative estimates on the accuracy of any numerical approximation $\hat{f}$ of $\bar{f}$. In particular, if $\hat{f}$ is determined with a machine learning method that is difficult to interpret, our approach contributes to trustworthy AI.

While the empirical mean squared distance (1.2) can directly be minimized using realizations $(\mathcal {X}^m, \mathcal {Y}^m)$ of (X, Y), our approach to derive error bounds for the approximation of $\bar{f}$ requires Y to be of the form $Y = h(X,V)$ for a known function $h :\mathbb {R}^{d+k} \rightarrow \mathbb {R}$ and a k-dimensional random vector V independent of X. In typical statistical applications, only realizations of (X, Y) can be observed and a structure of the form $Y = h(X,V)$ would have to be inferred from the data. But in many of the computational problems mentioned above, Y is directly given in the form $Y = h(X,V)$.

The rest of the paper is organized as follows: In Sect. 2, we first introduce the notation and some preliminary results before we formulate the precise mean squared distance minimization problem we are considering along with its empirical counterpart. Then we discuss upper bounds of the minimal mean squared distance and their approximation with Monte Carlo averages. In Sect. 3 we derive an expected value representation of the minimal mean squared distance which makes it possible to derive bounds on the $L^2$-error of any numerical approximation $\hat{f}$ of the true regression function $\bar{f}$. In Sect. 4 we compute conditional expectations in different examples using linear regression, polynomial regression and feedforward neural networks with varying activation functions. We benchmark the numerical results against values obtained from our expected value representation of the minimal mean squared distance and derive $L^2$-error estimates. Section 5 concludes, and in the Appendix we report auxiliary numerical results used to compute the figures shown in Sect. 4.

2 Numerical Approximation of Conditional Expectations

2.1 Notation and Preliminaries

Let us first note that the mean squared distance (1.1) does not necessarily have to be minimized with respect to the original probability measure $\mathbb {P}$. Indeed, the regression function $\bar{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ only depends on the conditional distribution of Y given X and not on the distribution $\nu _X$ of X. More precisely, the measure $\mathbb {P}$ can be disintegrated as

$$\begin{aligned} \mathbb {P}[A] = \int _{\mathbb {R}^d} \mathbb {P}[A \mid X = x] d\nu _X(x), \quad A \in \mathcal{F}, \end{aligned}$$

where $\mathbb {P}[. \mid X = x]$ is a regular conditional version of $\mathbb {P}$ given X. For any Borel probability measure $\nu$ on $\mathbb {R}^d$ that is absolutely continuous with respect to $\nu _X$,

$$\begin{aligned} \mathbb {P}^{\nu }[A]:= \int _{\mathbb {R}^d} \mathbb {P}[A \mid X = x] d\nu (x), \quad A \in \mathcal{F}, \end{aligned}$$

defines a probability measure on $\Omega$ under which X has the modified distribution $\nu$ while the conditional distribution of Y given X is the same as under $\mathbb {P}$. Let us denote by $\mathbb {E}^{\nu }$ the expectation with respect to $\mathbb {P}^{\nu }$ and by $\mathcal{B}(\mathbb {R}^d; \mathbb {R})$ the set of all Borel functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$. With this notation, one has the following.

Lemma 2.1

Assume $\mathbb {E}^{\nu } Y^2 < \infty$. Then a minimizer $\tilde{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ of the distorted minimal mean squared distance

$$\begin{aligned} D^{\nu }:= \min _{f \in \mathcal{B}(\mathbb {R}^d; \, \mathbb {R})} \mathbb {E}^{\nu } \! \left[ \left( Y - f(X) \right) ^2 \right] \end{aligned}$$

(2.1)

agrees with $\bar{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ $\nu$-almost surely. In particular, if $\nu$ has the same null sets as $\nu _X$, then $\tilde{f} = \bar{f}$ $\nu _X$-almost surely.

Proof

A Borel function $\tilde{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ minimizes (2.1) if and only if

$$\begin{aligned} \tilde{f}(x) = {{\,\mathrm{arg\,min}\,}}_{z \in \mathbb {R}} \int _{\mathbb {R}} (y - z)^2 \, \mathbb {P}[Y \in dy \mid X = x] \quad \hbox {for }\nu \hbox {-almost all } x \in \mathbb {R}^d. \end{aligned}$$

Since $\bar{f}$ has an analogous representation holding for $\nu _X$-almost all $x \in \mathbb {R}^d$, it follows that $\tilde{f}$ agrees with $\bar{f}$ $\nu$-almost surely. In particular, if $\nu$ has the same null sets as $\nu _X$, then $\tilde{f} = \bar{f}$ $\nu _X$-almost surely. $\square$

Lemma 2.1 gives us the flexibility to choose a distribution $\nu$ on $\mathbb {R}^d$ which assigns more weight than $\nu _X$ to regions of $\mathbb {R}^d$ that are important in a given application. For instance, $\nu \ll \nu _X$ can be chosen so as to concentrate more weight around a given point $x_0$ in the support of $\nu _X$; see Lemma 3.6 and Sect. 4.2.2 below. On the other hand, in financial risk management one is usually concerned with the tails of loss distributions. Then the distribution $\nu _X$ can be tilted in the direction of large losses of a financial exposure; see Sect. 4.4.2 below.

2.2 Upper Bound of the Minimal Mean Squared Distance

In many situations, the minimization problem (2.1) cannot be solved exactly. But if one has access to $\mathbb {P}^{\nu }$-realizations $(\mathcal {X}^m, \mathcal {Y}^m)$ of (X, Y), the true regression function $\bar{f}$ can be approximated by minimizing the empirical mean squared distance

$$\begin{aligned} \frac{1}{M} \sum _{m =1}^M \left( \mathcal {Y}^m - f(\mathcal {X}^m) \right) ^2 \end{aligned}$$

(2.2)

over f in a subset $\mathcal{S}$ of $\mathcal{B}(\mathbb {R}^d; \mathbb {R})$. In the examples of Sect. 4 below, we compare results obtained by using linear combinations of $1, X_1, \dots , X_d$, second order polynomials in $X_1, \dots , X_d$ as well as feedforward neural networks with different activation functions.

But irrespective of the method used to obtain an approximation of $\bar{f}$, any Borel measurable candidate regression function $\hat{f}: \mathbb {R}^d \rightarrow \mathbb {R}$ yields an upper bound

$$\begin{aligned} U^{\nu }:= \mathbb {E}^{\nu } \! \left[ \left( Y - \hat{f}(X) \right) ^2 \right] \end{aligned}$$

(2.3)

of the minimal mean squared distance $D^{\nu }$. However, since in typical applications, $U^{\nu }$ cannot be calculated exactly, we approximate it with a Monte Carlo estimate

$$\begin{aligned} U^{\nu }_N:= \frac{1}{N} \sum _{n =1}^{N} \left( Y^n - \hat{f}(X^n) \right) ^2 \end{aligned}$$

(2.4)

based on N independent $\mathbb {P}^{\nu }$-realizations $(X^n, Y^n)_{n =1}^{N}$ of (X, Y) drawn independently of any data $(\mathcal {X}^m, \mathcal {Y}^m)_{m = 1}^M$ used to determine $\hat{f}$.

Provided that $\mathbb {E}^{\nu } [ (Y -\hat{f}(X))^2] < \infty$, one obtains from the strong law of large numbers that

$$\begin{aligned} \lim _{N \rightarrow \infty } U^{\nu }_N = U^{\nu } \quad \mathbb {P}^{\nu }\hbox {-almost surely.} \end{aligned}$$

To derive confidence intervals, we compute the sample variance

$$\begin{aligned} v^{U,\nu }_{N}:= \frac{1}{N-1} \sum _{n=1}^{N} \left( \left( Y^n - \hat{f}(X^n) \right) ^2 - U^{\nu }_N \right) ^2 \end{aligned}$$

and denote, for $\alpha \in (0,1)$, by $q_{\alpha }$ the $\alpha$-quantile of the standard normal distribution. Then the following holds.

Lemma 2.2

Assume $\mathbb {E}^{\nu } \, Y^4 < \infty$ and $\mathbb {E}^{\nu } \, |\hat{f}(X)|^4 < \infty$. Then, for every $\alpha \in (1/2,1)$,

$$\begin{aligned} \liminf _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ \left| U^{\nu } - U^{\nu }_N \right| \le q_{1 - \alpha }\sqrt{\frac{v^{U,\nu }_{N}}{N}} \; \right] \ge 1 - 2 \alpha . \end{aligned}$$

(2.5)

Proof

In the special case where $Y = \hat{f}(X)$ $\mathbb {P}^{\nu }$-almost surely, one has $U^{\nu } = U^{\nu }_N = v^{U,\nu }_N = 0$   $\mathbb {P}^{\nu }$-almost surely for all $N \ge 1$. So (2.5) holds trivially. On the other hand, if $\mathbb {P}^{\nu }[Y \ne \hat{f}(X)] > 0$, it follows from the assumptions and the strong law of large numbers that $v^{U,\nu }_N$ converges $\mathbb {P}^{\nu }$-almost surely to ${\text {Var}}^{\mathbb {P}^{\nu }} \left( (Y - \hat{f}(X))^2 \right) > 0$ for $N \rightarrow \infty .$ Therefore, one obtains from the central limit theorem and Slutky’s theorem that

$$\begin{aligned} \lim _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ \sqrt{\frac{N}{v^{U,\nu }_N}} \, \left| U^{\nu } - U^{\nu }_{N} \right| \le q_{1-\alpha } \right] = 1- 2\alpha , \end{aligned}$$

which shows (2.5). $\square$

3 Error Estimates

Now, our goal is to derive bounds on the approximation error $\hat{f} - \bar{f}$ for a given candidate regression function $\hat{f} :\mathbb {R}^d \rightarrow \mathbb {R}$. To do that we assume in this section that Y has a representation of the form:

Remark 3.1

Provided that the probability space $(\Omega , \mathcal{F}, \mathbb {P}^{\nu })$ is rich enough, Y can always be assumed to be of the form (R). Indeed, if $(\Omega , \mathcal{F}, \mathbb {P}^{\nu })$ supports a random variable V which, under $\mathbb {P}^{\nu }$, is uniformly distributed on the unit interval (0, 1) and independent of X, the function $h :\mathbb {R}^d \times (0,1) \rightarrow \mathbb {R}$ can be chosen as a conditional $\mathbb {P}^{\nu }$-quantile function of Y given X and extended to the rest of $\mathbb {R}^{d+1}$ arbitrarily. Then (X, h(X, V)) has the same $\mathbb {P}^{\nu }$-distribution as (X, Y), and, in particular,

$$\begin{aligned} \mathbb {E}^{\nu } [h(X,V) \mid X] = \bar{f}(X) \quad \nu \hbox {-almost surely.} \end{aligned}$$

However, for our method to be applicable, the function h needs to be known explicitly.

A representation of the form (R) with a known function h is available in computational problems involving numerical regressions, such as regression methods to solve PDEs and BSDEs [see, e.g., [4, 7, 10, 19, 21, 25, 26]], SPDEs [see, e.g., [6]], financial valuation problems [see, e.g. [8, 11, 12, 16, 35, 37]] or financial risk management problems [see, e.g. [5, 13, 18, 28, 34]].

3.1 Alternative Representation of the Minimal Mean Squared Distance

The key ingredient of our approach is an alternative representation of the minimal mean squared distance

$$\begin{aligned} D^{\nu } = \min _{f \in \mathcal{B}(\mathbb {R}^d; \, \mathbb {R})} \mathbb {E}^{\nu } \! \left[ \left( Y - f(X) \right) ^2 \right] = \mathbb {E}^{\nu } \! \left[ \left( Y - \bar{f}(X) \right) ^2 \right] \end{aligned}$$

(3.1)

which does not involve a minimization problem or require knowledge of the true regression function $\bar{f}$ and, at the same time, can be approximated efficiently. An analogous representation exists for the squared $L^2$-norm of the conditional expectation

$$\begin{aligned} C^{\nu }:= \mathbb {E}^{\nu } \, \bar{f}^2(X) = \left\| [\mathbb {E}^{\nu }[Y \mid X] \right\| ^2_{L^2(\mathbb {P}^{\nu })}, \end{aligned}$$

(3.2)

which will be helpful in the computation of relative approximation errors in Sect. 4 below. If necessary, by enlarging² the probability space $(\Omega , \mathcal{F}, \mathbb {P}^{\nu }$), we can assume it supports a k-dimensional random vector $\tilde{V}$ that has the same $\mathbb {P}^{\nu }$-distribution as V and is independent of (X, V) under $\mathbb {P}^{\nu }$. Let us define

$$\begin{aligned} Z:= h(X,\tilde{V}). \end{aligned}$$

Then, we have the following.

Proposition 3.2

If $\mathbb {E}^{\nu } \, Y^2 < \infty$, then

$$\begin{aligned} C^{\nu } = \mathbb {E}^{\nu } \! \left[ Y Z \right] \quad \hbox {and} \quad D^{\nu } = \mathbb {E}^{\nu } \! \left[ Y (Y- Z) \right] . \end{aligned}$$

Proof

It follows from independence of X, V and $\tilde{V}$ that

$$\begin{aligned} \mathbb {E}^{\nu } \! \left[ Y Z \right] = \mathbb {E}^{\nu } \! \left[ \mathbb {E}^{\nu } \! \left[ h(X,V) h(X,\tilde{V}) \mid X \right] \right] = \mathbb {E}^{\nu } \! \left[ \bar{f}^2(X) \right] = C^{\nu }. \end{aligned}$$

Similarly, one has

$$\begin{aligned} \mathbb {E}^{\nu } \! \left[ Y \bar{f}(X) \right] = \mathbb {E}^{\nu } \! \left[ \mathbb {E}^{\nu }[Y \mid X] \bar{f}(X) \right] = \mathbb {E}^{\nu } \! \left[ \bar{f}^2(X) \right] , \end{aligned}$$

from which one obtains

$$\begin{aligned} \mathbb {E}^{\nu } \! \left[ Y (Y-Z) \right]= & {} \mathbb {E}^{\nu } \! \left[ Y^2 - \bar{f}^2(X) \right] = \mathbb {E}^{\nu } \! \left[ Y^2 - 2 Y \bar{f}(X) + \bar{f}^2(X) \right] \\= & {} \mathbb {E}^{\nu } \! \left[ \left( Y - \bar{f}(X) \right) ^2 \right] = D^{\nu }. \end{aligned}$$

$\square$

3.2 Approximation of $C^{\nu }$ and $D^{\nu }$

To approximate $C^{\nu }$ and $D^{\nu }$, we use $\mathbb {P}^{\nu }$-realizations $Z^n:= h(X^n, \tilde{V}^n)$, $n = 1, \dots , N$, of Z based on independent copies $\tilde{V}^n$ of V drawn independently of $(\mathcal {X}^m, \mathcal {Y}^m)$, $m = 1, \dots , M$, and $(X^n, Y^n, V^n)$, $n = 1, \dots , N$. The corresponding Monte Carlo approximations of $C^{\nu }$ and $D^{\nu }$ are

$$\begin{aligned} C^{\nu }_N:= \frac{1}{N} \sum _{n=1}^{N} Y^n Z^n \quad \hbox {and} \quad D^{\nu }_N:= \frac{1}{N} \sum _{n=1}^{N} Y^n (Y^n- Z^n), \end{aligned}$$

(3.3)

respectively. If $\mathbb {E}^{\nu } \, Y^2 < \infty$, then $\mathbb {E}^{\nu } \, Z^2 < \infty$ too, and one obtains from the strong law of large numbers that

$$\begin{aligned} \lim _{N \rightarrow \infty } C^{\nu }_N = C^{\nu } \quad \hbox {and} \quad \lim _{N \rightarrow \infty } D^{\nu }_N = D^{\nu } \quad \mathbb {P}^{\nu }\hbox {-almost surely.} \end{aligned}$$

Moreover, for the sample variances

$$\begin{aligned} v^{C,\nu }_N:= \frac{1}{N-1} \sum _{n=1}^{N} \left( Y^n Z^n - C^{\nu }_N \right) ^2 \quad \hbox {and} \quad v^{D,\nu }_N:= \frac{1}{N-1} \sum _{n=1}^{N} \left( Y^n (Y^n-Z^n) - D^{\nu }_N \right) ^2, \end{aligned}$$

the following analog of Lemma 2.2 holds.

Lemma 3.3

If $\mathbb {E}^{\nu } \, Y^4 < \infty$, then, for every $\alpha \in (1/2,1)$,

$$\begin{aligned} \liminf _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ \left| C^{\nu } - C^{\nu }_N \right| \le q_{1 - \alpha }\sqrt{\frac{v^{C,\nu }_{N}}{N}} \; \right] \ge 1 - 2 \alpha \end{aligned}$$

(3.4)

and

$$\begin{aligned} \liminf _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ \left| D^{\nu } - D^{\nu }_N \right| \le q_{1 - \alpha }\sqrt{\frac{v^{D,\nu }_{N}}{N}} \; \right] \ge 1 - 2 \alpha . \end{aligned}$$

(3.5)

Proof

If $C^{\nu } = Y Z$ $\mathbb {P}^{\nu }$-almost surely, then $C^{\nu } - C^{\nu }_N = v^{C,\nu }_N = 0$ $\mathbb {P}^{\nu }$-almost surely for all $N \ge 1$, and (3.4) is immediate. On the other hand, if $\mathbb {P}^{\nu }[C^{\nu } \ne YZ] > 0$, one obtains from the strong law of large numbers that $v^{C,\nu }_N \rightarrow {\text {Var}}^{\mathbb {P}{\nu }} \left( YZ \right) > 0$ $\mathbb {P}^{\nu }$-almost surely for $N \rightarrow \infty$, and it follows from the central limit theorem together with Slutky’s theorem that

$$\begin{aligned} \lim _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ \sqrt{\frac{N}{v^{C,\nu }_N}} \, \left| C^{\nu } - C^{\nu }_{N} \right| \le q_{1-\alpha } \right] = 1- 2\alpha . \end{aligned}$$

This shows (3.4). Equation (3.5) follows analogously. $\square$

3.3 $L^2$-Bounds on the Approximation Error

We now derive $L^2$-bounds on the error resulting from approximating the true regression function $\bar{f}$ with a candidate regression function $\hat{f}$. Let us denote by $L^2(\nu )$ the space of all Borel functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$ satisfying

$$\begin{aligned} \Vert f \Vert ^2_{L^2(\nu )}:= \mathbb {E}^{\nu } f^2(X) = \int _{\mathbb {R}^d} f^2(x) d \nu (x) < \infty \end{aligned}$$

and consider the squared $L^2(\nu )$-norm of the approximation error

$$\begin{aligned} F^{\nu }:= \Vert \hat{f} - \bar{f} \Vert ^2_{L^2(\nu )} = \mathbb {E}^{\nu } \! \left[ \left( \hat{f}(X) - \bar{f}(X) \right) ^2 \right] . \end{aligned}$$

(3.6)

$F^{\nu }$ has the following alternative representation.

Theorem 3.4

If $\mathbb {E}^{\nu } \, Y^2 < \infty$ and $\mathbb {E}^{\nu } \hat{f}^2(X) < \infty$, then

$$\begin{aligned} F^{\nu } = \mathbb {E}^{\nu } \! \left[ YZ + \hat{f}(X) \left( \hat{f}(X) - Y - Z \right) \right] . \end{aligned}$$

(3.7)

Proof

Since $\bar{f}(X) = \mathbb {E}^{\nu }[Y \mid X]$, it follows from $\mathbb {E}^{\nu } \, Y^2 < \infty$ and the conditional Jensen inequality that $\mathbb {E}^{\nu } \bar{f}^2(X) < \infty$ as well. Furthermore, $Y - \bar{f}(X)$ is orthogonal to $\hat{f}(X) - \bar{f}(X)$ in $L^2(\mathbb {P}^{\nu })$. Therefore, one obtains from Pythagoras’ theorem that

$$\begin{aligned} F^{\nu } = \left\| \hat{f}(X) - \bar{f}(X) \right\| ^2_{L^2(\mathbb {P}^{\nu })} = \left\| Y - \hat{f}(X) \right\| ^2_{L^2(\mathbb {P}^{\nu })} - \left\| Y - \bar{f}(X) \right\| ^2_{L^2(\mathbb {P}^{\nu })}. \end{aligned}$$

(3.8)

In addition, we know from Proposition 3.2 that

$$\begin{aligned} \left\| Y - \bar{f}(X) \right\| ^2_{L^2(\mathbb {P}^{\nu })} = \mathbb {E}^{\nu } \! \left[ \left( Y - \bar{f}(X) \right) ^2 \right] = \mathbb {E}^{\nu }[Y(Y-Z)]. \end{aligned}$$

(3.9)

So, since

$$\begin{aligned} \mathbb {E}^{\nu } \! \left[ Y \hat{f}(X) \right]= & {} \mathbb {E}^{\nu } \! \left[ \mathbb {E}^{\nu }[h(X,V) \mid X] \, \hat{f}(X) \right] = \mathbb {E}^{\nu } \! \left[ \mathbb {E}^{\nu }[h(X,\tilde{V}) \mid X] \, \hat{f}(X) \right] \\= & {} \mathbb {E}^{\nu } \! \left[ Z \hat{f}(X) \right] , \end{aligned}$$

we obtain from (3.8) and (3.9) that

$$\begin{aligned} F^{\nu }= & {} \mathbb {E}^{\nu } \! \left[ Y^2 - (Y+Z) \hat{f}(X) + \hat{f}^2(X)- Y(Y-Z) \right] \\= & {} \mathbb {E}^{\nu } \! \left[ YZ + \hat{f}(X) \left( \hat{f}(X) - Y - Z \right) \right] , \end{aligned}$$

which shows (3.7). $\square$

In view of (3.7), we approximate $F^{\nu }$ with the Monte Carlo average

$$\begin{aligned} F^{\nu }_N:= \frac{1}{N} \sum _{n = 1}^{N} \left\{ Y^n Z^n + \hat{f}(X^n) \left( \hat{f}(X^n) - Y^n - Z^n \right) \right\} \end{aligned}$$

(3.10)

and denote the corresponding sample variance by

$$\begin{aligned} v^{F, \nu }_N:= \frac{1}{N-1} \sum _{n=1}^{N} \left\{ Y^n Z^n + \hat{f}(X^n) \left( \hat{f}(X^n) - Y^n - Z^n \right) - F^{\nu }_N \right\} ^2. \end{aligned}$$

The following lemma provides approximate confidence upper bounds for the true squared $L^2$-approximation error (3.6).

Lemma 3.5

If $\mathbb {E}^{\nu } \, Y^4 < \infty$ and $\mathbb {E}^{\nu } \hat{f}^4(X) < \infty$, one has for all $\alpha \in (0,1)$,

$$\begin{aligned} \liminf _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ F^{\nu } \le F^{\nu }_N + q_{\alpha } \, \sqrt{\frac{v^{F,\nu }_N}{N}} \; \right] \ge \alpha . \end{aligned}$$

(3.11)

Proof

In the special case, where

$$\begin{aligned} YZ + \hat{f}(X)(\hat{f}(X) - Y - Z) = F^{\nu } \quad \mathbb {P}^{\nu }\hbox {-almost surely,} \end{aligned}$$

one has

$$\begin{aligned} F^{\nu } - F^{\nu }_N = v^{F,\nu }_N = 0 \quad \mathbb {P}^{\nu }\hbox {-almost surely for all } N \ge 1, \end{aligned}$$

and (3.11) is clear. On the other hand, if

$$\begin{aligned} \mathbb {P}^{\nu } \! \left[ YZ + \hat{f}(X)(\hat{f}(X) - Y - Z) \ne F^{\nu } \right] > 0, \end{aligned}$$

it follows from the strong law of large numbers that

$$\begin{aligned} \lim _{N \rightarrow \infty } v^{F,\nu }_N = \mathrm{Var}^{\mathbb {P}^{\nu }} \left( YZ + \hat{f}(X)(\hat{f}(X) - Y - Z \right) > 0 \quad \mathbb {P}^{\nu }\hbox {-almost surely.} \end{aligned}$$

So, one obtains from the central limit theorem and Slutky’s theorem that

$$\begin{aligned} \liminf _{N \rightarrow \infty } \mathbb {P}^{\nu } \! \left[ \sqrt{\frac{N}{v^{F,\nu }_N}} \left( F^{\nu } - F^{\nu }_N \right) \le q_{\alpha } \right] = \alpha , \end{aligned}$$

which implies (3.11). $\square$

In applications where $\bar{f}$ needs to be approximated well at a given point $x_0$ in the support of the distribution $\nu _X$ of X, $\nu _X$ can be distorted so as to obtain a probability measure $\nu \ll \nu _X$ on $\mathbb {R}^d$ that concentrates more weight around $x_0$. Then, provided that $\hat{f} - \bar{f}$ is continuous at $x_0$, $\Vert \hat{f} - \bar{f} \Vert _{L^2(\nu )}$ approximates the point-wise difference $|\hat{f}(x_0) - \bar{f}(x_0)|$. More precisely, if $\Vert . \Vert _2$ denotes the standard Euclidean norm on $\mathbb {R}^d$, the following holds.

Lemma 3.6

Assume $\mathbb {E}\, Y^2 < \infty$, $\mathbb {E}\, \hat{f}^2(X) < \infty$ and $\hat{f} - \bar{f}$ is continuous at a point $x_0 \in \mathbb {R}^d$. Let $(\nu _n)_{n \ge 1}$ be a sequence of Borel probability measures on $\mathbb {R}^d$ given by $d \nu _n/d\nu _X = p_n$ for a sequence of Borel functions $p_n :\mathbb {R}^d \rightarrow [0,\infty )$ satisfying

$$\begin{aligned} \int _{\mathbb {R}^d} p_n(x) d\nu _X(x) = 1 \; \hbox { for all } n \ge 1 \quad \hbox {and} \quad \sup _{x \in \mathbb {R}^d : \, \Vert x - x_0 \Vert _2 > 1/n} p_n(x) \rightarrow 0 \; \hbox { for}\ n \rightarrow \infty . \end{aligned}$$

Then

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert \hat{f} - \bar{f} \Vert _{L^2(\nu _n)} = |\hat{f}(x_0) - \bar{f}(x_0)|. \end{aligned}$$

Proof

It follows from $\mathbb {E}\, Y^2 < \infty$ that $\mathbb {E}\, \bar{f}^2(X) < \infty$, which together with the condition $\mathbb {E}\, \hat{f}^2(X) < \infty$, implies that $f:= \hat{f} - \bar{f} \in L^2(\nu _X)$. Moreover, one obtains from the assumptions that for every $\varepsilon > 0$, there exists an $n \ge 1$ such that

$$\begin{aligned} \left| f(x) - f(x_0) \right| \le \varepsilon \quad \hbox {for all } x \in \mathbb {R}^d \hbox { satisfying } \Vert x - x_0 \Vert _2 \le 1/n, \end{aligned}$$

and

$$\begin{aligned}&\int _{ \left\{ x \in \mathbb {R}^d : \, \Vert x - x_0 \Vert _2> 1/n \right\} } \left( f(x) - f(x_0) \right) ^2 d\nu _n(x)\\&\quad = \int _{ \left\{ x \in \mathbb {R}^d : \, \Vert x - x_0 \Vert _2 > 1/n \right\} } \left( f(x) - f(x_0) \right) ^2 p_n(x) d\nu _X(x) \le \varepsilon ^2. \end{aligned}$$

Hence,

$$\begin{aligned} \Vert f - f(x_0) \Vert ^2_{L^2(\nu _n)}= & {} \int _{ \left\{ x \in \mathbb {R}^d : \, \Vert x - x_0 \Vert _2 \le 1/n \right\} } \left( f(x) - f(x_0) \right) ^2 d\nu _n(x)\\&+ \int _{ \left\{ x \in \mathbb {R}^d : \, \Vert x - x_0 \Vert _2 > 1/n \right\} } \left( f(x) - f(x_0) \right) ^2 d\nu _n(x) \le 2 \varepsilon ^2, \end{aligned}$$

and therefore,

$$\begin{aligned} \left| \Vert f \Vert _{L^2(\nu _n)} - |f(x_0)| \right| \le \Vert f - f(x_0) \Vert _{L^2(\nu _n)} \le \sqrt{2}\, \varepsilon . \end{aligned}$$

Since $\varepsilon > 0$ was arbitrary, this proves the lemma. $\square$

4 Examples

In all our examples we compute a candidate regression function $\hat{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ by minimizing an empirical mean squared distance of the form (2.2). For comparison reasons we minimize (2.2) over different families $\mathcal{S}$ of Borel measurable functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$, in each case using a numerical method suited to the specific form of $\mathcal{S}$.

• 1. First, we use linear regression on $1, X_1, \dots , X_d$. The corresponding function family $\mathcal{S}$ consists of all linear combinations of $1, x_1, \dots , x_d$, and the minimization of the empirical mean squared distance (2.2) becomes the ordinary least squares problem

  $$\begin{aligned} \min _{\beta \in \mathbb {R}^{d+1}} \sum _{m=1}^M \left( \mathcal {Y}^m - \beta _0 - \sum _{i=1}^d \beta _i \mathcal {X}^m_i \right) ^2. \end{aligned}$$

  This yields a candidate regression function of the form $\hat{f}(x) = \hat{\beta }_0 + \sum _{i=1}^d \hat{\beta }_i x_i$, where $\hat{\beta } \in \mathbb {R}^{d+1}$ is a solution of the normal equation

  $$\begin{aligned} A^T A \, \hat{\beta } = A^T y \end{aligned}$$

  (4.1)

  for $A \in \mathbb {R}^{M \times (d+1)}$ and $y \in \mathbb {R}^M$ given by

  $$\begin{aligned} A = \left( \begin{array}{cccc} 1 &{} \mathcal {X}^1_1 &{} \cdots &{} \mathcal {X}^1_d\\ 1 &{} \mathcal {X}^2_1 &{} \cdots &{} \mathcal {X}^2_d\\ \cdots &{} \cdots &{}\cdots &{} \cdots \\ 1 &{} \mathcal {X}^M_1 &{} \cdots &{} \mathcal {X}^M_d \end{array} \right) \quad \hbox {and} \quad y = \left( \begin{array}{cccc} \mathcal {Y}^1\\ \dots \\ \dots \\ \mathcal {Y}^M \end{array} \right) . \end{aligned}$$

  In Sects. 4.1 and 4.2 we use $M = 2 \times 10^6$ independent Monte Carlo simulations $(\mathcal {X}^m, \mathcal {Y}^m)$ for the linear regression, while in Sects. 4.3 and 4.4, where the examples are higher-dimensional, we use $M = 5 \times 10^5$ of them. If the matrix $A^T A$ is invertible, Eq. (4.1) has a unique solution given by $\hat{\beta } = (A^T A)^{-1} A^T y$. If $A^T A$ is invertible and, in addition, well-conditioned, $\hat{\beta }$ can efficiently be computed using the Cholesky decomposition $R^TR$ of $A^T A$ to solve $R^T z = A^T y$ and $R \hat{\beta } = z$ in two steps. On the other hand, if $A^T A$ is not invertible or ill-conditioned, the Cholesky method is numerically unstable. In this case, we compute a singular value decomposition $U \Sigma V^T$ of A for orthogonal matrices $U \in \mathbb {R}^{M \times M}$, $V \in \mathbb {R}^{(d+1) \times (d+1)}$ and a diagonal matrix $\Lambda \in \mathbb {R}^{M \times (d+1)}$ with diagonal entries $\lambda _1 \ge \lambda _2 \ge \dots \ge \lambda _{d+1} \ge 0$. The solution of (4.1) with the smallest Euclidean norm is then given by

  $$\begin{aligned} \hat{\beta } = V \left( \begin{array}{lllll} \lambda _1^{-1} 1_{ \left\{ \lambda _1> 0 \right\} } &{} 0 &{} \dots &{} \dots &{} 0\\ 0 &{} \lambda ^{-1}_2 1_{ \left\{ \lambda _2> 0 \right\} } &{} \dots &{} \dots &{} 0\\ 0 &{} \dots &{} \dots &{} \dots &{} 0\\ 0 &{} \dots &{} \dots &{} \dots &{} \lambda _{d+1}^{-1} 1_{ \left\{ \lambda _{d+1} > 0 \right\} }\\ 0 &{} \dots &{} \dots &{} \dots &{} 0\\ \dots &{} \dots &{} \dots &{} \dots &{} \dots \\ 0 &{} \dots &{} \dots &{} \dots &{} 0 \end{array} \right) U^T y, \end{aligned}$$

  which, for numerical stability reasons, we approximate with a truncated SVD solution

  $$\begin{aligned} \hat{\beta }_c = V \left( \begin{array}{lllll} \lambda _1^{-1} 1_{ \left\{ \lambda _1> c \right\} } &{} 0 &{} \dots &{} \dots &{} 0\\ 0 &{} \lambda ^{-1}_2 1_{ \left\{ \lambda _2> c \right\} } &{} \dots &{} \dots &{} 0\\ 0 &{} \dots &{} \dots &{} \dots &{} 0\\ 0 &{} \dots &{} \dots &{} \dots &{} \lambda _{d+1}^{-1} 1_{ \left\{ \lambda _{d+1} > c \right\} }\\ 0 &{} \dots &{} \dots &{} \dots &{} 0\\ \dots &{} \dots &{} \dots &{} \dots &{} \dots \\ 0 &{} \dots &{} \dots &{} \dots &{} 0 \end{array} \right) U^T y \end{aligned}$$

  (4.2)

  for a small cutoff value $c > 0$; see, e.g., e.g., Björck [9].

• 2. As second method we use second order polynomial regression; that is, we regress on $1, X_1, \dots , X_d$ and all second order terms $X_i X_j$, $1 \le i \le j \le d$. $\mathcal{S}$ is then the linear span of $1, x_1, \dots , x_d$ and $x_ix_j$, $1 \le i \le j \le d$, and a canditate regression function can be computed as in 1. above, except that now the feature matrix A has $1 + 3d/2 + d^2/2$ columns. As before, we use $M = 2 \times 10^6$ independent Monte Carlo simulations $(\mathcal {X}^m, \mathcal {Y}^m)$ in Sects. 4.1–4.2 and $M = 5 \times 10^5$ of them in Sects. 4.3–4.4, and again, we use the Cholesky decomposition of $A^T A$ to solve (4.1) if $A^T A$ is well-conditioned and a truncated SVD solution otherwise.³

• 3. In our third method, $\mathcal{S}$ consists of all neural networks of a given architecture. In this paper we focus on feedforward neural networks of the form

  $$\begin{aligned} f^{\theta } = a_{D}^{\theta }\circ \varphi \circ a_{D-1}^{\theta } \circ \dots \circ \varphi \circ a_{1}^{\theta }, \end{aligned}$$

  (4.3)

  where

  • $D \ge 1$ is the depth of the network;

  • $a^{\theta }_{i}: \mathbb {R}^{q_{i-1}} \rightarrow \mathbb {R}^{q_{i}}$, $i = 1, \dots , D$, are affine transformations of the form $a^{\theta }_{i}(x) = A_ix + b_i$ for matrices $A_i \in \mathbb {R}^{q_i \times q_{i-1}}$ and vectors $b_i \in \mathbb {R}^{q_i}$, where $q_0$ is the input dimension, $q_D = 1$ the output dimension and $q_i$, $i = 1, \dots , D - 1$, the number of neurons in the i-th hidden layer;

  • $\varphi :\mathbb {R}\rightarrow \mathbb {R}$ is a non-linear activation function applied component-wise in each hidden layer.

  In the examples below, we use networks of depth $D = 4$ and 128 neurons in each of the three hidden layers. We compare the commonly used activation functions $\varphi = \tanh$ and $\mathrm{ReLU}(x):= \max \{0,x\}$ to the following smooth version of $\mathrm{Leaky ReLU}(x):= \max \{\alpha x, x\}$:

  $$\begin{aligned} \mathrm{LSE}(x):= \log \left( e^{\alpha x} + e^x \right) \quad \hbox {for } \alpha = 0.01, \end{aligned}$$

  which is efficient to evaluate numerically and, by the LogSumExp inequality, satisfies

  $$\begin{aligned} \mathrm{LeakyReLU}(x) \le \mathrm{LSE}(x) \le \mathrm{LeakyReLU}(x) + \log {2}. \end{aligned}$$

  In addition, $\mathrm{LSE}$ is everywhere differentiable with non-vanishing derivative, which alleviates the problem of vanishing gradients that can arise in the training of $\tanh$ and $\mathrm{ReLU}$ networks. We initialize the parameter vector $\theta$ according to Xavier initialization [24] and then optimize it by iteratively decreasing the empirical mean squared distance (2.2) with Adam stochastic gradient descent [33] using mini-batches of size $2^{13}$ and batch-normalization⁴ [30] before each activation $\varphi$. We perform 250,000 gradient steps with standard Adam parameters, except that we start with a learning rate of 0.1, which we manually reduce to 0.05, $10^{-2}$, $10^{-3}$, $10^{-4}$, $10^{-5}$ and $10^{-6}$ after 1000, 5000, 25,000, 50,000, 100,000 and 150,000 iterations, respectively. To avoid slow cross device communications between the CPU and GPU, we generate all simulations on the fly during the training procedure. Since we simulate from a model, we can produce a large training set and therefore, do not need to worry about overfitting to the training data.

Remark 4.1

In many applications, the performance of the numerical regression can be improved with little additional effort by adding a redundant feature of the form a(X) for a Borel measurable function $a :\mathbb {R}^d \rightarrow \mathbb {R}$ capturing important aspects of the relation between X and Y. For instance, if Y is given by $Y = h(X,V)$ for a Borel function $h :\mathbb {R}^{d+k} \rightarrow \mathbb {R}$ and a k-dimensional random vector V, adding the additional feature $a(X) = h(X,0)$, or something similar, often yields good results. Instead of minimizing the mean squared distance (2.1), one then tries to find a Borel function $\hat{g} :\mathbb {R}^{d+1} \rightarrow \mathbb {R}$ that minimizes $\mathbb {E}^{\nu } \! \left[ \left( Y - \hat{g}(X, a(X)) \right) ^2 \right]$ and approximates the regression function $\bar{f} :\mathbb {R}^d \rightarrow \mathbb {R}$ with $\hat{f}(x) = \hat{g}(x, a(x))$, $x \in \mathbb {R}^d$.

In all examples, we report for all different methods used to determine a candidate regression function $\hat{f}$,

• an approximate 95% confidence interval for $U^{\nu } = \mathbb {E}^{\nu } \! \left[ \left( Y - \hat{f}(X) \right) ^2 \right]$ using (2.5).

• an approximate 95% confidence interval for $D^{\nu } = \mathbb {E}^{\nu } \! \left[ \left( Y - \bar{f}(X) \right) ^2 \right]$ using (3.5).

• an estimate of the relative error $\Vert \hat{f} - \bar{f} \Vert _{L^2(\nu )}/ \Vert \bar{f} \Vert _{L^2(\nu )}$ of the form $\sqrt{F^{\nu }_N/C^{\nu }_N}$ for $C^{\nu }_N$ and $F^{\nu }_N$ given in (3.3) and (3.10), respectively. Note that while the theoretical values $C^{\nu } = \Vert \bar{f} \Vert _{L^2(\nu )}$ and $F^{\nu } = \Vert \hat{f} - \bar{f} \Vert ^2_{L^2(\nu )}$ are both non-negative, in some of our examples, $F^{\nu }$ is close to zero. So due to Monte Carlo noise, the estimate $F^{\nu }_N$ can become negative. In these cases, we report $- \sqrt{- F^{\nu }_N/C^{\nu }_N}$ instead of $\sqrt{F^{\nu }_N/C^{\nu }_N}$.

• an approximate 95% confidence upper bound for the error $\Vert \hat{f} - \bar{f} \Vert _{L^2(\nu )}$ based on (3.11) expressed as a fraction of $\Vert \bar{f} \Vert _{L^2(\nu )}$ as estimated by $C^{\nu }_N$ given in (3.3).

• The time in seconds it took to compute the approximate regression function $\hat{f}$.

In Sects. 4.1 and 4.2 below we used $N = 6 \times 10^8$ independent Monte Carlo simulations $(X^n, Y^n, Z^n)$ to compute the estimates $U^{\nu }_N$, $D^{\nu }_N$, $F^{\nu }_N$, $C^{\nu }_N$ together with the corresponding confidence intervals, whereas in Sects. 4.3 and 4.4, due to the higher dimensionality of the examples, we only worked with $N = 6 \times 10^7$ independent Monte Carlo simulations. To fit such large test data sets into the computer memory, we split them into 6,000 independent batches of 100,000 or 10,000 data points, respectively. In most examples, we chose $\nu$ to be equal to the original distribution $\nu _X$ of X, in which case $\mathbb {E}^{\nu }$ equals $\mathbb {E}$.

All computations were performed on a Nvidia GeForce RTX 2080 Ti GPU together with Intel Core Xeon CPUs using Python 3.9.6, TensorFlow 2.5.0 with eager mode disabled and TensorFlow Probability 0.13.0 on Fedora 32.

4.1 A Four-Dimensional Polynomial Example

In our first example, we consider a simple non-linear model for (X, Y) in which the conditional expectation $\mathbb {E}[Y \mid X]$ can be computed explicitly. This enables us to benchmark our numerical results against the theoretical values. Let $X = (X_1,X_2,X_3,X_4)$ be a four-dimensional random vector and V, Y random variables such that $X_1, \dots , X_4, V$ are i.i.d. standard normal and Y is of the form

$$\begin{aligned} Y = X_1 + X_2^2 + X_3 X_4 + V. \end{aligned}$$

(4.4)

Then the conditional expectation is

$$\begin{aligned} \mathbb {E}[Y \mid X]=X_1+ X_2^2 + X_3 X_4, \end{aligned}$$

(4.5)

from which the minimal mean squared distance under $\mathbb {P}$ can be seen to be

$$\begin{aligned} D^{\nu _X} = \mathbb {E}\! \left[ \left( Y - \mathbb {E}[Y \mid X] \right) ^2 \right] = \mathbb {E}\! \left[ V^2 \right] = 1.\end{aligned}$$

Replacing V by 0 in the expression (4.4) would suggest to use the additional feature $a(X) = X_1 + X^2_2 + X_3 X_4$. However, since this would directly solve the problem, we are not using it in this example.

Our numerical results are listed in Table 1. More details are provided in Table 7 in the Appendix. As could be expected, since the true regression function (4.5) is a second order polynomial, the accuracy of the linear regression is poor, while the the second order polynomial regression works very well. All three neural networks provide results comparable to the one of the second order polynomial regression, albeit with more computational effort.

Table 1 Numerical results for the polynomial example (4.4)

4.2 A Five-Dimensional Non-polynomial Example

In our second example, we consider a non-polynomial relationship between Y and X. More precisely, we let $X_1, V_1, \dots , X_5, V_5$ be i.i.d. standard normal and assume that Y is of the form

$$\begin{aligned} Y = 5 \log \left( 5 + (X_1+V_1)^2 X_2^2 + V^2_2 \right) \tanh \left( (X_3 + V_3) (X_4 + V_4) (X_5 + V_5)^2 \right) . \end{aligned}$$

(4.6)

Then the conditional expectation $\mathbb {E}[Y \mid X]$ is not known in closed form. Setting $V_1 = \dots = V_5 = 0$ in (4.6) suggests to use the additional feature

$$\begin{aligned} a(X) = 5 \log \left( 5 + X_1^2 X_2^2 \right) \tanh \left( X_3 X_4 X_5^2 \right) . \end{aligned}$$

(4.7)

4.2.1 Minimizing the Mean Squared Distance under $\mathbb {P}$

We first search for the function $f :\mathbb {R}^d \rightarrow \mathbb {R}$ minimizing the mean squared distance $\mathbb {E}[\left( Y - f(X) \right) ^2]$ under the original measure $\mathbb {P}$. The numerical results are reported in Table 2, and more details can be found in Table 8 in the Appendix. It can be seen that the second order polynomial regression yields better results than the linear regression, but now, both are clearly outperformed by the three neural network approaches. Moreover, the inclusion of the additional feature (4.7) improves the accuracy of the linear and second order polynomial regressions, while it does not increase the performance of the neural networks significantly.

Table 2 Numerical results for the non-polynomial example (4.6) regressed under $\mathbb {P}$

Table 3 Numerical results for the non-polynomial example (4.6) regressed under $\mathbb {P}^{\nu }$

4.2.2 Minimizing the Mean Squared Distance under a Distorted Measure $\mathbb {P}^{\nu }$

As a variant, we numerically minimize the mean squared distance $\mathbb {E}^{\nu } [\left( Y - f(X) \right) ^2]$ in the model (4.6) with respect to a distorted measure $\mathbb {P}^{\nu }$ under which $X_1, V_1 \dots , X_5, V_5$ are independent with $X_1, \dots X_5 \sim N(1,1/10)$ and $V_1, \dots , V_5 \sim N(0,1)$. The measure $\nu$ concentrates more mass around the point $(1,\dots , 1) \in \mathbb {R}^5$ than the original distribution $\nu _X$ of X. But since $(V_1, \dots , V_5)$ has the same distribution as under $\mathbb {P}$, the minimizing function f coincides with the same theoretical regression function $\bar{f}$ as before. However, $L^2$-norms are now measured with respect to $\mathbb {P}^{\nu }$ instead of $\mathbb {P}$, which leads to different numerical results in Tables 3 and 9 compared to Tables 2 and 8. It can be seen that, as before in the $\mathbb {P}$-minimization, the three neural networks provide better results than the second order polynomial regression, which works better than the linear regression. But now, including the additional feature (4.7) only improves the accuracy of the linear regression slightly, while it does not help the other methods.

4.3 Max-Call Options

Different pricing and risk management problems require a conditional valuation of a financial product conditional on the state of the world at a later time [see, e.g. [5, 8, 11,12,13, 16, 18, 28, 34, 35, 37]].

Financial market model We assume there exists a financial market consisting of a money market account offering zero interest rate and d risky securities with risk-neutral dynamics⁵

$$\begin{aligned} S^i_t = S^i_0 \exp \left( \sigma _i B^i_t - \frac{1}{2} \sigma ^2_i t \right) , \quad t \ge 0, \end{aligned}$$

(4.8)

for initial prices $S^i_0 = 10$, volatilities $\sigma _i = (10+i/2)\%$ and Brownian motions $B^i$, $i = 1, \dots , d$, with instantaneous correlation $\rho = 30\%$ between them. We denote the current time by 0 and consider a financial derivative on $S^1, \dots , S^d$ with payoff $\phi (S_T)$ at maturity $T = 1/3$ (four months) for a payoff function $\phi :\mathbb {R}^d \rightarrow \mathbb {R}$. Suppose we are interested in the value of the derivative at time $t = 1/52$ (one week from now) conditional on the prices $S^1_t, \dots , S^d_t$. According to standard no-arbitrage arguments [see, e.g., [32]], it is given by $\mathbb {E}\! \left[ \phi (S_T) \mid S_t \right]$, which can be written as $\mathbb {E}[Y \mid X]$ for $Y = \phi (S_T)$ and $X_i = S^i_t, \; i = 1, \dots , d$. Note that Y has an explicit representation of the form (R) (see the beginning of Sect. 3) since Y can be written as $Y= h(X,V)$ for

$$\begin{aligned} h(x,v) = \phi \left( x_1 \exp \left\{ v_1 - \frac{\sigma ^2_1}{2} (T-t) \right\} , \dots , x_d \exp \left\{ v_d - \frac{\sigma ^2_d}{2} (T-t) \right\} \right) \end{aligned}$$

and the random variables

$$\begin{aligned} V_i = \sigma _i (B^i_T - B^i_t), \quad i = 1, \dots , d, \end{aligned}$$

which are independent of $X_1, \dots , X_d$.

Let us first consider a $d=100$-dimensional max-call option with a time-T payoff of the form

$$\begin{aligned} \phi (S_T) = \left( \max _{1 \le i \le d} S^i_T - K \right) ^+ \end{aligned}$$

(4.9)

with strike price⁶$K=16.3$. Since the time-t price

$$\begin{aligned} \mathbb {E}\! \left[ \left( \max _{1 \le i \le d} S^i_T - K \right) ^+ \, \bigg | \, S_t \right] \end{aligned}$$

does not admit a closed form solution, it has to be computed numerically. In this example,

$$\begin{aligned} h(X, 0) = \left( \max _{1 \le i \le d} S^i_t e^{- \sigma ^2_i (T-t)/2} - K \right) ^+ \end{aligned}$$

is zero with high probability. Therefore, it is not useful as an additional feature. Instead, we use the additional feature

$$\begin{aligned} a(X) = \max _{1 \le i \le d} X_i = \max _{1 \le i \le d} S^i_{t}. \end{aligned}$$

(4.10)

The numerical results are reported in Table 4. Additional results are given in Table 10 in the Appendix. It can be seen that the three neural networks outperform the second order polynomial regression, which works better than the linear regression. The additional feature (4.10) does not improve the results of any of the methods significantly.

Table 4 Numerical results for the max-call option (4.9)

4.4 Binary Options

In our next example we consider a $d=100$-dimensional binary option in the Financial Market Model of Sect. 4.3 with time-T payoff

$$\begin{aligned} \phi (S_T) = 10 \times 1_{ \left\{ \max _{1 \le i \le d} S^i_T \ge K \right\} }, \end{aligned}$$

(4.11)

where, as above, we choose $K=16.3$. Again, the time-t price

$$\begin{aligned} 10 \, \mathbb {E}\! \left[ 1_{ \left\{ \max _{1 \le i \le d} S^i_T \ge K \right\} } \, \Big | \, S_t \right] = 10 \, \mathbb {P}\! \left[ \max _{1 \le i \le d} S^i_T \ge K \, \Big | \, S_t \right] \end{aligned}$$

cannot be computed exactly and therefore, has to be evaluated numerically. As in Sect. 4.3, we use

$$\begin{aligned} a(X) = \max _{1 \le i \le d} X_i = \max _{1 \le i \le d} S^i_t \end{aligned}$$

(4.12)

as additional feature.

4.4.1 Minimizing the Mean Squared Distance Under $\mathbb {P}$

We first compute a function f minimizing the mean squared distance $\mathbb {E}[\left( Y - f(X) \right) ^2]$ under the original measure $\mathbb {P}$. Our main numerical results are listed in Table 5. Additional results are given in Table 11 in the Appendix. Again, the three neural networks work better than the second order polynomial regression, which is more accurate than the linear regression. Adding the additional feature (4.12) does not have a significant influence on any of the methods.

Table 5 Numerical results for the binary option (4.11) regressed under $\mathbb {P}$

Table 6 Numerical results for the binary option (4.11) regressed under $\mathbb {P}^{\nu }$

4.4.2 Minimizing the Mean Squared Distance Under a Distorted Measure $\mathbb {P}^{\nu }$

In financial risk management, one usually is interested in the tail of a loss distribution. If a financial institution sold a contract promising a contingent payoff of $\phi (S_T)$ at time $T > 0$, the resulting exposure at time $t < T$ is $\mathbb {E}[Y \mid X] = \mathbb {E}[\phi (S_T) \mid S_t]$. To obtain a better approximation of $\bar{f} = \mathbb {E}[Y \mid X]$ with $\hat{f}(X)$ in the right tail, the least squares regression (2.2) can be performed under a measure $\mathbb {P}^{\nu }$ assigning more weight to the right tail of $\bar{f}(X)$ than $\mathbb {P}$. This can be done as in Cheridito et. al [18]. By (4.8), $X = S_t$ can be written as $X = u(QW)$ for a d-dimensional standard normal random vector W, a $d \times d$-matrix Q satisfying

$$\begin{aligned} Q Q^T = \left( \begin{array}{ccccc} 1 &{} 0.3 &{} \dots &{} \dots &{} 0.3\\ 0.3 &{} 1 &{} \dots &{} \dots &{} 0.3\\ \dots &{} \dots &{} \dots &{} \dots &{} \dots \\ 0.3 &{} \dots &{} \dots &{} 1 &{} 0.3\\ 0.3 &{} \dots &{} \dots &{} 0.3 &{} 1 \end{array} \right) \end{aligned}$$

and the function $u :\mathbb {R}^d \rightarrow \mathbb {R}^d$ given by

$$\begin{aligned} u(x_1, \dots , x_d) = \left( S^1_0 \exp \left( \sigma _1 \sqrt{t} \, x_1 - \frac{1}{2} \sigma ^2_1 t \right) , \dots , S^d_0 \exp \left( \sigma _d \sqrt{t} \, x_d - \frac{1}{2} \sigma ^2_d t \right) \right) . \end{aligned}$$

Even though the regression function $\bar{f}$ is not known in closed form, it follows by monotonicity from the form of the payoff (4.11) that the mapping $\bar{f} \circ u :\mathbb {R}^d \rightarrow \mathbb {R}$ is increasing in the direction $v = (1, \dots , 1)^T$. So, $\bar{f}(X)$ tends to be large if $v^T Q W$ is large. Therefore, we tilt $\mathbb {P}$ so that the distribution of W shifts in the direction of $Q^T v$. Let us denote by $q_{\alpha }$ the standard normal quantile at level $\alpha \in (0,1)$. Since $v^T Q W/\Vert v^T Q\Vert _2$ is one-dimensional standard normal, W lies in the region

$$\begin{aligned} G = \left\{ w \in \mathbb {R}^d: \frac{v^T Q w}{\Vert v^T Q\Vert _2} \ge q_{\alpha } \right\} \end{aligned}$$

with probability $1 - \alpha$, whereas, for

$$\begin{aligned} b = \frac{Q^T v}{\Vert Q^T v\Vert _2} q_{\alpha } \in \mathbb {R}^d, \end{aligned}$$

$W + b$ lies in G with probability 1/2. So if $\nu$ is the distribution of $u(Q(W+b))$, the $\mathbb {P}^{\nu }$-probability that $\bar{f}(X)$ is in its right $\mathbb {P}$-$(1-\alpha )$-tail is approximately 1/2. Table 6 shows results for the approximation of $\bar{f}$ under $\nu$ corresponding to $\alpha = 0.99$. More details are given in Table 12 in the Appendix. Again, the three neural networks outperform the polynomial regression, which is more accurate than the linear regression, and the inclusion of the additional feature (4.12) does not improve the performance of any of the methods significantly.

5 Conclusion

In this paper, we have studied the numerical approximation of the conditional expectation of a square-integrable random variable Y given a number of explanatory random variables $X_1, \dots , X_d$ by minimizing the mean squared distance between Y and $f(X_1, \dots , X_d)$ over a family $\mathcal{S}$ of Borel functions $f :\mathbb {R}^d \rightarrow \mathbb {R}$. The accuracy of the approximation depends on the suitability of the function family $\mathcal{S}$ and the performance of the numerical method used to solve the minimization problem. Using an expected value representation of the minimal mean squared distance which does not involve a minimization problem or require knowledge of the true regression function, we have derived $L^2$-bounds for the approximation error of a numerical solution to a given least squares regression problem. We have illustrated the method by computing approximations of conditional expectations in a range of examples using linear regression, polynomial regression as well as different neural network regressions and estimating their $L^2$-approximation errors. Our results contribute to trustworthy AI by providing numerical guarantees for a computational problem lying at the heart of different applications in various fields.

A Additional Numerical Results

In this appendix we report in Tables 7, 8, 9, 10, 11, 12 for all our numerical experiments of Sect. 4 our estimates

• $U^{\nu }_N$ of the upper bound $U^{\nu } = \mathbb {E}^{\nu }[(Y - \hat{f}(X))^2]$, see (2.4) and (2.3),

• $D^{\nu }_N$ of the minimal mean squared distance $D^{\nu } = \mathbb {E}^{\nu }[(Y - \bar{f}(X))^2]$, see (3.3) and (3.1),

• $F^{\nu }_N$ of the the squared $L^2$-approximation error $F^{\nu } = \Vert \hat{f} - \bar{f} \Vert ^2_{L^2(\nu )}$, see (3.10) and (3.6),

• $C^{\nu }_N$ of the squared $L^2$-norm $C^{\nu } = \Vert \bar{f} \Vert ^2_{L^2(\nu )}$, see (3.3) and (3.2),

together with the corresponding sample standard errors $\sqrt{v_N^{U,\nu }/N}$, $\sqrt{v_N^{D,\nu }/N}$, $\sqrt{v_N^{F,\nu }/N}$ and $\sqrt{v_N^{C,\nu }/N}$, which were used to compute⁷ the quantities in Tables 1, 2, 3, 4, 5, 6 in Sect. 4.

Table 7 Additional numerical results for the polynomial example (4.4)

Table 8 Additional numerical results for the non-polynomial example (4.6) regressed under $\mathbb {P}$

Table 9 Additional numerical results for the non-polynomial example regressed under $\mathbb {P}^{\nu }$

Table 10 Additional numerical results for the max-call option (4.9)

Table 11 Additional numerical results for the binary option (4.11) regressed under $\mathbb {P}$

Table 12 Additional numerical results for the binary option (4.11) regressed under $\mathbb {P}^{\nu }$