An Energy-based Overset Finite Element Method for Pseudo-static Structural Analysis

Abstract

This paper addresses a simple energy-based overset finite element method (EbO-FEM) to solve pseudo-static deformation problems consisting of overlapped meshes based on the domain composition method (DCM). This scheme is a non-iterative equation-based method for enforcing the continuity of the displacement field. Hence, the scheme consumes possible minimal computational costs for deformation problems with non-conforming overlapping meshes. The system’s total energy is augmented with continuity constraint energy (CCE) which is a function of the gaps in the displacement field between two overlapping regions. Subsequently, two conventional integration schemes, the Gauss-point projection, and the point-to-point projection, are utilized to discretize the CCE. It is confirmed that both schemes can yield accurate and unique solutions in the overlapped region of the finite element meshes. Further, we proposed a dimensionless relative penalty parameter (DRP). We found that DRP ranging between 1 to 10 is appropriate to robustly obtain accurate solutions for a wide range of scales, stiffness, and geometries, which is supported by three numerical simulations without increasing computational costs after assembling the global matrices and vectors.

1 Introduction

The finite element method (FEM) has been successfully employed to obtain numerical solutions to problems in the fields of fluid dynamics [1], poromechanics [2, 3], solid and structural deformation [4,5,6,7,8], contact mechanics [9,10,11,12], transport phenomenon [13], and several others. FEM is a mesh-based numerical method in which the problem’s spatial domain is discretized using finite elements [14]. A collection of such finite elements is called the domain’s mesh, and mesh creation is an integral part of finite element analysis. The accuracy of the finite element solution depends on the mesh quality and geometrical errors induced due to the spatial discretization of the computation domain. Thus, when the computation domain contains complex-shaped parts, the analyst must use fine-mesh in these parts to represent the shape as accurately as feasible [6, 15, 16]. Some approaches have been developed to create a fine mesh with high-quality [17, 18]. However, the computation cost of creating such high-quality fine meshes is still a challenge in computational mechanics.

Several researchers have shifted their focus to developing mesh-free methods to avoid the issues of mesh creation and distortion. Some examples of these methods include the material point method [19, 20], the smooth-particle-hydrodynamics [21, 22], and the particle FEM [23]. Although mesh-free methods solve the problem of mesh creation [24], they face new challenges due to their inefficiency in representing the boundary of the computation domain and material interfaces. Some of these challenges are prescribing boundary conditions and interface conditions. These issues can be handled easily and effectively using FEM through essential and natural boundary conditions.

Therefore, efforts have been made to improve FEMs to reduce the need for such high-quality fine meshes in the complex shape of the computation domain. In this regard, overset mesh schemes and the automatic meshing with overlapping and regular elements (AMORE) framework were proposed as an innovative method by Bathe et al. [25,26,27,28]. The method allows separately built meshes to overlap [25]. Applying a consistent test function to the overlapping region makes it possible to obtain a solution that satisfies the governing equations over the overlapping and non-overlapping regions [26]. The AMORE framework has been validated for convergence, accuracy, and applicability. This framework has high accuracy and applicability when the geometric data are known in advance, such as machine parts that are artificially built. In addition, nonconforming meshes should be rearranged to be conformed. For fluid analysis and multi-physical simulations, the Domain Composition Method (DCM) has been developed as a parallelization-friendly method [29,30,31,32,33,34] the method is applicable for both conforming/non-conforming meshes. Through these investigations, it is shown that the DCM reduces the computational costs [29], typically memory consumption.

Further, when FE-analysis is applied to civil/rural engineering [35,36,37,38,39] or plant biomechanics [40,41,42,43,44], the cost of handling meshes in the overlap domain is an inevitable problem. For example, even a simple irrigation system (refer to Fig. 1) or RC frame bridges usually contain tiny but physically essential parts such as joints, shoes, piers and parapets. Moreover, as depicted in Fig. 1, a typical matured soybean plant can have more than 200 joints between organs such as leaves, stems, and fruits[40, 41, 45,46,47]. Thanks to the advance in imaging technologies, it is currently possible to computationally create partially overlapped objects by combining 3-D scan data [40, 48], reconstructed CAD data [38, 39], and algorithm-generated 3-D point cloud or mesh data[45, 47, 49]. However, these computational schemes provide a large number of overlapping sections and increase the number of iterations or the number of unknowns to obtain the uniform solution based on the conventional DCM.

These problems for civil/rural engineering invariably necessitate two expensive computation costs: (1) the generation of nonconforming meshes for each part and (2) the conversion of nonconforming meshes to conforming mesh by nodal point rearrangement. Besides, the number of areas where overlaps occur increases drastically. Therefore, there is a need to develop a simple computational approach for enforcing continuity of the displacement field in the overlap regions for nonconforming meshes. Especially, it is necessary to minimize the extra computational costs to prevent unnatural gaps among overlapping meshes. It should be avoided that (1) iteration or trial-and-error procedure to enforce the gap-minimizing constraints [50] and (2) dynamic change in the size of the unknowns; the first one appears in the conventional equation-based methods [29], and the second procedure is required in the Lagrange multiplier methods.

This paper aims to describe a non-iterative, equation-based overset mesh scheme for pseudo-static deformation problems. Our key ideas are (1) to design a continuity constraint energy (CCE) function and (2) to find a solution to minimize the sum of the total energy of the system considering CCE and the conventional elastic potential energy, which are explained in Sect. 2. The proposed approach does not require iterative procedures such as Newton’s loop nor extra terms such as the Lagrange multipliers. We also introduced dimensionless relative penalty parameters (DRP) to provide a concrete form of the CCE, and numerically find the optimal range of the DRP value through three numerical simulations with various scales, stiffness and geometries as shown in Sects. 3 and 4. Further, the uniqueness and the existance of the solution is stated in Sect. 3.

Fig. 1

Target problem of energy-based overset mesh method. EbO-FEM targets pseudo-static deformation analysis for complex structures consisting of multiple members (left), where a 3D model is created for each member (centre), and numerical analysis is performed by overlaying the models (right)

2 Energy-based Overset Mesh Method

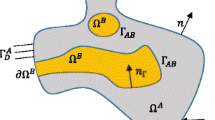
In the EbO-FEM, the analyst manually creates the system’s computation domain as a collection of finite element meshes of different subdomains ($\Omega ^{n}, n=1,2, \cdots$). In the present method, the meshes can overlap, unlike in the classical FEM. Figure 1 shows that such a scheme is desirable when the computation domain in a target control volume comprises multiple solid bodies or materials with complex shapes.

Let us now consider two computation domains, denoted by $\Omega ^p$ and $\Omega ^s$, where the superscripts p and s represent the primary and secondary domains, respectively. The primary and secondary domains are allowed to overlap, and the overlapped domain, designated by $\Omega ^{ps}$, is given by the following:

$$\begin{aligned} \Omega ^{ps} := \Omega ^{p} \cap \Omega ^{s}. \end{aligned}$$

Thus, any point $\textbf{x}_{i} \in \Omega ^{ps}$ also belongs to the spatial domains $\Omega ^{p}$ and $\Omega ^{s}$. Let us now denote the displacement field in $\Omega ^{p}$ and $\Omega ^{s}$ by $\textbf{u}^p := \textbf{u}(\textbf{x}), \textbf{x} \in \Omega ^{p}$, and $\textbf{u}^{s} := \textbf{u}(\textbf{x}), \textbf{x} \in \Omega ^{s}$, respectively. Similarly, the solution field in $\Omega ^{ps}$ is represented by $\textbf{u}^{ps}$. The strong condition of displacement consistency states that at any point $\textbf{x} \in \Omega ^{ps}$, $\textbf{u}^{ps}=\textbf{u}^{s}=\textbf{u}^{p}$. The requirement is expressed by introducing an energy function $\Pi _{g}$ :

$$\begin{aligned} \Pi _{g}( \textbf{u}^s, \textbf{u}^p ) = \int _{\Omega ^{ps}} \mathcal {G} \left( \textbf{u}^s-\textbf{u}^p \right) d\Omega = \int _{\Omega ^{ps}} \mathcal {G} \left( \textbf{g} \right) d\Omega , \end{aligned}$$

(1)

where, $\textbf{g}$ denotes the jump discontinuity in the displacement field as shown in Eq. (2).

$$\begin{aligned} \textbf{g} \left( \textbf{x}\right) = \textbf{u}^{p} - \textbf{u}^{s}. \end{aligned}$$

(2)

In Eq. (1), for simplicity, we have used:

$$\begin{aligned} \mathcal {G}(\textbf{x}) = \frac{\epsilon }{2} \textbf{g}(\textbf{x}) \cdot \textbf{g}(\textbf{x}), \end{aligned}$$

(3)

where, $\epsilon$ is a penalty parameter.

Finally, the problem statement is to minimize

$$\begin{aligned} \bar{\Pi } + \Pi _{g} \rightarrow MIN, \end{aligned}$$

(4)

where $\bar{\Pi }$ denotes the summation, $\bar{\Pi } = \sum \bar{\Pi }_d$, of energy function for each domain, $\bar{\Pi }_d$, which can be obtained from the governing equations.

The statement is expressed by the variational principle.

$$\begin{aligned} \delta \bar{\Pi } +\delta \Pi _{g} = 0. \end{aligned}$$

(5)

Using Eqs. (1) and (2), the variation $\delta \Pi$ in Eq. (5) is defined as a Gateaux derivative with respect to space $\textbf{x}$:

$$\begin{aligned} \delta \Pi = \frac{\partial \Pi }{\partial U_i (\textbf{x})} \delta U_i (\textbf{x}). , \end{aligned}$$

(6)

where $\delta U_i (\textbf{x})$ is a variation of the displacement field.

In the following subsections, we implement this formulation by discretizing Eq. (6) using the FEM. The first term can be discretized using conventional FEM formulations [51]; however, the discretization method for the second term must be carefully designed to enforce continuity condition as depicted in Fig. 1. We investigate the accuracy and characteristics of two of the most simple methods, Gauss-point and point-to-point projections.

Remark 1

Conventional DCM proposes an equation-based constraint

$$\begin{aligned} \int _{\Omega } \delta u \left( u_1 - u_2 \right) d\Omega = 0, \end{aligned}$$

(7)

where $\delta u$ is a test function, $u_1$ and $u_2$ are the unknown defined with respect to the subdomains $\Omega _1$ and $\Omega _2$, respectively. There are three possible strategies for implementing the constraint condition for the pseudo-static deformation problems: (1) iterative approach such as Dirichlet-Dirichlet or Dirichlet-Neumann approaches [29], (2) Lagrange multiplier method, and (3) penalty method. (1) requires iteration such as Newton’s method and (2) needs additional unknowns, Lagrange multipliers, which increases computational costs as the number of overlapping elements increases. The motivation of this study is to provide a non-iterative, computationally inexpensive approach. From this standpoint, we take (3) approach and provide (a) a simple and linear formulation to enforce continuity in the displacement field which does not requires iterative algorithm to obtain the solution and (b) a procedure to determine the optimal penalty parameter.

3 Finite Element Formulation for Mechanical Problem

3.1 Variational Equality

We use the EbO-FEM to solve a pseudo-static deformation problem based on FEM, where the energy function, $\Pi$, is regarded as the elastic/kinetic energy of the system, and the energy function, $\Pi _g$, represents free energy induced by the continuity constraint. The condition of consistency of the solution field state that at any $\textbf{x} \in \Omega ^{ps}$, the gap function, denoted here as $\textbf{g}^{p \rightarrow s}$, and given by the following:

$$\begin{aligned} \textbf{g}^{p \rightarrow s} = \textbf{u}^{s} - \textbf{u}^{p}, \end{aligned}$$

(8)

should be minimized. The aforementioned definition reveals that $\textbf{g}^{p \rightarrow s}$ is the measure of the solution field’s jump discontinuity in the overlapping region, and is given as follows:

$$\begin{aligned} \textbf{g}^{p \rightarrow s} + \textbf{g}^{s \rightarrow p} = \textbf{0}. \end{aligned}$$

(9)

In this study, the displacement consistency condition is enforced by employing the penalty method. Thus, the energy term associated with the gap function (denoted here as $\Pi _{\textbf{g}}^{p \rightarrow s}$) is given as follows:

$$\begin{aligned} \Pi _{\textbf{g}}^{p \rightarrow s} = \int _{\Omega ^{ps}} \varepsilon \frac{1}{2} \left\Vert \textbf{g}^{p \rightarrow s}\right\Vert ^{2} d \Omega , \end{aligned}$$

(10)

where $\varepsilon$ is a penalty parameter and $\left\Vert \star \right\Vert$ denotes the Euclidean norm of $\star$. Therefore, the displacement consistency condition can be given by the following energy minimization statement [52]:

$$\begin{aligned} \delta \Pi _\textbf{g}^{p \rightarrow s} + \delta {\bar{\Pi }} = 0 \end{aligned}$$

(11)

Consequently, the variational equality (11) can be expressed as follows:

$$\begin{aligned} \delta \Pi _\textbf{g}^{p \rightarrow s} + \delta {\bar{\Pi }} = \int _{\Omega ^{PS}} \varepsilon \delta \textbf{g}^{p \rightarrow s} \cdot \textbf{g}^{p \rightarrow s} d \Omega + \delta {\bar{\Pi }} = 0, \end{aligned}$$

(12)

where $(\cdot )$ denotes the inner product operation of two vectors.

$$\begin{aligned} \delta \textbf{g}^{p \rightarrow s} = \delta \textbf{u}^{s} - \delta \textbf{u}^{p}. \end{aligned}$$

(13)

Similarly, the variational equality in the opposite direction is given by the following:

$$\begin{aligned} \delta \Pi _\textbf{g}^{s \rightarrow p} + \delta {\bar{\Pi }} = \int _{\Omega ^{PS}} \varepsilon \delta \textbf{g}^{s \rightarrow p} \cdot \textbf{g}^{s \rightarrow p} d \Omega + \delta {\bar{\Pi }} = 0, \end{aligned}$$

(14)

with,

$$\begin{aligned} \delta \textbf{g}^{s \rightarrow p} = \delta \textbf{u}^{p} - \delta \textbf{u}^{s} \end{aligned}$$

(15)

3.2 Consistent Discretization Based on Finite Element Method

Let $N_{A}^{p}, A=1,2, \cdots n^{p}$ and $N_{A}^{s}, A=1,2, \cdots n^{s}$ be the shape functions of the solution field in $\Omega ^{p}$ and $\Omega ^{s}$, respectively (Fig. 3). Here, $n^{p}$ and $n^{s}$ are the total number of spatial nodes in the computation mesh of $\Omega ^{s}$ and $\Omega ^{p}$, respectively. Then, the nodal interpolation of $\textbf{u}^{s}$ and $\textbf{u}^{p}$ can be written by following expressions:

$$\begin{aligned} \textbf{u}^{p} = \sum _{A=1}^{n^{p}}{N_{A}^{p} \textbf{u}_{A}^{p}}, \end{aligned}$$

(16)

and

$$\begin{aligned} \textbf{u}^{s} = \sum _{A=1}^{n^{s}}{N_{A}^{s} \textbf{u}_{A}^{s}}, \end{aligned}$$

(17)

where $\textbf{u}_{I}^{s}$ denotes descritized displacement field. By substituting Eqs. (16) and (17) into Eqs. (8) and (13), the discretized jump functions and its variation are obtained as follows:

$$\begin{aligned} \begin{aligned} g_i^{p \rightarrow s}&= N_A^{s} u_{Ai}^{s} - N_A^{p} u_{Ai}^{p}\\ \delta g_i^{p \rightarrow s}&= \delta \left( N_A^{s} u_{Ai}^{s}\right) - \delta \left( N_A^{p} u_{Ai}^{p}\right) = N_A^{s} \delta u_{Ai}^{s} - N_A^{p} \delta u_{Ai}^{p}. \end{aligned} \end{aligned}$$

(18)

The variational equality (Eq. (12)) is discretized as

$$\begin{aligned} \begin{aligned} \delta \Pi _g^{p \rightarrow s}&= \int _{\Omega ^{PS}} \epsilon \delta g_i^{p \rightarrow s} g_i^{p \rightarrow s} d \Omega \\&= \epsilon \left( N_A^{s} \delta u_{Ai}^{s} - N_A^{p} \delta u_{Ai}^{p} \right) \left( N_A^{s} u_{Ai}^{s} - N_A^{p} u_{Ai}^{p}\right) J \cdot w, \end{aligned} \end{aligned}$$

(19)

where J is a determinant of the Jacobian matrix and w is a weight for the Gauss-Legendre integral.

Although the constraint should be given for all points, $x_i \in \Omega ^{ps}$, it is computationally inefficient to do so throughout the intersection. Therefore, consider a set of representative points, ${\hat{\Omega }^{ps}} \subset \Omega ^{ps}$, and weakly enforce the constraint condition in ${\hat{\Omega }^{ps}}$ rather than $\Omega ^{ps}$.

There are various options for ${\hat{\Omega }^{ps}}$; for instance, the set of representative points can be a set of nodes from the mesh in $\Omega ^{s}$. In this case, Eq. (19) is rewritten as follows:

$$\begin{aligned} \begin{aligned} {\hat{\delta }\Pi _g^{p \rightarrow s} }&= \epsilon \left( N_A^{s} \delta u_{Ai}^{s} - N_A^{p} \delta u_{Ai}^{p} \right) \left( N_A^{s} u_{Ai}^{s} - N_A^{p} u_{Ai}^{p}\right) \\&=\epsilon \left( \delta u_{i}^{s} - N_A^{p} \delta u_{Ai}^{p} \right) \left( u_{i}^{s} - N_B^{p} u_{B i}^{p}\right) \\ \end{aligned} \end{aligned}$$

(20)

where ${\hat{\delta }\Pi _g^{p \rightarrow s} }$ is the variational equality defined in ${\hat{\Omega }^{ps}}$. Finally, a matrix form of the energy variation is given as follows:

$$\begin{aligned} \begin{aligned} {\hat{\delta }\Pi _g^{p \rightarrow s} }&= \delta \textbf{u}_I \epsilon B_{I J}^T B_{J K} \textbf{u}_K J \cdot w, \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} B = \left( \begin{array}{rrrrrrrrrr} 1&{}0&{}0&{}-N_1^p&{}0 &{}0 &{}-N_2^p&{}0 &{}0 &{}...\\ 0&{}1&{}0&{}0 &{}-N_1^p&{}0 &{}0 &{}-N_2^p&{}0 &{}...\\ 0&{}0&{}1&{}0 &{}0 &{}-N_1^p&{}0 &{}0 &{}-N_2^p&{}...\\ \end{array}\right) \end{aligned}$$

(22)

$$\begin{aligned} \textbf{u}_{I} = \begin{pmatrix} {u}_x^{s}\\ {u}_y^{s}\\ {u}_z^{s}\\ {u}_{x1}^{p}\\ {u}_{y1}^{p}\\ {u}_{z1}^{p}\\ \vdots \end{pmatrix}, \delta \textbf{u}_{I} = \begin{pmatrix} \delta {u}_x^{s}\\ \delta {u}_y^{s}\\ \delta {u}_z^{s}\\ \delta {u}_{x1}^{p}\\ \delta {u}_{y1}^{p}\\ \delta {u}_{z1}^{p}\\ \vdots \end{pmatrix} \end{aligned}$$

(23)

where $^T$ indicates a transpose operator for a matrix.

Fig. 2

Schematics of the Jump-minimizing problems for domains undergo pseudo-static deformation

3.3 Discretization by Gauss-point Projection

Fig. 3

Schematic diagram of Gauss-point (top) and point-to-point (bottom) projections

In this subsection, we propose Gauss-point projection as a method for computing the numerical integrals in Eq. (1) based on the Gauss-Legendre quadrature points. Figure 3 depicts the schematic of the Gauss-point projection. We now consider the scenario where two finite elements denoted p and s undergo overlap. Here, we begin by locating all Gauss-points of finite element p that are included within finite element s. Next, the position vector of the identified effective Gauss-points in the entire coordinate system is determined. Then, the equivalent local position vector for the global position vector of the element s is determined. Eq. (1) is evaluated for each element based on the local position vector and shape functions for those p and s by the following equation under three-dimensional space ($a=1,2,3$ and $b=1,2,3$):

$$\begin{aligned} \Pi _{e}^{GP}= & {} \sum _{i}^{ngp} w_i \epsilon \left( N_a^s (\bar{g}) x_a^s - N_b^p (g_i) x_b^p \right) ^2 \det \frac{\partial \textbf{x}}{\partial \mathbf \xi } \end{aligned}$$

(24)

$$\begin{aligned}= & {} \sum _{i}^{ngp} w_i \epsilon \left( N_a^s (\bar{g}) u_a^s - N_b^p (g_i) u_b^p \right) ^2 \det \frac{\partial \textbf{x}}{\partial \mathbf \xi } , \end{aligned}$$

(25)

where $x_a^p$ and $x_a^s$ are the nodal positions for the primary and the secondary elements, respectively. $\Pi _{e}^{GP}$ is a gap-energy function for an element, ngp denotes the number of Gauss-points, $N_a^s (\bar{g})$ and $N_b^p (g_i)$ are shape functions for each hexahedron element, $u_a^s$ and $x_a^p$ are nodal value of unknowns, $\mathbf {\xi }$ is a local coordinate, and $\textbf{x}$ is a global coordinate. It is worth noting that the left hand side term is equal to zero in case that no projection from the primary domain to the secondary domain are found. Here, $\bar{\Pi }$ and $\Pi$ share the same Gaussian quadrature for simplicity. In addition, the accuracy can be improved by increasing the number of integration points, making the method simple and scalable. Section 4 contains the concrete formulations for one-dimensional and three-dimensional problems.

3.4 Discretization by Point-to-Point Projection

Although the Gauss-point projection introduced in the previous subsection can accurately discretize the numerical integration term, evaluating the energy at each Gauss-point is computationally expensive. The search cost of effective Gauss-points is up to NM when the number of elements is N and the number of Gauss-points per element is M, which is also similar to the Gauss-point projection or closest point projection in terms of contact mechanics[10, 52,53,54,55] and DCM [29]. In addition, it takes up to N times to search for a pair of elements for each effective Gauss-point and perform the projection, requiring a total of $MN^2$ orders of computation times. To reduce this computational cost, we also propose a simpler algorithm, point-to-point projection, that employs the sum of the energies for the sampled points rather than evaluating the integral term. We investigate the accuracy and applicability by numerical experiments in the following sections. A concrete formulation for the closest-point projection is shown in the Eqs. (21) to (23).

3.5 Dimension of the Consistent Penalty Parameter

It should be considered that the penalty parameter has different unit between the point-to-point projection and the Gauss-point projection. This subsection discusses the consistent unit for the penalty parameters.

An increment of internal energy of the thermodynamical system is given from the first law of the thermodynamics

$$\begin{aligned} \Delta U = Q - W, \end{aligned}$$

(26)

where $\Delta U$ is the internal energy of a closed system, Q is the quantity of the incoming energy as heat and W is an amount of the thermodynamical work done by the system and has a dimension of $kN \cdot m$, respectively. W is rewritten using Cauchy’s stress tensor and the strain tensor

$$\begin{aligned} W = \bar{\Pi } = \int _{\Omega } \sigma _{ij} \epsilon _{ij} d \Omega . \end{aligned}$$

(27)

Considering the extra energy term of Eq. (3), we obtain

$$\begin{aligned} W = \bar{\Pi } + \Pi _{g}= \int _{\Omega } \sigma _{ij} \epsilon _{ij} d \Omega + \mathcal {G}(\textbf{x}) . \end{aligned}$$

(28)

therefore, Eq. (26) is rewritten as

$$\begin{aligned} \Delta U = Q - \bar{\Pi } = Q - \int _{\Omega } \sigma _{ij} \epsilon _{ij} d \Omega - \mathcal {G}(\textbf{x}) . \end{aligned}$$

(29)

Energy-minimizing problem under the adiabatic process is given by

$$\begin{aligned} \Delta U =- \bar{\Pi } -\Pi _{g} = - \int _{\Omega } \sigma _{ij} \epsilon _{ij} d \Omega -\mathcal {G}(\textbf{x}) \rightarrow MIN \end{aligned}$$

(30)

The unit of the first term is $kN \cdot m$, hence, the unit of the second term should be the same. In the case of the point-to-point projection approach under three dimensional Cartesian coordinate, the unit of the penalty parameter should be kN/m and the unit for the Gauss-point projection approach is $kN/m^4$.

3.6 Algorithm

Figure 4 depicts the visual algorithm. First, the elemental stiffness matrix is created as in (1). There are no constraints in the overset region at this stage, implying that the coefficient matrix is orthogonal to each subregion. The next step calculates the overset stiffness matrix using Gauss-point or point-to-point projections and adds it to the global coefficient matrix. Here, the overset stiffness matrix is introduced between stiffness matrices for adjacent subdomains as a patch shown in (2), and its location can be estimated in advance using geometric correlations. Finally, the solution can be obtained immediately by introducing the Dirichlet condition and solving the system of linear equations (3).

Fig. 4

Solution algorithm and schematic diagram for EbO-FEM

3.7 Uniqueness and Existance of the Solution

The Lax-Milgram’s theorem has been widely used to confirm the uniqueness and the existence of the solution for constraint deformation problems [6, 56, 57]. We also utilize Lax-Milgram’s theorem for the proof. The problem is written in terms of the bilinear form,

$$\begin{aligned} a(u,v) + \hat{a}(u,v) = \langle f, v\rangle \end{aligned}$$

(31)

where $a(u,v) = \int _{\Omega } \sigma (v) \epsilon (u) d \Omega$ and $\hat{a}(u,v) = \int _{\Omega } \epsilon g(u) g(v) d \Omega$, and $\langle ,\rangle$ is an inner product operator.

Lemma 3.1

$B(u,v) = a(u,v) + \hat{a}(u,v)$ is a bilinear map on the real linear vector space $\textbf{V}$

Proof

In case that the constitutive equation is linear, for arbitrary vectors u, v, w, in $\textbf{V}$,

$$\begin{aligned} B(u+v,w)= & {} a(u+v,w) + \hat{a}(u+v,w)\nonumber \\= & {} \int _{\Omega } \sigma (w) \epsilon (u+v) d \Omega + \int _{\Omega } \epsilon g(u+v) g(w) d \Omega \nonumber \\= & {} \int _{\Omega } \sigma (w) \epsilon (u) d \Omega +\int _{\Omega } \sigma (w) \epsilon (v) d \Omega \nonumber \\{} & {} + \int _{\Omega } \epsilon (u_{1}+v_{1} - u_{2}-v_{2}) g(w) d \Omega \nonumber \\= & {} a(u,w) + a(v,w) + \hat{a}(u,w) + \hat{a}(u,w)\nonumber \\= & {} B(u,w) + B(v,w). \end{aligned}$$

(32)

Similarly,

$$\begin{aligned} B(u,v+w)= & {} a(u,v+w) + \hat{a}(u,v+w)\nonumber \\= & {} B(u,v) + B(u,w) \end{aligned}$$

(33)

Furthermore, for arbitrary real scalar value k, one holds

$$\begin{aligned} B(ku,v)= & {} a(ku,w) + \hat{a}(ku,v) \nonumber \\= & {} \int _{\Omega } \sigma (v) \epsilon (ku) d \Omega + \int _{\Omega } \epsilon g(ku) g(v) d \Omega \nonumber \\= & {} k \int _{\Omega } \sigma (v) \epsilon (u) d \Omega + \int _{\Omega } k \epsilon g(u) g(v) d \Omega \nonumber \\= & {} k \cdot B(u,v) \nonumber \\= & {} \int _{\Omega } \sigma (kv) \epsilon (u) d \Omega + \int _{\Omega } \epsilon g(u) g(kv) d \Omega \nonumber \\= & {} B(u,kv) \end{aligned}$$

(34)

Lemma 3.2

For Hilbert space $H(\textbf{V}, \Vert \cdot \Vert )$, $\hat{a}$ is bounded.

Proof

Considering arbitrary vectors $(u,v) \in \textbf{V}$, it holds that

$$\begin{aligned} | \hat{a}(u,v) |= & {} \sqrt{ \hat{a}(u,v)\hat{a}(u,v) } \nonumber \\= & {} \sqrt{ \int _{\Omega } \epsilon g(u) g(v) d \Omega \int _{\Omega } \epsilon g(u) g(v) d \Omega } \nonumber \\= & {} \sqrt{ \int _{\Omega } \epsilon (u_{1}-u_{2}) (v_{1}-v_{2}) d \Omega \int _{\Omega } \epsilon (u_{1}-u_{2}) (v_{1}-v_{2}) d \Omega } \nonumber \\ {}\le & {} \sqrt{ C^2 \Vert (u_{1} - u_{2})\Vert ^2\Vert (v_{1}-v_{2})\Vert ^2} \nonumber \\= & {} \sqrt{ C^2 \Vert u\Vert ^2\Vert v\Vert ^2}\nonumber \\= & {} C \Vert u\Vert \Vert v\Vert \end{aligned}$$

is shown by the Cauchy-Schwarz inequality, where $C_1$ and $C_2$ are positive real values since $\epsilon$ is a positive definite.

Lemma 3.3

For Hilbert space $H(\textbf{V}, \Vert \cdot \Vert )$, B is bounded and coercive.

Proof

Considering arbitrary vectors $(u,v) \in \textbf{V}$, it holds that

$$\begin{aligned} | B(u,v) |= & {} \sqrt{\Vert a(u,v) + \hat{a}(u,v)\Vert } \nonumber \\= & {} \sqrt{ a(u,v)a(u,v) +2a(u,v)\hat{a}(u,v) + \hat{a}(u,v)\hat{a}(u,v) } \nonumber \\\le & {} \sqrt{ C_1^2 \Vert u\Vert ^2\Vert v\Vert ^2 +2 C_1 \Vert u\Vert \Vert v\Vert C_2 \Vert u\Vert \Vert v\Vert + C_2^2 \Vert u\Vert ^2\Vert v\Vert ^2} \nonumber \\= & {} \sqrt{ C_1^2 +2 C_1 C_2 + C_2^2 } \Vert u\Vert \Vert v\Vert \nonumber \\= & {} (C_1 + C_2) \Vert u\Vert \Vert v\Vert \end{aligned}$$

is shown by the Cauchy-Schwarz inequality, where $C_1$ and $C_2$ are positive real values.

Also, considering $\hat{a}(u,u) \ge 0$, the Korn’s inequality shows that

$$\begin{aligned} B(u,u)= & {} a(u,u) + \hat{a}(u,u)\nonumber \\\ge & {} \int _{\Omega } \sigma (u) \epsilon (u) d \Omega \nonumber \\\ge & {} D \Vert u\Vert ^2 \end{aligned}$$

where $D_c$ is a Korn’s constant shown in [6], D is a positive scalar value. $\square$

After the above-mentioned mathematical preparations, the existence and the uniqueness of the weak form is proofed as shown below.

Proof

We consider the weak form

$$\begin{aligned} B(u,v) = \langle f, v\rangle , \end{aligned}$$

(35)

where f(v) is a bounded linear functional [6]. Using the Lemmas 3.1 to 3.3 and the Lax-Milgram’s theorem, Eq. (35) has a unique solution u for arbitrary v

4 Numerical Examples

In the previous section, we described our proposed EbO-FEM and presented its two possible formulations: Gauss-point and point-to-point projection. The energy-based overset mesh method requires that the overset domains of two discrete domains satisfy $C^0$ continuity. When two physical quantities, in this case, displacements, are given for the same position and a difference exists, energy exists and minimizes the difference.

Specific numerical examples are used to illustrate the possible basic considerations. We apply the overset mesh schemes to deformation problems. Here, the displacement field is unknown. The first and most significant question is how to determine the size of the penalty parameter a priori. The proposed method will fail if the penalty parameter is zero. By contrast, the proposed method should succeed if the penalty parameter is large, but it is unclear how large the penalty parameter should be. If the penalty parameter is extremely large, the condition number will increase and the problem will become ill-conditioned, which results in a drastic increase in the computation time. We employed two projection frameworks to analyze one-dimensional (1-D) and three-dimensional (3-D) problems for addressing these questions.

4.1 Example 1: 1-D Tensile Problem of an Elastic Cantilever

Fig. 5

A schematic of 1-D tensile problem with overset

The simplest problem to solve is the tensile problems for a 1-D cantilever. As shown in Fig. 5, let us consider pulling a bar consisting of two overset meshes, where the left side of $\Omega ^s$ is fixed on the left wall, and displacement, $\bar{u}$, is loaded on the right side of $\Omega ^p$. The case is formulated using FEM and the current method. The discretized equations are provided in Appendix.

Fig. 6

Numerical solutions of 1-D tensile problem with overset

Young’s modulus is set to 1.0 for the two components for simplicity, and the penalty parameter is varied from 0.00001 to 10.0 to examine the solution’s response to each penalty parameter. It is expected that given a larger penalty parameter, the jump-minimizing constraint will be satisfied more strictly. However, the previous study for contact analysis such as Zavarise and De Lorenzis (2009) [58] shows that the penalty parameter cannot be too large, since it induces so-called ill-conditioning of the stiffness matrix. From the engineering standpoint, it should be carefully clarified to figure out the inf-sup conditions where the analyst can obtain accurate enough solutions with avoiding the ill-conditioning. Hence this section observes the asymptotic behaviour of the approximate solution to the exact solution as the penalty parameter is increased.

The length of total bar was initially $3.5L_e$ but became $3.5 L_e + {\bar{u}}$, then the analytical solution on the 6 points $x_i (i=1,6)$

$$\begin{aligned} \begin{pmatrix} x_1 \\ x_2\\ x_3 \\ u_4\\ u_5 \\ u_6 \end{pmatrix} = \begin{pmatrix} 0 \\ L_e\\ 2 L_e \\ 1.5 L_e \\ 2.5 L_e \\ 3.5 L_e \end{pmatrix} \end{aligned}$$

(36)

are given as $u_i (i=1,6)$ with

$$\begin{aligned} \begin{pmatrix} u_1 \\ u_2\\ u_3 \\ u_4\\ u_5 \\ u_6 \end{pmatrix}= \begin{pmatrix} 0 \\ \frac{3.5L_e + {\bar{u}}}{3.5L_e}L_e - L_e\\ \frac{3.5L_e + {\bar{u}}}{3.5L_e}2 L_e - 2 L_e \\ \frac{3.5L_e + {\bar{u}}}{3.5L_e}1.5 L_e - 1.5 L_e \\ \frac{3.5L_e + {\bar{u}}}{3.5L_e}2.5 L_e - 2.5 L_e \\ \frac{3.5L_e + {\bar{u}}}{3.5L_e}3.5 L_e - 3.5 L_e \end{pmatrix} = \begin{pmatrix} 0 \\ \frac{2}{7}{\bar{u}}\\ \frac{4}{7}{\bar{u}}\\ \frac{3}{7}{\bar{u}}\\ \frac{5}{7}{\bar{u}}\\ {\bar{u}} \end{pmatrix} \end{aligned}$$

(37)

The numerical solutions obtained by the proposed methods are compared with the analytical solution to verify the accuracy and properties of the proposed method. $L_e=2$ is used for simplicity.

Figure 6 shows the exact solution and calculation results for the displacement at each nodal position. The figure shows that as the DRP increases from zero to 1.0, the results becomes closer to the exact solution. The solution was more accurate in cases of the Gauss-point projection than the point-to-point. The figure, however, implies that only $C^0$-continuity is almost satisfied in point-to-point projection, and nothing above $C^1$ is guaranteed. The phenomena has been also reported [29] and caused by the Dirichlet-Dirichlet type constraint. Alternatively, Gauss-point projection approximates both $C^2$ and $C^0$ continuity around the projection point. The overset mesh scheme was initially intended to satisfy only the $C^0$ continuity, and both solutions do so; however, the Gauss-point projection also satisfies higher-order continuity near the projection.

Overall, the current scheme successfully minimizes the gap as intended. As expected, increasing the penalty parameter yields a solution that is close to the exact solution. The smallest feasible penalty parameter is 1.0 and the results are unaffected if the penalty parameters are more than 10.0 at the projection point.

Notably, the penalty parameters in point-to-point and Gauss-point projections have different implications and dimensions. For 3-D cases, the former has a dimension of N/m and the latter has a dimension of $N/m^4$ as discussed in the previous section. This difference results in the difference in the dimension of the dimensionless relative penalty-parameters (DRP) $\mathscr {E}$ by

$$\begin{aligned} \mathscr {E} = \frac{\epsilon _{P}}{E} \times UL^{-1} = \frac{\epsilon _{G}}{E} \times UL^2 \end{aligned}$$

(38)

Notably, the penalty parameters in point-to-point and Gauss-point projections have different implications and dimensions. For 3-D cases, the former has a unit of N/m while the latter has $N/m^4$ as discussed in the previous section.

4.2 Example 2: 3-D Bending Problem of an Elastic Cantilever

Figure 7 shows the initial and boundary conditions of the problem. The cantilever (Young’s modulus = 1000.0, Poisson ratio = 0.0) is divided into three discrete cantilevers for EbO-FEM: The left cantilever is fixed in the left rigid wall, the right one is loaded displacement, and the middle one is traction-free. In the conventional one-domain FEM formulation, the problem has a solution where the three are connected into a uniform cantilever. Each subdomain in the overlapping mesh has $30 \times 9\times 9 = 2730$ elements and the mesh for the one-domain FEM has $90 \times 9 \times 9 = 2730$ elements. Each mesh overlaps 0.1 m each other for the overlapping mesh.

Fig. 7

Schematic diagram of 3-D bending problem of a cantilever beam

Figure 8 shows the deformed mesh and the effect of the penalty parameter. The figure shows that the results of the point-to-point and Gauss-point projections are identical to the analytical and FEM solutions. In terms of the penalty parameter, a relative penalty parameter of 1.0 appears to be sufficient, implying that the penalty parameter can be the same as Young’s modulus.

Fig. 8

Deformed mesh of a bending problem of 3-D cantilevers

Figure 9 shows the relationship between the force-curve and displacement. The DRP here is 10.0, the length of the bar is 5.8 m, the width is changed from 0.3 m to 0.7 m for each case. The current method’s solution is quantitatively almost the same as the analytical solution and the one-domain FEM solutions in any width.

Fig. 9

Force-curves of a bending problem of 3-D cantilevers, where the DRP is 10.0

Figure 10 plots the relationship between DRP and the number of iterations required for the convergence at the BiCGSTAB algorithm where the tolerance of the energy norm is $1.0 \times 10^{-10}$. For both cases, DRP $< 0.1$ enforces too weak constraint, which results in inaccurate solutions as visible in Fig. 9. By contrast, DRP $> 1000.0$ causes severe ill-condition in the case of Gauss-point projection, as well as DRP $> 10.0$ in the point-to-point projection. Hence, it is difficult for the point-to-point projection to obtain accurate and robust solutions. The Gauss-point projection gives accurate and robust solutions in case the DRP is in between 1 to 1000, at least in these initial/boundary conditions. The results also show that the Gauss-point projection cases only require 0.1 to 2.0 times larger number of iterations, which are sufficiently small computational costs as an overset mesh scheme compared to that of the one-domain case.

Fig. 10

DRP vs number of iteration in BiCGSTAB solver

Figure 11 shows how the condition number of the coefficient matrix varies with a change in relative penalty parameters. Since it is necessary to use a dense matrix to compute a condition number, we use a more coarse mesh (30 $\times$4 times 4 elements for each subdomain) due to the limitation of the computational resources. The result indicates that the condition numbers are minimized when the relative penalty parameter is about 1.0 in both cases. Alternatively, when the relative penalty parameter is smaller than 0.01 or larger than 10.0, the condition number increases drastically. Figs. 9, 10, and 11 indicate that a penalty parameter of 1.0 is optimal for both projection schemes.

Fig. 11

Relationship between DRP and condition number

4.3 Example 3: 3-D Deformation Analysis of Self-Weighted RC Frame Bridge

Investigating the applicability of the method to practical problems, we simulate here a four-spanned reinforced concrete (RC) frame bridge under a self-weighted condition (Fig. 12). Although similar simulations can be conducted by using the conventional FEM, it is a huge efforts to create such a qualified conforming mesh. By contrast, it is cost-efficient to use non-conforming mesh as shown in Fig. 13, if the proposed method provides similar solutions as ones of conventional FEM.

Figure 12 shows the initial and boundary condition of the computational domain. The RC frame bridge is a typical one for a railway bridge in Japan, with 40 m in length, 10 m in width and 7 m in height. The Young modulus, the shear modulus, and the density are $2.5 \times 10^7$ kPa, $1.0 \times 10^7$ kPa, and 25.0 kN/m$^3$, respectively. The bottom of the piers is fixed on the ground for simplicity.

The mesh consists of 74,201 points and 48,832 hexahedral elements for FEM. The EbO-FEM case uses a non-conforming mesh consisting of three parts as visible in Fig. 13, where the centre part consists of 71,119 points with 50368 elements, the set of floor parts has 4,848 points/3,000 elements, and the pair of the edge parts has 3,333 points/2,000 elements.

Figure 14 shows the deformed mesh with $\sigma _{zz}$ components of the Cauchy stress. As can be seen, the solution of EbO-FEM is consistent with the FEM solution in cases where the dimensionless relative penalty parameter (DRP) is greater than 1.0. On the other hand, the EbO-FEM solution is inconsistent in cases where the parameter is smaller than 1.0. The phenomena are also observed in the previous sections for 1-D and 3-D problems, which again suggests that (1) the DRP can be a universal measure for EbO-FEM scheme and (2) DRP should be greater than 1.0 to obtain consistent solutions.

Fig. 12

Initial and boundary condition of 3-D deformation analysis of RC rigid frame under self-weighted condition

Fig. 13

One-domain FEM mesh (top left) and equivalent overlapping mesh (right and bottom)

Fig. 14

Stress contour of $\sigma _{zz}$ with deformed mesh

5 Conclusion

In this study, an EbO-FEM, based on FEM, is proposed for nonconforming meshes to solve the multibody mesh overlap problem. To apply the continuity condition, we introduce a continuity constraint energy, which is analogous to the contact constraint energy in the node-to-segment method [10, 54, 58] based on the equation-based DCM [29]. It has been confirmed that the method can produce almost continuous and unique solutions on separately defined overlapping finite element meshes. We utilized two projection methods, point-to-point projection and the Gauss-point projection, and showed that the Gauss-point projection is a better strategy because it is more robust and requires less computation time for solving linear equations based on BiCGSTAB procedure. Also, we proposed a dimensionless measure, DRP, to evaluate the magnitude of the constraint, and showed that the DRP of 0.1 to 10.0 is the best from the standpoints of accuracy, robustness, and computation costs. Surprisingly, the present scheme does not increase the computation costs after assembling the global matrix, which is a great benefit for problems with many overlapping regions as these 3-D complex problems.

The proposed non-iterative, energy-based overset scheme helps solve pseudo-static deformation problems with multi-overlapping meshed appearing in civil engineering structures on vegetated ground[59, 60] and plant growth [40, 44, 61]. In addition, this EbO-FEM can be combined with discretization methods other than FEM as long as the continuous constraint energy is well-defined among nonconforming meshes. Therefore, this approach can be extended for dynamic elastic problems or wave propagation problems. Future studies will apply the method to dynamic analysis to see if it can provide an accurate solution for elastodynamic problems.

Appendix

Governing equation is

$$\begin{aligned} E \frac{d^2 u}{d x^2} = 0, \end{aligned}$$

(A.1)

where E is Young modulus, u is displacement and x is the coordinate. The weak form is derived based on Galerkin method

$$\begin{aligned} \begin{aligned} \int _{x_l}^{x_r} w E \frac{d^2 u}{d x^2} dx&= \\ \left[ w E \frac{d u}{d x} \right] _{x_l}^{x_r} - \int _{x_l}^{x_r} E \frac{d w}{d x} \frac{d u}{d x} dx&= 0, \end{aligned} \end{aligned}$$

(A.2)

where w is a weight function, $x_r$ and $x_l$ are the coordinate of the left and right sides of the bar, respectively. Here, no traction is loaded in the boundary, then $\frac{d u}{d x}=0$ in the boundary, hence,

$$\begin{aligned} \begin{aligned} \int _{x_l}^{x_r} E \frac{d w}{d x} \frac{d u}{d x} dx =0. \end{aligned} \end{aligned}$$

(A.3)

Introducing linear shape-functions, w and u are written as following expression

$$\begin{aligned} \begin{aligned} w&= (1-\xi ) w_l + \xi w_r\\ u&= (1-\xi ) u_l + \xi u_r. \end{aligned} \end{aligned}$$

(A.4)

The $\xi$ is a local coordinate defined in $[ 0 \le \xi \le 1 ]$, and the subscription $_r$ and $_l$ indicates the left and right nodes of a line element for unknowns w and u, respectively. Then the weak form is discretized as shown below

$$\begin{aligned} \begin{pmatrix} w_l&w_r \end{pmatrix} \begin{pmatrix} \int _{0}^{1} E \frac{d (1-\xi ) }{d \xi } \frac{d (1-\xi ) }{d \xi } \frac{d\xi }{dx} d\xi &{} \int _{0}^{1} E \frac{d (\xi ) }{d \xi } \frac{d (1-\xi ) }{d \xi } \frac{d\xi }{dx} d\xi \\ \int _{0}^{1} E \frac{d (\xi ) }{d \xi } \frac{d (1-\xi ) }{d \xi } \frac{d\xi }{dx} d\xi &{} \int _{0}^{1} E \frac{d (\xi ) }{d \xi } \frac{d \xi }{d \xi } \frac{d\xi }{dx} d\xi \\ \end{pmatrix} \begin{pmatrix} u_l \\ u_r \end{pmatrix}=0 . \end{aligned}$$

(A.5)

The $\frac{dx}{d\xi }$ is the length of the element $L_e$, consequently, the discretized equations are given.

$$\begin{aligned} \begin{pmatrix} \frac{E}{L_e} &{} -\frac{E}{L_e} \\ -\frac{E}{L_e} &{} \frac{E}{L_e}\\ \end{pmatrix} \begin{pmatrix} u_l \\ u_r \end{pmatrix}=0 \end{aligned}$$

(A.6)

The global equation is assembled as Eq. (A.7)

$$\begin{aligned} \begin{pmatrix} \frac{E_1}{L_e} &{} -\frac{E_1}{L_e} &{}0&{}0&{}0&{}0\\ -\frac{E_1}{L_e} &{} \frac{E_1}{L_e}+\frac{E_2}{L_e} &{}-\frac{E_2}{L_e}&{}0&{}0&{}0\\ 0&{}-\frac{E_2}{L_e}&{}\frac{E_2}{L_e}&{}0&{}0&{}0\\ 0&{}0&{}0&{}\frac{E_3}{L_e}&{}-\frac{E_3}{L_e}&{}0\\ 0&{}0&{}0&{}-\frac{E_3}{L_e}&{}\frac{E_3}{L_e}+\frac{E_4}{L_e}&{}-\frac{E_4}{L_e}\\ 0&{}0&{}0&{}0&{}-\frac{E_4}{L_e}&{}\frac{E_4}{L_e}\\ \end{pmatrix} \begin{pmatrix} u_1 \\ u_2\\ u_3 \\ u_4\\ u_5 \\ u_6 \end{pmatrix}= \begin{pmatrix} 0 \\ 0\\ 0 \\ 0\\ 0 \\ 0 \end{pmatrix} , \end{aligned}$$

(A.7)

where $u_n$ $(n=1,2,...,6)$ are nodal values of displacement field.

1.1 Formulation Based on Gauss-Point Projection

From Eq. (20), the constraint condition is active in $\Omega _{ps}$, then, the system of equation based on Eqs. (13) and (15) is given

$$\begin{aligned} \delta \Pi ^{gp}= & {} {\epsilon }{L_e} \begin{pmatrix} u_4&u_5&u_2&u_3 \end{pmatrix} \nonumber \\ {}{} & {} \begin{pmatrix} \frac{1}{2} + \frac{1}{2\sqrt{3}} \\ \frac{1}{2} - \frac{1}{2\sqrt{3}} \\ -\frac{1}{2\sqrt{3}} \\ -1 + \frac{1}{2\sqrt{3}}\\ \end{pmatrix} \begin{pmatrix} \frac{1}{2} + \frac{1}{2\sqrt{3}} &{} \frac{1}{2} - \frac{1}{2\sqrt{3}} &{} -\frac{1}{2\sqrt{3}} &{} -1 + \frac{1}{2\sqrt{3}}\\ \end{pmatrix} \begin{pmatrix} u_4 \\ u_5 \\ u_2 \\ u_3 \end{pmatrix} \end{aligned}$$

(A.8)

$$\begin{aligned} \delta \Pi ^{gp}= & {} {\epsilon }{L_e} \begin{pmatrix} u_4&u_5&u_2&u_3 \end{pmatrix} \begin{pmatrix} \frac{1}{3} + \frac{1}{2\sqrt{3}} &{} \frac{1}{6} &{} -\frac{1}{12} -\frac{1}{4\sqrt{3}} &{} -\frac{5}{12} - \frac{1}{4\sqrt{3}} \\ \frac{1}{6} &{} \frac{1}{3} - \frac{1}{2\sqrt{3}} &{} \frac{1}{12} - \frac{1}{4\sqrt{3}} &{} -\frac{7}{12} + \frac{1}{4\sqrt{3}} \\ -\frac{1}{12} - \frac{1}{4 \sqrt{3}} &{} \frac{1}{12} - \frac{1}{4\sqrt{3}} &{} \frac{1}{12} &{} -\frac{1}{12} + \frac{1}{2\sqrt{3}} \\ -\frac{5}{12} - \frac{1}{4\sqrt{3}} &{} -\frac{7}{12} +\frac{3}{4\sqrt{3}} &{} -\frac{1}{12} + \frac{1}{2\sqrt{3}} &{} \frac{13}{12} - \frac{1}{\sqrt{3}} \\ \end{pmatrix} \begin{pmatrix} u_4 \\ u_5 \\ u_2 \\ u_3 \end{pmatrix}\nonumber \\= & {} \delta u_A \bar{K}_{AB}^{gp} u_B \end{aligned}$$

(A.9)

The global equation is assembled as Eq. (A.10).

$$\begin{aligned} \begin{pmatrix} \frac{E_1}{L_e} &{} -\frac{E_1}{L_e} &{}0&{}0&{}0&{}0\\ -\frac{E_1}{L_e} &{} \frac{E_1}{L_e}+\frac{E_2}{L_e}+K_{22}^{gp} &{}-\frac{E_2}{L_e}+K_{23}^{gp}&{}K_{24}^{gp}&{}K_{25}^{gp}&{}0\\ 0&{}-\frac{E_2}{L_e}+K_{32}^{gp}&{}\frac{E_2}{L_e}+K_{33}^{gp}&{}K_{34}^{gp}&{}K_{35}^{gp}&{}0\\ 0&{}K_{42}^{gp}&{}K_{43}^{gp}&{}\frac{E_3}{L_e} + K_{4,4}^{gp}+K_{44}^{gp} &{}-\frac{E_3}{L_e}+K_{45}^{gp}&{}0\\ 0&{}K_{52}^{gp}&{}K_{53}^{gp}&{}-\frac{E_3}{L_e}+K_{54}^{gp}&{}\frac{E_3}{L_e}+\frac{E_4}{L_e}+K_{55}^{gp}&{}-\frac{E_4}{L_e}\\ 0&{}0&{}0&{}0&{}-\frac{E_4}{L_e}&{}\frac{E_4}{L_e}\\ \end{pmatrix} \begin{pmatrix} u_1 \\ u_2\\ u_3 \\ u_4\\ u_5 \\ u_6 \end{pmatrix}= \begin{pmatrix} 0 \\ 0\\ 0 \\ 0\\ 0 \\ 0 \end{pmatrix} , \end{aligned}$$

(A.10)

where $K_{AB}^{gp}$ is a globally assembled matrix of $\bar{K}_{AB}^{gp}$.

1.2 Formulation Based on Point-to-Point Projection

From Eq. (20), the constraint condition is active in $\Omega _{ps}$, then, the system of equation based on Eqs. (13) and (15) is given

$$\begin{aligned} \delta \Pi ^{p \rightarrow s}= & {} \epsilon \begin{pmatrix} \delta u_4&\delta u_2&\delta u_3 \end{pmatrix} \begin{pmatrix} 1\\ frac{1}{2}\\ frac{1}{2} \end{pmatrix} \begin{pmatrix} 1&-\frac{1}{2}&-\frac{1}{2} \end{pmatrix} \begin{pmatrix} u_4 \\ u_2 \\ u_3 \end{pmatrix}=0 \end{aligned}$$

(A.11)

$$\begin{aligned} \delta \Pi ^{s \rightarrow p}= & {} \epsilon \begin{pmatrix} \delta u_3&\delta u_4&\delta u_5 \end{pmatrix} \begin{pmatrix} 1\\ frac{1}{2}\\ frac{1}{2} \end{pmatrix} \begin{pmatrix} 1&-\frac{1}{2}&-\frac{1}{2} \end{pmatrix} \begin{pmatrix} u_3 \\ u_4 \\ u_5 \end{pmatrix}=0 \end{aligned}$$

(A.12)

and finally the matrix forms are obtained.

$$\begin{aligned} \delta \Pi ^{p \rightarrow s}= & {} \begin{pmatrix} \delta u_4&\delta u_2&\delta u_3 \end{pmatrix} \begin{pmatrix} \epsilon &{}-\frac{\epsilon }{2}&{}-\frac{\epsilon }{2}\\ -\frac{\epsilon }{2}&{}\frac{\epsilon }{4}&{}\frac{\epsilon }{4}\\ -\frac{\epsilon }{2}&{}\frac{\epsilon }{4}&{}\frac{\epsilon }{4} \end{pmatrix} \begin{pmatrix} u_4 \\ u_2 \\ u_3 \end{pmatrix}=0 \end{aligned}$$

(A.13)

$$\begin{aligned} \delta \Pi ^{s \rightarrow p}= & {} \begin{pmatrix} \delta u_3&\delta u_4&\delta u_5 \end{pmatrix} \begin{pmatrix} \epsilon &{}-\frac{\epsilon }{2}&{}-\frac{\epsilon }{2}\\ -\frac{\epsilon }{2}&{}\frac{\epsilon }{4}&{}\frac{\epsilon }{4}\\ -\frac{\epsilon }{2}&{}\frac{\epsilon }{4}&{}\frac{\epsilon }{4} \end{pmatrix} \begin{pmatrix} u_3 \\ u_4 \\ u_5 \end{pmatrix}=0 \end{aligned}$$

(A.14)

Substituting Eq. (A.14) into Eq. (A.7), a set of consistent equations are provided.

$$\begin{aligned} \begin{pmatrix} \frac{E_1}{L_e} &{} -\frac{E_1}{L_e} &{}0&{}0&{}0&{}0\\ -\frac{E_1}{L_e} &{} \frac{E_1}{L_e}+\frac{E_2}{L_e} &{}-\frac{E_2}{L_e}&{}0&{}0&{}0\\ 0&{}-\frac{E_2}{L_e}&{}\frac{E_2}{L_e}+\epsilon &{}-\frac{1}{2}\epsilon &{}-\frac{1}{2}\epsilon &{}0\\ 0&{}0&{}-\frac{1}{2}\epsilon &{}\frac{E_3}{L_e}+\frac{1}{4}\epsilon &{}-\frac{E_3}{L_e}+\frac{1}{4}\epsilon &{}0\\ 0&{}0&{}-\frac{1}{2}\epsilon &{}-\frac{E_3}{L_e}+\frac{1}{4}\epsilon &{}\frac{E_3}{L_e}+\frac{E_4}{L_e}+\frac{1}{4}\epsilon &{}-\frac{E_4}{L_e}\\ 0&{}0&{}0&{}0&{}-\frac{E_4}{L_e}&{}\frac{E_4}{L_e}\\ \end{pmatrix} \begin{pmatrix} u_1 \\ u_2\\ u_3 \\ u_4\\ u_5 \\ u_6 \end{pmatrix}= \begin{pmatrix} 0 \\ 0\\ 0 \\ 0\\ 0 \\ 0 \end{pmatrix} \end{aligned}$$

(A.15)

Finally, the boundary condition $u_6 = {\bar{u}}$ and $u_1 = 0$ is introduced.

$$\begin{aligned} \begin{pmatrix} 1 &{} 0 &{}0&{}0&{}0&{}0\\ 0 &{} \frac{E_1}{L_e}+\frac{E_2}{L_e} &{}-\frac{E_2}{L_e}&{}0&{}0&{}0\\ 0&{}-\frac{E_2}{L_e}&{}\frac{E_2}{L_e}+\epsilon &{}-\frac{1}{2}\epsilon &{}-\frac{1}{2}\epsilon &{}0\\ 0&{}0&{}-\frac{1}{2}\epsilon &{}\frac{E_3}{L_e}+\frac{1}{4}\epsilon &{}-\frac{E_3}{L_e}+\frac{1}{4}\epsilon &{}0\\ 0&{}0&{}-\frac{1}{2}\epsilon &{}-\frac{E_3}{L_e}+\frac{1}{4}\epsilon &{}\frac{E_3}{L_e}+\frac{E_4}{L_e}+\frac{1}{4}\epsilon &{}0\\ 0&{}0&{}0&{}0&{}0&{}1\\ \end{pmatrix} \begin{pmatrix} u_1 \\ u_2\\ u_3 \\ u_4\\ u_5 \\ u_6 \end{pmatrix}= \begin{pmatrix} 0 \\ 0\\ 0 \\ 0\\ \frac{E_4}{L_e}{\bar{u}} \\ {\bar{u}} \end{pmatrix} \end{aligned}$$

(A.16)

Solving this set of equations yields the results shown in Fig. 6.