Space-Time Discontinuous Galerkin Methods for Weak Solutions of Hyperbolic Linear Symmetric Friedrichs Systems

Abstract

We study weak solutions and its approximation of hyperbolic linear symmetric Friedrichs systems describing acoustic, elastic, or electro-magnetic waves. For the corresponding first-order systems we construct discontinuous Galerkin discretizations in space and time with full upwind, and we show primal and dual consistency. Stability and convergence estimates are provided with respect to a mesh-dependent DG norm which includes the ${\textrm{L}}_2$ norm at final time. Numerical experiments confirm that the a priori results are of optimal order also for solutions with low regularity, and we show that the error in the DG norm can be closely approximated with a residual-type error indicator.

1 Introduction

Linear wave equations are hyperbolic, and the formulation as first-order symmetric Friedrichs system provides a well established setting for analyzing and approximating solutions. A specific feature of hyperbolic systems is the transport of discontinuities along characteristics. Our goal is to provide a numerical scheme which is efficient for smooth solutions as well as for weak solutions with discontinuities.

For smooth solutions of linear symmetric Friedrichs systems ${\mathcal {O}}(h^{s-1/2})$ convergence can be established for discontinuous Galerkin approximations in space with respect to suitable mesh-dependent DG norm [9, Chap. 57], [5, Chap. 7]. For acoustics, the convergence analysis of a space-time approximation in a DG semi-norm provides estimates for all discrete time steps [2, Prop. 6.5].

Finite volume convergence ${\mathcal {O}}(h^{1/2})$ for hyperbolic linear symmetric Friedrichs systems is established in [18] combined with first-order time-stepping. Discontinuous Galerkin methods in time are analyzed in [12] for tent-type space-time meshes. This is adapted to space-time discontinuous Galerkin methods on general space-time meshes with upwind flux for acoustics in [2], where the convergence is established for sufficiently smooth solutions based on estimates in a suitable DG semi-norm. In particular, the analysis includes the adaptive approximation of corner singularities.

Here, we consider a DG method in space and time for linear symmetric Friedrichs systems, and we show inf-sup stability and convergence in the DG norm. Therefore we transfer our results for space-time Petrov–Galerkin methods in [6, 7] with continuous approximations in time and for the DPG method in [10, 11], where convergence in a stronger graph norm is considered. Our analysis includes bounds for the consistency error in the case that piecewise discontinuous material parameters are not aligned with the mesh. Convergence in the limit for piecewise discontinuous solutions of Riemann problems is established only in ${\textrm{L}}_2$.

The space-time method is realized in the parallel finite element system M++ [4]. In our numerical examples we confirm the a priori estimates for weak as well as for smooth solutions, and we demonstrate the efficiency of the p-adaptive scheme.

Space-time computations have a long history in practical engineering applications and in parallel time integration [13, 26]. The space-time approach allows for large-scale parallel computing and in case of point sources the reduction to the time cone within the space-time cylinder. Moreover, it allows for dual-primal goal-oriented error control and applications to inverse and optimal control problems where the adjoint problem is backward in time and relies on the forward solution in the full space-time cylinder. Space-time discretizations for the wave equation are constructed within a second-order approach in [19, 25], with isogeometric methods in [27], a very weak approach is presented in [15], a quasi-Trefftz method is considered in [17], and a new approach to space-time boundary integral equations for the wave equation is developed in [24]. In comparison with these methods the first-order DG approach is numerically expensive. On the other hand, convergence can be established with minimal regularity assumptions, the method easily extends to more general material laws and to more general hyperbolic conservation laws.

The paper is organized as follows. In Sect. 2 we introduce the notation and the formulation of wave equations as first-order systems, in Sect. 3 we introduce the DG discretization in time and in space. In Sect. 4 we consider well-posedness and stability, in Sect. 5 we prove existence of weak solutions and convergence estimates, in Sect. 5.3 we introduce an a posteriori error indicator, and in Sect. 6 we present numerical results. In Sect. 7 we conclude with a discussion of possible extensions and open problems.

2 Symmetric Friedrichs Systems

We consider weak solutions of linear hyperbolic first-order systems in the form of symmetric Friedrichs systems. Let $\Omega \subset {{\mathbb {R}}}^d$ be a bounded domain in space with Lipschitz boundary $\partial \Omega$, $I = (0,T)$ a time interval, and we denote the space-time cylinder by $Q = (0,T)\times \Omega$. Boundary conditions will be imposed on $\Gamma _k\subset \partial \Omega$ for $k=1,\ldots ,m$ depending on the model, where m is the dimension of the first-order system.

For $S \subset Q$ the ${\textrm{L}}_2$ norm and inner product are denoted by $\Vert \cdot \Vert _S$ and $(\cdot ,\cdot )_S$.

Let $L = M\partial _t +A$ be a linear differential operator in space and time, where $(M{{\textbf {v}} })(t,{{\textbf {x}} }) = \underline{M}({{\textbf {x}} }){\textbf {v}} (t,{{\textbf {x}} })$ defines the operator M with a uniformly positive definite matrix-valued function $\underline{M}\in {\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{m\times m}_\text {sym})$, and where $A {{\textbf {v}} } = \sum _{j=1}^d \underline{A}_j \partial _j {{\textbf {v}} }$ is a differential operator in space with matrices $\underline{A}_j\in {{\mathbb {R}}}^{m\times m}_\text {sym}$. Since $\underline{M}$ is uniformly positive definite, constants $C_M\ge c_M > 0$ exists such that

$$\begin{aligned} c_M \, \mathbf{{y}}^\top \mathbf{{y}} \le \mathbf{{y}}^\top \underline{M}(\mathbf{{x}}) \mathbf{{y}} \le C_M \, \mathbf{{y}}^\top \mathbf{{y}}\,,\qquad \mathbf{{y}}\in {\mathbb {R}}^m \text { and a.a. } \mathbf{{x}}\in \Omega \,. \end{aligned}$$

We observe

$$\begin{aligned} \big (L{{\textbf {v}} },{{\textbf {w}} }\big )_Q = \big (M\partial _t{{\textbf {v}} },{{\textbf {w}} }\big )_Q + \big (A{{\textbf {v}} },{{\textbf {w}} }\big )_Q&= -\big ({{\textbf {v}} },M\partial _t{{\textbf {w}} }\big )_Q -\big ({{\textbf {v}} },A{{\textbf {w}} }\big )_Q \\&= -\big ({{\textbf {v}} },L{{\textbf {w}} }\big )_Q \,,\qquad {{\textbf {v}} },{{\textbf {w}} } \in {\textrm{C}}^1_\text {c}(Q;{{\mathbb {R}}}^m) \,, \end{aligned}$$

so that $L^* = -L$ is the adjoint differential operator. This is now complemented by initial and boundary conditions.

For the unit normal vector ${{\textbf {n}} }\in {\textrm{L}}_\infty (\partial \Omega ;{{\mathbb {R}}}^d)$ we define the matrix $\underline{A}_{{{\textbf {n}} }} = \sum _{j=1}^d n_j \underline{A}_j \in {{\mathbb {R}}}^{m\times m}_\text {sym}$, so that

$$\begin{aligned} \big (A{{\textbf {v}} },{{\textbf {w}} }\big )_\Omega +\big ({{\textbf {v}} },A{{\textbf {w}} }\big )_\Omega = \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{\partial \Omega } =\big ({{\textbf {v}} },\underline{A}_{{{\textbf {n}} }}{{\textbf {w}} }\big )_{\partial \Omega } \,,\qquad {{\textbf {v}} },{{\textbf {w}} } \in {\textrm{C}}^1(\overline{\Omega };{{\mathbb {R}}}^m) \,. \end{aligned}$$

Correspondingly, we get for the operator L in space and time

$$\begin{aligned} \big (L{{\textbf {v}} },{{\textbf {w}} }\big )_Q + \big ({{\textbf {v}} },L{{\textbf {w}} }\big )_Q&= \big (M{{\textbf {v}} }(T),{{\textbf {w}} }(T)\big )_\Omega - \big (M{{\textbf {v}} }(0),{{\textbf {w}} }(0)\big )_\Omega \\&\qquad + \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } \,,\qquad {{\textbf {v}} },{{\textbf {w}} } \in {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m) \,, \end{aligned}$$

i.e., inserting $L^* = -L$,

$$\begin{aligned} \big ({{\textbf {v}} },L^*{{\textbf {w}} }\big )_Q&= \big (L{{\textbf {v}} },{{\textbf {w}} }\big )_Q - \big (M{{\textbf {v}} }(T),{{\textbf {w}} }(T)\big )_\Omega \\&\qquad + \big (M{{\textbf {v}} }(0),{{\textbf {w}} }(0)\big )_\Omega - \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } \,,\quad {{\textbf {v}} },{{\textbf {w}} } \in {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m) \,. \end{aligned}$$

In order to define weak solutions, we include initial values for $t=0$ and boundary conditions on $\Gamma _k$ for $k=1,\ldots ,m$ in the right-hand side. Therefore, we use a test space ${\mathcal {V}}^*\subset {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m)$ such that

$$\begin{aligned} \big ({{\textbf {v}} },L^*{{\textbf {w}} }\big )_Q&= \big (L{{\textbf {v}} },{{\textbf {w}} }\big )_Q + \big (M{{\textbf {v}} }(0),{{\textbf {w}} }(0)\big )_\Omega - \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } \,, \\&\qquad \qquad {{\textbf {v}} } \in {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m)\,,\ {{\textbf {w}} } \in {\mathcal {V}}^* \end{aligned}$$

with

$$\begin{aligned} \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega }= \sum _{k=1}^m&\big ((\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} })_k,w_k\big )_{(0,T)\times \Gamma _k} \,, \nonumber \\&\qquad {{\textbf {v}} } \in {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m)\,,\ {{\textbf {w}} } =(w_1,\ldots ,w_m)\in {\mathcal {V}}^* \,. \end{aligned}$$

(1)

The property (1) characterizes adjoint boundaries $\Gamma _k^*\subset \partial \Omega$ for $k=1,\ldots ,m$, so that the test space is defined by

$$\begin{aligned} {\mathcal {V}}^* = \big \{&{{\textbf {w}} } \in {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m) :{{\textbf {w}} }(T) = {\textbf {0}} \text { in } \Omega \,,\ {{\textbf {w}} }(t)\in {\mathcal {S}}^* \text { for } t\in [0,T) \big \}\\&\text {with}\quad {\mathcal {S}}^* = \big \{ {{\textbf {w}} } \in {\textrm{C}}^1(\overline{\Omega };{{\mathbb {R}}}^m) :(\underline{A}_{{{\textbf {n}} }}{{\textbf {w}} })_k = 0 \text { on } \Gamma _k^*\,,\ k=1,\ldots ,m \big \} \end{aligned}$$

with homogeneous final values at $t=T$ and homogenous values at the adjoint boundaries.

Our aim is to find a weak solution ${{\textbf {u}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ solving

$$\begin{aligned} \big ({{\textbf {u}} },L^*{{\textbf {w}} }\big )_Q = \big \langle \ell ,{{\textbf {w}} }\big \rangle \,,\qquad {{\textbf {w}} }\in {\mathcal {V}}^* \end{aligned}$$

(2)

with

$$\begin{aligned} \big \langle \ell ,{{\textbf {w}} }\big \rangle = \big ({{\textbf {f}} },{{\textbf {w}} }\big )_Q + \big (M{{\textbf {u}} }_0,{{\textbf {w}} }(0)\big )_\Omega - \big ({{\textbf {g}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } \,,\qquad {{\textbf {w}} }\in {\mathcal {V}}^* \end{aligned}$$

for given volume data ${{\textbf {f}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$, initial data ${{\textbf {u}} }_0\in {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)$, and boundary data ${{\textbf {g}} }\in {\textrm{L}}_2((0,T)\times \partial \Omega ;{{\mathbb {R}}}^m)$, where the boundary data ${{\textbf {g}} } = (g_k)_{k=1,\ldots ,m}$ are extended to $\partial \Omega$ by $g_k = 0$ on $\partial \Omega \setminus \Gamma _k$ for $k=1,\ldots ,m$.

Testing the weak solution ${{\textbf {u}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ in (2) with functions in ${{\textbf {v}} }\in {\textrm{C}}^1_\textrm{c}(Q;{{\mathbb {R}}}^m)$ defines the weak derivative $L{{\textbf {u}} } = {{\textbf {f}} }$ in ${\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$. If in addition ${{\textbf {u}} }(0) \in {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)$ and $\underline{A}_{{{\textbf {n}} }} {\textbf {u}} |_{(0,T)\times \Gamma _k} \in {\textrm{L}}_2((0,T)\times \Gamma _k)$ for $k=1,\ldots ,m$, the weak solution is also a strong solution characterized by

$$\begin{aligned} L{{\textbf {u}} } = {{\textbf {f}} } \text { in } {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)\,,\qquad&{{\textbf {u}} }(0) = {{\textbf {u}} }_0 \text { in } {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)\,,\qquad \nonumber \\&(\underline{A}_{{{\textbf {n}} }} {{\textbf {u}} })_k = g_k \text { on } {\textrm{L}}_2((0,T)\times \Gamma _k)\,,\ k= 1,\ldots ,m \,. \end{aligned}$$

(3)

This is now specified for acoustic, elastic and electro-magnetic waves.

Acoustic waves The second-order wave equation

$$\begin{aligned} \varrho \partial _t^2 \phi -\nabla \cdot (\kappa \nabla \phi ) = b \end{aligned}$$

is considered as first-order system with $p = \partial _t \phi$ and ${{\textbf {q}} } = -\kappa \nabla \phi$, i.e.,

$$\begin{aligned} \varrho \partial _t p + \nabla \cdot {\textbf {q}} = b&\ \text { and } \partial _t {\textbf {q}} + \kappa \nabla p = {\textbf {0}} \qquad \qquad{} & {} \text {in } (0,T)\times \Omega \,, \\ p(0) = p_0&\ \text { and } {\textbf {q}} (0) = {\textbf {q}} _0{} & {} \text { in } \Omega \text { at } t=0\,, \\ p(t) = p_\textrm{D}(t) \text { on } \Gamma _\textrm{D}&\ \text { and } {\textbf {n}} \cdot {\textbf {q}} (t) = g_\textrm{N}(t) \text { on } \Gamma _\textrm{N}{} & {} \text { on } \partial \Omega \text { for } t\in (0,T) \end{aligned}$$

for volume data b, boundary data $g_\textrm{N}$, $p_\textrm{D}$, initial data ${{\textbf {q}} }_0$, $p_0$, positive parameters $\varrho ,\kappa$, and the disjoint decomposition of the boundary $\partial \Omega = \Gamma _\textrm{D}\cup \Gamma _\textrm{N}$ into Dirichlet and Neumann part. The corresponding Friedrichs system with $m = 1+d$ components is given by

$$\begin{aligned} {{\textbf {u}} } = \begin{pmatrix} p \\ {{\textbf {q}} }\end{pmatrix}\,, \quad M{{\textbf {u}} } = \begin{pmatrix} \varrho p \\ \kappa ^{-1} {{\textbf {q}} }\end{pmatrix}\,, \quad A{{\textbf {u}} } = \begin{pmatrix} \nabla \cdot {{\textbf {q}} } \\ \nabla p\end{pmatrix} \,, \quad \nonumber \\ \underline{A}_{{{\textbf {n}} }}{{\textbf {u}} } = \begin{pmatrix} {{\textbf {n}} } \cdot {{\textbf {q}} } \\ p {{\textbf {n}} } \\ \end{pmatrix} \,, \quad {{\textbf {f}} } = \begin{pmatrix} b \\ {\textbf {0}} \end{pmatrix} \,, \quad {{\textbf {g}} } = \begin{pmatrix} g_\textrm{N}\\ p_\textrm{D}{{\textbf {n}} }\end{pmatrix} \,, \end{aligned}$$

(4)

so that for smooth functions $\varphi ,{\varvec{\psi }}$ with $\varphi = 0$ on $(0,T)\times \Gamma _\textrm{D}$ and ${{\textbf {n}} }\cdot {\varvec{\psi }} = 0$ on $(0,T)\times \Gamma _\textrm{N}$

$$\begin{aligned} \big (\underline{A}_{{{\textbf {n}} }}(p,{{\textbf {q}} }),(\varphi ,{\varvec{\psi }}) \big )_{(0,T)\times \partial \Omega } = \big ({{\textbf {n}} }\cdot {{\textbf {q}} },\varphi \big )_{(0,T)\times \Gamma _\textrm{N}} +\big (p,{{\textbf {n}} }\cdot {\varvec{\psi }}\big )_{(0,T)\times \Gamma _\textrm{D}}\,. \end{aligned}$$

In two space dimensions, this corresponds to the boundary parts $\Gamma _1 = \Gamma _1^* = \Gamma _\textrm{D}$ and $\Gamma _2 = \Gamma _2^* = \Gamma _3 = \Gamma _3^* = \Gamma _\textrm{N}$, and

$$\begin{aligned} \underline{M} = \begin{pmatrix} \varrho &{} 0 &{} 0 \\ 0 &{} \kappa ^{-1}&{} 0\\ 0 &{} 0 &{} \kappa ^{-1}\\ \end{pmatrix} \in {\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{3\times 3}_\text {sym}) \,, \quad \\ \underline{A}_1 = \begin{pmatrix} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{pmatrix} \in {{\mathbb {R}}}^{3\times 3}_\text {sym} \,, \quad \underline{A}_2 = \begin{pmatrix} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \\ \end{pmatrix} \in {{\mathbb {R}}}^{3\times 3}_\text {sym} \,. \end{aligned}$$

Elastic waves Linear elastic waves are described by the first-order system for velocity ${{\textbf {v}} }$ and stress ${\varvec{\sigma }}$

$$\begin{aligned} \varrho \partial _t {{\textbf {v}} } - \nabla \cdot {\varvec{\sigma }} = {{\textbf {b}} }&\ \text { and }\ \partial _t {\varvec{\sigma }} - {{\textbf {C}} } {\varvec{\varepsilon }}({{\textbf {v}} }) = {\textbf {0}} \qquad \qquad&\text {in } (0,T)\times \Omega \,, \\ {{\textbf {v}} }(0) = {{\textbf {v}} }_0&\ \text { and }\ {\varvec{\sigma }}(0) = {\varvec{\sigma }}_0&\text {in } \Omega \text { at } t=0\,, \\ {{\textbf {v}} }(t) = {{\textbf {v}} }_\textrm{D}(t) \text { on } \Gamma _\textrm{D}&\ \text { and }\ {\varvec{\sigma }} (t) {{\textbf {n}} } = {{\textbf {g}} }_\textrm{N}(t) \text { on } \Gamma _\textrm{N}&\text {on } \partial \Omega \text { for } t\in (0,T) \end{aligned}$$

with mass density $\varrho$, the symmetric gradient ${\varvec{\varepsilon }} ={\varvec{\varepsilon }}({{\textbf {v}} })$ of ${{\textbf {v}} }$, and, in isotropic media, with ${{\textbf {C}} }{\varvec{\varepsilon }}= 2\mu {\varvec{\varepsilon }} + \lambda {\text {*}}{trace}({\varvec{\varepsilon }}){{\textbf {I}} }_3$ depending on the Lamé parameters $\mu ,\lambda >0$. This corresponds to the Friedrichs system with

$$\begin{aligned} {{\textbf {u}} } = \begin{pmatrix} {{\textbf {v}} } \\ {\varvec{\sigma }}\end{pmatrix},\ M{{\textbf {u}} } = \begin{pmatrix} \varrho {{\textbf {v}} } \\ {{\textbf {C}} }^{-1} {\varvec{\sigma }}\end{pmatrix},\ A{{\textbf {u}} } = \begin{pmatrix} -\nabla \cdot {\varvec{\sigma }} \\ -{\varvec{\varepsilon }}({{\textbf {v}} })\end{pmatrix},\ \nonumber \\ \underline{A}_{{{\textbf {n}} }}{{\textbf {u}} } = \begin{pmatrix} -{\varvec{\sigma }} {{\textbf {n}} } \\ -{{\textbf {n}} } {{\textbf {v}} }^\top -{{\textbf {v}} } {{\textbf {n}} }^\top \end{pmatrix} , \ {{\textbf {f}} } = \begin{pmatrix} {{\textbf {b}} } \\ {\textbf {0}} \end{pmatrix} , \ {{\textbf {g}} } = \begin{pmatrix} -{{\textbf {g}} }_\textrm{N}\\ -{{\textbf {n}} } {{\textbf {v}} }_\textrm{D}^\top -{{\textbf {v}} }_\textrm{D}{{\textbf {n}} }^\top \end{pmatrix} . \end{aligned}$$

(5)

For $d=3$ we have $m = 9$ and $\Gamma _k= \Gamma _k^* = \Gamma _\textrm{D}$ for $k=1,2,3$, and $\Gamma _k= \Gamma _k^* = \Gamma _\textrm{N}$ for $k=4,\ldots ,9$.

Electro-magnetic waves The first-order system for the electric field ${{\textbf {E}} }$ and the magnetic field intensity ${{\textbf {H}} }$

$$\begin{aligned} \varepsilon \partial _t {{\textbf {E}} } - \nabla \times {{\textbf {H}} } = - {{\textbf {J}} } \ {}&\text { and }\ \mu \partial _t {{\textbf {H}} } + \nabla \times {{\textbf {E}} } = {\textbf {0}}&\text {in } (0,T)\times \Omega \,, \\ {{\textbf {E}} }(0) = {{\textbf {E}} }_0 \ {}&\text { and }\ {{\textbf {H}} }(0) = {{\textbf {H}} }_0\qquad \qquad&\text {in } \Omega \text { at } t=0\,, \\ {{\textbf {n}} } \times {{\textbf {E}} }(t) = {\textbf {0}} \text { on } \Gamma _\textrm{E}\ {}&\text { and }\ {{\textbf {n}} } \times {{\textbf {H}} }(t) = {{\textbf {g}} }_\textrm{M}\text { on } \Gamma _\textrm{M}&\text {on } \partial \Omega \text { for } t\in (0,T) \end{aligned}$$

with permittivity $\varepsilon$, permeability $\mu$, and boundary decomposition $\partial \Omega = \Gamma _\textrm{E}\cup \Gamma _\textrm{M}$ corresponds to a Friedrichs system with

$$\begin{aligned} {{\textbf {u}} } = \begin{pmatrix} {{\textbf {E}} } \\ {{\textbf {H}} }\end{pmatrix}, \quad M{{\textbf {u}} } = \begin{pmatrix} \varepsilon {{\textbf {E}} } \\ \mu {{\textbf {H}} }\end{pmatrix}, \quad A{{\textbf {u}} } = \begin{pmatrix} - \nabla \times {{\textbf {H}} } \\ \nabla \times {{\textbf {E}} }\end{pmatrix}, \quad \nonumber \\ \underline{A}_{{{\textbf {n}} }}{{\textbf {u}} } = \begin{pmatrix} -{{\textbf {n}} } \times {{\textbf {H}} }\\ {{\textbf {n}} } \times {{\textbf {E}} } \end{pmatrix} , \quad {{\textbf {f}} } = \begin{pmatrix} -{{\textbf {J}} } \\ {\textbf {0}} \end{pmatrix} , \quad {{\textbf {g}} } = \begin{pmatrix} -{{\textbf {g}} }_\textrm{M}\\ {\textbf {0}} \end{pmatrix} . \end{aligned}$$

(6)

For $d=3$ we have $m = 6$ and $\Gamma _k= \Gamma _k^* = \Gamma _\textrm{E}$ for $k=1,2,3$, and $\Gamma _k= \Gamma _k^* = \Gamma _\textrm{M}$ for $k=4,5,6$.

Remark 1

We only consider the case that the symmetric matrices $\underline{A}_j$, $j=1,\ldots ,d$, are constant in $\Omega$. In general, $\underline{A}_j$ may depend on ${{\textbf {x}} }\in \Omega$, e.g., for the linear transport equation $Lu = \partial _tu + {{\textbf {a}} }\cdot \nabla u$ with $m=1$ and transport vector ${{\textbf {a}} }({{\textbf {x}} })\in {{\mathbb {R}}}^d$. Then, $\Gamma _1$ is the inflow boundary, and for the adjoint equation we obtain $L^* v= -\partial _tv - {{\textbf {a}} }\cdot \nabla v - (\nabla \cdot {{\textbf {a}} } )v$ with $\Gamma _1^* = \partial \Omega \setminus \Gamma _1$. For the DG analysis of this case we refer to [5, Chap. 2] in the steady case and to [6] for a Petrov–Galerkin space-time method.

The suitable choice of the subsets $\Gamma _k\subset \partial \Omega$ for $k=1,\ldots ,m$ for the boundary conditions in general Friedrichs systems is discussed in [5, Chap. 7.2]. Here we consider the special case for wave systems. The property (1) characterizes the adjoint boundaries $\Gamma _k^*\subset \partial \Omega$ for $k=1,\ldots ,m$, and we observe

$$\begin{aligned} \sum _{k=1}^m \big ((\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} })_k,w_k\big )_{(0,T)\times \Gamma _k}&= \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } \\&= \big ({{\textbf {v}} },\underline{A}_{{{\textbf {n}} }}{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } = \sum _{k=1}^m \big (v_k,(\underline{A}_{{{\textbf {n}} }}{{\textbf {w}} })_k\big )_{(0,T)\times \partial \Omega \setminus \Gamma _k^*} \end{aligned}$$

for ${{\textbf {v}} } = (v_1\ldots ,v_m)\in {\textrm{C}}^1(Q;{{\mathbb {R}}}^m)$ and ${{\textbf {w}} } =(w_1,\ldots ,w_m)\in {\mathcal {V}}^*$ and thus, defining

$$\begin{aligned} {\mathcal {V}} = \big \{ {{\textbf {v}} } \in {\textrm{C}}^1(\overline{Q};{{\mathbb {R}}}^m) :&{{\textbf {v}} }(0) = {\textbf {0}} \text { in } \Omega \,,\ \\&(\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} })_k = 0 \text { on } (0,T]\times \Gamma _k\,,\ k=1,\ldots ,m \big \} \end{aligned}$$

with homogeneous initial value at $t=0$ and homogeneous boundary values on $\Gamma _k$, we obtain

$$\begin{aligned} \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {v}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } = \big ({{\textbf {v}} },\underline{A}_{{{\textbf {n}} }}{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } = 0 \,,\qquad {{\textbf {v}} }\in {\mathcal {V}}\,,\ {{\textbf {w}} } \in {\mathcal {V}}^* \,. \end{aligned}$$

Boundary conditions are required in order to obtain uniqueness and well-posedness of the solution. Therefore, we require for the subsets $\Gamma _k\subset \partial \Omega$, for $k=1,\ldots ,m$, that the operators L and $L^*$ are injective on ${\mathcal {V}}$ and ${\mathcal {V}}^*$, respectively, i.e.,

$$\begin{aligned} \big \{ {{\textbf {v}} } \in {\mathcal {V}} :L {{\textbf {v}} } = {\textbf {0}} \big \} = \{ {\textbf {0}} \} \,,\qquad \big \{ {{\textbf {w}} } \in {\mathcal {V}}^* :L^* {{\textbf {w}} } = {\textbf {0}} \big \} = \{ {\textbf {0}} \} \,, \end{aligned}$$

(7)

where the relatively open adjoint boundaries $\Gamma _k^*\subset \partial \Omega$ for $k=1,\ldots ,m$ are determined by property (1).

Now we show that both conditions in (7) are necessary. The first condition for $\Gamma _k$ is required for uniqueness for strong solutions: if ${{\textbf {v}} }\in {\mathcal {V}}\setminus \{{\textbf {0}} \}$ exists with $L {{\textbf {v}} } ={\textbf {0}}$, then this is a non-trivial homogeneous strong solution, i.e., ${{\textbf {v}} }$ solves (3) with ${{\textbf {u}} }_0 = {\textbf {0}}$, ${{\textbf {f}} } = {\textbf {0}}$, and ${{\textbf {g}} } = {\textbf {0}}$. On the other hand, if the second condition is violated, weak solutions do not exist for all volume data: if ${{\textbf {w}} }\in {\mathcal {V}}^*\setminus \{{\textbf {0}} \}$ and ${{\textbf {f}} } \in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ exists with $L^* {{\textbf {w}} } ={\textbf {0}}$ and $({{\textbf {f}} },{\textbf {w}} )_Q \ne 0$, no weak solution of (2) with homogeneous initial and boundary data ${{\textbf {u}} }_0 = {\textbf {0}}$ and ${{\textbf {g}} } = {\textbf {0}}$ exists.

Remark 2

The formulation of wave equations in our examples as Friedrichs systems yields symmetric matrices of the form $\underline{A}_j = \begin{pmatrix} \underline{0} &{} \underline{{\tilde{A}}}_j \\ \underline{{\tilde{A}}}_j^\top \!\!\!\!\! &{} \underline{0} \end{pmatrix}$ with $\underline{{\tilde{A}}}_j\in {{\mathbb {R}}}^{m_1\times m_2}$ and $m = m_1+m_2$. For the boundary conditions we can select a relatively open set $\Gamma _1\subset \partial \Omega$. Then, defining $\Gamma _k=\Gamma _1$ for $k=2,\ldots ,m_1$, $\Gamma _k=\partial \Omega \setminus \overline{\Gamma }_1$ for $k=m_1+1,\ldots ,m$, and $\Gamma _k^*=\Gamma _k$ for $k=1,\ldots ,m$, we observe that property (1) and conditions (7) are satisfied.

Remark 3

For smooth domains and data, the solution is also smooth, e.g., for acoustics $\phi (t)\in {\textrm{H}}^s(\Omega )$ for all $t\in [0,T]$ with $s\ge 2$. This allows for improved approximation orders ${\mathcal {O}}(h^s)$ for $\phi$. On the other hand, the necessary regularity requirements are quite restrictive [21], and the second-order formulation does not allow for the convergence analysis of piece-wise discontinuous solutions.

Remark 4

Waves in real media are dissipative and dispersive; e.g., modeling electro-magnetic waves in matter needs to include conductivity and impedance. The DG analysis can be extended to this case; see, e.g., [5, Chap. 7] for the steady case and [8] for visco-elastic waves with impedance boundary conditions.

In the elastic model for Rayleigh damping or for the Kelvin–Voigt model, the linear operator takes the form $L= M\partial _t + D + A$ with $(D{{\textbf {v}} })(t,{{\textbf {x}} }) = \underline{D}({{\textbf {x}} }) {\textbf {v}} (t,{{\textbf {x}} })$ and $\underline{D}\in {\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{d\times d}_\text {sym})$ symmetric positive semi-definite; then, $L^*= -M\partial _t + D - A$.

All our subsequent results extend to this case, but for simplicity we only consider the case $\underline{D} = \underline{0}$.

3 The Full-Upwind Discontinuous Galerkin Discretization

In this section we introduce an upwind DG discretization for the first-order system.

3.1 The DG Finite Element Space in the Space-Time Cylinder

For the discretization, we use tensor product space-time cells combining the mesh in space with a decomposition in time. For $0=t_0<t_1<\cdots < t_N = T$, we define time intervals $I_{n,h} = (t_{n-1},t_n)$, time-step sizes ${\vartriangle } t_n = t_n-t_{n-1}$, and

$$\begin{aligned} I_h = (t_0,t_1)\cup \cdots \cup (t_{N-1},t_N)\subset I = (0,T) \,, \qquad \partial I_h = \{t_0,t_1,\ldots ,t_{N-1},t_N\} \,. \end{aligned}$$

We set ${\vartriangle } t = \max {\vartriangle } t_n$, and we assume quasi-uniformity, i.e., ${\vartriangle } t_n \in [C_\text {sr} {\vartriangle } t,{\vartriangle } t]$ with $C_\text {sr}\in (0,1]$ independent of N.

Let ${\mathcal {K}}_h$ be a mesh so that $\Omega _h = \bigcup _{K\in {\mathcal {K}}_h} K$ is a decomposition in space into open cells $K\subset \Omega \subset {{\mathbb {R}}}^d$. Then, we obtain a tensor-product decomposition into space-time cells $R =I_{n,h}\times K$

$$\begin{aligned} Q_h&= I_h\times \Omega _h =\bigcup _{n=1}^N Q_{n,h} =\bigcup \limits _{R\in {\mathcal {R}}_h} R \;\subset \; Q = I\times \Omega \subset {{\mathbb {R}}}^{1+d}\,,\qquad \\ Q_{n,h}&=\bigcup \limits _{K\in {\mathcal {K}}_h} I_{n,h}\times K \;\subset \; I_{n,h}\times \Omega \end{aligned}$$

of the space-time cylinder Q. Let $F\in {\mathcal {F}}_K$ be the faces of the element K, and we set ${\mathcal {F}}_h = \bigcup _K {\mathcal {F}}_K$, so that $\partial \Omega _h = \overline{ \bigcup _{F\in {\mathcal {F}}_h} F}$ is the skeleton in space; $\partial Q_h = \bigcup _{n=0}^N \{t_n\}\times \partial \Omega _h$ is the corresponding space-time skeleton. For inner faces $F \in {\mathcal {F}}_h\cap \Omega$ and $K\in {\mathcal {K}}_h$, let $K_F$ be the neighboring cell such that ${\bar{F}}= \partial K \cap \partial K_F$. On boundary faces $F \in {\mathcal {F}}_h\cap \partial \Omega$ we set $K_F = K$. Let ${{\textbf {n}} }_K$ be the outer unit normal vector on $\partial K$. We assume that $\overline{\Omega }= \Omega _h \cup \partial \Omega _h$ and that the boundary decomposition is compatible with the mesh, i.e., $\overline{\Gamma }_k = \overline{\bigcup _{F\in {\mathcal {F}}_K\cap \Gamma _k} F}$ for $k=1,\ldots ,m$.

We set $h_K = {\text {*}}{diam}K$, $h_F = {\text {*}}{diam}F$, and $h = \max h_K$. We assume quasi-uniform meshes and shape-regularity, i.e., $h_F \ge c_\text {sr} h_K$ for $F\in {\mathcal {F}}_K$ with $c_\text {sr}> 0$ independent of $h_K$. In the following, we use the mesh-dependent norms

$$\begin{aligned} \big \Vert h^{\alpha /2} {{\textbf {v}} }_h\big \Vert _Q = \Big (\sum _{n=1}^{N} \sum _{K\in {\mathcal {K}}_h } h_K^\alpha \Vert {{\textbf {v}} }_h\Vert _{I_{n,h}\times K}^2\Big )^{1/2} \,,\qquad \alpha \in {{\mathbb {R}}}\,. \end{aligned}$$

(8)

In order to calibrate the accuracy in space and time, we assume, depending on a reference velocity $c_\text {ref}>0$, that the mesh size in time and space are well balanced satisfying

$$\begin{aligned} c_\text {ref}{\vartriangle } t\le h \,. \end{aligned}$$

(9)

Since we only consider fully implicit methods, we have no restriction with respect to stability of the time integration.

Remark 5

For simplicity we use only tensor-product space-time meshes. For the extension to more general meshes in the space-time cylinder we refer to [14], see also the analysis in [2]. General meshes in ${{\mathbb {R}}}^{1+d}$ are considered in [22]. Then, the condition (9) can be relaxed to a local condition.

The DG discretization is defined for a finite dimensional subspace $V_h\subset {\mathcal {V}}_h \subset {\textrm{C}}^1(I_h;{\mathcal {S}}_h)$, where

$$\begin{aligned} {\mathcal {V}}_h = \big \{ {{\textbf {v}} }_h\in {\textrm{C}}^1(Q_h;{{\mathbb {R}}}^m) :&{{\textbf {v}} }_{n,h,K} = {{\textbf {v}} }_h|_{I_{n,h}\times K} \text { extends continuously to }\\&{{\textbf {v}} }_{n,h,K} \in {\textrm{C}}^0(\overline{I_{n,h}\times K};{{\mathbb {R}}}^m) \big \}\,,\\ {\mathcal {S}}_h = \big \{ {{\textbf {v}} }_h\in {\textrm{C}}^1(\Omega _h;{{\mathbb {R}}}^m) :&{{\textbf {v}} }_{h,K} = {{\textbf {v}} }_h|_{K} \text { extends continuously to }\\&{{\textbf {v}} }_{h,K} \in {\textrm{C}}^0(\overline{K};{{\mathbb {R}}}^m) \big \}\,. \end{aligned}$$

On the space-time skeleton $\partial Q_h$, we define

$$\begin{aligned} \big \Vert {{\textbf {v}} }_h\big \Vert _{\partial Q_h} = \Big (\sum _{n=1}^{N} \sum _{K\in {\mathcal {K}}_h } \Vert {{\textbf {v}} }_{n,h,K}\Vert _{\partial (I_{n,h}\times K)}^2\Big )^{1/2} \,,\qquad {{\textbf {v}} }_h\in {\mathcal {V}}_h \,. \end{aligned}$$

(10)

For the positive definite matrix function $\underline{M}\in {\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{m\times m}_\text {sym})$ let $\underline{M}_h\in {\textrm{L}}_\infty (\Omega _h;{{\mathbb {R}}}^{m\times m}_\text {sym})$ be a piecewise constant approximation, and for $K\in {\mathcal {K}}_h$ let $\underline{M}_{h,K}\in \mathrm {{\mathbb {R}}}^{m\times m}_\text {sym}$ be the continuous extension of $\underline{M}_h|_K$ to $\overline{K}$; in case of material jumps this can result to different values on the left and right side of a face, i.e., $M_{h,K}|_F \ne M_{h,K_F}|_F$.

Let $L_h = M_h\partial _t +A$ be the corresponding linear differential operator, where the approximated operator $M_h$ is given by $(M_h{{\textbf {v}} })(t,{{\textbf {x}} }) = \underline{M}_h({{\textbf {x}} }){\textbf {v}} (t,{{\textbf {x}} })$. Note that then $L_h(V_h) \subset V_h$.

For our applications, we use a tensor-product construction of the finite element space.

For every space-time cell $R = I_{n,h}\times K$ we select polynomial degrees $p_R =p_{n,K}\ge 0$ in time and $q_R =q_{n,K}\ge 0$ in space. With this we define the discontinuous finite element spaces

$$\begin{aligned} S_{n,h}&= \prod \limits _{K\in {\mathcal {K}}_h} \mathbb P_{q_{n,K}}(K;{{\mathbb {R}}}^m) \subset {\mathcal {S}}_h \,,\qquad&S_h = S_{1,h}+\cdots + S_{N,h} \,, \end{aligned}$$

(11a)

$$\begin{aligned}&V_{n,h} = \prod \limits _{K\in {\mathcal {K}}_h} \mathbb P_{p_{n,K}}\otimes \mathbb P_{q_{n,K}}(K;{{\mathbb {R}}}^m) \,,&V_h = V_{1,h}+\cdots + V_{N,h} \subset {\mathcal {V}}_h \,, \end{aligned}$$

(11b)

where $\mathbb P_p$ denotes the set of polynomials up to order p. For the following, we fix $p = \max p_R$ and $q = \max q_R$, so that

$$\begin{aligned} S_{n,h}&\subset S_h\subset \mathbb P_q(\Omega _h;{{\mathbb {R}}}^m) \subset {\mathcal {S}}_h \,,\qquad \qquad \\ V_h&\subset \mathbb P_p(I_h)\otimes S_h\subset \mathbb P_p(I_h)\otimes \mathbb P_q(\Omega _h;{{\mathbb {R}}}^m) \subset {\mathcal {V}}_h \,. \end{aligned}$$

On the space-time skeleton $\partial Q_h = \bigcup _{n=0}^N \{t_n\}\times \overline{\Omega }\;\cup \; I_h\times \partial \Omega _h$, the inverse inequality and the discrete trace inequality [5, Lem. 1.44 and Lem. 1.46] yield

$$\begin{aligned}&\big \Vert h^{1/2}M_h^{-1/2}L_h{{\textbf {v}} }_h\big \Vert _{Q_h} \le C_\text {inv} \, \big \Vert h^{-1/2}M_h^{1/2}{{\textbf {v}} }_h\big \Vert _{Q} \,,\qquad \end{aligned}$$

(12a)

$$\begin{aligned}&\big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _{\partial Q_h} \le C_\text {tr} \big \Vert h^{-1/2}M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q\,,\qquad {{\textbf {v}} }_h\in V_h \,, \end{aligned}$$

(12b)

with $C_\text {inv},C_\text {tr}>0$ depending on the space-time mesh regularity (and thus also on $c_\text {ref}$), the polynomial degrees in $V_h$, and the material parameters.

Let $\Pi _h:{\textrm{L}}_2(Q;{{\mathbb {R}}}^m)\longrightarrow V_h$ be the space-time ${\textrm{L}}_2$ projection defined by

$$\begin{aligned} \big (M_h\Pi _h{{\textbf {v}} },{{\textbf {v}} }_h\big )_Q&= \big (M_h{{\textbf {v}} },{{\textbf {v}} }_h\big )_Q \,,\qquad&{{\textbf {v}} }_h\in V_h \,. \end{aligned}$$

(13)

For ${{\textbf {v}} }_h\in V_h$, let ${{\textbf {v}} }_{n,h}\in {\textrm{C}}^0\big ([t_{n-1},t_{n}];\mathrm L_2(\Omega _h;{{\mathbb {R}}}^m)\big )$ be the extension of ${{\textbf {v}} }_h|_{Q_{n,h}}\in {\textrm{L}}_2(Q_{n,h};{{\mathbb {R}}}^m)$ to $[t_{n-1},t_{n}]$.

In every time interval $I_{n,h}$ we use the projection $\Pi _{n,h}:{\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)\longrightarrow S_{n,h}\subset S_h$ defined by

$$\begin{aligned} \big (M_h\Pi _{n,h}{{\textbf {w}} },{{\textbf {w}} }_{n,h}\big )_\Omega&= \big (M_h{{\textbf {w}} }_n,{{\textbf {w}} }_{n,h}\big )_\Omega \,,\qquad&{{\textbf {w}} }_{n,h}\in S_{n,h} \,. \end{aligned}$$

In the following, we derive the discretizations in the infinite dimensional piecewise continuous spaces ${\mathcal {S}}_h$ and ${\mathcal {V}}_h$, since several properties only rely on the mesh. We use the finite dimensional DG spaces $V_h\subset {\mathcal {V}}_h$ and $S_h\subset {\mathcal {S}}_h$ if we require additional properties of the discrete space such as inverse and trace inequalities.

3.2 A Discontinuous Galerkin Method in Time

For ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {V}}_h$ we obtain after integration by parts in all intervals $I_{n,h} \subset I_h$

$$\begin{aligned} \big (M_h\partial _t{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{Q_{h}} = \sum _{n=1}^N \Big (&- \big (M_h{{\textbf {v}} }_{n,h},\partial _t{{\textbf {w}} }_{n,h}\big )_{Q_{n,h}} + \big (M_h{{\textbf {v}} }_{n,h}(t_n),{{\textbf {w}} }_{n,h}(t_n)\big )_{\Omega } \\ {}&-\big (M_h{{\textbf {v}} }_{n,h}(t_{n-1}),{{\textbf {w}} }_{n,h}(t_{n-1})\big )_{\Omega } \Big ) \,. \end{aligned}$$

Introducing the jump terms $[{{\textbf {w}} }_h]_n = {{\textbf {w}} }_{n+1,h}(t_n)-{\textbf {w}} _{n,h}(t_n)$ for $n=1,\ldots ,N-1$ and $[{{\textbf {w}} }_h]_N = - {{\textbf {w}} }_{N,h}(t_N)$, we define the dual representation of the full upwind DG method in time for ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {V}}_h$

$$\begin{aligned} m_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)&= -\big (M_h{{\textbf {v}} }_{n,h},\partial _t{{\textbf {w}} }_{n,h}\big )_{Q_{h}} -\sum _{n=1}^{N} \big (M_h{{\textbf {v}} }_{n,h}(t_n),[{{\textbf {w}} }_h]_n\big )_{\Omega } \,. \end{aligned}$$

(14)

We have dual consistency by construction, i.e.,

$$\begin{aligned} m_h({{\textbf {v}} }_h,{{\textbf {w}} }) = -\big (M_h{{\textbf {v}} }_h,\partial _t{{\textbf {w}} }\big )_{Q_{h}} \,,\qquad {{\textbf {w}} } \in {\mathcal {V}}^* \,. \end{aligned}$$

(15)

Again integrating by parts and defining $[{{\textbf {v}} }_h]_0 = {{\textbf {v}} }_{1,h}(0)$ yields the primal representation

$$\begin{aligned} m_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)&= \big (M_h\partial _t{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{Q_h} +\sum _{n=1}^N \big (M_h[{{\textbf {v}} }_h]_{n-1},{{\textbf {w}} }_{n,h}(t_{n-1})\big )_{\Omega } \,. \end{aligned}$$

(16)

Together, we obtain

$$\begin{aligned} 2\, m_h({{\textbf {v}} }_h,{{\textbf {v}} }_h)&= m_h({{\textbf {v}} }_h,{{\textbf {v}} }_h) + m_h({{\textbf {v}} }_h,{{\textbf {v}} }_h) \\ {}&= \sum _{n=1}^N \Big ( \big (M_h[{{\textbf {v}} }_h]_{n-1},{{\textbf {v}} }_{n,h}(t_{n-1})\big )_{\Omega } - \big (M_h{{\textbf {v}} }_{n,h}(t_n),[{{\textbf {v}} }_h]_n\big )_{\Omega } \Big )\\&=\big (M_h{{\textbf {v}} }_h(0),{{\textbf {v}} }_h(0)\big )_{\Omega } + \big (M_h{{\textbf {v}} }_h(T),{{\textbf {v}} }_h(T)\big )_{\Omega } \\ {}&\quad + \sum _{n=1}^{N-1} \Big ( \big (M_h[{{\textbf {v}} }_h]_{n},{{\textbf {v}} }_{n+1,h}(t_{n})\big )_{\Omega } \!- \big (M_h{{\textbf {v}} }_{n,h}(t_n),[{{\textbf {v}} }_h]_n\big )_{\Omega } \Big ) \,, \end{aligned}$$

which yields

$$\begin{aligned} m_h({{\textbf {v}} }_h,{{\textbf {v}} }_h)&= \frac{1}{2} \sum _{n=0}^N \big (M_h[{{\textbf {v}} }_h]_n,[{{\textbf {v}} }_h]_n\big )_{\Omega } \ge 0 \,, \qquad {{\textbf {v}} }_h\in {\mathcal {V}}_h \,, \end{aligned}$$

(17)

so that

$$\begin{aligned} m_h\big ({{\textbf {v}} }_h,{{\textbf {v}} }_h\big )= 0 \quad \Longrightarrow \quad m_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big )&= -\big (M_h{{\textbf {v}} }_h,\partial _t{{\textbf {w}} }\big )_{Q_{h}} \nonumber \\ {}&= \big (M_h\partial _t{{\textbf {v}} }_h,{{\textbf {w}} }\big )_{Q_{h}} \,,\qquad {{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {V}}_h \,. \end{aligned}$$

(18)

For $m_h({{\textbf {v}} }_h,{{\textbf {v}} }_h) = 0$ we observe ${{\textbf {v}} }_h\in {\textrm{H}}^1_0(0,T;{\mathcal {S}}_h)$.

This yields with ${d_T}(t) = T-t$

$$\begin{aligned} \big (M_h{{\textbf {v}} }_h,{{\textbf {v}} }_h\big )_Q&= \int _0^T \big (M_h{{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t)\big )_{\Omega }\, {\textrm{dt}} \\&= -\int _0^T \big (M_h{{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t)\big )_{\Omega }\partial _t{d_T}(t)\, {\textrm{dt}} \\&= 2\int _0^T \big ( M_h\partial _t{{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t)\big )_{\Omega }{d_T}(t)\, {\textrm{dt}} \\&\le 2T\, \big \Vert M_h^{-1/2}\partial _t{{\textbf {v}} }_h\big \Vert _{Q_h} \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _{Q} \,, \end{aligned}$$

i.e., we have $\big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q\le 2T\, \big \Vert M_h^{-1/2}\partial _t{{\textbf {v}} }_h\big \Vert _{Q_h}$.

This extends to discontinuous functions in ${\mathcal {V}}_h$ as follows.

Lemma 1

We have

$$\begin{aligned} \big (M_h{{\textbf {v}} }_h,{{\textbf {v}} }_h\big )_Q +\sum _{n=0}^{N-1}{d_T}(t_n)\big (M_h[{{\textbf {v}} }_h]_n,[{{\textbf {v}} }_h]_n\big )_{\Omega }&\le 2\, m_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h)\,,\quad {{\textbf {v}} }_h \in {\mathcal {V}}_h\,. \end{aligned}$$

Proof

The assertion follows from

$$\begin{aligned} \big (M_h{{\textbf {v}} }_h,{{\textbf {v}} }_h\big )_Q&= -\sum _{n=1}^N\int _{t_{n-1}}^{t_n} \big (M_h{{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t)\big )_{\Omega }\partial _t{d_T}(t)\,\mathrm dt\\&= 2\int _0^T \big (M_h\partial _t{{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t)\big )_{\Omega } {d_T}(t)\,\mathrm dt\\&\quad -\sum _{n=1}^N \Big ({d_T}(t_n) \big (M_h{{\textbf {v}} }_{n,h}(t_n),{{\textbf {v}} }_{n,h}(t_n)\big )_{\Omega }\\&\quad -{d_T}(t_{n-1}) \big (M_h{{\textbf {v}} }_{n,h}(t_{n-1}),{{\textbf {v}} }_{n,h}(t_{n-1})\big )_{\Omega } \Big )\\&= 2\big (M_h\partial _t{{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h\big )_{Q_h} -T\,\Vert M_h^{1/2}{{\textbf {v}} }_{1,h}(0)\Vert _{\Omega }^2\\&\quad +\sum _{n=1}^{N-1} {d_T}(t_n) \Big ( \big (M_h{{\textbf {v}} }_{n+1,h}(t_n),{{\textbf {v}} }_{n+1,h}(t_n)\big )_{\Omega } \\&\qquad - \big (M_h{{\textbf {v}} }_{n,h}(t_n),{{\textbf {v}} }_{n,h}(t_n)\big )_{\Omega } \Big ) \\&\le 2\big (M_h\partial _t{{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h\big )_{Q_h} +2\sum _{n=1}^{N-1} {d_T}(t_n) \big (M_h[{{\textbf {v}} }_h]_n,{{\textbf {v}} }_{n+1,h}(t_n)\big )_{\Omega } \\&\qquad -\sum _{n=1}^{N-1}{d_T}(t_n)\big (M_h[{{\textbf {v}} }_h]_n,[{{\textbf {v}} }_h]_n\big )_{\Omega } -T\,\Vert M_h^{1/2}{{\textbf {v}} }_{1,h}(0)\Vert _{\Omega }^2 \\&\le 2\, m_h\big ({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h\big ) -\sum _{n=0}^{N-1}{d_T}(t_n)\big (M_h[{{\textbf {v}} }_h]_n,[{{\textbf {v}} }_h]_n\big )_{\Omega } \end{aligned}$$

using

$$\begin{aligned}&\big (M_h{{\textbf {v}} }_{n+1,h}(t_n),{{\textbf {v}} }_{n+1,h}(t_n)\big )_{\Omega } - \big (M_h{{\textbf {v}} }_{n,h}(t_n),{{\textbf {v}} }_{n,h}(t_n)\big )_{\Omega } \\&\qquad = \big (M_h({{\textbf {v}} }_{n+1,h}(t_n)-{{\textbf {v}} }_{n,h}(t_n)), {{\textbf {v}} }_{n+1,h}(t_n)+{{\textbf {v}} }_{n,h}(t_n)\big )_{\Omega } \\&\qquad = \big (M_h[{{\textbf {v}} }_h]_n,{{\textbf {v}} }_{n+1,h}(t_n)\big )_{\Omega } + \big (M_h[{{\textbf {v}} }_h]_n,{{\textbf {v}} }_{n,h}(t_n)\big )_{\Omega } \\&\qquad = 2\big (M_h[{{\textbf {v}} }_h]_n,{{\textbf {v}} }_{n+1,h}(t_n)\big )_{\Omega } -\big (M_h[{{\textbf {v}} }_h]_n,[{{\textbf {v}} }_h]_n\big )_{\Omega } \,. \end{aligned}$$

$\square$

3.3 A Discontinuous Galerkin Method in Space

For ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {S}}_h$ we observe, integrating by parts for all elements $K\in {\mathcal {K}}_h$,

$$\begin{aligned} \big (A{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{\Omega _{h}}&= \sum _{K\in {\mathcal {K}}_h} \left( - \big ({{\textbf {v}} }_{h,K},A{{\textbf {w}} }_{h,K}\big )_K + \sum _{F\in {\mathcal {F}}_K} \big (\underline{A}_{{{\textbf {n}} }_K}{{\textbf {v}} }_{h,K},{{\textbf {w}} }_{h,K}\big )_F \right) \,. \end{aligned}$$

For conforming functions ${{\textbf {v}} }$, we have for the flux $\underline{A}_{{{\textbf {n}} }_K}{{\textbf {v}} }= -\underline{A}_{{{\textbf {n}} }_{K_F}}{{\textbf {v}} }$ on inner faces $F\subset \Omega$, and for discontinuous functions we define the jump term $[{{\textbf {w}} }_h]_{K,F} = {{\textbf {w}} }_{h,K_F}-{{\textbf {w}} }_{h,K}$. On boundary faces $F\subset \partial \Omega$ this depends on the boundary conditions, and we set $(\underline{A}_{{{\textbf {n}} }} [{\textbf {v}} _h])_k = -2 (\underline{A}_{{{\textbf {n}} }} {{\textbf {v}} }_h)_k$ on $\Gamma _k\subset \partial \Omega$ and $(\underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h])_k = 0$ on $\partial \Omega \setminus \Gamma _k$ for $k=1,\ldots ,m$.

We use the discontinuous Galerkin method with full upwind discretization in space which is of the form

$$\begin{aligned} a_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)&= - \big ({{\textbf {v}} }_h,A{{\textbf {w}} }_h\big )_{\Omega _h} + \sum _{K\in {\mathcal {K}}_h} \sum _{F\in {\mathcal {F}}_K} \big ({{\textbf {v}} }_{h,K},\underline{A}_{{{\textbf {n}} }_K}^\text {up}[{{\textbf {w}} }_h]_{K,F}\big )_F \,, \end{aligned}$$

where the upwind flux $\underline{A}_{{{\textbf {n}} }_K}^\text {up}\in {{\mathbb {R}}}^{m\times m}$ is obtained by solving local Riemann problems.

For the DG method we require dual consistency for the bilinear form and the right hand side for the boundary values for ${{\textbf {v}} }_h\in {\mathcal {S}}_h$, ${{\textbf {w}} } \in {\mathcal {S}}^*$

$$\begin{aligned} a_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }\big ) = -\big ({{\textbf {v}} }_h,A{{\textbf {w}} }\big )_{\Omega _h} \quad&\text {and}\quad \big \langle \ell _{\partial \Omega ,h}(t),{{\textbf {w}} }\big \rangle = \big ({{\textbf {g}} }(t),{{\textbf {w}} }\big )_{\partial \Omega } \,, \end{aligned}$$

(19)

and for the inconsistency complement we require that $C_1\ge c_1>0$ exists such that

$$\begin{aligned} c_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h]\big \Vert _{\partial \Omega _h}^2 \le a_h\big ({{\textbf {v}} }_h,{{\textbf {v}} }_h\big ) \le C_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h]\big \Vert _{\partial \Omega _h}^2 \,,\qquad {{\textbf {v}} }_h\in {\mathcal {S}}_h \,, \end{aligned}$$

(20)

so that for ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {S}}_h$

$$\begin{aligned} a_h\big ({{\textbf {v}} }_h,{{\textbf {v}} }_h\big )= 0 \quad \Longrightarrow \quad a_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big ) = -\big ({{\textbf {v}} }_h,A{{\textbf {w}} }_h\big )_{\Omega _h} = \big (A{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{\Omega _h} \,. \end{aligned}$$

(21)

We assume that $C_1 > 0$ only depends on the material parameters, and that

$$\begin{aligned} \big | a_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big ) + \big ({{\textbf {v}} }_h,A{{\textbf {w}} }_h\big )_{\Omega _h} \big |&\le C_1 \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _{\partial \Omega _h} \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {w}} }_h]\big \Vert _{\partial \Omega _h} \,, \end{aligned}$$

(22a)

$$\begin{aligned} \big | a_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big ) + \big (A{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{\Omega _h} \big |&\le C_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h]\big \Vert _{\partial \Omega _h} \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _{\partial \Omega _h} \,, \end{aligned}$$

(22b)

$$\begin{aligned} \big | \big \langle \ell _{\partial \Omega ,h}(t),{{\textbf {w}} }_h\big \rangle - \big ({{\textbf {g}} }(t),{{\textbf {w}} }_h\big )_{\partial \Omega } \big |&\le C_1 \big \Vert {{\textbf {g}} }(t)\big \Vert _{\partial \Omega _h} \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _{\partial \Omega _h} \end{aligned}$$

(22c)

for ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {S}}_h$.

For acoustic, elastic and electro-magnetic waves the upwind flux is explicitly evaluated, e.g., in [16, Sect. 4.3]. Here, we only consider the dual representation; integration by parts yields the primal representation.

Acoustic waves

The full upwind DG approximation for the acoustic wave equation (4) is given by

$$\begin{aligned}&a_h\big ((p_h,{{\textbf {q}} }_h),(\varphi _h,{\varvec{\psi }}_h)\big ) \! = \! \sum _{K\in {\mathcal {K}}_h} \Bigg ( \! -\big ({{\textbf {q}} }_{h,K},\nabla \varphi _{h,K}\big )_{K} - \big (p_{h,K},\nabla \cdot {\varvec{\psi }}_{h,K}\big )_{K} \! \! \! \\&\quad -\sum _{F\in {\mathcal {F}}_K} \frac{1}{Z_K + Z_{K_F}} \big (p_{K,h} + Z_{K_F}{{\textbf {n}} }_K\cdot {{\textbf {q}} }_{K,h} , [\varphi _h]_{K,F} + Z_K{{\textbf {n}} }_K\cdot [{\varvec{\psi }}_h]_{K,F}\big )_{F} \Bigg ) \end{aligned}$$

for $(p_h,{{\textbf {q}} }_h),(\varphi _h,{\varvec{\psi }}_h)\in {\mathcal {S}}_h$ with impedance $Z_K = \sqrt{\kappa _{h,K}\varrho _{h,K}}$ depending on the piecewise constant approximations for the material parameters $\kappa ,\varrho >0$. On inner boundaries material discontinuities can result in $Z_K \ne Z_{K_F}$, on boundary faces we define $Z_h = Z_K$ on $\partial \Omega \cap \partial K$. On Dirichlet boundary faces $F\in {\mathcal {F}}_h\cap \Gamma _\textrm{D}$, we set $[p_h]_{K,F} = -2 p_h$ and ${{\textbf {n}} }\cdot [{{\textbf {q}} }_h]_{K,F} = 0$. On Neumann boundary faces $F\in {\mathcal {F}}_h\cap \Gamma _\textrm{N}$, we set $[p_h]_{K,F} = 0$ and ${{\textbf {n}} }\cdot [{{\textbf {q}} }_h]_{K,F} = -2\, {{\textbf {n}} }\cdot {{\textbf {q}} }_h$. The right-hand side is complemented by the stabilization, so that

$$\begin{aligned} \big \langle \ell _{\partial \Omega ,h}(t),(\varphi _h,{\varvec{\psi }}_h)\big \rangle&=-\big (p_\textrm{D}(t),{{\textbf {n}} }\cdot {\varvec{\psi }}_h\big )_{\Gamma _\textrm{D}} -\big (g_\textrm{N}(t) ,\varphi _h\big )_{\Gamma _\textrm{N}} \nonumber \\&\quad +\big (p_\textrm{D}(t),Z_h^{-1}\varphi _h\big )_{\Gamma _\textrm{D}} +\big (g_\textrm{N}(t) ,Z_h{{\textbf {n}} }\cdot {\varvec{\psi }}_h\big )_{\Gamma _\textrm{N}} \,. \end{aligned}$$

(23)

Integration by parts gives

$$\begin{aligned}&a_h\big ((p_h,{{\textbf {q}} }_h),(p_h,{{\textbf {q}} }_h)\big ) = \\&\qquad \frac{1}{2} \sum _{K\in {\mathcal {K}}_h} \sum _{F\in {\mathcal {F}}_K} \frac{1}{Z_K + Z_{K_F}} \Bigg ( \big \Vert [p_h]_{K,F}\big \Vert _{F}^2 + Z_KZ_{K_F} \big \Vert {{\textbf {n}} }_K\cdot [{{\textbf {q}} }_h]_{K,F} \big \Vert _{F}^2 \Bigg ) \,. \end{aligned}$$

Elastic waves

The full upwind DG approximation for the elastic wave equation (5) is given by

$$\begin{aligned} &a_h\big (({{\textbf {v}} }_h,{\varvec{\sigma }}_h),({{\textbf {w}} }_h,{\varvec{\eta }}_h)\big ) = \! \sum _{K\in {\mathcal {K}}_h} \Bigg ( \! \big ({\varvec{\sigma }}_{h.K},{\varvec{\varepsilon }}({{\textbf {w}} }_{h,K})\big )_{K} \! +\big ({{\textbf {v}} }_{h,K}, \nabla \cdot {\varvec{\eta }}_{h,K}\big )_{K} \! \nonumber \\&-\sum _{F\in {\mathcal {F}}_K}\!\! \frac{ \Big ({{\textbf {n}} }_K\cdot \big ({\varvec{\sigma }}_{h,K}{{\textbf {n}} }_K -Z_{K_F}^\text {p}{{\textbf {v}} }_{h,K}\big ), {{\textbf {n}} }_K\cdot \big ([{\varvec{\eta }}_h]_{K,F}{{\textbf {n}} }_K -Z_K^\text {p} [{{\textbf {w}} }_h]_{K,F}\big )\Big )_{F} }{Z_K^\text {p} + Z_{K_F}^\text {p}} \nonumber \\&- \sum _{F\in {\mathcal {F}}_K}\!\! \frac{ \Big ({{\textbf {n}} }_K\times \big ({\varvec{\sigma }}_{h,K}{{\textbf {n}} }_K -Z_{K_F}^\text {s}{{\textbf {v}} }_{h,K}\big ), {{\textbf {n}} }_K\times \big ([{\varvec{\eta }}_h]_{K,F}{{\textbf {n}} }_K -Z_K^\text {s} [{{\textbf {w}} }_h]_{K,F}\big )\Big )_{F} }{Z_K^\text {s} + Z_{K_F}^\text {s}} \Bigg ) \end{aligned}$$

(24)

for $({{\textbf {v}} }_h,{\varvec{\sigma }}_h),({{\textbf {w}} }_h,{\varvec{\eta }}_h) \in {\mathcal {S}}_h$. The coefficients $Z_K^\text {p} = \sqrt{(2\mu _{h,K}+\lambda _{h,K})\varrho _{h,K}}$ and $Z_K^\text {s} = \sqrt{\mu _{h,K}\varrho _{h,K}}$ are the impedance of compressional waves and shear waves, respectively. On Dirichlet boundary faces $F\in {\mathcal {F}}_h\cap \Gamma _\textrm{D}$, we set $[{{\textbf {v}} }_h]_{K,F} = -2{{\textbf {v}} }_h$ and $[{\varvec{\sigma }}_h]_{K,F}{{\textbf {n}} }_K = {\textbf {0}}$, and on Neumann faces $F\in {\mathcal {F}}_h \cap \Gamma _\textrm{N}$ we set $[{\textbf {v}} _h]_{K,F} = {\textbf {0}}$ and $[{\varvec{\sigma }}_h]_{K,F}{{\textbf {n}} }_K = -2\, {\varvec{\sigma }}_h{{\textbf {n}} }_K$. The right-hand side is given by

$$\begin{aligned}&\big \langle \ell _{\partial \Omega ,h}(t),({{\textbf {w}} }_h,{\varvec{\eta }}_h)\big \rangle = \big ({{\textbf {v}} }_\textrm{D}(t),{\varvec{\eta }}_h{{\textbf {n}} }\big )_{\Gamma _\textrm{D}} +\big ({{\textbf {g}} }_\textrm{N}(t),{{\textbf {w}} }_h\big )_{\Gamma _\textrm{N}} \\&\qquad +\big ({{\textbf {n}} }\cdot {{\textbf {v}} }_\textrm{D}(t),(Z_h^\text {p})^{-1}{{\textbf {n}} }\cdot {{\textbf {w}} }_h\big )_{\Gamma _\textrm{D}} +\big ({{\textbf {n}} }\cdot {{\textbf {g}} }_\textrm{N}(t),Z_h^\text {p}{{\textbf {n}} }\cdot {\varvec{\eta }}_h{{\textbf {n}} }\big )_{\Gamma _\textrm{N}} \\&\qquad +\big ({{\textbf {n}} }\times {{\textbf {v}} }_\textrm{D}(t),(Z_h^\text {s})^{-1}{{\textbf {n}} }\times {{\textbf {w}} }_h\big )_{\Gamma _\textrm{D}} +\big ({{\textbf {n}} }\times {{\textbf {g}} }_\textrm{N}(t),Z_h^\text {s}{{\textbf {n}} }\times {\varvec{\eta }}_h{{\textbf {n}} }\big )_{\Gamma _\textrm{N}} \end{aligned}$$

with $Z_h^\text {p}= Z_K^\text {p}$ and $Z_h^\text {s}= Z_K^\text {s}$ on $\partial K \cap \partial \Omega$. Integrating by parts yields

$$\begin{aligned} a_h\big (&({{\textbf {v}} }_h,{\varvec{\sigma }}_h),({{\textbf {v}} }_h,{\varvec{\sigma }}_h)\big ) = \nonumber \\&\frac{1}{2} \sum _{K\in {\mathcal {K}}_h} \sum _{F\in {\mathcal {F}}_K} \Bigg ( \frac{ \big \Vert {{\textbf {n}} }_K\cdot \big ([{\varvec{\sigma }}_h]_{K,F}{{\textbf {n}} }_K\big )\big \Vert _{F}^2 +Z_K^\text {p}Z_{K_F}^\text {p} \big \Vert {{\textbf {n}} }_K\cdot [{{\textbf {v}} }_h]_{K,F}\big \Vert _{F}^2}{Z_K^\text {p} + Z_{K_F}^\text {p}} \nonumber \\&\qquad + \frac{ \big \Vert {{\textbf {n}} }_K\times \big ([{\varvec{\sigma }}_h]_{K,F}{{\textbf {n}} }_K\big )\big \Vert _{F}^2 +Z_K^\text {s}Z_{K_F}^\text {s}\big \Vert {{\textbf {n}} }_K\times [{{\textbf {v}} }_h]_{K,F}\big \Vert _{F}^2}{Z_K^\text {s} + Z_{K_F}^\text {s}} \Bigg ) \,. \end{aligned}$$

(25)

Electro-magnetic waves

The full upwind DG approximation for the electro-magnetic wave equation (6) is given by

$$\begin{aligned}&a_h\big ( ({{\textbf {E}} }_h,{{\textbf {H}} }_h),({\varvec{\varphi }}_h,{\varvec{\psi }}_h)\big ) =\sum _{K\in {\mathcal {K}}_h} \Bigg ( \big ({{\textbf {E}} }_{h,K}, \nabla \times {\varvec{\psi }}_{h,K}\big )_K - \big ({{\textbf {H}} }_{h,K}, \nabla \times {\varvec{\varphi }}_{h,K}\big )_K \nonumber \\&\qquad + \sum _{F\in {\mathcal {F}}_K} \frac{1}{Z_{K} +Z_{K_F}} \Big ( \big (Z_K {{\textbf {E}} }_{h,K} - {{\textbf {n}} }_K\times {{\textbf {H}} }_{h,K}, {{\textbf {n}} }_K\times [{\varvec{\psi }}_h]_{K,F}\big )_F \nonumber \\&\qquad - \big (Z_K{{\textbf {n}} }_K\times {{\textbf {E}} }_{h,K} + {{\textbf {H}} }_{h,K}, Z_{K_F}{{\textbf {n}} }_K\times [{\varvec{\varphi }}_h]_{K,F}\big )_F \Big ) \Bigg ) \end{aligned}$$

(26)

for $({{\textbf {E}} }_h,{{\textbf {H}} }_h), ({\varvec{\varphi }}_h,{\varvec{\psi }}_h) \in {\mathcal {S}}_h$ with coefficient $Z_{K} = \sqrt{\varepsilon _K/\mu _K}$. On the boundary faces, we set ${\textbf {n}} _K\times [{{\textbf {E}} }]_{K,F} = -2 {{\textbf {n}} }_K\times {{\textbf {E}} }_{h,K}$ and ${\textbf {n}} _K\times [{{\textbf {H}} }_h]_{K,F} = {\textbf {0}}$ on $F\in {\mathcal {F}}_h\cap \Gamma _\textrm{E}$, and on impedance boundary faces $F\in {\mathcal {F}}_h\cap \Gamma _\textrm{M}$, we set ${{\textbf {n}} }_K\times [{\textbf {E}} ]_{K,F} ={\textbf {0}}$ and ${{\textbf {n}} }_K\times [{{\textbf {H}} }]_{K,F} = -2 {\textbf {n}} _K\times {{\textbf {H}} }_{h,K}$. The right-hand side is given by

$$\begin{aligned} \big \langle \ell _{\partial \Omega ,h}(t),({\varvec{\varphi }}_h,{\varvec{\psi }}_h)\big \rangle&= \big ({{\textbf {g}} }_\textrm{M}(t) ,{\varvec{\varphi }}_h - Z_h^{-1}{{\textbf {n}} }\times {\varvec{\psi }}_h\big )_{\Gamma _\textrm{M}} \end{aligned}$$

with $Z_h = Z_K$ on $\partial K \cap \Gamma _\textrm{M}$. Again, integration by parts yields

$$\begin{aligned}&a_h\big (({{\textbf {E}} }_h,{{\textbf {H}} }_h), ({{\textbf {E}} }_{h},{{\textbf {H}} }_{h})\big ) = \\&\frac{1}{2} \sum _{K\in {\mathcal {K}}_h} \sum _{F\in {\mathcal {F}}_K} \frac{1}{Z_{K} + Z_{K_F}} \left( Z_{K}Z_{K_F} \big \Vert {{\textbf {n}} }_K\times [{{\textbf {E}} }_h]_{K,F}\big \Vert ^2_F + \Vert {{\textbf {n}} }_K\times [{{\textbf {H}} }_h]_{K,F}\big \Vert ^2_F \right) \,. \end{aligned}$$

3.4 A Discontinuous Galerkin Method in Time and Space

Combining the two semi-discretizations, we obtain the full DG discretization

$$\begin{aligned} b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)&= m_h({{\textbf {v}} }_h,{{\textbf {w}} }_h) + \int _0^T a_h\big ({{\textbf {v}} }_h(t),{{\textbf {w}} }_h(t)\big ) \,\mathrm dt \,,\qquad {{\textbf {v}} }_h\,,\ {{\textbf {w}} }_h\in {\mathcal {V}}_h\, \end{aligned}$$

(27)

with right-hand side in the space-time cylinder for ${{\textbf {v}} }_h \in {\mathcal {V}}_h$

$$\begin{aligned} \big \langle \ell _h,{{\textbf {w}} }_h\big \rangle&= \big ({{\textbf {f}} },{{\textbf {w}} }_h\big )_Q + \big (M_h{{\textbf {u}} }_0,{{\textbf {w}} }_h(0)\big )_{\Omega } + \int _0^T \big \langle \ell _{\partial \Omega ,h}(t),{{\textbf {w}} }_h(t)\big \rangle \,\mathrm dt \,. \end{aligned}$$

(28)

For the space-time DG method we have by construction dual consistency for the bilinear form and the right hand side

$$\begin{aligned} b_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }\big ) = \big ({{\textbf {v}} }_h,L_h^*{{\textbf {w}} }\big )_{Q_h} \,,\qquad {{\textbf {v}} }_h\in {\mathcal {V}}_h\,,\ {{\textbf {w}} } \in \mathcal V^* \,, \end{aligned}$$

(29)

and

$$\begin{aligned} \big \langle \ell _h,{{\textbf {w}} }\big \rangle = \big ({{\textbf {f}} },{{\textbf {w}} }\big )_Q + \big (M_h{{\textbf {u}} }_0,{{\textbf {w}} }(0)\big )_{\partial \Omega } + \big ({{\textbf {g}} },{{\textbf {w}} }\big )_{(0,T)\times \partial \Omega } \,,\qquad {{\textbf {w}} } \in \mathcal V^* \,, \end{aligned}$$

and positivity for the inconsistency complement

$$\begin{aligned} b_h\big ({{\textbf {v}} }_h,{{\textbf {v}} }_h\big )&\ge \frac{1}{2} \sum _{n=0}^N \big \Vert M_h^{1/2}[{{\textbf {v}} }_h]_n\big \Vert _{\Omega }^2 + c_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h]\big \Vert _{I_h\times \partial \Omega _h}^2 \,,\qquad {{\textbf {v}} }_h\in {\mathcal {V}}_h \end{aligned}$$

(30)

by combining (17) and (20). Together with (18) and (21) we obtain

$$\begin{aligned} b_h\big ({{\textbf {v}} }_h,{{\textbf {v}} }_h\big )= 0 \quad \Longrightarrow \quad b_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big ) = \big ({{\textbf {v}} }_h,L_h^*{{\textbf {w}} }_h\big )_{Q_h} = \big (L_h{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{Q_h} \end{aligned}$$

(31)

for ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {V}}_h$, and (22) yields with $C_1>0$

$$\begin{aligned}&\big | b_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big ) - \big ({{\textbf {v}} }_h,L_h^*{{\textbf {w}} }_h\big )_{\Omega _h} \big | \nonumber \\&\qquad \le \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _{\partial Q_h} \sqrt{ \big \Vert M_h^{1/2}[{{\textbf {w}} }_h]\big \Vert _{\partial I_h\times \Omega }^2 + C_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {w}} }_h]\big \Vert _{I_h\times \partial \Omega _h}^2} \,, \end{aligned}$$

(32a)

$$\begin{aligned}&\big | b_h\big ({{\textbf {v}} }_h,{{\textbf {w}} }_h\big ) - \big (L_h{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{\Omega _h} \big | \nonumber \\&\qquad \le \sqrt{ \big \Vert M_h^{1/2}[{{\textbf {v}} }_h]\big \Vert _{\partial I_h\times \Omega }^2 + C_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h]\big \Vert _{I_h\times \partial \Omega _h}^2 }\, \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _{\partial Q_h} \end{aligned}$$

(32b)

$$\begin{aligned}&\big | \big \langle \ell ,{{\textbf {w}} }_h\big \rangle - \big \langle \ell _h,{{\textbf {w}} }_h\big \rangle \big | \nonumber \\&\qquad \le \big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _{\Omega } \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _{\Omega } + C_1 \big \Vert {{\textbf {g}} }\big \Vert _{I_h\times \partial \Omega } \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _{I_h\times \partial \Omega } \,. \end{aligned}$$

(32c)

For sufficiently smooth functions ${{\textbf {v}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ with $L_h{{\textbf {v}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$, ${{\textbf {v}} }(0) \in {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)$, $[{{\textbf {v}} }]_n={\textbf {0}}$ for $n=1,\ldots ,N-1$, $A_{{{\textbf {n}} }} [{{\textbf {v}} }] = {\textbf {0}}$ on $I_h\times F$ for inner faces $F\in {\mathcal {F}}_h\setminus \partial \Omega$, and $A_{{{\textbf {n}} }} [{{\textbf {v}} }]\in {\textrm{L}}_2(I\times \partial \Omega ;{{\mathbb {R}}}^m)$, we obtain consistency of the form

$$\begin{aligned}&\big | b_h\big ({{\textbf {v}} },{{\textbf {w}} }_h\big ) - \big \langle \ell _h,{{\textbf {w}} }_h\big \rangle - \big (L_h{{\textbf {v}} } -{{\textbf {f}} },{{\textbf {w}} }_h\big )_{Q} - \big (M_h({{\textbf {v}} }(0)-{{\textbf {u}} }_0),{{\textbf {w}} }_h\big )_\Omega \big | \nonumber \\&\qquad \le C_1 \sum _{k=1}^m \big \Vert (A_{{{\textbf {n}} }} {{\textbf {v}} })_k - g_k\big \Vert _{I_h\times \Gamma _k} \big \Vert w_{h,k}\big \Vert _{I_h\times \Gamma _k} \,. \end{aligned}$$

(33)

Lemma 2

We have, depending on $c_1>0$ in (20),

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q^2&+ \sum _{n=0}^{N-1}{d_T}(t_n) \big \Vert M_h^{1/2}[{{\textbf {v}} }_h]_n\big \Vert _{\Omega }^2 + 2c_1\int _0^T{d_T}(t) \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t)]\big \Vert _{\partial \Omega _h}^2 \,\mathrm dt \\&\le 2\, b_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h) \,,\qquad {{\textbf {v}} }_h\in {\mathcal {V}}_h \,. \end{aligned}$$

Proof

By inserting ${{\textbf {v}} }_h(t)$ into (20) and integrating over time we find

$$\begin{aligned} c_1\int _0^T{d_T}(t) \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t)]\big \Vert _{\partial \Omega _h}^2 \,\mathrm dt&\le \int _0^T{d_T}(t)a_h({{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t))\,\mathrm dt \,, \end{aligned}$$

and thus with Lem. 1 we get for all ${{\textbf {v}} }_h\in {\mathcal {V}}_h$

$$\begin{aligned}&\big (M_h{{\textbf {v}} }_h,{{\textbf {v}} }_h\big )_Q + \sum _{n=0}^{N-1}{d_T}(t_n)\big (M_h[{{\textbf {v}} }_h]_n,[{{\textbf {v}} }_h]_n\big )_{\Omega } \le 2\, m_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h)\\&\qquad \le 2\, m_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h) + 2\int _0^T{d_T}(t)\,a_h\big ({{\textbf {v}} }_h(t),{{\textbf {v}} }_h(t)\big ) \,{\textrm{dt}} \\&\qquad \quad - 2c_1\int _0^T{d_T}(t) \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t)]\big \Vert _{\partial \Omega _h}^2 \,{\textrm{dt}}\\&\qquad = 2\, b_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h) - 2c_1\int _0^T{d_T}(t) \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t)]\big \Vert _{\partial \Omega _h}^2 \,{\textrm{dt}} \,. \end{aligned}$$

$\square$

4 Well-posedness and Stability

We show that the discrete problem has a unique solution and is stable with respect to different norms.

4.1 Well-Posedness of the Space-Time DG Discretization

The well-posedness of the discrete equation is now established as in [2, Prop. 5.1].

Lemma 3

A unique discrete approximation ${{\textbf {u}} }_h\in V_h$ exists solving

$$\begin{aligned} b_h({{\textbf {u}} }_h,{{\textbf {v}} }_h)&= \big \langle \ell _h,{{\textbf {v}} }_h\big \rangle \,,\qquad {{\textbf {v}} }_h\in V_h\,. \end{aligned}$$

(34)

Proof

Since $\dim V_h <\infty$, it is sufficient to show that ${{\textbf {u}} }_h = {\textbf {0}}$ is the unique solution of the homogeneous problem

$$\begin{aligned} b_h({{\textbf {u}} }_h,{{\textbf {v}} }_h)&= 0 \,,\qquad {{\textbf {v}} }_h\in V_h\,. \end{aligned}$$

(35)

Since (35) implies $b_h({{\textbf {u}} }_h,{{\textbf {u}} }_h)= 0$, we obtain by (30) for the jump terms $\big \Vert M_h^{1/2}[{{\textbf {u}} }_h]\big \Vert _{\partial I_h \times \Omega _h}= \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {u}} }_h]\big \Vert _{I_h \times \partial \Omega _h}= 0$, so that $b_h({{\textbf {u}} }_h,{{\textbf {v}} }_h) = \big (L_h{\textbf {u}} _h,{{\textbf {v}} }_h\big )_{Q_{h}} = 0$. Since $M_h$ is piecewise constant in $K\in {\mathcal {K}}_h$, we observe $L_h{{\textbf {u}} }_h\in V_h$, so that we can test with ${{\textbf {v}} }_h = L_h{{\textbf {u}} }_h$; thus, also $\big (L_h{\textbf {u}} _h,L_h{{\textbf {u}} }_h\big )_{Q_{h}} = 0$, i.e., $L_h{{\textbf {u}} }_h={\textbf {0}}$. Now the assertion follows from Lem. 2 and (31) by

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2 = \big (M_h{{\textbf {u}} }_h,{{\textbf {u}} }_h\big )_Q&\le 2\, b_h({{\textbf {u}} }_h,{d_T}{{\textbf {u}} }_h) = 2\, \big (L_h{{\textbf {u}} }_h,{d_T}{{\textbf {u}} }_h\big )_Q = 0 \,. \end{aligned}$$

$\square$

Remark 6

The previous lemma shows that the discrete graph norm defined by

$$\begin{aligned} \Vert {{\textbf {v}} }_h\Vert _{V_h} = \sup _{{{\textbf {w}} }_h\in V_h\setminus \{{\textbf {0}} \}} \frac{b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)}{\big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _Q} \,,\qquad {{\textbf {v}} }_h\in V_h\,, \end{aligned}$$

(36)

is well defined and a norm in $V_h$.

Since the discrete graph norm is only a semi-norm in ${\mathcal {V}}_h$, we have to use stronger norms for the convergence analysis.

4.2 Stability in Space and Time

Let $0=c_{p,0}<c_{p,1}<\cdots<c_{p,p}<1$ be the Radau Ia collocation points, so that

$$\begin{aligned} \int _0^1 \phi (s)\,\mathrm ds = \sum _{k=0}^p \omega _{p,k} \phi (c_{p,k})\,,\qquad \phi \in \mathbb P_{2p} \end{aligned}$$

(with quadrature weights $\omega _{p,k}>0$ for $k=0,\ldots ,p$), and let $\lambda _{p,k}\in \mathbb P_p$ be the corresponding Lagrange polynomials

$$\begin{aligned} \lambda _{p,k}(s) = \prod _{j=0,\ j\ne k}^p \frac{s-c_{p,j}}{c_{p,k}-c_{p,j}} \,,\qquad s\in [0,1] \,. \end{aligned}$$

This defines $\lambda _{n,h,k}\in {\mathbb {P}}_{p_n}(I_{n,h})$ by $\lambda _{n,h,k}(t_{n-1}+s{\vartriangle } t_n) = \lambda _{p_n,k}(s)$ for $s\in [0,1]$ and $t_{n,k} = t_{n-1}+ c_{p_n,k}{\vartriangle } t_n$.

Together this is combined to the corresponding interpolation ${\mathcal {I}}_h:{\mathcal {V}}_h \longrightarrow V_h$ by

$$\begin{aligned} ({\mathcal {I}}_{n,h}{{\textbf {v}} }_{n,h})(t, {{\textbf {x}} }) =&\sum _{k=0}^{p_{n}} \lambda _{n,h,k}(t) {{\textbf {v}} }_{n,h} (t_{n,k},{{\textbf {x}} }) \,,\quad (t,{{\textbf {x}} }) \in I_{n,h}\times \Omega _h,\\&{{\textbf {v}} }_{n,h}\in {\textrm{C}}^0([t_{n-1},t_n];{\mathcal {S}}_h), \ n = 1,\ldots , N \,. \end{aligned}$$

For the interpolation we will use in the following the estimate

$$\begin{aligned} \big \Vert M_h^{1/2}{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big \Vert _Q^2&= \sum _{n=1}^N \sum _{k=0}^{p_n} \omega _{p_n,k} \big \Vert M_h^{1/2}{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)(t_{n,k})\big \Vert _{\Omega }^2 \nonumber \\&= \sum _{n=1}^N \sum _{k=0}^{p_n} {d_T}(t_{n,k})^2 \omega _{p_n,k} \big \Vert M_h^{1/2}{{\textbf {v}} }_h(t_{n,k})\big \Vert _{\Omega }^2 \nonumber \\&\le T^2\sum _{n=1}^N \sum _{k=0}^{p_n} \omega _{p_n,k} \big \Vert M_h^{1/2}{{\textbf {v}} }_h(t_{n,k})\big \Vert _{\Omega }^2 = T^2\,\big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q^2 \,. \end{aligned}$$

(37)

Lemma 4

If $p_{n,K} = p_{n}$ for all $K\in {\mathcal {K}}_h$ and $n=1,\ldots ,N$, we have for ${{\textbf {v}} }_h\in V_h$

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {v}} }_h&\big \Vert _Q^2 + \sum _{n=1}^N \Big ( {d_T}(t_{n-1}) \big \Vert M_h^{1/2}[{{\textbf {v}} }_h]_{n-1}\big \Vert _{\Omega }^2 \\&+ 2c_1 \sum _{k=0}^{p_n} {d_T}(t_{n,k}) \omega _{p_n,k} \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t_{n,k})]\big \Vert _{\partial \Omega _h}^2 \Big )&\le 2\, b_h\big ({{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big ) \,. \end{aligned}$$

Proof

We observe

$$\begin{aligned} \big (M_h\partial _t{{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h\big )_{Q_h}&= \sum _{n=1}^N \big (M_h\partial _t{{\textbf {v}} }_{n,h},{d_T}{{\textbf {v}} }_{n,h}\big )_{I_{n,h}\times \Omega } \\&= \sum _{n=1}^N \sum _{k=0}^{p_n} \omega _{p_n,k} \big (M_h(\partial _t{{\textbf {v}} }_{n,h})(t_{n,k}),{d_T}(t_{n,k}) {{\textbf {v}} }_{n,h}(t_{n,k})\big )_\Omega \\&= \sum _{n=1}^N \sum _{k=0}^{p_n} \omega _{p_n,k} \big (M_h(\partial _t{{\textbf {v}} }_{n,h})(t_{n,k}), {\mathcal {I}}_{n,h}({d_T}{{\textbf {v}} }_{n,h})(t_{n,k})\big )_\Omega \\&= \big (M_h\partial _t{{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big )_{Q_h} \,. \end{aligned}$$

Using ${\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)(t_{n-1}) = {d_T}(t_{n-1}){\textbf {v}} _{n,h}(t_{n-1})$ for $n=1,\ldots ,N$, we have

$$\begin{aligned} m_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h)&= \big (M_h\partial _t{{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h\big )_{Q_h} + \sum _{n=1}^{N} \big (M_h[{{\textbf {v}} }_h]_n,{d_T}(t_{n-1}){{\textbf {v}} }_{n,h}(t_{n-1})\big )_{\Omega } \nonumber \\&= \big (M_h\partial _t{{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big )_{Q_h} + \sum _{n=1}^{N} \big (M_h[{{\textbf {v}} }_h]_n,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)(t_{n-1})\big )_{\Omega } \\&= m_h\big ({{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big ) \,, \end{aligned}$$

and together with Lem. 1 we obtain

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q^2 +&\sum _{n=1}^N {d_T}(t_{n-1}) \big \Vert M_h^{1/2}[{{\textbf {v}} }_h]_{n-1}\big \Vert _{\Omega }^2 \\&\le 2\, m_h({{\textbf {v}} }_h,{d_T}{{\textbf {v}} }_h) = 2\, m_h\big ({{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big ) \,. \end{aligned}$$

For the upwind DG discretization in space we obtain by (20)

$$\begin{aligned} 0&\le c_1 \sum _{n=1}^N \sum _{k=0}^{p_n} {d_T}(t_{n,k}) \omega _{p_n,k} \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t_{n,k})]\big \Vert _{\partial \Omega _h}^2 \\&\le \sum _{n=1}^N \sum _{k=0}^{p_n} {d_T}(t_{n,k}) \omega _{p_n,k} \, a_h\big ({{\textbf {v}} }_h(t_{n,k}),{{\textbf {v}} }_h(t_{n,k})\big ) \\&= \sum _{n=1}^N \sum _{k=0}^{p_n} \omega _{p_n,k} \, a_h\big ({{\textbf {v}} }_h(t_{n,k}),{\mathcal {I}}_{n,h}({d_T}{{\textbf {v}} }_{n,h})(t_{n,k})\big ) \\&= \sum _{n=1}^N \int _{t_{n-1}}^{t_n} a_h\big ({{\textbf {v}} }_h(t),{\mathcal {I}}_{n,h}({d_T}{{\textbf {v}} }_{n,h})(t)\big )\,{\textrm{dt}} \\&= \int _0^T a_h\big ({{\textbf {v}} }_h(t),{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)(t)\big )\,{\textrm{dt}} \,, \end{aligned}$$

so that together we obtain the assertion by

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q^2 + \sum _{n=1}^N&\Big ( {d_T}(t_{n-1}) \big \Vert M_h^{1/2}[{{\textbf {v}} }_h]_{n-1}\big \Vert _{\Omega }^2 \\&\qquad + 2c_1 \sum _{k=0}^{p_n} {d_T}(t_{n,k}) \omega _{p_n,k} \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {v}} }_h(t_{n,k})]\big \Vert _{\partial \Omega _h}^2 \Big ) \\&\le 2\, m_h\big ({{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big )+ \int _0^T a_h\big ({{\textbf {v}} }_h(t),{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)(t)\big )\,{\textrm{dt}} \\&= 2\, b_h\big ({{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big ) \,. \end{aligned}$$

$\square$

Remark 7

Together with (36) and (37) we obtain ${\textrm{L}}_2$ stability with respect to the discrete graph norm by

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q&\le 2 \frac{b_h\big ({{\textbf {v}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big )}{\big \Vert {M_h^{1/2}}{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big \Vert _Q} \frac{\big \Vert {M_h^{1/2}}{\mathcal {I}}_h({d_T}{{\textbf {v}} }_h)\big \Vert _Q}{\big \Vert M_h^{1/2}{{\textbf {v}} }_h\big \Vert _Q} \le 2T\, \Vert {{\textbf {v}} }_h\Vert _{V_h} \end{aligned}$$

for ${{\textbf {v}} }_h\in V_h\setminus \{0\}$, i.e., $\Vert M_h^{1/2}{{\textbf {v}} }_h\Vert _Q \le 2 T\, \Vert {{\textbf {v}} }_h\Vert _{V_h}$.

Corollary 1

Let ${{\textbf {u}} }_h\in V_h$ be the discrete solution (34), and assume homogeneous boundary data ${{\textbf {g}} } = {\textbf {0}}$.

If $p_{n,K} = p_{n}$ for all $K\in {\mathcal {K}}_h$ and $n=1,\ldots ,N$, the solution is bounded by

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2&+ \sum _{n=1}^N {d_T}(t_{n-1}) \left( \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_{n-1}\big \Vert _{\Omega }^2 + 2c_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {u}} }_h]\big \Vert _{I_{n,h}\times \partial \Omega _h}^2 \right) \\&\le 4\, \big \Vert {d_T}M_h^{-1/2}{{\textbf {f}} }\big \Vert _{Q}^2 + 4T\, \big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _\Omega ^2 \,. \end{aligned}$$

Proof

We have for $n=1,\ldots ,N$

$$\begin{aligned} {d_T}(t_{n-1}) \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {u}} }_h]\big \Vert _{I_{n,h}\times \partial \Omega _h}^2&= {d_T}(t_{n-1}) \sum _{k=0}^{p_n} \omega _{p_n,k} \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {u}} }_h(t_{n,k})]\big \Vert _{\partial \Omega _h}^2 \\&\le \sum _{k=0}^{p_n} {d_T}(t_{n,k}) \omega _{p_n,k} \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {u}} }_h(t_{n,k})]\big \Vert _{\partial \Omega _h}^2 \,, \end{aligned}$$

so that together with Lem. 4 and ${\mathcal {I}}_h(d_Tu_h)(0) = Tu_h(0)$ we get the assertion by

$$\begin{aligned} \frac{1}{2} \big \Vert M_h^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2&+ \frac{1}{2} \sum _{n=1}^N {d_T}(t_{n-1}) \left( \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_{n-1}\big \Vert _{\Omega }^2 + 2c_1 \big \Vert \underline{A}_{{{\textbf {n}} }} [{{\textbf {u}} }_h]\big \Vert _{I_{n,h}\times \partial \Omega _h}^2 \right) \\&\le b_h\big ({{\textbf {u}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {u}} }_h)\big ) = \langle \ell _h,{\mathcal {I}}_h({d_T}{{\textbf {u}} }_h)\rangle \\&= \big ({{\textbf {f}} },{d_T}{{\textbf {u}} }_h\big )_{Q} + \big (M_h{{\textbf {u}} }_0,T{{\textbf {u}} }_h(0)\big )_\Omega \\&\le \big \Vert {d_T}M_h^{-1/2}{{\textbf {f}} }\big \Vert _Q^2 + \frac{1}{4} \big \Vert M_h^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2 \\&\qquad +T \big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _\Omega ^2 + \frac{T}{4} \big \Vert M_h^{1/2}{{\textbf {u}} }_h(0)\big \Vert _\Omega ^2 \,. \end{aligned}$$

$\square$

Remark 8

The estimate in Lem. 2 directly implies that the Petrov–Galerkin method with test space $V_h^* = d_TV_h$ is well-defined and ${\textrm{L}}_2$ stable: the Petrov–Galerkin solution ${{\textbf {u}} }_h^{\textrm{PG}}\in V_h$ given by

$$\begin{aligned} b_h({{\textbf {u}} }_h^{\textrm{PG}},{d_T}{{\textbf {v}} }_h) = \langle \ell _h,{d_T}{{\textbf {v}} }_h\rangle \,,\qquad {{\textbf {v}} }_h\in V_h \end{aligned}$$

(38)

is bounded by

$$\begin{aligned} \frac{1}{2} \big \Vert M_h^{1/2}{{\textbf {u}} }_h^{\textrm{PG}}\big \Vert _{Q}^2 + \frac{T}{2} \big \Vert M_h^{1/2}{{\textbf {u}} }_h^{\textrm{PG}}(0)\big \Vert _\Omega ^2 \le b_h({{\textbf {u}} }_h^{\textrm{PG}},{d_T}{{\textbf {u}} }_h^{\textrm{PG}}) = \langle \ell _h,{d_T}{{\textbf {u}} }_h^{\textrm{PG}}\rangle \,, \end{aligned}$$

and thus, in case of homogeneous boundary data ${{\textbf {g}} } = {\textbf {0}}$ we obtain

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {u}} }_h^{\textrm{PG}}\big \Vert _{Q}^2 + T\, \big \Vert M_h^{1/2}{{\textbf {u}} }_h^{\textrm{PG}}(0)\big \Vert _\Omega ^2 \le 4\, \big \Vert {d_T}M_h^{-1/2}{{\textbf {f}} }\big \Vert _{Q}^2+ 4T\, \big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _\Omega ^2 \,. \end{aligned}$$

This is proposed and analyzed in [1] in the semi-discrete case for the advection-diffusion problem. Our numerical tests indicate, that the Petrov–Galerkin modification does not improve the approximation quality, and in the next section we show, that stability and convergence in the DG norm can be established also for the Galerkin method with ansatz and test space $V_h$ and with adaptively chosen $p_{n,K}$.

4.3 Inf-Sup Stability in the DG Norm

Suitable mesh-dependent DG semi-norms and norms can be defined for all ${{\textbf {v}} }_h\in {\mathcal {V}}_h$ by

$$\begin{aligned} \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}&=\sqrt{b_h({{\textbf {v}} }_h,{{\textbf {v}} }_h)}\,, \nonumber \\ \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}^+}&= \Bigg ( \sum \limits _{n=1}^N \Big (\big \Vert M_h^{1/2}{{\textbf {v}} }_{n,h}(t_{n-1})\big \Vert _{\Omega }^2+ \big \Vert M_h^{1/2}{{\textbf {v}} }_{n,h}(t_n)\big \Vert _{\Omega }^2\Big ) \nonumber \\&\qquad + C_1 \sum _{K\in {\mathcal {K}}_h}\big \Vert M_h^{1/2}{\textbf {v}} _h\big \Vert _{I_h\times \partial K}^2 \Bigg )^{1/2} \,, \nonumber \\ \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}&= \sqrt{ \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 + \big \Vert h^{1/2}\,M_h^{-1/2}L_h{{\textbf {v}} }_h\big \Vert _{Q_h}^2} \,, \quad \nonumber \\ \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}^+}&= \sqrt{ \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}^+}^2 + \big \Vert h^{-1/2}M_h^{1/2}{{\textbf {v}} }_h\big \Vert _{Q}^2} \,, \end{aligned}$$

(39)

see [5, Chap. 2 and 7]. Analogously to the proof of Lem. 3 we observe that $\big \Vert {\textbf {v}} _h\big \Vert _{h,\textrm{DG}} = 0$ implies ${{\textbf {v}} }_h = {\textbf {0}}$, so that $\big \Vert \cdot \big \Vert _{h,\textrm{DG}}$ indeed is a norm. Using (32), we obtain for ${{\textbf {v}} }_h,{{\textbf {w}} }_h\in {\mathcal {V}}_h$

$$\begin{aligned} \big | b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h) + \big ({{\textbf {v}} }_h,L_h{{\textbf {w}} }_h\big )_{Q_h} \big |&\le \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}^+} \big |{{\textbf {w}} }_h\big |_{h,\textrm{DG}} \,, \nonumber \\ \big | b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h) - \big (L_h{{\textbf {v}} }_h,{{\textbf {w}} }_h\big )_{Q_h} \big |&\le \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}} \big |{{\textbf {w}} }_h\big |_{h,\textrm{DG}^+} \,. \end{aligned}$$

(40)

We have

$$\begin{aligned} 2\,\big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2&= 2\, b_h({{\textbf {v}} }_h,{{\textbf {v}} }_h) + \big (L_h{{\textbf {v}} }_h,{{\textbf {v}} }_h\big )_{Q_h} - \big ({{\textbf {v}} }_h,L_h{{\textbf {v}} }_h\big )_{Q_h} \\&\le 2\, \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}^+} \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}} \,, \end{aligned}$$

i.e., $\big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}} \le \big |{\textbf {v}} _h\big |_{h,\textrm{DG}^+}$, and continuity of the bilinear form $b_h({\textbf {v}} _h,{{\textbf {w}} }_h)\le \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}} \big \Vert {\textbf {w}} _h\big \Vert _{h,\textrm{DG}^+}$ and $b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)\le \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}^+} \big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}$.

The inf-sup stability for the advection equation [5, Lem. 2.35] can be transferred to our setting.

Theorem 1

A constant $c_{\mathrm{inf-sup}}>0$ exists such that

$$\begin{aligned} \sup _{{{\textbf {w}} }_h\in V_h\setminus \{{\textbf {0}} \}} \frac{b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)}{\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}} \ge c_{\mathrm{inf-sup}} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}} \,,\qquad {{\textbf {v}} }_h\in V_h \,. \end{aligned}$$

Proof

For given ${{\textbf {v}} }_h\in V_h\setminus \{{\textbf {0}} \}$ we define ${{\textbf {z}} }_h = h M_h^{-1}L_h{{\textbf {v}} }_h\in V_h$, and we obtain by the discrete trace inequality (12b)

$$\begin{aligned} \big |{{\textbf {z}} }_h\big |_{h,\textrm{DG}^+}&\le C_\text {tr} \big \Vert h^{-1/2}M_h^{1/2}{{\textbf {z}} }_h\big \Vert _{Q_h} = C_\text {tr} \big \Vert h^{1/2}M_h^{-1/2}L_h{{\textbf {v}} }_h\big \Vert _{Q_h} \\&\le C_\text {tr} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}} \,, \end{aligned}$$

and together with the inverse inequality (12a) this yields

$$\begin{aligned} \big \Vert {{\textbf {z}} }_h\big \Vert _{h,\textrm{DG}}^2&= \big |{{\textbf {z}} }_h\big |_{h,\textrm{DG}}^2 + \big \Vert h^{1/2}M_h^{-1/2}L_h{{\textbf {z}} }_h\big \Vert _{Q_h}^2 \nonumber \\&\le \big |{{\textbf {z}} }_h\big |_{h,\textrm{DG}^+}^2 + C_\text {inv}^2 \big \Vert h^{-1/2}M_h^{1/2}{{\textbf {z}} }_h\big \Vert _{Q_h}^2 \le \big (C_\text {tr}^2+C_\text {inv}^2\big ) \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}^2 \,. \end{aligned}$$

(41)

We observe, using (40),

$$\begin{aligned} \big (L_h{{\textbf {v}} }_h,{{\textbf {z}} }_h\big )_{Q_h} - b_h({{\textbf {v}} }_h,{{\textbf {z}} }_h)&\le \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}} \big |{{\textbf {z}} }_h\big |_{h,\textrm{DG}^+} \\&\le \frac{C_\text {tr}^2}{2} \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 + \frac{1}{2C_\text {tr}^2} \big |{{\textbf {z}} }_h\big |_{h,\textrm{DG}^+}^2 \\&\le \frac{C_\text {tr}^2}{2} \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 + \frac{1}{2} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}^2 \,. \end{aligned}$$

This yields, inserting $\big \Vert h^{1/2}M_h^{-1/2}L_h{\textbf {v}} _h\big \Vert _{Q_h}^2 = \big (L_h{{\textbf {v}} }_h,{{\textbf {z}} }_h\big )_{Q_h}$,

$$\begin{aligned} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}^2&=\big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 + \big (L_h{{\textbf {v}} }_h,{{\textbf {z}} }_h\big )_{Q_h} \\&\le \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 + \frac{C_\text {tr}^2}{2} \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 + \frac{1}{2} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}^2 + b_h({{\textbf {v}} }_h,{{\textbf {z}} }_h) \,, \end{aligned}$$

so that with $C_2 = 2 + C_\text {tr}^2$

$$\begin{aligned} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}^2&\le C_2 \big |{{\textbf {v}} }_h\big |_{h,\textrm{DG}}^2 +2\, b_h({{\textbf {v}} }_h,{{\textbf {z}} }_h) = b_h({{\textbf {v}} }_h,C_2{{\textbf {v}} }_h+2{{\textbf {z}} }_h) \,. \end{aligned}$$

(42)

Using (41), we obtain the assertion with $c_{\mathrm{inf-sup}} = \big (C_2+2\sqrt{C_\text {tr}^2+C_\text {inv}^2}\big )^{-1}$ by

$$\begin{aligned} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}^2&\le \big \Vert C_2{{\textbf {v}} }_h + 2{{\textbf {z}} }_h\big \Vert _{h,\textrm{DG}} \frac{b_h({{\textbf {v}} }_h,C_2{{\textbf {v}} }_h+2{{\textbf {z}} }_h)}{\big \Vert C_2{{\textbf {v}} }_h + 2{{\textbf {z}} }_h\big \Vert _{h,\textrm{DG}}} \\&\le c_{\mathrm{inf-sup}}^{-1} \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}} \sup _{{{\textbf {w}} }_h\in V_h\setminus \{{\textbf {0}} \}} \frac{b_h({{\textbf {v}} }_h,{{\textbf {w}} }_h)}{\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}} \,. \end{aligned}$$

$\square$

5 Convergence of the DG Space-Time Approximation

In the first step, we show that stability in ${\textrm{L}}_2$ implies convergence in the limit of the DG approximation. Then, by assuming some regularity of the solution, qualitative convergence results are obtained in the DG norm.

5.1 Convergence in the Limit

Let $\big (Q_h\big )_{h\in {\mathcal {H}}}$ be a shape-regular family of space-time meshes with mesh sizes ${\mathcal {H}}=\{h_0,h_1,h_2,\cdots \}\subset (0,\infty )$ and $0\in \overline{{\mathcal {H}}}$.

Let $\big (V_h\big )_{h\in {\mathcal {H}}}$ be corresponding DG finite element spaces, so that

$$\begin{aligned} \lim _{h\in {\mathcal {H}}} \inf _{{{\textbf {v}} }_h\in V_h} \big \Vert {{\textbf {v}} } -{{\textbf {v}} }_h\big \Vert _Q = 0 \,,\qquad {{\textbf {v}} }\in {\mathcal {V}}^* \,. \end{aligned}$$

(43)

For $h\in {\mathcal {H}}$, let ${{\textbf {u}} }_h\in V_h$ be the solution of the discrete problem (34).

The proof of existence of a unique discrete solution in Lem. 3 only relies on the properties (30) and (31) of the DG bilinear form and thus only implicitly on the boundary parts $\Gamma _k\subset \partial \Omega$. In order to obtain a unique weak solution of (2) in the limit, constraints for the selection of $\Gamma _k\subset \partial \Omega$, $k=1,\ldots ,m$, are necessary, cf. (7). This is used in the following.

Theorem 2

Assume that $p_{n,K} = p_n \ge 1$ and $q_{n,K}\ge 1$. In case of homogeneous boundary data ${{\textbf {g}} }= {\textbf {0}}$ and convergent approximations of the material parameters $M_h\longrightarrow M$, $M_h^{-1}\longrightarrow M^{-1}$ in ${\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{m\times m}_\text {sym})$, the discrete solutions $\big ({{\textbf {u}} }_h\big )_{h\in {\mathcal {H}}}$ are converging to a weak solution ${{\textbf {u}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ of (2). Moreover, ${{\textbf {u}} }$ is a strong solution satisfying (3), and the strong solution is unique.

Proof

By the assumption $p_{n,K} = p_n$ we can apply Lem. 4 with the construction of the interpolation ${\mathcal {I}}_h$ and Cor. 1, so that $({{\textbf {u}} }_h)_{h\in {\mathcal {H}}}$ is uniformly bounded by

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2 +T\, \big \Vert M_h^{1/2}{{\textbf {u}} }_h(0)\big \Vert _{\Omega }^2&\le 4T\, \Big (\big \Vert M_h^{-1/2}{{\textbf {f}} }\big \Vert _Q^2 + \big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _{\Omega }^2\Big ) \,. \end{aligned}$$

By (30) and the definition of $\ell _h$ (with ${\textbf {g}} = {\textbf {0}}$), this also implies that

$$\begin{aligned} c_1 \sum _{k=1}^m&\big \Vert (\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} }_h)_k \big \Vert _{(0,T)\times \Gamma _k}^2 = c_1 \big \Vert \underline{A}_{{{\textbf {n}} }}[{{\textbf {u}} }_h]\big \Vert _{(0,T)\times \partial \Omega _h}^2 \\&\le b({{\textbf {u}} }_h,{{\textbf {u}} }_h) = \big \langle \ell _h,{{\textbf {u}} }_h\big \rangle = \big ({{\textbf {f}} },{{\textbf {u}} }_h\big )_Q + \big (M_h{{\textbf {u}} }_0,{{\textbf {u}} }_h(0)\big )_{\Omega } \\&\le \frac{1}{2}\big \Vert M_h^{-1/2}{{\textbf {f}} }\big \Vert _Q^2 + \frac{1}{2}\big \Vert M_h^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2 + \frac{1}{2T}\big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _{\Omega }^2 + \frac{T}{2}\big \Vert M_h^{1/2}{{\textbf {u}} }_h(0)\big \Vert _{\Omega }^2 \\&\le \Big (\frac{1}{2}+2T\Big ) \big \Vert M_h^{-1/2}{{\textbf {f}} }\big \Vert _Q^2 + \Big (\frac{1}{2T}+2T\Big )\big \Vert M_h^{1/2}{{\textbf {u}} }_0\big \Vert _{\Omega }^2 \end{aligned}$$

is uniformly bounded for $h\in {\mathcal {H}}$, so that together with the asymptotic consistency of the material parameters $M_h\longrightarrow M$, $M_h^{-1}\longrightarrow M^{-1}$ in ${\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{m\times m}_\text {sym})$ we obtain with a constant $C_{{{\textbf {f}} },{{\textbf {u}} }_0}>0$ depending on the data

$$\begin{aligned} \big \Vert M^{1/2}{{\textbf {u}} }_h\big \Vert _Q^2 +T\, \big \Vert M^{1/2}{{\textbf {u}} }_h(0)\big \Vert _{\Omega }^2 + c_1 \sum _{k=1}^m \big \Vert (\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} }_h)_k \big \Vert _{(0,T)\times \Gamma _k}^2&\le C_{{{\textbf {f}} },{{\textbf {u}} }_0} \,,\ h\in {\mathcal {H}}\,. \end{aligned}$$

The uniform stability in ${\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ implies, that a subsequence ${\mathcal {H}}_0\subset {\mathcal {H}}$ with $0\in \overline{{\mathcal {H}}}_0$ and a weak limit ${{\textbf {u}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ with ${{\textbf {u}} }(0)\in {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)$ and $(\underline{A}_{{{\textbf {n}} }}{\textbf {u}} )_k|_{(0,T)\times \Gamma _k}\in {\textrm{L}}_2((0,T)\times \Gamma _k)$ for $k=1,\ldots ,m$ exists, i.e.,

$$\begin{aligned} \big (M{{\textbf {u}} },{{\textbf {v}} }\big )_Q&= \lim _{h\in {\mathcal {H}}_0} \big (M_h{{\textbf {u}} }_h,{{\textbf {v}} }\big )_Q \,,\qquad&{{\textbf {v}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m) \\ \big (M{{\textbf {u}} }(0),{{\textbf {v}} }_0\big )_\Omega&= \lim _{h\in {\mathcal {H}}_0} \big (M_h{{\textbf {u}} }_h(0),{{\textbf {v}} }_0\big )_\Omega \,,\qquad&{{\textbf {v}} }_0\in {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m) \\ \big ((\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} })_k,v\big )_{(0,T)\times \Gamma _k}&= \lim _{h\in {\mathcal {H}}_0} \big ((\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} }_h)_k,v\big )_{(0,T)\times \Gamma _k} \,,\qquad&v\in {\textrm{L}}_2((0,T)\times \Gamma _k),\forall k \,. \end{aligned}$$

Then we obtain for all ${{\textbf {v}} }\in {\mathcal {V}}_h$

$$\begin{aligned} \big ({{\textbf {u}} },L^*{{\textbf {v}} }\big )_Q = \lim _{h\in {\mathcal {H}}_0} \big ({{\textbf {u}} }_h,L^*{{\textbf {v}} }\big )_{Q_h} = \lim _{h\in {\mathcal {H}}_0} \big ({{\textbf {u}} }_h,L_h^*{{\textbf {v}} }\big )_{Q_h} = \lim _{h\in {\mathcal {H}}_0} b_h({{\textbf {u}} }_h,{{\textbf {v}} }) \end{aligned}$$

using dual consistency (29) for the last step. This extends to ${\textrm{H}}^1_0(Q;{{\mathbb {R}}}^m)$, and by the assumption $p_{n,K},q_{n,K}\ge 1$, for all ${{\textbf {v}} }\in {\textrm{H}}^1_0(Q;{{\mathbb {R}}}^m)$ a sequence $({{\textbf {v}} }_h)_{h\in {\mathcal {H}}_0}$ exists with ${{\textbf {v}} }_h\in V_h\cap {\textrm{H}}^1_0(Q;{{\mathbb {R}}}^m)$ and $\lim \limits _{h\in {\mathcal {H}}_0}{{\textbf {v}} }_h= {{\textbf {v}} }$, so that by (29)

$$\begin{aligned} \big ({{\textbf {u}} },L^*{{\textbf {v}} }\big )_Q = \lim _{h\in {\mathcal {H}}_0} b_h({{\textbf {u}} }_h,{{\textbf {v}} }) = \lim _{h\in {\mathcal {H}}_0} b_h({{\textbf {u}} }_h,{{\textbf {v}} }_h) = \lim _{h\in {\mathcal {H}}_0} \big ({{\textbf {f}} },{{\textbf {v}} }_h\big )_Q = \big ({{\textbf {f}} },{{\textbf {v}} }\big )_Q \,, \end{aligned}$$

i.e., for the limit ${{\textbf {u}} }$ the weak derivative $L{{\textbf {u}} }= {{\textbf {f}} }$ in ${\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ exists. This extends to initial and boundary data. Therefore, let $\overline{{\mathcal {V}}}^*\subset {\textrm{H}}^1(Q;{{\mathbb {R}}}^m)$ be the closure of ${\mathcal {V}}^*$ in ${\textrm{H}}^1(Q;{{\mathbb {R}}}^m)$; then, for all ${{\textbf {v}} }\in {\mathcal {V}}^*$ a sequence $({{\textbf {v}} }_h)_{h\in {\mathcal {H}}_0}$ with ${{\textbf {v}} }_h \in V_h\cap \overline{{\mathcal {V}}}^*$ and $\lim \limits _{h\in {\mathcal {H}}_0}{{\textbf {v}} }_h= {{\textbf {v}} }$ exists, and we get again by (29)

$$\begin{aligned} \big ({{\textbf {u}} },L^*{{\textbf {v}} }\big )_Q&= \lim _{h\in {\mathcal {H}}_0} b_h({{\textbf {u}} }_h,{{\textbf {v}} }) = \lim _{h\in {\mathcal {H}}_0} b_h({{\textbf {u}} }_h,{{\textbf {v}} }_h) = \lim _{h\in {\mathcal {H}}_0} \big \langle \ell _h,{{\textbf {v}} }_h\big \rangle \\&= \big ({{\textbf {f}} },{{\textbf {v}} }\big )_{Q} + \big (M{{\textbf {u}} }_0,{{\textbf {v}} }(0)\big )_{\Omega } \,. \end{aligned}$$

Thus, using ${{\textbf {v}} }(T) = {\textbf {0}}$ for ${{\textbf {v}} } = (v_1\ldots ,v_m)\in {\mathcal {V}}^*$ yields

$$\begin{aligned} 0&= \big ({{\textbf {u}} },L^*{{\textbf {v}} }\big )_Q - \big ({{\textbf {f}} },{{\textbf {v}} }\big )_{Q} - \big (M{{\textbf {u}} }_0,{{\textbf {v}} }(0)\big )_{\Omega } \\&= \big ({{\textbf {u}} },L^*{{\textbf {v}} }\big )_Q - \big (L{{\textbf {u}} },{{\textbf {v}} }\big )_{Q} - \big (M{{\textbf {u}} }_0,{{\textbf {v}} }(0)\big )_{\Omega } \\&= \big (M{{\textbf {u}} }(0),{{\textbf {v}} }(0)\big )_{\Omega } - \big (\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} },{{\textbf {v}} }\big )_{(0,T)\times \partial \Omega } - \big (M{{\textbf {u}} }_0,{{\textbf {v}} }(0)\big )_{\Omega } \\&= \big (M({{\textbf {u}} }(0)-{{\textbf {u}} }_0),{{\textbf {v}} }(0)\big )_{\Omega } + \sum _{k=1}^m \big ((\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} })_k,v_k\big )_{(0,T)\times \Gamma _k} \,, \end{aligned}$$

so that ${{\textbf {u}} }(0) = {{\textbf {u}} }_0$ in $\Omega$ and $(\underline{A}_{{\textbf {n}} }{{\textbf {u}} })_k = 0$ on $(0,T)\times \Gamma _k$ for $k=1,\ldots ,m$, and thus ${{\textbf {u}} }$ is indeed a strong solution with homogeneous boundary conditions at $(0,T)\times \partial \Omega$.

Next, we show that the weak limit is unique. Therefore, select another subsequence ${\mathcal {H}}_1\subset {\mathcal {H}}$ with $0\in \overline{{\mathcal {H}}}_1$ and with a weak limit $\tilde{{{\textbf {u}} }}\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ with $\tilde{{\textbf {u}} }(0)\in {\textrm{L}}_2(\Omega ;{{\mathbb {R}}}^m)$ and $(\underline{A}_{{\textbf {n}} }\tilde{{{\textbf {u}} }})_k|_{(0,T)\times \Gamma _k} \in {\textrm{L}}_2((0,T)\times \Gamma _k)$ for $k=1,\ldots ,m$. Then, we also obtain $\tilde{{{\textbf {u}} }}(0) = {{\textbf {u}} }_0$ and $(\underline{A}_{{\textbf {n}} }\tilde{{{\textbf {u}} }})_k = 0$ for $k=1,\ldots ,m$. A sequence $({\textbf {e}} _h)_{h\in {\mathcal {H}}}$ with ${{\textbf {e}} }_h\in V_h$ exists such that $\lim _{h\in {\mathcal {H}}} {{\textbf {e}} }_h= {{\textbf {u}} }-\tilde{{{\textbf {u}} }}$, and we get

$$\begin{aligned} \frac{1}{2} \big \Vert M^{1/2}({{\textbf {u}} }-\tilde{{{\textbf {u}} }})\big \Vert _Q^2&= \frac{1}{2} \lim _{h\in {\mathcal {H}}} \big \Vert M^{1/2}{{\textbf {e}} }_h\big \Vert _Q^2 \\&\le \lim _{h\in {\mathcal {H}}} b_h\big ({{\textbf {e}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {e}} }_h)\big ) \\&= \lim _{h\in {\mathcal {H}}_0} b_h\big ({{\textbf {u}} }_h,{\mathcal {I}}_h({d_T}{{\textbf {e}} }_h)\big ) - \lim _{h\in {\mathcal {H}}_1} b_h\big (\tilde{{{\textbf {u}} }},{\mathcal {I}}_h({d_T}{{\textbf {e}} }_h)\big ) \\&= \lim _{h\in {\mathcal {H}}_0} \big \langle \ell _h,{\mathcal {I}}_h({d_T}{{\textbf {e}} }_h)\big \rangle - \lim _{h\in {\mathcal {H}}_1} \big \langle \ell _h,{\mathcal {I}}_h({d_T}{{\textbf {e}} }_h)\big \rangle \\&= \big \langle \ell ,{d_T}({{\textbf {u}} }-\tilde{{{\textbf {u}} }})\big \rangle - \big \langle \ell ,{d_T}({{\textbf {u}} }-\tilde{{{\textbf {u}} }})\big \rangle = 0 \,, \end{aligned}$$

so that ${{\textbf {u}} } =\tilde{{{\textbf {u}} }}$. This shows that the weak limit is unique, so that the full sequence is converging, i.e., $\lim _{h\in {\mathcal {H}}} {{\textbf {u}} }_h= {{\textbf {u}} }$.

The same argument applies to all strong solutions, i.e., ${{\textbf {u}} }$ is the unique strong solution of (3). $\square$

Remark 9

The result extends to inhomogeneous boundary data ${{\textbf {g}} }\ne {\textbf {0}}$, if ${{\textbf {u}} }_{{{\textbf {g}} }}\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ exists with $L{{\textbf {u}} }_{{{\textbf {g}} }}\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ and $(A_{{{\textbf {n}} }}{{\textbf {u}} }_{{{\textbf {g}} }})_k\in {\textrm{L}}_2(I\times \Gamma _k)$ satisfying $(A_{{{\textbf {n}} }}{\textbf {u}} _{{{\textbf {g}} }})_k =g_k$, $k=1,\ldots ,m$. In particular, the regularity result that the limit of the DG approximations is a strong solution requires sufficient regularity of the boundary data.

5.2 Convergence in the DG Norm

We adapt the convergence result for the DG norm (39) in [5, Thm. 2.37] to our setting.

Theorem 3

Assume that the strong solution of (3) is sufficiently smooth satisfying ${{\textbf {u}} } \in {\textrm{H}}^s(Q;{{\mathbb {R}}}^m)$ with $s \ge 1$ and $s\le \min _{n,K}\{p_{n,K},q_{n,K}\}+1$. Then, the error for the discrete solution ${{\textbf {u}} }_h\in V_h$ of (34) is bounded by

$$\begin{aligned} \big \Vert {{\textbf {u}} } - {{\textbf {u}} }_h\big \Vert _{h,\textrm{DG}} \le C h^{s-1/2}\, \big \Vert \mathrm D^s{{\textbf {u}} }\big \Vert _Q + CT h^{-1/2} \big \Vert M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \end{aligned}$$

with $C>0$ depending on the mesh regularity, the polynomial degrees in $V_h$, and the material parameters.

Proof

Since we assume for the solution ${{\textbf {u}} }\in {\textrm{H}}^1(Q;{{\mathbb {R}}}^m)$, we have $L{{\textbf {u}} }, L_h{{\textbf {u}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$, for all traces ${{\textbf {u}} }|_{\partial Q_h} \in {\textrm{L}}_2(\partial Q_h;{{\mathbb {R}}}^m)$, $[{{\textbf {u}} }]_n={\textbf {0}}$ for $n=1,\ldots ,N-1$, and $A_{{{\textbf {n}} }} [{{\textbf {v}} }] = {\textbf {0}}$ on $I_h\times F$ for inner faces $F\in {\mathcal {F}}_h\setminus \partial \Omega$, and $(\underline{A}_{{{\textbf {n}} }}{{\textbf {u}} })_k = g_k$ on $I\times \Gamma _k$ for $k=1,\ldots ,m$, so that $b_h({{\textbf {u}} },{{\textbf {v}} }_h)$ is well defined with

$$\begin{aligned} b_h({{\textbf {u}} },{{\textbf {w}} }_h)&= \big (L_h{{\textbf {u}} },{{\textbf {w}} }_h\big )_Q \!+ (M_h{{\textbf {u}} }(0),{{\textbf {w}} }_h)_Q + \!\int _0^T \big \langle \ell _{\partial \Omega ,h}(t),{{\textbf {w}} }_h\big \rangle \,\mathrm dt \nonumber \\&= \big \langle \ell _h,{{\textbf {w}} }_h\big \rangle + \big ((M_h-M)\partial _t{{\textbf {u}} },{{\textbf {w}} }_h\big )_Q \,,\quad {{\textbf {w}} }_h\in V_h \,. \end{aligned}$$

(44)

Thus we obtain for the discrete solution ${{\textbf {u}} }_h\in V_h$ Galerkin orthogonality up to data error

$$\begin{aligned} b_h({{\textbf {u}} }_h,{{\textbf {w}} }_h)&= b_h({{\textbf {u}} },{{\textbf {w}} }_h) + \big ((M-M_h)\partial _t{{\textbf {u}} },{{\textbf {w}} }_h\big )_Q \,,\qquad {{\textbf {w}} }_h\in V_h \,. \end{aligned}$$

By the trace estimate (12) we obtain $\big \Vert {\textbf {w}} _h\big \Vert _{h,\textrm{DG}^+}^2 \le (C_\text {tr}^2+1)h^{-1}\big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _Q^2$, so that by Lem. 2

$$\begin{aligned} \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _Q^2&\le 2\, b_h({{\textbf {w}} }_h,d_T{{\textbf {w}} }_h) \le 2\,\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}} \big \Vert d_T{{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}^+} \\&\le 2T\,\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}} \big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}^+} \\&\le 2T^2(C_\text {tr}^2+1) h^{-1}\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}^2 + \frac{1}{2(C_\text {tr}^2+1)}h\,\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}^+}^2 \\&\le 2T^2(C_\text {tr}^2+1)h^{-1}\,\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}^2 + \frac{1}{2} \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _Q^2 \,, \end{aligned}$$

so that the consistency term can by bounded by

$$\begin{aligned} \big ((M-M_h)\partial _t{{\textbf {u}} },{{\textbf {w}} }_h\big )_Q&\le \Vert \big (M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \big \Vert M_h^{1/2}{{\textbf {w}} }_h\big \Vert _Q \\&\le 2T\sqrt{C_\text {tr}^2+1} h^{-1/2} \Vert \big (M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}} \,. \end{aligned}$$

For all ${{\textbf {v}} }_h\in V_h$ this yields the estimate, using Thm. 1 and continuity of the bilinear form $b_h(\cdot ,\cdot )$ in the DG norms

$$\begin{aligned} c_{\mathrm{inf-sup}} \big \Vert {{\textbf {u}} }_h - {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}&\le \sup _{{{\textbf {w}} }_h\in V_h\setminus \{{\textbf {0}} \}} \frac{b_h({{\textbf {u}} }_h - {{\textbf {v}} }_h,{{\textbf {w}} }_h)}{\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}} \\&= \sup _{{{\textbf {w}} }_h\in V_h\setminus \{{\textbf {0}} \}} \frac{b_h({{\textbf {u}} } - {{\textbf {v}} }_h,{{\textbf {w}} }_h) + \big ((M-M_h)\partial _t{{\textbf {u}} },{{\textbf {w}} }_h\big )_Q}{\big \Vert {{\textbf {w}} }_h\big \Vert _{h,\textrm{DG}}} \\&\le \big \Vert {{\textbf {u}} } - {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}^+} \\&\qquad + 2T\sqrt{C_\text {tr}^2+1} h^{-1/2} \Vert \big (M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \,. \end{aligned}$$

Now select an ${\textrm{H}}^1$-stable quasi-interpolation ${{\textbf {v}} }_h = \Pi _h^\text {Cl}{{\textbf {u}} }$ of Clement-type [3, Sect. 4.4.2] with

$$\begin{aligned} \big \Vert M^{1/2}({{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} })\big \Vert _{Q}&\le C_4 h\, \big \Vert \mathrm D{{\textbf {u}} }\big \Vert _{Q}\,,\qquad \\ \big \Vert M^{-1/2}L_h({{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} })\big \Vert _{Q}&\le C_5 \big \Vert \mathrm D{{\textbf {u}} }\big \Vert _{Q} \end{aligned}$$

and constants $C_4,C_5$ depending on the mesh regularity and the polynomial degrees in $V_h$. Using $s\le \min \{p,q\}+1$,

$$\begin{aligned} \big \Vert M^{1/2}({{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} })\big \Vert _{\partial Q_h}&+ h^{-1/2}\big \Vert M^{1/2}({{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} })\big \Vert _Q \\&+ h^{1/2}\big \Vert M^{-1/2}L_h({{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} })\big \Vert _Q \le C_6 h^{s-1/2} \big \Vert \mathrm D^s{{\textbf {u}} }\big \Vert _{Q} \,. \end{aligned}$$

Then, the result follows from interpolation estimates using [5, Lem. 1.59] and

$$\begin{aligned} \big \Vert {{\textbf {u}} } - {{\textbf {u}} }_h\big \Vert _{h,\textrm{DG}}&\le \big \Vert {{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} }\big \Vert _{h,\textrm{DG}} + \big \Vert {{\textbf {u}} }_h - \Pi _h^\text {Cl}{{\textbf {u}} }\big \Vert _{h,\textrm{DG}} \\&\le \big \Vert {{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} }\big \Vert _{h,\textrm{DG}} + c_{\mathrm{inf-sup}}^{-1} \big \Vert {{\textbf {u}} } - \Pi _h^\text {Cl}{{\textbf {u}} }\big \Vert _{h,\textrm{DG}^+} \\&\qquad + 2T\sqrt{C_\text {tr}^2+1}\,c_{\mathrm{inf-sup}}^{-1} h^{-1/2} \big \Vert M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \\&\le C_6 h^{s-1/2} \big \Vert \mathrm D^s{{\textbf {u}} }\big \Vert _{Q} + C_7 T h^{-1/2} \big \Vert M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \,. \end{aligned}$$

$\square$

This recovers the convergence result [2, Prop. 6.5] for the DG semi-norm (39).

Corollary 2

Assume that the strong solution of (3) is sufficiently smooth satisfying ${{\textbf {u}} } \in {\textrm{H}}^s(Q;{{\mathbb {R}}}^m)$ with $s \ge 1$.

Then, the error for the discrete solution ${{\textbf {u}} }_h\in V_h$ of (34) is bounded in every time step by

$$\begin{aligned} \big \Vert M_h^{1/2}\big ({{\textbf {u}} }(t_n) - {{\textbf {u}} }_{n,h}(t_n)\big )\big \Vert _{\Omega }&\le C h^{s-1/2}\, \big \Vert \mathrm D^s{{\textbf {u}} }\big \Vert _{(0,t_n)\times \Omega } \\&\qquad + CT h^{-1/2} \big \Vert M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _{(0,t_n)\times \Omega } \end{aligned}$$

with $C>0$ depending on the mesh regularity, the polynomial degree, and the material parameters.

For the proof Thm. 3 is applied with $T= t_n$; then, the assertion directly follows from $\frac{1}{2} \big \Vert M_h^{1/2}{\textbf {v}} _h(T)\big \Vert _{\Omega }\le \big \Vert {{\textbf {v}} }_h\big \Vert _{h,\textrm{DG}}$.

Remark 10

If $M\in {\textrm{L}}_\infty (\Omega ;{{\mathbb {R}}}^{m\times m}_{{\text {sym}}})$ is smooth, the consistency term can be estimated by

$$\begin{aligned} \big \Vert M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q \le \big \Vert M_h^{-1/2}(M-M_h)M^{-1/2}\big \Vert _\infty \big \Vert M^{1/2}\partial _t{{\textbf {u}} }\big \Vert _Q \,. \end{aligned}$$

If M is discontinuous and if the jumps of the material parameters are not resolved by the mesh, the consistency error can be estimated in case of higher regularity of the solution: if $\partial _t{\textbf {u}} \in {\textrm{L}}_2(0,T;{\textrm{L}}_q(\Omega ;{{\mathbb {R}}}^m))$ with $q>2$, we obtain

$$\begin{aligned} \big \Vert M_h^{-1/2}(M_h-M)\partial _t{{\textbf {u}} }\big \Vert _Q&\le \big \Vert M_h^{-1/2}(M-M_h)M^{-1/2}\big \Vert _{{\textrm{L}}_{2q/(2-q)}(\Omega ;{{\mathbb {R}}}^{m\times m}_{{\text {sym}}})} \\&\qquad \cdot \big \Vert M^{1/2}\partial _t{{\textbf {u}} }\big \Vert _{{\textrm{L}}_2(0,T;{\textrm{L}}_q(\Omega ;{{\mathbb {R}}}^m))} \,. \end{aligned}$$

Remark 11

For the continuous solution the energy is conserved, i.e.,

$$\begin{aligned} \big (M{{\textbf {u}} }(t_n),{{\textbf {u}} }(t_n)\big )_\Omega = \big (M{{\textbf {u}} }(0),{{\textbf {u}} }(0)\big )_\Omega + \int _0^{t_n} \langle \ell (t),{{\textbf {u}} }(t)\rangle \,\mathrm dt \,. \end{aligned}$$

From Lem. 4 and Cor. 2 we obtain energy conservation in the limit

$$\begin{aligned} \big (M{{\textbf {u}} }(t_n),{{\textbf {u}} }(t_n)\big )_\Omega = \big (M_h{{\textbf {u}} }_h(t_n),{{\textbf {u}} }_h(t_n)\big )_\Omega + {\mathcal {O}}(h^{2s-1}) \end{aligned}$$

in case of consistent data $M = M_h$.

Remark 12

The constants in Thm. 1 and 3 depend on the mesh and polynomial degrees p. For triangulations and a quasi-uniform distribution of p it is known that $C_{\text { inv}} \sim p^2$, $C_{\text { tr}} \sim p$ [23, Thm. 4.7]. Estimates of quasi-interpolations are considered in [20, Thm. 3.1] where it is shown that the classical Clément interpolation estimate holds with h replaced by h/p.

5.3 Error Control

For the error ${{\textbf {u}} }-{{\textbf {u}} }_h$ in the DG semi-norm we obtain from (18) and (20)

$$\begin{aligned} \big |{{\textbf {u}} }-{{\textbf {u}} }_h\big |_{h,\textrm{DG}}^2&\le \frac{1}{2} \Big ( \big \Vert M_h^{1/2}({{\textbf {u}} }_h(0)-{{\textbf {u}} }_0)\big \Vert _\Omega ^2 + \sum _{n=1}^{N-1} \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_n\big \Vert _\Omega ^2 \nonumber \\&\qquad + \big \Vert M_h^{1/2}({{\textbf {u}} }_h(T)-{{\textbf {u}} }(T))\big \Vert _\Omega ^2 \Big ) \nonumber \\&\qquad + \sum _{k=1}^m \big \Vert (A_{{{\textbf {n}} }}{{\textbf {u}} }_h)_k- g_k\big \Vert _{I_h\times \Gamma _k}^2 + C_1 \big \Vert A_{{{\textbf {n}} }}[{{\textbf {u}} }_h]\big \Vert _{I_h\times (\partial \Omega _h\cap \Omega )}^2 \end{aligned}$$

(45)

and in the DG norm

$$\begin{aligned} \big \Vert {{\textbf {u}} }-{{\textbf {u}} }_h\big \Vert _{h,\textrm{DG}}^2&= \big |{{\textbf {u}} }-{{\textbf {u}} }_h\big |_{h,\textrm{DG}}^2 + \big \Vert h^{1/2}M_h^{-1/2}L_h({{\textbf {u}} }-{{\textbf {u}} }_h)\big \Vert _{Q_h}^2 \nonumber \\&\le \big |{{\textbf {u}} }-{{\textbf {u}} }_h\big |_{h,\textrm{DG}}^2 + 2\,\big \Vert h^{1/2}M_h^{-1/2}(L_h{{\textbf {u}} }_h-{{\textbf {f}} })\big \Vert _{Q_h}^2 \nonumber \\&\quad + 2\,\big \Vert h^{1/2}M_h^{-1/2}(M-M_h)\partial _t{{\textbf {u}} } \big \Vert _{Q_h}^2 \,. \end{aligned}$$

(46)

Up to the error ${{\textbf {u}} }_h-{{\textbf {u}} }$ at final time T in (45) and the parameter approximation error $M-M_h$ in (46), this can be evaluated explicitly by the residual error indicator $\displaystyle \eta _{\text { res},h} = \Big (\sum _{R\in {\mathcal {R}}_h}\eta _{\text { res},R}^2 \Big )^{1/2}$ given by the local contributions

$$\begin{aligned}&\eta _{\text { res},R}^2 = \eta _{\text { res},n,K}^2 +2h_K\,\big \Vert M_h^{-1/2}(L_h{{\textbf {u}} }_h-{{\textbf {f}} })\big \Vert _R^2\\&\quad + \sum _{k=1}^m \big \Vert (A_{{{\textbf {n}} }}{{\textbf {u}} }_h)_k- g_k\big \Vert _{(t_{n-1},t_n)\times (\Gamma _k\cap \partial K)}^2 + C_1 \big \Vert A_{{{\textbf {n}} }}[{{\textbf {u}} }_h]\big \Vert _{(t_{n-1},t_n)\times (\Omega \cap \partial K)}^2 \end{aligned}$$

for $R = (t_{n-1},t_n)\times K$, $n=1,\ldots ,N$, with

$$\begin{aligned} \eta _{\text { res},1,K}^2&= \frac{1}{2} \big \Vert M_h^{1/2}({{\textbf {u}} }_h(0)-{{\textbf {u}} }_0)\big \Vert _K^2 + \frac{1}{2} \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_1\big \Vert _K^2 \,,\quad R = (0,t_1)\times K \,,\\ \eta _{\text { res},n,K}^2&= \frac{1}{2} \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_{n-1}\big \Vert _K^2 + \frac{1}{2} \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_n\big \Vert _K^2 \,,\quad R = (t_{n-1},t_n)\times K\\&\qquad 1< n < N \,,\\ \eta _{\text { res},N,K}^2&= \frac{1}{2} \big \Vert M_h^{1/2}[{{\textbf {u}} }_h]_{N-1}\big \Vert _K^2 \,,\quad R = (t_{N-1},T)\times K \,. \end{aligned}$$

Lemma 5

Let ${{\textbf {u}} }\in {\textrm{L}}_2(Q;{{\mathbb {R}}}^m)$ be the weak solution of (2) and ${{\textbf {u}} }_h\in V_h$ the discrete solution of (34). Then, if ${{\textbf {u}} }$ is a strong solution, the error in the DG norm is bounded by

$$\begin{aligned} \big \Vert {{\textbf {u}} }-{{\textbf {u}} }_h\big \Vert _{h,\textrm{DG}}&\le \Big ( \eta _{\text { res},h}^2 + \big \Vert M_h^{1/2}({{\textbf {u}} }_h(T)-{{\textbf {u}} }(T))\big \Vert _\Omega ^2 \\&\qquad + 2\,\big \Vert h^{1/2}M_h^{-1/2}(M-M_h)\partial _t{{\textbf {u}} } \big \Vert _{Q_h}^2 \Big )^{1/2} \!\!. \end{aligned}$$

Fig. 1

Convergence test for the first experiment with $\gamma = 0.5$ and ${{\textbf {m}} } = (0,1)^{\textsc {t}}$

6 Numerical Experiments

The convergence estimates in the DG norm are illustrated by numerical experiments for acoustics (4) for cases where the exact solution is know which is then used for Dirichlet boundary conditions. The results for uniform refinement are compared with a simple adaptive strategy by increasing the polynomial degree for $\eta _{\text {res},R}\ge \theta _1 \max \limits _{R'}\eta _{\text { res},R'}$ and decreasing the polynomial degree for $\eta _{\text { res},R}\le \theta _0 \max \limits _{R'}\eta _{\text { res},R'}$, see [6] for details. In addition, we consider an example motivated from the application to seismic imaging where the exact solution is not known, and the convergence is demonstrated with respect to the residual error indicator.

Experiment 1 We test the convergence of the solution in $Q = (0,1) \times (0,1)^2$ and ${{\textbf {f}} } = {\textbf {0}}$ with smooth initial value and piecewise constant material

$$\begin{aligned} \varrho ({{\textbf {x}} }) = {\left\{ \begin{array}{ll} 1 ~ &{}{{\textbf {x}} }\cdot {{\textbf {m}} }\le \gamma \,,\\ 2 &{} {{\textbf {x}} }\cdot {{\textbf {m}} }> \gamma \,,\\ \end{array}\right. } \quad \kappa ({{\textbf {x}} }) = 1/\varrho ({{\textbf {x}} }) \,, \ \gamma \in (0,1)\,,\ {{\textbf {m}} }\in {\mathbb {R}}^2\,,\ {{\textbf {m}} }\cdot {{\textbf {m}} } = 1 \,, \end{aligned}$$

so that the impedance is constant across the interface. We start with

$$\begin{aligned} {{\textbf {u}} }_0({{\textbf {x}} }) = a_0({{\textbf {x}} }\cdot {{\textbf {m}} }) \begin{pmatrix} 1 \\ {{\textbf {m}} }\end{pmatrix} \qquad \text {with} \quad a_0(x) = {\left\{ \begin{array}{ll} \sin (3\pi x)^2 &{} x \in [0,1/3] \\ 0 &{}\text {else.} \end{array}\right. } \end{aligned}$$

Then, the solution is given by $\displaystyle {{\textbf {u}} }(t,{{\textbf {x}} }) = {\left\{ \begin{array}{ll} {{\textbf {u}} }_0({{\textbf {x}} } - t {{\textbf {m}} }) &{} {{\textbf {x}} }\cdot {{\textbf {m}} }\le \gamma \,,\\ {{\textbf {u}} }_0(2{{\textbf {x}} } - (t+2/3) {{\textbf {m}} }) ~ &{} {{\textbf {x}} }\cdot {{\textbf {m}} }> \gamma \,. \end{array}\right. }$

Fig. 2

Convergence test for the first experiment with $\gamma = 4/7$ and m =(0.8,0.6)$^{\textsc {t}}$

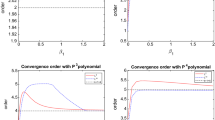
Case a) If the material interface is resolved by the mesh ($M = M_h$), we observe for linear approximations in space and time on uniformly refined meshes the expected convergence rate in the DG norm (Fig. 1). For this configuration also the dual problem is smooth which results in better convergence rates for the ${\textrm{L}}_2$ error, in particular in the adaptive case.

Case b) If the material interface cannot be resolved by the mesh ($M \ne M_h$), the consistency error gets relevant, which is observed by the results in Fig. 2.

Although the material interface cannot be resolved by the mesh, the solution is sufficiently smooth so that the approximation error of the material data $M_h-M$ can be estimated by Rem. 10. We observe nearly optimal convergence in the DG norm, but now the ${\textrm{L}}_2$ convergence gets worse in comparison with the first case.

In both cases, the convergence of ${{\textbf {u}} }(T) - {{\textbf {u}} }_h(T)$ in ${\textrm{L}}_2$ is faster than the convergence in the DG norm, and the residual error indicator yields results close to the error in the DG norm; this confirms the estimate in Lem. 5. We observe that adaptivity provides better solutions with a substantial reduction of the required problem size $\dim V_h$ to achieve a certain accuracy. Therefore a single adaptive step is sufficient, where the polynomial degree in space and time is increased for $\eta _{\text { res},R} \ge \vartheta _1 \max _{R'\in \mathrm R_h} \eta _{\text { res},R'}$ and decreased for $\eta _{\text { res},R} \le \vartheta _0 \max _{R'\in \mathrm R_h}\eta _{\text { res},R'}$, depending on $\vartheta _1>\vartheta _0 > 0$. Note that this results in a different refinement pattern in every time interval, and a simple refinement in space is not sufficient for a strong reduction of the required degrees of unknowns. Here, we select $\vartheta _1 = 0.3$ and $\vartheta _0 = 0.02$, and in the figures for the adaptive results the mesh size is logarithmically interpolated depending on the degrees of freedom.

Experiment 2 At next, we test the convergence of a Riemann problem in $Q = (0,1/2) \times (-1,1) \times (0,1)$ with ${{\textbf {f}} } = {\textbf {0}}$, where the solution is given by

$$\begin{aligned} {{\textbf {u}} }(t,{{\textbf {x}} }) = {\left\{ \begin{array}{ll} \begin{pmatrix} 0 \\ {\textbf {0}} \end{pmatrix} &{} {{\textbf {x}} } \cdot {{\textbf {m}} }< -t\,,\\ \begin{pmatrix} 1 \\ {{\textbf {m}} }\end{pmatrix} &{} -t< {{\textbf {x}} } \cdot {{\textbf {m}} }< t\,,\\ \begin{pmatrix} 1 \\ {\textbf {0}} \end{pmatrix}&t < {{\textbf {x}} } \cdot {{\textbf {m}} } \,, \end{array}\right. } \quad {{\textbf {m}} }= \begin{pmatrix} 0.8 \\ 0.6\end{pmatrix} \,, \quad \kappa = 1\,,\quad \varrho = 1 \,. \end{aligned}$$

Then, $L{{\textbf {u}} }= {\textbf {0}}$, so that ${{\textbf {u}} }$ is a strong solution, and since the condition in Rem. 9 applies, we obtain convergence in the limit by Thm. 2. On the other hand, the solution is piecewise discontinuous, so that the smoothness assumption in Thm. 3 is not satisfied.

Fig. 3

Convergence test for the Riemann Problem

We also observe convergence, cf. Fig. 3, but with a reduced rate ${\mathcal {O}}(h^{1/3})$. In particular, the rate is not improved for the ${\textrm{L}}_2$ error, and simple adaptivity is not sufficient to increase the efficiency.

Here, the solution is not smooth, and the results do not improve if the material parameters are aligned with the mesh. Moreover, further tests show that the convergence order of approximately ${\mathcal {O}}(h^{0.4})$ in the DG norm cannot be improved by adaptivity, which indicates that without sufficient regularity and jumps along the characteristics the DG norm is not appropriate for a qualitative convergence analysis, as it is possible for point singularities, see [2]. Then, the convergence analysis requires high regularity in weighted Sobolev spaces.

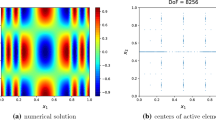
Experiment 3 In our final example we test the space-time method for the forward problem in seismic imaging. Here, we only consider 2d acoustics in $\Omega = (0,10)\times (0,3)$ and $I=(0,4)$ with homogeneous initial and Neumann boundary conditions. For this test we use a piecewise constant right-hand side $b(t,{\textbf {x}} ) = 1$ for $(t,{{\textbf {x}} })\in (0,0.5)\times (0.25,0.75)\times (0,0.5)$ and $b = 0$ else.

Fig. 4

Convergence test for a forward problem in seismic imaging in a truncated space-time domain

The configuration, the distribution of the the piecewise constant parameters $\varrho$ and $\kappa$, and the parallel solution framework in M++ are described in detail in [8]. Since in this application only the evaluation in a small measurement region $(4.75,7.25)\times (0,0.4)\subset \Omega$ is of interest, the space-time domain can be truncated, see [10, Lem. 2]. Here the convergence is only tested by evaluating the residual error indicator on uniformly refined meshes and for one and two p-adaptive steps with $\theta _0 = 0.01$ and $\theta _1 = 0.1$. Since all data are aligned with the mesh but discontinuous, the regularity of the solution is limited. We observe approximately linear convergence with respect to the estimate of the DG norm, and again we observe improved convergence by space-time adaptivity, cf. Fig. 4.

7 Conclusion and Outlook

The convergence analysis in the DG norm only assumes regularity of the space-time solution ${{\textbf {u}} }$ in ${\textrm{H}}^1(Q;{{\mathbb {R}}}^m)$; this implies regularity of the solution ${{\textbf {u}} }(t_n)$ at all time steps in ${\textrm{H}}^{1/2}(\Omega ;{{\mathbb {R}}}^m)$. This clearly extends convergence results with respect to the graph norm, where the analysis requires higher regularity. Moreover, the simple residual error indicator yields estimates very close to the error in the DG norm. On the other hand, for discontinuous Riemann problems we can prove only convergence in the limit, and the numerical experiments demonstrate that we obtain convergence in ${\textrm{L}}_2$ but with a reduced rate, which can be improved by adaptivity in ${\textrm{L}}_2$ but not in the DG norm.

All our estimates rely on a Hilbert space setting. This may be not appropriate for hyperbolic systems, and numerical tests demonstrate better convergence rates in ${\textrm{L}}_1(Q;{{\mathbb {R}}}^m)$, but a corresponding analysis remains an open problem.