A Time-Continuous Embedding Method for Scalar Hyperbolic Conservation Laws on Manifolds

Abstract

A time-continuous (tc-)embedding method is first proposed for solving nonlinear scalar hyperbolic conservation laws with discontinuous solutions (shocks and rarefaction waves) on codimension 1, connected, smooth, and closed manifolds (surface PDEs or SPDEs in ${\mathbb {R}}^2$ and ${\mathbb {R}}^3$). The new embedding method improves upon the classical closest point (cp-)embedding method, which requires re-establishments of the constant-along-normal (CAN-)property of the extension function at every time step, in terms of accuracy and efficiency, by incorporating the CAN-property analytically and explicitly in the embedding equation. The tc-embedding SPDEs are solved by the second-order nonlinear central finite volume scheme with a nonlinear minmod slope limiter in space, and the third-order total variation diminished Runge-Kutta scheme in time. An adaptive nonlinear essentially non-oscillatory polynomial interpolation is used to obtain the solution values at the ghost cells. Numerical results in solving the linear wave equation and the Burgers’ equation show that the proposed tc-embedding method has better accuracy, improved resolution, and reduced CPU times than the classical cp-embedding method. The Burgers’ equation, the traffic flow problem, and the Buckley-Leverett equation are solved to demonstrate the robust performance of the tc-embedding method in resolving fine-scale structures efficiently even in the presence of a shock and the essentially non-oscillatory capturing of shocks and rarefaction waves on simple and complex shaped one-dimensional manifolds. Burgers’ equation is also solved on the two-dimensional torus-shaped and spherical-shaped manifolds.

1 Introduction

Partial differential equations on a surface (surface PDEs or SPDEs) have received growing interest over the last years. Problems of interest areas arise in a wide range of fields such as image processing (e.g., the restoration of a damaged pattern on a surface [4] and image of the human brain [24]), biological systems (e.g., study domain formation in vesicles [2] and wound healing process [27]), mathematical physics (e.g., flows and solidification on surfaces [25, 26]) and computer graphics (e.g., real-time fluid visualization on surfaces [1]).

Instead of studying linear and quasi-linear SPDEs with smooth solutions ( [12, 14] for level set approach, [31] for a semi-Lagrangian method, [37] for meshfree finite difference method, [3, 7, 10, 22, 28,29,30] for closest point (cp-)embedding methods) on Cartesian grids and orthogonal gradient grids, as a proof of concept, this study explores the application of the embedding methods and develops a numerical scheme, based on our extensive knowledge of essentially non-oscillatory shock-capturing schemes, to solve the (nonlinear scalar) hyperbolic conservation laws (Burgers’ equation) with a discontinuous solution on one-dimensional manifolds. For the rest of the paper, the manifold is implicitly referred to as the one-dimensional, connected, smooth, closed, and complex (or simple) manifold unless specified otherwise.

After reviewing some necessary definitions and assumptions in Sec. 2, we propose a new time-continuous (tc-)embedding method based on the classical closest point (cp-)embedding in [30] in Sect. 3. The new tc-embedding method improves upon the classical cp-embedding method, which requires re-establishments of the constant-along-normal (CAN-)property of the extension function at every time step, in terms of accuracy and efficiency by incorporating the CAN-property analytically and explicitly in the embedding equation. The tc-embedding SPDEs are solved by the second-order nonlinear central finite volume scheme (CFV) with a nonlinear minmod slope limiter in space, and the third-order total variation diminished Runge–Kutta scheme (RK-TVD) in time. An adaptive nonlinear essentially non-oscillatory polynomial (ENO) interpolation is used to obtain the solution values at the ghost cells required by the CFV scheme. The main contributions of this study are in the following two areas. They are i) a novel time-continuous (tc-)embedding that holds for all time continuously in contrast to the classical cp-embedding that is only true at a fixed time (see Theorem 1 for the formal statement), and ii) the first attempt in solving hyperbolic SPDEs with discontinuous solutions on a manifold. In Sect. 4, we detail a numerical recipe (CFV, RK-TVD, and ENO interpolation) for solving the resulting embedded SPDEs. In Sect. 5.1, accuracy and efficiency tests of the tc-embedding method versus the cp-embedding method are given. The results indicate that the tc-embedding method has a lesser numerical dissipation, resolves the fine-scale structures more efficiently, and is roughly two and half times faster CPU times than the cp-embedding method. In Sect. 5.2, the Burgers’ equation with convex flux, the traffic flow problem with concave flux, and the Buckley-Leverett equation with non-convex flux demonstrate the essentially non-oscillatory shock-capturing property and the efficient resolution of fine-scale structures of the tc-embedding method on a complex manifold. In Sect. 5.3, numerical results are also given for extending the tc-embedding method for solving the Burgers’ equation on two-dimensional torus-shaped and spherical-shaped manifolds embedded in ${\mathbb {R}}^3$. Conclusion and future works are given in Sect. 6.

2 PDEs on Manifolds

Let ${\mathcal {M}}\subseteq {\mathbb {R}}^2$ be a (one-dimensional, connected, smooth, and closed) manifold with well-defined unit outward normal vector and tangent space, denoted by ${\hat{\textbf{n}}}\in {\mathbb {R}}^2$ and ${{{\mathcal {T}}}}_{\mathcal {M}}$, respectively, for every point ${\varvec{p}}\in {\mathcal {M}}$.

Also, let $Q_{\mathcal {M}}:{\mathcal {M}}\times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}$ be some conserved variables associated with a smooth flux function $F:{\mathbb {R}}\rightarrow {\mathbb {R}}$. In this paper, we consider SPDEs of scalar hyperbolic type for the unknown conserved function $Q_{\mathcal {M}}\in H^1(H^2({\mathcal {M}});[0,T])$ in the form of

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial }{\partial t} Q_{\mathcal {M}}+ {{\varvec{v}}}_{\mathcal {M}}{{\,{\varvec{\cdot }}\,}}\nabla _{\mathcal {M}}F(Q_{\mathcal {M}}) = 0, &{}\qquad \hbox {on}\,\, {\mathcal {M}}\hbox {,}\,\, t\in (0,T], \\ Q_{\mathcal {M}}({{\,{\varvec{\cdot }}\,}},0) ~= Q_{{\mathcal {M}},0}, &{}\qquad \hbox {on}\ \,\mathcal {M},\, \end{array} \right. \end{aligned}$$

(1)

for some known vector field ${{\varvec{v}}}_{\mathcal {M}}: {\mathcal {M}}\rightarrow {{{\mathcal {T}}}}_{\mathcal {M}}$. The surface gradient operator $\nabla _{\mathcal {M}}$ in (1) can be defined as

$$\begin{aligned} \nabla _{\mathcal {M}}:= (I_{2\times 2} -{\hat{\textbf{n}}}{\hat{\textbf{n}}}^T) \nabla , \end{aligned}$$

(2)

in terms of the standard Euclidean gradient $\nabla$ in ${\mathbb {R}}^2$ via projections to ${{{\mathcal {T}}}}_{\mathcal {M}}$.

2.1 Embedded PDEs

For some $\delta >0$, we begin by defining the narrow band domain around the manifold by

$$\begin{aligned} \Omega : = \left\{ {{\varvec{x}}}\in {\mathbb {R}}^2:\, \inf _{{\varvec{p}}\in {\mathcal {M}}} \Vert {{\varvec{x}}}-{\varvec{p}}\Vert < \delta \right\} \supseteq {\mathcal {M}}. \end{aligned}$$

(3)

The goal of this section is to recast the well-posed PDEs on ${\mathcal {M}}$ in (1) in $\Omega$. Firstly, we need the relationship between surface and Euclidean gradient operators on time-independent functions on the manifold and their extensions.

Proposition 1

([9]) Let ${\mathcal {M}}$ be $C^3$-smooth and $q_E\in (C^2\cap H^{2+\frac{1}{2}})(\Omega )$ be an extension of some manifold function $q_{\mathcal {M}}\in H^2({\mathcal {M}})$ with $q_E|_{{\mathcal {M}}}=q_{\mathcal {M}}$, then we have

$$\begin{aligned} \nabla _{\mathcal {M}}q_{\mathcal {M}}= \nabla q_E - {\hat{\textbf{n}}}\frac{\partial }{\partial {\hat{\textbf{n}}}} q_E, \qquad \textrm{on}~ {\mathcal {M}}. \end{aligned}$$

(4)

Proposition 1 gives a strong motivation to extend manifold functions $Q_{\mathcal {M}}$ to $Q_E$ in such a way that the normal-derivative $\partial _{\hat{\textbf{n}}}Q_E$ remains zero everywhere on ${\mathcal {M}}$. Note that this is not yet a unique extension operator.

Before proceeding, let us define the closest point mapping ${{\text {cp}}}: \Omega \subset {\mathbb {R}}^2 \rightarrow {\mathcal {M}}$ by

$$\begin{aligned} {{\text {cp}}}({{\varvec{x}}})=\underset{{\varvec{p}}\in {\mathcal {M}}}{\arg \inf }\ \Vert {\varvec{p}}-{{\varvec{x}}}\Vert _{\ell ^2({\mathbb {R}}^2)}, \end{aligned}$$

(5)

on $\Omega$ in (3) with some sufficiently small $\delta$ [30]. The existence of such $\Omega$, in which ${{\text {cp}}}$ is well-defined, is guaranteed provided that ${\mathcal {M}}$ has enough smoothness; see [8]. For any (time-independent) manifold function $Q_{\mathcal {M}}\in {\mathcal {M}}\rightarrow {\mathbb {R}}$, the constant-along-normal (CAN) extension is given by

$$\begin{aligned} Q_{{{\text {cp}}}}:= Q_{\mathcal {M}}\circ {{\text {cp}}}: \Omega \rightarrow {\mathbb {R}}, \end{aligned}$$

(6)

whose function value is constant along with normal directions of ${\mathcal {M}}$.

So far, we follow the setting of the closest point embedding method [30]. For any fixed $t_0\ge 0$, the SPDEs in (1) can be embedded to $\Omega \supset {\mathcal {M}}$ using CAN-extension $Q_{{\text {cp}}}$ to $Q_{\mathcal {M}}(\cdot , t_0)$ and yield

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial }{\partial t} Q_{{{\text {cp}}}} + ({{\varvec{v}}}_{{\mathcal {M}}}\circ {{\text {cp}}}) {{\,{\varvec{\cdot }}\,}}\nabla {F}(Q_{{{\text {cp}}}}) = 0,&{} \qquad \hbox {in}\;\Omega \;\hbox {,}\quad t=t_0, \\ Q_{{\text {cp}}}({{\,{\varvec{\cdot }}\,}},t_0) = {Q_{{\mathcal {M}}}}({{\text {cp}}}({{\,{\varvec{\cdot }}\,}}),t_0), &{}\qquad \text{ in } \Omega , \\ \displaystyle \frac{\partial }{\partial {\hat{\textbf{n}}}} Q_{{{\text {cp}}}}~ = 0, &{}\qquad \hbox {on}\,\, \partial \Omega \;\hbox {,}\quad t=t_0. \end{array}\right. \end{aligned}$$

(7)

Since the CAN-property of $Q_{{{\text {cp}}}}$ carries over to ${F}(Q_{{{\text {cp}}}})$, Proposition 1 ensures that

$$\begin{aligned} \nabla _{\mathcal {M}}{F}(Q_{\mathcal {M}})=\big (\nabla {F}(Q_{{{\text {cp}}}})\big )|_{{\mathcal {M}}} \qquad \hbox {on}\,\, {\mathcal {M}}\,\, \hbox {and}\,\, t=t_0. \end{aligned}$$

(8)

The solution of the embedded PDEs (7), when restricted to the surface ${\mathcal {M}}$, coincides with the solution of the SPDEs (1) with $Q_{{\mathcal {M}}}({{\,{\varvec{\cdot }}\,}},t_0)=Q_{{{\text {cp}}}}({{\,{\varvec{\cdot }}\,}},t_0)|_{\mathcal {M}}$ at the fixed $t_0$.

Numerically, the spatial operator (in this case, the gradient of the flux) in the embedded PDEs (7) can be discretized by any finite volume scheme. The resulting semi-discrete temporal ODEs can be integrated to advance the solution of the SPDEs (1) near the surface of the manifold for one time step (or one stage of a multi-stage Runge-Kutta scheme). Note that there is no temporal treatment in this formulation. More precisely, once (7) is advanced in time, the numerical solution $Q_{{{\text {cp}}}}({{\,{\varvec{\cdot }}\,}},t_0+\triangle t)$ will violate the CAN-property for any $\triangle t>0$. An interpolation process of all grid points is needed to reconstruct the CAN-property of the numerical solution, which is mathematically equivalent to constructing a new CAN-extension based on $Q_{{\mathcal {M}}}({{\,{\varvec{\cdot }}\,}},t_0+\triangle t)$. This classical (spatial) cp-embedding method was commonly used for solving time-dependent problems, see [21,22,23, 28, 30].

3 Time-Continuous Embedded PDEs

We desire to have the CAN-extension $Q_E$ of the exact solution $Q_{\mathcal {M}}$ to (1) such that

$$\begin{aligned} Q_E({{\varvec{x}}},t):= Q_{\mathcal {M}}( {{\text {cp}}}({{\varvec{x}}}),t) \qquad \text{ for } {{\varvec{x}}}\in \Omega \hbox { and } t\in [0,T], \end{aligned}$$

(9)

and solve the tc-embedded PDEs in the form of

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial }{\partial t} Q_{E} + {{\varvec{v}}}_E {{\,{\varvec{\cdot }}\,}}\nabla {F}(Q_E) = 0, &{}\qquad \quad \text{ in } \Omega , t\in (0,T], \\ Q_E({{\,{\varvec{\cdot }}\,}},0) = Q_{\mathcal {M}}({{\text {cp}}}({{\,{\varvec{\cdot }}\,}}),0), &{}~~\qquad \hbox { in}\ \Omega , \\ \displaystyle \frac{\partial }{\partial {\hat{\textbf{n}}}} Q_E~= 0, &{}\qquad ~~~ \hbox {on}~ \partial \Omega \hbox {,}\,\, t\in (0,T], \end{array}\right. \end{aligned}$$

(10)

where ${{\varvec{v}}}_{E}=(u,v)$ is the vector field with u and v as its x- and y-direction components, respectively, defined in the Theorem (1) below. For clarity of later discussion, we define the continuous spatial operator ${{\mathcal {L}}}$ as

$$\begin{aligned} {{\mathcal {L}}}(Q_E):={{\varvec{v}}}_E {{\,{\varvec{\cdot }}\,}}\nabla {F}(Q_E)=u \frac{\partial {F}(Q_E)}{\partial x}+v \frac{\partial {F}(Q_E)}{\partial y}, \end{aligned}$$

(11)

and (10) can be written compactly as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial }{\partial t} Q_{E} + {{\mathcal {L}}}(Q_E) = 0, &{}\qquad ~\hbox {in}\, \Omega \hbox {,}\quad \, t\in (0,T], \\ Q_E({{\,{\varvec{\cdot }}\,}},0)= Q_{\mathcal {M}}({{\text {cp}}}({{\,{\varvec{\cdot }}\,}}),0), &{}\qquad \hbox { in}\, \Omega , \\ \displaystyle \frac{\partial }{\partial {\hat{\textbf{n}}}} Q_E = 0,&{}\qquad ~\hbox {on}\,\, \partial \Omega \;\hbox {,}\quad \,t\in (0,T]. \end{array}\right. \end{aligned}$$

(12)

Although the notation difference between (7) and (12) is small, the implication is huge in the computational aspect. Instead of embedding the original problem (1) in the form of (7) at every time step, we only need to tc-embed (1) once and solve (12) until we reach the final time T. It is because, as shown later, the extended velocity field ${{\varvec{v}}}_E$ depends exclusively on the geometric properties of the manifold, which is time-independent in this study.

One can easily see that the requirement (9) implies

$$\begin{aligned} \frac{\partial }{\partial t} Q_{E}({{\varvec{x}}},t) =\frac{\partial }{\partial t} Q_{\mathcal {M}}( {{\text {cp}}}({{\varvec{x}}}),t), \quad {{\varvec{x}}}\in \;\Omega , \quad t \ge 0. \end{aligned}$$

The realization of the proposed tc-embedding hence lies on finding an appropriate extended velocity field ${{\varvec{v}}}_E:\Omega \rightarrow {\mathbb {R}}^2$ to the vector field ${{\varvec{v}}}_{\mathcal {M}}:{\mathcal {M}}\rightarrow {\mathbb {R}}^2$. To do so, we define the signed-distance function ${\text {dist}}:\Omega \times {\mathcal {M}}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\text {dist}}({{\varvec{x}}},{{\text {cp}}}({{\varvec{x}}})):= \text {sign}\big ({\hat{\textbf{n}}}{{\,{\varvec{\cdot }}\,}}({{\varvec{x}}}- {{\text {cp}}}({{\varvec{x}}})) \big ) \Vert {{\varvec{x}}}-{{\text {cp}}}({{\varvec{x}}})\Vert _{\ell ^2({\mathbb {R}}^2)}. \end{aligned}$$

Now, the following theorem provides the mean to adjust the extended velocity field ${{\varvec{v}}}_E$ so that the CAN-property of $Q_E$ is preserved over time.

Theorem 1

Suppose that ${\mathcal {M}}$ is smooth enough and $\Omega$ in (3) is chosen so that Proposition 1 holds. For any $q:\Omega \rightarrow {\mathbb {R}}$ to be any (time-independent) $C^1$-function satisfying the CAN-property with respect to the manifold ${\mathcal {M}}$. If an extended velocity field ${{\varvec{v}}}_E:\Omega \rightarrow {\mathbb {R}}^2$ to ${{\varvec{v}}}_{\mathcal {M}}$ in (1) defined by

$$\begin{aligned} {{\varvec{v}}}_E({{\varvec{x}}}):= \Big (1+{\text {dist}}\big ({{\varvec{x}}},{{\text {cp}}}({{\varvec{x}}})\big ) \tilde{\kappa }({{\text {cp}}}({{\varvec{x}}})) \Big ){{\varvec{v}}}_{\mathcal {M}}({{\text {cp}}}({{\varvec{x}}}) ), \quad {{\varvec{x}}}\in \Omega , \end{aligned}$$

(13)

where $\kappa ({{\text {cp}}}({{\varvec{x}}}))$ and $\tilde{\kappa }({{\text {cp}}}({{\varvec{x}}}))$ denoting the absolute and signed curvature of ${\mathcal {M}}$ at ${{\text {cp}}}({{\varvec{x}}})$, respectively, finite and exist, then

$$\begin{aligned} {{\varvec{v}}}_{\mathcal {M}}({{\text {cp}}}({{\varvec{x}}}) ){{\,{\varvec{\cdot }}\,}}\nabla _{\mathcal {M}}q ( {{\text {cp}}}({{\varvec{x}}}) ) = {{\varvec{v}}}_E({{\varvec{x}}}){{\,{\varvec{\cdot }}\,}}\nabla q ({{\varvec{x}}}). \end{aligned}$$

(14)

Proof

Due to the CAN-property, it suffices to show that

$$\begin{aligned} {{\varvec{v}}}_{\mathcal {M}}({{\text {cp}}}({{\varvec{x}}}) ){{\,{\varvec{\cdot }}\,}}\nabla q ( {{\text {cp}}}({{\varvec{x}}}) ) = {{\varvec{v}}}_E({{\varvec{x}}}){{\,{\varvec{\cdot }}\,}}\nabla q ({{\varvec{x}}}), \end{aligned}$$

for any fixed ${{\varvec{x}}}\in \Omega \supset {\mathcal {M}}$. Note that the right-hand side of (14) is a ${{\varvec{v}}}_{\mathcal {M}}$-directional derivative of q at ${{\text {cp}}}({{\varvec{x}}})\in {\mathcal {M}}$. Consider a (local) arc-length parameterization ${\varvec{\gamma }}(s)$ of the manifold ${\mathcal {M}}$ defined by its arc-length variable $s\in {\mathcal {N}}_\epsilon (0)$ in some $\epsilon$-neighborhood around the origin with ${\varvec{\gamma }}(0)={{\text {cp}}}({{\varvec{x}}})$ and orientation given by the unit tangent vector $\frac{d}{d s} {\varvec{\gamma }}(0)= {{\varvec{v}}}_{\mathcal {M}}/\Vert {{\varvec{v}}}_{\mathcal {M}}\Vert =: {\hat{\textbf{T}}}(0)$. Now we have

$$\begin{aligned} {{\varvec{v}}}_{\mathcal {M}}({{\text {cp}}}({{\varvec{x}}})){{\,{\varvec{\cdot }}\,}}\nabla q({{\text {cp}}}({{\varvec{x}}})) = \Vert {{\varvec{v}}}_{\mathcal {M}}({{\text {cp}}}({{\varvec{x}}})) \Vert \, \frac{\partial }{\partial {\hat{\textbf{T}}}} q({{\text {cp}}}({{\varvec{x}}})). \end{aligned}$$

(15)

Obviously, ${{\varvec{v}}}_E$ must point to the ${\hat{\textbf{T}}}$ direction. We only need to study the scaling effect when the point of evaluation in the directional-derivative $\frac{\partial }{\partial {\hat{\textbf{T}}}}q$ is shifted from ${{\text {cp}}}({{\varvec{x}}})$ to ${{\varvec{x}}}$.

Let $D:={\text {dist}}\big ({{\varvec{x}}},{{\text {cp}}}({{\varvec{x}}})\big )$, that is a fixed real number because ${{\varvec{x}}}$ is considered as fixed. Since the outward unit normal vector ${\hat{\textbf{n}}}({{\text {cp}}}({{\varvec{x}}}))={\hat{\textbf{n}}}({\varvec{\gamma }}(0))$ of ${\mathcal {M}}$ depends on the orientation of the manifold (definition of counterclockwise) and the normal vector ${\hat{\textbf{N}}}(0)$ obtained from ${\varvec{\gamma }}(s)$ depends on the orientation of the curve ${\varvec{\gamma }}(s)$, we have

$$\begin{aligned} {{\varvec{x}}}={\varvec{\gamma }}(0)+D{{\hat{\textbf{n}}}}({\varvec{\gamma }}(0))={\varvec{\gamma }}(0)\pm D{\hat{\textbf{N}}}(0). \end{aligned}$$

We begin by considering the directional derivative as a derivative on ${\varvec{\gamma }}(s)$, i.e., Gateaux derivative, and shifted the point of evaluation using the CAN-property as follows:

$$\begin{aligned} \frac{\partial }{\partial {\hat{\textbf{T}}}} q\big ({{\text {cp}}}({{\varvec{x}}})\big ):= & {} \lim _{h\rightarrow 0} \frac{q\big ( {\varvec{\gamma }}(h)\big )-q\big ({\varvec{\gamma }}(0)\big )}{h} \\= & {} \lim _{h\rightarrow 0} \frac{q\big ( {\varvec{\gamma }}(h) \pm D{\hat{\textbf{N}}}(h) \big )-q\big ({\varvec{\gamma }}(0)\pm D{\hat{\textbf{N}}}(0)\big )}{h} \\= & {} \lim _{h\rightarrow 0} \frac{q\big ( {{\varvec{x}}}+ h\{{\hat{\textbf{T}}}(0) \pm D {\hat{\textbf{N}}}'(0)\} + {\mathcal {O}}(h^2) \big )-q\big ({{\varvec{x}}}\big )}{h} \\=: & {} \Big \Vert {\hat{\textbf{T}}}(0) \pm D {\hat{\textbf{N}}}'(0) \Big \Vert \, \frac{\partial }{\partial {\hat{\textbf{T}}}} q\big ({{\varvec{x}}}\big ). \end{aligned}$$

The last equality uses another definition for directional derivative based on the rate of change in the direction ${\hat{\textbf{T}}}\pm D{\hat{\textbf{N}}}'$, i.e., Fréchet derivative. Using the Frenet-Serret formula and the fact that ${\mathcal {M}}$ is planar, we find that

$$\begin{aligned} \big \Vert {\hat{\textbf{T}}}(s)\pm D {\hat{\textbf{N}}}'(s) \big \Vert =\big \Vert {\hat{\textbf{T}}}(s)\pm D \kappa (s) {\hat{\textbf{T}}}(s) \big \Vert = 1+D \tilde{\kappa }(s),\qquad \text{ for } s\in {\mathcal {N}}_\epsilon (0). \end{aligned}$$

(16)

The scaling factor we desired is given by (16) at $s=0$, and hence, the formula for ${{\varvec{v}}}_E$ in (13) is deduced. $\square$

In the proof above, we have used the definition of the absolute and signed curvatures, that is, $\tilde{\kappa }({{\text {cp}}}({{\varvec{x}}})) = \pm \kappa ({{\text {cp}}}({{\varvec{x}}}))$. Once again, if the ${{\varvec{v}}}_{\mathcal {M}}\circ {{\text {cp}}}({{\varvec{x}}})$ does not change in time, ${{\varvec{v}}}_E$ in (13) is time-independent. It can be pre-computed once at each point ${{\varvec{x}}}$ in the initialization stage of the algorithm and used subsequently in the time-stepping scheme.

Now that the embedding process is completed solving the SPDEs (1) can be transformed into solving the tc-embedded PDEs (12) in a narrow computational domain $\Omega$ with any suitable spatial solver in the two-dimensional Euclidean space. In the coming sections, we will describe the tc-embedding method for solving (12) based on the governing equations and the CAN-property in its solution, i.e., instead of the zero Neumann boundary conditions. Using this alternative approach, we propose an easy recipe to propagate non-smooth solutions on one-dimensional manifolds.

4 Implementation of the Tc-Embedding Method

This section will describe the numerical method in solving tc-embedded PDEs (12) with the spatial operator ${{\mathcal {L}}}$ (11) in a computational tube of radius $\delta$.

Fig. 1

Simple illustration of the distribution of data points $\varvec{X}= { \varvec{X}_I} \bigcup { \varvec{X}_G} \subset \Omega$ in the computational tube with the sets of interior $\varvec{X}_I$ (blue) and ghost $\varvec{X}_G$ (red) points. The black line represents the manifold ${\mathcal {M}}$ (Color figure online)

We shall denote the computational domain in the two-dimensional Cartesian domain as $\Omega$ (bounded within two pink lines) where the one-dimensional manifold ${\mathcal {M}}$ (black line) is embedded inside as illustrated in Fig. 1 with a circular manifold. With the Cartesian domain $\Omega$, we discretize the domain with uniformly spaced computational cells with cell sizes ${{\triangle x}}$ and ${{\triangle y}}$ in the horizontal x-direction and the vertical y-direction, respectively. In Fig. 1, the cell centers ${{\varvec{x}}}= (x_i, y_j)$ are shown. Following the suggestion in [28], we restrict the computational tube radius $\delta$ to be

$$\begin{aligned} \delta \ge \max \left( p\sqrt{{{\triangle x}}^2+{{\triangle y}}^2} + p/2\max ({{\triangle x}},{{\triangle y}}), \delta ^* \right) , \end{aligned}$$

(17)

where the critical radius $\delta ^*$ satisfies the condition $\delta ^* \max \{\kappa ({{\varvec{x}}}):{{\varvec{x}}}\in {\mathcal {M}}\}< 1$, where $\kappa$ is the curvature of ${\mathcal {M}}$. Since we will be using a second-order finite volume scheme (CFV) and a second-order ENO interpolation, to solve (12) at a given ${{\varvec{x}}}= (x_i, y_j)$ (excluding the ghost cells), the computational stencil is $p=2$ cells in all directions. This lower bound of $\delta$ ensures that there is always a sufficient number of computational cells available in the neighborhood of a given cell center ${{\varvec{x}}}$ to perform the necessary spatial operations given the order of the numerical scheme p.

Together, as illustrated in Fig. 1, we define a set of uniform spaced cell center (grid) points $(x_i, y_j)$ with cell size ${{\triangle x}}$ and ${{\triangle y}}$ in $\Omega$ by

$$\begin{aligned} \varvec{X}:= \Omega \cap \left( ({{\triangle x}}\, {\mathbb {Z}}) \otimes ({{\triangle y}}\, {\mathbb {Z}}) \right) , \end{aligned}$$

(18)

contained inside the computational tube of radius $\delta$. The set $\varvec{X}$ is further sub-divided into two subsets;

• The set of interior cells (blue solid symbol) ${ \varvec{X}_I}:=\{ {{\varvec{x}}}\in \varvec{X}\,:\,\text{ for } \text{ computing } \text{ the } \text{ flux } \text{ gradient } \text{ in }(11) \}$,

• The set of ghost cells (red hollow symbol)

  ${ \varvec{X}_G}:=\varvec{X}\setminus { \varvec{X}_I}$.

Ghost cells $\varvec{X}_G$ are near-boundary cells that cannot be updated due to missing stencil’s information, but are needed to compute the flux gradients in (11) for those cells at the edges of $\varvec{X}_I$. The size of $\varvec{X}_G$ generally grows linearly as the spatial order of the scheme. For the second-order scheme used here, one cell is needed inside the domain boundary.

At any given time $t\ge 0$, we can use the available numerical solution $Q_E(\varvec{X},t)$ at $\varvec{X}$ to compute the numerical flux gradient at $\varvec{X}_I$ by

$$\begin{aligned} \nabla {F}(Q_E)\bigg |_{\varvec{X}_I}=\left( \frac{\partial {F}(Q_E)}{\partial x},\frac{\partial {F}(Q_E)}{\partial y} \right) ^T\bigg |_{\varvec{X}_I}, \end{aligned}$$

which will be discussed in greater detail below. Together with the extended velocity field ${{\varvec{v}}}_E =(u,v)$ defined in (13), the semi-discrete approximation ${{\mathcal {L}}}_N$ of the spatial operator ${{\mathcal {L}}}$ defined in (11) becomes

$$\begin{aligned} {{\mathcal {L}}}_N(Q_E)\bigg |_{\varvec{X}_I} = {{\varvec{v}}}_E\bigg |_{\varvec{X}_I} {{\,{\varvec{\cdot }}\,}}\nabla {F}(Q_E)\bigg |_{\varvec{X}_I} = \left( u \frac{\partial {F}(Q_E)}{\partial x}+v \frac{\partial {F}(Q_E)}{\partial y}\right) \bigg |_{\varvec{X}_I}. \end{aligned}$$

(19)

Finally, we obtain the semi-discrete system of ODEs

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d}{d t}{Q_E(\varvec{X}_I,t)} = -{{\mathcal {L}}}_N(Q_E(\varvec{X},t))\bigg |_{\varvec{X}_I},\\ Q_E(\varvec{X},0)~= Q_{\mathcal {M}}({{\text {cp}}}(\varvec{X}),0), \end{array} \right. \end{aligned}$$

(20)

where the initial condition is specified by applying the ${{\text {cp}}}$-mapping to the initial conditions in (1). We note that while the system of ODEs is evaluated only at the interior points $\varvec{X}_I$, the initial condition must be made available in the whole computational tube $\varvec{X}$ that includes the ghost cells $\varvec{X}_G$.

The numerical solution $Q_E(\varvec{X}_I, t)$ of (20) can be solved by advancing in time via the explicit third-order total variation diminishing (TVD) low-storage Runge-Kutta (RK-TVD) scheme [13] from time $t=t_n$ with the discrete solution $Q_I^n=Q_E^{n}(\varvec{X}_I)=Q_E(\varvec{X}_I, t_n)$, to time $t=t_{n+1} = t_n+{{\triangle t}}$ with a time step ${{\triangle t}}$, $Q_I^{n+1} =Q_E^{n+1}(\varvec{X}_I)=Q_E(\varvec{X}_I, t_{n+1})$, $n=0,1,2,\ldots$ as

$$\begin{aligned} \begin{aligned} Q^{(1)}_I&=Q^{n}_I-{{\triangle t}}\, {{\mathcal {L}}}_N\left( Q^{n}_I \right) , \\Q^{(2)}_I&=\frac{3}{4}Q^{n}_I+\frac{1}{4} Q^{(1)}_I-\frac{1}{4}{{\triangle t}}\, {{\mathcal {L}}}_N\left( Q^{(1)}_I\right) , \\Q^{n+1}_I&=\frac{1}{3}Q^{n}_I+\frac{2}{3} Q^{(2)}_I-\frac{2}{3}{{\triangle t}}\, {{\mathcal {L}}}_N\left( Q^{(2)}_I\right) , \end{aligned} \end{aligned}$$

(21)

with the given initial condition $Q^{0}_I = Q_E(\varvec{X}_I,0)$ (20). $\{Q^{(k)}_I = Q_E(\textbf{X}_I, t_k), k = \{1, 2\}\}$ are the intermediate solutions and times ($t_1=t_n+{{\triangle t}}, t_2 = t_n + {{\triangle t}}/2)$ at the kth RK-TVD stage. The time step ${{\triangle t}}$ at each RK-TVD step is determined by the CFL stability condition ${{\triangle t}}\left( \alpha \left| \left| {{\varvec{v}}}_E \cdot \frac{1}{\triangle r}\right| \right| _p\right) =\text {CFL} < 1$, for some $p-$norm ($p=1,2,\infty$) and $\frac{1}{\triangle r}=(\frac{1}{{{\triangle x}}}, \frac{1}{{{\triangle y}}})$, where $\alpha =\displaystyle \max _{{{\varvec{x}}}\in \varvec{X}}\left| {\partial {F}}/{\partial {Q}} \right|$ is the maximum characteristic speed of the hyperbolic conservation laws on $\varvec{X}$. The CFL stability condition for an explicit numerical SPDE solver depends not only on the time step ${{\triangle t}}$, grid spacing $\triangle r$, and spectral radius of the Jacobian of the flux, but also on the geometric properties, namely, curvature $\kappa$ expressed via ${{\varvec{v}}}_E$ (13), of the given manifold. For a manifold with a large curvature $\kappa$, the time step ${{\triangle t}}$ will be reduced accordingly. In the following discussion, for simplicity, we shall take ${{\triangle x}}={{\triangle y}}$ and $\text {CFL}=0.45$ unless stated otherwise. Readers are reminded that $t_k, k=\{1,2\}$ are the intermediate times between the times $t_n$ (at the time step n) and $t_{n+1}$ (at the time step $n+1$).

Since the tc-embedded PDEs (9) with the extended velocity field ${{\varvec{v}}}_E$ satisfies the CAN-property intrinsically, the Neumann boundary condition in (12) is discarded in exchange for finding the solution $Q_E({{\varvec{x}}},t)$ at the ghost cells ${{\varvec{x}}}\in \varvec{X}_G$.

Given the numerical solutions $\{Q_{\varvec{X}}^{(k)}=Q_E(\varvec{X},t_k), k = \{n, 1, 2, n+1\}\}$, the two missing components of the numerical scheme in the discussion are:

• 1. At the beginning of each RK-TVD stage with $k=\{n, 1, 2\}$ and for all ${{\varvec{x}}}\in {\varvec{X}_I}$, computing the flux gradient $\nabla F(Q_E(\varvec{X}_I,t_k))$ using the shock-capturing central finite volume (CFV) scheme with the nonlinear minmod slope limiter (see Sect. 4.1), and

• 2. At the end of each RK-TVD stage with $k=\{1,2,n+1\}$ and for all ${{\varvec{x}}}_g \in {\varvec{X}_G}$, updating the numerical solution for the ghost cells $Q_E(\varvec{X}_G,t_k)$ with the essentially non-oscillatory (ENO) interpolation at $\xi ={{\text {cp}}}({{\varvec{x}}}_g) \in {\mathcal {M}}$, which satisfies the CAN-property, based on a few specially selected $\textbf{Q}_E(\varvec{X}_I,t_k)$ in the closest neighboring cells around $\xi$ (see Sect. 4.2).

4.1 Nonlinear Construction of the Flux Gradient $\nabla F(Q_E(\varvec{X}_I,t_k))$

At any given time $t=t_k, k=\{n,1,2\}$, the numerical flux gradient

$$\begin{aligned} \nabla {F}(Q_E)\bigg |_{\varvec{X}_I} = \left( \frac{\partial {F}(Q_E)}{\partial x},\frac{\partial {F}(Q_E)}{\partial y}\right) ^T\bigg |_{\varvec{X}_I}, \end{aligned}$$

at a given cell center ${{\varvec{x}}}= (x_i,y_j) \in \varvec{X}_I$ is approximated via a second-order shock-capturing nonlinear central finite volume (CFV) scheme with the nonlinear minmod slope limiter [19] in the two-dimensional Euclidean space, which is a class of nonlinear numerical schemes designed for solving nonlinear hyperbolic partial differential equations. Since the computational stencils $\varvec{X}$ are embedded in the Cartesian rectangular domain with uniform cell-sizes ${{\triangle x}}$ and ${{\triangle y}}$ in both x- and y-directions, respectively, the numerical approximation of the flux gradients can be carried out simply in a dimension-by-dimension order. Without loss of generality, we will only briefly describe a generic numerical framework in computing the x-component $\frac{\partial F}{\partial x}$ via a one-dimensional CFV scheme by assuming the solution $Q_E$ and the flux F are functions of x alone and independent of y. The same numerical framework for computing the y-component $\frac{\partial F}{\partial y}$ can be carried out similarly by assuming the solution $Q_E$ and the flux F are functions of y alone and independent of x. Therefore, we will describe the one-dimensional CFV scheme’s generic numerical framework without the burden of irrelevant superscript and subscript notations needed in a multi-dimensional case. Furthermore, since we are only interested in finding the spatial gradient of the flux at a given time t, the time-dependency of the solution $Q_E$ and the flux F and their corresponding subscript and superscript notations are also ignored in the discussion below.

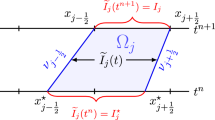
In a one-dimensional generic numerical framework of the CFV scheme, at a given cell $I_i = [x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}]$ with the cell center $x_i$, cell boundaries $x_{i\pm \frac{1}{2}}$, and cell-size ${{\triangle x}}$, the computational stencil $\{I_{i-1},I_{i},I_{i+1} \}$ and their corresponding numerical solution $\{Q_{i-1},Q_{i},Q_{i+1}\}$ are employed to compute the gradient of the flux written in the conservative form at $x_i$ exactly as

$$\begin{aligned} \frac{\partial {F}}{\partial x} \bigg |_{x_i} = \frac{{\mathcal {F}}_{i+\frac{1}{2}}-{\mathcal {F}}_{i-\frac{1}{2}}}{{{\triangle x}}}, \end{aligned}$$

(22)

to guarantee the numerical solution of the CFV scheme is a weak solution of the hyperbolic conservation laws. The numerical flux ${\mathcal {F}}_{i+\frac{1}{2}}$ at the cell boundary $x_{i+\frac{1}{2}}$ can be approximated by the global Lax-Friedrichs (LF) flux as

$$\begin{aligned} {\mathcal {F}}_{i+\frac{1}{2}}=\frac{1}{2}\left[ {F}\left( {Q}_{i+\frac{1}{2}}^{-}\right) +{F}\left( {Q}_{i+\frac{1}{2}}^{+}\right) \right] -\frac{1}{2} \alpha \left( {Q}_{i+\frac{1}{2}}^{+}-{Q}_{i+\frac{1}{2}}^{-}\right) , \end{aligned}$$

(23)

where $\alpha = \max _Q |{{\partial F} \over {\partial Q}}|$ is the global maximum speed of propagation.

To obtain a formal second-order accuracy when the solution Q(x) is sufficiently smooth, the numerical solution ${Q}_{i+\frac{1}{2}}^{\pm }$ at the (+) right and (-) left sides of the cell boundary $x_{i+\frac{1}{2}}$, respectively, are reconstructed via a piece-wise linear polynomial, as

$$\begin{aligned} {Q}_{i+\frac{1}{2}}^{+}={{Q}}_{i+1}-\frac{{{\triangle x}}}{2}\left( {Q}_{x}\right) _{i+1}, \quad \text{ and } \quad {Q}_{i+\frac{1}{2}}^{-}={{Q}}_{i}+\frac{{{\triangle x}}}{2}\left( {Q}_{x}\right) _{i}, \end{aligned}$$

(24)

where the slopes are approximated as

$$\begin{aligned} \left( {Q}_{x}\right) _{i+1} = \frac{{{Q}}_{i+1}-{{Q}_{i}}}{{{\triangle x}}}, \quad \text{ and } \quad \left( {Q}_{x}\right) _{i} = \frac{{{Q}}_{i}-{{Q}}_{i-1}}{{{\triangle x}}}. \end{aligned}$$

Due to the non-linearity of the hyperbolic PDEs, a finite-time singularity (discontinuity) might formed. To mitigate the Gibbs oscillations from polluting the solution and destabilizing the numerical scheme, the slope $\left( {Q}_{x} \right) _{i}$ should be limited. Therefore, we apply the generalized nonlinear minmod slope limiter [19]

$$\begin{aligned} \left( {Q}_{x}\right) _{i}={\text {minmod}}\left( \omega \frac{{{Q}}_{i+1}-{{Q}_{i}}}{{{\triangle x}}}, \frac{{{Q}}_{i+1}-{{Q}}_{i-1}}{2{{\triangle x}}},\omega \frac{{{Q}}_{i}-{{Q}}_{i-1}}{{{\triangle x}}}\right) , \quad \omega \in [0,2], \end{aligned}$$

(25)

where the general multivariate minmod function is

$$\begin{aligned} {\text {minmod}}\left( x_{1}, x_{2}, \ldots \right) =\left\{ \begin{array}{ll} \min _{i}\left\{ x_{i}\right\} , &{} \text{ if } x_{i}>0~~\forall ~ i, \\ \max _{i}\left\{ x_{i}\right\} , &{} \text{ if } x_{i}<0~~\forall ~ i, \\ 0, &{} \text{ otherwise } . \end{array}\right. \end{aligned}$$

(26)

In this study, unless otherwise specified, we take $\omega =1.25$ for all the numerical examples.

4.2 Essentially Non-Oscillatory (ENO) Interpolation for Ghost Cells $\varvec{X}_G$

At any given time $t=t_k, k=\{1,2,n+1\}$, the numerical solution at all ghost cells $Q_E(\varvec{X}_G,t_k)$ are needed to be specified to allow an update of the numerical flux gradient in the interior cells $\nabla {F}(\varvec{X}_I,\cdot )$ in the next RK-TVD stage/step. Using the CAN-property of the embedding method and the closest point mapping ${{\text {cp}}}({{\varvec{x}}})$, the value $Q_E({{\varvec{x}}}_g,t_k), {{\varvec{x}}}_g \in \varvec{X}_G$ are mapped to the closest point $\xi _{\mathcal {M}}\in {\mathcal {M}}$ via the cp-mapping (5), that is, $\xi _{\mathcal {M}}= {{\text {cp}}}({{\varvec{x}}}_g)$ and $Q_E({{\varvec{x}}}_g,t_k) = Q_{\mathcal {M}}(\xi _{\mathcal {M}},t_k)$. By denoting $\xi _{\mathcal {M}}= {{\varvec{x}}}_0 = (x_0, y_0)$, we shall employ a two-dimensional Lagrange interpolation polynomial $P({{\varvec{x}}}_0)=Q_E({{\varvec{x}}}_g,t_k)=f({{\varvec{x}}}_0)$ with the known data $Q_E(\varvec{X}_I,t_k)=f(\varvec{X}_I)$ at the end of the RK-TVD stage/step. Without loss of generality, we shall ignore the time-dependency of the variables and their corresponding superscript notations in the discussion for simplicity.

One can argue that a linear (e.g. central polynomial) interpolation method should work well if the underlining function is sufficiently smooth. However, one cannot assume any smoothness of the nonlinear hyperbolic PDEs’ solution in general. The solution can become discontinuous at any spatial location and time. Hence, one should not use the linear high order interpolation method near a discontinuity lest the interpolation across the discontinuity will result in numerical oscillations. To get around this predicament, a nonlinear interpolation method that biases the interpolation stencils adaptively according to the local smoothness of the data should be employed instead. Hence, to maintain the formal high order of the numerical scheme, a more computational expensive ENO interpolation process (see [15,16,17,18, 32, 33, 35, 36] for details) is employed to avoid the interpolation across any potential discontinuity. Furthermore, since the data $f(\varvec{X}_I)$ are distributed uniformly on a two-dimensional Cartesian grid, a one-dimensional ENO interpolation process can be applied to the two-dimensional data in a tensorial, aka, dimension-by-dimension, manner.

Hence, the Lagrange interpolation polynomial can be written as

$$\begin{aligned} P(x,y) = \sum _{k=\mathfrak {n}_i}^{\mathfrak {n}_i+K} \, \sum _{m=\mathfrak {n}_j}^{\mathfrak {n}_j+M} f_{km} \, l_{k}(x) \, l_{m}(y), \end{aligned}$$

(27)

where $f_{km} = f(x_k,y_m)$, and $l_k(x)$ and $l_m(y)$ are the one-dimensional Lagrange interpolation polynomial of degrees K and M, respectively.

The index k (m) will be biased according to the local smoothness of the solution that would minimize two $(K+1){\text {th}}$-order ($(M+1){\text {th}}$-order) divided differences of $f_{km}$ if a data point is added either to the right (top) or to the left (bottom) of the $K{\text {th}}$-order ($M{\text {th}}$-order) divided difference stencil, and $\mathfrak {n}_i$ ($\mathfrak {n}_j$) represents the left-most (bottom-most) index. The process of moving the indices k and m above will give the adaptive ENO interpolation. This is essentially a one-dimensional process, and hence we will describe it in a generic one-dimensional framework by assuming the data is a function of x only and independent of y for simplicity.

We will begin by giving the construction of the $K{\text {th}}$-order divided difference;

• The $0\text {th}$-order divided difference of $f_i$ is defined by:

  $$\begin{aligned} f[x_i] = f(x_i). \end{aligned}$$

  (28)

• The $k\text {th}$-order divided difference is then defined recursively by:

  $$\begin{aligned} f[x_i, \ldots , x_{i+k}] = \frac{f[x_{i+1}, \ldots , x_{i+k}]- f[x_i, \ldots , x_{i+k-1}] }{x_{i+k} - x_i}, \quad k =1,\ldots , K. \end{aligned}$$

  (29)

The interpolation polynomial, in general, can be written as

$$\begin{aligned} P(x) = \sum _{k=\mathfrak {n}_i}^{\mathfrak {n}_i + K} f_{k} \, l_{k}(x). \end{aligned}$$

(30)

The $\mathfrak {n}_i$ is the left-most index determined by the local smoothness of f(x) at $x_i$ as measured by the $K{\text {th}}$-order divided differences.

• For the starting point $\mathfrak {n}_i$ with the given $x_0$: We first locate the nearest neighboring point $x_i$ such that $|x_i-x_0| \le {{\triangle x}}/2$ and set $\mathfrak {n}_i=i$.

• For the $0\text {th}$-order divided difference $f[x_{\mathfrak {n}_i}]$: $f[x_{\mathfrak {n}_i}]$ is formed across the one-point ENO stencil $S_1=\{x_{\mathfrak {n}_i}\}$.

• For the $1\text {st}$-order divided difference $f[x_{\mathfrak {n}_i},x_{\mathfrak {n}_i+1}]$:

  • If $x_{\mathfrak {n}_i}\ge x_0$, then $\mathfrak {n}_i$ is updated by $\mathfrak {n}_i\leftarrow (\mathfrak {n}_i-1)$.

  • $f[x_{\mathfrak {n}_i},x_{\mathfrak {n}_i+1}]$ is formed across the two-points ENO stencil $S_2=\{x_{\mathfrak {n}_i},x_{\mathfrak {n}_i+1}\}$.

• For the $k\text {th}$-order divided difference $f[x_{\mathfrak {n}_i},...,x_{\mathfrak {n}_i+k}]$ ($k=2,\ldots ,K$): Given the k-points ENO stencil $S_{k}=\{x_{\mathfrak {n}_i},...,x_{\mathfrak {n}_i+k-1}\}$,

  • if $\left| f[I_{k}\cup x_{\mathfrak {n}_i-{1}}]\right| <\left| f[I_{k}\cup x_{\mathfrak {n}_i+{k}}]\right|$, then $\mathfrak {n}_i$ is updated by $\mathfrak {n}_i\leftarrow (\mathfrak {n}_i-1)$.

  • $f[x_{\mathfrak {n}_i},...,x_{\mathfrak {n}_i+k}]$ is formed across the ($k+1$)-points ENO stencil $S_{k+1}=\{x_{\mathfrak {n}_i},...,x_{\mathfrak {n}_i+k}\}$.

5 Numerical Results

To demonstrate the numerical performance of the cp- and tc-embedding methods (refer collectively as embedding methods), we present several classical benchmark problems in one-dimensional scalar hyperbolic conservation laws with a linear, and both convex and non-convex nonlinear fluxes $F(Q_{\mathcal {M}})$ on a manifold.

The tested problems are given on three representative manifolds with an increasing complexity

$$\begin{aligned} {\mathcal {M}}_k: {\varvec{p}}= (R_{x}\cos (\theta ),R_{y}\sin (\theta )),~~ k=1,2,3, \end{aligned}$$

where $R_{x}$ and $R_{y}$ are the radii in the x- and y-directions as given in Table 1.

The manifolds ${\mathcal {M}}_1, {\mathcal {M}}_2$, and ${\mathcal {M}}_3$ are a unit circle, an ellipse, and a complex closed curve, respectively, as illustrated in Fig. 2.

Fig. 2

The shapes of the three manifolds of ${\mathcal {M}}_1, {\mathcal {M}}_2$ and ${\mathcal {M}}_3$

The counterclockwise direction is defined as a positive direction. Therefore, the tangential vector at (x, y) is ${{\varvec{v}}}_{{\mathcal {M}}}({{\text {cp}}}({{\varvec{x}}}))=\frac{{\varvec{p}}'(\theta )}{||{\varvec{p}}'(\theta )||_2}\in {{{\mathcal {T}}}}_{{\mathcal {M}}}$, and the arc-length¹ of the manifold ${\mathcal {M}}_k$ is

$$\begin{aligned} C_k=\int _{0}^{2 \pi } ||{\varvec{p}}'(\theta )||_2 d \theta . \end{aligned}$$

(31)

Fig. 3

The global and (a,b,c) zoom-in extended velocity field ${{\varvec{v}}}_E\in \Omega$ around the manifold ${\mathcal {M}}_3$. The color indicates the magnitude of the velocity (Color figure online)

Figure 3 shows the global and local extended velocity field ${{\varvec{v}}}_E\in \Omega$ around the manifold ${\mathcal {M}}_3$ as depicted by (13). The velocity ${{\varvec{v}}}_E$ increases (decreases) in speed gradually from the ${{\varvec{v}}}_{\mathcal {M}}$ on the manifold away radially outward (inward) according to the locally signed curvature $\tilde{\kappa }({{\text {cp}}}({{\varvec{x}}}))$ and follows the same direction as the direction of the tangent vector at a given point ${{\varvec{x}}}$ on ${\mathcal {M}}_3$.

The computational Cartesian domain $x\times y$, the number of grid points $N_x\times N_y$, and the mesh resolution ${{\triangle x}}={{\triangle y}}$ and other relevant parameters employed in this study are summarized in Table 1 unless specified otherwise.

Table 1 The radius $(R_{x}$, $R_{y})$ with $\alpha =\frac{3}{2}\theta +\frac{\pi }{8},\beta =e^{\cos (2\theta )}$, the arc-length $C_k$, the computational Cartesian domain $x\times y$, the numbers of grid points $N_x\times N_y$, and the mesh resolution ${{\triangle x}}={{\triangle y}}$ of the three manifolds ${\mathcal {M}}_1, {\mathcal {M}}_2$, and ${\mathcal {M}}_3$

Under this spatial discretization setting, the corresponding collocating points on the manifolds will not be uniformly distributed and tend to cluster around a large curvature. For presentations of the results in the following numerical experiments, by the second-order ENO interpolation from the collocation points on the manifold, we will obtain and plot 500 data points of the numerical results and the reference solutions distributed evenly along the angle $\theta$ of the manifolds.

By considering a (local) parameterization ${\varvec{\gamma }}(s)$ with s being the arc-length of the manifold ${\mathcal {M}}_k$, one has

$$\begin{aligned} {{\varvec{v}}}_{{\mathcal {M}}} {{\,{\varvec{\cdot }}\,}}\nabla _{{\mathcal {M}}} F= \frac{ \partial F}{\partial {\varvec{\gamma }}}\frac{\partial {\varvec{\gamma }}}{\partial s} = {{\partial F} \over {\partial s}}. \end{aligned}$$

(32)

The SPDEs of scalar hyperbolic type (1) can be written in the equivalent form of

$$\begin{aligned} \left\{ \begin{aligned}&{{\partial Q_{{\mathcal {M}}}} \over {\partial t}} + {{\partial F_{{\mathcal {M}}}} \over {\partial s}} = 0, \qquad \hbox {on}\,\, {\mathcal {M}}\hbox {,}\, t\in (0,T], \quad s\in [0,C_k],\\&Q_{\mathcal {M}}(s,0)~ = Q_{0}(s), \qquad \hbox { on}\ {\mathcal {M}}. \end{aligned} \right. \end{aligned}$$

(33)

We will begin by examining the accuracy and rate of convergence of the cp- and tc-embedding methods in solving a linear wave advection with a smooth solution on the manifolds. We will then examine the essentially non-oscillatory shock-capturing performance by solving the inviscid nonlinear Burgers’ equation with a composite-waves initial condition on the manifold ${\mathcal {M}}_1$. The numerical dissipation property and the resolution efficiency in resolving fine-scale structures in the complex solution are also studied.

Finally, several sets of benchmark one-dimensional shock-tube problems are simulated on ${\mathcal {M}}_3$ with the tc-embedding method are presented. In particular, the nonlinear hyperbolic conservation laws with a convex flux (e.g., inviscid Burgers’ equation) and a concave flux (e.g., traffic flow problem) that forms isolated shock or isolated rarefaction wave, and a non-convex flux (e.g., Buckley-Leverett equation) that forms compound wave are used to validate the performance of the tc-embedding method on a complex manifold.

5.1 The Accuracy, Resolution, and Efficiency of the Embedding Methods

As for any newly developed numerical scheme, it is essential to examine the accuracy and rate of convergence of the scheme in solving a linear wave equation with a smooth solution. The $L^1, L^2$, and $L^\infty$ errors of the embedding methods in solving the linear wave equation show quantitatively the accuracy and the rate of convergence on the three manifolds ${\mathcal {M}}_1, {\mathcal {M}}_2$, and ${\mathcal {M}}_3$. For a non-smooth solution, the nonlinear inviscid Burgers’ equation with the composite multi-waves initial condition is solved using the embedding methods to assess their relative performance in essentially non-oscillatory shock-capturing and resolution of smooth fine-scale structures. Their results are compared qualitatively with the reference solution on the manifold ${\mathcal {M}}_1$. The CPU times of the embedding methods are also obtained to demonstrate their relative computational efficiency.

5.1.1 Example 1: Linear Wave Equation

The linear wave equation with a smooth solution is used to obtain the errors in examining the accuracy and the convergence rate of the embedding methods.

The linear flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = Q_{{\mathcal {M}}}, \end{aligned}$$

(34)

and the initial condition is

$$\begin{aligned} \begin{aligned} Q_0(s)=\sin (2\pi s/C_k). \end{aligned} \end{aligned}$$

(35)

The exact solution is $Q_{{\mathcal {M}}}(s,t)=Q_0(2\pi (s-t)/C_k)$. The final time is $T=C_k$.

Figure 4 shows the errors without the nonlinear minmod slope limiter ($\omega =0$ in (25)) in the CFV scheme since the solution is smooth. In the figure, a thick black line with a slope of two is included for easy reference when comparing the convergence rate of different methods. The errors of the cp- and tc-embedding methods are shown with the dashed and solid lines, respectively. It is easy to see that the errors of the tc-embedding method are about ten times smaller than the errors of the cp-embedding method for all three manifolds. The convergence rates of both embedding methods, as expected, are second-order.

Fig. 4

(Example 1 without the nonlinear minmod slope limiter) Errors of the cp-embedding (dashed lines) and the tc-embedding (solid lines) methods of the wave equation with the smooth initial condition at $T=C_k$

Fig. 5

(Example 1 with the nonlinear minmod slope limiter) Errors of the cp-embedding (dashed lines) and the tc-embedding (solid lines) methods of the wave equation with the smooth initial condition at $T=C_k$

Since we are attempting to solve the hyperbolic conservation laws with non-smooth solutions, the nonlinear minmod slope limiter needs to be activated to suppress any Gibbs oscillations that might appear in the solution. Figure 5 shows the errors in the CFV scheme with the nonlinear minmod slope limiter ($\omega =1.25$ in (25)) activated. Here, we include another thick black line with a slope of one as the limiter might reduce the convergence rate by a half order. It is easy to see that the errors of the tc-embedding method are still smaller than the errors of the cp-embedding method for all three manifolds. The convergence rate is reduced slightly to around 1.5 in the $L^2$ norm and 1.2 in the $L^\infty$ norm. These results are consistent with the results in [19]. In summary, the results here show that the tc-embedding method is more accurate than the cp-embedding method, and both methods converge at the same rate as the mesh is refined.

5.1.2 Example 2: Inviscid Burgers’ Equation with Composite Waves IC

The inviscid Burgers’ equation with the composite waves initial condition is employed to demonstrate the essentially non-oscillatory shock-capturing capability near the discontinuities and the high-resolution at the fine-scale smooth structures of the scheme.

The nonlinear convex flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = \frac{1}{2}Q_{{\mathcal {M}}}^2, \end{aligned}$$

(36)

and the initial condition consisting of composite waves is

$$\begin{aligned} \begin{aligned} Q_{0}(s)=\left\{ \begin{array}{lc} \sin ( \pi \eta ), &{} -4 \le \eta<-1, \\ 3, &{} ~~-1 \le \eta<-0.5, \\ 1, &{} -0.5 \le \eta< 0,~~ \\ 3, &{} ~~~~0 \le \eta< 0.5, \\ 2, &{} 0.5 \le \eta <1,\\ \sin (4 \pi \eta ), &{} 1 \le \eta \le 4, \end{array}\right. \end{aligned} \end{aligned}$$

(37)

with $\eta =4\left( \frac{2 s}{C_k}-1\right)$. The final time is $T=\frac{1}{20}C_k$. Since there is no exact solution to the Burgers’ equation with this complex initial condition, the solution of the cp-embedding method with the mesh resolution ${{\triangle x}}={{\triangle y}}=\frac{1}{250}$ is used as the reference solution.

Fig. 6

Example 2 (The Burgers’ equation with composite waves on the unit circle ${\mathcal {M}}_1$): (Left) The solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T = \frac{1}{20}C_1$ and (Right) the zoomed-in figure computing by the tc-embedding and the cp-embedding methods with the mesh resolutions ${{\triangle x}}={{\triangle y}}=\frac{1}{30}$ and ${{\triangle x}}={{\triangle y}}=\frac{1}{40}$

In Fig. 6, the solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T = \frac{1}{20}C_1$ on the manifold ${\mathcal {M}}_1$ computed by the embedding methods with the mesh resolution ${{\triangle x}}={{\triangle y}}=\frac{1}{30}$ and ${{\triangle x}}={{\triangle y}}=\frac{1}{40}$ are shown. The solution on the manifold exhibits multiple shocks and fine-scale structures. Both embedding methods can capture multiple discontinuities in an essentially non-oscillatory manner as the solution evolves in space and time, forming discontinuities from an otherwise smooth solution. If not well-captured by the locally adaptive numerical dissipation at a strong gradient, the Gibbs oscillations will pollute the smooth fine-scale structures. Furthermore, as shown in the right sub-figure of Fig. 6, the tc-embedding method has less numerical dissipation than the cp-embedding method allowing an efficient resolution of the fine-scale structures, which is a very important feature for a long time simulation.

Table 2 The CPU times (in seconds) of the wave equation with smooth initial condition on ${\mathcal {M}}_1$ (Example 1) at final time $T=C_1$ and speedup factors (SF) of the cp- and tc-embedding methods

Table 3 The CPU times (in seconds) of the wave equation with smooth initial condition on ${\mathcal {M}}_3$ (Example 1) after 20 Runge-Kutta time steps and speedup factors (SF) of the cp- and tc-embedding methods

Finally, we present the CPU times of the embedding methods to demonstrate their relative computational efficiency. Both embedding methods are written in Matlab version R2019a and ran on a desktop computer equipped with a four cores Intel(R) Core(TM) i7-6700 CPU with a clock speed of 3.40 GHz. Tables 2 and 3 show the CPU times of the cp-embedding method ($\text {CPU}_\text {cp}$) and the tc-embedding method ($\text {CPU}_\text {tc}$), and the speedup factors ($\text {SF}=\text {CPU}_\text {cp}/\text {CPU}_\text {tc}$) for an increasing resolution. The CPU times are obtained by running the Example 1 on the unit circle ${\mathcal {M}}_1$ to the final time $T=C_1$ and the complex manifold ${\mathcal {M}}_3$ with 20 Runge-Kutta time steps. We shall also denote $n(\varvec{X}_I)$ and $n(\varvec{X}_G)$ as the number of cells in the sets $\varvec{X}_I$ and $\varvec{X}_G$, respectively. The total CPU times ($\text {CPU}_\text {total}$) of the embedding methods are mainly composed of the CPU times used in the CFV method ($\text {CPU}_\text {cfv}$) and the ENO interpolation ($\text {CPU}_\text {eno}$), that is, $\text {CPU}_\text {total}\approx \text {CPU}_\text {cfv} + \text {CPU}_\text {eno}$. In terms of $\text {CPU}_\text {cfv}$, the embedding methods are basically the same ($\text {SF}\approx 1$). In terms of $\text {CPU}_\text {eno}$, the tc-embedding method is about 3.5 times faster than the cp-embedding method ($\text {SF}\approx 3.5$). Although $n(\varvec{X}_I)/n(\varvec{X}_G)\approx 3$, the $\text {CPU}_\text {eno}$ dominates over the $\text {CPU}_\text {cfv}$. In terms of $\text {CPU}_\text {total}$, the tc-embedding method is about 2.5 times faster than the cp-embedding method ($\text {SF}\approx 2.5$). The reason for such large speedup factors is that the former eliminates the costly computations in reconstructing the CAN-property for all ${{\varvec{x}}}\in \varvec{X}_I$ at each RK-TVD stage required by the latter.

In summary, the tc-embedding method has better accuracy, improved resolution, and reduced CPU time than the cp-embedding method.

5.2 The One-Dimensional Benchmark Shocked Flow Problems on ${\mathcal {M}}_3$

This section presents the numerical results of solving the hyperbolic conservation laws on ${\mathcal {M}}_3$ with several benchmark one-dimensional scalar hyperbolic conservation laws with discontinuous solutions. Both the linear ($F''= 0$), convex ($F'' > 0$), concave ($F'' < 0$), and non-convex ($F''$ changes sign) fluxes of the hyperbolic conservation laws are considered. The problems are the linear advection equation with a discontinuous initial condition (linear flux), the inviscid Burgers’ equation with a stationary shock and with an interaction of the moving shock and composite waves (convex flux), the traffic flow problem (concave flux), and the Buckley-Leverett equation (non-convex flux). These problems demonstrate the robust performance of the tc-embedding method in resolving fine-scale structures efficiently even in the presence of a shock and the essentially non-oscillatory capturing of complex shocks and rarefaction waves existed in the nonlinear PDEs. As the results computed on the other two manifolds ${\mathcal {M}}_1$ and ${\mathcal {M}}_2$ are essentially the same as the one computed on the ${\mathcal {M}}_3$ when the final time T is scaled proportionally with their respective arc-length $C_k$; they are omitted here for saving space.

In the figure of each following example, three sub-figures are included. The solution at the final time $Q_{{\mathcal {M}}}(s, T)$, the space-time ($s-t$) evolution of $Q_{{\mathcal {M}}}(s,t)$ in terms of arc-length s and the space-time (${{\varvec{x}}}-t$) evolution of $Q_{{\mathcal {M}}}({{\varvec{x}}},t)$ in terms of ${{\varvec{x}}}\in \Omega$ in the left, middle, and right sub-figures, respectively. In the right sub-figure, the vertical axis z represents the increasing time t, and the manifold ${\mathcal {M}}_3 \in \Omega$ resides on the $x\!-\!y$ plane. In the left sub-figure, the symbols are placed with a fixed spacing distance of $3\%$ between symbols to avoid clustering of the symbols for clarity. For all the test problems, the solutions of the tc-embedding method with the mesh resolution ${{\triangle x}}={{\triangle y}}=\frac{1}{250}$ on ${\mathcal {M}}_3$ are used as the reference solutions. The solution’s space-time evolution is illustrated with color-flooded and black solid lines contour in the middle and right sub-figures.

5.2.1 Example 3: Linear Advection Equation with Multi-Waves IC

In this example, the simple linear advection problem is solved with the linear flux $F(Q_{\mathcal {M}})$ and a piece-wise continuous multi-waves initial condition $Q_0(s)$ in (33) as given below.

The linear flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = Q_{{\mathcal {M}}}, \end{aligned}$$

(38)

and the multi-wave initial condition consists of a smooth Gaussian function, a discontinuous square function, a piece-wise continuous triangle function, and a smooth elliptic function,

$$\begin{aligned} \begin{aligned} Q_0(s)=\left\{ \begin{array}{ll} \frac{1}{6}(G(\eta ,\beta ,z-\delta )+G(\eta ,\beta ,z-\delta )+4G(\eta ,\beta ,z)), &{} -0.8 \le \eta \le -0.6, \\ 1, &{} -0.4 \le \eta \le -0.2, \\ 1-|10(\eta -0.1)|, &{} 0\le \eta \le 0.2, \\ \frac{1}{6}(H(\eta ,\alpha ,a-\delta )+H(\eta ,\alpha ,a-\delta )+4H(\eta ,\alpha ,a)), &{} 0.4 \le \eta \le 0.6, \\ 0, &{} \text {otherwise}, \end{array}\right. \end{aligned} \end{aligned}$$

(39)

where $\eta =2s/C_3 - 1$, $G(x,\beta ,z)=e^{-\beta (x-z)^2}, H(x,\alpha ,a)=\sqrt{\max (0,1-\alpha ^2(x-a)^2)}$ with $a=0.5, z=-0.7, \delta = 0.005, \alpha = 10$ and $\beta = \frac{\log 2}{36\delta ^2}$. The exact solution is $Q_{{\mathcal {M}}}(s,t)=Q_0(2 (s-t)/C_3 - 1)$. The final time is $T=C_3$.

Fig. 7

Example 3 (The linear advection of the multi-wave on ${\mathcal {M}}_3$): (Left) The solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T=C_3$. The space-time evolution of the solution (Middle) $Q_{{\mathcal {M}}}(s,t)$ in terms of arc-length s and (Right) $Q_{{\mathcal {M}}}({{\varvec{x}}},t)$ in terms of physical location ${{\varvec{x}}}$

As shown in Fig. 7, the tc-embedding method is capable of advecting the discontinuous solution in an essentially non-oscillatory manner while resolving the piece-wise smooth solutions well spatially and temporally. The result is very encouraging.

Next, we shall solve the SPDEs with a nonlinear convex and non-convex flux, giving rise to complex finite-time singularity even with a smooth initial condition.

5.2.2 Example 4: Inviscid Burgers’ Equation with Stationary Shock

Inviscid Burgers’ equation is the simplest prototype for the scalar hyperbolic conservation laws with a nonlinear convex flux that the solution can develop either an isolated shock wave (discontinuity in the solution) or an isolated rarefaction wave (discontinuity in the first derivative of the solution). They are the weak solutions of the inviscid Burgers’ equation and satisfy an entropy inequality with entropy function $\eta = Q^2$ [20]. The Burgers’ equation is a fundamental partial differential equation in applied mathematics, such as fluid mechanics and gas dynamics. Here we solve (33) on ${\mathcal {M}}_3$ with the nonlinear convex flux F and a smooth initial condition $Q_0(s)$ given below with the tc-embedding method.

The nonlinear convex flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = \frac{1}{2}Q_{{\mathcal {M}}}^2, \end{aligned}$$

(40)

and the smooth initial condition is

$$\begin{aligned} \begin{aligned} Q_0(s)=\sin (2\pi s/C_3). \end{aligned} \end{aligned}$$

(41)

The final time is $T=\frac{1}{4}C_3$.

Fig. 8

Example 4 (The Burgers’ equation with stationary shock on ${\mathcal {M}}_3$): (Left) The solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T=\frac{1}{4}C_3$. The space-time evolution of the solution (Middle) $Q_{{\mathcal {M}}}(s,t)$ in terms of arc-length s and (Right) $Q_{{\mathcal {M}}}({{\varvec{x}}},t)$ in terms of physical location ${{\varvec{x}}}$

Figure 8 shows the numerical results of the simulations. As shown in the space-time evolution of the solution $Q_{\mathcal {M}}(s,t)$ in the middle sub-figure, the initial smooth function develops into a stationary discontinuity (shock) at arc-length $s = C_3/2$ and the wave breaking time $t = C_3/(2 \pi )$, as predicted by the theory when the left- and right-going characteristics have collided together. The weak solution also satisfies the Rankine-Hugoniot condition for the shock speed. The simple piece-wise continuous numerical solution has no discernible Gibbs oscillations. The example demonstrates that the tc-embedding method can capture the shock wave adaptively in an essentially non-oscillatory manner while resolving the piece-wise smooth solutions well spatially and temporally.

This problem is relatively easy to handle as the discontinuity is stationary in space and time. Next, we shall tackle the same problem but with moving shocks and with a complex initial condition consists of composite waves. This problem will challenge the space-time adaptivity characteristic of the tc-embedding method.

5.2.3 Example 5: Inviscid Burgers’ Equation with Composite Waves IC

This example is given to show the performance of the tc-embedding method on ${\mathcal {M}}_3$. The initial condition is complex, including four discontinuous with different jump ratios and two smooth sine functions with different wave frequencies.

The nonlinear convex flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = \frac{1}{2}Q_{{\mathcal {M}}}^2, \end{aligned}$$

(42)

and the initial condition consisting of composite waves is given in (37). The final time is $T=\frac{1}{20}C_3$.

Fig. 9

Example 5 (The Burgers’ equation with composite waves on ${\mathcal {M}}_3$): (Left) The solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T = \frac{1}{20}C_3$. The space-time evolution of the solution (Middle) $Q_{{\mathcal {M}}}(s,t)$ in terms of arc-length s and (Right) $Q_{{\mathcal {M}}}({{\varvec{x}}},t)$ in terms of physical location ${{\varvec{x}}}$

Figure 9 shows the Burgers’ equation with the composite waves initial condition. As shown in the space-time evolution of the solution $Q_{\mathcal {M}}(s,t)$ in the middle sub-figure, the left-most sine wave develops into stationary shock at $s = C_3/8$, while the right-most high-frequency sine wave to the right of the strong shock develops into a train of shocklets. The two right-moving shocks are formed in the middle and moves to the right. They are captured essentially non-oscillatory as they evolve around the manifold ${\mathcal {M}}_3$ in space and time, as shown in the right sub-figure. This challenging example demonstrates the space-time adaptivity characteristic of the tc-embedding method on a non-trivial shape of the manifold.

5.2.4 Example 6: Traffic Flow Problem

In mathematics and transportation engineering, traffic flow is a fundamental theory to analyze and study the interactions between travellers (mainly cars) and infrastructure, with the aim of understanding the relationship between traffic flow, velocity and density, reducing the occurrence of accidents, and improving the efficiency movement of traffic.

The nonlinear concave flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = v_{\max } Q_{{\mathcal {M}}}(1-Q_{{\mathcal {M}}}/Q_{\max }), \end{aligned}$$

(43)

where $Q_{{\mathcal {M}}}$ is the cars’ density. We take $v_{\max }=1$ and $Q_{\max }=1$ as the limited speed and density, respectively. The initial condition is

$$\begin{aligned} \begin{aligned} Q_0(s)=\left\{ \begin{array}{lc} 1, &{} -0.2 \le \eta \le 0.6, \\ \frac{1}{2}, &{} \text {otherwise}, \end{array}\right. \end{aligned} \end{aligned}$$

(44)

where $\eta =\frac{2s}{C_3}-1$. The final time is $T=\frac{2}{5}C_3$.

Fig. 10

Example 6 (The traffic flow problem on ${\mathcal {M}}_3$): (Left) The solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T = \frac{2}{5}C_3$. The space-time evolution of the solution (Middle) $Q_{{\mathcal {M}}}(s,t)$ in terms of arc-length s and (Right) $Q_{{\mathcal {M}}}({{\varvec{x}}},t)$ in terms of physical location ${{\varvec{x}}}$

As shown in Fig. 10, there are two strong discontinuities (front and back of the traffic jam) in the initial conditions. The left discontinuity (shock) propagates to the left as the cars in the low-density region slow down and become congested as cars enter the high-density region. The right discontinuity evolves into a rarefaction wave as cars’ density reduces gradually, as the cars speeding up, from the high-density region toward the low-density region. The left-going shock and the left-going rarefaction waves are well-captured in an essentially non-oscillatory manner by the tc-embedding method on ${\mathcal {M}}_3$ spatially and temporally, as shown in the middle and right sub-figures.

The examples above show that the tc-embedding method performs equally well for both the convex and concave fluxes. We will conclude the study showing that the tc-embedding method also works well with a non-convex flux, where the second derivative of the flux changes sign, on ${\mathcal {M}}_3$.

5.2.5 Example 7: Buckley-Leverett Problem

In fluid dynamics, the Buckley-Leverett equation is a model for a two-phase oil–water immiscible displacement process in porous media in a one-dimensional or quasi-one-dimensional reservoir.

The nonlinear non-convex flux F is

$$\begin{aligned} F(Q_{{\mathcal {M}}}) = \frac{Q_{{\mathcal {M}}}^2}{Q_{{\mathcal {M}}}^2+\mu (1-Q_{{\mathcal {M}}})^2}, \end{aligned}$$

(45)

with the viscosity $\mu =1/4$. The initial condition is

$$\begin{aligned} \begin{aligned} Q_0(s)=\left\{ \begin{array}{lc} 1, &{} -0.5 \le \eta \le 0, \\ 0, &{} \text {otherwise}, \end{array}\right. \end{aligned} \end{aligned}$$

(46)

where $\eta =\frac{2 s}{C_3} - 1$. The final time is $T=\frac{1}{5}C_3$.

Fig. 11

Example 7 (The Buckley-Leverett problem on ${\mathcal {M}}_3$): (Left) The solution $Q_{{\mathcal {M}}}(s, T)$ at the final time $T = \frac{1}{5}C_3$. The space-time evolution of the solution (Middle) $Q_{{\mathcal {M}}}(s,t)$ in terms of arc-length s and (Right) $Q_{{\mathcal {M}}}({{\varvec{x}}},t)$ in terms of physical location ${{\varvec{x}}}$

The flux is S-shaped with an inflection point and, therefore, non-convex. It yields a rarefaction-shock compound wave, also known as the Buckley-Leverett (BL) profile, which consists of a shock wave immediately followed by a rarefaction wave (see [20] for details). Figure 11 shows that the BL profile is captured essentially non-oscillatory and sharply by the tc-embedding method. The space-time evolution of the solution shows the formation process of the BL profile as the shock waves move towards the right stably together with the expanding rarefaction fans attached.

5.3 The Burgers’ Equation on the Two-Dimensional Manifolds

This section presents preliminary numerical results for applying the tc-embedding method for solving the moving Burgers’ equation on two-dimensional manifolds embedded in ${\mathbb {R}}^3$. More specifically, they are the torus-shaped and spherical-shaped manifolds. We conjuncture that the generalization of Theorem 2 to ${\mathbb {R}}^3$ can be done by using extended velocity field as in (13) on codimension-2 manifolds constructed by slicing ${\mathcal {M}}$ along $v_{\mathcal {M}}$ direction. We leave the proof to our future work.

We first illustrate the performance of the tc-embedding method in solving SPDEs on a two-dimensional parametrized torus surface:

$$\begin{aligned} x(\theta , \phi )=(R+r\cos \phi )\cos \theta , ~y(\theta , \phi )=(R+r\cos \phi )\sin \theta , ~z(\theta , \phi )=r\sin \theta . \end{aligned}$$

(47)

where the parametrization parameters are $\theta \in [-\pi ,\pi )$ and $\phi \in [-\pi , \pi )$. $R=1$ is the distance from the center of the tube to the center of the torus, and $r=0.5$ is the radius of the tube. The SPDEs Burgers’ equation simulates the finite-time formation of shock waves and their movement on a surface. The initial condition is

$$\begin{aligned} \begin{aligned} Q_0(\theta +\phi )= \frac{1}{2}+ \sin (\theta +\phi ). \end{aligned} \end{aligned}$$

(48)

The final time is $T=\pi$. In Fig. 12, the solutions $Q_{{\mathcal {M}}}(\varvec{x}, t)$ of the Burgers’ equation at times ($t=0, 1, 2$) on the torus surface computed by the tc-embedding methods with the mesh resolution ${{\triangle x}}={{\triangle y}}={{\triangle z}}=\frac{1}{25}$ are shown. The results show that the tc-embedding method can capture the formation of the strong gradient and shock sharply and essentially non-oscillatory and its later evolution on the torus-shaped manifold.

Fig. 12

The solution of the Burgers’ equation computed by the tc-embedding methods on the torus surface at times $t=0,1,2$

We conclude this study by performing a similar but slightly more complex evolution of four Gaussian-shaped spots distributed on a spherical-shaped surface:

$$\begin{aligned} x(\theta , \phi )=R\sin \phi \cos \theta , ~y(\theta , \phi )=R\sin \phi \sin \theta , ~z(\theta , \phi )=R\cos \phi . \end{aligned}$$

(49)

where the parametrization parameters are $\theta \in [0,2\pi )$ and $\phi \in [0, \pi )$. $R=1$ is the radius. The initial condition is

$$\begin{aligned} \begin{aligned} Q_0(\theta , \phi )= C + \frac{1}{\sqrt{2\pi }\sigma }\sum _{i=1}^{4} e^{-\frac{\left( \theta -a_1k_i\right) ^2+ \left( \phi -a_2h_i\right) ^2}{2\sigma ^2}}, \end{aligned} \end{aligned}$$

(50)

where $C=10^{-5}$, $a_1=\frac{\pi }{4}$, $k_i=2i-1$, $a_2=\frac{\pi }{5}$, $h_i=i$, and $\sigma =\frac{\pi }{8}$. The final time is $T=\pi$. In Fig. 13, the solutions $Q_{{\mathcal {M}}}(\varvec{x}, t)$ of the Burgers’ equation at times ($t=0, 1, 2$) on the spherical surface computed by the tc-embedding methods with the mesh resolution ${{\triangle x}}={{\triangle y}}={{\triangle z}}=\frac{1}{25}$ are shown. The initial condition ($t=0$) shows the four peaks on the spherical surface. Similar to the single shock formation in the previous example, the proposed algorithm can capture the formation of the strong gradient and shock sharply and essentially non-oscillatory. The movements and mutual interactions among the Gaussian functions are well-resolved, and discontinuities are well-captured, as depicted in the middle and right subfigures.

Fig. 13

The solution of the Burgers’ equation computed by the tc-embedding methods on the spherical surface at times $t=0,1,2$

6 Conclusion

A new closest point time-continuous embedding (tc-embedding) method is developed for solving nonlinear scalar hyperbolic conservation law (PDEs) on one-dimensional, connected, smooth, and closed manifolds (SPDEs). It improves upon the classical closest point embedding (cp-embedding) method that requires a costly re-establishment of the extension function’s constant-along-normal (CAN) property at every time step; the tc-embedding method incorporates the CAN-property analytically and explicitly in the SPDEs directly. The main idea in the tc-embedding method for solving SPDEs on a one-dimensional manifold is that under certain minor restrictions, the time-independent extended velocity field only needs to be determined once at the initialization stage and then used subsequently for all times in the method; thus, a substantial saving in the computational times can be realized.

Due to the nonlinear nature of the PDEs, finite-time singularities, such as shocks and rarefaction waves, can appear spontaneously in the solution. A second-order central finite volume scheme with a nonlinear minmod slope limiter is used to approximate the flux gradients discretely in a computational tube placed inside a Cartesian rectangular uniformly spaced mesh to mitigate Gibbs oscillations. It requires values at the ghost cells to compute the flux gradients at the boundary cell at the edges of the computational tube. By using the cp-mapping and CAN-property to map the location of a ghost cell to a point on the manifold, the ENO interpolation process updates the values of the ghost cells using data around the point on the manifold. The adaptive ENO interpolation is an essential technique in obtaining an essentially non-oscillatory value by avoiding interpolating across any potential discontinuity or high gradient in the solution. The third-order total variation diminishing Runge-Kutta (RK-TVD) scheme integrates the numerical solution in time.

We compared both methods’ accuracy on the linear advection equation with a smooth solution on simple and complex manifolds. While both methods are formally second order, the tc-embedding method is more accurate than the cp-embedding method overall. We have also compared both embedding methods’ resolution power and CPU times in solving the Burgers’ equation with a piece-wise continuous solution on a circular manifold. The results indicate that the tc-embedding method has a lesser numerical dissipation, resolves the fine-scale structures more efficiently, and is roughly two and half times faster CPU times than the cp-embedding method. Finally, several one-dimensional benchmark shocked flow problems, such as the Burgers’ equation with convex flux, the traffic flow problem with concave flux, and the Buckley-Leverett equation with non-convex flux, are used to demonstrate the essentially non-oscillatory shock-capturing property and the efficient resolution of fine-scale structures of the tc-embedding method on a complex manifold. The numerical results of the Burgers’ equation are also given for the two-dimensional torus-shaped and spherical-shaped manifolds.

These preliminary results show the potential synergy between the embedding method for solving SPDEs with smooth solutions and the nonlinear shock-capturing scheme for hyperbolic conservation laws with non-smooth (discontinuous) solutions. This study serves as the starting point, and there are more challenges in the theoretical and numerical aspects of combining both for solving more sophisticated hyperbolic SPDEs. As immediate follow-up work, extending the theoretical and numerical frameworks of the tc-embedding method for solving the scalar hyperbolic conservation laws on a two-dimensional complex connected manifold with a well-defined velocity field is challenging and will be investigated. As for future works, we will study if the tc-embedding method can help solve the one-dimensional or multi-dimensional system of hyperbolic conservation laws, for example, shallow water equations, Euler equations, multi-phases flow, and multi-components flow, on a stationary or moving manifold. Moreover, high-order shock-capturing schemes, with improved resolution, for example, the weighted ENO (WENO) finite volume/finite difference schemes [5, 6, 34] on a regular Cartesian mesh and the discontinuous Galerkin [11] method (DG) on a structured and unstructured triangular mesh, is also currently under consideration.