Deep-HyROMnet: A Deep Learning-Based Operator Approximation for Hyper-Reduction of Nonlinear Parametrized PDEs

Abstract

To speed-up the solution of parametrized differential problems, reduced order models (ROMs) have been developed over the years, including projection-based ROMs such as the reduced-basis (RB) method, deep learning-based ROMs, as well as surrogate models obtained through machine learning techniques. Thanks to its physics-based structure, ensured by the use of a Galerkin projection of the full order model (FOM) onto a linear low-dimensional subspace, the Galerkin-RB method yields approximations that fulfill the differential problem at hand. However, to make the assembling of the ROM independent of the FOM dimension, intrusive and expensive hyper-reduction techniques, such as the discrete empirical interpolation method (DEIM), are usually required, thus making this strategy less feasible for problems characterized by (high-order polynomial or nonpolynomial) nonlinearities. To overcome this bottleneck, we propose a novel strategy for learning nonlinear ROM operators using deep neural networks (DNNs). The resulting hyper-reduced order model enhanced by DNNs, to which we refer to as Deep-HyROMnet, is then a physics-based model, still relying on the RB method approach, however employing a DNN architecture to approximate reduced residual vectors and Jacobian matrices once a Galerkin projection has been performed. Numerical results dealing with fast simulations in nonlinear structural mechanics show that Deep-HyROMnets are orders of magnitude faster than POD-Galerkin-DEIM ROMs, still ensuring the same level of accuracy.

1 Introduction

Mathematical models involving partial differential equations (PDEs) depending on a set of parameters are ubiquitous in applied sciences and engineering. These input parameters are defined to characterize, e.g., material properties, loads, boundary/initial conditions, source terms, or geometrical features. High-fidelity simulations based on full-order models (FOMs), like the finite element (FE) method, entail huge computational costs in terms of CPU time and memory, if a large number of degrees of freedom dofs) is required. Complexity is amplified whenever interested to go beyond a single direct simulation, such as in the multi-query contexts of optimization, parameter estimation and uncertainty quantification. To face these problems, several strategies to build reduced order models (ROMs) have been developed over the years, aiming at computing reliable solutions to parametrized PDEs at a greatly reduced cost. A large class of ROMs relies on a projection-based approach, which aims at approximating the unknown state quantities as a linear superimposition of basis functions; these latter then span a subspace which the governing equations are projected onto [8, 9]. Among these, the reduced basis (RB) method [35, 49] is a powerful and widely used technique, characterized by a splitting of the reduction procedure into an expensive, parameter-independent offline phase (however performed once and for all) and an efficient, parameter-dependent online phase. Its efficiency mainly relies on two crucial assumptions:

• 1. The solution manifold is low-dimensional, so that the FOM solutions can be approximated as a linear combination of few reduced modes with a small error;

• 2. The online stage is completely independent of the high-fidelity dimension [21].

Assumption 1 concerns the approximability of the solution set and is associated with the slow decay of the Kolmogorov N-width [46]. However, for physical phenomena characterized by a slow N-width decay, such as those featuring coherent structures that propagate over time [25], the manifold spanned by all the possible solutions is not of small dimension, so that ROMs relying on linear (global) subspaces might be inefficient. Alternative strategies to overcome this bottleneck can be, e.g., local RB methods [2, 43, 55], or nonlinear approximation techniques, mainly based on deep learning architectures, see, e.g., [22,23,24, 37, 39].

Assumption 2 is automatically verified in linear, affinely parametrized problems [49], but cannot be fulfilled when dealing with nonlinear problems, as the online assembling of the reduced operators requires to reconstruct the high-fidelity ones. To overcome this issue, a further level of approximation, or hyper-reduction, must be introduced. State-of-the-art methods, such as the empirical interpolation method (EIM) [6], the discrete empirical interpolation method (DEIM) [15], its variant matrix DEIM (MDEIM) [42], the missing point estimation [4] and the Gauss-Newton with approximated tensors (GNAT) [13], aim at recovering an affine expansion of the nonlinear operators by computing only a few entries of the nonlinear terms. EIM, DEIM and GNAT can be seen as approximate-then-project techniques, since operator approximation is performed at the level of FOM quantities, prior to the projection stage. On the other hand, project-then-approximate strategies have also been introduced, aiming at approximating directly ROM operators, such as the reduced nonlinear residual and its Jacobian. An option in this sense is represented by the so-called Energy Conserving Sampling and Weighting (ECSW) technique [20]; see. e.g., [21] for a detailed review.

Although extensively used in many applications, spanning from fluid flows models to cardiac mechanics [2, 11, 19, 27, 50, 54], these strategies are code-intrusive and, more importantly, might impact on the overall efficiency of the ROM approximation in complex applications. Indeed, when dealing with highly nonlinear problems, expensive hyper-reduction strategies are usually required if aiming at preserving the physical constraints at the ROM level, that is, if ROMs are built consistently with the FOM through a projection-based procedure. For instance, a large number of DEIM basis vectors are required to ensure the convergence of the reduced Newton systems arising from the linearization of the nonlinear hyper-ROM when dealing with highly nonlinear elastodynamics problems [17], even if few basis functions are required to approximate the state solution in a low-dimensional subspace through, e.g., proper orthogonal decomposition (POD). An alternative formulation of DEIM in a finite element framework, known as unassembled DEIM (UDEIM) [53], has been proposed to preserve the sparsity of the problem, while in [44] a localized DEIM selecting smaller local subspace for the approximation of the nonlinear term is presented.

Semi-intrusive strategies, avoiding the ROM construction through a Galerkin projection, have been recently proposed exploiting surrogate models to determine the RB approximation. For instance, neural networks (NNs) or Gaussian process regression can be employed to learn the map between the input parameters and the reduced-basis expansion coefficients in a non-intrusive way [32, 33, 36, 52]. An approximation of the nonlinear term arising in projection-based ROMs is obtained in [26] through deep NNs (DNNs) that exploit the projection of FOM solutions. NNs have also also been recently applied in the context of operator inference for (parametrized) differential equations, combining ideas from classical model reduction with data-driven learning. For instance, the design of NNs able to accurately represent linear/nonlinear operators, mapping input functions to output functions, has been proposed recently in [40]; based on the universal approximation theorem of operators [16], a general deep learning framework, called DeepONet, has been introduced to learn continuous operators, such as solution operators of PDEs, using DNNs; see also [56]. In [45] a non-intrusive projection-based ROM for parametrized time-dependent PDEs including low-order polynomial nonlinear terms is considered, inferring an approximation of the reduced operators directly from data of the FOM. Finally, the obtained low-dimensional system is solved—in this case, the learning task consists in the solution to a least squares problem; see also [7]. Projection-based ROMs and machine learning have been fused in [47] aiming at the approximation of linear and quadratic ROM operators, focusing on the solution to a large class of fluid dynamics applications. Similarly, in [5] a non-intrusive technique, exploiting machine learning regression algorithms, is proposed for the approximation of ROM operators related to projection-based methods for the solution of parametrized PDEs. Finally, principal component analysis-based model reduction with a NNs for approximation has been combined in [10], in a purely data-driven fashion, of infinite-dimensional solution maps, such as the solution operator for time-dependent PDEs.

In this paper, we develop a novel semi-intrusive, deep learning-enhanced hyper-reduced order modeling strategy, which hereon we refer to as shape Deep-HyROMnet, by leveraging a Galerkin-RB method for solution dimensionality reduction and DNNs to perform hyper-reduction. Since the efficiency of the nonlinear ROM hinges upon the cost-effective approximation of the projections of the (discrete) reduced residual operator and its Jacobian (when an implicit numerical scheme is employed), the key idea is to overcome the computational bottleneck associated with classical, intrusive hyper-reduction techniques, like DEIM, by relying on DNNs to approximate otherwise expensive reduced nonlinear operators at a greatly reduced cost. Unlike data-driven-based methods, for which the predicted output is not guaranteed to satisfy the underlying PDE, our proposed method is physics-based, as it computes the ROM solution by actually solving the reduced nonlinear systems by means of the Newton method, thus exploiting the physics of the problem. A further benefit of the proposed Deep-HyROMnet method lies on the fact that the inputs given to the NNs are low-dimensional arrays, so that the overwhelming training times and costs that may be required by even moderately large FOM dimensions can be avoided. Note that we aim at efficiently approximating the nonlinear operators that result from the composition of the reduced solution operator—that maps the input parameter vector and time to the corresponding ROM solution—and the reduced residual/Jacobian operator, that maps the ROM solution to the reduced residual/Jacobian evaluated on the ROM solution. We apply the proposed methodology to the solution of problems in nonlinear solid mechanics, focusing on parametrized nonlinear elastodynamics and complex (e.g., exponential nonlinear) constitutive relations of the material undergoing large deformations, showing that the Deep-HyROMnet approach outperforms the Galerkin-RB method equipped with DEIM in terms of computational speed-up during the online stage, achieving the same level of accuracy results.

The paper is structured as follows. We recall the formulation of the RB method for nonlinear unsteady parametrized PDEs in Sect. 2, relying on POD for the construction of the reduced subspace and on DEIM as hyper-reduction technique (hence obtaining POD-Galerkin-DEIM ROMs). The proposed Deep-HyROMnet and the DNN architecture employed to perform reduced operator approximation are detailed in Sect. 3. The numerical performances of the resulting method are assessed in Sect. 4 on several benchmark problems related with nonlinear elastodynamics, highlighting some conclusions in Sect. 5.

2 Projection-Based ROMs: The Reduced Basis Method

Our goal is to pursue an efficient solution to nonlinear unsteady PDE problems depending on a set of input parameters, which can be written in abstract form as follows: given an input parameter vector ${\varvec{\mu }}\in \mathcal {P}$ and $\textbf{u}(0;{\varvec{\mu }})$, find $\textbf{u}(t;{\varvec{\mu }})\in V$ such that, $\forall t\in (0,T]$,

$$\begin{aligned} R(\textbf{u}(t;{\varvec{\mu }}),t;{\varvec{\mu }})=0 \quad \text {in } V', \end{aligned}$$

(1)

where the parameter space $\mathcal {P}\subset \mathbb {R}^P$ is a compact set, R is the residual of a second-order differential equation, and $V'$ is the dual of a suitable functional space $H^1_0(\varOmega )^m\subseteq V \subseteq H^1(\varOmega )^m$ over the bounded domain $\varOmega \subset \mathbb {R}^d$, where V depends on the boundary conditions at hand. In particular, we are interested in vector problems ($m=3$) set in $d=3$ dimensions. The role of the parameter vector ${\varvec{\mu }}$ depends on the particular application at hand; in the case of nonlinear elastodynamics, ${\varvec{\mu }}$ is for instance related to the coefficients of the constitutive relation, the material properties and the boundary conditions.

After discretising problem (1) in space and time, we end up with a fully-discrete nonlinear system

$$\begin{aligned} \textbf{R}(\textbf{u}_h^n({\varvec{\mu }}),t^n;{\varvec{\mu }}) = \textbf{0} \quad \text {in } \mathbb {R}^{N_h}, \end{aligned}$$

(2)

at each time step $t^n$, $n=1,\ldots ,N_t$, which can be solved by means of the Newton method: given ${\varvec{\mu }}\in \mathcal {P}$ and an initial guess $\textbf{u}_h^{n,(0)}({\varvec{\mu }})$, for $k\ge 0$, find $\mathbf {\delta u}_h^{n,(k)}({\varvec{\mu }})\in \mathbb {R}^{N_h}$ such that

$$\begin{aligned} \left\{ \begin{array}{llll} \textbf{J}(\textbf{u}_h^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }})\mathbf {\delta u}_h^{n,(k)}({\varvec{\mu }}) = - \textbf{R}(\textbf{u}_h^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }}) \\ \textbf{u}_h^{n,(k+1)}({\varvec{\mu }}) = \textbf{u}_h^{n,(k)}({\varvec{\mu }}) + \mathbf {\delta u}_h^{n,(k)}({\varvec{\mu }}) \end{array} \right. \end{aligned}$$

(3)

until suitable stopping criteria are fulfilled. Here, $\textbf{u}_h^{n,(k)}({\varvec{\mu }})$ represents the solution vector for a fixed parameter ${\varvec{\mu }}$ computed at time step $t^{n}$ and Newton iteration k, while $\textbf{R}\in \mathbb {R}^{N_h}$ and $\textbf{J}\in \mathbb {R}^{N_h\times N_h}$ denote the residual vector and the corresponding Jacobian matrix, respectively. In particular, $\textbf{u}_h^{n,(0)}({\varvec{\mu }})$ is selected as the solution vector obtained at time $t^{n-1}$ once Newton iterations have converged. We refer to (3) as the high-fidelity, FOM for problem (1). In particular, we rely on a Galerkin-FE method for space approximation, and consider implicit finite difference schemes for time discretization, which do not require restrictions on $\Delta t$ [48]. The high-fidelity dimension $N_h$ is determined by the underlying mesh and the chosen FE polynomial order and can be extremely large in case of very fine meshes.

To reduce the FOM numerical complexity, we introduce a projection-based ROM, by relying on the RB method [49]. The idea of the RB method is to suitably select $N\ll N_h$ vectors of $\mathbb {R}^{N_h}$, forming the so-called RB matrix $\textbf{V}\in \mathbb {R}^{N_h\times N}$, and to generate a reduced problem by performing a Galerkin projection of the FOM onto the subspace $V_N=\text {Col}(\textbf{V})\subset \mathbb {R}^{N_h}$ generated by these vectors. This method relies on the assumption that the reduced-order approximation can be expressed as a linear combination of few, problem-dependent, basis functions, that is

$$\begin{aligned} \textbf{u}_h^{n}({\varvec{\mu }})\approx \textbf{Vu}_N^{n}({\varvec{\mu }}) \end{aligned}$$

for $n=1,\ldots ,N_t$, where $\textbf{u}_N^{n}({\varvec{\mu }})\in \mathbb {R}^N$ denotes the vector of the ROM-dofs at time $t^n\ge 0$. The latter is obtained by imposing that the projection of the FOM residual computed on the ROM solution is orthogonal to the trial subspace (in the case of a Galerkin projection): given ${\varvec{\mu }}\in \mathcal {P}$, at each time $t^{n}$, for $n=1,\ldots ,N_t$, we seek $\textbf{u}_N^{n}({\varvec{\mu }})\in \mathbb {R}^{N}$ such that

$$\begin{aligned} \textbf{V}^T\textbf{R}(\textbf{Vu}_N^{n}({\varvec{\mu }}),t^{n};{\varvec{\mu }}) = \textbf{0}. \end{aligned}$$

From now on, we will denote the reduced residual $\textbf{V}^T\textbf{R}$ and the corresponding Jacobian $\textbf{V}^T\textbf{JV}$ as $\textbf{R}_N$ and $\textbf{J}_N$, respectively. Then, the associated reduced Newton problem at time $t^{n}$ reads: given $\textbf{u}_N^{n,(0)}({\varvec{\mu }})$, for $k\ge 0$, find $\mathbf {\delta u}_N^{n,(k)}({\varvec{\mu }})\in \mathbb {R}^{N}$ such that

$$\begin{aligned} \left\{ \begin{array}{llll} \textbf{J}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }})\mathbf {\delta u}_N^{n,(k)}({\varvec{\mu }}) = - \textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }}), \\ \textbf{u}_N^{n,(k+1)}({\varvec{\mu }}) = \textbf{u}_N^{n,(k)}({\varvec{\mu }}) + \mathbf {\delta u}_N^{n,(k)}({\varvec{\mu }}), \end{array} \right. \end{aligned}$$

(4)

until a suitable stopping criterion is fulfilled.

2.1 Solution-Space Reduction: Proper Orthogonal Decomposition

In this section we provide an overview of the proper orthogonal decomposition (POD) technique used to compute the reduced basis $\textbf{V}$ through the so-called method of snapshots [8, 14]. Let

$$\begin{aligned} \mathcal {M}_{u_h} = \{\textbf{u}_h^n({\varvec{\mu }})\in \mathbb {R}^{N_h}~|~{\varvec{\mu }}\in \mathcal {P}, ~n=1,\ldots ,N_t \} \end{aligned}$$

be the (discrete) solution manifold identified by the image of $\textbf{u}_h$, that is, the set of all the PDE solutions for ${\varvec{\mu }}$ varying in the parameter space and $t^n$ in the partition of the time interval. Our goal is to approximate $\mathcal {M}_{u_h}$ with a reduced linear manifold, the trial manifold

$$\begin{aligned} \mathcal {M}_{u_N}^{lin} = \{\textbf{Vu}_N^n({\varvec{\mu }})~|~\textbf{u}_N^n({\varvec{\mu }})\in \mathbb {R}^N, ~{\varvec{\mu }}\in \mathcal {P},~n=1,\ldots ,N_t \}. \end{aligned}$$

To do this, given $n_s<N_h$ sampled instances of ${\varvec{\mu }}\in \mathcal {P}$, the snapshots matrix $\textbf{S}$ is constructed by collecting column-wise the FOM solution $\textbf{u}_h^n({\varvec{\mu }}_\ell )$ at each time step $n=1,\ldots ,N_t$, for $\ell =1,\ldots ,n_s$, that is

$$\begin{aligned} \textbf{S} = \left[ \textbf{u}_h^1({\varvec{\mu }}_1)\left| \ldots \right| \textbf{u}_h^{N_t}({\varvec{\mu }}_1)\left| \ldots \right| \textbf{u}_h^1({\varvec{\mu }}_{n_s})\left| \ldots \right| \textbf{u}_h^{N_t}({\varvec{\mu }}_{n_s})\right] \in \mathbb {R}^{N_h\times N_t n_s}. \end{aligned}$$

Sampling can be performed, e.g., through a latin hypercube sampling design, as well as through suitable low-discrepancy points sets. The POD basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$ spanning the subspace $V_N$ is usually obtained by performing the singular value decomposition $\textbf{S}=\mathbf {U\Sigma Z}^T$ of $\textbf{S}$, and then collecting the first N columns of $\textbf{U}$, corresponding to the N largest singular values stored in the diagonal matrix ${\varvec{\Sigma }}= \text {diag}(\sigma _1,\ldots ,\sigma _{r})\in \mathbb {R}^{n_s\times n_s}$, with $\sigma _1\ge \dots \ge \sigma _{r}\ge 0$ and $r\le N_h\wedge n_s$ being the rank of $\textbf{S}$. This yields an orthonormal basis such that

$$\begin{aligned}&\Vert \textbf{S} - \textbf{V}\textbf{V}^T\textbf{S} \Vert _F^2 = \underset{\textbf{W}\in \mathbb {R}^{N_h\times N}:\textbf{W}^T\textbf{W}=\textbf{I}_N}{\min } \Vert \textbf{S} - \textbf{W}\textbf{W}^T\textbf{S} \Vert _F^2 = \sum _{i=N+1}^r \sigma _i^2, \end{aligned}$$

where $\Vert \cdot \Vert _F$ is the Frobenius norm. Hence, singular values’ decay directly impacts on the size N, which can be computed as the minimum integer satisfying

$$\begin{aligned} RIC(N) = \frac{\sum _{\ell =1}^{N}\sigma _i^2}{\sum _{\ell =1}^{r}\sigma _i^2} \ge 1-\varepsilon _{POD}^2 \end{aligned}$$

(5)

for a given tolerance $\varepsilon _{POD}>0$. In this work we exploit the so-called randomized-SVD, which offers a powerful tool to perform low-rank matrix approximations when dealing with massive datasets [34], such as high-dimensional snapshots matrices.

2.2 Hyper-Reduction: The Discrete Empirical Interpolation Method

In the case of parametrized PDEs featuring nonaffine dependence on the parameter and/or nonlinear (high-order polynomial or nonpolynomial) dependence on the field variable, a further level of reduction, known as hyper-reduction, must be introduced [30, 42]. Note that if nonlinearities only include quadratic (or, at most, cubic) terms and do not feature any parameter dependence, assembling of nonlinear terms in the ROM can be performed by projection of the corresponding FOM quantities, once and for all [28].

For the case at hand, the residual $\textbf{R}_N$ and the Jacobian $\textbf{J}_N$ appearing in the reduced Newton system (4) depend on the solution at the previous iteration and, therefore, must be computed at each step $k\ge 0$. It follows that, for any new instance of the parameter ${\varvec{\mu }}$, we need to assemble the high-dimensional FOM-arrays before projecting them onto the reduced subspace, entailing a computational complexity which is still of order $N_h$. To setup an efficient offline–online computational splitting, an approximation of the nonlinear operators that is independent of the high-fidelity dimension is required.

Several techniques have been employed to provide this further level of approximation [4, 6, 13, 15, 20]; among these, DEIM has been successfully applied to stationary or quasi-static nonlinear mechanical problems [11, 27]. Its key idea is to replace the nonlinear arrays in (4) with a collateral reduced basis expansion, computed through an inexpensive interpolation procedure. In this framework, the high-dimensional residual $\textbf{R}({\varvec{\mu }})$ is projected onto a reduced subspace of dimension $m<N_h$ spanned by a basis ${\varvec{\Phi }}_\mathcal {R}\in \mathbb {R}^{N_h\times m}$

$$\begin{aligned} \textbf{R}({\varvec{\mu }}) \approx {\varvec{\Phi }}_\mathcal {R}\textbf{r}({\varvec{\mu }}), \end{aligned}$$

where $\textbf{r}({\varvec{\mu }})\in \mathbb {R}^m$ is the vector of the unknown amplitudes. The matrix ${\varvec{\Phi }}_\mathcal {R}$ can be precomputed offline by performing POD on a set of high-fidelity residuals collected when solving (4) for $n_s'$ training input parameters

$$\begin{aligned} \textbf{S}_{{\varvec{\rho }}} =\left[ \textbf{R}(\textbf{Vu}_N^{n,(k)}({\varvec{\mu }}_\ell ),t^{n};{\varvec{\mu }}_\ell )), k\ge 0\right] _{n=1,\ldots ,N_t}^{\ell =1,\ldots ,n_s'}. \end{aligned}$$

The unknown parameter-dependent coefficient $\textbf{r}({\varvec{\mu }})$ is obtained online by collocating the approximation at the m components selected by a greedy procedure, and requiring that, for these components, $\textbf{P}^T\textbf{R}({\varvec{\mu }}) = \textbf{P}^T{\varvec{\Phi }}_\mathcal {R}\textbf{r}({\varvec{\mu }})$, so that

$$\begin{aligned} \textbf{r}({\varvec{\mu }}) = (\textbf{P}^T{\varvec{\Phi }}_\mathcal {R})^{-1}\textbf{P}^T\textbf{R}({\varvec{\mu }}), \end{aligned}$$

where $\textbf{P}\in \mathbb {R}^{N_h\times m}$ is the boolean matrix associated with the interpolation constraints. We thus define the hyper-reduced residual vector as

$$\begin{aligned} \textbf{R}_{N,m}({\varvec{\mu }}) := \textbf{V}^T{\varvec{\Phi }}_\mathcal {R}(\textbf{P}^T{\varvec{\Phi }}_\mathcal {R})^{-1}\textbf{P}^T\textbf{R}({\varvec{\mu }}) \approx \textbf{R}_N \equiv \textbf{V}^T\textbf{R}({\varvec{\mu }}). \end{aligned}$$

Finally, the associated Jacobian approximation $\textbf{J}_{N,m}({\varvec{\mu }})$ can be computed as the derivative of $\textbf{R}_{N,m}({\varvec{\mu }})$ with respect to the reduced displacement, obtaining

$$\begin{aligned} \textbf{J}_{N,m}({\varvec{\mu }}) = \textbf{V}^T{{\varvec{\Phi }}_\mathcal {R}}(\textbf{P}^T{{\varvec{\Phi }}_\mathcal {R}})^{-1} \textbf{P}^T\textbf{J}({\varvec{\mu }})\textbf{V}, \end{aligned}$$

or relying on the MDEIM algorithm [42], see [11, 41].

However, the application of DEIM in the case of nonlinear time-dependent PDEs can be rather inefficient, especially when turning to complex problem which require a high number of residual basis (and, thus, of interpolation points) to ensure the convergence of the hyper-reduced Newton system

$$\begin{aligned} \left\{ \begin{array}{llll} \textbf{J}_{N,m}(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }})\mathbf {\delta u}_N^{n,(k)}({\varvec{\mu }}) = - \textbf{R}_{N,m}(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }}) \\ \textbf{u}_N^{n,(k+1)}({\varvec{\mu }}) = \textbf{u}_N^{n,(k)}({\varvec{\mu }}) + \mathbf {\delta u}_N^{n,(k)}({\varvec{\mu }}). \end{array} \right. \end{aligned}$$

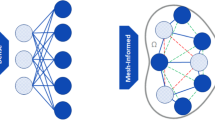
In fact, the m points selected by the DEIM algorithm correspond to a subset of nodes of the computational mesh, which, together with the neighboring nodes (i.e. those sharing the same cell), form the so-called reduced mesh; see, e.g., the sketch reported in Fig. 1. Since the entries of any FE-vector are associated with the dofs of the problem, $\textbf{P}^T\textbf{R}({\varvec{\mu }})$ is computed by integrating the residual only on the quadrature points belonging to the elements forming the reduced mesh, which, nevertheless, can be rather dense.

Fig. 1

Sketch of a reduced mesh for an hexahedral computational grid in two dimensions. The red dots represent the points selected by the DEIM algorithm and, together with the blue ones, yield the vertices of the elements (light blue) of the reduced mesh (Color figure online)

A modification of the DEIM algorithm, UDEIM, has been proposed in [54] to exploit the sparsity of the problem and minimize the number of element function calls. However, a high number of nonlinear function evaluations is still required when the number of magic points is sufficiently large. Indeed, DEIM-based affine approximations are effective, in terms of computational costs, provided that few entries of the nonlinear terms can be cheaply computed; however, this situation does not occur neither for dynamical systems arising from the linearization of a nonlinear system around a steady state, nor when dealing with global nonpolynomial nonlinearities.

In this paper, we propose an alternative technique to perform hyper-reduction, which is independent of the underlying mesh and relies on a DNN architecture to approximate reduced residual vectors and Jacobian matrices. The introduction of a surrogate model to perform operator approximation is justified by the fact that, often, most of the CPU time needed online for each new parameter instance is required by POD-Galerkin-DEIM ROMs for assembling arrays such as residual vectors or corresponding Jacobian matrices on the reduced mesh.

3 Operator Approximation: A Deep Learning-Based Technique (Deep-HyROMnet)

To recover the offline–online efficiency of the RB method, overcoming the need to assemble the nonlinear arrays onto the computational mesh as in the case of DEIM, we present a novel projection-based method which relies on DNNs for the approximation of the nonlinear terms. We refer to this strategy as to a hyper-reduced order model enhanced by deep neural networks (Deep-HyROMnet). Our goal is the efficient numerical approximation of the sets

which represents the reduced residual manifold and reduced Jacobian manifold, respectively, in a way that depends only on the ROM dimension N and on the number of parameters P. To achieve this task, we employ the DNN architecture developed in [23] for the so-called DL-ROM techniques. It is worthy to note that, except for the approximation error of the reduced nonlinear operators, the proposed Deep-HyROMnet approach is a physics-based method and that the computed solution satisfies the nonlinear equation of the problem at hand, up to a further approximation of ROM residual and Jacobian arrays—thus, similarly to what happened for a POD-Galerkin-DEIM ROM. The main idea of the deep learning-based operator approximation approach that replaces DEIM in our new Deep-HyROMnet strategy, is to learn the following input-to-residual and input-to-Jacobian maps, respectively:

$$\begin{aligned} {\varvec{\rho }}_N:({\varvec{\mu }},t^n,k)&\longmapsto \textbf{R}_N(\textbf{Vu}^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }}), \\ {\varvec{\iota }}_N:({\varvec{\mu }},t^n,k)&\longmapsto \textbf{J}_N(\textbf{Vu}^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }}), \end{aligned}$$

provided $({\varvec{\mu }},t^n,k)\in \mathcal {P}\times \{t^1,\ldots ,t^{N_t}\}\times \mathbb {N}^+$ as inputs and to finally replace the linear system in (4) with

$$\begin{aligned} {{\varvec{\iota }}}_N({\varvec{\mu }},t^n,k)\mathbf {\delta u}^{n,(k)}({\varvec{\mu }}) = - {{\varvec{\rho }}}_N({\varvec{\mu }},t^n,k). \end{aligned}$$

Hence, we aim at approximating the residual vector and the Jacobian matrix obtained after their projection onto the reduced space of dimension $N\ll N_h$. Indeed, performing a Galerkin projection onto the POD solution space allows to severely reduce the problem dimension from $N_h$ to N and, hence, to ease the learning task with respect the reconstruction of the full-order residual $\textbf{R}$ and Jacobian $\textbf{J}$.

Remark 1

As an alternative to Newton iterative scheme, we can rely on Broyden’s method [12], which belongs to the class of quasi-Newton methods. This allows to avoid the computation of the Jacobian matrix at each iteration $k\ge 0$ by relying on rank-one updates, based on residuals computed at previous iterations. However, we are able to compute Jacobian matrices very efficiently using automatic differentiation (AD), so that the computational burden is the assembling of residual vectors. For this reason, in this paper we will focus on the Newton method only, that is, the solution of problem (4).

To summarize, in the case of the Newton approach, we end up with the following reduced problem: given ${\varvec{\mu }}\in \mathcal {P}$ and, for $n=1,\ldots ,N_t$, the initial guess $\textbf{u}_N^{n,(0)}({\varvec{\mu }}) = \textbf{u}_N^{n-1}({\varvec{\mu }})$, find $\delta \textbf{u}_N^{n,(k)}\in \mathbb {R}^N$ such that, for $k\ge 0$,

$$\begin{aligned} \left\{ \begin{array}{llll} {\varvec{\iota }}_N({\varvec{\mu }},t^{n},k) \delta \textbf{u}_N^{n,(k)}({\varvec{\mu }}) = - {\varvec{\rho }}_N({\varvec{\mu }},t^{n},k), \\ \textbf{u}_N^{n,(k+1)}({\varvec{\mu }}) = \textbf{u}_N^{n,(k)}({\varvec{\mu }}) + \delta \textbf{u}_N^{n,(k)}({\varvec{\mu }}), \end{array} \right. \end{aligned}$$

(6)

until $\Vert {\varvec{\rho }}_N({\varvec{\mu }},t^n,k)\Vert _2 / \Vert {\varvec{\rho }}_N({\varvec{\mu }},t^n,0)\Vert _2 < \varepsilon$, where $\varepsilon >0$ is a given tolerance. In Algorithms 1 and 2, we report a summary of the offline and online stages of Deep-HyROMnet, respectively.

3.1 Deep Neural Network Construction

For the sake of generality, we will focus on the DNN-based approximation of the reduced residual vector only, that is

$$\begin{aligned} {{\varvec{\rho }}}_N({\varvec{\mu }},t^n,k) \approx \textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }})\in \mathbb {R}^N. \end{aligned}$$

In fact, by relying on a suitable transformation, we can easily write the Jacobian matrix as a vector of dimension $N^2$ and apply to it the same procedure described in the following for the residual vector. In particular, we define the transformation

$$\begin{aligned} vec:\mathbb {R}^{N\times N}\rightarrow \mathbb {R}^{N^2}, \quad vec(\textbf{J}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }})) = \textbf{j}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }}), \end{aligned}$$

which consists in stacking the columns of $\textbf{J}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }})$ in a vector that is passed to the DNN as training sample, thus obtaining

$$\begin{aligned} \widetilde{{\varvec{\iota }}}_N({\varvec{\mu }},t^n,k)\approx \textbf{j}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }})\in \mathbb {R}^{N^2}. \end{aligned}$$

Finally, the vec operation is reverted, so that ${{\varvec{\iota }}}_N({\varvec{\mu }},t^n,k) = vec^{-1}(\widetilde{{\varvec{\iota }}}_N({\varvec{\mu }},t^n,k))$.

We thus aim at efficiently approximating the whole set $\mathcal {M}_{R_N}$ by means of the reduced residual trial manifold, defined as

$$\begin{aligned} \mathcal {M}_{\rho _N} = \{ {{\varvec{\rho }}}_N({\varvec{\mu }},t^n,k) ~|~{\varvec{\mu }}\in \mathcal {P}, ~n=1,\ldots ,N_t, ~k\ge 0\}\subset \mathbb {R}^{N}. \end{aligned}$$

The approximation of the ROM residual $\textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }})$ takes the form

$$\begin{aligned} {\varvec{\rho }}_N({\varvec{\mu }},t^n,k) = \widetilde{\textbf{R}}_N({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{DF},{\varvec{\theta }}_{D}) = \textbf{f}^D_N({\varvec{\phi }}_q^{DF}({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{DF});{\varvec{\theta }}_{D}) \end{aligned}$$

where:

• ${\varvec{\phi }}_q^{DF}(\cdot ~;{\varvec{\theta }}_{DF}):\mathbb {R}^{P+2}\rightarrow \mathbb {R}^q$ such that

  $$\begin{aligned} {\varvec{\phi }}_q^{DF}({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{DF}) = \textbf{R}_q({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{DF}) \end{aligned}$$

  is a deep feedforward neural network (DFNN), consisting in the subsequent composition of a nonlinear activation function, applied to a linear transformation of the input, multiple times. Here, ${\varvec{\theta }}_{DF}$ denotes the vector of parameters of the DFNN, collecting all the corresponding weights and biases of each layer and q is as close as possible to the input size $P+2$;

• $\textbf{f}^D_N(\cdot ~;{\varvec{\theta }}_{D}):\mathbb {R}^q\rightarrow \mathbb {R}^N$ such that

  $$\begin{aligned} \textbf{f}^D_N(\textbf{R}_q({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{DF});{\varvec{\theta }}_{D}) = \widetilde{\textbf{R}}_N({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{DF},{\varvec{\theta }}_{D}) \end{aligned}$$

  is the decoder function of a convolutional autoencoder (CAE), obtained as the composition of several layers (some of which are convolutional), depending upon a vector ${\varvec{\theta }}_{D}$ collecting all the corresponding weights and biases.

The encoder function of the CAE is exploited, during the training stage only, to map the reduced residual $\textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }})$ associated to $({\varvec{\mu }},t^n,k)$ onto a low-dimensional representation

$$\begin{aligned} \textbf{f}^E_q(\textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }});{\varvec{\theta }}_{E}) = \widetilde{\textbf{R}}_q({\varvec{\mu }},t^n,k;{\varvec{\theta }}_{E}), \end{aligned}$$

where $\textbf{f}^E_q(\cdot ~;{\varvec{\theta }}_{E}):\mathbb {R}^N\rightarrow \mathbb {R}^q$ denotes the encoder function, depending upon a vector ${\varvec{\theta }}_{E}$ of parameters. The choice of a CAE is due to the fact that, thanks to the shared parameters and local connectivity properties which allow to reduce the numbers of parameters of the network and the number of associated computations, convolutional layers are better suited than dense layers to handle high-dimensional correlated data.

Remark 2

We point out that the input of the encoder function—that is, the reduced residual vector $\textbf{R}_N$—is reshaped into a square matrix by rewriting its elements in row-major order, thus obtaining $\textbf{R}_N^{reshape}\in \mathbb {R}^{\sqrt{N}\times \sqrt{N}}$. If N is not a square, the input $\textbf{R}_N$ is zero-padded as explained in [29], and the additional elements are subsequently discarded.

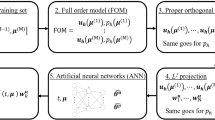
Regarding the prediction of the reduced residual for new unseen instances of the inputs, computing ${\varvec{\rho }}_N({\varvec{\mu }}_{test},t^n,k)$ for any given ${\varvec{\mu }}_{test}\in \mathcal {P}$, and for any possible $n=1,\ldots ,N_t$, $k\ge 0$, corresponds to the testing stage of a DFNN and of the decoder function of a convolutional AE. Thus, we discard the encoder function at testing time. The architecture used during the training stage is reported in Fig. 2; only the block highlited in the inner (red) box is then used during the testing phase.

Fig. 2

DNN architecture for the approximation of the reduced residual vector. A similar architecture is considered to approximate the reduced Jacobian matrix

Let $\textbf{M}\in \mathbb {R}^{(P+2)\times N_{train}}$, with $N_{train}=n_s'N_tN_k$, be the parameter matrix of the input triples, i.e.

$$\begin{aligned} \textbf{M} = \left[ \left( {\varvec{\mu }}_\ell ,t^n,k\right) \right] _{\ell =1,\ldots ,n_s',n=1,\ldots ,N_t,k\ge 0}. \end{aligned}$$

The corresponding training dataset for ${\varvec{\rho }}_N$ is given by the reduced residual snapshots matrix $\textbf{S}_{{\varvec{\rho }}}\in \mathbb {R}^{N\times N_{train}}$ defined as

$$\begin{aligned} \textbf{S}_{{\varvec{\rho }}} = \left[ \right.&\textbf{R}_N(\textbf{Vu}_N^{1,(1)}({\varvec{\mu }}_1),t^1;{\varvec{\mu }}_1)|\dots |\textbf{R}_N(\textbf{Vu}_N^{1,(N_{k_1})}({\varvec{\mu }}_1),t^1;{\varvec{\mu }}_1)|\\&\textbf{R}_N(\textbf{Vu}_N^{2,(1)}({\varvec{\mu }}_1),t^2;{\varvec{\mu }}_1)|\dots |\textbf{R}_N(\textbf{Vu}_N^{2,(N_{k_2})}({\varvec{\mu }}_1),t^2;{\varvec{\mu }}_1)|\\&\vdots \\&\textbf{R}_N(\textbf{Vu}_N^{N_t,(1)}({\varvec{\mu }}_{n_s'}),t^{N_t};{\varvec{\mu }}_{n_s'})|\dots |\textbf{R}_N(\textbf{Vu}_N^{N_t,(N_{k_{n_s'}})}({\varvec{\mu }}_{n_s'}),t^{N_t};{\varvec{\mu }}_{n_s'}) \left. \right] \\ =&\left[ \textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}),t^n;{\varvec{\mu }}_\ell )\right] _{\ell =1,\ldots ,n_s',n=1,\ldots ,N_t,k\ge 0}, \end{aligned}$$

that is, by the matrix collecting column-wise ROM residuals computed for $n_s'$ sampled parameters ${\varvec{\mu }}_\ell \in \mathcal {P}$, at different time instances $t^1,\ldots ,t^{N_t}$ and for each Newton iteration $k\ge 0$. The training stage consists in solving the following optimization problem in the weights variable ${\varvec{\theta }}= ({\varvec{\theta }}_{E},{\varvec{\theta }}_{DF},{\varvec{\theta }}_{D})$:

$$\begin{aligned} \mathcal {J}({\varvec{\theta }}) = \dfrac{1}{N_{train}}\sum _{\ell =1}^{n_s'}\sum _{n=1}^{N_t}\sum _{k=0}^{N_k}\mathcal {L}({\varvec{\mu }}_\ell ,t^n,k;{\varvec{\theta }}) \rightarrow \underset{{\varvec{\theta }}}{\min } \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \mathcal {L}({\varvec{\mu }}_\ell ,t^n,k;{\varvec{\theta }})&= \dfrac{1}{2} \Vert \textbf{R}_N(\textbf{V}\textbf{u}_N^{n,(k)}({\varvec{\mu }}_\ell ),t^n;{\varvec{\mu }}_\ell ) - \widetilde{\textbf{R}}_N({\varvec{\mu }}_\ell ,t^n,k;{\varvec{\theta }}_{DF},{\varvec{\theta }}_{D}) \Vert ^2 \\&\quad + \dfrac{1}{2} \Vert \widetilde{\textbf{R}}_q({\varvec{\mu }}_\ell ,t^n,k;{\varvec{\theta }}_{E}) - \textbf{R}_q({\varvec{\mu }}_\ell ,t^n,k;{\varvec{\theta }}_{DF}) \Vert ^2. \end{aligned} \end{aligned}$$

(7)

The loss function (7) combines the reconstruction error, i.e. the error between the ROM residual and the corresponding DNN approximation, and the error between the intrinsic coordinates and the output of the encoder. The training stage of the DNN involved in Deep-HyROMnet is detailed in Algorithm 3; in particular, we denote by $\alpha$ the training-validation splitting fraction, by $\eta$ the starting learning rate of the ADAM optimizer, by $N_b$ the batch size, by $n_b = (1-\alpha )N_{train}/N_b$ the number of minibatches and by $N_e$ the maximum number of epochs. We recall that the total number of training samples is given by $N_{train}= n_s'N_tN_k$. The testing stage of the DNN is detailed in Algorithm 4. As suggested by [23, 24], we set $\alpha =8:2$, $\eta =10^{-4}$, $N_b=20$ and $N_e=10^4$. To avoid overfitting, we employ the early-stopping regularization technique [29], that is, we stop the training if (and when) the loss evaluated on the validation set does not decrease over 500 epochs. Regarding the NN architecture, a 12-layer DFNN with 50 neurons per hidden layer and q neurons in the output layer is employed, where q is problem-dependent and set equal to the intrinsic dimension, i.e. $q = P + 2$ (the time instant and the Newton iteration are considered as additional parameters); further details about the CAE architecture are summarized in Tables 1 and 2. In all cases, except for the last convolutional layer of the decoder, we consider the ELU nonlinear activation function [18], selected by assessing the impact of different activation functions on the validation loss.

Table 1 Attributes of convolutional and dense layers of the encoder function of the CAE

Table 2 Attributes of dense and transposed convolutional layers of the decoder function of the CAE

Remark 3

Differently from the min-max scaling used in [23, 24], we standardize the input and output of the DNN as follows. After splitting the data into training and validation sets according to a user-defined training-validation splitting fraction ${\varvec{\alpha }}$, $\textbf{M} = \left[ \textbf{M}^{train},\textbf{M}^{val}\right]$ and $\textbf{S}_{{\varvec{\rho }}} = \left[ \textbf{S}_{{\varvec{\rho }}}^{train},\textbf{S}_{{\varvec{\rho }}}^{val}\right]$, we define for each row of the training set the corresponding mean and standard deviation

$$\begin{aligned} M_{mean}^i = \dfrac{1}{N_{train}} \sum _{j=1}^{N_{train}} M_{ij}^{train}, \quad M_{sd}^i = \sqrt{\dfrac{1}{N_{train}-1} \sum _{j=1}^{N_{train}} (M_{ij}^{train}-M_{mean}^i)^2}, \end{aligned}$$

so that parameters are normalized by applying the following transformation

$$\begin{aligned} M_{ij}^{train} \mapsto \dfrac{M_{ij}^{train}-M_{mean}^i}{M_{sd}^i}, \quad i=1,\ldots ,P+2, \quad j=1,\ldots ,N_{train}, \end{aligned}$$

(8)

that is, each feature of the training parameter matrix is standardized. The same procedure is applied to the training snapshots matrix $\textbf{S}_{{\varvec{\rho }}}^{train}$ by replacing $M^i_{*}$ with $S^i_{*}$, where $*\in \{mean,sd\}$ respectively. Transformation (8) is applied to the validation and testing sets as well, but considering the mean and the standard deviation computed over the training set. In order to rescale the reconstructed solution to the original values, we apply the inverse transformation.

4 Numerical Results

In this section we assess the performances of the proposed Deep-HyROMnet strategy on different applications related to parametrized nonlinear time-dependent PDE problems, focusing on structural mechanics. In particular, we consider (1) a series of structural tests on a rectangular beam, with different loading conditions and a simple nonlinear constitutive law, and then (2) a test case on an idealized left ventricle geometry, simulating cardiac contraction.

4.1 Nonlinear Elastodynamics

Let us consider a continuum body $\mathcal {B}$ embedded in a three-dimensional Euclidean space. For a given parameter vector ${\varvec{\mu }}\in \mathcal {P}$, the displacement vector field

$$\begin{aligned} \textbf{u}(\textbf{X},t;{\varvec{\mu }}) = \chi (\textbf{X},t;{\varvec{\mu }}) - \textbf{X} \end{aligned}$$

relates the material position $\textbf{X}$ of a particle in the reference configuration $\varOmega _0$, which we assume to coincide with the initial configuration, to its spatial position $\textbf{x}$ in the current configuration $\varOmega _t$ at time $t>0$, being $\chi (\textbf{X},t;{\varvec{\mu }}) = \textbf{x}$ the motion of the body. The corresponding deformation gradient

$$\begin{aligned} \textbf{F}(\textbf{X},t;{\varvec{\mu }}) = \frac{\partial \chi (\textbf{X},t;{\varvec{\mu }})}{\partial \textbf{X}} = \textbf{I} + \nabla _0 \textbf{u}(\textbf{X},t;{\varvec{\mu }}), \end{aligned}$$

characterizes the change of material elements during motion, so that the change in volume between the reference and the current configurations at time $t>0$ is given by $J(\textbf{X},t;{\varvec{\mu }}) = \det \textbf{F}(\textbf{X},t;{\varvec{\mu }})>0$. The equation of motion for a continuous medium reads as follows:

$$\begin{aligned} \rho _0\partial _t^2\textbf{u}(\textbf{X},t;{\varvec{\mu }}) - \nabla _0\cdot \textbf{P}(\textbf{F}(\textbf{X},t;{\varvec{\mu }})) = \textbf{b}_0(\textbf{X},t;{\varvec{\mu }}), \qquad \textbf{X}\in \varOmega _0,~t>0 \end{aligned}$$

where $\rho _0$ is the density of the body, $\mathbf {P(F)}$ is the first Piola-Kirchhoff stress tensor and $\textbf{b}_0$ is an external body force. Proper boundary and initial conditions must be specified to ensure the well-posedness of the problem. In addition, we need a constitutive equation for $\textbf{P}$, that is, a stress-strain relationship describing the material behavior. Here, we consider hyperelastic materials, for which the existence of a strain-energy density function $\mathcal {W}:Lin^+\rightarrow \mathbb {R}$ such that

$$\begin{aligned} \mathbf {P(F)} = \frac{\partial \mathcal {W}(\textbf{F})}{\partial \textbf{F}} \end{aligned}$$

is postulated. Note that, since $\textbf{F}$ depends on the displacement $\textbf{u}$, we can equivalently write $\mathbf {P(F)}$ or $\textbf{P}(\textbf{u})$.

The strong formulation of a general initial boundary-valued problem in elastodynamics thus reads as follows: given a body force $\textbf{b}_0 = \textbf{b}_0(\textbf{X},t;{\varvec{\mu }})$, a prescribed displacement $\bar{\textbf{u}} = \bar{\textbf{u}}(\textbf{X},t;{\varvec{\mu }})$ and surface traction $\bar{\textbf{T}} = \bar{\textbf{T}}(\textbf{X},t,\textbf{N};{\varvec{\mu }})$, find the unknown displacement field $\textbf{u}({\varvec{\mu }}):\varOmega _0\times (0,T]\rightarrow \mathbb {R}^3$ so that

$$\begin{aligned} \left\{ \begin{array}{lllr} \rho _0\partial ^2_t {\textbf{u}}(\textbf{X},t;{\varvec{\mu }}) - \nabla _0\cdot \textbf{P}(\textbf{u}(\textbf{X},t;{\varvec{\mu }})) = \textbf{b}_0(\textbf{X},t;{\varvec{\mu }}) &{}&{} \text {in } &{} \varOmega _0\times (0,T]\\ \textbf{u}(\textbf{X},t;{\varvec{\mu }}) = \bar{\textbf{u}}(\textbf{X},t;{\varvec{\mu }}) &{}&{} \text {on } &{} \Gamma _0^{D}\times (0,T]\\ \textbf{P}(\textbf{u}(\textbf{X},t;{\varvec{\mu }}))\textbf{N} = \bar{\textbf{T}}(\textbf{X},t,\textbf{N};{\varvec{\mu }}) &{}&{} \text {on } &{} \Gamma _0^{N}\times (0,T]\\ \textbf{P}(\textbf{u}(\textbf{X},t;{\varvec{\mu }}))\textbf{N} + \alpha \textbf{u}(\textbf{X},t;{\varvec{\mu }}) + \beta \partial _t\textbf{u}(\textbf{X},t;{\varvec{\mu }}) = \textbf{0} &{}&{} \text {on } &{} \Gamma _0^{R}\times (0,T]\\ \textbf{u}(\textbf{X},0;{\varvec{\mu }}) = \textbf{u}_0(\textbf{X};{\varvec{\mu }}),~~ \partial _t{\textbf{u}}(\textbf{X},0;{\varvec{\mu }}) = \dot{\textbf{u}}_0(\textbf{X};{\varvec{\mu }}) &{}&{} \text {in } &{} \varOmega _0\times \{0\} \end{array} \right. \end{aligned}$$

(9)

where $\textbf{N}$ is the outer normal unit vector and $\alpha ,\beta \in \mathbb {R}$. The boundary of the reference domain is partitioned such that $\Gamma _0^D\cup \Gamma _0^N\cup \Gamma _0^R = \Gamma$, with $\Gamma _0^i\cap \Gamma _0^j=\emptyset$ for $i,j\in \{D,N,R\}$. This equation is inherently nonlinear and additional source of nonlinearity is introduced in the material law, i.e. when using a nonlinear strain-energy density function $\mathcal {W} =\mathcal {W}(\textbf{F})$, which is often the case of engineering applications. For the sake of simplicity, in all test cases, we neglect the body forces $\textbf{b}_0({\varvec{\mu }})$ and consider zero initial conditions $\textbf{u}_0({\varvec{\mu }}) = \dot{\textbf{u}}_0({\varvec{\mu }}) = \textbf{0}$. Regarding boundary conditions, we consider $\bar{\textbf{u}}({\varvec{\mu }}) = \textbf{0}$ on the Dirichlet boundary $\Gamma _0^D$ and always assume $\alpha =\beta =0$, so that we actually impose homogeneous Neumann conditions on $\Gamma _0^R$. Finally, the traction vector is given by

$$\begin{aligned} \bar{\textbf{T}}(\textbf{X},t,\textbf{N};{\varvec{\mu }}) = -\textbf{g}(t;{\varvec{\mu }})J\textbf{F}^{-T}\textbf{N}, \end{aligned}$$

where $\textbf{g}(t;{\varvec{\mu }})$ represents an external load and will be specified according to the application at hand. Finally, the residual in (2) is given by

$$\begin{aligned} \begin{aligned} \textbf{R}(\textbf{u}_h^{n}({\varvec{\mu }}), t^{n};{\varvec{\mu }})&:= \left( \dfrac{\rho _0}{\Delta t^2}\mathcal {M} + \dfrac{1}{\Delta t}\mathcal {F}_{\beta }^{int} + \mathcal {F}_{\alpha }^{int}\right) \textbf{u}_h^{n}({\varvec{\mu }}) + \mathcal {S}(\textbf{u}_h^{n}({\varvec{\mu }})) \\ {}&\quad - \left( \dfrac{2\rho _0}{\Delta t^2}\mathcal {M} + \dfrac{1}{\Delta t}\mathcal {F}_{\beta }^{int}\right) \textbf{u}_h^{n-1}({\varvec{\mu }}) + \dfrac{\rho _0}{\Delta t^2}\mathcal {M}\textbf{u}_h^{n-2}({\varvec{\mu }}) - \mathcal {F}^{ext,n}({\varvec{\mu }}), \end{aligned} \end{aligned}$$

for $n=1,\ldots ,N_t$, where $\textbf{u}_h^0({\varvec{\mu }})$ and $\textbf{u}_h^{-1}({\varvec{\mu }})$ are known for the initial condition, and

$$\begin{aligned}&[\mathcal {M}]_{ij} = \int _{\varOmega _0} {\varvec{\varphi }}_j\cdot {\varvec{\varphi }}_id\varOmega , \\&[\mathcal {F}_{\beta }^{int}]_{ij} = \int _{\Gamma _0^R} \beta ~{\varvec{\varphi }}_j\cdot {\varvec{\varphi }}_i d\Gamma , \qquad [\mathcal {F}_{\alpha }^{int}]_{ij} = \int _{\Gamma _0^R} \alpha ~{\varvec{\varphi }}_j\cdot {\varvec{\varphi }}_i d\Gamma ,\\&[\mathcal {S}(\textbf{u}_h^n({\varvec{\mu }}))]_{i} = \int _{\varOmega _0} \textbf{P}(\textbf{u}_h^n({\varvec{\mu }})):\nabla {{\varvec{\varphi }}_i}d\varOmega , \\&[\mathcal {F}^{ext,n}({\varvec{\mu }})]_{i} = \int _{\Gamma _0^N} \bar{\textbf{T}}^n(\textbf{N};{\varvec{\mu }})\cdot {{\varvec{\varphi }}_i}d\Gamma + \int _{\varOmega _0} \textbf{b}_0^n({\varvec{\mu }})\cdot {{\varvec{\varphi }}_i}d\varOmega , \end{aligned}$$

for all $i,j=1,\ldots ,N_h$, being $\{{\varvec{\varphi }}_i\}_{i=1}^{N_h}$ a basis for the FE space.

As a measure of accuracy of the reduced approximations with respect to the FOM solution, we consider time-averaged $L^2$-errors of the displacement vector, that are defined as follows:

$$\begin{aligned} \begin{aligned} \epsilon _{abs}({\varvec{\mu }})&= \frac{1}{N_t}\sum _{n=1}^{N_t} \Vert \textbf{u}_h(\cdot ,t^n;{\varvec{\mu }}) - \textbf{Vu}_N(\cdot ,t^n;{\varvec{\mu }})\Vert _{2}, \\ \epsilon _{rel}({\varvec{\mu }})&= \frac{1}{N_t}\sum _{n=1}^{N_t} \frac{\Vert \textbf{u}_h(\cdot ,t^n;{\varvec{\mu }}) - \textbf{Vu}_N(\cdot ,t^n;{\varvec{\mu }})\Vert _{2}}{\Vert \textbf{u}_h(\cdot ,t^n;{\varvec{\mu }})\Vert _{2}}. \end{aligned} \end{aligned}$$

(10)

The CPU time ratio, that is the ratio between FOM and ROM computational times, is used to measure efficiency, since it represents the speed-up offered by the ROM with respect to the FOM. The code is implemented in Python in our software package pyfe$^\text {x}$, a Python binding with the in-house Finite Element library life$^\texttt {x}$ (https://lifex.gitlab.io/lifex), a high-performance C++ library based on the deal.II (https://www.dealii.org) Finite Element core [3]. Computations have been performed on a PC desktop computer with 3.70GHz Intel Core i5-9600K CPU and 16GB RAM, except for the training of the DNNs and the prediction of the reduced nonlinear operators that have been carried out on a Tesla V100 32GB GPU.

Furthermore, we introduce the following measures to evaluate the performance of the DNNs during the training process:

$$\begin{aligned} \begin{aligned}&\epsilon _{rel,\textbf{R}_N}=\frac{1}{n_s' N_t} \sum _{\ell =1}^{n_s'}\sum _{n=1}^{N_t} \textbf{E}(\textbf{R}_N,\widetilde{\textbf{R}}_N; {\varvec{\mu }}_\ell , t^n),\\&\epsilon _{rel,\textbf{J}_N}=\frac{1}{n_s' N_t} \sum _{\ell =1}^{n_s'}\sum _{n=1}^{N_t} \textbf{E}(vec(\textbf{J}_N),vec(\widetilde{\textbf{J}}_N); {\varvec{\mu }}_\ell , t^n), \end{aligned} \end{aligned}$$

(11)

for residual vectors and Jacobian matrices, respectively, where

$$\begin{aligned} \textbf{E}(\textbf{w},\widetilde{\textbf{w}};{\varvec{\mu }}_\ell , t^n) = \left( \frac{\sqrt{ \sum _{k=1}^{N_{k_\ell }} \Vert \textbf{w}(\textbf{Vu}_N^{n,(k)}({\varvec{\mu }}_\ell ),t^n;{\varvec{\mu }}_\ell ) - \widetilde{\textbf{w}}({\varvec{\mu }}_\ell ,t^n,k;\varvec{\theta }_{DF},\varvec{\theta }_{D})\Vert ^2}}{\sqrt{ \sum _{k=1}^{N_{k_\ell }} \Vert \textbf{w}(\textbf{Vu}_N^{n,(k)}({\varvec{\mu }}_\ell ),t^n;{\varvec{\mu }}_\ell )\Vert ^2}} \right) . \end{aligned}$$

4.2 Deformation of a Clamped Rectangular Beam

The first series of test cases represents a typical structural mechanical problem, with reference geometry $\bar{\varOmega }_0 = [0,10^{-2}]\times [0,10^{-3}]\times [0,10^{-3}]$ m$^3$, reported in Fig. 3.

Fig. 3

Rectangular beam geometry (left) and computational grid (right)

We consider a nearly-incompressible neo-Hookean material, which is characterized by the following strain density energy function

$$\begin{aligned} \mathcal {W}(\textbf{F}) = \frac{G}{2}(\mathcal {I}_1 - 3) + \frac{K}{4}( (J-1)^2 + \ln ^2(J) ), \end{aligned}$$

where $G>0$ is the shear modulus, $\mathcal {I}_1 = J^{-\frac{2}{3}}\det (\textbf{C})$ and the latter term is needed to enforce incompressibility, being the bulk modulus $K>0$ the penalization factor. This choice leads to the following first Piola-Kirchhoff stress tensor, characterized by a nonpolynomial nonlinearity,

$$\begin{aligned} \textbf{P}(\textbf{F}) = GJ^{-\frac{2}{3}}\left( \textbf{F} - \frac{1}{3}\mathcal {I}_1\textbf{F}^T\right) + \frac{K}{2}J\left( J-1+\frac{1}{J}\ln (J)\right) \textbf{F}^T. \end{aligned}$$

The beam is clamped at the left-hand side, that is, Dirichlet boundary conditions are imposed on the left face $x=0$, whilst a pressure load changing with the deformed surface orientation is applied to the entire bottom face $z=0$ (i.e. $\Gamma _0^N$). Homogeneous Neumann conditions are applied on the remaining boundaries (i.e. $\Gamma _0^R$ with $\alpha =\beta =0$). As possible functions for the external load $\textbf{g}(t;{\varvec{\mu }})$, we choose

• 1. A linear function $\textbf{g}(t;{\varvec{\mu }}) = \widetilde{p}~t/T$;

• 2. A triangular or hat function $\textbf{g}(t;{\varvec{\mu }}) = \widetilde{p}~\left( 2t~\chi _{\left( 0,\frac{T}{2}\right] }(t) + 2(T-t)~\chi _{\left( \frac{T}{2},T\right] }(t)\right)$;

• 3. A step function $\textbf{g}(t;{\varvec{\mu }}) = \widetilde{p}~\chi _{\left( 0,\frac{T}{3}\right] }(t)$, so that the presence of the inertial term is not negligible.

Here, $\widetilde{p}>0$ is a parameter controlling the maximum load. The FOM is built on a hexahedral mesh with 640 elements and 1025 vertices, resulting in a high-fidelity dimension $N_h=3075$ (since $\mathbb {Q}_1$-FE are employed). The resulting computational mesh in the reference configuration is reported in Fig. 3.

The following sections are organized as follows: first, we analyze the accuracy and the efficiency of the POD-Galerkin ROM without hyper-reduction with respect to the POD tolerance $\varepsilon _{POD}$, thus resulting in reduced subspaces of different dimensions $N\in \mathbb {N}$. Then, for a fixed basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$, POD-Galerkin-DEIM approximation capabilities are investigated for different sizes of the reduced mesh, associated with different values of the DEIM tolerance $\varepsilon _{DEIM}$ for the computation of the residual basis ${\varvec{\Phi }}_{\mathcal {R}}\in \mathbb {R}^{N_h\times m}$. Finally, the performances of Deep-HyROMnet are assessed and compared to those of DEIM-based hyper-ROMs.

4.2.1 Test Case 1: Linear Function for the Pressure Load

Let us consider the parametrized linear function

$$\begin{aligned} \textbf{g}(t;{\varvec{\mu }}) = \widetilde{p}~t/T, \end{aligned}$$

for the pressure load, describing a situation in which a structure is progressively loaded. We choose a time interval $t\in [0,0.25]$ s and employ a uniform time step $\Delta t = 5\times 10^{-3}$ s for the time discretization scheme, resulting in a total number of 50 time iterations. As parameters, we consider:

• The shear modulus $G\in [0.5\times 10^4,1.5\times 10^4]$ Pa;

• The bulk modulus $K\in [2.5\times 10^4,7.5\times 10^4]$ Pa;

• The external load parameter $\widetilde{p}\in [2,6]$ Pa.

Given a training set of $n_s=50$ points generated from the three-dimensional parameter space $\mathcal {P}$ through latin hypercube sampling (LHS), we compute the reduced basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$ using the POD method with tolerance

$$\begin{aligned} \varepsilon _{POD}\in \{10^{-3}, 5\times 10^{-4}, 10^{-4}, 5\times 10^{-5}, 10^{-5}, 5\times 10^{-6}, 10^{-6}\}. \end{aligned}$$

The corresponding reduced dimensions are $N=3$, 4, 5, 6, 8, 9 and 15, respectively. In Fig. 4 we show the singular values of the snapshot matrix related to the FOM displacement $\textbf{u}_h$, where a rapid decay of the plotted quantity means that a small number of RB functions is needed to correctly approximate the FOM solution.

Fig. 4

Test case 1. Decay of the singular values of the FOM solution snapshots matrix

The average relative error $\epsilon _{rel}$ between the FOM and the POD-Galerkin ROM solutions computed over a testing set of 50 randomly chosen parameters, different from the ones used to compute the solution snapshots, is reported in Fig. 5, together with the CPU time ratio. The approximation error decreases up to an order of magnitude when reducing the POD tolerance $\varepsilon _{POD}$ from $10^{-3}$ to $10^{-6}$, corresponding to an increase of the RB dimension from $N=3$ to $N=15$. Despite the low dimension of the POD space, the computational speed-up achieved by the reduced model is negligible. This is due to the fact that the ROM still depends on the FOM dimension $N_h$ during the online stage. For this reason, we need to rely on suitable hyper-reduction techniques.

Fig. 5

Test case 1. Average over 50 testing parameters of relative error $\epsilon _{rel}$ (left) and average speed-up (right) of ROM without hyper-reduction

For the construction of the hyper-reduced models, i.e. POD-Galerkin-DEIM ROMs and Deep-HyROMnet, we first need to compute snapshots from the ROM solutions for given parameter values and time instants, in order to build either the DEIM residual basis ${\varvec{\Phi }}_\mathcal {R}$ or train the DNNs. To this goal, we choose a POD-Galerkin ROM with dimension $N=4$, yielding a good balance between accuracy and computational effort for the test case at hand, and perform ROM simulations for a given set of $n_s'=200$ parameter samples to collect residual and Jacobian data. To investigate the impact of hyper-reduction on the ROM solution error, we compute the DEIM basis $\mathbf {{\varvec{\Phi }}}_{\mathcal {R}}$ for approximating the residual using different DEIM tolerances,

$$\begin{aligned} \varepsilon _{DEIM}\in \{10^{-3}, 5\times 10^{-4}, 10^{-4}, 5\times 10^{-5}, 10^{-5}, 5\times 10^{-6}, 10^{-6}\}, \end{aligned}$$

corresponding to $m=22$, 25, 30, 33, 39, 43, 51, respectively, DEIM basis functions. Larger tolerances were not sufficient to ensure the convergence of the Newton method for all considered combinations of parameters, so that higher speed-ups cannot be achieved by decreasing the basis dimension m. The average relative error $\epsilon _{rel}$ is evaluated over the testing set and plotted in Fig. 6, as well as the CPU time ratio. To compute the high-fidelity solutions, 26 s are required in average, while a POD-Galerkin-DEIM ROM, with $N=4$ and $m=22$, requires only 2.4 s, thus yielding a speed-up about 11 times compared to the FOM.

Fig. 6

Test case 1. Average over 50 testing parameters of relative error $\epsilon _{rel}$ (left) and average speed-up (right) of POD-Galerkin-DEIM with $N=4$

Data related to the performances of the POD-Galerkin-DEIM ROMs for $N=4$ and different values of m are shown in Table 3. The number of elements of the reduced mesh represents a small percentage of the one forming the original grid, so that the cost related to the residual assembling is remarkably alleviated. Nonetheless, it is evident how the main computational bottleneck is the construction of the reduced system at each Newton iteration, and in particular the assembling of the residual vector on the reduced mesh, which requires between $78\%$ and $88\%$ of the total (online) CPU time. In particular, almost $90\%$ of this computational time is required for assembling the residual $\textbf{R}(\textbf{Vu}_N^{n,(k)}({\varvec{\mu }}),t^{n};{\varvec{\mu }})$ on the reduced mesh, while computing the associated Jacobian matrix using the AD tool takes less than $1\%$.

Table 3 Test case 1. Computational data related to POD-Galerkin-DEIM with $N=4$ and different values of m

The performances of Deep-HyROMnet are first analyzed by considering different sizes of the training set, and then compared in terms of both accuracy and efficiency with those of different POD-Galerkin-DEIM ROMs.

From the evolution of the $L^2(\varOmega )$-absolute error displayed in Fig. 7 (left), averaged over 50 testing parameters values, we observe that relying on a training set of $n_s'=200$ ROM simulations results in an approximation accuracy up to two orders of magnitude higher than the one obtained for $n_s'=100$. On the other hand, further increasing the dimension of the dataset, e.g. $n_s'=300$, does not affect the results due to the fact that the NN architecture is kept fixed and, consequently, the additional information becomes redundant. For this reason, we focus on the results obtained with $n_s'=200$, corresponding to the same training parameters used for the construction of the DEIM bases.

Fig. 7

Test case 1. Evolution in time of the average $L^2(\varOmega _0)$-absolute error for $N=4$ computed using Deep-HyROMnet for different sizes of the training set (left) and that obtained using POD-Galerkin-DEIM and Deep-HyROMnet (for $n_s'=200$) hyper-ROMs (right)

The average of the absolute error $\epsilon _{abs}$, the relative error $\epsilon _{rel}$ and the CPU time ratio are reported in Table 4. Moreover, in Table 5 we report the relative errors (11) for the approximation of the reduced nonlinear arrays by means of the DNNs, computed on both training and testing sets, showing that the approximation of the ROM residual is the most challenging task due to the higher variability of the data. In terms of efficiency, Deep-HyROMnets outperform DEIM-based hyper-ROMs substantially, being almost 100 times faster than the POD-Galerkin-DEIM ROM exploiting $m=22$ DEIM basis functions, whilst achieving the same accuracy for $n_s'=200$. In particular, our Deep-HyROMnet approach allows us to compute the reduced solutions in less than 0.02 s, thus yielding an overall speed-up of order $\mathcal {O}(10^3)$ compared to the FOM.

Table 4 Test case 1. Computational data related to POD-Galerkin-DEIM ROMs and Deep-HyROMnet, for $N=4$

Table 5 Test case 1. Accuracy of the DNNs predictions on training and test sets

The evolution of the $L^2(\varOmega _0)$-absolute error, averaged over the testing parameters, is reported in Fig. 7 for both the reduction approaches considered. The final accuracy of the hyper-ROMs equals that of the ROM without hyper-reduction, i.e. $\epsilon _{rel}\approx 10^{-2}$, meaning that the projection error dominates over the nonlinear operators approximation error. The difference between the FOM and Deep-HyROMnet solutions at time $T=0.25$ s is shown in Fig. 8 in two scenarios.

Fig. 8

Test case 1. FOM (wireframe) and Deep-HyROMnet (colored) solutions at time $T=0.25$ s for ${\varvec{\mu }}= [1.3225\times 10^4~\text {Pa}, 3.9875\times 10^4~\text {Pa}, 3.43~\text {Pa}]$ (left) and ${\varvec{\mu }}= [0.6625\times 10^4~\text {Pa}, 5.8625\times 10^4~\text {Pa}, 4.89~\text {Pa}]$ (right) (Color figure online)

Table 6 collects the offline CPU time required for building the POD basis and collecting the ROM nonlinear operators, as well as the offline GPU time needed for training the DNN. Moreover, we report the total offline computational time—assuming that the training stages are run sequentially—and the break even point, that is the number of online FOM simulations that make the construction of the ROM affordable. We recall that FOM and POD-Galerkin ROM simulations are run in serial on a PC desktop computer with 3.70GHz Intel Core i5-9600K CPU and 16GB RAM, whereas the DNN are trained on a Tesla V100 32GB GPU.

Table 6 Test case 1. Offline time required for the construction of the ROMs (for $N=4$) and the equivalence in terms of FOM simulations

In order to improve the accuracy of the reduced solution, we should consider higher values of the RB dimension N. Nonetheless, by increasing the number of the POD basis functions, thus the size of the reduced nonlinear data, the task of the DNNs becomes more complex. As a matter of fact, from the results reported in Fig. 9, we observe that more training samples and a larger size of the neural networks are required when N increases, in order to achieve comparable results with the ones obtained for smaller values of the POD dimension. In particular, we have included an additional hidden layer in both the encoder and the decoder of the CAE, and considered a larger numbers of neurons in the dense layers. To conclude, we report in Table 7 the computational data associated with POD-Galerkin-DEIM and Deep-HyROMnet hyper-ROMs when $N=8$, but the same number of training snapshots and the same DNN architectures of previous case (i.e. $N=4$) are employed. As expected, the POD-Galerkin-DEIM method is able to provide more accurate approximations of the FOM solution by increasing the size m of the residual basis, albeit reducing the online speed-up substantially.

Fig. 9

Test case 1. Evolution in time of the average $L^2(\varOmega _0)$-absolute error computed using Deep-HyROMnet for different RB dimensions N (left) and different features of the DNNs, i.e. amount of training data and architecture size (right)

Table 7 Test case 1. Computational data related to POD-Galerkin-DEIM ROMs and Deep-HyROMnet, for $N=8$

4.2.2 Test Case 2: Hat Function for the Pressure Load

Let us now consider a piecewise linear pressure load given by

$$\begin{aligned} \textbf{g}(t;{\varvec{\mu }}) = \widetilde{p}~\left( 2\frac{t}{T}~\chi _{\left( 0,\frac{T}{2}\right] }(t) + 2\frac{T-t}{T}~\chi _{\left( \frac{T}{2},T\right] }(t)\right) , \end{aligned}$$

describing the case in which a structure is increasingly loaded until a maximum pressure is reached, and then linearly unloaded in order to recover the initial resting state. For the case at hand, we choose $t\in [0,0.35]$ s and $\Delta t = 5\times 10^{-3}$ s, resulting in a total number of 70 time steps. As parameter, we consider the external load parameter $\widetilde{p}\in [2,12]$ Pa; the shear modulus G and the bulk modulus K are fixed to $10^4$ Pa and $5\times 10^4$ Pa, respectively. Let us consider a training set of $n_s=50$ points generated from $\mathcal {P}=[2,12]$ Pa through LHS and build the RB basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$ with $N=4$, corresponding to $\varepsilon _{POD}=10^{-4}$. The singular values of the solution snapshots matrix are reported in Fig. 10.

Fig. 10

Test case 2. Decay of the singular values of the FOM solution

Given the Galerkin-ROM nonlinear data collected for $n_s'=300$ sampled parameters, different DEIM residual bases $\mathbf {{\varvec{\Phi }}}_{\mathcal {R}}$ are computed using different tolerances

$$\begin{aligned} \varepsilon _{DEIM}\in \{10^{-3}, 5\times 10^{-4}, 10^{-4}, 5\times 10^{-5}, 10^{-5}, 5\times 10^{-6}, 10^{-6}\}, \end{aligned}$$

corresponding to $m=14$, 16, 22, 24, 29, 31, 37 DEIM basis functions, respectively. Tolerances $\varepsilon _{DEIM}$ larger than the values reported above were not sufficient to ensure convergence of the Newton method for all the considered parameters.

Fig. 11

Test case 2. Average over 50 testing parameters of relative error $\epsilon _{rel}$ (left) and average speed-up (right) of POD-Galerkin-DEIM with $N=4$

The relative error $\epsilon _{rel}$, evaluated over a testing set of 50 parameters, is about $10^{-2}$ when using $m=14$ residual basis functions, and can be further reduced of one order of magnitude when increasing the DEIM dimension to $m=29$, albeit highly decreasing the CPU time ratio, as shown in Fig. 11.

Table 8 shows the comparison between the POD-Galerkin-DEIM (with $m=14$ and $m=29$) and the Deep-HyROMnet hyper-reduced models on a testing set of 50 parameter instances. As observed in the previous test case, Deep-HyROMnet is able to achieve good results in terms of accuracy, comparable with the fastest POD-Galerkin-DEIM ROM ($m=14$), at a greatly reduced cost. Also in this case, the speed-up achieved by our Deep-HyROMnet is of order $\mathcal {O}(10^3)$ with respect to the FOM, since less than 0.04 s are needed to compute the reduced solution for each new instance of the parameter, against a time of about 40 s required by the FOM, and of (at least) 3 s required by POD-Galerkin-DEIM ROMs.

Table 8 Test case 2. Computational data related to POD-Galerkin-DEIM ROMs and Deep-HyROMnet, for $N=4$

Fig. 12

Test case 2. Evolution in time of the average $L^2(\varOmega _0)$-absolute error for $N=4$ computed using POD-Galerkin-DEIM and Deep-HyROMnet

The evolution in time of the average $L^2(\varOmega _0)$-absolute error for the POD-Galerkin-DEIM and the Deep-HyROMnet models is shown in Fig. 12. The accuracy obtained using Deep-HyROMnet, although slightly lower than the ones achieved using a DEIM-based approximation, is satisfying in all the considered scenarios. Figure 13 shows the FOM and the Deep-HyROMnet displacements at different time instances obtained for a given testing parameter.

Fig. 13

Test case 2. FOM (wireframe) and Deep-HyROMnet (colored) solutions computed at different times for ${\varvec{\mu }}= [10.7375~\text {Pa}]$ (Color figure online)

We finally report in Table 9 the offline CPU and GPU times required for the test case at hand.

Table 9 Test case 2. Offline time required for the construction of the ROMs and the equivalence in terms of FOM simulations

4.2.3 Test Case 3: Step Function for the Pressure Load

As last test case for the beam geometry, we consider a pressure load acting on the bottom surface area for only a third of the whole simulation time, that is

$$\begin{aligned} \textbf{g}(t;{\varvec{\mu }}) = \widetilde{p}~\chi _{\left( 0,\frac{T}{3}\right] }(t), \end{aligned}$$

such that the resulting deformation features oscillations. This case is of particular interest in nonlinear elastodynamics, since the inertial term cannot be neglected, as it has a crucial impact on the deformation of the body. For the case at hand, we choose $t\in [0,0.27]$ s and a uniform time step $\Delta t = 3.6\times 10^{-3}$ s, resulting in a total number of 75 time iterations. Concerning the input parameters, we vary the external load $\widetilde{p}\in [2,12]$ Pa and consider $G=10^4$ Pa and $K=5\times 10^4$ Pa fixed.

We build the POD basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$ from a training set of $n_s=50$ FOM solutions using $\varepsilon _{POD}=10^{-3}$, obtaining also in this case a reduced dimension of $N=4$, and perform POD-Galerkin ROM simulations for a given set of $n_s'=300$ parameter samples to collect the nonlinear terms data necessary for the construction of both POD-Galerkin-DEIM and Deep-HyROMnet models. The DEIM basis $\mathbf {{\varvec{\Phi }}}_{\mathcal {R}}$ for the approximation of the residual is computed using as tolerances

$$\begin{aligned} \varepsilon _{DEIM}\in \{10^{-3}, 5\times 10^{-4}, 10^{-4}, 5\times 10^{-5}, 10^{-5}, 5\times 10^{-6}, 10^{-6}\}, \end{aligned}$$

where $\varepsilon _{DEIM}=10^{-3}$ is the larger tolerance that ensures the convergence of the reduced Newton algorithm for all testing parameters. The corresponding number of bases for $\textbf{R}$ is $m=18$, 20, 27, 30, 38, 40, 50, respectively. The results regarding the average relative error $\epsilon _{rel}$ and the computational speed-up, evaluated over 50 instances of the parameter, are shown in Fig. 14.

Fig. 14

Test case 3. Average over 50 testing parameters of relative error $\epsilon _{rel}$ (left) and average speed-up (right) of POD-Galerkin-DEIM with $N=4$

Like for the previous test cases, we compare POD-Galerkin-DEIM and Deep-HyROMnet ROMs, with respect to the displacement error and the CPU time ratio.

Table 10 Test case 3. Computational data related to POD-Galerkin-DEIM ROMs and Deep-HyROMnet, for $N=4$

As reported in Table 10, DNNs outperform DEIM substantially in terms of efficiency also in this case when handling the nonlinear terms. Indeed, Deep-HyROMnet yields a ROM that is more than 1000 times faster than the FOM (this latter requiring 51 s in average to be solved), still providing satisfactory results in terms of accuracy.

Fig. 15

Test case 3. FOM (wireframe) and Deep-HyROMnet (colored) solutions computed at different times (Color figure online)

In Fig. 15 the Deep-HyROMnet solution at different time instants for two different values of the parameter is shown, highlighting that our hyper-ROM is able to correctly capture the nonlinear behavior of the continuum body also when the inertial term cannot be neglected. Table 11 reports the offline times required for the construction of the ROMs in the present case.

Table 11 Test case 3. Offline time required for the construction of the ROMs and the equivalence in terms of FOM simulations

4.3 Passive Inflation and Active Contraction of an Idealized Left Ventricle

The second problem we are interested in is the inflation and contraction of a prolate spheroid geometry representing an idealized left ventricle (see Fig. 16) where the boundaries $\Gamma _0^R$, $\Gamma _0^N$ and $\Gamma _0^D$ represent the epicardium, the endocardium and the base of a left ventricle, respectively, the latter being the artificial boundary resulting from truncation of the heart below the valves in a short axis plane. We consider transversely isotropic material properties for the myocardial tissue, adopting a nearly-incompressible formulation of the constitutive law proposed in [31], whose strain-energy density function is given by $\mathcal {W}(\textbf{F}) = \frac{C}{2}(e^{Q(\textbf{F})} - 1)$, with the following form for Q to describe three-dimensional transverse isotropy with respect to the fiber coordinate system,

$$\begin{aligned} Q = b_{f} E_{ff}^2 + b_{s} E_{ss}^2 + b_{n} E_{nn}^2 + b_{fs}(E_{fs}^2 + E_{sf}^2) + b_{fn}(E_{fn}^2 + E_{nf}^2) + b_{sn}(E_{sn}^2 + E_{ns}^2). \end{aligned}$$

Fig. 16

Passive inflation and active contraction of an idealized left ventricle. Idealized truncated ellipsoid geometry (left) and computational grid (right)

here $E_{ij}$, $i,j\in \{f,s,n\}$, are the components of the Green-Lagrange strain tensor $\textbf{E} =\frac{1}{2}(\textbf{F}^T\textbf{F}-\textbf{I})$, the material constant $C>0$ scales the stresses and the coefficients $b_f$, $b_s$, $b_n$ are related to the material stiffness in the fiber, sheet and transverse directions, respectively. This leads to a (passive) first Piola-Kirchhoff stress tensor characterized by exponential nonlinearity. In order to enforce the incompressibility constraint, we consider an additional term $\mathcal {W}_{vol}(J)$ in the definition of the strain-energy density function, which must grow as the deformation deviates from being isochoric. A common choice for $\mathcal {W}_{vol}$ is a convex function with null slope in $J=1$, e.g.,

$$\begin{aligned} \mathcal {W}_{vol}(J) = \frac{K}{4}( (J-1)^2 + \ln ^2(J) ), \end{aligned}$$

where the penalization factor is the bulk modulus $K>0$. Furthermore, to reproduce the typical twisting motion of the ventricular systole, we need to take into account a varying fiber distribution and contractile forces. The fiber direction is computed using the rule-based method proposed in [51], which depends on parameter angles ${\varvec{\alpha }}^{epi}$ and ${\varvec{\alpha }}^{endo}$. Active contraction is modeled through the active stress approach [1], so that we add to the passive first Piola-Kirchoff stress tensor a time-dependent active tension, which is assumed to act only in the fiber direction

$$\begin{aligned} \textbf{P} = \left( \frac{\partial \mathcal {W}(\textbf{F})}{\partial \textbf{F}} + \frac{\partial \mathcal {W}_{vol}(J)}{\partial \textbf{F}}\right) + T_a(t)(\textbf{Ff}_0\otimes \textbf{f}_0), \end{aligned}$$

where $\textbf{f}_0\in \mathbb {R}^3$ denotes the reference unit vector in the fiber direction and $T_a$ is a parametrized function that surrogates the active generation forces. In our case, since we are modeling only the systolic contraction, we define

$$\begin{aligned} T_a(t) = \widetilde{T}_a~t/T, \quad t\in (0,T), \end{aligned}$$

with $\widetilde{T}_a>0$. To model blood pressure inside the chamber we assume a linearly increasing external load

$$\begin{aligned} \textbf{g}(t;{\varvec{\mu }}) = \hat{p}~t/T, \quad t\in (0,T). \end{aligned}$$

Since we want to assess the performance of Deep-HyROMnet in enhancing the myocardium contraction problem, we consider as unknown parameters those related to the active components of the strain-energy density function:

• The maximum value of the active tension $\widetilde{T}_a\in [49.5\times 10^3,70.5\times 10^3]$ Pa, and

• The fiber angles ${\varvec{\alpha }}^{epi}\in [-105.5,-74.5]^\circ$ and ${\varvec{\alpha }}^{endo}\in [74.5,105.5]^\circ$.

All other parameters are fixed to the reference values taken from [38], namely $b_{f}=8$, $b_{s}=b_{n}=b_{sn}=2$, $b_{fs}=b_{fn}=4$, $C=2\times 10^3$ Pa, $K=50\times 10^3$ Pa and $\widetilde{p}=15\times 10^3$. Regarding time discretization, we choose $t\in [0,0.25]$ s and a uniform time step $\Delta t = 5\times 10^{-3}$ s, resulting in a total number of 50 time iterations. The FOM is built on a hexahedral mesh with 4804 elements and 6455 vertices, depicted in Fig. 16, corresponding to a high-fidelity dimension $N_h=19365$, since $\mathbb {Q}_1$-FE (that is, linear FE on a hexahedral mesh) are used. In this case, the FOM requires almost 360 s to compute the solution dynamics for each parameter instance.

Given $n_s=50$ points obtained by sampling the parameter space $\mathcal {P}$, we construct the corresponding solution snapshots matrix $\textbf{S}_u$ and compute the POD basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$ using the POD method with tolerance

$$\begin{aligned} \varepsilon _{POD}\in \{10^{-3}, 5\times 10^{-4}, 10^{-4}, 5\times 10^{-5}, 10^{-5}, 5\times 10^{-6}, 10^{-6}\}. \end{aligned}$$

From Fig. 17, we observe a slower decay of the singular values of $\textbf{S}_u$ with respect to the structural problems of Sect. 4.2. In fact, we obtain larger reduced basis dimensions $N=16$, 22, 39, 50, 87, 109 and 178, respectively.

Fig. 17

Passive inflation and active contraction of an idealized left ventricle. Decay of the singular values of the FOM solution snapshots matrix

The error and the CPU speed-ups averaged over a testing set of 20 parameters are both shown in Fig. 18, as functions of the POD tolerance $\varepsilon _{POD}$.

Fig. 18

Passive inflation and active contraction of an idealized left ventricle. Average over 20 testing parameters of relative error $\epsilon _{rel}$ (left) and average speed-up (right) of ROM without hyper-reduction

Also in this case, the speed-up achieved by the ROM is negligible, since at each Newton iteration without hyper-reduction the ROM still depends on the high-fidelity dimension $N_h$. For what concerns the approximation error, we observe a reduction of almost two orders of magnitude when going from $N=16$ to $N=178$. The fact that greater POD dimension with respect to the previous test cases are now obtained, allows us to assess the performances of the Deep-HyROMnet approach both on small and large values of N.

Given the reduced basis $\textbf{V}\in \mathbb {R}^{N_h\times N}$ with $N=16$, we construct the POD-Galerkin-DEIM approximation by considering $n_s'=200$ parameter samples. Fig. 19 shows the decay of the singular values of $\textbf{S}_R$, that is, the snapshots matrix of the residual vectors $\textbf{R}(\textbf{Vu}_N^{n,(k)}({\varvec{\mu }}_{\ell '}),t^n;{\varvec{\mu }}_{\ell '})$. We observe that the reported curve decreases very slowly, so that we expect that a large number of basis functions is required to correctly approximate the nonlinear operators.

Fig. 19

Passive inflation and active contraction of an idealized left ventricle. Decay of the singular values of the ROM residual snapshots matrix

In fact, by computing ${\varvec{\Phi }}_{\mathcal {R}}\in \mathbb {R}^{N_h\times m}$ using the following DEIM tolerances,

$$\begin{aligned} \varepsilon _{DEIM}\in \{5\times 10^{-4}, 10^{-4}, 5\times 10^{-5}, 10^{-5}, 5\times 10^{-6}, 10^{-6}\}, \end{aligned}$$

we obtain $m=303$, 456, 543, 776, 902 and 1233, respectively. Higher values of $\varepsilon _{DEIM}$ (related to smaller dimensions m) were not sufficient to guarantee the convergence of the reduced Newton problem for all testing parameters. The average relative error over a set of 20 parameters and the computational speed-up are both reported in Fig. 20. In particular, we observe that the relative error is between $4\times 10^{-3}$ and $8\times 10^{-3}$, as we could expect from the projection error reported in Fig. 18, that is, POD-Galerkin-DEIM ROMs are able to achieve the same accuracy of the ROM without hyper-reduction.

Fig. 20

Passive inflation and active contraction of an idealized left ventricle. Average over 20 testing parameters of relative error $\epsilon _{rel}$ (left) and average speed-up (right) of POD-Galerkin-DEIM ROMs with $N=16$

The data reported in Table 12 leads to the same conclusions regarding the computational bottleneck of DEIM technique as those reported in Table 3. In fact, assembling the residual on the reduced mesh requires around $85\%$ of the online CPU time, thus undermining the hyper-ROM efficiency.

Table 12 Passive inflation and active contraction of an idealized left ventricle

Table 13 Passive inflation and active contraction of an idealized left ventricle

Table 14 Passive inflation and active contraction of an idealized left ventricle. Offline time required for the construction of the ROMs and the equivalence in terms of FOM simulations

Fig. 21

Passive inflation and active contraction of an idealized left ventricle. Evolution in time of the average $L^2(\varOmega _0)$-absolute error computed using POD-Galerkin-DEIM ROMs and Deep-HyROMnet, for $N=16$

Fig. 22

Passive inflation and active contraction of an idealized left ventricle. FOM (wireframe) and Deep-HyROMnet (colored) displacements (frontal view on top, lateral view in the middle) and corresponding difference (bottom) at time $T=0.25$ s for ${\varvec{\mu }}= [61942.5~\text {Pa},-77.5225^\circ , 87.9075^\circ ]$ (left), ${\varvec{\mu }}= [59737.5~\text {Pa},-102.3225^\circ , 91.1625^\circ ]$ (center) and ${\varvec{\mu }}= [50497.5~\text {Pa},-100.9275^\circ , 80.0025^\circ ]$ (right) (Color figure online)

Finally, Table 13 reports the computational data of POD-Galerkin-DEIM ROMs (for a number of magic points equals to $m=303$ and $m=543$) and Deep-HyROMnet, clearly showing that the latter outperforms the classical reduction strategy regarding the computational speed-up. In fact, Deep-HyROMnet is able to approximate the solution dynamics in 0.1 s, that is even faster than real-time given the timescale of the phenomenon at hand, while a POD-Galerkin-DEIM ROM requires 1 min in average, where the final simulation time T is set equal to 0.25 s. The offline CPU and GPU times are reported in Table 14. Although the Deep-HyROMnet error is slightly larger than the one obtained with a DEIM-based hyper-ROM (see Fig. 21), the results are satisfactory in terms of accuracy. In Fig. 22 the FOM and the Deep-HyROMnet displacements at time $T=0.25$ s are reported for three different values of the parameters, together with the error between the high-fidelity and the reduced solutions.

Table 15 reports the accuracy of the prediction on the interpolation functions, showing that the error on the reduced Jacobian matrix $\textbf{J}_N$ is of the same order of the corresponding reduced residual vector $\textbf{R}_N$ and one order of magnitude higher than in test case 4.2. This fact might be due to several issues, such as the larger dimension of the input, i.e., $N^2=256$ instead of $N^2=16$, the smaller size of the training set, and the overall increased complexity of the problem, either in the constitutive law and the geometry.

To conclude, we assess the performances of Deep-HyROMnet on a problem involving a higher FOM dimension. We still consider the test case described in this Section, however using a finer hexahedral mesh with 9964 elements and 13025 vertices, thus obtaining $N_h=39075$ as FOM dimension. In this case, about 13 minutes are required to compute the high-fidelity solution. On the other hand, a reduced basis of dimension $N=16$ is computed for $\varepsilon _{POD}=10^{-3}$; the computational data, averaged over a testing set of 20 parameter samples, are reported in Table 16. The online CPU time required by Deep-HyROMnet doubles as we double $N_h$, despite the same POD dimension $N=16$ has been selected, and the same level of accuracy is obtained. This mild dependence of our hyper-ROM on the FOM dimension $N_h$ is due to the reconstruction of the reduced solutions $\textbf{Vu}_N^n({\varvec{\mu }})$, for $n=1,\ldots ,N_t$, whereas the same computational time is required for the online assembling and solution of the reduced Newton systems. Nonetheless, the overall computational speed-up of Deep-HyROMnet increases as $N_h$ grows, while the number N of reduced basis function remains small, so that reduced solutions can be computed extremely fast.

Table 15 Passive inflation and active contraction of an idealized left ventricle

Table 16 Passive inflation and active contraction of an idealized left ventricle

5 Conclusions

In this work we have addressed the solution to parametrized, nonlinear, time-dependent PDEs arising in elastodynamics, by means of a new projection-based ROM, developed to accurately capture the state solution dynamics at a reduced computational cost with respect to high-fidelity FOMs. We focused on Galerkin-RB methods, characterized by a projection of the differential problem onto a low-dimensional subspace built, e.g., by performing POD on a set of FOM solutions, and by the splitting of the reduction procedure into a costly offline phase and an inexpensive online phase. Numerical experiments showed that, despite their highly nonlinear nature, elastodynamics problems can be reduced by exploiting projection-based strategies in an effective way, with POD-Galerkin ROMs achieving very good accuracy even in presence of a handful of basis functions. However, when dealing with nonlinear problems, a further level of approximation is required to make the online stage independent of the high-fidelity dimension.

Hyper-reduction techniques, such as DEIM, are necessary to efficiently handle the nonlinear operators. However, a serious issue is represented by the assembling (albeit onto a reduced mesh) of the approximated nonlinear operators in this framework. This observation suggested the idea of relying on surrogate models to perform operator approximation, overcoming the need to assemble the nonlinear terms onto the computational mesh. Pursuing this strategy, we have proposed a new projection-based, deep learning-based ROM, Deep-HyROMnet, which combines the Galerkin-RB approach with DNNs to assemble the reduced Newton system in an efficient way, thus avoiding the computational burden entailed by classical hyper-reduction strategies. This approach allows to rely on physics-based ROMs retaining the underlying structure of the physical model, as DNNs are employed only for the approximation of the reduced nonlinear operators. Regarding the offline cost of this hybrid reduction strategy, we point out that:

• FOM solutions are only required to build the POD-Galerkin ROM;

• A small number N of reduced basis functions is sufficient to accurately approximate the high-fidelity solution manifold, so that the arising reduced nonlinear systems can be solved efficiently;

• Since data on nonlinear operators are collected during Newton iterations at each time step, a smaller number of ROM simulations—compared to purely data-driven approaches—is sufficient for training the DNNs;

• Since training data are low-dimensional, we can avoid the overwhelming training times and costs that would be required by DNNs if FOM arrays were used.

The Deep-HyROMnet approach has been successfully applied on several test cases in nonlinear solid mechanics, showing remarkable improvements in terms of online CPU time with respect to POD-Galerkin-DEIM ROMs. Our goal in future works is to apply the developed strategy to other classes of nonlinear problems for which traditional hyper-reduction techniques represent a computational bottleneck.