1 Introduction

Convection-diffusion equations have been widely used to model many applications in engineering involving advection of scalar quantities such as density, temperature or concentration among others. For instance, convection-diffusion problems have been proposed to study water transport in soils [25], heat transfer of nanofluids [36], and the transport in ferrofluids under rotating magnetic fields [10]. On the other hand, various numerical methods have been developed in recent years to solve the convection-diffusion equations. Most of these computational techniques can be classified into three main categories: (i) Eulerian methods, (ii) Lagrangian methods and (iii) semi-Lagrangian methods. In the framework of finite elements, the most popular Eulerian methods are the streamline upwind Petrov-Galerkin methods [9, 11], Galerkin/least-squares methods [9, 26] and Taylor-Galerkin methods [12, 13]. However, it is well known that these Eulerian methods do not perform very satisfactory in the case of convection-dominated problems unless small time steps and highly refined grids are used in the simulations. In the case of pure convection problems as those considered in this study, these requirements are practically not feasible and may limit the performance of these Eulerian methods. The Lagrangian techniques on the other hand, are theoretically well suited for the numerical solution of advection problems due to the possibility of using large time steps in the simulations. In practice, the computational mesh for the Lagrangian methods moves along the fluid particle trajectory which may yield to mesh distortion after few time steps in the computations. Thus, because of this drawback, the Lagrangian methods are not recommended for the numerical solution of complex convection-diffusion problems. In the semi-Lagrangian methods known also in the framework of finite elements by Galerkin-characteristics, the computational mesh is taken to be fixed to overcome the drawback of the Lagrangian methods while keeping the advantage of the Lagrangian tracking algorithm along the characteristic curves. The main advantage of the Galerkin-characteristics method lies on the fact that the Courant-Friedrichs-Lewy (CFL) condition is highly relaxed compared to its Eulerian counterparts, see for example [15,16,17,18, 32, 39, 42]. In addition, the Lagrangian treatment in the Galerkin-characteristics algorithms greatly reduces the time truncation errors in the Eulerian methods, see [7, 8, 15, 38, 41] among others. Thus, the Galerkin-characteristics finite element method has the potential to be more suitable than the Eulerian and Lagrangian methods for convection-diffusion problems on unstructured meshes. Numerical assessment of the conventional Galerkin-characteristics method has been carried out in [16] for convection problems and comparisons to well-established Eulerian methods can also been found in this reference.

In general, most of Galerkin-characteristics finite element methods are second-order accurate in space and time but the accuracy of this class of numerical methods depends on the order of the interpolation polynomials used to compute the solution in the convection stage and on the time integration procedure for the diffusion operator. For example, to achieve a second-order accuracy in the Galerkin-characteristics finite element method, the interpolation polynomials have to be at least second-order accurate and the time integration must be at least semi-implicit for the diffusion terms. In addition, it has been observed that the error in the conventional Galerkin-characteristics finite element method for convection-diffusion problems decreases as the time step increases at certain range of parameters, see for instance [17, 18, 20]. High-order accurate numerical methods for convection-dominated problems have the potential to reduce the computational effort required for a given order of solution accuracy. The state of the art in this field is more advanced for the Eulerian methods than for the semi-Lagrangian methods. For example, high-order discretization techniques such as those relying on spectral or hp-finite element method have been shown to achieve fast convergence with low numerical diffusion and dispersion errors for advection-diffusion problems [22, 28]. The p-finite element method and hp-finite element method where introduced by Babuška, Szabó and their coworkers in the mid-1970s. It was shown that the hp-finite element method delivers exponential convergence for elliptic problems with piecewise analytic data, see the survey [6] and further references are therein. A similar performance was also proven for boundary-layer and singularly perturbed problems [33, 37]. A study reported in [5] reveals that the choice of high-order shape functions is critical to the stability and efficiency of the finite element procedure. Particularly, high-order finite elements based on Lobatto shape functions have proven to possess better conditioning compared to other types of high-order shape functions widely used in the literature [43]. Assessment of different high-order shape functions in [35], including Bernstein, Lobatto and Lagrange Gauss-Lobatto polynomials for interior acoustic problems, has shown the advantage of high-order polynomials in reducing the pollution errors and the good performance of Bernstein polynomials when combined with the Krylov subspace solvers. In a closely related study [19], Bernstein shape functions have been demonstrated to yield comparable, and even better performance in terms of accuracy and memory requirements compared to the well-established partition of unity finite method. The Bernstein polynomials are well known in the field of computer aided geometric design and computer graphics. However, their applications in the finite element community have until now not been widely adopted. Although hierarchical basis functions are often chosen in the design of high-order finite elements for their suitability in p-adaptivity, recently attention has been paid to the favorable properties of the Bernstein polynomials [1, 24, 29]. Especially, it has been shown that Bernstein-Bézier finite elements over simplicial domains, hexahedra and pyramids yield optimal complexity for the standard finite element spaces. In a more recent work [3], the Bernstein basis functions combined to an additive Schwarz preconditioner was successfully implemented for challenging applications including boundary layers, non-linear reaction-diffusion problems and wave propagation of solitons.

The main focus of the present study is the development of a class of high-order Galerkin-characteristics finite element methods to numerically solve convection-dominated problems. This goal is achieved by the implementation of Bernstein-Bézier finite elements for the Galerkin-characteristics method. It should be stressed that combining the Galerkin-characteristics method with the Bernstein-Bézier finite elements, to the best of our knowledge, is reported for the first time. In the context of Galerkin-characteristics finite element methods, Bernstein polynomials are used as shape functions associated with elements of the computational mesh to calculate the departure points and update the global solutions. The positivity of these local basis functions and the variation diminishing properties make them a very attractive alternative to the standard Lagrange polynomials. To increase the efficiency of the proposed method, we also implement an efficient preconditioned iterative solver using the mass matrix as a preconditioner as proposed in [3]. The key idea behind this considered algorithm lies on the static condensation of the cell-based Degrees of Freedoms (DoFs) on each element and it can be viewed as an extension of the Additive Schwarz method. This results in a p-independent uniform bound on the growth of the associated condition number. It should also be noted that in case of the pure convection problem, the resulting linear system in the proposed semi-Lagrangian method consists of the mass matrix which make the proposed preconditioned conjugate gradient solver more convenient than its convection-diffusion counterpart. Furthermore, for the convection-dominated problems the growth of the condition number is relaxed by the viscosity coefficient and therefore, the performance of the considered linear solver is not affected. Numerical results presented in this work demonstrate that an interesting feature of the Bernstein-Bézier finite elements is to allow large time steps and coarse meshes in the simulations without deteriorating the high-order accuracy of the computed solutions.

This paper is organized as follows. Introduction of the Bernstein-Bézier finite element discretization is presented in Sect. 2. Section 3 is devoted to the formulation of the Bernstein-Bézier Galerkin-characteristics finite element method for pure convection problems. This section includes the calculation of characteristic curves and the implementation of the computational algorithm. The extension of the method for solving convection-diffusion equations is discussed in Sect. 4. In Sect. 5, we examine the numerical performance of the proposed method using several test examples of convection-diffusion problems including the viscous Burger equation. The proposed Bernstein-Bézier Galerkin-characteristics finite element method is demonstrated to enjoy the expected high-order accuracy as well as efficiency. Concluding remarks are summarized in Sect. 6.

2 Bernstein-Bézier Finite Element Approximation

In order to formulate our Galerkin-characteristics method, the computational domain \(\Omega \) assumed for simplicity to be a two dimensional bounded and polygonal domain, is first partitioned into non-overlapping triangular finite elements. Let \(\widehat{T}\) be the reference element defined by

(1)

where \(\widehat{q}_1 = (0,0)\), \(\widehat{q}_2 = (1,0)\) and \(\widehat{q}_3 = (0,1)\) are vertices of the reference element as shown in Fig. 1. The barycentric coordinates \(\lambda _i\) (\(i=1,2,3\)) relative to the reference element \(\widehat{T}\) are defined by

$$\begin{aligned} \lambda _1(\varvec{\xi })= \xi _1, \qquad \lambda _2(\varvec{\xi })=\xi _2\qquad \text {and}\quad \lambda _3(\varvec{\xi })=1-\xi _1-\xi _2. \end{aligned}$$
(2)

The Bernstein-Bézier basis for the space \(\mathbb {P}_p(\widehat{T})\) of polynomials of total degree at most p consists of the following shape functions:

  • Vertex-based shape functions defined by

    $$\begin{aligned} B_{(p,0,0)}^p(\varvec{\xi })= \lambda _{1}^{p}(\varvec{\xi }),\qquad B_{(0,p,0)}^p(\varvec{\xi }) = \lambda _{2}^{p}(\varvec{\varvec{\xi }}),\qquad B_{(0,0,p)}^p(\varvec{\xi }) = \lambda _{3}^{p}(\varvec{\xi }), \end{aligned}$$

  • Edge-based shape functions defined by

    $$\begin{aligned} B_{(p-k,k,0)}^{p}(\varvec{\xi }) = \begin{pmatrix} p\\ k \end{pmatrix} \lambda _{1}^{p-k}(\varvec{\xi })\lambda _{2}^{k}(\varvec{\xi }),&\qquad 1 \leqslant k \leqslant p-1,\\ B_{(0,p-k,k)}^{p}(\varvec{\xi }) = \begin{pmatrix} p\\ k \end{pmatrix} \lambda _{2}^{p - k}(\varvec{\xi })\lambda _{3}^{k}(\varvec{\xi }),&\qquad 1 \leqslant k \leqslant p-1,\\ B_{(k,0,p-k)}^{p}(\varvec{\xi }) = \begin{pmatrix} p \\ k \end{pmatrix} \lambda _{3}^{p- k}(\varvec{\xi })\lambda _{1}^{k}(\varvec{\xi }),&\qquad 1 \leqslant k \leqslant p-1. \end{aligned}$$

  • Cell-based shape functions defined by

$$\begin{aligned} B^{p}_{(i,j,p-i-j)}(\varvec{\xi })\! = \!\begin{pmatrix} p \\ i+j \end{pmatrix}\begin{pmatrix} i+j \\ i \end{pmatrix} \lambda _{1}^i(\varvec{\xi })\lambda _{2}^j(\varvec{\xi })\lambda _{3}^{ p-i-j}(\varvec{\xi }),\!\!\quad 1 \!\leqslant \! i \!\leqslant \! p-2,\!\!\quad 1 \!\leqslant \! i+j\! \leqslant \! p-1. \end{aligned}$$

For a multi-index \(\varvec{\alpha }\in \mathbb {Z}^3_+\), we define \(\displaystyle |\varvec{\alpha }|=\sum ^3_{i=1}\alpha _i\) and \(\displaystyle \varvec{\alpha }!=\prod ^3_{i=1}\alpha _i!\). Let \(\varvec{\alpha },\varvec{\beta }\in \mathbb {Z}^3_+\) such that \(\varvec{\beta }\geqslant \varvec{\alpha }\) i.e., \(\beta _i \geqslant \alpha _i\) for \(\leqslant i \leqslant 3\), we set \(\displaystyle \left( {\begin{array}{c}\varvec{\beta }\\ \varvec{\alpha }\end{array}}\right) =\prod ^3_{i=1}\left( {\begin{array}{c}\beta _i\\ \alpha _i\end{array}}\right) \). Using these notations, the Bernstein-Bézier shape functions can also be formulated in a simple compact form as

$$\begin{aligned} B^{p}_{\varvec{\alpha }}=\left( {\begin{array}{c}p\\ \varvec{\alpha }\end{array}}\right) \prod ^3_{i=1}\lambda ^{\alpha _i}_i, \end{aligned}$$
(3)

where \(\left( {\begin{array}{c}p\\ \varvec{\alpha }\end{array}}\right) = \frac{p!}{\varvec{\alpha }!}\) and \(|\varvec{\alpha }|=p.\) It should also be stressed that one of the most important proprieties of the Bernstein polynomials lies on the fact that their product yields a scaled Bernstein polynomial as

$$\begin{aligned} B^{p}_{\varvec{\alpha }}(\varvec{\xi })B^{q}_{\varvec{\beta }}(\varvec{\xi })=\frac{\begin{pmatrix} \varvec{\alpha }+\varvec{\beta }\\ \varvec{\alpha } \end{pmatrix}}{\begin{pmatrix} p+q\\ p \end{pmatrix}}B^{p+q}_{\varvec{\alpha }+\varvec{\beta }}(\varvec{\xi }), \end{aligned}$$
(4)

where \(|\varvec{\alpha }|=p\) and \(|\varvec{\beta }|=q\). Furthermore the integral of a Bernstein polynomial over the reference triangle element has a simple form

$$\begin{aligned} {\displaystyle \int _{\widehat{T}} B^{p}_{\varvec{\alpha }}(\varvec{\xi }) d\varvec{\xi } = \frac{|\widehat{T}|}{\begin{pmatrix} p+2\\ 2 \end{pmatrix}}} \end{aligned}$$
(5)

On the other hand the gradient of Bernstein polynomials can be computed as follows:

$$\begin{aligned} {\displaystyle \nabla B^{p}_{\varvec{\alpha }}(\varvec{\xi }) = p\sum _{k=1}^{3}B^{p-1}_{\varvec{\alpha }-\varvec{e}_k}(\varvec{\xi })\nabla \lambda _k }, \end{aligned}$$
(6)

where \(\varvec{e}_k\) is a multi-index with its kth entry is a unity and its remaining entries are zero, and \(B^{p-1}_{\varvec{\alpha }-\varvec{e}_k}=0\) if \(\varvec{\alpha }-\tilde{\varvec{e}}_k\) has a negative component. It should be noted that the Bernstein polynomials are non-negative and form a partition of unity on the element \(\widehat{T}\). Moreover, these polynomials have some attractive features such as variation diminishing and monotonicity preserving properties, see for instance [21, 23] and further references can be found therein.

Fig. 1
figure 1

A schematic diagram showing the main quantities used in the approximation of the departure points. Here, T is a given mesh element, \(\varvec{\xi }_{\varvec{j}}\) is a Stroud quadrature point used in the reference element \(\widehat{T}\) and mapped onto \(\varvec{x}_{h{\varvec{j}}}\) in the element T, \(T^*_{\varvec{j}}\) is the host element where the departure point \({{\varvec{\mathcal {X}}}_{h\varvec{j}}^n}\) belongs, and \(\Phi _{T}\) is the affine one-to-one mapping

Full size image

Following the same procedure carried out in the classical finite element methods, each mesh element T in the triangulation \(\mathcal {T}_h\) is mapped to the reference element \(\widehat{T}\) in which all computations are performed. Here, we use the following reference affine map

$$\begin{aligned} \varvec{x}=\Phi _{T}(\varvec{\xi })=\lambda _1(\varvec{\xi })\varvec{q}_1+\lambda _2(\varvec{\xi })\varvec{q}_2+\lambda _3(\varvec{\xi })\varvec{q}_3, \end{aligned}$$
(7)

where \(\varvec{q}_1\), \(\varvec{q}_2\) and \(\varvec{q}_3\) are the vertices of the physical element T. The conforming finite element space for the solution that we consider is defined as

$$\begin{aligned} {\displaystyle {V}_h } = {\displaystyle \left\{ {w}_h\in {C}^0(\bar{\Omega }):\quad {w}_h\Big |_{T}\circ \Phi _{T}\in \mathbb {P}_p ( \widehat{T} ),\quad \forall ~T \in \mathcal {T}_h \right\} }. \end{aligned}$$
(8)

For a polynomial degree \(p\geqslant 1\), the number of Degrees of Freedom (DoF) per element is given by

$$\begin{aligned} N^e={\left\{ \begin{array}{ll} 3, &{}\quad \text {if}\quad p=1,\\ 6, &{}\quad \text {if}\quad p=2,\\ 3 + 3(p-1)+\dfrac{(p-2)(p-1)}{2}, &{}\quad \text {if}\quad p\geqslant 3. \end{array}\right. } \end{aligned}$$
(9)

Note that, in contrast to the Lagrange finite elements where the degrees of freedom refer to nodal point evaluations, a global orientation of edges is required to enable matching edge modes of a similar shape, thus ensuring \(C^0\) conformity [19, 28, 43]. Finite element approximations with varying polynomial order can also be used by assigning to each vertex, edge and cell in the mesh an arbitrary polynomial degree, see [1, 19] among others.

3 Bernstein-Bézier Finite Element Galerkin-Characteristics Method

To describe the formulation of the proposed Bernstein-Bézier finite element Galerkin-characteristics method, we consider the following two-dimensional Cauchy problem for the convection equation

$$\begin{aligned} \frac{Dc}{Dt} := \frac{\partial c}{\partial t} + {{\varvec{v}}}(\varvec{x},t)\cdot \nabla {c}= & {} 0,\qquad ({\varvec{x}},t) \in \Omega \times (0,T],\nonumber \\ c({\varvec{x}},0)= & {} c_0({\varvec{x}}),\qquad {\varvec{x}} \in \Omega , \end{aligned}$$
(10)

where \({\varvec{x}} = (x,y)^{\top }\) is the space variable, \(\nabla {c} = (\frac{\partial c}{\partial x},\frac{\partial c}{\partial y})^{\top }\) is the gradient vector, \(\Omega \) is a spatial bounded domain in with boundary \(\partial \Omega \), and [0, T] is a time interval. Here, \(c({\varvec{x}},t)\) denotes the concentration of some species, \({{\varvec{v}}}({\varvec{x}},t) = \left( u({\varvec{x}},t),v({\varvec{x}},t)\right) ^\top \) is the velocity field assumed to depend on the solution c as well, and \(c_0({\varvec{x}})\) is a given initial function. We assume that appropriate boundary conditions are given in such a way the problem is well defined and has a unique solution. Note that \(\frac{Dc}{Dt}\) in (10) measures the rate of change of the concentration c following the trajectories of the flow particles. The main idea behind the Galerkin-characteristics method is to impose a regular grid at the new time level and to backtrack the flow trajectories to the previous time level. At the old time level, the quantities that are needed are evaluated by interpolation from their known values on a regular grid.

Next, we divide the time interval [0, T] into N subintervals \([t_n,t_{n+1}]\) with length \(\Delta t = t_{n+1}-t_n\) for \(n = 0,1,\dots ,N\). We use the notation \(w^n\) to denote the value of a generic function w at time \(t_n\). Hence, the characteristic curves associated with the convection problem (10) are the solution of the backward differential equation

$$\begin{aligned} \frac{d{\varvec{\mathcal {X}}}(\tau ;\varvec{x},t_{n+1})}{d\tau }= & {} {\varvec{v}}\bigl (\varvec{\mathcal {X}}(\tau ;\varvec{x},t_{n+1}),\tau \bigr ),\quad \tau \in [t_n,t_{n+1}],\nonumber \\ \varvec{\mathcal {X}}(t_{n+1};t_{n+1},\varvec{x})= & {} \varvec{x}, \end{aligned}$$
(11)

where \(\varvec{\mathcal {X}}(\tau ;\varvec{x},t_{n+1}) = \bigl (X(\tau ;\varvec{x},t_{n+1}),Y(\tau ;\varvec{x},t_{n+1})\bigr )^\top \) is the departure point at time \(\tau \) of a particle that will arrive at \(\varvec{x}= \left( x,y\right) ^\top \) at time \(t_{n+1}\). Note that the Galerkin-characteristics methods do not follow the flow particles forward in time, as the Lagrangian schemes do, instead they trace backwards the position at time \(t_n\) of particles that will reach the points of a fixed mesh at time \(t_{n+1}\), see Fig. 1 for an illustration. By so doing, the Galerkin-characteristics methods avoid the grid distortion difficulties that the conventional Lagrangian methods have. The solution of the differential eq. (11) can be expressed as

$$\begin{aligned} {{\varvec{\mathcal {X}}}(t_n;{\varvec{x}},t_{n+1})} = {\varvec{x}}-\int _{t_n}^{t_{n+1}}{{\varvec{v}}}\left( {\varvec{\mathcal {X}}}(\tau ;{\varvec{x}},t_{n+1}),\tau \right) \;d\tau . \end{aligned}$$
(12)

Hence, integrating the convection eq. (10) along the characteristic curves yields

$$\begin{aligned} {{c}}^{n+1}({\varvec{x}})= {{c}}^{n}\left( {\varvec{\mathcal {X}}}(t_n;{\varvec{x}},t_{n+1})\right) . \end{aligned}$$
(13)

Note that the Bernstein polynomials are not interpolatory by reconstruction i.e., the degrees of freedom associated to the shape functions do not directly lie on the solution evaluated at control points. Hence, the solution at the next time level should be obtained by a weak formulation. Thus, multiplying both sides of equation (13) by a test function \(w \in H^1\left( \Omega \right) \) and integrating over \(\Omega \), it leads to the following weak form

$$\begin{aligned} \int _\Omega w\;{{c}}^{n+1}\;d\varvec{x}=\int _\Omega w\;{{c}}^{n}\circ {\varvec{\mathcal {X}}}^n\;d\varvec{x}. \end{aligned}$$
(14)

Here, the finite element solution \(c^{n+1}_h\) is sought element-wise at each time step as

$$\begin{aligned} c^{n+1}_h(\varvec{x})=\sum _{|\varvec{\alpha }|=p}C^{n+1}_{\varvec{\alpha }} B^{p}_{\varvec{\alpha }}(\varvec{\xi }), \end{aligned}$$
(15)

with \(\varvec{x} = \Phi _{T}(\varvec{\xi })\) and \(T \in \mathcal {T}_h\). The approximation of the weak form (14) using the conforming finite element space \(V_h\) yields the following linear system of algebraic equations

$$\begin{aligned} \varvec{M}\varvec{C}^{n+1}= \varvec{b}^n, \end{aligned}$$
(16)

with \(\varvec{M}\) is an \(n_{\text {ndof}}\times n_{\text {ndof}}\)-valued sparse symmetric matrix, \(\varvec{b}\) is an \(n_{\text {ndof}}\)-valued right-hand side column vector and \(\varvec{C}\) is \(n_{\text {ndof}}\)-valued column vector of the unknowns, where \(n_{\text {ndof}}\) is the total number of degrees of freedom. The entries of the mass element matrix can be written as

$$\begin{aligned} M^{p}_{\varvec{\alpha },\varvec{\beta }}= & {} \displaystyle \int _{\widehat{T}} \det (\varvec{J}_T)B^{p}_{\varvec{\alpha }}(\varvec{\xi })B^{p}_{\varvec{\beta }}(\varvec{\xi })\;\text {d}\varvec{\xi }, \end{aligned}$$
(17)

where \(|\varvec{\alpha }|=|\varvec{\beta }|=p\) and \(\varvec{J}_T=\left( \frac{\text {d}\Phi _T}{\text {d}\varvec{\xi }}\right) ^{\top }\) is the Jacobian matrix. Since the geometry is interpolated using the affine map \(\Phi _T\), analytical integration rules as those proposed in [1, 29] can be used for the evaluation of the element mass matrix. Thus, using the proprieties (4) and (5), the integral in (17) can be evaluated as

$$\begin{aligned} M^{p}_{\varvec{\alpha },\varvec{\beta }}= & {} \frac{|T|}{|\widehat{T}|}\frac{\left( {\begin{array}{c}\varvec{\alpha }+\varvec{\beta }\\ \varvec{\beta }\end{array}}\right) }{\left( {\begin{array}{c}2p\\ p\end{array}}\right) }\displaystyle \int _{\widehat{T}} B^{2p}_{\varvec{\alpha }+\varvec{\beta }}(\varvec{\xi })\;\text {d}\varvec{\xi }=\frac{|T|}{|\widehat{T}|}\frac{\left( {\begin{array}{c}\varvec{\alpha }+\varvec{\beta }\\ \varvec{\beta }\end{array}}\right) }{\left( {\begin{array}{c}2p\\ p\end{array}}\right) \left( {\begin{array}{c}2p+2\\ 2\end{array}}\right) }. \end{aligned}$$
(18)

Note that the crucial step in this approach is the evaluation of the right-hand entries in (16) given by

$$\begin{aligned} b^{n}_{\varvec{\alpha }}= & {} \displaystyle \int _{\widehat{T}} \det (\varvec{J}_T)\;c^{n}_h\circ {\varvec{\mathcal {X}}}_h^n\;B^{p}_{\varvec{\alpha }}(\varvec{\xi })\;\text {d}\varvec{\xi }. \end{aligned}$$
(19)

is evident that, if the above integrals are evaluated exactly then it is easy to show that the Galerkin-characteristics method is unconditionally stable in the \(L^2\)-norm, see for instance [15, 40]. In a general framework, this cannot be done and one has to approximate the integrals by numerical integration.

It has shown in [1] that the Duffy transformation enables a tensorial reconstruction of the Bernstein-Bézier basis on simplices. Thus, the well-established sum factorization is used to efficiently evaluate and integrate these polynomials based on the Stroud conical quadrature. This transformation maps the unit quadrilateral with coordinates \(\varvec{t} = (t_1,t_2) \in \widehat{S} = [0,1]^2\) to the reference triangle \(\widehat{T}\) and it can be defined by

$$\begin{aligned} F(\varvec{t}) = \varvec{\xi } = \Bigl (t_1, (1-t_1)t_2\Bigr )^{\top }. \end{aligned}$$
(20)

Let us denote by \(B^p_i = \left( {\begin{array}{c}p\\ i\end{array}}\right) t^i(1-t)^{p-i}\) the one-dimensional Bernstein polynomial on the unit interval [0, 1]. Hence, it is shown in [1] that

$$\begin{aligned} B^{p}_{\varvec{\alpha }}(\varvec{\xi }) = B^p_{\alpha _1}(t_1)B^{p-\alpha _1}_{\alpha _2}(t_2), \end{aligned}$$
(21)

where \(\left| \varvec{\alpha }\right| = p\). Therefore, the Bernstein polynomial form (15) becomes

$$\begin{aligned} c^{n+1}_h(\varvec{x})=\sum _{\alpha _1=0}^{p}B^p_{\alpha _1}(t_{1}) \sum ^{p-\alpha _1}_{\alpha _2=0}C^{n+1}_{\varvec{\alpha }}\;B^{p-\alpha _1}_{\alpha _2}(t_{2}), \end{aligned}$$
(22)

with \(\varvec{x}=\Phi _{T}\circ F(\varvec{t})\) and \(T\in \mathcal {T}_h.\) Recall the q-point Gauss-Jacobi quadrature defined as

$$\begin{aligned} \int ^1_{0}w(t)f(t)\;\text {d}t\approx \sum ^{q}_{i=0}w^{(a,b)}_{i}f(s^{(a,b)}_i), \end{aligned}$$
(23)

where the weight function \(w(t)=(1-t)^a t^b\), with \(a,b >-1\), \(\{s^{(a,b)}_i\}\) is the set of nodes, and \(\{w^{(a,b)}_{i}\}\) are the weights. Thus, using the Stroud quadrature rule, the relations (20) and (22), the evaluation of the integral (19) yields

$$\begin{aligned} b^n_{\varvec{\alpha }}= & {} \frac{|T|}{|\widehat{T}|}\displaystyle \int ^1_{0}\left( \int ^1_{0} (1-t_1)B^p_{\alpha _1}(t_1)c^{n}_h\circ {\varvec{\mathcal {X}}}_h^n\;\text {d}t_1\right) B^{p-\alpha _1}_{\alpha _2}(t_2)\;\text {d}t_2,\nonumber \\\approx & {} \frac{|T|}{|\widehat{T}|}\displaystyle \sum ^{q}_{j_2=1}w^{(0,0)}_{j_2}B^{p-\alpha _1}_{\alpha _2}\left( s^{(0,0)}_{j_2}\right) \left( \sum ^{q}_{{j_1}=1}w^{(1,0)}_{{j_1}} \;B^p_{\alpha _1}(s^{(1,0)}_{j_1})\;c^n_h\left( \varvec{\mathcal {X}}_{h\varvec{j}}^n\right) \right) , \end{aligned}$$
(24)

where \(\varvec{j}=(j_1,j_2)\). By setting \(\displaystyle \varvec{\xi }_{\varvec{j}}^*=\Phi ^{-1}_{T_{\varvec{j}}^*}({\varvec{\mathcal {X}}}_{h\varvec{j}}^n)\), \(\displaystyle t^*_{\varvec{j},1}=\xi ^*_{\varvec{j},1}\) and \(\displaystyle t^*_{\varvec{j},2}=\frac{\xi ^*_{\varvec{j},2}}{1-\xi ^*_{\varvec{j},1}}\), the solution \(c^{n}_h\) can be evaluated at the point \({\varvec{\mathcal {X}}}_{h\varvec{j}}^n\) as

$$\begin{aligned} c^{n}_h({\varvec{\mathcal {X}}}^n_{h\varvec{j}})= & {} \sum _{|\varvec{\alpha }|=p}C^{n}_{\varvec{\alpha }} B^{p}_{\varvec{\alpha }}\left( {\varvec{\xi }}_{\varvec{j}}^*\right) ,\nonumber \\= & {} \sum _{\alpha _1=0}^{p}B^p_{\alpha _1}\left( t^*_{\varvec{j},1}\right) \sum ^{p-\alpha _1}_{\alpha _2=0}C^{n}_{\varvec{\alpha }}\;B^{p-\alpha _1}_{\alpha _2}\left( t^*_{\varvec{j},2}\right) . \end{aligned}$$
(25)

Note that if \(1-\xi ^*_{\varvec{j},1}=0\) the Duffy transformation degenerates and since in this case \(\lambda _1(\xi ^*_{\varvec{j},1})=1\) and \(\lambda _2(\xi ^*_{\varvec{j},1})=\lambda _2(\xi ^*_{\varvec{j},1})=0\), it follows that \(c^{n}_h({\varvec{\mathcal {X}}}^n_{h\varvec{j}})=C^{n}_{(p,0,0)}\).

The evaluation step (25) requires finding for each arrival point \(\varvec{x}_{h\varvec{j}}=\Phi _T(\varvec{\xi }_{\varvec{j}})\), the host element \(T_{\varvec{j}}^*\) where the departure point \({\varvec{\mathcal {X}}}_{h\varvec{j}}^n={\varvec{\mathcal {X}}}_h\left( t_n;\varvec{x}_{h\varvec{j}},t_{n+1}\right) \) is located, with

$$\begin{aligned} \xi _{j_1} = s^{(1,0)}_{j_1}\qquad \text {and}\qquad \xi _{j_2}=(1-s^{(1,0)}_{j_1})s^{(0,0)}_{j_2}. \end{aligned}$$
(26)

At the implementation level, the interpolation of \(c^{n}_h\) at the departure point \({\varvec{\mathcal {X}}}^n_{h\varvec{j}}\) is performed in the same manner as in [1], by exploiting property (25). Thus, we first evaluate all the univariate Bernstein polynomials \(B^p_{\alpha _1}\) and \(B^{p-\alpha _1}_{\alpha _2}\), with \(\alpha _1=0,1,\dots ,p\) and \(\alpha _2=0,1,\dots ,p-\alpha _1\), at the points \(t^*_{\varvec{j},1}\) and \(t^*_{\varvec{j},2}\), respectively, based on the recursion formula

$$\begin{aligned} B^{k+1}_{\alpha }(t)=t B^{k}_{\alpha -1}(t)+(1-t)B^{k}_{\alpha }(t), \end{aligned}$$
(27)

where \(B^{k}_{-1}=B^{k}_{k+1}=0\) and \(B^{0}_{0}=1\). Note that this procedure requires \(\mathcal {O}(p^2)\) floating point operations. Next, for \(\alpha _1 = 0,1,\dots ,p\), we compute the auxiliary coefficients

$$\begin{aligned} C^{*}_{\alpha _1}=\sum ^{p-\alpha _1}_{\alpha _2=0}C^{n}_{\varvec{\alpha }}\;B^{p-\alpha _1}_{\alpha _2}(t^*_{\varvec{j},2}), \end{aligned}$$
(28)

which yields a cost of \(\mathcal {O}(p^2)\). Hence, we evaluate \(c^{n}_h({\varvec{\mathcal {X}}}^n_{h\varvec{j}})\) as

$$\begin{aligned} c^{n}_h({\varvec{\mathcal {X}}}^n_{h\varvec{j}})= & {} \sum _{\alpha _1=0}^{p}C^{*}_{\alpha _1}B^p_{\alpha _1}(t^*_{\varvec{j},1}). \end{aligned}$$
(29)

Notice that the computational cost of this algorithm per point is of \(\mathcal {O}(p^2)\) operations for an arbitrary point. It should also be stressed that De Casteljau’s algorithm [31] can be used for evaluating the previous coefficients. However, this results in \(\mathcal {O}(p^3)\) operations, unless the given point \({\varvec{\mathcal {X}}}^n_{h\varvec{j}}\) belongs to an edge of the triangle for which the computational cost will decrease to \(\mathcal {O}(p^2)\) operations. Once \(c^{n}_h({\varvec{\mathcal {X}}}^n_{h\varvec{j}})\) is computed for all \(j_1, j_2=1,\dots ,q\), each entry \(b^{n}_{\varvec{\alpha }}\) given by (24) can be evaluated in \(\mathcal {O}(q^2)\) operations. Since the required number q of quadrature points should be chosen such that \(q=\mathcal {O}(p)\) to ensure a sufficiently accurate numerical integration, the total cost to set up the element right-hand side is \(\mathcal {O}(p^2)\).

In the current study, to compute the departure point \({\varvec{\mathcal {X}}}_{h{\varvec{j}}}^n\) from a given integration point \(\varvec{x}_{h{\varvec{j}}}\), the discrete analogous of (12) is first reformulated as

$$\begin{aligned} {\varvec{\mathcal {X}}}_{h{\varvec{j}}}^n={\varvec{x}}_{h{\varvec{j}}}-\varvec{\delta }_{h{\varvec{j}}}, \end{aligned}$$
(30)

where the displacement \(\varvec{\delta }_{h{\varvec{j}}}\) is evaluated using the following iterative procedure based on the Adams-Bashforth method

$$\begin{aligned} \varvec{\delta }_{h{\varvec{j}}} ^{(0)}= & {} \frac{\Delta t}{2}\Biggl ({\varvec{v}}^n\left( {\varvec{x}}_{h{\varvec{j}}} \right) - {\varvec{v}}^{n-1}\left( {\varvec{x}}_{h{\varvec{j}}}\right) \Biggr ),\nonumber \\[-1ex] \nonumber \\ \varvec{\delta }_{h{\varvec{j}}} ^{(k+1)}= & {} \frac{\Delta t}{2}\Biggl (3{\varvec{v}}^n\left( {\varvec{x}}_{h{\varvec{j}}}-\frac{1}{2}\varvec{\delta }_{h{\varvec{j}}} ^{(k)}\right) - {\varvec{v}}^{n-1}\left( {\varvec{x}}_{h{\varvec{j}}}-\frac{1}{2}\varvec{\delta }_{h{\varvec{j}}} ^{(k)}\right) \Biggr ),\qquad k = 0,1,\dots , \end{aligned}$$
(31)

with the velocity fields \({\varvec{v}}^n\bigl ({\varvec{x}}_{h{\varvec{j}}}-\frac{1}{2}\varvec{\delta }_{h{\varvec{j}}}^{(k)}\bigr )\) and \({\varvec{v}}^{n-1}\bigl ({\varvec{x}}_{h{\varvec{j}}}-\frac{1}{2}\varvec{\delta }_{h{\varvec{j}}} ^{(k)}\bigr )\) evaluated based on the finite element interpolation on the mesh element where \({\varvec{x}}_{h{\varvec{j}}}-\frac{1}{2}\varvec{\delta }_{h{\varvec{j}}}^{(k)}\) is located. This iterative procedure was first proposed in [41] for the finite difference semi-Lagrangian methods and investigated in [15] for the finite element discretizations. In the present work, the iterations (31) are stopped when the following criteria

$$\begin{aligned} \frac{\left\| \varvec{\delta }_{h{\varvec{j}}}^{(k+1)}-\varvec{\delta }_{h{\varvec{j}}}^{(k)}\right\| }{\left\| \varvec{\delta }_{h{\varvec{j}}}^{(k)}\right\| } \le \epsilon , \end{aligned}$$
(32)

is satisfied for the Euclidean norm \(\Vert \cdot \Vert \) and a given tolerance \(\epsilon \). In general, the departure points do not coincide with the spatial position of a mesh point in the triangular mesh. Therefore, the method used to compute \({\varvec{\mathcal {X}}}_{h{\varvec{j}}}^n\) should be equipped with a search-locate algorithm to find the host element where such point is located. In our simulations presented in Sect. 5, we have implemented a search-locate algorithm designed in [4] for the semi-Lagrangian methods in unstructured finite element discretizations. In addition, the iterations in (31) were continued until the trajectory changed by less than \(\epsilon = 10^{-6}\).

4 Implementation for Convection-Diffusion Problems

In this section we consider convection-diffusion problems reformulated using the total derivative as

$$\begin{aligned} \frac{D{{c}}}{D t} - \nu \Delta {{c}}= & {} {f}({\varvec{x}},t),\qquad ({\varvec{x}},t) \in \Omega \times (0,T],\nonumber \\ c({\varvec{x}},0)= & {} c_0({\varvec{x}}),\qquad {\varvec{x}} \in \Omega , \end{aligned}$$
(33)

where \(\nu \) is the diffusion coefficient and \({f}(\mathbf{x},t)\) the source term. We assume that eq. (33) is equipped with well defined boundary and initial conditions depending on the problem under study. In the current study, to deal with the diffusion part in the eq. (33) we consider a second-order implicit scheme of Gear type also known in the literature by backward differentiation formula (BDF2). Using the same notations introduced in the previous section, the time semi-discrete form of the eq. (33) reads

$$\begin{aligned} \frac{3c^{n+1} -4c^{n}\circ {\varvec{\mathcal {X}}}^n + c^{n-1}\circ {\varvec{\mathcal {X}}}^{n-1}}{2\Delta t}-\nu \Delta c^{n+1} = f^{n+1}, \end{aligned}$$
(34)

which can be rearranged in a compact form as

$$\begin{aligned} \dfrac{3}{2\Delta t}c^{n+1}-\nu \Delta c^{n+1} = F^{n}, \end{aligned}$$
(35)

with \(F^{n} = \frac{4}{2\Delta t}c^{n}\circ {\varvec{\mathcal {X}}}^n - \frac{1}{2\Delta t}c^{n-1}\circ {\varvec{\mathcal {X}}}^{n-1}+f^{n+1}\). Notice that to advance the solution \(c^{n+1}\) in time in (34), the two solutions \(c^{n-1}\) and \(c^{n}\) are required. At time \(t = 0\) only one initial condition is provided and to obtain the second condition we use the implicit Euler scheme. Suppose for simplicity purposes, the convection-diffusion problem (33) is supplied with an homogeneous Dirichlet boundary condition on \(\partial \Omega \). Then, the discrete weak form of (35) reads as: Find \(c_h^{n+1}\in V^0_h=V_h\cap H^1_0(\Omega )\), such that

$$\begin{aligned} \dfrac{3}{2\Delta t}\int _\Omega v_h\;c_h^{n+1}\;d\varvec{x}+\nu \int _\Omega \nabla v_h\cdot \nabla c_h^{n+1}\;d\varvec{x}=\int _\Omega v_h\;F^{n}\;d\varvec{x},\quad \forall v_h\in V^0_h, \end{aligned}$$
(36)

where \({V}_h\) is the conforming finite element space defined in (8). By virtue of definitions of the finite element operators given above, this reduces to the following linear system of algebraic equations

$$\begin{aligned} \frac{3}{2\Delta t}\varvec{M} \varvec{C}^{n+1} + \nu \varvec{K}\varvec{C}^{n+1} = \varvec{b}^{n}, \end{aligned}$$
(37)

where \(\varvec{K}\) is an \(n_{\text {ndof}}\times n_{\text {ndof}}\)-valued sparse symmetric matrix and \(\varvec{b}^n\) is an \(n_{\text {ndof}}\)-valued right-hand side column vector. It should also noted that since the Bernstein polynomials are only interpolatory at the mesh grid vertices, a numerical procedure is needed to impose nonhomogeneous Dirichlet type boundary condition. In the present work, this is achieved by using the \(L^2\) projection on the Bernstein-Bézier basis of the local boundary data Lagrange interpolate.

The entries \(K_{\varvec{\alpha },\varvec{\beta }}\) of the element stiffness matrix \(\varvec{K}\) are given by

$$\begin{aligned} K_{\varvec{\alpha },\varvec{\beta }} = \displaystyle \int _{\widehat{T}} \det (\varvec{J}_T)\;\left( \varvec{J}^{-1}_T\widehat{\nabla }B^p_{\varvec{\beta }}\right) \cdot \left( \varvec{J}^{-1}_T\widehat{\nabla }B^p_{\varvec{\alpha }}\right) \;\text {d}\varvec{\xi }, \end{aligned}$$
(38)

and the entries \(b^n_{\varvec{\alpha }}\) of the right-hand side column vector \(\varvec{b}^{n}\) are given by

$$\begin{aligned} b^{n}_{\varvec{\alpha }}= & {} \displaystyle \int _{\widehat{T}} \det (\varvec{J}_T)\;\left( \frac{4}{2\Delta t}c^{n}\circ {\varvec{\mathcal {X}}}^n - \frac{1}{2\Delta t}c^{n-1}\circ {\varvec{\mathcal {X}}}^{n-1}+f^{n+1}\right) \;B^{p}_{\varvec{\alpha }}(\varvec{\xi })\;\text {d}\varvec{\xi }. \end{aligned}$$
(39)

where \(|\varvec{\alpha }|=|\varvec{\beta }|=p\), \(\widehat{\nabla }\) refers to the gradient with respect to the local coordinates \({\varvec{\xi }}\). Following the same procedure used in the previous section to compute analytically the entries of the elements mass matrix, one can easily verify that the computation of the entries of the element stiffness matrix can be carried out analytically using eq. (6) as

$$\begin{aligned} K_{\varvec{\alpha },\varvec{\beta }} = p^2\frac{|T|}{|\widehat{T}|}\displaystyle \sum _{k,l=1}^{3}\left( \varvec{J}^{-1}_T\widehat{\nabla }\lambda _k\right) \cdot \left( \varvec{J}^{-1}_T\widehat{\nabla }\lambda _l\right) M^{p-1}_{\varvec{\alpha }-\varvec{e_k},\varvec{\beta -\varvec{e_l}}}, \end{aligned}$$
(40)

where \(M^{p-1}_{\varvec{\alpha }-\varvec{e_k},\varvec{\beta -\varvec{e_l}}}\) is deduced from the closed form (18). In addition, the integral in (39) is computed in the same manner as previously based on the Stroud quadrature and property (22). Here, a rule of \(q=p + 2\) quadrature points which is exact if the integrand is a polynomial of degree no higher than \(2p + 3\) is adopted.

In summary, the Bernstein-Bézier Galerkin-characteristics finite element method to solve either the convection problem (10) or convection-diffusion problem (33) is carried out in the following steps:

figure a

Note that, since the cell-based shape functions are internal i.e., they vanish on the element boundaries and are therefore not connected to the neighboring elements, the static condensation can be applied at the elemental level to remove the internal DoFs from the global finite element system during the assembly. Once the matrix and the right-hand side of the statically condensed system are formed, the internal DoFs in the solution can be recovered during the post-processing by solving element-wise local linear problems. This procedure is very efficient in reducing the size and enhancing the condition number of hp-finite element system matrices. Furthermore, the considered method requires solution of uncoupled elliptic problems such that their finite element discretization leads to linear systems of algebraic equations for which, very efficient solvers can be implemented. Therefore, by taking advantage of these properties, we solve the linear systems in (16) or (37) by the preconditioned conjugate gradient solver. This yields an efficient method for solving this class of linear systems of algebraic equations for which the preconditioner is implemented at a cost of \(\mathcal {O}(p^3)\) operations as discussed in [3]. Here, the additive Schwarz preconditioner is used in the same manner as studied in [3]. The key idea consists in using the relationship between the Bernstein and Jacobi polynomials which makes the passage from the Jacobi to the Bernstein basis functions and vice versa easy without inverting any matrix. These techniques have been proposed in [3] to build a preconditionner for the Bernstein polynomials using the well-established preconditionner introduced in [2] for the Jacobi polynomials but with less computational cost. This gives rise to a preconditioned system for which the condition number is bounded independently of the polynomial order p and the mesh size h.

5 Results and Examples

A number of numerical examples are selected to illustrate the accuracy of the new Galerkin-characteristics method with Bernstein-Bézier finite elements introduced in the above sections. These examples range from a linear passive advection of some initial conditions to a nonlinear viscous Burgers problem. For some of these test examples the analytical solutions are known, so that we can evaluate the relative \(L^1\)-error and relative \(L^2\)-error at time \(t_n\) as

$$\begin{aligned} L^1\text {-error} = \frac{\displaystyle \int _\Omega \bigl |c_{h}^n - c^n_{\mathrm {exact}}\bigr |\;d\varvec{x}}{\displaystyle \int _\Omega \bigl |c^n_{\mathrm {exact}}\bigr |\;d\varvec{x}},\qquad \qquad L^2\text {-error} = \frac{\sqrt{\displaystyle \int _\Omega \bigl |c_{h}^n - c^n_{\mathrm {exact}}\bigr |^2\;d\varvec{x}}}{\displaystyle \sqrt{\int _\Omega \bigl |c^n_{\mathrm {exact}}\bigr |^2\;d\varvec{x}}}, \end{aligned}$$
(41)

where \(c^n_{\mathrm {exact}}\) and \(c^n_{h}\) are respectively, the exact and numerical solutions at gridpoint \({\varvec{x}}_{h}\) and time \(t_n\). We also define the CFL number associated to the problems (10) and (33) as

$$\begin{aligned} \mathrm {CFL} = \max _{x,y}\left( \sqrt{\left| u\right| ^2 + \left| v\right| ^2}\right) \frac{\Delta t}{h/p}. \end{aligned}$$
(42)

In all our computations carried out in this section, the resulting linear systems of algebraic equations are solved using the preconditioned conjugate gradient solver and stopping criteria set to \(10^{-6}h/p\), which is small enough to guarantee that the algorithm truncation errors dominate the total numerical errors. All the computations were performed on an Intel Core(TM) i7-7700HQ CPU@2.80GHz with 8 GB of RAM. It should be pointed out that in all our simulations reported in this section, the number iterations in the linear solver do not exceed 30 iterations.

Table 1 Results for pure advection of the Gaussian pulse test after one revolution using gradually refined meshes, polynomial degrees and CFL numbers. The CPU times are given in seconds
Full size table

5.1 A Gaussian Pulse Example

In this example we consider the advection-diffusion of a Gaussian pulse in a rotating velocity field widely used in the literature to ascertain the performance of transport schemes, see for example [18, 41]. Thus, the governing equations are of the form (33) with \({\varvec{v}}= (-\omega y,\omega x)^\top \) and \(\omega = 4\). Initial and boundary conditions are taken from the exact solution

$$\begin{aligned} c_{\mathrm {exact}}(x,y,t) = \frac{\sigma ^2}{\sigma ^2 + 4\nu t}\exp \left( -\frac{(\bar{x} - x_0)^2 + (\bar{y} - y_0)^2}{\sigma ^2 + 4\nu t}\right) , \end{aligned}$$

where \(\bar{x} = x\cos (\omega t)+y\sin (\omega t)\), \(\bar{y} = -x\sin (\omega t)+y\cos (\omega t)\), \(x_0=-0.25\), \(y_0=0\) and \(\sigma ^2=0.002\). The computational domain \(\Omega = [-0.5,0.5]\times [-0.5,0.5]\) is covered by different uniform finite element meshes and the time period required for one complete rotation is \(\frac{\pi }{2}\). From the definition (42), the CFL number associated to this example is \(\omega \frac{\sqrt{2}}{2}\frac{\Delta t}{h/p}\) and it is set to different values in our simulations.

Table 2 Results for advection-diffusion of the Gaussian pulse test with \(\nu = 10^{-6}\) after one revolution using gradually refined meshes, polynomial degrees and CFL numbers. The CPU times are given in seconds
Full size table

The purpose of this test example is to quantify the errors and convergence rates for the proposed Bernstein-Bézier Galerkin-characteristics finite element method. First we consider the case of pure advection for this example corresponding to \(\nu = 0\) in (33). In Table 1 we summarize the results obtained for the \(L^1\)-error and convergence rate after one revolution using different meshes, polynomial degrees and CFL numbers. In this table we also include the CPU times for each run. In terms of \(L^1\)-error, keeping the polynomial degree p fixed and refining the spatial step h results in a substantial decrease in the computed \(L^1\)-errors. From the values of convergence rates in Table 1 we observe that the expected order of convergence is achieved for each selected polynomial degree p. It has also been observed that these convergence rates have not been deteriorated by the increase in the values of CFL, and the order of the Bernstein-Bézier Galerkin-characteristics finite element method remains almost the same for the considered CFL numbers of 2.5, 5 and 10. Notice that to reduce the computational cost, these CFL numbers are chosen as large as possible which yield explicit Eulerian-based methods noncompetitive.

Next we include the physical diffusion in this problem by solving the advection-diffusion of the Gaussian pulse with diffusion coefficient \(\nu = 10^{-6}\). As in the previous case, Table 2 summarizes the results obtained for the \(L^1\)-error and convergence rate after one revolution using different meshes, polynomial degrees and CFL numbers. It is clear from the results in Table 2 that for the considered diffusion coefficient, the expected convergence rates are preserved in the Bernstein-Bézier Galerkin-characteristics finite element method for the considered CFL numbers of 2.5, 5 and 10. Notice that, to be confined with convection-dominated problems only small values of the diffusion coefficient are accounted for in our simulations. Furthermore, for the considered small values of the diffusion coefficient, the time steps obtained according to the selected CFL numbers are small enough such that the errors associated with the discretization of the advection term are the dominant ones. Therefore, no substantial decrease in the computed errors is achieved when decreasing the CFL number. From the computational results obtained for the advection-diffusion of a Gaussian pulse, one may conclude the following: (i) the Bernstein-Bézier Galerkin-characteristics finite element method highly solve this test problem on coarse meshes, (ii) the convergence rate of the method is not deteriorated when increasing the CFL numbers.

Table 3 Results for the time-dependent Burgers example with \(\nu = 10^{-2}\) at time \(t = 2\) using gradually refined meshes, polynomial degrees and two CFL numbers
Full size table
Table 4 Results for the time-dependent Burgers example with \(h=\frac{1}{32}\) at time \(t = 2\) using different time steps, polynomial degrees and two different viscosity coefficients
Full size table

5.2 Time-Dependent Burgers Example

To further quantify the errors for the proposed Bernstein-Bézier Galerkin-characteristics finite element method for time-dependent problems, we solve the following nonlinear Burgers problem

$$\begin{aligned} \frac{\partial c}{\partial t} + c\frac{\partial c}{\partial x} + c\frac{\partial c}{\partial y} - \nu \Delta c = 0, \end{aligned}$$

in the squared domain \(\Omega = [0,2]\times [0,2]\) subject to initial and boundary conditions obtained from the following exact solution

$$\begin{aligned} c(x,y,t) = \frac{1}{1+\exp \left( \displaystyle \frac{x+y-t}{2\nu }\right) }. \end{aligned}$$

It is clear that the velocity field in this example depends on the time for which time accuracy of the proposed method can be evaluated. A similar example has been considered in [27] using a spectral volume method. In Table 3 we present the results obtained for the \(L^1\)-error, \(L^2\)-error and convergence rates at time \(t = 2\) for \(\nu = 10^{-2}\) using different meshes, different polynomial degrees and two CFL numbers CFL = 2.5 and CFL = 5. As in the previous simulations, keeping the polynomial degree p fixed and refining the mesh size h results in a substantial decrease in the computed \(L^1\)-error, \(L^2\)-error for both selected CFL numbers. The convergence rates in Table 3 confirm the expected order of convergence of the proposed Bernstein-Bézier Galerkin-characteristics finite element method for each selected polynomial degree p. It should be also noted that lower convergence rates have been observed for this test example using CFL = 2.5 than the case using CFL = 5. These features can be attributed to the nonlinear nature of the problem and also to the time dependence of the velocity field involved in the calculation of departure points.

The next idea is to check the convergence rates in time of the proposed Bernstein-Bézier Galerkin-characteristics finite element method for this test example. In doing so, we compute the \(L^1\)-error and \(L^2\)-error using a fixed mesh with \(h=\frac{1}{32}\) and carry out some numerical experiments varying the polynomial degree and the time step \(\Delta t\). The obtained results at time \(t = 2\) for two different diffusion coefficient \(\nu = 10^{-2}\) and \(\nu = 10^{-3}\) are listed in Table 4. It is clear that decreasing the time step \(\Delta t\) yields a decrease in both \(L^1\)-error and \(L^2\)-error for all considered polynomial degrees p and diffusion coefficients. A second-order convergence in time is also clearly observed in Table 4 for the considered polynomial degrees p and diffusion coefficients. Note that for this test example, better convergence results are obtained for the simulations with \(\nu = 10^{-2}\) than the simulations with \(\nu = 10^{-3}\).

5.3 Deformational Flow Example

In this example we solve the deformational flow problem widely used in the literature to examine the performance of Galerkin-characteristics methods, see for example [14, 18, 34]. Here, the problem statement consists of the linear advection eq. (10) in a circular spatial domain centered at \((x_0 = 0,y_0 = 0)\) with radius 4 and equipped with a highly deformational velocity defined by a steady circular vortex with tangential velocity depending on the radius of the vortex as

$$\begin{aligned} v_t(x,y) = v_0\mathrm {sech}^2\left( R\right) \tanh \left( R\right) , \end{aligned}$$

where \(v_0 = 2.58\) and the radial distance \(R = \sqrt{\left( x-x_0\right) ^2+\left( y-y_0\right) ^2}\) is the radius of the vortex. Initial and boundary conditions are obtained from the analytical solution

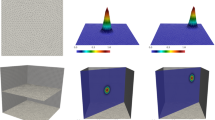
$$\begin{aligned} c_{\mathrm {exact}}(x,y,t) = -\tanh \left( \frac{y - y_0}{\eta }\cos \left( \omega t\right) - \frac{x - x_0}{\eta }\sin \left( \omega t\right) \right) , \end{aligned}$$
(43)

with \(\displaystyle \omega = \frac{v_t}{R}\) is the angular velocity of the circular vortex and \(\eta \) is a parameter controlling the steepness of the solution (43). Here, \(\eta = 0.05\) which yields a tight hyperbolic tangent profile in the initial condition that results in a non-smooth solution as the problem is integrated forward in time. Figure 2 illustrates the computational mesh and the initial condition used in the simulations for this test example. The steep gradient at the centerline of the computational domain can be clearly seen in the initial condition. The unstructured mesh shown in Fig. 2 contains 237 elements. This coarse mesh is considered in the simulations to demonstrate the high accuracy of the proposed Bernstein-Bézier Galerkin-characteristics finite element method to solve highly deformational flow problems without need to very fine meshes.

Fig. 2
figure 2

Computational mesh (left) and initial solution (right) for the deformational flow problem

Full size image
Fig. 3
figure 3

Results for the deformational flow example at time \(t = 4\) using different polynomial degrees \(p = 2\), 4, 6, 8, 10 and the exact solution

Full size image
Fig. 4
figure 4

Cross-sections of the results in Fig. 3 at \(y = 0\) (left) and at \(x = 0\) (right) using different polynomial degrees

Full size image
Table 5 Results for the deformational flow problem at time \(t = 4\) using different meshes and polynomial degrees
Full size table

In Fig. 3 we display the results obtained at time \(t = 4\) and \({\mathrm {CFL}} = 3\) using different values for the polynomial degree p. We also include the analytical solution in this figure for comparison reasons. For a better insight, Fig. 4 exhibits cross-sections at \(x = 0\) and \(y = 0\) of the results using the considered polynomial degrees. It is clear that, using \(p = 2\) in the Bernstein-Bézier Galerkin-characteristics finite element method, nonphysical oscillations are generated in the obtained results, specially at the center of the spatial domain where the gradient is sharper. Increasing the value of polynomial degree to \(p = 4\), the amplitude of these oscillations is reduced but the numerical dissipation is still present in these results. From the same figures we observe a complete absence of these oscillations and numerical diffusion in the results obtained using \(p = 8\) and \(p = 10\). Observe the good agreement between the numerical results and the analytical solutions in Fig. 4 even when using the coarse mesh and the large CFL number. Since the analytical solution for this flow problem is provided in (43), errors can be quantified. In Table 5 we present the \(L^1\)-error and \(L^2\)-error obtained using three meshes and different polynomial degrees. These unstructured meshes are used such that the number of elements in one mesh is about the double of its coarser counterpart. It is clear that increasing the polynomial order or refining the mesh result in a decrease in both \(L^1\)-error and \(L^2\)-error. This confirms the high accuracy and the good convergence of the proposed method for solving deformational flow problems. It should be pointed out that the performance of the proposed Bernstein-Bézier Galerkin-characteristics finite element method is very attractive since the computed solutions remain stable and highly accurate even when coarse meshes are used without requiring nonlinear solvers or small time steps to be taken in the simulations.

Fig. 5
figure 5

Computational meshes used for the moving fronts problem

Full size image

5.4 Moving Fronts Example

We consider the problem of moving fronts modeled by the convection-diffusion eq. (33) equipped with a time-dependent velocity field. Initially, two separate fronts propagate along the main diagonal of the computational domain at different speeds and eventually coalesce into a single front for a longer time. This problem has also been solved in [30] using a family of finite element alternating-direction methods combined with a modified method of characteristics. Here, we solve this problem in a squared domain \(\Omega = [0,1]\times [0,1]\) with the velocity field defined as

$$\begin{aligned} u(x,y,t)= & {} \frac{\displaystyle -0.1e^{-A(x,t)} + 0.5e^{-B(x,t)} + e^{-C(x,t)}}{\displaystyle e^{-A(x),t} + e^{-B(x,t)} + e^{-C(x,t)}},\\ v(x,y,t)= & {} \frac{\displaystyle -0.1e^{-A(y,t)} + 0.5e^{-B(y,t)} + e^{-C(y,t)}}{\displaystyle e^{-A(y,t)} + e^{-B(y,t)} + e^{-C(y,t)}}, \end{aligned}$$

where

$$\begin{aligned}&A(\alpha ,t) = \frac{0.05}{\nu }\left( \alpha - 0.5 + 4.95t\right) ,\qquad B(\alpha ,t) = \frac{0.25}{\nu }\left( \alpha - 0.5 + 0.75t\right) ,\\&\qquad C(t,\alpha ) = \frac{0.50}{\nu }\left( \alpha - 0.375\right) , \end{aligned}$$

with \(\alpha = x\) for the velocity u and \(\alpha = y\) for the velocity v. Initial and boundary conditions are defined by the following exact solution

$$\begin{aligned} c(x,y,t)= u(x,y,t)v(x,y,t). \end{aligned}$$

First we examine the mesh convergence in the proposed Bernstein-Bézier Galerkin-characteristics finite element method. To this end, we consider three structured meshes Mesh A, Mesh B and Mesh C with different element densities as depicted in Fig. 5. Here, the number of triangular elements in Mesh A, Mesh B and Mesh C is 32, 128 and 512, respectively. In Fig. 6 we present 20 equi-distributed contourlines of the solutions obtained at \(t = 0.2\) using CFL = 3 and \(p = 10\). Here, results are presented for four different diffusion coefficients namely, \(\nu = 5\times 10^{-4}\), \(\nu = 10^{-4}\), \(\nu = 5\times 10^{-3}\) and \(\nu = 10^{-2}\). The analytical solutions are also included in Fig. 6 for comparison purposes. It is clear that, by decreasing the values of the physical diffusion \(\nu \), the convective term becomes dominant and steep internal layers are formed near the vicinity of front lines in the computational domain. The mesh convergence on these results is clearly shown for the Bernstein-Bézier Galerkin-characteristics finite element method using the selected polynomial degree \(p = 10\). However, noticeable oscillations are detected for results obtained on the coarse mesh Mesh A. These results give a clear view of the overall transport pattern and effects of the diffusion coefficient \(\nu \) on the structure of moving fronts in the computational domain. It is worth remarking that the thinning of the internal layers with decreasing \(\nu \) is evident from these plots and the rate of this thinning is slower for \(\nu = 5\times 10^{-4}\) than for \(\nu = 10^{-3}\). These features clearly demonstrate the high accuracy achieved by the proposed Bernstein-Bézier Galerkin-characteristics finite element method for solving moving fronts problems using coarse meshes and large time steps. In addition, compared to the results published for example in [30], it can be seen that our method resolves accurately the solution features and the moving fronts seem to be localized in the correct place in the flow domain without requiring very fine meshes as those reported in [30].

Fig. 6
figure 6

Results for the moving fronts problem at time \(t = 0.2\) using \(p = 10\) and \(\nu = 5\times 10^{-4}\) (first row), \(\nu = 10^{-3}\) (second row), \(\nu = 5\times 10^{-3}\) (third row) and \(\nu = 10^{-2}\) (fourth row) on Mesh A (first column), Mesh B (second column), Mesh C (third column) and exact solution (fourth column)

Full size image
Fig. 7
figure 7

Cross-sections of the results for the moving fronts problem at the main diagonal \(y = 1-x\) using \(\nu = 5\times 10^{-4}\) and different polynomial degrees on the considered three meshes

Full size image
Fig. 8
figure 8

Same as Fig. 7 but using \(\nu = 10^{-3}\)

Full size image

To further qualify the results for these meshes, we plot in Fig. 7 the cross-section results at the main diagonal \(y = 1-x\) using \(\nu = 5\times 10^{-4}\) on the considered three meshes using different polynomial degrees. Those results obtained using \(\nu = 10^{-3}\) are depicted in Fig. 8. For large values of p, it is clear that the method on the three meshes produces practically identical results. This can be attributed to the high accuracy achieved by Bernstein-Bézier Galerkin-characteristics finite element method using \(p = 12\) even on the coarse mesh Mesh A. However, using low polynomial degrees on the meshes Mesh A and Mesh B, nonphysical oscillations are clearly visible in those regions where the solution gradients are steep such as the moving fronts. Apparently, the solution structures are in good agreement with the exact solutions presented in these figures. Needless to say that for convection-dominated simulations, keeping the mesh fixed and changing the polynomial degree, the Bernstein-Bézier Galerkin-characteristics finite element method does not diffuse the fronts or yields spurious oscillations near the steep gradients.

Fig. 9
figure 9

Computational mesh (left) and initial solution (right) for the viscous Burgers problem. We set \(c = 0.5\) on both center lines in the initial solution

Full size image
Fig. 10
figure 10

Results for the viscous Burgers equation with \(\lambda =1\) (first column), \(\lambda =5\) (second column) and \(\lambda =10\) (third column) using \(p = 6\) (first row), \(p = 10\) (second row) and exact solution (third row)

Full size image
Fig. 11
figure 11

Cross-sections at \(y = x\) of the results for the viscous Burgers problem using \(\lambda =1\) (first column), \(\lambda =5\) (second column) and \(\lambda =10\) (third column)

Full size image

5.5 Viscous Burgers Flow Example

Our final example solves the following viscous Burgers equation which evolves to a highly convective steady-state

$$\begin{aligned} \frac{\partial c}{\partial t} + \lambda y\left( c - \frac{1}{2}\right) \frac{\partial c}{\partial x} + \lambda x\left( c - \frac{1}{2}\right) \frac{\partial c}{\partial y} - \Delta c = 0, \end{aligned}$$

where \(\lambda \) is a constant controlling the magnitude of the nonlinear convective term. The boundary conditions are of Dirichlet type given by the exact steady-state solution

$$\begin{aligned} c(x,y) = \frac{1}{2}\left( 1 - \tanh \left( \frac{\lambda xy}{2}\right) \right) . \end{aligned}$$

This problem has been solved in a squared domain in [30] using a modified method of characteristics. Here, this problem is solved in a circular domain with radius 5 and centered at the origin. The domain dimensions and the initial conditions used in our computations are illustrated in Fig. 9. We use the Bernstein-Bézier Galerkin-characteristics finite element method to compute the steady-state solutions for three different values of \(\lambda \) namely, \(\lambda = 1\), \(\lambda = 5\) and \(\lambda = 10\). For these steady-state solutions, the time integration process is stopped when the inequality

$$\begin{aligned} \frac{\left\| c^{n+1} - c^n\right\| }{\left\| c^{n}\right\| } \le \tau , \end{aligned}$$
(44)

is satisfied. Here \(\Vert \cdot \Vert \) denotes the \(L^1\)-norm and \(\tau \) is a given tolerance fixed to \(10^{-6}\Delta t\) in our computations. It should be pointed out that, the number of iterations to reach this tolerance depends on the values taken by \(\lambda \) such that, for a fixed CFL number, more iterations are required for larger values of \(\lambda \).

Figure 10 illustrates the obtained results using a mesh of 432 elements and \({\mathrm {CFL}} = 3\). Here, we plot 10 equi-distributed contours of the solutions using two values of the polynomial degree \(p=6\) and \(p=10\). For comparison, we have also included analytical steady-state solutions in this figure. It is clear that, by increasing the values of \(\lambda \), the convective term becomes dominant and steep internal boundary layers are formed near the vicinity of center lines. For low values of \(\lambda \), the internal boundary layers are wide and diffuse in the flow domain. As \(\lambda \) increases, the internal boundary layers concentrate and move towards the domain center. It is apparent that the flow structure is in good agreement with the previous work in [30]. These plots give a clear view of the overall flow pattern and the effect of the convection control parameter \(\lambda \) on the structure of steady internal boundary layers in the cavity. It is worth remarking that the thinning of the internal boundary layers with increasing \(\lambda \) is evident from these plots, although the rate of this thinning is slower for \(p=6\) method than for \(p=10\). These features clearly demonstrate the high accuracy achieved by the proposed Bernstein-Bézier Galerkin-characteristics finite element method for solving viscous Burgers problems at steady-state regimes. In addition, compared to the results published for example in [30], it can be seen that our method resolves accurately the flow structures and the boundary layers seem to be localized in the correct place in the flow domain.

For visualizing the comparisons, we display in Fig. 11 a cross-section at the main diagonal \(y = x\) using the selected values of \(\lambda \) and p. For \(\lambda = 1\), it is clear that the results obtained using \(p=6\) and \(p=10\) produce practically identical results. This can be attributed to the large physical diffusion presented in the problem. However, increasing the value of \(\lambda \) to 5 and 10 the results computed using \(p=10\) are more accurate than those computed using \(p=6\). Apparently, By using \(p=10\), high resolution is achieved in those regions where the flow gradients are steep such as the moving fronts. Comparing the results obtained using the considered values of p, it is clear that using \(p=6\) produces diffusive solutions resulting in smearing the shocks. On the other hand, this numerical diffusion has remarkably been reduced in the results computed using \(p=10\).

6 Conclusions

In this paper, we have presented a Bernstein-Bézier Galerkin-characteristics finite element method for solving convection-diffusion equations on unstructured meshes. The proposed solver inherits the advantages of semi-Lagrangian integration (unconditional stability and reduction of time truncation errors) while preserving high-order accuracy. Moreover, this implementation simplifies the computational complexity of the Bernstein-Bézier Galerkin-characteristics solver for a fixed polynomial approximation during the time integration process. To increase the performance of the proposed method the element-level static condensation is implemented. The favorable performance of the developed algorithm is demonstrated using a series of numerical examples including the viscous Burgers equation. The results obtained for these examples show that the Bernstein-Bézier Galerkin-characteristics finite element method has the advantage of requiring less computational resources for the integration of convection-dominated problems than an Eulerian-based finite element methods, typical of those widely used in Eulerian algorithms for convection-dominated problems. This fact, as well as its favorable high-order accuracy and strong stability properties, make it an attractive alternative for convection solvers based on Galerkin-characteristic techniques. Finally, the method presented in this paper is not appropriate for nonlinear invscid equations with strong shocks. However, using the idea of the limiting techniques studied in [17], and following the arguments of Sect. 3, it is possible to reconstruct a shock-preserving Bernstein-Bézier Galerkin-characteristics finite element method for nonlinear equations. Results on these schemes will be reported in the near future. Future work will also concentrate on extending these methods for the incompressible viscous flows in three space dimensions using unstructured meshes and developing highly efficient preconditioned iterative solvers for the associated linear systems.