A Mass-Preserving Two-Step Lagrange–Galerkin Scheme for Convection-Diffusion Problems

Abstract

A mass-preserving two-step Lagrange–Galerkin scheme of second order in time for convection-diffusion problems is presented, and convergence with optimal error estimates is proved in the framework of $L^2$-theory. The introduced scheme maintains the advantages of the Lagrange–Galerkin method, i.e., CFL-free robustness for convection-dominated problems and a symmetric and positive coefficient matrix resulting from the discretization. In addition, the scheme conserves the mass on the discrete level if the involved integrals are computed exactly. Unconditional stability and error estimates of second order in time are proved by employing two new key lemmas on the truncation error of the material derivative in conservative form and on a discrete Gronwall inequality for multistep methods. The mass-preserving property is achieved by the Jacobian multiplication technique introduced by Rui and Tabata in 2010, and the accuracy of second order in time is obtained based on the idea of the multistep Galerkin method along characteristics originally introduced by Ewing and Russel in 1981. For the first time step, the mass-preserving scheme of first order in time by Rui and Tabata in 2010 is employed, which is efficient and does not cause any loss of convergence order in the $\ell ^\infty (L^2)$- and $\ell ^2(H^1_0)$-norms. For the time increment $\Delta t$, the mesh size h and a conforming finite element space of polynomial degree $k \in {\mathbb {N}}$, the convergence order is of $O(\Delta t^2 + h^k)$ in the $\ell ^\infty (L^2)\cap \ell ^2(H^1_0)$-norm and of $O(\Delta t^2 + h^{k+1})$ in the $\ell ^\infty (L^2)$-norm if the duality argument can be employed. Error estimates of $O(\Delta t^{3/2}+h^k)$ in discrete versions of the $L^\infty (H^1_0)$- and $H^1(L^2)$-norm are additionally proved. Numerical results confirm the theoretical convergence orders in one, two and three dimensions.

1 Introduction

The convection-diffusion equation is one of the important equations in flow problems, as it is considered a simplification of the Navier–Stokes equations. To deal with the equation especially in convection-dominant cases, nowadays, many finite element schemes have been proposed and analyzed, e.g., upwind methods [2, 9, 10, 21, 22, 38], characteristics(-based) methods [4,5,6, 11, 13,14,15,16,17, 30,31,32, 34, 35, 39] and so on. The Lagrange–Galerkin method (also called characteristic(-curve) finite element method or Galerkin-characteristics method) belongs to the latter group and is a finite element method based on the method of characteristics, where the idea is to consider the trajectory of a fluid particle and discretize the material derivative along this trajectory. It is known that the Lagrange–Galerkin method has many advantages including robustness for convection-dominated problems without needing any stabilization parameters, symmetry of the resulting coefficient matrix, and no requirement of the so-called CFL condition, which enables the use of large time increments. Hence, the Lagrange–Galerkin method has also been applied to other equations, e.g., the Oseen/Navier–Stokes/viscoelastic/natural convection equations, cf. [3, 7, 8, 23,24,25,26,27,28,29, 37] and references therein.

Some Lagrange–Galerkin schemes of second order in time for convection-diffusion problems have already been proposed, including single step methods [4, 5, 34] and multistep methods [6, 16]. However, in general, the mass-preserving property is often not satisfied by Lagrange–Galerkin methods. Recently mass-preserving Lagrange–Galerkin schemes for convection-diffusion problems in conservative form and hyperbolic conservation laws, i.e., pure convection problems in conservative form, with arbitrary orders in time and space have been proposed by Colera et al. [13, 14] but error estimates are not yet given. About a decade ago, Rui and Tabata [32] has proposed a mass-preserving Lagrange–Galerkin scheme of first order in time for convection-diffusion problems by a Jacobian multiplication technique and proved error estimates of first order in time. To the best of our knowledge, however, there are no Lagrange–Galerkin schemes of second order in time having both, a mass-preserving property and error estimates.

In this paper, we propose a Lagrange–Galerkin scheme of second order in time for convection-diffusion problems and prove its mass-preserving property and error estimates. Stability and convergence with optimal error estimates are proved in the framework of $L^2$-theory. We devise the scheme based on two ideas; one is the multistep (two-step) Galerkin method along characteristics by Ewing and Russel [16], and the other one is the Jacobian multiplication technique by Rui and Tabata [35]. To find the numerical solution at time step n, we employ two Jacobians for the time steps $n-1$ and $n-2$. The Jacobians are of the forms, $1 - \Delta t (\nabla \cdot u^n) + O(\Delta t^2)$ and $1 - 2\Delta t (\nabla \cdot u^n) + O(\Delta t^2)$, respectively, where $\Delta t$ is a time increment and $u^n$ is the velocity at time step n. For this reason it is not obvious that our scheme is of second order in time and that the mass-preserving property is satisfied. We, therefore, prove these properties in this paper. As two-step methods require solutions at two prior time steps, we propose to employ the mass-preserving Lagrange–Galerkin scheme of first order in time by Rui and Tabata [35] for the first time step. This construction is efficient and does not cause any loss of convergence order in the $\ell ^\infty (L^2)$- and $\ell ^2(H^1_0)$-norms.

The main results for our scheme including the construction of the solution at the first time step are as follows. (i) The mass-preserving property is proved, cf. Theorem 1. (ii) Stability in $\ell ^\infty (L^2)\cap \ell ^2(H^1_0)$ and $\ell ^\infty (H^1_0)$ is proved, cf. Theorem 2. (iii) An error estimate of $O(\Delta t^2 + h^k)$ in the $\ell ^\infty (L^2)\cap \ell ^2(H^1_0)$-norm is proved, where h is the mesh size in space and $k \in {\mathbb {N}}$ is the polynomial degree of a conforming finite element space for the numerical solution, cf. Theorem 3-(i). (iv) An error estimate of $O(\Delta t^2 + h^{k+1})$ in the $\ell ^\infty (L^2)$-norm is proved under the assumption that the duality argument can be employed, cf. Theorem 3-(ii). Furthermore, in Theorem 3-(i), we prove an error estimate of $O(\Delta t^{3/2} + h^k)$ in a discrete version of the $L^\infty (H^1_0)\cap H^1(L^2)$-norm. Although the convergence order in the $L^\infty (H^1_0)\cap H^1(L^2)$-norm is slightly reduced to $\Delta t^{3/2}$ due to the construction of the solution at the first time step, it is still higher than first order. When we consider an application of the scheme to the Navier–Stokes equations, the further analysis will be useful for the estimate of the pressure.

Here, we make two further remarks. (i) In real computations our scheme is only approximately mass conservative, since numerical integration is in general required to compute the integrals occuring in the scheme. This introduces an approximation error in the total mass of the discrete solution. In this paper, in place of mass-conservative, which we only use if no mass is lost (in the discrete case up to machine precison), we employ the term mass-preserving to refer to schemes that are mass-conservative if the involved integrals are computed exactly. (ii) While there are $\ell ^\infty (L^2)$-error estimates for single-step Lagrange–Galerkin methods (including space-time versions) for convection-diffusion problems that are independent of the viscosity constant, cf., e.g., [11, 35, 39], the error estimates in this paper are dependent on the viscosity constant. This is caused by an estimate of the discrete material derivative using the two-step backward differentiation formula in combination with the discrete Gronwall’s inequality for the two-step method and to the best of our knowledge no viscosity-independent error estimates for multi-step Lagrange–Galerkin methods exist. Furthermore, in applications to the Navier–Stokes equations, viscosity-dependent error estimates are usually obtained even for single-step Lagrange–Galerkin methods due to the nonlinearity.

This paper is organized as follows. Our mass-preserving two-step Lagrange–Galerkin scheme for convection-diffusion problems is presented in Sect. 2. The main results on the mass-preserving property, the stability, and the convergence with optimal error estimates are stated in Sect. 3, and they are proved in Sect. 4. The theoretical convergence orders are numerically confirmed by one-, two- and three-dimensional numerical experiments in Sect. 5. The conclusions are given in Sect. 6. In the Appendix three lemmas used in Sect. 4 are proved.

2 A Lagrange–Galerkin Scheme

The function spaces and the notations used throughout the paper are as follows. Let $\Omega$ be a bounded domain in ${\mathbb {R}}^d$ for $d = 1, 2$ or 3, $\Gamma :=\partial \Omega$ the boundary of $\Omega$, and T a positive constant. For $m \in {\mathbb {N}}\cup \{0\}$ and $p\in [1,\infty ]$, we use the Sobolev spaces $W^{m,p}(\Omega )$, $W^{1,\infty }_0(\Omega )$, $H^m(\Omega ) \, (=W^{m,2}(\Omega ))$ and $H^1_0(\Omega )$. For any normed space S with norm $\Vert \cdot \Vert _S$, we define function spaces $H^m(0,T; S)$ and C([0, T]; S) consisting of S-valued functions in $H^m(0,T)$ and C([0, T]), respectively. We use the same notation $(\cdot , \cdot )$ to represent the $L^2(\Omega )$ inner product for scalar- and vector-valued functions. The norm on $L^2(\Omega )$ is simply denoted by $\Vert \cdot \Vert$, i.e., $\Vert \cdot \Vert :=\Vert \cdot \Vert _{L^2(\Omega )}$. The dual pairing between S and the dual space $S^\prime$ is denoted by $\langle \cdot , \cdot \rangle$. The notation $\Vert \cdot \Vert$ is employed not only for scalar-valued functions but also for vector-valued ones. For $t_0$ and $t_1\in {\mathbb {R}}$ $(t_0 < t_1)$, we introduce the function space

$$\begin{aligned} Z^m(t_0, t_1)&:=\bigl \{ \psi \in H^j(t_0, t_1; H^{m-j}(\Omega ));~j=0,\ldots ,m,\ \Vert \psi \Vert _{Z^m(t_0, t_1)} < \infty \bigr \} \end{aligned}$$

with the norm

$$\begin{aligned} \Vert \psi \Vert _{Z^m(t_0, t_1)}&:=\biggl [ \sum _{j=0}^m \Vert \psi \Vert _{H^j(t_0,t_1; H^{m-j}(\Omega ))}^2 \biggr ]^{1/2}, \end{aligned}$$

and set $Z^m :=Z^m(0, T)$. We often omit [0, T], $\Omega$, and the superscript d if there is no confusion, e.g., we shall write $C(L^\infty )$ in place of $C([0,T]; L^\infty (\Omega )^d)$. We denote by c and $c(a_1, a_2, \ldots )$ a generic positive constant and a positive constant dependent on $a_1, a_2, \ldots$, respectively, and introduce the following constants, for $i=0,1$,

$$\begin{aligned} c_\nu&= c (1/\nu ),&c_0&= c \bigl ( \Vert u\Vert _{C(L^{\infty })} \bigr ),&c_1&= c \bigl ( \Vert u\Vert _{C(W^{1,\infty })} \bigr ), \\ c_{i,\nu }&= c ( c_i, 1/\nu ),&c_{i,T}&= c ( c_i, T ),&c_{i,\nu ,T}&= c ( c_i, 1/\nu , T ). \end{aligned}$$

We consider a convection-diffusion problem; find $\phi :\Omega \times (0, T)\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned}&\frac{\partial {\phi }}{\partial {t}} + \nabla \cdot (u \phi ) - \nu \Delta \phi&= f&\mathrm{in}\ \Omega \times (0, T),&\end{aligned}$$

(1a)

$$\begin{aligned}&\nu \frac{\partial {\phi }}{\partial {n}} - \phi u\cdot n&= g&\mathrm{on}\ \Gamma \times (0, T),&\end{aligned}$$

(1b)

$$\begin{aligned}&\phi&=\phi ^0&\mathrm{in}\ \Omega ,\ \mathrm{at}\ t=0,&\end{aligned}$$

(1c)

where $u:\Omega \times (0, T)\rightarrow {\mathbb {R}}^d$, $f:\Omega \times (0, T)\rightarrow {\mathbb {R}}$, $g: \Gamma \times (0, T) \rightarrow {\mathbb {R}}$ and $\phi ^0:\Omega \rightarrow {\mathbb {R}}$ are given functions, $n: \partial \Omega \rightarrow {\mathbb {R}}^d$ is the outward unit normal vector, $\nu \in (0, \nu _0]$ is a viscosity constant, and $\nu _0 (>0)$ is an upper bound of $\nu$. Since we are interested in problems with a small $\nu$, i.e., convection-dominated problems, we assume without loss of generality $\nu _0 = 1$ in this paper.

Let $\Psi :=H^1(\Omega )$. A weak formulation to problem (1) is to find $\{\phi (t) = \phi (\cdot ,t) \in \Psi ;\ t \in (0, T)\}$ such that, for $t\in (0, T)$,

$$\begin{aligned}&\Bigl ( \frac{\partial {\phi }}{\partial {t}} (t), \psi \Bigr ) + a_0(\phi (t), \psi ) + a_1(\phi (t), \psi ; u(t))&= \langle F(t), \psi \rangle ,&\forall \psi&\in \Psi&\end{aligned}$$

(2)

with $\phi (0) = \phi ^0$, where $a_0(\cdot ,\cdot )$ and $a_1(\cdot \,,\cdot ) = a_1(\cdot \,,\cdot \,;u)$ are bilinear forms defined by

$$\begin{aligned} a_0(\phi , \psi )&:=\nu (\nabla \phi , \nabla \psi ),&a_1(\phi , \psi ; u)&:=-(\phi , u\cdot \nabla \psi ), \end{aligned}$$

and $F(t)\in \Psi ^\prime$, $t\in (0,T)$, is a functional defined by

$$\begin{aligned} \langle F(t), \psi \rangle&:=( f(t), \psi ) + [g(t), \psi ]_\Gamma ,&[g(t), \psi ]_\Gamma&:=\int _\Gamma g(t) \psi \, ds \end{aligned}$$

(3)

for $f(t) = f(\cdot ,t) \in L^2(\Omega )$ and $g(t) = g(\cdot ,t) \in L^2(\Gamma )$.

Let us assume $f\in L^2(0,T;L^2(\Omega ))$ and $g\in L^2(0,T;L^2(\Gamma ))$. Substituting $1\in \Psi$ into $\psi$ in (2) and integrating over (0, t), one can easily obtain the so-called mass-balance identity, i.e., for $t\in (0, T)$,

$$\begin{aligned} \int _\Omega \phi (x, t)\,dx = \int _\Omega \phi ^0(x)\,dx + \int _0^td\tau \int _\Omega f(x, \tau )\,d\tau + \int _0^td\tau \int _\Gamma g(x, \tau ) ds, \end{aligned}$$

(4)

which is an important property of problem (1). This property is, therefore, desired to hold also on the discrete level. It is known that conventional Galerkin, streamline diffusion (SD) [18, 22], streamline upwind/Petrov–Galerkin (SUPG), and least square schemes [10, 20] satisfy a discrete version of (4). In [35], a characteristic finite element (Lagrange–Galerkin) scheme of first order in time satisfying a discrete version of (4) has been proposed and analyzed.

Let $\Delta t >0$ be a time increment, $t^n :=n\Delta t~(n\in {\mathbb {Z}})$, and $N_T :=\lfloor T/\Delta t\rfloor$. For a function $\rho$ defined in $\Omega \times (0, T)$, $\rho (\cdot , t^n)$ is simply denoted by $\rho ^n$. Let ${\mathcal {T}}_h$ be a triangulation of $\Omega$, and $\Omega _h :=\mathrm{int} ( \bigcup _{K\in {\mathcal {T}}_h} K )$ the approximate domain, where h is the maximum mesh size of ${\mathcal {T}}_h$, i.e., $h :=\max \{ h_K;\ K\in {\mathcal {T}}_h \}$ for $h_K:=\mathrm {diam} (K)$ $(K\in {\mathcal {T}}_h)$. For the sake of simplicity, we assume that $\Omega _h = \Omega$ throughout this paper. Let $\Psi _h$ be a finite element space defined by

$$\begin{aligned} \Psi _h :=\Bigl \{ \psi _h \in C({\bar{\Omega }});\ \psi _{h|K} \in P_k(K),\ \forall K\in {\mathcal {T}}_h \Bigr \}, \end{aligned}$$

(5)

where $P_k(K)$ is the space of polynomial functions of degree $k \in {\mathbb {N}}$ on $K \in {\mathcal {T}}_h$. For a velocity $v: \Omega \rightarrow {\mathbb {R}}^d$, let $X_1 (v,\Delta t): \Omega \rightarrow {\mathbb {R}}^d$ be the mapping defined by

$$\begin{aligned} X_1 (v,\Delta t) (x) :=x - v(x)\Delta t, \end{aligned}$$

(6)

which is called the upwind point of x with respect to the velocity v and the time increment $\Delta t$. We define mappings $X_1^n, {\tilde{X}}_h^n: \Omega \rightarrow {\mathbb {R}}^d$ and their Jacobians $\gamma ^n, {\tilde{\gamma }}^n: \Omega \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} X_1^n (x)&:=X_1(u^n,\Delta t)(x) = x - u^n(x) \Delta t,&{\tilde{X}}_1^n(x)&:=X_1(u^n, 2\Delta t)(x) = x - 2 u^n(x) \Delta t, \\ \gamma ^n (x)&:=\mathrm {det} \biggl ( \frac{\partial {X_1^n}}{\partial {x}} (x)\biggr ),&{\tilde{\gamma }}^n (x)&:=\mathrm {det} \biggl ( \frac{\partial {{\tilde{X}}_1^n}}{\partial {x}} (x) \biggr ). \end{aligned}$$

The scheme proposed in [35] is to find at each time step $\phi _h^n\in \Psi _h$ such that

$$\begin{aligned}&\Biggl ( \frac{\phi _h^n-\phi _h^{n-1} \circ X_1^n\gamma ^n}{\Delta t}, \psi _h \Biggr ) + a_0(\phi _h^n, \psi _h)&= \langle F^n, \psi _h \rangle ,&\forall \psi _h&\in \Psi _h.&\end{aligned}$$

(7)

By multiplication with the Jacobian $\gamma ^n$ the mass of $\phi _h^{n-1}$ is conserved after taking the composite with the mapping $X_i^n$ and we call this “the Jacobian multiplication technique.” That is substituting $1\in \Psi _h$ into $\psi$ in (7) and using the identity

$$\begin{aligned} \int _\Omega \phi _h^{n-1} \circ X_1^n\gamma ^n\,dx&= \int _\Omega \phi _h^{n-1}\,dx, \end{aligned}$$

we obtain a discrete mass-balance identity, cf. [35] for detail.

Moreover, a multistep (two-step) Galerkin method along characteristics of second order in time [16] is well known; at each time step $n \in \{ 2, \ldots , N_T\}$, find $\phi _h^n\in \Psi _h$ such that

$$\begin{aligned}&\Biggl ( \frac{3\phi _h^n-4\phi _h^{n-1} \circ X_1^n+\phi _h^{n-2} \circ {\tilde{X}}_1^n}{2\Delta t}, \psi _h \Biggr ) + a_0(\phi _h^n, \psi _h)&= \langle F^n, \psi _h \rangle ,&\forall \psi _h&\in \Psi _h.&\end{aligned}$$

(8)

Scheme (8) is of second order in time but does not satisfy the mass-balance identity in general.

Combining the Jacobian multiplication technique (7) with the multistep (two-step) Galerkin method along characteristics (8), we obtain the Lagrange–Galerkin scheme proposed in this paper.

Let $\phi _h^0 \in \Psi _h$ and $F \in H^1(0,T; \Psi ^\prime )$ be given. We propose a mass-preserving two-step Lagrange–Galerkin scheme of second order in time; find $\{\phi _h^n\in \Psi _h;\ n=1, \ldots , N_T\}$ such that, for $n=1, \ldots , N_T$,

$$\begin{aligned}&\Biggl ( \frac{\phi _h^n-\phi _h^{n-1} \circ X_1^n\gamma ^n}{\Delta t}, \psi _h \Biggr ) + a_0( \phi _h^n, \psi _h ) = \langle F^n, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h,\ n=1, \end{aligned}$$

(9a)

$$\begin{aligned}&\Biggl ( \frac{3\phi _h^n-4\phi _h^{n-1} \circ X_1^n \gamma ^n + \phi _h^{n-2} \circ {\tilde{X}}_1^n {\tilde{\gamma }}^n}{2\Delta t}, \psi _h \Biggl ) + a_0( \phi _h^n, \psi _h ) = \langle F^n, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h,\ n \ge 2. \end{aligned}$$

(9b)

Since the Jacobians $\gamma ^n$ and $\tilde{\gamma ^n}$ are of the forms $1 - \Delta t (\nabla \cdot u^n) + O(\Delta t^2)$ and $1 - 2\Delta t (\nabla \cdot u^n) + O(\Delta t^2)$, respectively, it is not clear that the combined scheme is of second order in time and that the mass-balance identity is satisfied. These properties are therefore proved in this paper. In the following, we rewrite scheme (9) simply as

$$\begin{aligned} ( {\mathcal {A}}_{\Delta t} \phi _h^n, \psi _h ) + a_0( \phi _h^n, \psi _h ) = \langle F^n, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h, \end{aligned}$$

for $n \in \{1,\ldots , N_T\}$, where, for a series $\{\rho ^n\}_{n=0}^{N_T} (\subset \Psi )$, the function ${\mathcal {A}}_{\Delta t} \rho ^n: \Omega \rightarrow {\mathbb {R}}$ is defined by

$$\begin{aligned} {\mathcal {A}}_{\Delta t} \rho ^n :=\left\{ \begin{aligned}&{\mathcal {A}}_{\Delta t}^{(1)} \rho ^n :=\frac{1}{\Delta t} \Bigl ( \rho ^n-\rho ^{n-1} \circ X_1^n\gamma ^n \Bigr ),&n&= 1, \\&{\mathcal {A}}_{\Delta t}^{(2)} \rho ^n :=\frac{1}{2\Delta t} \Bigl ( 3\rho ^n-4\rho ^{n-1} \circ X_1^n \gamma ^n + \rho ^{n-2} \circ {\tilde{X}}_1^n {\tilde{\gamma }}^n \Bigr ),&n&\ge 2. \end{aligned} \right. \end{aligned}$$

Remark 1

(i) The first order scheme (9a) is employed in the first time step, since then the approximate solution $\phi _h^1$ needed in (9b) with $n=2$ is not yet available. This construction of $\phi _h^1$ is efficient and has no adverse effect on the convergence order in the $\ell ^\infty (L^2)$-norm, cf. Theorem 3.

(ii) $F \in H^1(0,T; \Psi ^\prime )$ implies that $F \in C([0,T]; \Psi ^\prime )$ and $\{F^n\}_{n=1}^{N_T} \subset \Psi ^\prime$.

3 Main Results

We start this section, by setting hypotheses for the velocity u and the time increment $\Delta t$, and reviewing previous results.

Hypothesis 1

The function u satisfies $u \in C([0,T]; W^{1,\infty }_0(\Omega )^d)$.

Hypothesis 2

The time increment $\Delta t$ satisfies the condition $\Delta t |u|_{C(W^{1,\infty })} \le 1/8$.

Proposition 1

[34, 40] (i) Under Hypothesis 1 and $\Delta t |u|_{C(W^{1,\infty })} < 1/2$, it holds that $X_1^n(\Omega )={\tilde{X}}_1^n(\Omega ) = \Omega$ for $n=0, \ldots , N_T$.

(ii) Under Hypotheses 1 and 2, it holds that $1/2 \le \gamma ^n, {\tilde{\gamma }}^n \le 3/2$ for $n=0, \ldots , N_T$.

For $n=0, \ldots , N_T$, let ${\mathcal {M}}_h^n$ be an approximate value of mass at $t=t^n$ defined by

$$\begin{aligned} {\mathcal {M}}_h^n&:=\left\{ \begin{aligned}&\int _\Omega \phi _h^n dx,&n = 0, 1, \\&\int _\Omega \Bigl ( \frac{3}{2}\phi _h^n-\frac{1}{2}\phi _h^{n-1} \Bigr ) dx,&n\ge 2. \end{aligned} \right. \end{aligned}$$

Remark 2

The value ${\mathcal {M}}_h^n$ is an approximation of $\int _\Omega \phi ^n dx$ due to the relation $\frac{3}{2}\phi ^n-\frac{1}{2}\phi ^{n-1} (= \phi ^{n+1/2} + O(\Delta t^2)) = \phi ^n + O(\Delta t)$ for any smooth function $\phi$.

Theorem 1

(conservation of mass) Suppose that Hypotheses 1 and 2 hold true. Let $\phi _h = \{\phi _h^n\}_{n=1}^T$ be a solution to scheme (9) for a given $\phi _h^0$. Then, we have the following.

(i) It holds that, for $n=0,\ldots , N_T$,

$$\begin{aligned} {\mathcal {M}}_h^n = {\mathcal {M}}_h^0 + \Delta t \sum _{i=1}^n \Bigl ( \int _\Omega f^i dx + \int _\Gamma g^i ds \Bigr ). \end{aligned}$$

(10)

(ii) Assume $f=0$ and $g=0$ additionally. Then, for the solution to scheme (9), it holds that, for $n=0,\ldots , N_T$,

$$\begin{aligned} \int _\Omega \phi _h^n dx = \int _\Omega \phi _h^0 dx. \end{aligned}$$

(11)

Remark 3

The identity (10) is equivalent to

$$\begin{aligned} \int _\Omega \phi _h^n dx&= \int _\Omega \phi _h^0 dx + \Delta t \sum _{i=1}^n \Bigl ( \int _\Omega f^i dx + \int _\Gamma g^i ds \Bigr ), \quad n=0, 1, \\ \int _\Omega \Bigl (\frac{3}{2}\phi _h^n - \frac{1}{2}\phi _h^{n-1} \Bigr ) dx&= \int _\Omega \phi _h^0 dx + \Delta t \sum _{i=1}^n \Bigl ( \int _\Omega f^i dx + \int _\Gamma g^i ds \Bigr ), \quad n\ge 2. \end{aligned}$$

For a sequence $\{\rho ^n\}_{n = 0}^{N_T}$, let ${\bar{D}}_{\Delta t}$ be the backward quotient operator defined by

$$\begin{aligned} {\bar{D}}_{\Delta t}\rho ^n :=\left\{ \begin{aligned}&{\bar{D}}_{\Delta t}^{(1)}\rho ^n,&n = 1, \\&{\bar{D}}_{\Delta t}^{(2)}\rho ^n,&n \ge 2, \end{aligned} \right. \end{aligned}$$

where ${\bar{D}}_{\Delta t}^{(1)}$ and ${\bar{D}}_{\Delta t}^{(2)}$ are the first- and second-order backward difference quotient operators,

$$\begin{aligned} {\bar{D}}_{\Delta t}^{(1)} \rho ^n :=\frac{\rho ^n-\rho ^{n-1}}{\Delta t}, \qquad {\bar{D}}_{\Delta t}^{(2)} \rho ^n :=\frac{3\rho ^n-4\rho ^{n-1}+\rho ^{n-2}}{2\Delta t}. \end{aligned}$$

Let $m \in \{ 0,\ldots ,N_T\}$ be an integer and Y be a normed space. When $\{\rho ^n\}_{n = 0}^{N_T} \subset Y$, we define the norms $\Vert \cdot \Vert _{\ell ^\infty _m(Y)}$ and $\Vert \cdot \Vert _{\ell ^2_m(Y)}$ by

$$\begin{aligned} \Vert \rho \Vert _{\ell ^\infty _m(Y)}&:=\max _{n=m,\ldots ,N_T} \Vert \rho ^n\Vert _Y,&\Vert \rho \Vert _{\ell ^2_m (Y)}&:=\biggl \{ \Delta t \sum _{n=m}^{N_T} \Vert \rho ^n\Vert _{Y}^2 \biggr \}^{1/2}, \end{aligned}$$

and let $\Vert \rho \Vert _{\ell ^\infty (Y)} :=\Vert \rho \Vert _{\ell ^\infty _1(Y)}$ and $\Vert \rho \Vert _{\ell ^2(Y)} :=\Vert \rho \Vert _{\ell ^2_1(Y)}$. When $Y = L^2(\Omega )$, we omit $\Omega$ from the norms, e.g., $\Vert \rho \Vert _{\ell ^\infty (L^2)}$, and use the same notations $\Vert \cdot \Vert _{\ell ^\infty _m (L^2)}$, $\Vert \cdot \Vert _{\ell ^2_m (L^2)}$, $\Vert \cdot \Vert _{\ell ^\infty (L^2)}$ and $\Vert \cdot \Vert _{\ell ^2 (L^2)}$ also for a sequence of vector valued functions, e.g., $\Vert \nabla \rho \Vert _{\ell ^\infty (L^2)} = \max _{n=1,\ldots ,N_T} \Vert \nabla \rho ^n\Vert _{L^2(\Omega )^d}$.

Proposition 2

(stability for a given $\phi _h^1$) Suppose that Hypothesis 1 holds true. Let $F \in H^1(0,T; \Psi ^\prime )$ be given. Suppose that Hypothesis 2 holds true, and assume $\Delta t \in {(0, 1)}$. For given functions $\phi _h^0, \phi _h^1 \in \Psi _h$, let $\{\phi _h^n\}_{n=2}^{N_T} \subset \Psi _h$ be the solution to scheme (9b). Then, we have the following:

(i) There exists a positive constant $c_\dagger = c_\dagger ( \Vert u\Vert _{C(W^{1,\infty })}, T, 1/\nu )$ independent of h and $\Delta t$ such that

$$\begin{aligned} \Vert \phi _h\Vert _{\ell ^\infty _2(L^2)} + \sqrt{\nu } \Vert \nabla \phi _h\Vert _{\ell ^2_2(L^2)} \le c_\dagger \left( \Vert \phi _h^0\Vert + \Vert \phi _h^1\Vert + \Vert F\Vert _{\ell ^2_2(\Psi _h^\prime )} \right) . \end{aligned}$$

(12)

(ii) Assume $F \in H^1(0,T; L^2(\Omega ))$ additionally. Then, there exists a positive constant ${\bar{c}}_\dagger = {\bar{c}}_\dagger (\Vert u\Vert _{C(W^{1,\infty })}, T, 1/\nu )$ independent of h and $\Delta t$ such that

$$\begin{aligned} \sqrt{\nu } \Vert \nabla \phi _h\Vert _{\ell ^\infty _2(L^2)} + \Vert {\bar{D}}_{\Delta t}\phi _h\Vert _{\ell ^2_2(L^2)} \le {\bar{c}}_\dagger (\Vert \phi _h^0\Vert _{H^1(\Omega )} + \Vert \phi _h^1\Vert _{H^1(\Omega )} + \Vert F\Vert _{\ell ^2_2(L^2)}). \end{aligned}$$

(13)

Theorem 2

(stability) Suppose that Hypothesis 1 holds true. Let $F \in H^1(0,T; \Psi ^\prime )$ be given. Suppose that Hypothesis 2 holds true, and assume $\Delta t \in {(0, 1)}$. For a given function $\phi _h^0 \in \Psi _h$, let $\{\phi _h^n\}_{n=1}^{N_T} \subset \Psi _h$ be the solution to scheme (9). Then, we have the following:

(i) There exists a positive constant $c_\ddagger =c_\ddagger (\Vert u\Vert _{C(W^{1,\infty })}, T, 1/\nu )$ independent of h and $\Delta t$ such that

$$\begin{aligned} \Vert \phi _h\Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } \Vert \nabla \phi _h\Vert _{\ell ^2(L^2)} \le c_\ddagger \left( \Vert \phi _h^0\Vert + \Vert F\Vert _{\ell ^2(\Psi _h^\prime )} \right) . \end{aligned}$$

(14)

(ii) Assume $F \in H^1(0,T; L^2(\Omega ))$ additionally. Then, there exists a positive constant ${\bar{c}}_\ddagger = {\bar{c}}_\ddagger (\Vert u\Vert _{C(W^{1,\infty })}, T, 1/\nu )$ independent of h and $\Delta t$ such that

$$\begin{aligned} \sqrt{\nu } \Vert \nabla \phi _h\Vert _{\ell ^\infty (L^2)} + \Vert {\bar{D}}_{\Delta t}\phi _h\Vert _{\ell ^2(L^2)} \le {\bar{c}}_\ddagger \bigl ( \Vert \phi _h^0\Vert _{H^1(\Omega )} + \Vert F\Vert _{\ell ^2(L^2)} \bigr ). \end{aligned}$$

(15)

Remark 4

The assumption $F \in H^1(0,T; L^2(\Omega ))$ in Theorem 2-(ii) implies $g=0$, which is explicitly written in Corollary 1-(ii) below.

Corollary 1

(i) Suppose that the functional $F \in H^1(0,T; \Psi ^\prime )$ is given by (3) with $f\in H^1(0,T;L^2(\Omega ))$ and $g\in H^1(0,T;L^2(\Gamma ))$, the stability estimate (14) in Theorem 2-(i) becomes

$$\begin{aligned} \Vert \phi _h\Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } \, \Vert \nabla \phi _h\Vert _{\ell ^2(L^2)} \le c_\ddagger \bigl ( \Vert \phi _h^0\Vert + \Vert f\Vert _{\ell ^2(L^2)} + \Vert g\Vert _{\ell ^2(L^2(\Gamma ))} \bigr ). \end{aligned}$$

(ii) Suppose that the functional $F \in H^1(0,T; \Psi ^\prime )$ is given by (3) with $f\in H^1(0,T;L^2(\Omega ))$ and $g=0$, the stability estimate (15) in Theorem 2-(ii) becomes

$$\begin{aligned} \sqrt{\nu } \, \Vert \nabla \phi _h\Vert _{\ell ^\infty (L^2)} + \Vert {\bar{D}}_{\Delta t}\phi _h\Vert _{\ell ^2(L^2)} \le {\bar{c}}_\ddagger \bigl ( \Vert \phi _h^0\Vert _{H^1(\Omega )} + \Vert f\Vert _{\ell ^2(L^2)} \bigr ). \end{aligned}$$

We present the convergence result of second order in time after stating regularity hypotheses for the solution to problem (2) given the polynomial degree $k\in {\mathbb {N}}$ of the finite element space $\Psi _h$ in Hypothesis 3 and for the solution of the Poisson problem in Hypothesis 4. Then we define the Poisson projection in Definition 1.

Hypothesis 3

The solution $\phi$ to (2) satisfies $\phi \in Z^3 \cap H^2(0,T; H^{k+1}(\Omega ))$.

Remark 5

We suppose $H^2(0,T; H^{k+1}(\Omega ))$, since the regularity $H^1(0,T; H^{k+1}(\Omega ))$ is not sufficient to get the convergence of second order in time, especially for the estimate of the solution at the first time step.

Hypothesis 4

The Poisson problem is regular on the domain $\Omega$, i.e., for any ${\tilde{f}}\in L^2(\Omega )$, there exists a unique solution to the Poisson problem; find $\rho \in \Psi$ such that

$$\begin{aligned} a_0(\rho ,\psi ) + (\rho , \psi ) = ({\tilde{f}},\psi ), \quad \forall \psi \in \Psi , \end{aligned}$$

and there exists a positive constant $c_R$ independent of ${\tilde{f}}$ and $\rho$ such that

$$\begin{aligned} \Vert \rho \Vert _{H^2(\Omega )} \le c_R \Vert {\tilde{f}}\Vert . \end{aligned}$$

Definition 1

For $\phi \in \Psi$, we define the Poisson projection ${\hat{\phi }}_h \in \Psi _h$ to $\phi$ by

$$\begin{aligned} a_0({\hat{\phi }}_h, \psi _h) + ({\hat{\phi }}_h, \psi _h) = a_0(\phi , \psi _h) + (\phi , \psi _h), \quad \forall \psi _h \in \Psi _h. \end{aligned}$$

(16)

Theorem 3

(error estimates) Suppose that Hypothesis 1 holds true. For a given $F\in H^1(0,T; \Psi ^\prime )$, let $\{\phi (t) = \phi (\cdot ,t)\in \Psi ;~t\in (0,T) \}$ be the solution to problem (2). Suppose that Hypothesis 3 holds true. Let $\Delta t\in {(0, 1)}$ be a time increment satisfying Hypothesis 2 and $\{\phi _h^n\}_{n=1}^{N_T} \subset \Psi _h$ be the solution to scheme (9) with the initial condition $\phi _h^0 = {\hat{\phi }}_h^0 \in \Psi _h$. Then, we have the following:

(i) There exist positive constants $c_*$ and $c_*^\prime$ independent of h and $\Delta t$ such that

$$\begin{aligned} \Vert \phi _h - \phi \Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } \, \Vert \nabla (\phi _h - \phi ) \Vert _{\ell ^2(L^2)}&\le c_*(\Delta t^2 + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}, \end{aligned}$$

(17a)

$$\begin{aligned} \sqrt{\nu } \Vert \nabla (\phi _h - \phi ) \Vert _{\ell ^\infty (L^2)} + \Bigl \Vert {\bar{D}}_{\Delta t}\phi _h - \frac{\partial {\phi }}{\partial {t}} \Bigr \Vert _{\ell ^2(L^2)}&\le c_*^\prime (\Delta t^{3/2} + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}. \end{aligned}$$

(17b)

(ii) Suppose that additionally Hypothesis 4 holds. Then, there exists a positive constant ${\bar{c}}_*$ independent of h and $\Delta t$ such that

$$\begin{aligned} \Vert \phi _h - \phi \Vert _{\ell ^\infty (L^2)} \le {\bar{c}}_*(\Delta t^2 + h^{k+1}) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}. \end{aligned}$$

(18)

4 Proofs

4.1 Proof of Theorem 1

We first note that due to Proposition 1-(i)

$$\begin{aligned} \int _{\Omega } \rho \circ X_1^n(x) \gamma ^n(x) dx = \int _\Omega \rho (x)\, dx, \quad \int _{\Omega } \rho \circ {{\tilde{X}}}_1^n(x) {{\tilde{\gamma }}}^n(x) dx = \int _\Omega \rho (x)\, dx \end{aligned}$$

(19)

hold for any $\rho \in \Psi$ and $n=1,\dots , N_t$. We substitute $1 \in \Psi _h$ into $\psi _h$ in scheme (9) in the following.

We prove (i) by induction.

(I) Initial steps ($n=0, 1$):    Since (10) with $n=0$ is trivial, we prove it for $n = 1$. We have

$$\begin{aligned} {\mathcal {M}}_h^1&= \int _\Omega \phi _h^1(x) dx \\&= \int _\Omega \phi _h^0\circ X_1^1(x)\gamma ^1(x) dx + \Delta t \Bigl ( \int _\Omega f^1(x) dx + \int _\Gamma g^1(x) ds \Bigr ) \qquad (\text{ by }~(9a)) \\&= \int _\Omega \phi _h^0 (y) dy + \Delta t \Bigl ( \int _\Omega f^1(x) dx + \int _\Gamma g^1(x) ds \Bigr ) \qquad (\text{ by }~(19)) \\&= {\mathcal {M}}_h^0 + \Delta t \Bigl ( \int _\Omega f^1(x) dx + \int _\Gamma g^1(x) ds \Bigr ). \end{aligned}$$

Hence, (10) holds for $n=0, 1$.

(II) General steps:    Let $m\in \{2,\ldots , N_T\}$ and suppose that (10) holds true for $n=m-1$. Then, we obtain (10) for $n=m$ as follows:

$$\begin{aligned} {\mathcal {M}}_h^m&= \int _\Omega \Bigl ( \frac{3}{2} \phi _h^m - \frac{1}{2} \phi _h^{m-1} \Bigr ) dx \\&= \int _\Omega \Bigl ( \frac{3}{2} \phi _h^m - \frac{1}{2} \phi _h^{m-1} \circ X_1^m \gamma ^m \Bigr ) dx \qquad (\text{ cf. }~(19)) \\&= \int _\Omega \Bigl ( \frac{3}{2} \phi _h^{m-1} \circ X_1^m \gamma ^m - \frac{1}{2} \phi _h^{m-2} \circ {\tilde{X}}_1^m {\tilde{\gamma }}^m \Bigr ) dx + \Delta t \Bigl ( \int _\Omega f^m(x) dx + \int _\Gamma g^m(x) ds \Bigr ) \quad (\text{ by }~(9b))\\&= \int _\Omega \Bigl ( \frac{3}{2} \phi _h^{m-1} - \frac{1}{2} \phi _h^{m-2} \Bigr ) dx + \Delta t \Bigl ( \int _\Omega f^m(x) dx + \int _\Gamma g^m(x) ds \Bigr ) \\&= {\mathcal {M}}_h^{m-1} + \Delta t \Bigl ( \int _\Omega f^m(x) dx + \int _\Gamma g^m(x) ds \Bigr ) \qquad (\text{ cf. }~(19)) \\&= {\mathcal {M}}_h^0 + \Delta t \sum _{i=1}^m \Bigl ( \int _\Omega f^i(x) dx + \int _\Gamma g^i(x) ds \Bigr ) \\&\qquad \text{(by } \text{ the } \text{ induction } \text{ assumption, } \text{ i.e., }~(10)~\text{ with }~n=m-1). \end{aligned}$$

From (I) and (II) the proof of (i) is completed.

We prove (ii) by induction.

(I’) Initial steps ($n=0, 1$):    The property (11) is obvious for $n=0, 1$, cf. (I) in the proof of (i).

(II’) General steps:    Let $m\in \{ 2, \ldots , N_T\}$ and assume that (11) holds true for $n = m-1$ and $m-2$, we prove that (11) also does for $n=m$. From (9b) with $f=0$, $g=0$ and the induction assumption, we obtain (11) with $n=m$ as follows:

$$\begin{aligned} \int _\Omega \phi _h^m dx&= \int _\Omega \Bigl ( \frac{4}{3} \phi _h^{m-1}\circ X_1^m\gamma ^m - \frac{1}{3}\phi _h^{m-2}\circ {\tilde{X}}_1^m {\tilde{\gamma }}^m \Bigr ) dx \\&= \int _\Omega \Bigl ( \frac{4}{3} \phi _h^{m-1} - \frac{1}{3} \phi _h^{m-2} \Bigr ) dx = \int _\Omega \phi _h^0 dx. \end{aligned}$$

From (I’) and (II’) the proof of (ii) is completed. $\square$

4.2 Proofs of Proposition 2 and Theorem 2

The proofs are given after stating two lemmas on a discrete Gronwall’s inequality and composite functions. The proof of the next lemma is given in Appendix A.1.

Lemma 1

Let $a_i, i=0,1,2,$ be non-negative numbers with $a_1 \ge a_2$, and $\Delta t\in (0, 3/(4a_0)]$. Let $\{x_n\}_{n\ge 0}$, $\{y_n\}_{n\ge 1}$, $\{z_n\}_{n\ge 2}$ and $\{b_n\}_{n\ge 2}$ be non-negative sequences. Suppose that

$$\begin{aligned} \frac{1}{\Delta t}\Bigl ( \frac{3}{2} x_n - 2 x_{n-1} + \frac{1}{2} x_{n-2} + y_n - y_{n-1} \Bigr ) + z_n \le a_0 x_n + a_1 x_{n-1} + a_2 x_{n-2} + b_n,\quad \forall n\ge 2 \end{aligned}$$

(20)

holds. Then, it holds that

$$\begin{aligned} x_n + \frac{2}{3} y_n + \frac{2}{3}\Delta t\sum _{i=2}^nz_i&\le \Bigl ( \exp ( 2 a_*n\Delta t ) +1 \Bigr ) \Biggl ( x_0 + \frac{3}{2} x_1 + y_1+\Delta t\sum _{i=2}^n b_i \Biggr ), \quad \forall n \ge 2, \end{aligned}$$

(21)

where $a_*:=a_0+a_1+a_2$.

We recall some results concerning the evaluation of composite functions, which are mainly due to Lemma 4.5 in [1] and Lemma 1 in [15].

Lemma 2

[1, 15, 29, 34] Let a be a function in $W^{1,\infty }_0(\Omega )^d$ satisfying $\Delta t \Vert a\Vert _{1,\infty } \le 1/4$ and consider the mapping $X_1(a,\Delta t)$ defined in (6). Then, the following inequalities hold.

$$\begin{aligned} \Vert \psi \circ X_1(a,\Delta t)\Vert&\le (1 + c_1 \Delta t) \Vert \psi \Vert ,&\forall \psi&\in L^2(\Omega ), \end{aligned}$$

(22a)

$$\begin{aligned} \Vert \psi - \psi \circ X_1(a,\Delta t)\Vert&\le c_0 \Delta t \Vert \psi \Vert _{H^1(\Omega )},&\forall \psi&\in H^1(\Omega ), \end{aligned}$$

(22b)

$$\begin{aligned} \Vert \psi - \psi \circ X_1(a,\Delta t) \Vert _{H^{1}(\Omega )^\prime }&\le c_1 \Delta t \Vert \psi \Vert ,&\forall \psi&\in L^2(\Omega ). \end{aligned}$$

(22c)

Proof of Proposition 2

The equation (9b) can be written as

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(2)}\phi _h^n, \psi _h \bigr ) + a_0(\phi _h^n, \psi _h)&= \langle F^n, \psi _h \rangle + \langle I_h^n, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h \end{aligned}$$

(23)

for $n \ge 2$, where $I_h^n \in \Psi _h^\prime$ with the norm $\Vert \cdot \Vert _{\Psi _h} :=\Vert \cdot \Vert _{\Psi } \ (= \Vert \cdot \Vert _{H^1(\Omega )})$ is defined for $n \in \{ 2, \ldots , N_T\}$ by

We prove (i). Substituting $\phi _h^n \in \Psi _h$ into $\psi _h$ in (23), we have

$$\begin{aligned}&\frac{1}{\Delta t} \Bigl [ \frac{3}{4} \Vert \phi _h^n\Vert ^2 - \Vert \phi _h^{n-1}\Vert ^2 + \frac{1}{4}\Vert \phi _h^{n-2}\Vert ^2 + \frac{1}{2}( \Vert \phi _h^n-\phi _h^{n-1}\Vert ^2-\Vert \phi _h^{n-1} - \phi _h^{n-2}\Vert ^2) \Bigr ]\nonumber \\&\qquad + \frac{\nu }{2} \Vert \nabla \phi _h^n\Vert ^2 \nonumber \\&\quad \le \frac{3}{8} \Vert \phi _h^n\Vert ^2 + c_{1,\nu } \Bigl ( \frac{1}{2} \Vert \phi _h^{n-1}\Vert ^2 + \frac{1}{2} \Vert \phi _h^{n-2}\Vert ^2 \Bigr ) + c_\nu \Vert F^n\Vert _{\Psi _h^\prime }^2 \end{aligned}$$

(24)

from the estimates, thanks to Young’s inequality and an identity in [33] for $({\bar{D}}_{\Delta t}^{(2)}\phi _h^n, \phi _h^n)$,

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(2)}\phi _h^n, \phi _h^n \bigr )&= \frac{1}{\Delta t} \Bigl [ \frac{3}{4} \Vert \phi _h^n\Vert ^2 - \Vert \phi _h^{n-1}\Vert ^2 + \frac{1}{4} \Vert \phi _h^{n-2}\Vert ^2 + \frac{1}{4} \Vert \phi _h^n-2\phi _h^{n-1}+\phi _h^{n-2}\Vert ^2 \nonumber \\&\qquad + \frac{1}{2} \Bigl ( \Vert \phi _h^n-\phi _h^{n-1}\Vert ^2 - \Vert \phi _h^{n-1}-\phi _h^{n-2}\Vert ^2 \Bigr ) \Bigr ] \nonumber \\&\ge \frac{1}{\Delta t} \Bigl [ \frac{3}{4} \Vert \phi _h^n\Vert ^2 - \Vert \phi _h^{n-1}\Vert ^2 + \frac{1}{4} \Vert \phi _h^{n-2}\Vert ^2 \nonumber \\&\qquad + \frac{1}{2} \Bigl ( \Vert \phi _h^n-\phi _h^{n-1}\Vert ^2 - \Vert \phi _h^{n-1}-\phi _h^{n-2}\Vert ^2 \Bigr ) \Bigr ], \nonumber \\ a_0(\phi _h^n, \phi _h^n)&= \nu \Vert \nabla \phi _h^n\Vert ^2, \nonumber \\ \langle F^n, \phi _h^n \rangle&\le \Vert F^n\Vert _{\Psi _h^\prime } \Vert \phi _h^n\Vert _{H^1(\Omega )} \le \Vert F^n\Vert _{\Psi _h^\prime } (\Vert \phi _h^n\Vert + \Vert \nabla \phi _h^n\Vert ) \nonumber \\&\le \frac{1}{8} \Vert \phi _h^n\Vert ^2 + \frac{\nu }{4}\Vert \nabla \phi _h^n\Vert ^2 + c_\nu \Vert F^n\Vert _{\Psi _h^\prime }^2 \quad (c_\nu = 2 + 1/\nu ), \end{aligned}$$

(25)

$$\begin{aligned} \Vert I_{h1}^n\Vert _{\Psi _h^\prime }&\le \Vert I_{h1}^n\Vert _{H^1(\Omega )^\prime } \le c_1(\Vert \phi _h^{n-1}\Vert +\Vert \phi _h^{n-2}\Vert ) \quad (\text{ by } \text{ Lem. }~2\hbox {-}(22c)), \nonumber \\ \Vert I_{h2}^n\Vert&\le \frac{c}{\Delta t} \Bigl ( \Vert \phi _h^{n-1} \circ X_1^n ( 1 - \gamma ^n ) \Vert + \Vert \phi _h^{n-2} \circ {\tilde{X}}_1^n ( 1 - {\tilde{\gamma }}^n ) \Vert \Bigr ) \nonumber \\&\le c_1 \bigl ( \Vert \phi _h^{n-1} \Vert + \Vert \phi _h^{n-2} \Vert \bigr ) \nonumber \\&\qquad (\text{ by }\, \Vert 1-\gamma \Vert _{C(L^\infty )},\ \Vert 1-{\tilde{\gamma }}\Vert _{C(L^\infty )} \le c_1 \Delta t,\ \ \text{ Lem. }~2\hbox {-}(22a)) \end{aligned}$$

(26)

$$\begin{aligned} \langle I_h^n, \phi _h^n \rangle&\le \Vert I_{h1}^n\Vert _{\Psi _h^\prime } \Vert \phi _h^n \Vert _{\Psi _h} + \Vert I_{h2}^n\Vert \Vert \phi _h^n \Vert \le \Vert I_{h1}^n\Vert _{\Psi _h^\prime } (\Vert \phi _h^n \Vert + \Vert \nabla \phi _h^n \Vert ) + \Vert I_{h2}^n\Vert \Vert \phi _h^n \Vert \nonumber \\&\le \Bigl ( 2 + \frac{1}{\nu } \Bigr ) \Vert I_{h1}^n\Vert _{\Psi _h^\prime }^2 + 2 \Vert I_{h2}^n\Vert ^2 + \frac{1}{4} \Vert \phi _h^n \Vert ^2 + \frac{\nu }{4} \Vert \nabla \phi _h^n \Vert ^2 \nonumber \\&\le \frac{1}{4}\Vert \phi _h^n\Vert ^2 + \frac{\nu }{4} \Vert \nabla \phi _h^n \Vert ^2 + c_{1,\nu } \Bigl ( \frac{1}{2} \Vert \phi _h^{n-1}\Vert ^2 + \frac{1}{2} \Vert \phi _h^{n-2}\Vert ^2 \Bigr ). \end{aligned}$$

(27)

The inequality (24) and Lemma 1 with

$$\begin{aligned} x_n&= \frac{1}{2}\Vert \phi _h^n\Vert ^2,&y_n&= \frac{1}{2}\Vert \phi _h^n-\phi _h^{n-1}\Vert ^2,&z_n&= \frac{\nu }{2} \Vert \nabla \phi _h^n\Vert ^2, \\ a_0&= \frac{3}{4},&a_1&= a_2 = c_{1,\nu },&b_n&= c_\nu \Vert F^n\Vert _{\Psi _h^\prime }^2 \end{aligned}$$

imply

$$\begin{aligned} \max _{n=2,\ldots ,N_T} \Vert \phi _h^n \Vert ^2 + \nu \Delta t\sum _{n=2}^{N_T} \Vert \nabla \phi _h^n \Vert ^2 \le c_{1,\nu ,T} \Bigl [ \Vert \phi _h^0 \Vert ^2 + \Vert \phi _h^1 \Vert ^2 + \Delta t \sum _{n=2}^{N_T} \Vert F^n\Vert _{\Psi _h^\prime }^2 \Bigr ], \end{aligned}$$

which completes the proof of (i).

Next we prove (ii). Substituting ${\bar{D}}_{\Delta t}^{(2)}\phi _h^n \in \Psi _h$ into $\psi _h$ in (23), we have

$$\begin{aligned}&\frac{\nu }{\Delta t} \biggl [ \frac{3}{4} \Vert \nabla \phi _h^n\Vert ^2 - \Vert \nabla \phi _h^{n-1}\Vert ^2 + \frac{1}{4} \Vert \nabla \phi _h^{n-2}\Vert ^2 + \frac{1}{2} \Bigl ( \Vert \nabla (\phi _h^n-\phi _h^{n-1})\Vert ^2\nonumber \\&\quad - \Vert \nabla (\phi _h^{n-1}-\phi _h^{n-2})\Vert ^2 \Bigr ) \biggr ] \nonumber \\&\quad + \frac{1}{2} \Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n \Vert ^2 \le \frac{c_1}{\nu } \biggl ( \frac{\nu }{2} \Vert \nabla \phi _h^{n-1}\Vert ^2 + \frac{\nu }{2} \Vert \nabla \phi _h^{n-2}\Vert ^2 \biggr )\nonumber \\&\quad + \Vert F^n\Vert ^2 + c_1^\prime \sum _{i=1}^2 \Vert \phi _h^{n-i}\Vert ^2 \end{aligned}$$

(28)

from the estimates

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(2)}\phi _h^n, {\bar{D}}_{\Delta t}^{(2)}\phi _h^n \bigr )&= \Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n \Vert ^2, \nonumber \\ a_0(\phi _h^n, {\bar{D}}_{\Delta t}^{(2)}\phi _h^n)&= \frac{\nu }{\Delta t} \Bigl [ \frac{3}{4} \Vert \nabla \phi _h^n\Vert ^2 - \Vert \nabla \phi _h^{n-1}\Vert ^2 + \frac{1}{4} \Vert \nabla \phi _h^{n-2}\Vert ^2 \nonumber \\&\quad + \frac{1}{4} \Vert \nabla (\phi _h^n-2\phi _h^{n-1}+\phi _h^{n-2})\Vert ^2 \nonumber \\&\quad + \frac{1}{2} \Bigl ( \Vert \nabla (\phi _h^n-\phi _h^{n-1})\Vert ^2 - \Vert \nabla (\phi _h^{n-1}-\phi _h^{n-2})\Vert ^2 \Bigr ) \Bigr ] \text{(by } \text{ an } \text{ identity } \text{ in } \text{[13]) } \nonumber \\&\ge \frac{\nu }{\Delta t} \Bigl [ \frac{3}{4} \Vert \nabla \phi _h^n\Vert ^2 - \Vert \nabla \phi _h^{n-1}\Vert ^2 + \frac{1}{4} \Vert \nabla \phi _h^{n-2}\Vert ^2 \nonumber \\&\quad + \frac{1}{2} \Bigl ( \Vert \nabla (\phi _h^n-\phi _h^{n-1})\Vert ^2 - \Vert \nabla (\phi _h^{n-1}-\phi _h^{n-2})\Vert ^2 \Bigr ) \Bigr ], \nonumber \\ \langle F^n, {\bar{D}}_{\Delta t}^{(2)}\phi _h^n \rangle&= ( F^n, {\bar{D}}_{\Delta t}^{(2)}\phi _h^n ) \le \Vert F^n\Vert ^2 + \frac{1}{4}\Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n\Vert ^2, \nonumber \\ \Vert I_{h1}^n \Vert&\le c_0 ( \Vert \phi _h^{n-1}\Vert _1 + \Vert \phi _h^{n-2}\Vert _1 ) \quad (\text{ by } \text{ Lem. }~2\text{- }(22b)), \nonumber \\ \Vert I_{h2}^n\Vert&\le c_1 \bigl ( \Vert \phi _h^{n-1} \Vert + \Vert \phi _h^{n-2} \Vert \bigr ) \quad (\text{ cf. }~(26)), \nonumber \\ \bigl \langle I_h^n, {\bar{D}}_{\Delta t}^{(2)}\phi _h^n \bigr \rangle&\le \Vert I_h^n\Vert ^2 + \frac{1}{4}\Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n\Vert ^2 \le c_1 ( \Vert \phi _h^{n-1}\Vert _1^2 + \Vert \phi _h^{n-2}\Vert _1^2 ) + \frac{1}{4}\Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n\Vert ^2 \nonumber \\&= c_1 \Bigl ( \Vert \nabla \phi _h^{n-1}\Vert ^2 + \Vert \nabla \phi _h^{n-2}\Vert ^2 \Bigr ) + c_1^\prime \sum _{i=1}^2 \Vert \phi _h^{n-i}\Vert ^2 + \frac{1}{4}\Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n\Vert ^2. \end{aligned}$$

(29)

From the inequality (28), applying Lemma 1 with

$$\begin{aligned} x_n&= \frac{\nu }{2} \Vert \nabla \phi _h^n\Vert ^2,&y_n&= \frac{\nu }{2}\Vert \nabla (\phi _h^n-\phi _h^{n-1})\Vert ^2,&z_n&= \frac{1}{2} \Vert {\bar{D}}_{\Delta t}^{(2)}\phi _h^n\Vert ^2,\\ a_0&= 0,&a_1&= a_2 = \frac{c_1}{\nu },&b_n&= \Vert F^n\Vert ^2 + c_1^\prime \sum _{i=1}^2 \Vert \phi _h^{n-i}\Vert ^2, \end{aligned}$$

and using the result of (i), we obtain

$$\begin{aligned}&\max _{n=2,\ldots ,N_T} \nu \Vert \nabla \phi _h^n \Vert ^2 + \Delta t\sum _{n=2}^{N_T} \Vert {\bar{D}}_{\Delta t}^{(2)} \phi _h^n \Vert ^2\\&\quad \le c_{1,\nu ,T} \left( \Vert \phi _h^0 \Vert _{H^1(\Omega )}^2 + \Vert \phi _h^1 \Vert _{H^1(\Omega )}^2 + \Delta t \sum _{n=2}^{N_T} \Vert F^n \Vert ^2 \right) , \end{aligned}$$

which completes the proof of (ii). $\square$

Proof of Theorem 2

We employ Proposition 2 for the proof. For the first step, $n=1$, scheme (9a) can be written as

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(1)}\phi _h^1, \psi _h \bigr ) + a_0(\phi _h^1, \psi _h)&= \langle F^1, \psi _h \rangle + \langle I_h^1, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h, \end{aligned}$$

(30)

where $I_h^1 \in \Psi _h^\prime$ is defined by

$$\begin{aligned} I_h^1&:=- \frac{1}{\Delta t} \bigl ( \phi _h^0 - \phi _h^0 \circ X_1^1 \gamma ^1 \bigr ). \end{aligned}$$

We first prove (i). Substituting $\phi _h^1 \in \Psi _h$ into $\psi _h$ in (30), and noting that

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(1)}\phi _h^1, \phi _h^1 \bigr )&= \frac{1}{\Delta t} \biggl ( \frac{1}{2} \Vert \phi _h^1\Vert ^2 - \frac{1}{2} \Vert \phi _h^0\Vert ^2 + \frac{1}{2} \Vert \phi _h^1-\phi _h^0\Vert ^2 \biggr ) \ge \frac{1}{\Delta t} \biggl ( \frac{1}{2} \Vert \phi _h^1\Vert ^2 - \frac{1}{2} \Vert \phi _h^0\Vert ^2 \biggr ), \\ a_0(\phi _h^1, \phi _h^1)&= \nu \Vert \nabla \phi _h^1\Vert ^2, \nonumber \\ \langle F^1, \phi _h^1 \rangle&\le \frac{1}{8} \Vert \phi _h^1\Vert ^2 + \frac{\nu }{4}\Vert \nabla \phi _h^1\Vert ^2 + c_\nu \Vert F^1\Vert _{\Psi _h^\prime }^2 \quad (\text{ cf. }~(25)), \nonumber \\ \langle I_h^1, \phi _h^1 \rangle&\le \frac{1}{4}\Vert \phi _h^1\Vert ^2 + \frac{\nu }{4} \Vert \nabla \phi _h^1 \Vert ^2 + \frac{c_{1,\nu }}{2} \Vert \phi _h^0\Vert ^2 \quad (\text{ cf. }~(27)), \end{aligned}$$

we have

$$\begin{aligned} \frac{1}{\Delta t} \biggl ( \frac{1}{2} \Vert \phi _h^1\Vert ^2 - \frac{1}{2} \Vert \phi _h^0\Vert ^2 \biggr ) + \frac{\nu }{2} \Vert \nabla \phi _h^1\Vert ^2&\le \frac{1}{2} \Vert \phi _h^1\Vert ^2 + \frac{c_{1,\nu }}{2} \Vert \phi _h^0\Vert ^2 + c_\nu \Vert F^1\Vert _{\Psi _h^\prime }^2, \end{aligned}$$

which implies

$$\begin{aligned} \Vert \phi _h^1\Vert ^2 + \nu \Delta t \Vert \nabla \phi _h^1\Vert ^2&\le c_{1,\nu } \Bigl ( \Vert \phi _h^0\Vert ^2 + \Delta t \Vert F^1\Vert _{\Psi _h^\prime }^2 \Bigr ). \end{aligned}$$

(31)

The result (14) is obtained by combining (31) with Proposition 2-(i).

We next prove (ii). Substituting ${\bar{D}}_{\Delta t}^{(1)}\phi _h^n \in \Psi _h$ into $\psi _h$ in (30), and noting that

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(1)}\phi _h^1, {\bar{D}}_{\Delta t}^{(1)}\phi _h^1 \bigr )&= \Vert {\bar{D}}_{\Delta t}^{(1)}\phi _h^1 \Vert ^2, \\ a_0 \bigl ( \phi _h^1, {\bar{D}}_{\Delta t}^{(1)}\phi _h^1 \bigr )&\ge \frac{1}{\Delta t} \biggl ( \frac{\nu }{2} \Vert \nabla \phi _h^1\Vert ^2 - \frac{\nu }{2} \Vert \nabla \phi _h^0\Vert ^2 \biggr ), \\ \langle F^1, {\bar{D}}_{\Delta t}^{(1)}\phi _h^1 \rangle&= (F^1, {\bar{D}}_{\Delta t}^{(1)}\phi _h^1) \le \Vert F^1\Vert ^2 + \frac{1}{4}\Vert {\bar{D}}_{\Delta t}^{(1)}\phi _h^1\Vert ^2, \\ \langle I_h^1, {\bar{D}}_{\Delta t}^{(1)}\phi _h^1 \rangle&\le c_1 \bigl ( \Vert \nabla \phi _h^0\Vert ^2 + \Vert \phi _h^0\Vert ^2 \bigr ) + \frac{1}{4}\Vert {\bar{D}}_{\Delta t}^{(1)}\phi _h^1\Vert ^2 \quad (\text{ cf. }~(29)), \end{aligned}$$

we have

$$\begin{aligned} \frac{1}{\Delta t} \biggl ( \frac{\nu }{2} \Vert \nabla \phi _h^1\Vert ^2 - \frac{\nu }{2} \Vert \nabla \phi _h^0\Vert ^2 \biggr ) + \frac{1}{2} \Vert {\bar{D}}_{\Delta t}^{(1)}\phi _h^1\Vert ^2&\le \frac{c_1}{\nu } \Bigl ( \frac{\nu }{2}\Vert \nabla \phi _h^0 \Vert ^2 \Bigr ) + \Vert F^1\Vert ^2 + c_1^\prime \Vert \phi _h^0\Vert ^2, \end{aligned}$$

which implies

$$\begin{aligned} \nu \Vert \nabla \phi _h^1\Vert ^2 + \Delta t \Vert {\bar{D}}_{\Delta t}^{(1)}\phi _h^1\Vert ^2&\le c_{1,\nu } \Bigl ( \Vert \phi _h^0\Vert _{H^1(\Omega )}^2 + \Delta t \Vert F^1\Vert ^2 \Bigr ), \end{aligned}$$

and, by taking into account (31) with $g=0$,

$$\begin{aligned} \Vert \phi _h^1\Vert _{H^1(\Omega )}^2 + \Delta t \Vert {\bar{D}}_{\Delta t}^{(1)}\phi _h^1\Vert ^2&\le c_{1,\nu } \Bigl ( \Vert \phi _h^0\Vert _{H^1(\Omega )}^2 + \Delta t \Vert F^1\Vert ^2 \Bigr ). \end{aligned}$$

(32)

The result (15) is obtained by combining (32) with Proposition 2-(ii). $\square$

4.3 Proof of Theorem 3

Error estimates for the Poisson projection are summarized in the following lemma.

Lemma 3

[12] Let $\Psi _h$ be the finite element space defined in (5) with polynomial degree $k\in {\mathbb {N}}$. Then, we have the following.

(i) There exists a positive constant c independent of h such that

$$\begin{aligned} \Vert {\hat{\psi }}_h - \psi \Vert _{H^1(\Omega )} \le c h^k \Vert \psi \Vert _{H^{k+1}(\Omega )}, \quad \forall \psi \in H^{k+1}(\Omega ). \end{aligned}$$

(ii) Under Hypothesis 4, there exists a positive constant $c^\prime$ independent of h such that

$$\begin{aligned} \Vert {\hat{\psi }}_h - \psi \Vert \le c^\prime h^{k+1} \Vert \psi \Vert _{H^{k+1}(\Omega )}, \quad \forall \psi \in H^{k+1}(\Omega ). \end{aligned}$$

The next lemma shows the truncation error of second order in time for the time-discretization of $\partial \phi /\partial t + \nabla \cdot ( u\phi )$, and plays an important role in the proof of Theorem 3.

Lemma 4

(truncation error) Suppose that Hypothesis 1 holds true. Assume $\phi \in Z^3$. Suppose that Hypothesis 2 holds true. Then, there exists a positive constant $c=c_1$ independent of $\Delta t$ such that

$$\begin{aligned} \Bigl \Vert {\mathcal {A}}_{\Delta t} \phi ^n - \Bigl [ \frac{\partial {\phi }}{\partial {t}} +\nabla \cdot \bigl ( u\phi \bigr ) \Bigr ] (\cdot ,t^n) \Bigr \Vert \le c \Delta t^{3/2} \Vert \phi \Vert _{Z^3(t^{n-2},t^n)}, \quad n\in \{2, \ldots , N_T\}. \end{aligned}$$

(33)

Proof

Let $n\in \{2, \ldots , N_T\}$ be fixed arbitrarily. From a simple calculation, the two Jacobians, $\gamma ^n$ and ${\tilde{\gamma }}^n$, are written as

$$\begin{aligned} \gamma ^n(x)&= 1 - \Delta t \nabla \cdot u^n(x) + \Delta t^2 \delta _1^n(x) + \Delta t^3 \delta _2^n(x), \end{aligned}$$

(34a)

$$\begin{aligned} {\tilde{\gamma }}^n(x)&= 1 - 2\Delta t \nabla \cdot u^n(x) + (2\Delta t)^2 \delta _1^n(x) + (2\Delta t)^3 \delta _2^n(x), \end{aligned}$$

(34b)

where $\delta _i: \Omega \times (0,T) \rightarrow {\mathbb {R}}$, $i = 1, 2$, are defined by

$$\begin{aligned} \delta _1&:=\left\{ \begin{aligned}&\ 0,&d&= 1, \\&\frac{\partial {u_1}}{\partial {x_1}} \frac{\partial {u_2}}{\partial {x_2}} - \frac{\partial {u_1}}{\partial {x_2}} \frac{\partial {u_2}}{\partial {x_1}} ,&d&= 2, \\&\frac{\partial {u_1}}{\partial {x_1}} \frac{\partial {u_2}}{\partial {x_2}} + \frac{\partial {u_2}}{\partial {x_2}} \frac{\partial {u_3}}{\partial {x_3}} + \frac{\partial {u_3}}{\partial {x_3}} \frac{\partial {u_1}}{\partial {x_1}} - \frac{\partial {u_1}}{\partial {x_2}} \frac{\partial {u_2}}{\partial {x_1}} - \frac{\partial {u_2}}{\partial {x_3}} \frac{\partial {u_3}}{\partial {x_2}} {- \frac{\partial {u_3}}{\partial {x_1}} \frac{\partial {u_1}}{\partial {x_3}} ,}&d&= 3, \end{aligned} \right. \\ \delta _2&:=\left\{ \begin{aligned}&\ 0,&d&= {1,\,} 2, \\&\quad - \frac{\partial {u_1}}{\partial {x_1}} \frac{\partial {u_2}}{\partial {x_2}} \frac{\partial {u_3}}{\partial {x_3}} - \frac{\partial {u_1}}{\partial {x_2}} \frac{\partial {u_2}}{\partial {x_3}} \frac{\partial {u_3}}{\partial {x_1}} - \frac{\partial {u_1}}{\partial {x_3}} \frac{\partial {u_2}}{\partial {x_1}} \frac{\partial {u_3}}{\partial {x_2}} \\&\quad + \frac{\partial {u_1}}{\partial {x_1}} \frac{\partial {u_2}}{\partial {x_3}} \frac{\partial {u_3}}{\partial {x_2}} + \frac{\partial {u_1}}{\partial {x_3}} \frac{\partial {u_2}}{\partial {x_2}} \frac{\partial {u_3}}{\partial {x_1}} + \frac{\partial {u_1}}{\partial {x_2}} \frac{\partial {u_2}}{\partial {x_1}} \frac{\partial {u_3}}{\partial {x_3}} ,&\quad \ d&= 3, \end{aligned} \right. \end{aligned}$$

with the estimates $\Vert \delta _i \Vert _{C(L^\infty )} \le c_1$, $i=1, 2$. The relations (34) imply the key identity

(35)

Let us introduce the notations

$$\begin{aligned} y(x,s)&= y(x,s;n) :=X_1 \bigl ( u^n, (1-s)\Delta t \bigr )(x) = x - u^n(x) (1-s)\Delta t, \\ t(s)&= t(s;n) :=t^{n-1}+s\Delta t. \end{aligned}$$

Applying the identities

$$\begin{aligned} \rho ^\prime (1) - \Bigl [ \frac{3}{2}\rho (1)-2\rho (0)+\frac{1}{2}\rho (-1) \Bigr ]&= 2\int _0^1sds\int _{2s-1}^s\rho ^{\prime \prime \prime }(s_1)ds_1,\\ \rho (1)-2\rho (0)+\rho (-1)&= \int _0^1ds\int _{s-1}^s \rho ^{\prime \prime }(s_1)ds_1, \\ \rho (0)-\rho (-1)&= \int _{-1}^0 \rho ^{\prime }(s)ds \end{aligned}$$

for ${\rho } (s) = \phi (y(\cdot ,s),t(s))$ we have the next expressions of $O(\Delta t^2)$,

$$\begin{aligned} I_1^n (x)&= -2\Delta t^2 \int _0^1 s ds \int _{2s-1}^s \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} +u^n(x)\cdot \nabla \Bigr )^3\phi \Bigr ] \bigl ( y(x,s_1), t(s_1) \bigr ) \, ds_1, \\ I_2^n (x)&= -\Delta t^2 (\nabla \cdot u^n)(x) \int _0^1ds\int _{s-1}^{s} \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} +u^n(x)\cdot \nabla \Bigr )^2\phi \Bigr ] \bigl ( y(x,s_1, t(s_1) \bigr ) \, ds_1, \\ I_3^n (x)&= -2\Delta t^2 \delta _1(x) \int _{-1}^0 \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} +u^n(x)\cdot \nabla \Bigr ) \phi \Bigr ] \bigl ( y(x,s), t(s) \bigr ) \, ds. \end{aligned}$$

We evaluate $\Vert I_i^n\Vert _{L^2(\Omega )}$, $i=1,\ldots ,4$, as follows:

$$\begin{aligned} \Vert I_1^n\Vert&= 2\Delta t^2 \biggl \Vert \int _0^1 s ds \int _{2s-1}^s \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} +u^n(\cdot )\cdot \nabla \Bigr )^3\phi \Bigr ] \bigl ( y(\cdot , s_1), t(s_1) \bigr ) \, ds_1 \biggr \Vert \nonumber \\&\le c_0 \Delta t^2 \int _0^1 s ds \int _{2s-1}^s \Bigl \Vert \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} + 1\cdot \nabla \Bigr )^3\phi \Bigr ] \bigl ( y(\cdot , s_1), t(s_1) \bigr ) \Bigr \Vert \, ds_1 \quad \text{( }1\cdot \nabla = \sum _{i=1}^d \frac{\partial {}}{\partial {x_i}} \text{) } \nonumber \\&\le c_1 \Delta t^2 \int _0^1 s ds\int _{2s-1}^s \Bigl \Vert \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} + 1\cdot \nabla \Bigr )^3\phi \Bigr ] \bigl (\, \cdot \, , t(s_1) \bigr ) \Bigr \Vert \, ds_1 \quad (\text{ by } \text{ Prop. }~1) \nonumber \\&\le c_1^\prime \Delta t \int _{t^{n-2}}^{t^n} \Bigl \Vert \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} + 1\cdot \nabla \Bigr )^3\phi \Bigr ] (\, \cdot \, , t) \Bigr \Vert \, dt \nonumber \\&\le \sqrt{2} \, c_1^\prime \Delta t^{3/2} \Bigl \Vert \Bigl ( \frac{\partial {}}{\partial {t}} + 1\cdot \nabla \Bigr )^3\phi \Bigr \Vert _{L^2(t^{n-2},t^n; L^2)} \nonumber \\&\le c_1^{\prime \prime } \Delta t^{3/2} \Vert \phi \Vert _{Z^3(t^{n-2},t^n)}, \end{aligned}$$

(36a)

$$\begin{aligned} \Vert I_2^n\Vert&\le c_1\Delta t^2 \int _0^1ds\int _{s-1}^s \Bigl \Vert \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} + 1\cdot \nabla \Bigr )^2\phi \Bigr ] \bigl ( y(\cdot ,s_1), t(s_1) \bigr ) \Bigr \Vert \, ds_1 \nonumber \\&\le c_1^\prime \Delta t \int _{t^{n-2}}^{t^n} \Bigl \Vert \Bigl [ \Bigl ( \frac{\partial {}}{\partial {t}} + 1\cdot \nabla \Bigr )^2\phi \Bigr ] ( \, \cdot \, , t ) \Bigr \Vert ds_1 \le c_1^{\prime \prime } \Delta t^{3/2} \Vert \phi \Vert _{Z^2(t^{n-2},t^n)}, \end{aligned}$$

(36b)

$$\begin{aligned} \Vert I_3^n\Vert&\le c_1 \Delta t^{3/2} \Vert \phi \Vert _{Z^1(t^{n-2},t^n)}, \end{aligned}$$

(36c)

$$\begin{aligned} \Vert I_4^n\Vert&\le c_1 \Delta t^2 ( \Vert \phi ^{n-1}\Vert + \Vert \phi ^{n-2}\Vert ) \le c_1^\prime \Delta t^{3/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n;L^2)}, \end{aligned}$$

(36d)

where for the last inequality in the estimate of $\Vert I_4^n\Vert$, we have employed the inequality,

$$\begin{aligned} \Vert \phi ^{n-1}\Vert + \Vert \phi ^{n-2}\Vert \le c\Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n;L^2)}. \end{aligned}$$

From the identity (35) and estimates (36), we obtain

$$\begin{aligned} \text{ LHS } \text{ of }~(33)&\le \sum _{i=1}^4 \Vert I_i^n\Vert _{L^2(\Omega )} \le c_1 \Delta t^{3/2} \Vert \phi \Vert _{Z^3(t^{n-2},t^n)}, \end{aligned}$$

which completes the proof. $\square$

Remark 6

([35]) For any $n\in \{1, \ldots , N_T\}$, there exists a positive constant $c = c_1$ independent of $\Delta t$ such that

$$\begin{aligned} \biggl \Vert {\mathcal {A}}_{\Delta t}^{(1)} \phi ^n - \Bigl [ \frac{\partial {\phi }}{\partial {t}} +\nabla \cdot \bigl ( u\phi \bigr ) \Bigr ] (\cdot ,t^n) \biggr \Vert \le c \Delta t^{1/2} \Vert \phi \Vert _{Z^2(t^{n-1},t^n)} \ \Bigl ( \le c^\prime \Delta t \Vert \phi \Vert _{Z^3} \Bigr ). \end{aligned}$$

(37)

Remark 7

Lemma 4 and Remark 6 with $u = 0$ imply that

$$\begin{aligned} \Bigl \Vert {\bar{D}}_{\Delta t}\phi ^n - \frac{\partial {\phi }}{\partial {t}} \Bigr \Vert&\le \left\{ \begin{aligned}&c \Delta t^{1/2} \Vert \phi \Vert _{H^2(t^0,t^1;L^2)} \le c^\prime \Delta t \Vert \phi \Vert _{H^3(0,T;L^2)}&(n = 1), \\&c^{\prime \prime } \Delta t^{3/2} \Vert \phi \Vert _{H^3(t^{n-2},t^n;L^2)}&(n \ge 2). \end{aligned} \right. \end{aligned}$$

Before the proof of Theorem 3, we prepare notations, equations and two lemmas to be employed. Let $\{\phi (t) = \phi (\cdot ,t) \in \Psi ;\ t\in [0,T]\}$ be the solution to problem (2), and for each $t\in [0, T]$, let ${\hat{\phi }}_h(t) = {\hat{\phi }}_h (\cdot , t) \in \Psi _h$ be the Poisson projection to $\phi (t)$, cf. Definition 1. Let $\{\phi _h^n\}_{n=1}^{N_T} \subset \Psi _h$ be the solution to scheme (9) with $\phi _h^0 = {\hat{\phi }}_h^0 \in \Psi _h$. We introduce the two functions $e_h^n$ and $\eta (t)$ defined by

$$\begin{aligned} e_h^n&:=\phi _h^n - {{\hat{\phi }}}_h^n \in \Psi _h,&\eta (t)&:=\phi (t) - {{\hat{\phi }}}_h (t) \in \Psi \end{aligned}$$

for $n\in \{0, \ldots , N_T\}$ and $t\in [0, T]$. Then, the series $\{e_h^n\}_{n=0}^{N_T} \subset \Psi _h$ satisfies

$$\begin{aligned} \bigl ( {\mathcal {A}}_{\Delta t} e_h^n, \psi _h \bigr ) + a_0( e_h^n, \psi _h ) = \langle R_h^n, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h \end{aligned}$$

(38)

for $n \in \{ 1, \ldots , N_T \}$, where $R_h^n \in \Psi _h^\prime$ is defined by

$$\begin{aligned} R_h^n&:=\sum _{i=1}^3 R_{hi}^n, \\ R_{h1}^n&:=\left\{ \begin{aligned}&\frac{\partial {\phi ^n}}{\partial {t}} + \nabla \cdot (u^n\phi ^n) - \frac{\phi _h^n-\phi _h^{n-1}\circ X_1^n \gamma ^n}{\Delta t},&n&= 1,\\&\frac{\partial {\phi ^n}}{\partial {t}} + \nabla \cdot (u^n\phi ^n) - \frac{3\phi _h^n-4\phi _h^{n-1}\circ X_1^n \gamma ^n + \phi _h^{n-2}\circ {\tilde{X}}_1^n {\tilde{\gamma }}^n}{2\Delta t},&n&\ge 2, \end{aligned} \right. \\ R_{h2}^n&:=\left\{ \begin{aligned}&\frac{\eta ^n-\eta ^{n-1}\circ X_1^n \gamma ^n}{\Delta t},&n&= 1, \\&\frac{3\eta ^n-4\eta ^{n-1}\circ X_1^n \gamma ^n + \eta ^{n-2}\circ {\tilde{X}}_1^n {\tilde{\gamma }}^n}{2\Delta t},&n&\ge 2, \end{aligned} \right. \\ R_{h3}^n&:=-\eta ^n. \end{aligned}$$

We summarize some estimates to be used in the proof of Theorem 3 in the next two lemmas. Their proofs are given in Appendix A.2 and A.3. The first lemma provides estimates for $R_h^n$ and $\eta ^n$ and the second lemma provides estimates for $e_h^1$.

Lemma 5

Suppose that Hypotheses 1, 2 and 3 hold true. Assume $\Delta t \in {(0, 1)}$. Then, we have the following.

(i) It holds that

$$\begin{aligned} \Vert \eta (\cdot ,t)\Vert&\le \Vert \eta (\cdot ,t)\Vert _{H^1(\Omega )} \le c h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1})} \le {c^\prime } h^k \Vert \phi \Vert _{H^2(H^{k+1})} \nonumber \\&\quad {(t\in [t^{n-1},t^n] \cap [0,T], n\in {\mathbb {N}}),} \end{aligned}$$

(39a)

$$\begin{aligned} \Vert {\bar{D}}_{\Delta t}\eta ^n\Vert&\le \left\{ \begin{aligned}&c h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})}&(n = 1), \\&c^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n;H^{k+1})}&(n \ge 2), \end{aligned} \right. \end{aligned}$$

(39b)

$$\begin{aligned} \Vert R_{h1}^n\Vert _{\Psi _h^\prime }&\le \Vert R_{h1}^n\Vert \le \left\{ \begin{aligned}&c_1 \Delta t^{1/2} \Vert \phi \Vert _{Z^2(t^0,t^1)}&(n = 1), \\&c_1^\prime \Delta t^{3/2} \Vert \phi \Vert _{Z^3(t^{n-2},t^n)}&(n \ge 2), \end{aligned} \right. \end{aligned}$$

(39c)

$$\begin{aligned} \Vert R_{h2}^n\Vert _{\Psi _h^\prime }&\le \left\{ \begin{aligned}&c_1 h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})}&(n = 1), \\&c_1^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n;H^{k+1})}&(n \ge 2), \end{aligned} \right. \end{aligned}$$

(39d)

$$\begin{aligned} \Vert R_{h3}^n\Vert _{\Psi _h^\prime }&\le \Vert R_{h3}^n\Vert \le c h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1})} \quad (n \ge 1), \end{aligned}$$

(39e)

$$\begin{aligned} \Vert R_{h2}^n\Vert&\le \left\{ \begin{aligned}&c_1 h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})}&(n = 1), \\&c_1^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n;H^{k+1})}&(n \ge 2). \end{aligned} \right. \end{aligned}$$

(39f)

(ii) Under Hypothesis 4, the estimates of $\Vert \eta (\cdot ,t)\Vert$, $\Vert R_{h2}^n\Vert _{\Psi _h^\prime }$ and $\Vert R_{h3}^n\Vert _{\Psi _h^\prime }$ are given as

$$\begin{aligned} \Vert \eta (\cdot ,t)\Vert&\le c h^{k+1} \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1})} \le {c^\prime } h^{k+1} \Vert \phi \Vert _{H^2(H^{k+1})} \nonumber \\&\quad {(t\in [t^{n-1},t^n] \cap [0,T], n\in {\mathbb {N}}),} \end{aligned}$$

(40a)

$$\begin{aligned} \Vert R_{h2}^n\Vert _{\Psi _h^\prime }&\le \left\{ \begin{aligned}&c_1 h^{k+1} \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})}&(n = 1), \\&c_1^\prime h^{k+1} \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n;H^{k+1})}&(n \ge 2), \end{aligned} \right. \end{aligned}$$

(40b)

$$\begin{aligned} \Vert R_{h3}^n\Vert _{\Psi _h^\prime }&\le \Vert R_{h3}^n\Vert \le c h^{k+1} \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1})} \quad (n \ge 1). \end{aligned}$$

(40c)

Remark 8

Hypotheses 1 and 2 are not needed for the estimates of (39a), (39b), (39e), (40a) and (40c).

Lemma 6

Suppose that Hypotheses 1, 2 and 3 hold true. Then, we have the following.

$$\begin{aligned} \Vert e_h^1\Vert \le \Vert e_h^1\Vert + \sqrt{\nu \Delta t} \, \Vert \nabla e_h^1\Vert&\le c_1 (\Delta t^2 + h^{k+1}) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}, \end{aligned}$$

(41a)

$$\begin{aligned} \sqrt{\nu } \, \Vert \nabla e_h^1 \Vert + \sqrt{\Delta t} \, \Vert {\bar{D}}_{\Delta t}^{(1)} e_h^1 \Vert&\le c_1 (\Delta t^{3/2} + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}. \end{aligned}$$

(41b)

Now, we give the proof of the error estimates.

Proof of Theorem 3

Considering the equation (38) for $e_h$, applying Proposition 2-(i) and (ii), and taking into account the fact $e_h^0 = 0$, we have

$$\begin{aligned} \Vert e_h\Vert _{\ell ^\infty _2(L^2)} + \sqrt{\nu } \Vert \nabla e_h\Vert _{\ell ^2_2(L^2)}&\le c_\dagger \left( \Vert e_h^1\Vert + \Vert R_h\Vert _{\ell ^2_2(\Psi _h^\prime )} \right) , \end{aligned}$$

(42)

$$\begin{aligned} \sqrt{\nu } \Vert \nabla e_h\Vert _{\ell ^\infty _2(L^2)} + \Vert {\bar{D}}_{\Delta t} e_h\Vert _{\ell ^2_2(L^2)}&\le {\bar{c}}_\dagger \left( \Vert e_h^1\Vert _{H^1(\Omega )} + \Vert R_h\Vert _{\ell ^2_2(L^2)} \right) . \end{aligned}$$

(43)

We prove (i). From Lemma 5-(i), it holds that:

$$\begin{aligned} \Vert R_{h1}\Vert _{\ell ^2_2(\Psi _h^\prime )}&\le \Vert R_{h1}\Vert _{\ell ^2_2(L^2)} = \Bigl ( \Delta t \sum _{n=2}^{N_T} \Vert R_{h1}^n\Vert ^2 \Bigr )^{1/2} \le c_1 \Bigl ( \Delta t \sum _{n=2}^{N_T} \Delta t^3 \Vert \phi \Vert _{Z^3(t^{n-2},t^n)}^2 \Bigr )^{1/2} \nonumber \\&\le c_1 \bigl ( 2 \Delta t^4 \Vert \phi \Vert _{Z^3}^2 \bigr )^{1/2} = c_1^\prime \Delta t^2 \Vert \phi \Vert _{Z^3} \quad (c_1^\prime = \sqrt{2}c_1), \nonumber \\ \Vert R_{h2}\Vert _{\ell ^2_2(\Psi _h^\prime )}&= \Bigl ( \Delta t \sum _{n=2}^{N_T} \Vert R_{h2}^n\Vert _{\Psi _h^\prime }^2 \Bigr )^{1/2} \nonumber \\&\le c_1 \Bigl [ \Delta t \sum _{n=2}^{N_T} \bigl ( h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n; H^{k+1})} \bigr )^2 \Bigr ]^{1/2} \nonumber \\&\le c_{1,T} h^k \Vert \phi \Vert _{H^1(H^{k+1})}, \nonumber \\ \Vert R_{h2}\Vert _{\ell ^2_2(L^2)}&= \Bigl ( \Delta t \sum _{n=2}^{N_T} \Vert R_{h2}^n\Vert ^2 \Bigr )^{1/2} \le c_{1,T} h^k \Vert \phi \Vert _{H^1(H^{k+1})}, \nonumber \\ \Vert R_{h3}\Vert _{\ell ^2_2(\Psi _h^\prime )}&\le \Vert R_{h3}\Vert _{\ell ^2_2(L^2)} = \Bigl ( \Delta t \sum _{n=2}^{N_T} \Vert \eta ^n\Vert ^2 \Bigr )^{1/2} \le c \Bigl [ \Delta t \sum _{n=2}^{N_T} \bigl ( h^k \Vert \phi \Vert _{H^1(0,T; H^{k+1}(\Omega ))} \bigr )^2 \Bigr ]^{1/2} \nonumber \\&\le c_T h^k \Vert \phi \Vert _{H^1(H^{k+1})} \quad {(c_T = c T^{1/2})}, \nonumber \\ \Vert R_h\Vert _{\ell ^2_2(\Psi _h^\prime )}&\le \sum _{i=1}^3 \Vert R_{hi}\Vert _{\ell ^2_2(\Psi _h^\prime )} \le c_{1,T} \bigl ( \Delta t^2 + h^k \bigr ) \Vert \phi \Vert _{Z^3\cap H^1(H^{k+1})}, \end{aligned}$$

(44)

$$\begin{aligned} \Vert R_h\Vert _{\ell ^2_2(L^2)}&\le \sum _{i=1}^3 \Vert R_{hi}\Vert _{\ell ^2_2(L^2)} \le c_{1,T} \bigl ( \Delta t^2 + h^k \bigr ) \Vert \phi \Vert _{Z^3\cap H^1(H^{k+1})}. \end{aligned}$$

(45)

Combining (41a) and (44) with (42), we obtain

$$\begin{aligned} \Vert e_h\Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } \, \Vert \nabla e_h\Vert _{\ell ^2(L^2)}&\le \bigl ( \Vert e_h^1\Vert + \sqrt{\nu \Delta t} \, \Vert \nabla e_h^1 \Vert \bigr ) + \Vert e_h\Vert _{\ell ^\infty _2(L^2)} + \sqrt{\nu } \, \Vert \nabla e_h\Vert _{\ell ^2_2(L^2)} \\&\le \bigl ( \Vert e_h^1\Vert + \sqrt{\nu \Delta t} \, \Vert \nabla e_h^1 \Vert \bigr ) + c_\dagger \Bigl ( \Vert e_h^1\Vert + \Vert R_h\Vert _{\ell ^2_2(\Psi _h^\prime )} \Bigr ) \\&\le c_{1,\nu ,T} ( \Delta t^2 + h^k ) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}, \end{aligned}$$

which implies the error estimate (17a) of (i), as

$$\begin{aligned}&\Vert \phi _h - \phi \Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } \, \Vert \nabla (\phi _h - \phi )\Vert _{\ell ^2(L^2)} \\&\quad \le \Vert e_h \Vert _{\ell ^\infty (L^2)} + \Vert \eta \Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } (\Vert \nabla e_h\Vert _{\ell ^2(L^2)} + \Vert \nabla \eta \Vert _{\ell ^2(L^2)}) \\&\quad \le \Vert e_h \Vert _{\ell ^\infty (L^2)} + \sqrt{\nu } \Vert \nabla e_h\Vert _{\ell ^2(L^2)} + c_T h^k \Vert \phi \Vert _{H^1(H^{k+1})} \quad (\text{ by }~(39a))\nonumber \\&\quad \le c_{1,\nu ,T} ( \Delta t^2 + h^k ) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}. \end{aligned}$$

For the error estimate (17b), we have

$$\begin{aligned}&\sqrt{\nu } \, \Vert \nabla e_h \Vert _{\ell ^\infty (L^2)} + \bigl \Vert {\bar{D}}_{\Delta t} e_h \bigr \Vert _{\ell ^2(L^2)} \nonumber \\&\quad \le \bigl ( \sqrt{\nu } \, \Vert \nabla e_h^1 \Vert + \sqrt{\Delta t} \, \bigl \Vert {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \Vert \bigr ) + \sqrt{\nu } \, \Vert \nabla e_h \Vert _{\ell ^\infty _2(L^2)} + \bigl \Vert {\bar{D}}_{\Delta t} e_h \bigr \Vert _{\ell ^2_2(L^2)} \nonumber \\&\quad \le \bigl ( \sqrt{\nu } \, \Vert \nabla e_h^1 \Vert + \sqrt{\Delta t} \, \bigl \Vert {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \Vert \bigr ) + {\bar{c}}_\dagger \bigl ( \Vert e_h^1 \Vert _{H^1(\Omega )} + \Vert R_h\Vert _{\ell ^2_2(L^2)} \bigr ) \quad \text{(by }~(36)) \nonumber \\&\quad \le c_{1,\nu ,T} (\Delta t^{3/2} + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} \quad \text{(by }~(39a), (39b)\hbox { and}~(47)). \end{aligned}$$

(46)

Noting the estimate

$$\begin{aligned} \Bigl \Vert {\bar{D}}_{\Delta t} \phi - \frac{\partial {\phi }}{\partial {t}} \Bigr \Vert _{\ell ^2(L^2)}&= \sqrt{ \Delta t \, \Bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \phi ^1 - \frac{\partial {\phi ^1}}{\partial {t}} \Bigr \Vert ^2 + \Delta t \sum _{n=2}^{N_T} \Bigl \Vert {\bar{D}}_{\Delta t}^{(2)} \phi ^n - \frac{\partial {\phi ^n}}{\partial {t}} \Bigr \Vert ^2 } \nonumber \\&\le \sqrt{ c (\Delta t^3 + \Delta t^4) \Vert \phi \Vert _{H^3(L^2)}^2 } \qquad (\text{ cf. } \text{ Rmk. }~7) \nonumber \\&\le c^\prime \Delta t^{3/2} \Vert \phi \Vert _{H^3(L^2)}, \end{aligned}$$

(47)

we obtain the estimate (17b) of (i), as

$$\begin{aligned}&\sqrt{\nu } \, \Vert \nabla (\phi _h - \phi ) \Vert _{\ell ^\infty (L^2)} + \Bigl \Vert {\bar{D}}_{\Delta t} \phi _h - \frac{\partial {\phi }}{\partial {t}} \Bigr \Vert _{\ell ^2(L^2)} \\&\quad \le \sqrt{\nu } \, \Bigl ( \Vert \nabla e_h \Vert _{\ell ^\infty (L^2)} + \Vert \nabla \eta \Vert _{\ell ^\infty (L^2)} \Bigr ) + \bigl \Vert {\bar{D}}_{\Delta t} e_h \bigr \Vert _{\ell ^2(L^2)}\\&\qquad + \bigl \Vert {\bar{D}}_{\Delta t} \eta \bigr \Vert _{\ell ^2(L^2)} + \Bigl \Vert {\bar{D}}_{\Delta t} \phi - \frac{\partial {\phi }}{\partial {t}} \Bigr \Vert _{\ell ^2(L^2)} \\&\quad \le c_{1,\nu , T} ( \Delta t^{3/2} + h^k ) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} + \Bigl \Vert {\bar{D}}_{\Delta t} \phi - \frac{\partial {\phi }}{\partial {t}} \Bigr \Vert _{\ell ^2(L^2)} \quad \text{(by }~(46), (39a)\hbox { and}~(39b)) \\&\le c_{1,\nu , T}^\prime ( \Delta t^{3/2} + h^k ) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} \quad \text{(by }~(47)). \end{aligned}$$

We next prove (ii). Under Hypothesis 4, we have, from Lemma 5-(ii),

$$\begin{aligned} \Vert R_{h2}\Vert _{\ell ^2_2(\Psi _h^\prime )}&\le c_{1,T} h^{k+1} \Vert \phi \Vert _{H^1(H^{k+1})}, \nonumber \\ \Vert R_{h3}\Vert _{\ell ^2_2(\Psi _h^\prime )}&\le c_T h^{k+1} \Vert \phi \Vert _{H^1(H^{k+1})}, \nonumber \\ \Vert R_h\Vert _{\ell ^2_2(\Psi _h^\prime )}&\le \sum _{i=1}^3 \Vert R_{hi}\Vert _{\ell ^2_2(\Psi _h^\prime )} \le c_{1,T} \bigl ( \Delta t^2 + h^{k+1} \bigr ) \Vert \phi \Vert _{Z^3\cap H^1(H^{k+1})}. \end{aligned}$$

(48)

Combining (41a) and (48) with (42) and taking into account Lemma 3-(ii), we obtain

$$\begin{aligned} \Vert \phi _h - \phi \Vert _{\ell ^\infty (L^2)}&\le \Vert e_h\Vert _{\ell ^\infty (L^2)} + \Vert \eta \Vert _{\ell ^\infty (L^2)} \\&\le \max \bigl \{ \Vert e_h^1\Vert , \Vert e_h\Vert _{\ell ^\infty _2(L^2)} \bigr \} + c h^{k+1} \Vert \phi \Vert _{H^1(H^{k+1})} \\&\le c_{1,\nu ,T} ( \Delta t^2 + h^{k+1} ) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}, \end{aligned}$$

which completes the proof of (ii). $\square$

5 Numerical Results

In this section we verify the theoretical orders of convergence from Theorem 3 in numerical experiments. To this end we solved an example problem by scheme (9) in a finite element space of polynomial order $k=1$. As initial data we set $\phi _h^0 = \Pi _h\phi ^0$ using the Lagrange interpolation operator $\Pi _h:C({\bar{\Omega }}) \rightarrow \Psi _h$, and note that this choice of $\phi _h^0$ does not cause any loss of convergence order in Theorem 3. For the computation of the integrals appearing in the scheme we employed numerical quadrature formulae of degree nine for $d=1$ (five points) and degree five for $d=2$ (seven points) and $d=3$ (fifteen points) [36]. While higher order quadrature formulae can improve numerical results of Lagrange-Galerkin methods, cf., e.g., [6, 14], we do not consider them in this paper. The linear systems were solved using the conjugate gradient method and meshes were generated using FreeFem++ [19].

Example 1

In problem (1), for $d=1,2,3$, we set $\Omega = (-1,1)^d$, $T=0.5$, $f=0$, $g=0$, and

$$\begin{aligned} u(x,t)&= \sum _{i=1}^d (1+\sin (t-x_i))e_i, \end{aligned}$$

where $\{e_i\}_{i=1}^d \subset {\mathbb {R}}^d$ is the standard basis in ${\mathbb {R}}^d$. The function $\phi ^0$ is given according to the exact solution

$$\begin{aligned} \phi (x,t) = \prod _{i=1}^d \exp \left( -\frac{1-\cos (t-x_i)}{\nu }\right) . \end{aligned}$$

The viscosity constant is set $\nu = 10^{-2}$ if not otherwise noted.

We applied scheme (9) to Example 1 and computed the errors

$$\begin{aligned} E_Y:=\frac{\Vert \phi _h - \Pi _h \phi \Vert _Y}{\Vert \Pi _h \phi \Vert _Y} \end{aligned}$$

for $Y=\ell ^\infty (L^2)$, $\ell ^2(H^1_0)$, $\ell ^{\infty }(H^1_0)$, where $\Vert \phi \Vert _{\ell ^2(H^1_0)} :=\Vert \nabla \phi \Vert _{\ell ^2(L^2)}$, $\Vert \phi \Vert _{\ell ^\infty (H^1_0)} :=\Vert \nabla \phi \Vert _{\ell ^\infty (L^2)}$ and $\Pi _h:C({\bar{\Omega }}) \rightarrow \Psi _h$ is the Lagrange interpolation operator. Tables 1–11 show the errors and the corresponding experimental orders of convergence (EOCs)¹ after grid refinement. The number N in the tables denotes the division number of the domain in each space dimension determining the mesh, whose size is taken as $h :=2/N$. We coupled time increment and mesh size by $\Delta t = c h^p$ and varied the constant c and the exponent p in the tables to see the theoretical convergence orders. According to Theorem 3 we expected to see experimental convergence orders 2 ($E_{\ell ^\infty (L^2)}$), 1 ($E_{\ell ^2(H^1_0)}$) and 1 ($E_{\ell ^\infty (H^1_0)}$) for $p=1$, 2 ($E_{\ell ^\infty (L^2)}$), 2 ($E_{\ell ^2(H^1_0)}$) and 3/2 ($E_{\ell ^\infty (H^1_0)}$) for $p=1/2$ and 2 ($E_{\ell ^\infty (L^2)}$), 3/2 ($E_{\ell ^2(H^1_0)}$) and 3/2 ($E_{\ell ^\infty (H^1_0)}$) for $p=2/3$. The EOCs in the tables either agree with or exceed our expectations and therefore support our theoretical results. To see $\Delta t$-convergence for a fixed $h~(=2/256)$ and h-convergence for a fixed $\Delta t~(=0.01)$, we present Tables 12 and 13, respectively, which further support the convergence rates in Theorem 3.

Table 1 Relative errors and EOCs for $\Delta t=4h$ in 1D $(d=1)$

Table 2 Relative errors and EOCs for $\Delta t=0.4\sqrt{h}$ in 1D $(d=1)$

Table 3 Relative errors and EOCs for $\Delta t=h^{2/3}$ in 1D $(d=1)$

Table 4 Relative errors and EOCs for $\Delta t=4h$ in 2D $(d=2)$

Table 5 Relative errors and EOCs for $\Delta t=0.4\sqrt{h}$ in 2D $(d=2)$

Table 6 Relative errors and EOCs for $\Delta t=h^{2/3}$ in 2D $(d=2)$

Table 7 Relative errors and EOCs for $\Delta t=2h$ in 3D $(d=3)$

Table 8 Relative errors and EOCs for $\Delta t=4h$ in 3D $(d=3)$

Table 9 Relative errors and EOCs for $\Delta t=0.2\sqrt{h}$ in 3D $(d=3)$

Table 10 Relative errors and EOCs for $\Delta t=0.4\sqrt{h}$ in 3D $(d=3)$

Table 11 Relative errors and EOCs for $\Delta t=h^{2/3}$ in 3D $(d=3)$

Table 12 Relative errors and EOCs for $N=256$ in 2D $(d=2)$ for $\nu =10^{-2}$

Table 13 Relative errors and EOCs in h (denoted by EOC$_h$ in the table) for $\Delta t=0.01$ in 2D $(d=2)$ for $\nu =10^{-2}$

The tables, i.e., Tables 1–13, moreover show a low relative loss of mass,

$$\begin{aligned} E_{\text {mass}} :=\frac{\left| \int _\Omega \phi _h^{N_T}\, dx - \int _\Omega \Pi _h \phi ^{N_T}\, dx\,\right| }{ \left| \int _\Omega \Pi _h \phi ^{N_T}\, dx \, \right| }, \end{aligned}$$

which decreases as the mesh is refined. Furthermore we computed the error formulas

$$\begin{aligned} E_{\text {mass}}^\prime :=\frac{\left| \int _\Omega \phi _h^{N_T} dx - \int _\Omega \phi _h^0\, dx\,\right| }{ \left| \int _\Omega \phi _h^0\, dx \, \right| }, \quad E_{\text {mass}}^{\prime \prime } :=\frac{\Delta t \sum _{n=1}^{N_T} \, \left| \int _\Omega \phi _h^n\, dx - \int _\Omega \Pi _h \phi ^n\, dx\,\right| }{ \Delta t \sum _{n=1}^{N_T} \, \left| \int _\Omega \Pi _h \phi ^n \, dx \, \right| }, \end{aligned}$$

for $\Delta t = 4h$ shown in Table 14 providing additional information on the error of mass within the computation and throughout all time steps. Both $E_{\text {mass}}^\prime$ and $E_{\text {mass}}^{\prime \prime }$ also decrease as the mesh is refined.

These results indicate that mass is lost only due to numerical integration and Lagrange interpolation of the exact solution and thus support the mass-preserving property of the scheme (Theorem 1). When the viscosity $\nu$ is decreased to $\nu = 10^{-3}$ or $10^{-4}$, we observe a reduction in the EOC in $\ell ^\infty (L^2)$ to orders smaller than 2 for some N but still larger than 1, and almost no effect in the EOCs in $\ell ^2(H^1_0)$ and $\ell ^\infty (H^1_0)$, as we show in Tables 15 and 16.

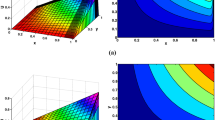
We further present numerical solutions for $d=2$ and 3 in Fig. 1.

Fig. 1

Employed meshes (left column) and numerical solutions of Example 1 for $d=2$ (top row) and $d=3$ (bottom row). Initial conditions (middle column) and numerical solutions at the final time $T=0.5$ (right column) computed by scheme (9) are shown

Table 14 Relative errors of mass for $\Delta t=4h$ in 2D $(d=2)$

Table 15 Relative errors and EOCs for $\Delta t=4h$ in 2D $(d=2)$ for $\nu =10^{-3}$

Table 16 Relative errors and EOCs for $\Delta t=4h$ in 2D $(d=2)$ for $\nu =10^{-4}$

6 Conclusions

We have presented a mass-preserving two-step Lagrange–Galerkin scheme of second order in time for convection-diffusion problems. Its mass-preserving property is achieved by the Jacobian multiplication technique, and its accuracy of second order in time is obtained based on the idea of the multistep Galerkin method along characteristics. For the first time step, we have proposed to employ a mass-preserving scheme of first order in time. This construction is efficient and does not decrease the convergence orders in the $\ell ^\infty (L^2)$- and $\ell ^2(H^1_0)$-norms.

Both main advantages of Lagrange–Galerkin methods, the CFL-free robustness for convection-dominated problems and the symmetric and positive coefficient matrix of the resulting system of linear equations, are kept in our scheme. Additionally, our scheme has a mass-preserving property as proved in Theorem 1. We have proved unconditional stability without any stabilization parameter in Theorem 2, and error estimates of second order in time in Theorem 3. For the error estimates two key lemmas on the truncation error analysis of the material derivative in conservative form, cf. Lemma 4, and a discrete Gronwall inequality for multistep methods, cf. Lemma 1, have been prepared.

We summarize the shown convergence orders as follows. The order in the $\ell ^\infty (L^2)\cap \ell ^2(H^1_0)$-norm is $O(\Delta t^2 + h^k)$, and the order in the $\ell ^\infty (L^2)$-norm is $O(\Delta t^2 + h^{k+1})$ if the duality argument can be employed. We have also proved the convergence order $O(\Delta t^{3/2}+h^k)$ in the discrete $\ell ^\infty (H^1_0)$- and $H^1(L^2)$-norm, which will be useful when we apply the scheme to, e.g., the Navier–Stokes equations. We have presented numerical results in one-, two- and three-dimensions, which have supported the theoretical convergence orders.

Appendix

1.1 Proof of Lemma 1

From the assumption (20), there exists a non-negative sequence $\{{\tilde{z}}_n\}_{n\ge 2}$ such that

$$\begin{aligned}&\frac{1}{\Delta t}\Bigl ( \frac{3}{2} x_n - 2 x_{n-1} + \frac{1}{2} x_{n-2} + y_n - y_{n-1} \Bigr ) + {\tilde{z}}_n \\&\quad = a_0 x_n + a_1 x_{n-1} + a_2 x_{n-2} + b_n,\quad \forall n\ge 2, \end{aligned}$$

where ${\tilde{z}}_n$ satisfies

$$\begin{aligned} z_n \le {\tilde{z}}_n, \quad \forall n\ge 2. \end{aligned}$$

Let p and q, $p < q$, be the roots of quadratic equation $f(x) :=(3/2-a_0\Delta t) x^2 - (2+a_1\Delta t) x + (1/2 -a_2\Delta t) = 0$, and let $\lambda :=2/3$ and $D :=(2+a_1\Delta t)^2 - (3-2a_0\Delta t)(1-2a_2\Delta t)$ $(= 1+2(a_0+2a_1+3a_2)\Delta t + (a_1^2-4a_0a_2)\Delta t^2)$. The numbers p and q have the properties

$$\begin{aligned} |p|&< 1 \le q,&2\lambda&\le p+q,&pq&\le \lambda ,&q - p&\ge \lambda ,&q^n - p^n&\le \exp (2 a_*n\Delta t) +1, \end{aligned}$$

(A.1)

which are obtained from $f(1) = - (a_0+a_1+a_2)\Delta t \le 0$, $f(-1) = 4 + (- a_0 + a_1 - a_2) \Delta t \ge {13/4} > 0$, $a_0\Delta t \le 3/4$, $1 \le D \le [1+(a_0+2a_1+3a_2)\Delta t]^2$, and

$$\begin{aligned} q^n - p^n&\le q^n + |p|^n \le q^n + 1 = \left( \frac{2+a_1\Delta t+\sqrt{D} }{3-2a_0\Delta t} \right) ^n + 1 \le \left( 1 + \frac{3 a_*\Delta t}{3-2a_0\Delta t} \right) ^n + 1 \\&\le ( 1 + 2 a_*\Delta t )^n {+1} \le \exp (2 a_*n\Delta t) {+ 1.} \end{aligned}$$

Let $n\ge 2$ be fixed arbitrarily. Then, we have

$$\begin{aligned} x_n - p x_{n-1} + \lambda (y_n - y_{n-1}) + \lambda \Delta t{\tilde{z}}_n&= q (x_{n-1}-p x_{n-2}) + \lambda \Delta t b_n, \\ x_n - q x_{n-1} + \lambda (y_n - y_{n-1}) + \lambda \Delta t{\tilde{z}}_n&= p (x_{n-1}-q x_{n-2}) + \lambda \Delta t b_n, \end{aligned}$$

which imply

$$\begin{aligned}&x_n - p x_{n-1} + \lambda \Biggl [ \sum _{i=2}^n q^{n-i} y_i - \sum _{i=1}^{n-1} q^{n-1-i} y_i \Biggr ] + \lambda \Delta t \sum _{i=2}^n q^{n-i} {\tilde{z}}_i \nonumber \\&\quad = q^{n-1} (x_1-p x_0) + \lambda \Delta t \sum _{i=2}^n q^{n-i} b_i, \end{aligned}$$

(A.2a)

$$\begin{aligned}&x_n - q x_{n-1} + \lambda \Biggl [ \sum _{i=2}^n p^{n-i} y_i - \sum _{i=1}^{n-1} p^{n-1-i}y_i \Biggr ] + \lambda \Delta t \sum _{i=2}^n p^{n-i} {\tilde{z}}_i\nonumber \\&\quad = p^{n-1} (x_1-q x_0) + \lambda \Delta t \sum _{i=2}^n p^{n-i} b_i. \end{aligned}$$

(A.2b)

Multiplying (A.2a) by q and (A.2b) by p and subtracting the second equation from the first, we get

$$\begin{aligned}&(q-p) x_n + \lambda \Biggl [ \sum _{i=2}^n (q^{n+1-i}-p^{n+1-i}) y_i - \sum _{i=1}^{n-1} (q^{n-i} - p^{n-i}) y_i \Biggr ] \nonumber \\&\qquad + \lambda \Delta t \sum _{i=2}^n (q^{n+1-i}-p^{n+1-i}) {\tilde{z}}_i \nonumber \\&\quad = (q^n-p^n) x_1 - pq (q^{n-1}-p^{n-1}) x_0 + \lambda \Delta t \sum _{i=2}^n (q^{n+1-i} - p^{n+1-i}) b_i. \end{aligned}$$

(A.3)

It is noted here that

$$\begin{aligned}&\sum _{i=2}^n (q^{n+1-i} - p^{n+1-i}) y_i - \sum _{i=1}^{n-1} (q^{n-i} - p^{n-i}) y_i \nonumber \\&\quad = (q-p) y_n + \sum _{i=2}^{n-1} \Bigl [ (q^{n+1-i}-p^{n+1-i}) - (q^{n-i} - p^{n-i}) \Bigr ] y_i - (q^{n-1}-p^{n-1})y_1 \nonumber \\&\quad \ge (q-p) y_n - (q^{n-1}-p^{n-1})y_1, \end{aligned}$$

(A.4)

where the following inequality has been employed:

$$\begin{aligned} q^{k+1}-p^{k+1} \ge q^k - p^k, \qquad \forall k\in {\mathbb {N}}\cup \{0\}. \end{aligned}$$

This inequality holds obviously from the first property in (A.1) for $p\ge 0$ or for $p < 0$ and an even number k. For $p < 0$ and an odd number k, it is proved by induction, and the key inequality in the induction is

$$\begin{aligned} q^{k+2}-p^{k+2}&= (q^{k+1}-p^{k+1})(p+q) -pq(q^k-p^k)\\&\ge (q^{k+1}-p^{k+1})(p+q) \ge q^{k+1}-p^{k+1}. \end{aligned}$$

Combining (A.1) and (A.4) with (A.3) and noting that $0 \le -pq/(q-p) \le q/(q-p) \le 1$ for $p \in (-1,0)$ and $-pq/(q-p) \le 0 < 1$ for $p \in [0,1)$, we obtain

$$\begin{aligned} x_n + \lambda y_n + \lambda \Delta t \sum _{i=2}^n {\tilde{z}}_i&\le \frac{q^n-p^n}{q-p} \Biggl [ x_1 - pq x_0 + \lambda y_1 + \lambda \Delta t \sum _{i=2}^n b_i \Biggr ] \nonumber \\&\le \Bigl ( \exp ( 2 a_*n\Delta t ) + 1 \Bigr ) \Biggl ( x_0 + \frac{3}{2} x_1 + y_1+\Delta t\sum _{i=2}^n b_i \Biggr ), \end{aligned}$$

which completes the proof.

1.2 Proof of Lemma 5

We prove (i). For the estimate (39a), from the next calculations,

$$\begin{aligned} \eta (\cdot ,t)&= \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} \eta (\cdot ,t)\, ds = \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} \Bigl ( \bigl [ \eta (\cdot ,s_1) \bigr ]_{s_1 = s}^t \Bigr ) ds + \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} \eta (\cdot ,s)\, ds \\&= \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n}ds \int _s^{t} \frac{\partial {\eta }}{\partial {t}} (\cdot ,s_1) \, ds_1 + \frac{1}{\Delta t} \Bigl [ \int _{t^{n-1}}^{t^n} \eta (\cdot ,s)^2 ds \Bigr ]^{1/2} \Bigl [ \int _{t^{n-1}}^{t^n} 1^2 ds \Bigr ]^{1/2} \\&\le \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} ds \Bigl [ \int _s^t \frac{\partial {\eta }}{\partial {t}} (\cdot ,s_1)^2 ds_1 \Bigr ]^{1/2} \Bigl [ \int _s^t 1^2 ds_1 \Bigr ]^{1/2} + \frac{1}{\sqrt{\Delta t}} \Bigl [ \int _{t^{n-1}}^{t^n} \eta (\cdot ,s)^2 ds \Bigr ]^{1/2} \\&\le \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} ds \Bigl [ \int _{t^{n-1}}^{t^n} \frac{\partial {\eta }}{\partial {t}} (\cdot ,s_1)^2 ds_1 \Bigr ]^{1/2} \Bigl [ \int _{t^{n-1}}^{t^n} 1^2 ds_1 \Bigr ]^{1/2} + \frac{1}{\sqrt{\Delta t}} \Bigl [ \int _{t^{n-1}}^{t^n} \eta (\cdot ,s)^2 ds \Bigr ]^{1/2} \\&= \sqrt{\Delta t} \Bigl [ \int _{t^{n-1}}^{t^n} \frac{\partial {\eta }}{\partial {t}} (\cdot ,s)^2 ds \Bigr ]^{1/2} + \frac{1}{\sqrt{\Delta t}} \Bigl [ \int _{t^{n-1}}^{t^n} \eta (\cdot ,s)^2 ds \Bigr ]^{1/2} \\&\le \sqrt{\frac{2}{\Delta t}}\, \Bigl [ \int _{t^{n-1}}^{t^n} \Bigl ( \eta (\cdot ,s)^2 + \frac{\partial {\eta }}{\partial {t}} (\cdot ,s)^2 \Bigr ) ds \Bigr ]^{1/2}, \end{aligned}$$

and Lemma 3-(i), we obtain the inequalities as

$$\begin{aligned} \Vert \eta (\cdot ,t) \Vert&\le \Vert \eta (\cdot ,t) \Vert _{H^1(\Omega )} \le \sqrt{2} \, \Delta t^{-1/2} \Vert \eta \Vert _{H^1(t^{n-1},t^n;H^1)} \le c h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-1},t^n;H^{k+1})} \\&\le c^\prime h^k \Vert \phi \Vert _{H^2(0,T; H^{k+1})} \quad \text{(by } \text{ the } \text{ Sobolev } \text{ embedding } \text{ theorem } \text{ with } \text{ respect } \text{ to } \text{ time). } \end{aligned}$$

For the estimate (39b), noting that

$$\begin{aligned} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert&= \frac{1}{\Delta t} \Vert \eta ^n - \eta ^{n-1}\Vert \le \frac{1}{\Delta t} \, \Bigl \Vert \bigl [ \eta (\cdot , s) \bigr ]_{s=t^{n-1}}^{t^n} \Bigr \Vert = \frac{1}{\Delta t} \Bigl \Vert \int _{t^{n-1}}^{t^n} \frac{\partial {\eta }}{\partial {t}} (\cdot , s) \, ds \Bigr \Vert \nonumber \\&\le \frac{1}{\Delta t} \int _{t^{n-1}}^{t^n} \Bigl \Vert \frac{\partial {\eta }}{\partial {t}} (\cdot , s) \Bigr \Vert \, ds \le \frac{1}{\sqrt{\Delta t}} \, \Bigl \Vert \frac{\partial {\eta }}{\partial {t}} \Bigr \Vert _{L^2(t^{n-1},t^n; L^2(\Omega ))} \nonumber \\&\le \Delta t^{-1/2} \Vert \eta \Vert _{H^1(t^{n-1},t^n; L^2(\Omega ))} \le c h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1}(\Omega ))}, \end{aligned}$$

(A.5)

$$\begin{aligned} \bigl \Vert {\bar{D}}_{\Delta t}^{(2)} \eta ^n \bigr \Vert&= \Bigl \Vert \frac{3}{2}{\bar{D}}_{\Delta t}^{(1)} \eta ^n - \frac{1}{2}{\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \Bigr \Vert \le \frac{3}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert + \frac{1}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \bigr \Vert \\&\le c h^k \Delta t^{-1/2} \bigl ( \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1}(\Omega ))} + \Vert \phi \Vert _{H^1(t^{n-2},t^{n-1}; H^{k+1}(\Omega ))} \bigr ) \\&\le c^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n; H^{k+1}(\Omega ))}. \end{aligned}$$

Thus, we obtain (39b). From Lemma 4 and Remark 6, the estimate of (39c) follows. Since we have

$$\begin{aligned}&\frac{1}{\Delta t} \bigl \Vert \eta ^0 - \eta ^0 \circ X_1^1 \gamma ^1 \bigr \Vert _{\Psi _h^\prime } \nonumber \\&\quad \le \frac{1}{\Delta t} \bigl \Vert \eta ^0 - \eta ^0 \circ X_1^1 \bigr \Vert _{\Psi _h^\prime } + \frac{1}{\Delta t} \bigl \Vert \eta ^0 \circ X_1^1 (1-\gamma ^1) \bigr \Vert _{\Psi _h^\prime } \nonumber \\&\quad \le c_1 \bigl ( \Vert \eta ^0 \Vert + \Vert \eta ^0 \circ X_1^1 \Vert \bigr ) \quad (\text{ by } \text{ Lem. }~2\hbox {-}(22c)\hbox { and } \Vert 1-\gamma ^1\Vert _{L^\infty (\Omega )} \le c_1\Delta t) \nonumber \\&\quad \le c_1^\prime \Vert \eta ^0 \Vert \quad (\text{ by } \text{ Lem. }~2\hbox {-}(22a)), \end{aligned}$$

(A.6)

the estimate (39d) is obtained as

$$\begin{aligned} \Vert R_{h2}^1\Vert _{\Psi _h^\prime }&= \frac{1}{\Delta t} \bigl \Vert \eta ^1 - \eta ^0 \circ X_1^1 \gamma ^1 \bigr \Vert _{\Psi _h^\prime } \le \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^1 \bigr \Vert _{\Psi _h^\prime } + \frac{1}{\Delta t} \bigl \Vert \eta ^0 - \eta ^0 \circ X_1^1 \gamma ^1 \bigr \Vert _{\Psi _h^\prime } \nonumber \\&\le \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^1 \bigr \Vert + c_1 \Vert \eta ^0 \Vert \le c_1^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})} \quad (\text{ by }~(A.4)~\hbox {and}~(39a)), \end{aligned}$$

(A.7)

$$\begin{aligned} \Vert R_{h2}^n\Vert _{\Psi _h^\prime }&= \frac{1}{2\Delta t} \bigl \Vert 3\eta ^n-4\eta ^{n-1}\circ X_1^n \gamma ^n + \eta ^{n-2}\circ {\tilde{X}}_1^n {\tilde{\gamma }}^n \bigr \Vert _{\Psi _h^\prime } \quad (\text{ for } \,n \ge 2) \nonumber \\&= \Bigl \Vert \frac{3}{2} {\bar{D}}_{\Delta t}^{(1)} \eta ^n - \frac{1}{2} {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} + \frac{2}{\Delta t} \bigl ( \eta ^{n-1} - \eta ^{n-1}\circ X_1^n \gamma ^n \bigr )\nonumber \\&\quad - \frac{1}{2\Delta t} \bigl ( \eta ^{n-2} - \eta ^{n-2} \circ {\tilde{X}}_1^n {\tilde{\gamma }}^n \bigr ) \Bigr \Vert _{\Psi _h^\prime } \nonumber \\&\le \frac{3}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert + \frac{1}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \bigr \Vert + \frac{2}{\Delta t} \bigl \Vert \eta ^{n-1} - \eta ^{n-1}\circ X_1^n \gamma ^n \bigr \Vert _{\Psi _h^\prime } \nonumber \\&\quad + \frac{1}{2\Delta t} \bigl \Vert \eta ^{n-2} - \eta ^{n-2} \circ {\tilde{X}}_1^n {\tilde{\gamma }}^n \bigr \Vert _{\Psi _h^\prime } \nonumber \\&\le c_1 \bigl ( \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert + \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \bigr \Vert + \Vert \eta ^{n-1} \Vert + \Vert \eta ^{n-2} \Vert \bigr ) \quad (\text{ cf. }~(A.6)) \nonumber \\&\le c_1^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n; H^{k+1})} \quad (\text{ by }~(A.5)~ \hbox {and}~(39a)). \end{aligned}$$

(A.8)

The estimate (39e) is obvious from (39a). Using a similar evaluation to (39d) with some modifications, we get (39f) by

$$\begin{aligned} \Vert R_{h2}^1\Vert&= \frac{1}{\Delta t} \bigl \Vert \eta ^1 - \eta ^0 \circ X_1^1 \gamma ^1 \bigr \Vert \le \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^1 \bigr \Vert + \frac{1}{\Delta t} \bigl \Vert \eta ^0 - \eta ^0 \circ X_1^1 \bigr \Vert + \frac{1}{\Delta t} \bigl \Vert \eta ^0 \circ X_1^1 (1-\gamma ^1) \bigr \Vert \nonumber \\&\le \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^1 \bigr \Vert + c_1 \Vert \eta ^0 \Vert _{H^1(\Omega )} \quad (\text{ by } \text{ Lem. }~2-(22b)~\hbox {and}~ \Vert 1-\gamma ^1\Vert _{L^\infty (\Omega )} \le c_1\Delta t) \nonumber \\&\le c_1^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})}, \nonumber \\ \Vert R_{h2}^n\Vert&\le \frac{3}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert + \frac{1}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \bigr \Vert + \frac{2}{\Delta t} \bigl \Vert \eta ^{n-1} - \eta ^{n-1} \circ X_1^n \bigr \Vert + \frac{2}{\Delta t} \bigl \Vert \eta ^{n-1} \circ X_1^n (1-\gamma ^n) \bigr \Vert \nonumber \\&\quad + \frac{1}{2\Delta t} \bigl \Vert \eta ^{n-2} - \eta ^{n-2} \circ {\tilde{X}}_1^n \bigr \Vert + \frac{1}{2\Delta t} \bigl \Vert \eta ^{n-2} \circ {\tilde{X}}_1^n (1-{\tilde{\gamma }}^n) \bigr \Vert \quad \text{(for } n \ge 2\text{) } \nonumber \\&\le c_1 \bigl ( \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert + \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \bigr \Vert + \Vert \eta ^{n-1} \Vert _{H^1(\Omega )} + \Vert \eta ^{n-2} \Vert _{H^1(\Omega )} \bigr ) \quad (\text{ cf. }~(A.9)) \nonumber \\&\le c_1^\prime h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n; H^{k+1})}. \end{aligned}$$

(A.9)

We prove (ii). The estimate (40a) is obvious from Lemma 3-(ii). We evaluate $\Vert R_{h2}^n\Vert _{\Psi _h^\prime }$. Recalling the calculation of $\Vert R_{h2}^n\Vert _{\Psi _h^\prime }$, cf. (A.7) and (A.8), in the proof of (i), and noting that

$$\begin{aligned} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert&\le \Delta t^{-1/2} \Vert \eta \Vert _{H^1(t^{n-1},t^n; L^2(\Omega ))} \quad (\text{ cf. }~(A.5)) \nonumber \\&\le c h^{k+1} \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-1},t^n; H^{k+1}(\Omega ))} \quad (\text{ by } \text{ Lem. }~3\hbox {-}{} \textit{(ii)}) \end{aligned}$$

for $n \ge 1$, we have the following estimates,

$$\begin{aligned} \Vert R_{h2}^1\Vert _{\Psi _h^\prime }&\le \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^1 \bigr \Vert + c_1 \Vert \eta ^0 \Vert \le c_1^\prime h^{k+1} \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})} \quad (\text{ by }~(40a)), \\ \Vert R_{h2}^n\Vert _{\Psi _h^\prime }&\le c_1 \bigl ( \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^n \bigr \Vert + \bigl \Vert {\bar{D}}_{\Delta t}^{(1)} \eta ^{n-1} \bigr \Vert + \Vert \eta ^{n-1} \Vert + \Vert \eta ^{n-2} \Vert \bigr ) \quad (\text{ for }\, n \ge 2) \\&\le c_1^\prime h^{k+1} \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^{n-2},t^n; H^{k+1})} \quad (\text{ by }~(40a)), \end{aligned}$$

which complete the proof of (40b). The estimate of (40c) is obvious under Hypothesis 4 from Lemma 3-(ii).

1.3 Proof of Lemma 6

We prove (i). From Lemma 5-(i), it holds that

$$\begin{aligned} \Vert R_h^1\Vert&\le \Delta t \sum _{i=1}^3 \Vert R_{hi}^1\Vert \le c_1 \bigl ( \Delta t^{1/2} \Vert \phi \Vert _{Z^2(t^0,t^1)} + h^k \Delta t^{-1/2} \Vert \phi \Vert _{H^1(t^0,t^1;H^{k+1})} \bigr ) \nonumber \\&\le c_1^\prime \bigl ( \Delta t \Vert \phi \Vert _{Z^3} + h^k \Vert \phi \Vert _{H^2(H^{k+1})} \bigr ) \le c_1^{\prime \prime } (\Delta t + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}. \end{aligned}$$

(A.10)

The equation (38) with $n=1$ is rewritten as

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(1)} e_h^1, \psi _h \bigr ) + a_0( e_h^1, \psi _h ) = \langle R_h^1, \psi _h \rangle , \quad \forall \psi _h \in \Psi _h \end{aligned}$$

(A.11)

from $e_h^0 = 0$ and, therefore, $\frac{1}{\Delta t} (e_h^1 - e_h^0 \circ X_1^n\gamma ^n) = {\bar{D}}_{\Delta t}^{(1)}e_h^1$. Substituting $e_h^1$ into $\psi _h$ in (A.11), dropping the positive term $a_0( e_h^1, e_h^1 )$, and using $e_h^0 = 0$ and $\langle R_h^1, e_h^1 \rangle \le \Vert R_h^1\Vert \Vert e_h^1\Vert$, we have

$$\begin{aligned} \Vert e_h^1\Vert&\le \Delta t \Vert R_h^1\Vert \le \Delta t \bigl [ c_1 (\Delta t + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} \bigr ] \quad (\text{ by }~(A.10)) \nonumber \\&\le c_1^\prime (\Delta t^2 + h^{k+1}) \, \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}, \end{aligned}$$

(A.12)

where for the last inequality we have employed

$$\begin{aligned} \Delta t h^k \le \frac{1}{2} (\Delta t^2 + h^{2k}) \le \frac{1}{2} (\Delta t^2 + h^{k+1}),\quad k \ge 1, \ h \in {(0,1).} \end{aligned}$$

Again, substituting $e_h^1$ into $\psi _h$ in (A.11), and using $e_h^0 = 0$ and $\langle R_h^1, e_h^1 \rangle \le \Vert R_h^1\Vert \Vert e_h^1\Vert$, we have

$$\begin{aligned}&\Vert e_h^1\Vert ^2 + \nu \Delta t \Vert \nabla e_h^1\Vert ^2\nonumber \\&\quad \le \Delta t \Vert R_h^1\Vert \Vert e_h^1\Vert \nonumber \\&\quad \le c_1 \Delta t (\Delta t + h^k) (\Delta t^2 + h^{k+1}) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})}^2 \quad (\text{ by }~(A.10) ~\hbox {and}~(A.12)) \nonumber \\&\quad \le c_1^\prime \bigl [ (\Delta t^2 + h^{k+1}) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} \bigr ]^2, \end{aligned}$$

(A.13)

which implies (41a).

Substituting ${\bar{D}}_{\Delta t}^{(1)}e_h^1$ into $\psi _h$ in (A.11) and using the estimates,

$$\begin{aligned} \bigl ( {\bar{D}}_{\Delta t}^{(1)}e_h^1, {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr )&= \bigl \Vert {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \Vert ^2,\\ a_0 \bigl ( e_h^1, {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr )&\ge \frac{1}{\Delta t} \biggl ( \frac{\nu }{2} \Vert \nabla e_h^1\Vert ^2 - \frac{\nu }{2} \Vert \nabla e_h^0\Vert ^2 \biggr ) = \frac{1}{\Delta t} \Bigl ( \frac{\nu }{2} \Vert \nabla e_h^1\Vert ^2 \Bigr ),\\ \bigl \langle R_h^1, {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \rangle&\le \bigl \Vert R_h^1\bigr \Vert \, \bigl \Vert {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \Vert \le \frac{1}{2}\bigl \Vert R_h^1\bigr \Vert ^2 + \frac{1}{2} \bigl \Vert {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \Vert \end{aligned}$$

we get

$$\begin{aligned} \nu \Vert \nabla e_h^1\Vert ^2 + \Delta t \bigl \Vert {\bar{D}}_{\Delta t}^{(1)}e_h^1 \bigr \Vert ^2&\le \Delta t\Vert R_h^1 \Vert ^2 \le \Delta t \bigl [ c_1 (\Delta t + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} \bigr ]^2 \quad (\text{ by }~(A.10)) \\&\le c_1^\prime \bigl [ (\Delta t^{3/2} + h^k) \Vert \phi \Vert _{Z^3\cap H^2(H^{k+1})} \bigr ]^2, \end{aligned}$$

which implies (41b).