The Convergence Analysis of Semi- and Fully-Discrete Projection-Decoupling Schemes for the Generalized Newtonian Models

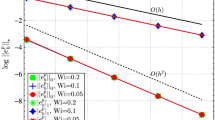
Abstract

We propose two linear schemes (1st- and 2nd-order) for the generalized Newtonian flow with the shear-dependent viscosity, which combine the decoupling techniques with the projection methods. The linear stabilization terms mimic $-k\partial _t \Delta {\varvec{u}}$ and $-k\partial _{tt} \Delta {\varvec{u}}$ from the PDE point of view. By our schemes, each velocity component can be computed in parallel efficiently using the same solver $(I-\alpha ^{-1}k\Delta )^{-1}$ at every time level. We analyze the convergence rates of the (temporally) semi- and the fully-discrete schemes. The theoretical results are testified by the numerical experiments.

Appendix A The Proof of (4.35)

For $B_{n+1} \in C^s$, the system (4.34) admits a unique solution $(\tilde{{\varvec{e}}}^{n+1}, q^{n+1}) \in H^{s+1} \times H^s$ $(s=1,2)$. The task here is to derive the a-priori estimate (4.35). For $i=1,2,\cdots ,m$, we reformulate (4.34) into

$$\begin{aligned}&\begin{aligned}&-\nabla \cdot [B_2 {\mathbb {D}}(\tilde{{\varvec{e}}}^{i+1})] - \alpha ^{-1} \Delta (\tilde{{\varvec{e}}}^{i+1} - I_k \tilde{{\varvec{e}}}^{i+1}) + \nabla \cdot [B_2 {\mathbb {D}}(\tilde{{\varvec{e}}}^{i+1} - I_k \tilde{{\varvec{e}}}^{i+1})] \\&\quad \quad + \nabla q^{i+1} = {\varvec{F}}^{i+1} + \nabla \cdot [(B_{i+1} - B_2) \nabla I_k \tilde{{\varvec{e}}}^{i+1}] =: \bar{{\varvec{F}}}^{i+1}, \end{aligned}&\quad \text { in } \Omega , \end{aligned}$$

(A.1a)

$$\begin{aligned}&\nabla \cdot \tilde{{\varvec{e}}}^{i+1} - k \beta \Delta (q^{i+1} - q^i) = - k \beta \Delta (p(t_{i+1}) - p(t_i))&\quad \text { in } \Omega , \end{aligned}$$

(A.1b)

with $\tilde{{\varvec{e}}}^{i+1} = \nabla q^{i+1} \cdot {\varvec{n}} = 0$ on $\Gamma$. By $\Vert B_i - B_j\Vert _{W^{2,\infty }} \le C|t_i - t_j|$, we have, for $s=0,1$,

$$\begin{aligned} \Vert \bar{{\varvec{F}}}^{i+1}\Vert _{H^s} \le \Vert {\varvec{F}}^{i+1}\Vert _{H^s} + C|t_{m+1} - t_{i+1}| \Vert I_k \tilde{{\varvec{e}}}^{i+1} \Vert _{H^s}. \end{aligned}$$

If we prove that

$$\begin{aligned} \sum _{i=1}^m \Vert \tilde{{\varvec{e}}}^{i+1} \Vert _{H^{s+2}}^2 \le C \sum _{i=0}^m ( \Vert \bar{{\varvec{F}}}^{i+1}\Vert _{H^s}^2 + k^2 \Vert p(t_{i+1})\Vert _{H^{s+4}}^2 + \Vert {\varvec{{\tilde{e}}}}^{i+1}\Vert _{H^1}^2) + C( \Vert \tilde{{\varvec{e}}}^1 \Vert _{H^{s+2}}^2 + \Vert \tilde{{\varvec{e}}}^0 \Vert _{H^{s+2}}^2 ),\nonumber \\ \end{aligned}$$

(A.2)

we can conclude (4.35) for $1 \le i \le m$. Then it is not difficult to proceed to $m+1 \le i \le 2m$, and furthermore to $1\le i \le n$, by induction. Therefore, it suffices to prove (A.2). The proof consists of two steps: (i) first we apply the Z-transform to the equations of $\{(\tilde{{\varvec{e}}}^{i+1}, q^{i+1})\}_{i=1}^m$; (ii) We derive the $H^2$ and $H^3$ regularity using the method of translation.

(i) For $\zeta \in {\mathbb {S}} = \{ \zeta \in {\mathbb {C}} \mid |\zeta |=1\}$, we introduce the Z-transform of $({\varvec{{\tilde{e}}}}^i,q^i,\bar{{\varvec{F}}}^i,p(t_i))$:

$$\begin{aligned} {\varvec{{\tilde{e}}}}(\zeta )&= \sum _{i=1}^\infty {\varvec{{\tilde{e}}}}^{i+1} \zeta ^{i+1}, \quad q(\zeta ) = \sum _{i=0}^\infty q^{i+1} \zeta ^{i+1}, \quad \bar{{\varvec{F}}}(\zeta ) = \sum _{i=0}^\infty \bar{{\varvec{F}}}^{i+1}\zeta ^i,\\&\quad {\bar{p}}(\zeta ) = \sum _{i=0}^\infty p(t_i) \zeta ^{i+1}, \end{aligned}$$

where $\{({\varvec{{\tilde{e}}}}^i, q^i)\}_{i=2}^\infty$ is the solution to the system (A.1) with $(\bar{{\varvec{F}}}^{i+1}, p(t_{i+1})) = ({\varvec{0}},0)$ for $i > m$. Multiplying (A.1) by $\zeta ^{i+1}$, we see that $({\varvec{{\tilde{e}}}}(\zeta ), q(\zeta ))$ satisfies the system

$$\begin{aligned}&\begin{aligned}&-(1-(1-\zeta )^2)\nabla \cdot [B_2 {\mathbb {D}}(\tilde{{\varvec{e}}})] - \alpha ^{-1} (1-\zeta )^2\Delta \tilde{{\varvec{e}}} + \nabla q = \bar{{\varvec{F}}} \\&\quad \quad \quad + \zeta ^2(\alpha ^{-1} \Delta I_k {\varvec{{\tilde{e}}}}^2 - \nabla \cdot [B_2 {\mathbb {D}}(I_k {\varvec{{\tilde{e}}}}^2)]) - \zeta ^3(\alpha ^{-1} \Delta {\varvec{{\tilde{e}}}}^1 - \nabla \cdot [B_2 {\mathbb {D}}({\varvec{{\tilde{e}}}}^1)]) =: {\varvec{G}} \end{aligned}&\quad \text { in } \Omega , \end{aligned}$$

(A.3a)

$$\begin{aligned}&\nabla \cdot \tilde{{\varvec{e}}} - k \beta (1-\zeta ) \Delta q = - k \beta (1-\zeta )\Delta {\bar{p}} + \zeta ^2 k \beta \Delta p^1 =: kg&\quad \text { in } \Omega , \end{aligned}$$

(A.3b)

with $\tilde{{\varvec{e}}}= \nabla q \cdot {\varvec{n}} = 0$ on $\Gamma$. By the Parseval equality

$$\begin{aligned} \int _{\mathbb {S}} \Vert w(\zeta ) \Vert _{H^s}^2 ~d\zeta = \sum _{i=0}^\infty \Vert w^i \Vert _{H^s}^2 \quad \forall w(\zeta ) = \sum _{i=0}^\infty \zeta ^i w^i({\varvec{x}}), \quad w^i({\varvec{x}}) \in H^s(\Omega ), \end{aligned}$$

we reduce the proof of (A.2) to the derivation of the a-priori estimate

$$\begin{aligned} \Vert {\varvec{{\tilde{e}}}} \Vert _{H^{s+2}}^2 \le C(\Vert {\varvec{G}}\Vert _{H^s}^2 + k^2 \Vert {\bar{p}} \Vert _{H^{s+4}}^2 + k^2 \Vert p^1\Vert _{H^{s+4}}^2 + \Vert {\varvec{{\tilde{e}}}} \Vert _{H^1}^2) \quad \quad s=0,1. \end{aligned}$$

(A.4)

The validation of (A.4) will be carried out in step (ii). As a previous step, we write out the variational form of (A.3) and investigate the ellipticity. For all $({\varvec{v}}, r) \in H_0^1(\Omega )^d \times H^1(\Omega )$,

$$\begin{aligned} \begin{aligned} a({\varvec{{\tilde{e}}}},q; {\varvec{v}},r)&:= (1-(1-\zeta )^2)(B_2{\mathbb {D}}({\varvec{{\tilde{e}}}}), {\mathbb {D}}({\varvec{v}})) + \alpha ^{-1}(1-\zeta )^2(\nabla {\varvec{{\tilde{e}}}}, \nabla {\varvec{v}}) - (q, \nabla \cdot {\varvec{v}}) \\&\quad + (\nabla \cdot {\varvec{{\tilde{e}}}}, r) + \beta k (1-\zeta ) (\nabla q, \nabla r) = ({\varvec{G}}, {\varvec{v}}) + k(g,r). \end{aligned} \nonumber \\ \end{aligned}$$

(A.5)

By Korn and Poincaré’s inequalities, there exist two constants $C_{B1}$ and $C_{B2}$ such that

$$\begin{aligned} C_{B1} \Vert \nabla {\varvec{v}} \Vert _{L^2}^2 \le \Vert B_i {\mathbb {D}}({\varvec{v}}) \Vert _{L^2}^2 \le C_{B2} \Vert \nabla {\varvec{v}} \Vert _{L^2}^2 \quad \forall {\varvec{v}} \in H^1_0, \ i = 1,\cdots ,N. \end{aligned}$$

Note that $\zeta = \cos \theta + {\mathfrak {i}} \sin \theta$ with $\theta \in [0,2\pi )$, and

$$\begin{aligned} \begin{aligned}&1-\zeta = 1-\cos \theta - \sin \theta {\mathfrak {i}},\quad 1-(1-\zeta )^2 = 2\cos \theta + 1 -2\cos ^2\theta + 2\sin \theta (1-\cos \theta ) {\mathfrak {i}}, \\&(1-\zeta )^2 = -2\cos \theta (1-\cos \theta ) - 2\sin \theta (1-\cos \theta ) {\mathfrak {i}}. \end{aligned} \end{aligned}$$

For a suitable constant $\kappa \in (0,1)$ (will be specified later), we consider the following three cases:

• (1) $\cos \theta \in (1 -\kappa , 1]$. Since $|1-\zeta |^2 = 2(1-\cos \theta )$, under the assumption that $\alpha > 2\kappa /C_{B1}$, the real part of $a({\varvec{v}},r; {\varvec{v}},r)$ is coercive:

  $$\begin{aligned} \begin{aligned} \mathrm {Re}[a({\varvec{v}},r; {\varvec{v}},r)]&\ge \left( (2\cos \theta + 1 - 2\cos ^2\theta )C_{B1} - \alpha ^{-1}2\cos \theta (1-\cos \theta ) \right) \Vert \nabla {\varvec{v}}\Vert _{L^2}^2 \\&\quad + \beta k (1-\cos \theta )\Vert \nabla q \Vert _{L^2}^2 \\&\ge ( C_{B1} - \alpha ^{-1} 2\kappa ) \Vert \nabla {\varvec{v}}\Vert _{L^2}^2 + \beta k |1-\zeta |^2 \Vert \nabla r \Vert _{L^2}^2/2 \ge 0. \end{aligned} \end{aligned}$$

• (2) $\cos \theta \in [-1, -1 + \kappa )$. If $\alpha < 2(2-\kappa )(1-\kappa )/(3C_{B2})$, then the coercivity of the real part holds true:

  $$\begin{aligned} \begin{aligned} \mathrm {Re}[a({\varvec{v}},r; {\varvec{v}},r)]&\ge \left( \alpha ^{-1}2(1-\kappa )(2-\kappa ) - 3C_{B2} \right) \Vert \nabla {\varvec{v}}\Vert _{L^2}^2 + \beta k |1-\zeta |^2 \Vert \nabla q \Vert _{L^2}^2/2 \ge 0. \end{aligned} \end{aligned}$$

• (3) $\cos \theta \in [-1+\kappa , 1-\kappa ]$. We have $|1-\zeta |^2 \in [2\kappa , 4-2\kappa ]$. When $\sin \theta \in [\sqrt{\kappa (2-\kappa )},1]$, if $\alpha < 1/(2C_{B2})$, we find that

  $$\begin{aligned} \begin{aligned} \mathrm {Re}[{\mathfrak {i}}a({\varvec{v}},r; {\varvec{v}},r)]&\ge ( \alpha ^{-1} \sin \theta (1-\cos \theta ) - \sin \theta (1-\cos \theta )2C_{B2} ) \Vert \nabla {\varvec{v}}\Vert _{L^2}^2 + \beta k \sin \theta \Vert \nabla q\Vert _{L^2}^2 \\&\ge \sin \theta (1-\cos \theta )(\alpha ^{-1} - 2C_{B2}) \Vert \nabla {\varvec{v}}\Vert _{L^2}^2 + \beta k |1-\zeta |^2 \Vert \nabla q\Vert _{L^2}^2/4 \ge 0. \end{aligned} \end{aligned}$$

  When $\sin \theta \in [-1, -\sqrt{\kappa (2-\kappa )}]$, we have

  $$\begin{aligned} \begin{aligned} \mathrm {Re}[-{\mathfrak {i}}a({\varvec{v}},r; {\varvec{v}},r)]&\ge -\sin \theta (1-\cos \theta )(\alpha ^{-1} - 2C_{B2}) \Vert \nabla {\varvec{v}}\Vert _{L^2}^2 + \beta k |1-\zeta |^2 \Vert \nabla q\Vert _{L^2}^2/4 \ge 0. \end{aligned} \end{aligned}$$

In summary, for sufficiently small $\alpha$ and $\kappa \in (0,1)$ satisfying $2\kappa /C_{B1}< \alpha < \min ((2C_{B2})^{-1}, 2(2-\kappa )(1-\kappa )/(3C_{B2}))$, there exists a constant $C>0$ such that

$$\begin{aligned} \mathrm {Re}[{\mathfrak {o}} a({\varvec{v}},r;{\varvec{v}},r) ] \ge C( \Vert \nabla {\varvec{v}} \Vert _{L^2}^2 + \beta k |1-\zeta |^2 \Vert \nabla q\Vert _{L^2}^2 ) \quad \quad {\mathfrak {o}} = 1, {\mathfrak {i}} \text { or } \mathfrak {-i}. \end{aligned}$$

(A.6)

(ii) In this step, we prove (A.4) by the method of translation. Without loss of generality, we consider two simple cases: (1) $\Omega = {\mathbb {R}}^d$ and (2) $\Omega = {\mathbb {R}}^d_+ := {\mathbb {R}}^d \cap \{x_d >0\}$, and assume that $({\varvec{{\tilde{e}}}},q)$ has compact support. The case of the general smooth domain can be reduced to these two cases essentially (cf. [29]). We denote by $({\varvec{\xi }}_1,\cdots ,{\varvec{\xi }}_d) = I \in {\mathbb {R}}^{d\times d}$.

• (1) $\Omega = {\mathbb {R}}^d$. For $i=1,2,\cdots ,d$ and $D_h w({\varvec{x}}) = (w({\varvec{x}} + h{\varvec{\xi }}_i) - w({\varvec{x}}))/h$, we substitute $({\varvec{v}},q) = (D_{-h}D_h {\varvec{{\tilde{e}}}}({\varvec{x}}), D_{-h}D_h q({\varvec{x}}))$ into (A.5) and obtain (by (A.6)):

  $$\begin{aligned} \begin{aligned}&C(\Vert \nabla D_h{\varvec{{\tilde{e}}}} \Vert _{L^2}^2 + \beta k |1-\zeta |^2 \Vert \nabla D_h q\Vert _{L^2}^2) - C\Vert D_h B_2\Vert _{L^\infty } \Vert {\mathbb {D}}(D_h{\varvec{{\tilde{e}}}}) \Vert _{L^2} \Vert {\mathbb {D}}({\varvec{{\tilde{e}}}}) \Vert _{L^2} \\&\le C\Vert {\varvec{G}}\Vert _{L^2} \Vert D_{-h}D_h {\varvec{{\tilde{e}}}}\Vert _{L^2} + k( \Vert \Delta D_{-h}D_h {\bar{p}}\Vert _{L^2} + \Vert \Delta D_{-h}D_h p^1\Vert _{L^2} )\Vert q\Vert _{L^2}, \end{aligned}\nonumber \\ \end{aligned}$$

  (A.7)

  which implies (A.4) with $s=0$. Differentiating (A.3) with respect to $x_i$, we can prove (A.4) with $s=1$ in a similar manner.

• (2) $\Omega = {\mathbb {R}}^d_+$. For $i=1,2,\cdots ,d-1$, we substitute $({\varvec{v}},q) = (D_{-h}D_h {\varvec{{\tilde{e}}}}({\varvec{x}}), D_{-h}D_h q({\varvec{x}}))$ into (A.5) and obtain (A.7), which yields: for $i=1,2,\cdots ,d-1$,

  $$\begin{aligned} \Vert \partial _{x_i} {\varvec{{\tilde{e}}}} \Vert _{H^1}^2 + \beta k |1-\zeta |^2 \Vert \nabla \partial _{x_i} q\Vert _{L^2}^2 \le C(\Vert {\varvec{G}}\Vert _{L^2}^2 + k^2 \Vert {\bar{p}}\Vert _{H^4}^2 + k^2 \Vert p^1\Vert _{H^4}^2). \end{aligned}$$

  (A.8)

  For $i=1,\cdots ,d-1$, differentiating (A.3b) with $x_i$, we get

  $$\begin{aligned} -k\beta (1-\zeta )\Delta \partial _{x_i} q = k \partial _{x_i} g - \nabla \cdot \partial _{x_i} {\varvec{{\tilde{e}}}}, \end{aligned}$$

  (A.9)

  with $\nabla \partial _{x_i} q \cdot {\varvec{n}} = 0$ on $\Gamma = {\mathbb {R}}^d \cap \{x_d= 0\}$. Multiplying (A.9) by $(1-{\bar{\zeta }})/|1-\zeta |$ and testing by $D_{-h}D_h \partial _{x_i} q$, we derive the estimate:

  $$\begin{aligned} \beta k |1-\zeta | \Vert \partial _{x_i} q \Vert _{H^2} \le C( k \Vert {\bar{p}}\Vert _{H^3} + k \Vert p^1\Vert _{H^3} + \Vert \nabla \cdot \partial _{x_i} {\varvec{{\tilde{e}}}}\Vert _{L^2}) \quad (i=1,\cdots ,d-1). \nonumber \\ \end{aligned}$$

  (A.10)

  Setting

  $$\begin{aligned} {\varvec{U}} = {\varvec{{\tilde{e}}}} - \beta k (1-\zeta ) \nabla q, \quad Q = q + \beta k (1-\zeta ) (\alpha ^{-1} (1-\zeta )^2 + (1-(1-\zeta )^2)b_2)\Delta q, \end{aligned}$$

  we find that $({\varvec{U}}, Q)$ satisfies the system:

  $$\begin{aligned} -(1-(1-\zeta )^2)\nabla \cdot [b_2 {\mathbb {D}}({\varvec{U}})] - \alpha ^{-1}(1-\zeta )^2 \Delta {\varvec{U}} + \nabla Q = \hat{{\varvec{G}}} , \quad \quad \nabla \cdot {\varvec{U}} = kg, \nonumber \\ \end{aligned}$$

  (A.11)

  where $\hat{{\varvec{G}}} := {\varvec{G}} + (1-(1-\zeta )^2) \Big ( \nabla \cdot [(B_2 - b_2 {\mathbb {I}}) {\mathbb {D}}({\varvec{U}}-{\varvec{{\tilde{e}}}})] + \beta k (1-\zeta ) (\nabla b_2 \cdot \nabla ^2 q + \Delta q \nabla b_2) \Big )$. Because $\Vert {\varvec{{\tilde{e}}}}\Vert _{H^\frac{3}{2}(\Gamma )}$ and $\Vert {\varvec{U}}\Vert _{H^\frac{3}{2}(\Gamma )}$ only involve $\Vert \partial _{x_i} {\varvec{{\tilde{e}}}}\Vert _{H^1}$ and $\Vert \partial _{x_i} \nabla q\Vert _{H^1}$ with $i=1,\cdots ,d-1$,

  $$\begin{aligned} \begin{aligned} \Vert {\varvec{{\tilde{e}}}}\Vert _{H^\frac{3}{2}(\Gamma )} + \Vert {\varvec{U}}\Vert _{H^{3/2}(\Gamma )}&\le C(\Vert {\varvec{G}}\Vert _{L^2} + k \Vert {\bar{p}}\Vert _{H^3} + k \Vert p^1\Vert _{H^3} + \Vert \nabla \cdot \partial _{x_i} {\varvec{{\tilde{e}}}}\Vert _{L^2}) \quad \text {(by} (A.10))\\&\le C(\Vert {\varvec{G}}\Vert _{L^2} + k \Vert {\bar{p}}\Vert _{H^4} + k \Vert p^1\Vert _{H^4}). \quad \text {(by} (A.8)) \end{aligned}\nonumber \\ \end{aligned}$$

  (A.12)

  Therefore, we achieve (by the regularity of Stokes equations)

  $$\begin{aligned} \begin{aligned} \Vert {\varvec{U}}\Vert _{H^2} + \Vert Q\Vert _{H^1}&\le C(\Vert \hat{{\varvec{G}}} \Vert _{L^2} + k \Vert g\Vert _{H^1} + \Vert {\varvec{U}}\Vert _{H^{3/2}(\Gamma )}) \\&\quad \le C(\Vert {\varvec{G}} \Vert _{L^2} + \Vert B_2 - b_2 {\mathbb {I}}\Vert _{W^{1,\infty }} (\Vert {\varvec{U}}\Vert _{H^2} + \Vert {\varvec{{\tilde{e}}}}\Vert _{H^2}) + k\Vert q\Vert _{H^2} \\&\quad + k \Vert {\bar{p}}\Vert _{H^4} + k \Vert p^1\Vert _{H^4}). \end{aligned} \end{aligned}$$

  Under the assumption that $\Vert B_i - b_i {\mathbb {I}}\Vert _{L^\infty } \le \epsilon$ $(\forall i \ge 2)$ with sufficiently small $\epsilon$, and in view of $k\Vert q\Vert _{H^2} \le C\Vert {\varvec{{\tilde{e}}}}\Vert _{H^1} + k\Vert g\Vert _{L^2}$ (by (A.3b)), we conclude

  $$\begin{aligned} \Vert {\varvec{U}}\Vert _{H^2} + \Vert Q\Vert _{H^1} \le C(\Vert {\varvec{G}}\Vert _{L^2} + \epsilon \Vert {\varvec{{\tilde{e}}}}\Vert _{H^2} + k \Vert {\bar{p}}\Vert _{H^4} + k \Vert p^1\Vert _{H^4}). \end{aligned}$$

  (A.13)

  Setting $Z(\zeta ) = \alpha ^{-1} (1-\zeta )^2 + (1-(1-\zeta )^2)b_2$, we obtain from (A.3a$- \nabla Z(\zeta )$ (A.3b)) that

  $$\begin{aligned} -(1-(1-\zeta )^2)\nabla \cdot [B_2 {\mathbb {D}}({\varvec{{\tilde{e}}}})] - \alpha ^{-1}(1-\zeta )^2 \Delta {\varvec{{\tilde{e}}}} - \nabla [Z(\zeta ) \nabla \cdot {\varvec{{\tilde{e}}}}] = -\nabla Q + {\varvec{G}} + k \nabla [Z(\zeta ) g], \end{aligned}$$

  which implies (by the coercivity of $a({\varvec{v}},r ;{\varvec{v}},r) + (Z(\zeta )\nabla \cdot {\varvec{v}}, \nabla \cdot {\varvec{v}})$)

  $$\begin{aligned} \begin{aligned} \Vert {\varvec{{\tilde{e}}}} \Vert _{H^2}&\le C (\Vert -\nabla Q + {\varvec{G}} + k \nabla [Z(\zeta ) g] \Vert _{L^2} + \Vert {\varvec{{\tilde{e}}}} \Vert _{H^{3/2}(\Gamma )}) \\&\le C ( \Vert {\varvec{G}}\Vert _{L^2} + k \Vert {\bar{p}}\Vert _{H^4} + k \Vert p^1\Vert _{H^4} ) \quad \text {(by }(A.13), (A.8) \text { and } (A.12)). \end{aligned} \end{aligned}$$

  We conclude (A.4) for $s=0$. The case of $s=1$ can be handled similarly.