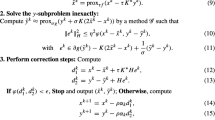Cubic Regularized Newton Method for the Saddle Point Models: A Global and Local Convergence Analysis

Abstract

In this paper, we propose a cubic regularized Newton method for solving the convex-concave minimax saddle point problems. At each iteration, a cubic regularized saddle point subproblem is constructed and solved, which provides a search direction for the iterate. With properly chosen stepsizes, the method is shown to converge to the saddle point with global linear and local superlinear convergence rates, if the saddle point function is gradient Lipschitz and strongly-convex-strongly-concave. In the case that the function is merely convex-concave, we propose a homotopy continuation (or path-following) method. Under a Lipschitz-type error bound condition, we present an iteration complexity bound of ${\mathcal {O}}\left( \ln \left( 1/\epsilon \right) \right)$ to reach an $\epsilon$-solution through a homotopy continuation approach, and the iteration complexity bound becomes ${\mathcal {O}}\left( \left( 1/\epsilon \right) ^{\frac{1-\theta }{\theta ^2}}\right)$ under a Hölderian-type error bound condition involving a parameter $\theta$ ($0<\theta <1$).

Appendix A Proofs of the Propositions and Theorems

1.1 A.1 Proof of Proposition 2.1

With Assumption 2.1, we have

$$\begin{aligned} f(x,y^*)-f(x^*,y^*)\ge \frac{\mu }{2}\Vert x-x^*\Vert ^2\qquad \text{ and }\qquad f(x^*,y^*)-f(x^*,y)\ge \frac{\mu }{2}\Vert y-y^*\Vert ^2. \end{aligned}$$

As a result, $\frac{\mu }{2}\Big (\Vert x-x^*\Vert ^2 + \Vert y-y^*\Vert ^2\Big )\le f(x,y^*)-f(x^*,y)$. Denote $z = (x;y)$ and $z^* = (x^*;y^*)$. By the Lipschitzian Assumption 2.2, it holds that $\Vert F(z)\Vert ^2=\Vert F(z)-F(z^*)\Vert ^2\le L^2\Vert z-z^*\Vert ^2$, which leads to the first half of our result

$$\begin{aligned} m(z) \le \frac{L^2}{2}\Vert z-z^*\Vert ^2 \le \frac{L^2}{\mu }(f(x,y^*)-f(x^*,y)) \le \frac{L^2}{\mu }\left( \max \limits _{y'\in {\mathbb {R}}^m} f(x,y')-\min \limits _{x'\in {\mathbb {R}}^n} f(x',y)\right) . \end{aligned}$$

On the other hand, denote

$$\begin{aligned} y^*(x)=\arg \max \limits _{y'\in {\mathbb {R}}^m}f(x,y') \qquad \text{ and }\qquad x^*(y)=\arg \min \limits _{x'\in {\mathbb {R}}^n}f(x',y). \end{aligned}$$

With this notation, the duality gap can be rewritten as $f(x,y^* (x))-f(x^*(y),y)$. By the first-order stationarity condition, we have

$$\begin{aligned} \nabla _xf(x^*(y),y)=0\qquad \text{ and }\qquad \nabla _yf(x,y^*(x))=0. \end{aligned}$$

Applying the Lipschitz continuity condition yields

$$\begin{aligned} \begin{array}{ll} f(x,y) &{} \le f(x^*(y),y)+\nabla _xf(x^*(y),y)^{\top }(x^*(y)-x)+\frac{L}{2}\Vert x^*(y)-x\Vert ^2 \\ &{} =f(x^*(y),y)+\frac{L}{2}\Vert x^*(y)-x\Vert ^2.\\ \end{array} \end{aligned}$$

Similarly, $f(x,y)\ge f(x,y^*(x))-\frac{L}{2}\Vert y^*(x)-y\Vert ^2$. Combining these two yields

$$\begin{aligned} \begin{array}{ll} f(x,y^*(x))-f(x^*(y),y) &{} = f(x,y^*(x))-f(x,y)+f(x,y)-f(x^*(y),y) \\ &{} \le \frac{L}{2}\left( \Vert x^*(y)-x\Vert ^2+\Vert y^*(x)-y\Vert ^2\right) . \\ \end{array} \end{aligned}$$

(32)

Additionally, the strong convexity/strong concavity of f gives

$$\begin{aligned} \begin{array}{ll} &{} \Vert \nabla _xf(x,y)\Vert ^2=\Vert \nabla _xf(x,y)-\nabla _xf(x^*(y),y)\Vert ^2\ge \mu ^2\Vert x-x^*(y)\Vert ^2, \\ &{} \Vert \nabla _yf(x,y)\Vert ^2=\Vert \nabla _yf(x,y)-\nabla _yf(x,y^*(x))\Vert ^2\ge \mu ^2\Vert y-y^*(x)\Vert ^2, \\ \end{array} \end{aligned}$$

resulting

$$\begin{aligned} \begin{array}{ll} \mu ^2(\Vert x^*(y)-x\Vert ^2+\Vert y^*(x)-y\Vert ^2) \le \Vert \nabla _xf(x,y)\Vert ^2+\Vert \nabla _yf(x,y)\Vert ^2 \le 2m(z). \\ \end{array} \end{aligned}$$

(33)

Combining (32),(33) we the second half of the result:

$$\begin{aligned} \max \limits _{y'\in {\mathbb {R}}^m} f(x,y')-\min \limits _{x'\in {\mathbb {R}}^n} f(x',y)=f(x,y^* (x))-f(x^*(y),y)\le \frac{L}{\mu ^2}m(z). \end{aligned}$$

$\square$

1.2 A.2 Proof of Proposition 3.3

We first prove that (8) can be achieved with small enough $\gamma ^k$. Note that $u^k,v^k$ are the solutions to the stationarity condition (7), which is equivalent to the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma ^k\Vert u^k\Vert u^k+Q_1u^k+H_{xy}^kv^k=-g_x^k,\\ \gamma ^k\Vert v^k\Vert v^k+Q_2v^k-(H_{xy}^k)^{\top }\!u^k\!=\!g_y^k, \end{array}\right. } \end{aligned}$$

(34)

where $Q_1 = H_{xx}^k \succeq \mu I$ and $Q_2 = -H_{yy}^k \succeq \mu I$ are positive definite matrices. Inner product the first equation in (34) with $u^k$ and the second with $v^k$ and then sum up the two, we get

$$\begin{aligned} \gamma ^k\big (\Vert u^k\Vert ^3+\Vert v^k\Vert ^3\big )+(u^k)^{\top }Q_1u^k+(v^k)^{\top }Q_2v^k= - (g_x^k)^{\top }u^k+(g_y^k)^{\top }v^k. \end{aligned}$$

Consequently, let $b = \max \big \{\Vert g_x^k\Vert ,\Vert g_y^k\Vert \big \}$, we have

$$\begin{aligned} \gamma ^k(\Vert u^k\Vert ^3+\Vert v^k\Vert ^3)+\mu (\Vert u^k\Vert ^2+\Vert v^k\Vert ^2)\le {b}(\Vert u^k\Vert +\Vert v^k\Vert ).\end{aligned}$$

Note that $\Vert u^k\Vert ^2+\Vert v^k\Vert ^2\ge \frac{1}{2}(\Vert u^k\Vert +\Vert v^k\Vert )^2$ and $\Vert u^k\Vert ^3+\Vert v^k\Vert ^3\ge \frac{1}{4}(\Vert u^k\Vert +\Vert v^k\Vert )^3$. As a result,

$$\begin{aligned} \gamma ^k(\Vert u^k\Vert +\Vert v^k\Vert )^3+2\mu (\Vert u^k\Vert +\Vert v^k\Vert )^2\le 4{b}(\Vert u^k\Vert +\Vert v^k\Vert ). \end{aligned}$$

Let $\omega = \gamma ^k(\Vert u^k\Vert +\Vert v^k\Vert )$, then the above inequality is equivalent to $\omega ^2 + 2\mu \omega - 4b\gamma ^k\le 0$. Solving this quadratic inequality yields that

$$\begin{aligned} \gamma ^k(\Vert u^k\Vert +\Vert v^k\Vert )\le \sqrt{\mu ^2+4{b}\gamma ^k}-\mu = \frac{4b\gamma ^k}{\sqrt{\mu ^2+4{b}\gamma ^k}+\mu }\rightarrow 0 \quad \text{ as }\quad \gamma ^k\rightarrow 0. \end{aligned}$$

(35)

We can see that the upper bound for $\gamma ^k(\Vert u^k\Vert +\Vert v^k\Vert )$ is an increasing function of $\gamma ^k$ with function values ranging from 0 to $\infty$. This indicates that by making $\gamma ^k$ small enough, condition (8) can then be satisfied.

Next, we proceed to prove descent result of Proposition 3.3. The proof of this part is based on the concept of the proof in [28]. By direct calculation,

$$\begin{aligned}&\langle \nabla m(z^k),d^k\rangle \nonumber \\&\quad = \langle H_{xx}^kg_x^k+H_{xy}^kg_y^k,u^k\rangle + \langle H_{yy}^kg_y^k+(H_{xy}^k)^{\top }g_x^k,v^k\rangle \nonumber \\&\quad = \langle H_{xx}^kg_x^k+H_{xy}^kg_y^k,u^k\rangle +\mu \cdot (u^k)^{\top }H_{xy}^kv^k+(g_x^k)^{\top }H_{xy}^kv^k-(u^k)^{\top }H_{xy}^kg_y^k\\&\qquad +\langle H_{yy}^kg_y^k+(H_{xy}^k)^{\top }g_x^k,v^k\rangle -\mu \cdot (u^k)^{\top }H_{xy}^kv^k-(g_x^k)^{\top }H_{xy}^kv^k+(u^k)^{\top }H_{xy}^kg_y^k.\nonumber \end{aligned}$$

(36)

Note that we added and subtracted the same three terms in the last equality. By rearranging the terms in the inner product, the first four terms on the RHS of (36) can be written as:

$$\begin{aligned}&\langle H_{xx}^kg_x^k+H_{xy}^kg_y^k,u^k\rangle +\mu \cdot (u^k)^{\top }H_{xy}^kv^k+(g_x^k)^{\top }H_{xy}^kv^k-(u^k)^{\top }H_{xy}^kg_y^k\nonumber \\&\quad = \langle g_x^k+H_{xx}^ku^k+H_{xy}^kv^k, g_x^k+\mu \cdot u^k\rangle -\Vert g_x^k\Vert ^2-\mu \cdot (u^k)^{\top }H_{xx}^ku^k -\mu \cdot (g_x^k)^{\top }u^k\nonumber \\&\quad \overset{\text {By} (7)}{=} \langle -\gamma ^k\Vert u^k\Vert u^k,g_x^k+\mu \cdot u^k\rangle -\Vert g_x^k\Vert ^2-\mu \cdot (u^k)^{\top }H_{xx}^ku^k-\mu \cdot (g_x^k)^{\top }u^k\nonumber \\&\quad \le -\mu ^2\Vert u^k\Vert ^2-\mu \gamma ^k\Vert u^k\Vert ^3-\gamma ^k\Vert u^k\Vert (u^k)^{\top }g_x^k-\Vert g_x^k\Vert ^2-\mu \cdot (g_x^k)^{\top }u^k \nonumber \\&\quad \overset{(i)}{\le } -\left( \frac{\mu ^2}{2}+\mu \gamma ^k\Vert u^k\Vert -\frac{1}{2}(\gamma ^k)^2\Vert u^k\Vert ^2\right) \Vert u^k\Vert ^2\nonumber \\&\quad \overset{(ii)}{\le } -\frac{\mu ^2}{2}\Vert u^k\Vert ^2 \end{aligned}$$

(37)

where inequality (ii) is because $\gamma ^k\Vert u^k\Vert \le \mu$ and inequality (i) is due to

$$\begin{aligned}&-\gamma ^k\Vert u^k\Vert (u^k)^{\top }g_x^k-\Vert g_x^k\Vert ^2-\mu \cdot (g_x^k)^{\top }u^k\\= & {} -\left( \frac{1}{2}\Vert g_x^k\Vert ^2+\gamma ^k\Vert u^k\Vert (u^k)^{\top }g_x^k\right) -\left( \frac{1}{2}\Vert g_x^k\Vert ^2+\mu (g_x^k)^{\top }u^k\right) \\\le & {} \frac{1}{2}(\gamma ^k)^2\Vert u^k\Vert ^4 + \frac{\mu ^2}{2}\Vert u^k\Vert ^2. \end{aligned}$$

Similarly, for the last four terms of (36), we have

$$\begin{aligned}&\langle H_{yy}^kg_y^k+(H_{xy}^k)^{\top }g_x^k,v^k\rangle -\mu \cdot (u^k)^{\top }H_{xy}^kv^k-(g_x^k)^{\top }H_{xy}^kv^k+(u^k)^{\top }H_{xy}^kg_y^k \\&\quad =\langle -g_y^k-H_{yy}^kv^k-(H_{xy}^k)^{\top }u^k, -g_y^k+\mu \cdot v^k\rangle -\Vert g_y^k\Vert ^2+\mu \cdot (v^k)^{\top }H_{yy}^kv^k+\mu \cdot (g_y^k)^{\top }v^k \\&\quad \le -\frac{\mu ^2}{2}\Vert v^k\Vert ^2. \end{aligned}$$

Adding (37) to the above inequality, combining with (36), we have $\langle \nabla m(z^k),d^k\rangle \le -\frac{\mu ^2}{2}\Vert d^k\Vert ^2$, which completes the proof. $\square$

1.3 A.3 Proof of Theorem 3.1

First of all, we establish the descent lemma for the mapping F(z) by observing that:

$$\begin{aligned} F(z^{k+1})=F(z^k+\alpha d^k)=F(z^k)+\alpha \nabla F(z^k)d^k+\int ^1_{t=0}(\nabla F(z^k+t\alpha d^k)-\nabla F(z^k))\alpha d^kdt. \end{aligned}$$

Then with Assumption 2.2, we have the following inequality:

$$\begin{aligned} \begin{array}{ll} \Vert F(z^{k+1})\Vert &{} \le \Vert F(z^k)+\alpha \nabla F(z^k)d^k\Vert +\alpha \Vert d^k\Vert \int _{t=0}^1\Vert \nabla F(z^k+t\alpha d^k)-\nabla F(z^k)\Vert dt \\ &{} \le \Vert F(z^k)+\alpha \nabla F(z^k)d^k\Vert +\frac{\alpha ^2L_2}{2}\Vert d^k\Vert ^2. \end{array} \end{aligned}$$

(38)

We can rewrite the expression for $\nabla F(z^k)d^k$ using stationarity condition (7):

$$\begin{aligned} \nabla F(z^k)d^k= \begin{pmatrix} H_{xx}^ku^k + H_{xy}^kv^k \\ -(H_{xy}^k)^{\top }u^k-H_{yy}^kv^k \end{pmatrix} = - F(z^k) - \gamma ^k\begin{pmatrix} \Vert u^k\Vert u^k \\ \Vert v^k\Vert v^k \end{pmatrix}. \end{aligned}$$

Putting the above identity back to (38) yields

$$\begin{aligned} \begin{array}{lcl} \Vert F(z^{k+1})\Vert &{} \le &{} (1-\alpha )\Vert F(z^k)\Vert +\alpha \gamma ^k\big (\Vert u^k\Vert ^2+\Vert v^k\Vert ^2\big )+\frac{\alpha ^2L_2}{2}\Vert d^k\Vert ^2\\ &{} \le &{} (1-\alpha )\Vert F(z^k)\Vert + \big (\alpha {\bar{\gamma }} + \frac{\alpha ^2L_2}{2}\big )\Vert d^k\Vert ^2. \end{array} \end{aligned}$$

(39)

Note that (9) indicates that $\Vert d^k\Vert ^2 \le \frac{8L_m}{\mu ^4}(m(z^k)-m(z^{k+1}))=\frac{4}{\alpha \mu ^2}(m(z^k)-m(z^{k+1}))$, which further yields

$$\begin{aligned} \begin{array}{ll} \Vert d^k\Vert ^2 &{} \le \frac{4}{\alpha \mu ^2}(m(z^k)-m(z^{k+1})) \\ &{} = \frac{2}{\alpha \mu ^2}(\Vert F(z^k)\Vert ^2-\Vert F(z^{k+1})\Vert ^2) \\ &{} = \frac{2}{\alpha \mu ^2}(\Vert F(z^k)\Vert +\Vert F(z^{k+1})\Vert )(\Vert F(z^k)-F(z^{k+1})\Vert ) \\ &{} \le \frac{4L D}{\alpha \mu ^2}(\Vert F(z^k)\Vert -\Vert F(z^{k+1})\Vert ). \end{array} \end{aligned}$$

(40)

where the last inequality is due to $\Vert F(z)\Vert = \Vert F(z)-F(z^*)\Vert \le L D$ for $\forall z\in \{z:m(z)\le m(z^0)\}.$ Define $\beta = \left( \frac{L_2}{L_m}+\frac{4\bar{\gamma }}{\mu ^2}\right) L D$. Then combining (40) and (39) yields that

$$\begin{aligned} \begin{array}{ll} \Vert F(z^{k+1})\Vert &{} \le (1-\alpha )\Vert F(z^k)\Vert +\beta (\Vert F(z^k)\Vert -\Vert F(z^{k+1})\Vert ), \\ \end{array} \end{aligned}$$

which results in:

$$\begin{aligned} \Vert F(z^{k+1})\Vert \le \frac{(1-\alpha )+\beta }{1+\beta }\Vert F(z^k)\Vert =\left( 1-\frac{\alpha }{1+\beta }\right) \Vert F(z^k)\Vert . \end{aligned}$$

(41)

Squaring both sides of (41) and dividing by half, we get the desired bound

$$\begin{aligned} m(z^{k+1})\le \Big (1-\frac{\alpha }{1+\beta }\Big )^2m(z^k). \end{aligned}$$

Finally, taking $\bar{\gamma }= \frac{L_2\mu ^2}{4L_m}$, we have $\beta =\left( \frac{L_2}{L_m}+\frac{4\bar{\gamma }}{\mu ^2}\right) L D=\frac{2L_2L D}{L_m}=\frac{2L_2LD}{L^2+L_2LD}\le 2$, which further yields

$$\begin{aligned} m(z^{k+1})\le \Big (1-\frac{\alpha }{3}\Big )^2m(z^k)=\left( 1-\frac{\mu ^2}{6L_m}\right) ^2m(z^k). \end{aligned}$$

$\square$

1.4 A.4 Proof of Lemma 5.1

Let $x_t=(M+tI_m)^{-1}b$ for some $t>0$. Suppose $r=\text{ rank } (M)$. If $r=m$ (namely M is invertible) then the lemma holds true trivially, by noting that $(M+tI_m)^{-1}=M^{-1}+{\mathcal {O}}(t)$ and $\Vert x_t-x_s\Vert =\Vert {\mathcal {O}}(t)b-{\mathcal {O}}(s)b\Vert ={\mathcal {O}}(|s-t|)$ for small $s,t>0$. Now, suppose $r<m$, we shall show the same holds by establishing the dependency on t for $x_t$. Let a singular value decomposition of M be

$$\begin{aligned} M=U^\top \varLambda V, \text{ where } \varLambda =\left( \begin{array}{cc} \varLambda _r &{} 0_{r\times (m-r)} \\ 0_{(m-r)\times r} &{} 0_{(m-r)\times (m-r)} \end{array}\right) , \end{aligned}$$

with $\varLambda _r$ being an $r\times r$ diagonal positive, and U and V are orthonormal matrices. The pseudo-inverse of M is $M^+=V^\top \varLambda ^+ U$, where $\varLambda ^+=\left( \begin{array}{cc} \varLambda _r^{-1} &{} 0_{r\times (m-r)} \\ 0_{(m-r)\times r} &{} 0_{(m-r)\times (m-r)} \end{array}\right)$. According to the theory of pseudo-inverse matrices (cf. [4]), $L_0=\{x: Mx=b\}\not =\emptyset$ if and only if $b=MM^+b$, or equivalently, the last $m-r$ elements of Ub are zero; that is, $U b=\left( \begin{array}{c} {\bar{b}}_r \\ 0_{m-r} \end{array}\right)$.

Now, let $G=UV^\top$, which is also orthonormal, and introduce

$$\begin{aligned} x_t:= & {} (M+t I)^{-1} b = (U^\top \varLambda V + t I)^{-1} b = V^\top (\varLambda + t G )^{-1} U b \\= & {} V^\top \left( \begin{array}{cc} \varLambda _r + t G_{11} &{} t G_{12} \\ t G_{21} &{} t G_{22} \end{array}\right) ^{-1} U b. \end{aligned}$$

In fact, observe that $G_{22}$ is invertible. To see this, let us first examine the order of t in $\det (M+tI_m)$. Note that $\det (M+tI_m)$ is exactly the characteristic polynomial of the matrix $-M$ (which has eigenvalues of opposite sign of M). Therefore, it can be written in the expression $\prod \limits _{i=1}^r(t+\sigma _i)t^{m-r}$ for a rank-r matrix M with non-zero eigenvalues $\sigma _i$, $i=1,...,r$. Therefore, the dominant order of t in $\det (M+tI_m)$ as $t\rightarrow 0$ is ${\mathcal {O}}(t^{m-r})$. However, if $G_{22}$ would be degenerate, then we can alternatively express the determinant as:

$$\begin{aligned} \det \left( \begin{array}{cc} \varLambda _r + t G_{11} &{} t G_{12} \\ t G_{21} &{} t G_{22} \end{array}\right) = \det (\varLambda _r + t G_{11}) \cdot \det \left( G_{22} - t G_{21} ( \varLambda _r + t G_{11})^{-1} G_{12} \right) \cdot t^{m-r}. \end{aligned}$$

We can see that the middle term is at least O(t), since if it is of constant order, then the value converges to $\det (G_{22})=0$ as $t\rightarrow 0$, which is already a contradiction. Therefore, the above expression concludes that $\det (M+tI_m)$ is at least of the order $O(t^{m-r+1})$ for sufficiently small $t>0$, which is a contradiction to the earlier conclusion. Therefore, $G_{22}$ must be invertible.

In general, consider a $2\times 2$ invertible block matrix $\left( \begin{array}{cc} A &{} B \\ C &{} D \end{array}\right)$, where A and its Schur complement $D-CA^{-1}B$ are invertible. Then (see [13]),

$$\begin{aligned}&\left( \begin{array}{cc} A &{} B \\ C &{} D \end{array}\right) ^{-1} \\&\quad = \left( \begin{array}{cc} A^{-1}+A^{-1}B(D-CA^{-1}B)^{-1}CA^{-1} &{} -A^{-1}B(D-CA^{-1}B)^{-1} \\ -(D-CA^{-1}B)^{-1}CA^{-1} &{} (D-CA^{-1}B)^{-1} \end{array}\right) . \end{aligned}$$

Substituting $A=\varLambda _r + t G_{11}$, $B=t G_{12}$, $C=t G_{21}$ and $D=t G_{22}$ into the above expression, we have

$$\begin{aligned} \left( \begin{array}{cc} \varLambda _r + t G_{11} &{} t G_{12} \\ t G_{21} &{} t G_{22} \end{array}\right) ^{-1} =\left( \begin{array}{cc} \varLambda _r^{-1} + O(t) &{} -\varLambda _r^{-1} G_{12} G_{22}^{-1} + O(t) \\ -G_{22}^{-1} G_{21} \varLambda _r^{-1} + O(t) &{} G_{22}^{-1}/t + O(t) \end{array}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} x_t = V^\top \left( \begin{array}{c} \varLambda _r^{-1} {\bar{b}} + O(t) \\ -G_{22}^{-1} G_{21} \varLambda _r^{-1} {\bar{b}} + O(t) \end{array}\right) . \end{aligned}$$

Since $L_0=\{x: Mx=b\}\not =\emptyset$, it follows that $M^+b \in L_0$. Let $x_0:=M^+b = V^\top \left( \begin{array}{c} \varLambda _r^{-1} {\bar{b}} \\ -\varLambda _r^{-1} G_{12} G_{22}^{-1} {\bar{b}} \end{array}\right) \in L_0$, we have $\Vert x_t - x_0\Vert =O(t)$. By the smoothness of the curve $\{x_t: 0<t<\delta \}$, we actually have $\Vert x_t-x_s\Vert =O(|t-s|)$ for sufficiently small positive t and s. $\square$

1.5 A.5 Proof of Lemma 5.6

First of all, note that since $0<\lambda _k<1$, the sequence $\{\nu _k\}$ is strictly decreasing. Let us first assume $\nu _0>1$. Then for $k<K$ such that $\nu _k>1$, we can take $\lambda _k=\lambda$ as a constant:

$$\begin{aligned} \lambda = \left( \frac{1}{4L_2C+2}\right) ^{\frac{1}{\theta }}\le \left( \frac{\nu _k^{1-\theta }}{4L_2C+2\nu _k^{1-\theta }}\right) ^{\frac{1}{\theta }}. \end{aligned}$$

The above inequality can be verified by taking reciprocal on both sides and noting that $\nu _k^{1-\theta }>1$. Indeed, for $K>(4L_2C+2)^{\frac{1}{\theta }}\cdot \ln \nu _0$, we have $\nu _K = (1-\lambda )^K\nu _0\le \exp (-K\lambda )\nu _0<1$.

Let us now focus on the case when $\nu _k<1$. Without loss of generality, take $\lambda _k$ as its upper bound in (24). Therefore we have

$$\begin{aligned} \nu _{k+1}=\left( 1-\left( \frac{\nu _k^{1-\theta }}{4L_2C+2\nu _k^{1-\theta }}\right) ^{\frac{1}{\theta }}\right) \nu _k=\nu _k-\frac{\nu _k^{\frac{1}{\theta }}}{(4L_2C+2\nu _k^{1-\theta })^{\frac{1}{\theta }}}\le \nu _k-\xi \cdot \nu _k^{\frac{1}{\theta }}, \end{aligned}$$

where $\xi <1$ is a constant defined as

$$\begin{aligned} \frac{1}{\xi }:=(4L_2C+2)^{\frac{1}{\theta }}\ge (4L_2C+2\nu _k^{1-\theta })^{\frac{1}{\theta }}, \end{aligned}$$

for $\nu _k<1$.

Therefore, to establish the convergence of $\{\nu _k\}$, we could instead establish the convergence of the following sequence:

$$\begin{aligned} a_0<1,\quad a_{k+1}=a_k-\xi \cdot a_k^{\frac{1}{\theta }}, \end{aligned}$$

(42)

for $\theta \in (0,1)$.

The remaining part of this proof follows from the proof of Theorem 1 in [20].

Let us first note that the function $f(x)=\frac{1}{(1+x)^p}$ is convex for $x\ge -1$ and $p>0$. Therefore, for $x\ge -1$, we have $f(x)=\frac{1}{(1+x)^p}\ge f(0)+f'(0)x=1-px$. Taking $p=\frac{1-\theta }{\theta }>0$ and $x=\frac{a_{k+1}-a_k}{a_k}>-1$, we obtain

$$\begin{aligned} \left( \frac{a_k}{a_{k+1}}\right) ^{\frac{1-\theta }{\theta }}=\frac{1}{\left( 1+\frac{a_{k+1}-a_k}{a_k}\right) ^{\frac{1-\theta }{\theta }}}\ge 1-\frac{1-\theta }{\theta }\cdot \frac{a_{k+1}-a_k}{a_k}. \end{aligned}$$

(43)

Then

$$\begin{aligned} a_{k+1}^{\frac{\theta -1}{\theta }}-a_{k}^{\frac{\theta -1}{\theta }}=a_{k}^{\frac{\theta -1}{\theta }}\left( \frac{a_{k+1}^{\frac{\theta -1}{\theta }}}{a_{k}^{\frac{\theta -1}{\theta }}}-1\right) \overset{(43)}{\ge }\frac{1-\theta }{\theta }\cdot \frac{a_k-a_{k+1}}{a_k^{\frac{1}{\theta }}}\overset{(42)}{=} \frac{1-\theta }{\theta }\cdot \xi . \end{aligned}$$

Summing up the above inequality from $a_0$ to $a_k$, we have

$$\begin{aligned} a_k^{\frac{\theta -1}{\theta }}\ge a_0^{\frac{\theta -1}{\theta }}+\frac{1-\theta }{\theta }\cdot k\xi \ge 1+\frac{1-\theta }{\theta }\cdot k\xi . \end{aligned}$$

Therefore, $a_k\le \left( \frac{1}{1+\frac{1-\theta }{\theta }\cdot k\xi }\right) ^{\frac{\theta }{1-\theta }}$. By the definition of $C'$ in Lemma 5.6, we obtain $\nu _k\le \left( \frac{1}{1+C'\cdot k}\right) ^{\frac{\theta }{1-\theta }}$, for all k such that $\nu _k<1$. $\square$