Low-CP-Rank Tensor Completion via Practical Regularization

Abstract

Dimension reduction is analytical methods for reconstructing high-order tensors that the intrinsic rank of these tensor data is relatively much smaller than the dimension of the ambient measurement space. Typically, this is the case for most real world datasets in signals, images and machine learning. The CANDECOMP/PARAFAC (CP, aka Canonical Polyadic) tensor completion is a widely used approach to find a low-rank approximation for a given tensor. In the tensor model (Sanogo and Navasca in 2018 52nd Asilomar conference on signals, systems, and computers, pp 845–849, https://doi.org/10.1109/ACSSC.2018.8645405, 2018), a sparse regularization minimization problem via $\ell _1$ norm was formulated with an appropriate choice of the regularization parameter. The choice of the regularization parameter is important in the approximation accuracy. Due to the emergence of the massive data, one is faced with an onerous computational burden for computing the regularization parameter via classical approaches (Gazzola and Sabaté Landman in GAMM-Mitteilungen 43:e202000017, 2020) such as the weighted generalized cross validation (WGCV) (Chung et al. in Electr Trans Numer Anal 28:2008, 2008), the unbiased predictive risk estimator (Stein in Ann Stat 9:1135–1151, 1981; Vogel in Computational methods for inverse problems, 2002), and the discrepancy principle (Morozov in Doklady Akademii Nauk, Russian Academy of Sciences, pp 510–512, 1966). In order to improve the efficiency of choosing the regularization parameter and leverage the accuracy of the CP tensor, we propose a new algorithm for tensor completion by embedding the flexible hybrid method (Gazzola in Flexible krylov methods for lp regularization) into the framework of the CP tensor. The main benefits of this method include incorporating the regularization automatically and efficiently as well as improving accuracy in the reconstruction and algorithmic robustness. Numerical examples from image reconstruction and model order reduction demonstrate the efficacy of the proposed algorithm.

1 Introduction

Tensor computations have become prevalent in across many fields in mathematics [16, 28], computer science [9, 22, 35], engineering [14] and data science [1, 27]. In particular, tensor methods are now ubiquitous in areas of numerical linear algebra [6, 7], imaging sciences [21, 55] and applied algebraic geometry [29]. In addition, tensor based methods are gaining grounds in solving complex problems in scientific computing. [11].

The tensor rank problem is crucial in reconstructing a given tensor ${\mathcal {T}}$. The rank of tensor is defined as the minimum number R of the summands in a sum of rank-one tensor product, $\sum ^{R}_{r = 1} \alpha _r{\mathbf {a}}_{r} \otimes {\mathbf {b}}_{r} \otimes {\mathbf {c}}_{r}$. In practice, the column vectors, ${\mathbf {a}}_{r}$, ${\mathbf {b}}_{r}$ and ${\mathbf {c}}_{r}$, are concatenated into what we call factor matrices, ${\mathbf {A}}$, ${\mathbf {B}}$ and ${\mathbf {C}}$. The elements of the vector $\alpha$ of size R are the scalings of the rank-one tensors. This tensor factorization is the well-known canonical polyadic or CANDECOMP/PARAFAC (CP) decomposition. Optimization techniques, namely the multi-block alternating methods are standard methods for finding the factor matrices of a given tensor and its rank.

A tensor model [45] which incorporates tensor rank approximation is

$$\begin{aligned} \min _{A,B,C,{{\alpha }}} \left\| {\mathcal {T}} - {\mathcal {S}} \right\| _F + \lambda \Vert {\alpha } \Vert _{\ell _1}, \end{aligned}$$

where $\lambda$ is a regularization parameter and ${\mathcal {S}} = \sum ^{U}_{r=1} \alpha _r {\mathbf {a}}_{r} \otimes {\mathbf {b}}_{r} \otimes {\mathbf {c}}_{r}$ with an upper bound tensor rank R. This sparse optimization problem is solved iteratively and the vector $\alpha$ reveals an approximated tensor rank R where $R<< U$. The main drawback of this model is that the accuracy of the computational results highly relies on an appropriate value of the regularization parameter $\lambda$. In [54], the choice of the regularization parameter is tied to two intrinsic parameters: variance of noise and incoherence of the given tensor data ${\mathcal {T}}$. One has to initialize $\lambda$ from a bound based on these two parameters from the tensor data with an upper bound rank R. In practice, a priori estimates of the variance and incoherence parameters are required based on a CP decomposition of the given data with an initial tensor rank guess R. Then $\lambda$ can be chosen accordingly from an estimated bound. The advantage of this approach is that it provides a theoretical bound for $\lambda$. However, it is not practical enough for real data implementation; the choice of $\lambda$ is only as good as the estimated intrinsic parameter. Moreover, the accuracy level is only around $10^{-2}$. In this paper, we present a more adaptive, practical and methodical way for calculating the regularization parameter $\lambda$ using the flexible hybrid method, which is tailored for the use in the canonical CP tensor framework. The flexible hybrid method is capable of computing the regularized solutions to large-scale linear inverse problems more efficiently than classical approaches [20], since the original regularized problem is iteratively projected onto small subspaces of increasing dimension and the regularization parameter $\lambda$ is estimated by implementing the standard regularization techniques, such as weighted generalized cross validation (WGCV) [15], unbiased predictive risk estimator [48, 51], and discrepancy principle [36], on the projected problem at each iteration. Our numerical results show that this new iterativedt8;333 ‘method gives more accurate results in tensor completion and model order reduction problems.

We have two application areas in this paper: tensor completion in image restoration and model order reduction. Matrix and tensor completion techniques provide major tools in recommender systems in computer science and in general in data science; it is about filling in missing entries from the partially observed entries of the matrix or tensor. The success of matrix completion methods are attributed to sparse optimization methods in compressed sensing [13]. These methods have been generalized iteratively to tensor completion problem [33] via Tucker models [4, 52] where missing entries are predicted through the matrix trace norm optimization. In fact, the tensor completion problem dates back as early as in 2000. Bro [12] had one of the earliest work on demonstrating two ways to handle missing data using CP. The first one is to estimate the model parameters iteratively while imputing the missing data. Another approach called Missing-Skipping skips the missing value and builds up the model based only on the observed part via a weighted least squares formulation in the CP format [2]. Our proposed tensor completion gives more accurate results in capturing more features in color images through low rank construction via our model and numerical technique.

Furthermore, we show that recent effort in tensor-based model reduction such as Randomized CP tensor decomposition [17] and tensor POD [56] have been rewarded with many promising developments leverage the computational effort for many-query computations and repeated output evaluations for different values of some inputs of interest where classical model order reduction approaches [38, 39] such as Reduced Basis Methods [8, 44] and Proper Orthogonal Decomposition (POD) faced with heavy computational burden. Compared with the classical model order reduction approaches, tensor-based model reduction algorithms allow us to achieve significant computational savings, especially for expensive high fidelity numerical solvers.

The paper is organized as follows. In Sect. 2, we provide some tensor backgrounds and basic tensor decomposition. Then, Sect. 3 deals with the derivations of the iterative equation by alternating block optimization containing the unfolding of the tensors in each mode. The proximal gradient formulation and the flexible hybrid method for the automatic selection of the regularization parameter are discussed. Experimental results are in Sect. 4, and the conclusions follow in Sect. 5.

2 Preliminaries

We denote a vector by a bold lower-case letter ${\mathbf {a}}$. The bold upper-case letter ${\mathbf {A}}$ represents a matrix and the symbol of tensor is a calligraphic letter ${\mathcal {A}}$. Throughout this paper, we focus on third-order tensors ${\mathcal {A}}=(a_{ijk})\in {{\mathbb {R}}}^{I\times J\times K}$ of three indices $1\le i\le I,1\le j\le J$ and $1\le k\le K$, but all are applicable to tensors of arbitrary order greater or equal to three.

A third-order tensor ${\mathcal {A}}$ has column, row and tube fibers, which are defined by fixing every index but one and denoted by ${\mathbf {a}}_{:jk}$, ${\mathbf {a}}_{i:k}$ and ${\mathbf {a}}_{ij:}$ respectively. Correspondingly, we can obtain three kinds ${\mathbf {A}}_{(1)},{\mathbf {A}}_{(2)}$ and ${\mathbf {A}}_{(3)}$ of matricization of ${\mathcal {A}}$ according to respectively arranging the column, row, and tube fibers to be columns of matrices. We can also consider the vectorization for ${\mathcal {A}}$ to obtain a row vector ${\mathbf {a}}$ such the elements of ${\mathcal {A}}$ are arranged according to k varying faster than j and j varying faster than i, i.e., ${\mathbf {a}}=(a_{111},\ldots ,a_{11K},a_{121},\ldots ,a_{12K},\ldots ,a_{1J1},\ldots ,a_{1JK},\ldots )$.

Henceforth, the outer product of a rank-one third order tensor is denoted as ${\mathbf {x}}\circ {\mathbf {y}}\circ {\mathbf {z}}\in {{\mathbb {R}}}^{I\times J\times K}$ of three nonzero vectors ${\mathbf {x}}, {\mathbf {y}}$ and ${\mathbf {z}}$ is a rank-one tensor with elements $x_iy_jz_k$ for all the indices. A canonical polyadic decomposition of ${\mathcal {A}}\in {{\mathbb {R}}}^{I\times J\times K}$ expresses ${\mathcal {A}}$ as a sum of rank-one outer products:

$$\begin{aligned} {\mathcal {A}}=\sum _{r=1}^{R} {\mathbf {x}}_r\circ {\mathbf {y}}_r\circ {\mathbf {z}}_r \end{aligned}$$

(2.1)

where ${\mathbf {x}}_r\in {{\mathbb {R}}}^I,{\mathbf {y}}_r\in {{\mathbb {R}}}^J,{\mathbf {z}}_r\in {{\mathbb {R}}}^K$ for $1\le r\le R$. Every outer product ${\mathbf {x}}_r\circ {\mathbf {y}}_r\circ {\mathbf {z}}_r$ is called as a rank-one component and the integer R is the number of rank-one components in tensor ${\mathcal {A}}$. The minimal number R such that the decomposition (2.1) holds is the rank of tensor ${\mathcal {A}}$, which is denoted by $\text{ rank }({\mathcal {A}})$. For any tensor ${\mathcal {A}}\in {{\mathbb {R}}}^{I\times J\times K}$, $\text{ rank }({\mathcal {A}})$ has an upper bound $\min \{IJ,JK,IK\}$ [30].

In this paper, we consider CP decomposition in the following form

$$\begin{aligned} {\mathcal {T}}=\sum _{r=1}^{R} \alpha _r{\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r \end{aligned}$$

(2.2)

where $\alpha _r\in {{\mathbb {R}}}$ is a rescaling coefficient of rank-one tensor ${\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r$ for $r=1,\ldots ,R$. For convenience, we let ${\alpha }=(\alpha _1,\ldots ,\alpha _R)\in {{\mathbb {R}}}^R$ and denote $[{\alpha };{\mathbf {A}},{\mathbf {B}},{\mathbf {C}}]_R = \sum _{r=1}^{R} \alpha _r{\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r$ in (2.2) where ${\mathbf {A}}=({\mathbf {a}}_1,\ldots ,{\mathbf {a}}_R)\in {{\mathbb {R}}}^{I\times R},{\mathbf {B}}=({\mathbf {b}}_1,\ldots ,{\mathbf {b}}_R)\in {{\mathbb {R}}}^{J\times R}$ and ${\mathbf {C}}=({\mathbf {c}}_1,\ldots ,{\mathbf {c}}_R)\in {{\mathbb {R}}}^{K\times R}$ are called the factor matrices of tensor ${\mathcal {A}}$.

In most iterative techniques for tensor decompositions, the high order tensor matricizations are transformed from tensor equations into matrix equations via the standard unfolding mechanishm. Here we describe a standard approach for a matricizing of a tensor. The Khatri-Rao product [47] of two matrices $X\in {{\mathbb {R}}}^{I\times R}$ and $Y \in {{\mathbb {R}}}^{J\times R}$ is defined as

$$\begin{aligned} {X\odot Y}=({x}_1\otimes {y}_1,\ldots , {x}_R \otimes {y}_R)\in {R}^{IJ\times R}, \end{aligned}$$

where the symbol “${\otimes }$” denotes the Kronecker product:

$$\begin{aligned} {x\otimes y}=(x_1y_1,\ldots ,x_1y_J,\ldots ,x_Iy_1,\ldots ,x_Iy_J)^T. \end{aligned}$$

Using the Khatri-Rao product, the CP model (2.2) can be written in three equivalent matrix equations:

$$\begin{aligned} {\mathbf {T}}_{(1)}&= \mathbf {A{Diag}}(\mathbf {C\odot B})^T, \end{aligned}$$

(2.3a)

$$\begin{aligned} {\mathbf {T}}_{(2)}&=\mathbf {B{Diag}}(\mathbf {C\odot A})^T, \end{aligned}$$

(2.3b)

$$\begin{aligned}&\text{ and } \nonumber \\ {\mathbf {T}}_{(3)}&=\mathbf {C{Diag}}(\mathbf {B\odot A})^T \end{aligned}$$

(2.3c)

where $\mathbf {{Diag}}$ is a diagonal matrix, where the diagonal entries are the elements of ${\alpha }$. To achieve CP decomposition of given tensor ${\mathcal {T}}$ with a known tensor rank R and an assumption that ${\mathbf {D}}={\mathbf {I}}$, the matrix equations Eqs. (2.3a)–(2.3c) are formulated into linear least-squares subproblems to solve iteratively for ${\mathbf {A}}$, ${\mathbf {B}}$ and ${\mathbf {C}}$, respectively. Here are the linear least-squares subproblems:

$$\begin{aligned}&\min \limits _{{\mathbf {A}}}\Vert {\mathbf {T}}_{(1)} - \mathbf {A{Diag}}(\mathbf {C\odot B})^T \Vert _F^2 , \end{aligned}$$

(2.4a)

$$\begin{aligned}&\min \limits _{{\mathbf {B}}} \Vert {\mathbf {T}}_{(2)} - \mathbf {B{Diag}}(\mathbf {C\odot A})^T \Vert _F^2, \end{aligned}$$

(2.4b)

$$\begin{aligned}&\text{ and } \nonumber \\&\min \limits _{{\mathbf {C}}} \Vert {\mathbf {T}}_{(3)} - \mathbf {C{Diag}}(\mathbf {B\odot A})^T \Vert _F^2. \end{aligned}$$

(2.4c)

This technique is the well known Alternating Least-Squares (ALS) [12, 31]. Typically, a normalization constraint on factor matrices such that each column is normalized to length one [3, 50] is required for convergence, which we denote by $\mathbf {N(A,B,C)}=1$.

3 Iterative Equations for Tensor Completion

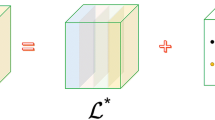
We will describe our low rank tensor model of a given tensor in a CP format with an approximated tensor rank for tensor completion. Our goal is to fill in the missing entries from a given tensor ${\mathcal {T}}$ with the partially observed entries by reconstructing a completed low rank tensor ${\mathcal {S}}$. To do so, we formulate a sparse optimization problem [45] for recovering CP decomposition from tensor ${\mathcal {T}} \in {{\mathbb {R}}}^{I \times J \times K}$ with partially observed entries on the index set $\Omega$:

$$\begin{aligned}&\min _{A,B,C,{\alpha }} \left\| {\mathcal {T}} - {\mathcal {S}} \right\| _F + \lambda \Vert \alpha \Vert _{\ell _1} \nonumber \\&\text{ subject } \text{ to } {\mathcal {S}}(\Omega )={\mathcal {T}}(\Omega ) \end{aligned}$$

(3.1a)

where $\lambda$ is a constant regularization parameter and ${\mathcal {S}}= \sum _r {\alpha _r} {\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r$.

We will now derive the iterative equations for A, B, C and $\alpha$. The equations are typically associated with Iterative Soft Thresholding Algorithm (ISTA) [5] whose derivation is based on the Majorization-Minimization (MM) [18] method. ISTA (Iterative Soft-Thresholding Algorithm) is a combination of the Landweber algorithm and soft-thresholding (so it is also called the thresholded-Landweber algorithm).

Suppose we have a minimization problem:

$$\begin{aligned} \min \limits _{{x}} f(x). \end{aligned}$$

(3.2)

By using the proximal operators formulation (see Appendix) and the MM approach, we first find an upper bound for f(x):

$$\begin{aligned} f(x) \le f(y) + \langle \nabla _x f(y) , x-y \rangle + \gamma \Vert x - y \Vert ^2_2 \end{aligned}$$

Let $g(x,y)=f(y) + \langle \nabla _x f(y) , x-y \rangle + \gamma \Vert x - y \Vert ^2_2$. Note that $f(x) \le g(x,y)$ for all x and $f(x) = g(x,y)$ when $y=x$. Thus, we can reformulate 3.2 as

$$\begin{aligned} \min \limits _{{x}} f(y) + \langle \nabla _x f(y) , x-y \rangle + \gamma \Vert x - y \Vert ^2_2. \end{aligned}$$

(3.3)

Since this is a minimization over x, then 3.3 is equivalent to

$$\begin{aligned} \min \limits _{{x}} \langle \nabla _x f(y) , x-y \rangle + \gamma \Vert x - y \Vert ^2_2. \end{aligned}$$

(3.4)

By gathering the terms with respect to x, the objective function in 3.4 can be expressed as

$$\begin{aligned} \gamma (-2b^Tx + x^Tx) + c, \end{aligned}$$

where $c=\gamma (y)^Ty - {\nabla _x} f(y)^Ty$ and $b = y - \frac{1}{2 \gamma } \nabla _x f(y)$. Since $b^Tb - 2b^Tx + x^Tx= \Vert b -x \Vert ^2_2$, we have a new formulation:

$$\begin{aligned} \min \limits _{{x}} \gamma \Vert x - b \Vert _2^2. \end{aligned}$$

(3.5)

Now from the least-squares problems (2.4a–2.4c) and using proximal gradient formulation, we have the following new formulations:

$$\begin{aligned} \begin{aligned} {\mathbf {A}}^*=&\arg \min \limits _{{\mathbf {A}}} \{\langle {\mathbf {A}}-{\mathbf {A}}^n,\nabla _{\mathbf {A}} f({\mathbf {A}}^n,{\mathbf {B}}^n,{\mathbf {C}}^n,{\alpha }^n)\rangle +\frac{sd_n}{2}\Vert {\mathbf {A}}-{\mathbf {A}}^n\Vert _F^2\}&\\&\quad \text{ s.t. }\ \Vert {\mathbf {a}}_i\Vert =1, i=1,\ldots ,R,&\\ {\mathbf {B}}^*=&\arg \min \limits _{{\mathbf {B}}} \{\langle {\mathbf {B}}-{\mathbf {B}}^n,\nabla _{\mathbf {B}} f({\mathbf {A}}^{n+1},{\mathbf {B}}^n,{\mathbf {C}}^n,{\alpha }^n)\rangle +\frac{se_n}{2}\Vert {\mathbf {B}}-{\mathbf {B}}^n\Vert _F^2\}&\\&\quad \text{ s.t. }\ \Vert {\mathbf {b}}_i\Vert =1, i=1,\ldots ,R,&\end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\mathbf {C}}^*=&\arg \min \limits _{{\mathbf {C}}} \{\langle {\mathbf {C}}-{\mathbf {C}}^n,\nabla _{\mathbf {C}} f({\mathbf {A}}^{n+1},{\mathbf {B}}^{n+1},{\mathbf {C}}^n,{\alpha }^n)\rangle +\frac{sf_n}{2}\Vert {\mathbf {C}}-{\mathbf {C}}^n\Vert _F^2\}&\\&\quad \text{ s.t. }\ \Vert {\mathbf {c}}_i\Vert =1, i=1,\ldots ,R,&\end{aligned} \end{aligned}$$

where $d_n=\max \{\Vert {\mathbf {U}}^n{{\mathbf {U}}^n}^T\Vert _F,1\}$, $e_n=\max \{\Vert {\mathbf {V}}^n{{\mathbf {V}}^n}^T\Vert _F,1\}$ and $f_n=\max \{\Vert {\mathbf {W}}^n{{\mathbf {W}}^n}^T\Vert _F,1\}$ with

$$\begin{aligned} {\mathbf {U}}=\mathbf {{Diag}} ({\mathbf {C}} \odot {\mathbf {B}})^T, {\mathbf {V}}=\mathbf {{Diag}}({\mathbf {C}} \odot {\mathbf {A}}^T), {\mathbf {W}}=\mathbf {{Diag}}({\mathbf {B}} \odot {\mathbf {A}})^T. \end{aligned}$$

(3.6)

The gradients of $f(\mathbf {A,B,C},{\alpha })=\frac{1}{2} \Vert {\mathcal {T}} - {\sum ^R_{r=1} \alpha _r} {\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r \Vert _F^2$ on $\mathbf {A,B,C}$ are the following in terms of the Khatri-Rao product via matricizations:

$$\begin{aligned} \nabla _{\mathbf {A}} f(\mathbf {A,B,C,}{\alpha })&=(\mathbf {A{Diag}}(\mathbf {C\odot B}) - {\mathbf {T}}_{(1)}) (\mathbf {C\odot B})^T \mathbf {{Diag}}^T , \end{aligned}$$

(3.7a)

$$\begin{aligned} \nabla _{\mathbf {B}} f(\mathbf {A,B,C,}{\alpha })&=(\mathbf {B{Diag}}(\mathbf {C\odot A})-{\mathbf {T}}_{(2)}) (\mathbf {C\odot A})^T\mathbf {{Diag}}^T, \end{aligned}$$

(3.7b)

$$\begin{aligned}&\text{ and } \nonumber \\ \nabla _{\mathbf {C}} f(\mathbf {A,B,C,}{\alpha })&=(\mathbf {C{Diag}}(\mathbf {B\odot A})-{\mathbf {T}}_{(3)}) (\mathbf {B\odot A})^T\mathbf {{Diag}}^T. \end{aligned}$$

(3.7c)

The gradient of $f(\mathbf {A,B,C},{\alpha })$ on $\alpha$ is described in Sect. 3.1. Based from the calculations (3.3–3.5), we obtain the following iterative formula for A:

$$\begin{aligned} \arg \min \limits _{{\mathbf {A}}} \{\Vert {\mathbf {A}}-{\mathbf {D}}^n\Vert _F^2\} \quad \text{ s.t. }\ \Vert {\mathbf {a}}_i\Vert =1, i=1,\ldots ,R. \end{aligned}$$

where ${\mathbf {D}}^n={\mathbf {A}}^n-\frac{1}{sd_n}\nabla _{\mathbf {A}} f({\mathbf {A}}^n,{\mathbf {B}}^n,{\mathbf {C}}^n,{\alpha }^n)$. We can break it further component-wise:

$$\begin{aligned} {\mathbf {a}}_i^{n+1}={\mathbf {d}}_i^n/\Vert {\mathbf {d}}_i^n\Vert , i=1,\ldots ,R, \end{aligned}$$

where ${\mathbf {a}}_i^{n+1}$ and ${\mathbf {d}}_i^n$ are the i-th columns of ${\mathbf {A}}^{n+1}$ and ${\mathbf {D}}^n$.

Similarly, the update of ${\mathbf {B}}$ is

$$\begin{aligned} \arg \min \limits _{{\mathbf {Y}}} \{\Vert {\mathbf {B}}-{\mathbf {E}}^n\Vert _F^2\} \quad \text{ s.t. }\ \Vert {\mathbf {b}}_i\Vert =1, i=1,\ldots ,R. \end{aligned}$$

where ${\mathbf {E}}^n={\mathbf {B}}^n-\frac{1}{se_n}\nabla _{\mathbf {B}} f({\mathbf {A}}^{n+1},{\mathbf {B}}^n,{\mathbf {C}}^n,{\alpha }^n)$. Column-wise, we have

$$\begin{aligned} {\mathbf {b}}_i^{n+1}={\mathbf {e}}_i^n/\Vert {\mathbf {e}}_i^n\Vert , i=1,\ldots ,R, \end{aligned}$$

where ${\mathbf {b}}_i^{n+1}$ and ${\mathbf {e}}_i^n$ are the i-th columns of ${\mathbf {B}}^{n+1}$ and ${\mathbf {E}}^n$.

Furthermore, the update of ${\mathbf {C}}$ is

$$\begin{aligned} \arg \min \limits _{{\mathbf {C}}} \{\Vert {\mathbf {C}}-{\mathbf {F}}^n\Vert _F^2\} \quad \text{ s.t. }\ \Vert {\mathbf {c}}_i\Vert =1, i=1,\ldots ,R. \end{aligned}$$

where ${\mathbf {F}}^n={\mathbf {C}}^n-\frac{1}{sf_n}\nabla _{\mathbf {C}} f({\mathbf {A}}^{n+1},{\mathbf {B}}^{n+1},{\mathbf {C}}^n,{\alpha }^n)$. Also, we update vector-wise:

$$\begin{aligned} {\mathbf {c}}_i^{n+1}={\mathbf {f}}_i^n/\Vert {\mathbf {f}}_i^n\Vert , i=1,\ldots ,R, \end{aligned}$$

where ${\mathbf {c}}_i^{n+1}$ and ${\mathbf {f}}_i^n$ are the i-th columns of ${\mathbf {C}}^{n+1}$ and ${\mathbf {F}}^n$.

3.1 Iterative Equation for $\alpha$

Using the vectorization of tensors in Sect. 2, we can vectorize every rank-one tensor of outer product ${\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r$ into a row vector ${\mathbf {q}}_r$ for $1\le r\le R$. We denote a matrix consisting of all ${\mathbf {q}}_r$ for $1\le r\le R$ by

$$\begin{aligned} {\mathbf {Q}}=({\mathbf {q}}_1^T,\ldots ,{\mathbf {q}}_R^T)^T. \end{aligned}$$

(3.8)

Thus the function $\frac{1}{2} \Vert {\mathcal {T}} - {\sum ^R_{r=1} \alpha _r} {\mathbf {a}}_r\circ {\mathbf {b}}_r\circ {\mathbf {c}}_r \Vert _F^2$ can be also written as $\frac{1}{2}\Vert {\mathbf {t}}-{\alpha {{\mathbf {Q}}}}\Vert _F^2$ where ${\mathbf {t}}$ is a vectorization for tensor ${\mathcal {T}}$. Also, the gradient of $f(\bullet )$ on $\mathbf {A,B,C,\alpha }$ is the following in terms of the Khatri-Rao product via matricizations:

$$\begin{aligned} \nabla _{\alpha } f(\mathbf {A,B,C,}{\alpha })=({\alpha }{\mathbf {Q}}-{\mathbf {t}}){\mathbf {Q}}^T. \end{aligned}$$

Then, the minimization problem for $\alpha$ is

$$\begin{aligned} \min \limits _{\alpha } \frac{1}{2} \Vert {\mathbf {t}}-{\alpha {\mathbf {Q}}}\Vert _F^2 + \lambda \Vert \alpha \Vert _1. \end{aligned}$$

(3.9)

Efficiently and appropriately choosing the regularization parameter $\lambda$ plays a crucial role in solving (3.9). In the papers [53, 54], the proximal operators formulation (see Appendix) and the MM approach are used to solve $\alpha$ iteratively via

$$\begin{aligned} \alpha ^{n+1}= \arg \min \limits _{{\alpha }} \{\langle {\alpha }-{\alpha }^n,\nabla _{{\alpha }} f({\mathbf {A}}^{n+1},{\mathbf {B}}^{n+1},{\mathbf {C}}^{n+1},{\alpha }^n)\rangle +\frac{s\eta _n}{2}\Vert {\alpha }-{\alpha }^n\Vert ^2+\lambda \Vert {\alpha }\Vert _1\}. \end{aligned}$$

which is equivalent to the following:

$$\begin{aligned} \alpha ^{n+1}=\arg \min \limits _{{\alpha }} \frac{1}{2} \left\| {\alpha }-{\alpha }^n+\frac{1}{s\eta _n}\nabla _{{\alpha }} f({\mathbf {A}}^{n+1},{\mathbf {B}}^{n+1},{\mathbf {C}}^{n+1},{\alpha }^n) \right\| ^2 +\frac{\lambda }{s\eta _n}\Vert {\alpha }\Vert _1\qquad \end{aligned}$$

(3.10)

where $\eta _n=\max \{\Vert {\mathbf {Q}}^{n+1}{{\mathbf {Q}}^{n+1}}^T\Vert _F,1\}$.

However, we found that the accuracy of these methods heavily depends on the choice of the initial value of $\alpha$, which reduces the robustness of the entire algorithm, especially for practical problems. To address this problem, we embed the flexible hybrid method introduced in the following section into the CP completion framework.

3.2 The Flexible Hybrid Method for $\ell _1$ Regularization

Efficiently and accurately solving (3.9) is important for the CP completion. Notice that (3.9) is an inverse problem with $\ell _1$ regularization. The iteratively reweighted norm (IRN) methods [24, 43] are typical strategies for solving the $\ell _p-$ regularization inverse problem. However, these methods assume that an appropriate value of the regularization parameter is known in advance, which is hard oftentimes. Therefore, there have been some recent works [19, 23] on selecting regularization parameters for $\ell _p$. In this work, we focus on $p = 1$ and employing the flexible method based on Golub–Kahan process [19] to solve the $\ell _1-$regularized problem. For the convenience of description, we rewrite problem (3.9) into a standard inverse problem with $\ell _1$ regularization as follows.

$$\begin{aligned} \underset{{\varvec{s}}}{\min }||{\varvec{H}}{\varvec{s}}- {\varvec{d}}||^2_2 + \lambda ||{\varvec{s}}||_1, \end{aligned}$$

(3.11)

where ${\varvec{d}}\in \mathbb {R}^m$ is the observed data, ${\varvec{H}}\in \mathbb {R}^{m \times n}$ models the forward process, ${\varvec{s}}\in \mathbb {R}^n$ is the approximation of the desired solution. The first step is to break the $\ell _1-$regularized problem (3.11) into a sequence of $\ell _2-$norm problems,

$$\begin{aligned} \underset{{\varvec{s}}}{\min }||{\varvec{H}}{\varvec{s}}- {\varvec{d}}||^2_2 + \lambda ||{\varvec{L}}({\varvec{s}}){\varvec{s}}||^2_2, \end{aligned}$$

(3.12)

where

$$\begin{aligned} {\varvec{L}}({\varvec{s}}) = \text {diag}\Big (\big (1/\sqrt{f_{\tau }([|{\varvec{s}}|]_i)}\big )_{i=1,\dots ,n} \Big ), \end{aligned}$$

(3.13)

and $f_{\tau }([|{\varvec{s}}|]_i) = {\left\{ \begin{array}{ll}_i &{} [|{\varvec{s}}|]_i \ge \tau _1 \\ \tau _2 &{} [|{\varvec{s}}|]_i < \tau _1\end{array}\right. }$. Here $0< \tau _2 < \tau _1$ are small thresholds enforcing some additional sparsity in $f_{\tau }([|{\varvec{s}}|]_i)$. Since directly solving (3.12) is not possible in real problems since the true ${\varvec{s}}$ is not available. To avoid nonlinearities and follow the common practice of iterative methods, ${\varvec{L}}({\varvec{s}})$ can be approximated by ${\varvec{L}}({\varvec{s}}_k)$, where ${\varvec{s}}_k$ is the numerical solution at the $(k-1)$-th iteration that can be treated as an approximation of the solution at k-th iteration. Since directly choosing regularization parameters for large problems is quite costly, the flexible hybrid approaches based on the flexible Golub–Kahan process[19] has been developed to solve the following variable-preconditioned Tikhonov problem,

$$\begin{aligned} \underset{{\varvec{s}}}{\min }||{\varvec{H}}{\varvec{s}}- {\varvec{d}}||^2_2 + \lambda ||{\varvec{L}}_k{\varvec{s}}||^2_2, \end{aligned}$$

(3.14)

which is equivalent to

$$\begin{aligned} \underset{{\varvec{s}}}{\min }||{\varvec{H}}{\varvec{L}}^{-1}_k\widehat{{\varvec{s}}} - {\varvec{d}}||^2_2 + \lambda ||\widehat{{\varvec{s}}}||^2_2, \end{aligned}$$

(3.15)

where $\widehat{{\varvec{s}}} = {\varvec{L}}_k{\varvec{s}}$, and ${\varvec{L}}_k = {\varvec{L}}({\varvec{s}}_k)$ may change at each iteration. To be able to incorporate the changing preconditioner, the flexible Golub–Kahan process (FGK) is used to generate the bases for the solution. Given ${\varvec{H}}, {\varvec{d}}$ and changing preconditioner ${\varvec{L}}_k$, the FGK iterative process can be described as follows. Let ${\varvec{u}}_1 = {\varvec{d}}/{\left\| {\varvec{d}}\right\| _{2}}$ and ${\varvec{v}}_1 = {\varvec{H}}^{\top }{\varvec{u}}_1/{\left\| {\varvec{H}}^{\top }{\varvec{u}}_1\right\| _{2}}$. Then at the k-th iteration, we generates vectors ${\varvec{p}}_k, {\varvec{v}}_k$ and ${\varvec{u}}_{k+1}$ such that

$$\begin{aligned} {\varvec{H}}{\varvec{P}}_k = {\varvec{U}}_{k+1}{\varvec{M}}_k \quad {{\text{ a }nd}} \quad {\varvec{H}}^{\top }{\varvec{U}}_{k+1} = {\varvec{V}}_{k+1}{\varvec{T}}_{k+1}, \end{aligned}$$

(3.16)

where ${\varvec{P}}_k = \begin{bmatrix}{\varvec{L}}^{-1}_1{\varvec{v}}_1&\dots&{\varvec{L}}^{-1}_k{\varvec{v}}_k\end{bmatrix} \in \mathbb {R}^{n \times k}, {\varvec{M}}_k \in \mathbb {R}^{(k+1)\times k}$ is upper Hessenberg, ${\varvec{T}}_{k+1} \in \mathbb {R}^{(k+1)\times (k+1)}$ is upper triangular, and ${\varvec{U}}_{k+1} = \begin{bmatrix}{\varvec{u}}_1&\dots&{\varvec{u}}_{k+1}\end{bmatrix} \in \mathbb {R}^{m \times (k+1)}$ and ${\varvec{V}}_{k+1} = \begin{bmatrix}{\varvec{v}}_1&\dots&{\varvec{v}}_{k+1}\end{bmatrix} \in \mathbb {R}^{n \times (k+1)}$ contain orthonormal columns. We remark that the column vectors of ${\varvec{P}}_k$ don’t span a Krylov subspace like conventional Golub–Kahan bidiagonalization process[10, 40], but they do provide a basis for the solution ${\varvec{s}}_k$ at k-th iteration. Given the relationships in (3.16), an approximate least-squares solution can be computed as ${\varvec{s}}_k = {\varvec{P}}_k{\varvec{q}}_k$, where ${\varvec{q}}_k$ is the solution to the projected least-squares problem,

$$\begin{aligned} \underset{{\varvec{s}}_k \in {\mathcal {R}}({\varvec{P}}_k)}{\min }||{\varvec{H}}{\varvec{s}}_k - {\varvec{d}}||^2_2 = \underset{{\varvec{q}}_k }{\min }||{\varvec{M}}_k{\varvec{q}}_k - \beta _1{\varvec{e}}_1||^2_2, \end{aligned}$$

(3.17)

where $\mathcal {R}({\varvec{P}}_k)$ denotes the range of ${\varvec{P}}_k$, ${\varvec{e}}_1 \in \mathbb {R}^{k+1}$ is the first column of $(k+1)$ by $(k+1)$ identity matrix. However, it is well-known that, for inverse problems, standard iterative methods, like LSQR, exhibit a semiconvergent behavior, whereby the solution improve in early iterations but become contaminated with inverted noise in later iterations [25]. This phenomennon, which is common for most ill-posed inverse problems, occurs also for the flexible methods. Thus, it is desirable to consider including a standard regularization term on the projected problem (3.17) to stabilize the reconstruction errors, so that

$$\begin{aligned} {\varvec{q}}_k = \arg \underset{{\varvec{q}}}{\min }||{\varvec{M}}_k{\varvec{q}}- \beta _1{\varvec{e}}_1||^2_2 + \lambda ||{\varvec{q}}||^2_2. \end{aligned}$$

(3.18)

Henceforth, ${\varvec{s}}_k = {\varvec{P}}_k{\varvec{q}}_k$ is the numerical solution at k-th iteration for the full problem. To get a better regularized solution, we consider using weighted generalized crossed validation (WGCV) method [15] to choose $\lambda$.

3.3 Practical Regularization CP Tensor

Recall that the low-rank CP tensor completion requiring solving $\alpha$ in (3.9) each iteration, can be computationally inaccurate and unstable since the forward matrix $\mathbf {Q}$ is ill-posed and that the regularization parameter $\lambda$ is hard to determine without enough prior knowledge. Our proposed practial regularization CP tensor method implements the flexible hybrid method in solving (3.9), which thus ameliorates the instability and improves the solution accuracy without sacrificing too much in speed by using standard parameter selection techniques such as WGCV to efficiently and automatically estimate the regularization parameter for the projected problem during the iterative process.

Notice that in practical regularization CP tensor method, iteratively updating $\alpha$ and $\lambda$ via the flexible hybrid method is independent of their initial settings. Furthermore, the flexible hybrid method has proven to be very effective for solving large linear inverse problems due to its inherent regularization properties as well as the added flexibility to select regularization parameters adaptively. Thus, compared with classical CP tensor, our proposed algorithm is more accurate and stable without sacrificing much efficiency. A summary pseudocode of the practical regularization CP tensor is provided in Algorithm 3.1, where $diag(a_1,\dots ,a_n)$ in the pseudocode denotes the diagonal matrix with the diagonal entries $a_1, \dots , a_n$.

4 Numerical Results

In this section, we consider various scenarios where our proposed algorithm can enhance the stability and accuracy compared with the classical CP tensor method. In all the simulations, the initial guesses are randomly generated. The stopping criterion used in all experiments depends on two parameters: one is the upper bound of the number of iterations $m_{\text {max}}$ and the other is the tolerance $\epsilon _{\text {tol}}$ of the relative difference between the observation and the approximation. The regularization parameter $\lambda$ is iteratively updated by the flexible Krylov method with weight generalized cross validation method. These experiments ran on a laptop computer with Intel i5 CPU 2GHz and 16G memory.

4.1 Image Recovering by Tensor Completion

For the first experiment, we test two cases for this example, where the missing pixels for the first case are randomly chosen while the miss part for the second case is deterministic. The reconstruction error is computed with the relative error $\frac{||{\mathcal {A}}_n - {\mathcal {A}}||_2}{|| {\mathcal {A}} ||_2}$, where ${\mathcal {A}}_n$ denotes the approximated tensor at the nth iteration, and ${\mathcal {A}}$ represents the true tensor we want to reconstruct.

Case 1 We implemented our algorithm on a color image ${\mathcal {A}} \in {{\mathbb {R}}}^{189 \times 267 \times 3}$ shown in Fig. 1. We recovered an estimated color image after removing $30\%$ of the entries from the origin color image, which is shown in Fig. 1. The upper bound R of rank$({\mathcal {A}})$ is fixed to 50 in the algorithm. The stopping criteria for this case are assumed to be $m_{\text {max}} = 500$ and the relative error tolerance is $\epsilon _{\text {tol}} = 10^{-3}$.

The recovered images by original CP tensor with different choices of $\lambda$ and practical regularization CP tensor are provided in Fig. 2. The results of these two approaches both correspond to 500 iterations. It is noted that, for the conventional CP tensor, the quality of image recovery highly depends on the choice of the regularization parameter $\lambda$. Our proposed practical regularization CP tensor produces recovered image that has much less noise than classical CP tensor, demonstrating that using flexible Krylov method to determine different regularization parameter for each iteration is beneficial. The comparison of the relative error shown in Fig. 2 also verifies the better performance of our practical regularization CP tensor. In terms of CPU time, original CP tensor with $\lambda = 35$ took 14.1 sec, and practical regularization CP tensor took 43.4 sec, since the automatic regularization parameter selection by flexible Krylov method is more expensive than predetermined regularization parameter that is cost-free.

Fig. 1

True image (left) and observation (right)

Fig. 2

Recovered color image with relative reconstruction error norms provided in the bracket

Case 2 We consider recovering the image ${\mathcal {A}} \in {{\mathbb {R}}}^{246\times 257\times 3}$ with the certain missing pixels as shown in Fig. 3, associating with its true image. The upper bound R of rank $({\mathcal {A}})$ is chosen to be 50. The stopping criteria are setup as $m_{\text {max}} = 250$ and the relative error tolerance is $\epsilon _{\text {tol}} = 10^{-3}$. For the classical CP tensor, we choose $\lambda = 35$.

The recovered images are provided in Fig. 4. The original CP tensor reached the stopping criteria at 12th iteration, and took 0.7 s for the quick convergence. For our proposed practical regularization CP tensor, the maximum number of iteration was reached, and the running time of it is 26.1 s. We observe that our algorithm provide more complete recovery than conventional CP tensor, which is also demonstrated by the relative error. To avoid the premature convergence problem, the results of original CP tensor corresponding to the maximum iterations has been checked, and is similar to the results at 12th iteration.

Fig. 3

True image (left) and observation (right)

Fig. 4

Recovered color image with relative reconstruction error norms provided in the bracket

4.2 Model Order Reduction

Next we investigate a scenario in model order reduction where the key snapshots needs to be obtained to capture the low rank structure of the solution manifold that has low Kolmogorov width [34, 42]. This example demonstrates some advantages of our practical regularization CP tensor. Model order reduction techniques such as the POD and the Reduced Basis Methods are typically used to solve the problems requiring one to query an expensive yet deterministic computational solver once for each parameter node. We show that hybridizing our approach with the regularized alternating block minimization method [32, 37] provides a novel way to do model reduction and pattern extraction. More specifically, assuming ${\mathcal {A}}$ is the collection of the solutions on sampled parameters. To select the snapshots (reduced bases) for the low rank approximation of the solution manifold, we employ our algorithm to give a prior knowledge of rank(${\mathcal {A}}$) denoted as R. Then we run the regularized alternating block minimization method according to the R to approximate ${\mathcal {A}}$ and construct the reduced bases, where the stopping criteria for the outer ALS step are also defined by the maximum number of the iteration, which we assume here to be 500, and a tolerance of the relative error $\frac{||{\mathcal {A}}_n - {\mathcal {A}}||_2}{|| {\mathcal {A}} ||_2}$, which we assume to be $\epsilon _{\text{ t }ol} = 10^{-2}$.

In this experiment, we consider the following two-dimensional diffusion equation that induces a solution manifold that requires many snapshots to achieve small error:

$$\begin{aligned} (1+\mu _1x)u_{xx} + (1+\mu _2y)u_{yy} = e^{4xy} \qquad \text {on} \quad \Omega . \end{aligned}$$

(4.1)

The physical domain is $\Omega = [-1, 1]\times [-1, 1]$ and we impose homogeneous Dirichlet boundary conditions on $\partial \Omega$. The truth approximation is a spectral Chebyshev collocation method [26, 49] with ${\mathcal {N}}_x = 100$ degrees of freedom in each direction. This means the truth approximation has dimension ${\mathcal {N}} = 10000 ({\mathcal {N}} = {\mathcal {N}}^2_x)$. The parameter domain ${\mathcal {D}}$ for $(\mu _1, \mu _2)$ is taken to be $[-0.99, 0.99]\times [-0.99, 0.99]$. For the parameter sample set, we discretize ${\mathcal {D}}$ using on a $9 \times 9$ cartesian grid, thus the size of training parameters is 81. The testing set $\Xi _{\text {test}}$ contains another 10 random samples in ${\mathcal {D}}$. The resulting tensor ${\mathcal {A}}$ is of dimension $100 \times 100 \times 81$. Given an initial value of the rank $R_0= 50$ and tolerance $\varepsilon = 10^{-2}$, we run our algorithm on ${\mathcal {A}}$ at first, then we sort the rescaling coefficients $\{\alpha _r\}_{r = 1}^{R_0}$ in descending order while discarding the coefficients below $\varepsilon \alpha _{\text{ m }ax}$, where $\alpha _{\text{ m }ax}$ is the maximum rescaling coefficients. Assuming that the number of the coefficients we keep is R which is much smaller than ${\mathcal {N}}$, then we run the regularized alternating optimization method with rank R to approximate

$$\begin{aligned} {\mathcal {A}} \approx \sum _{r=1}^{R} \alpha _{r}{\mathbf {x}}_r\circ {\mathbf {y}}_r\circ {\mathbf {z}}_r, \end{aligned}$$

(4.2)

and build up the reduced bases $\{\phi _r\}_{r=1}^{R}$ by orthonormalizing $\{{\widehat{\phi }}_r\}_{r=1}^{R}$, where ${\widehat{\phi }}_r$ is created by vectorizing ${\mathbf {x}}_r\circ {\mathbf {y}}_r$.

4.2.1 Computational Performance

Given initial value of $\lambda = 10$, our proposed approach chooses $R = 20$ reduced bases, while the classical CP tensor chooses $R = 7$ reduced bases with the same initialization. The absolute value of the coefficients $\alpha$ is shown in Fig. 5. We can see that original CP tensor does more rank reduction than practical regularization CP tensor. However, it is noted that, in (3.9), larger regularization parameter $\lambda$ always gives more sparse solution, which doesn’t mean solving this inverse problem more accurately. Thus, appropriate selection of $\lambda$ is crucial for solving (3.9), which is not easy if the prior knowledge or experience is not enough. In addition, in this model reduction example, we found that the sparsity of $\alpha$ is very sensitive to the choice of initial value of $\lambda$, that is, for classical CP tensor, much less(more) components of $\alpha$ will be close to zeros if we increase(decrease) $\lambda$ a little bit. To reduce the sensitivity caused by the determination of the initial value of $\lambda$, our practical regularization CP tensor includes the automatic regularization parameter selection, which is more robust than the conventional CP tensor since it doesn’t rely on the empirical choice of $\lambda$.

Fig. 5

Value of $|\alpha |$: the comparison between practical regularization CP tensor and original CP tensor

To gain the understanding of the quality of the reduced bases our proposed approach, the number of reduced bases constructed by the POD is also set to be 20 for comparative purposes. The algorithmic accuracy is evaluated by approximating the $u(x, \mu _1, \mu _2)$ via reduced bases, where $(\mu _1, \mu _2) \in \Xi _{\text {test}}$ and the error is measured by $\ell ^2$ norm. Fig. 6 displays the approximation of the solution at two parameters drawn from the testing set for the practical regularization CP tensor and the POD, since the 7 bases obtained by original CP tensor are too less to capture the main pattern of the solution. We observe that our proposed algorithm faithfully captures the feature of the solution, although the error is large compared to the POD. The performance of approximating the solutions at all the parameters in the testing set for our algorithm, canonical CP tensor and the POD is provided in Fig. 7. Table 1 further quantifies the range of the approximation results as well as the computational time. Although our practical regularization CP tensor is more expensive, the approximation quality of this method is better than original CP tensor since the automatic regularization parameter selection helps to reduce dependence on the initial guess of the regularization parameter. However, it can clearly be seen that POD is much faster and more accurate than the two CP tensor methods. Compared with POD, the main attraction of CP tensor methods is the low-cost storage, which is detailed in the following subsection.

Fig. 6

The approximation of the solution of Two-dimensional diffusion equation at two parameters in the testing set: $\mu _1 = -0.9193, \mu _2 = 0.6913$(left) and $\mu _1 = -0.8986, \mu _2 = -0.7977$(right)

Fig. 7

The approximation of $u(x, \mu _1, \mu _2)$ with $(\mu _1, \mu _2) \in \Xi _{\text {test}}$: CP tensor, practical regularization CP tensor and POD

Table 1 Summary of the computational results for the model reduction problem

4.2.2 A Note on Compression

For this model reduction problem, although both practical regularization CP tensor and CP tensor provide a more parsimonious representation of the data than the POD, comparing the compression ratios between the CP tensor techniques and the POD illustrates the difference and the benefit of the CP tensor techniques. For a rank $R = 20$ tensor of dimension ${\mathcal {A}} = 100 \times 100 \times 81$, the compression, the compression ratios are

$$\begin{aligned} {\mathcal {C}}_{\text {POD}}&= \frac{I \cdot J \cdot K}{R\cdot (I\cdot J + K + 1)} = \frac{100^2\cdot 81}{20\cdot (100^2 + 81 + 1)} \approx 4.02, \end{aligned}$$

(4.3)

$$\begin{aligned} {\mathcal {C}}_{\text {CP}}&= \frac{I \cdot J \cdot K}{R\cdot (I {+} J + K + 1)} = \frac{100^2\cdot 81}{20\cdot (100+100 + 81 + 1)} \approx 143.62. \end{aligned}$$

(4.4)

Notice that the POD requires the tensor to be reshaped in some direction. The comparison illustrates the striking difference between the compression ratios. It is worth mentioning that the CP tensor approaches requires much less memory to approximate the data. This can be of importance if the online stage (approximating the data) is in limited storage situations and that the accuracy requirement is not high.

5 Conclusion

In this paper, we have presented a new low-rank CP tensor completion algorithm by combining the flexible hybrid method and the CP tensor completion. A key advantage of this method is that the regularization parameter can be easily and automatically estimated during the iterative process, which substantially reduces the difficulty of initializing the regularization parameter and improves the robustness of the algorithm. In addition to memory savings, our proposed approach demonstrates outstanding performance on the model reduction example, compared to the POD. Moreover, our image recovery experiments show that our algorithm has a practical advantage in capturing more details in image reconstruction over the conventional CP tensor due to a more optimal choice of the regularization parameter. In our future outlook, we will extend this hybrid approach in a tensor based total variation formulation for denoising and deblurring multi-channel images and videos.

Appendix A: Proximal Gradient

Recall $g(\sigma )= \lambda \parallel \sigma \parallel _{1}$ is convex and non-differentiable. The function g can be turn into a proximal operator to find its minimum using the definition [41, 46] below:

Definition A.1

Given a proper closed convex function f: ${{\mathbb {R}}}^{n}\longrightarrow {{\mathbb {R}}}\bigcup {\infty }$, the proximal operator scaled by $\delta >0$, is a mapping from ${{\mathbb {R}}}^{n}\longrightarrow {{\mathbb {R}}}$ defined by

$$\begin{aligned} \mathbf{prox} _{\delta g}(v):= \begin{aligned}&\underset{y \in {{\mathbb {R}}}^{n} }{\text {argmin}}&\left( g(y) + \frac{1}{2\delta } \parallel y-v\parallel ^{2} \right) . \end{aligned} \end{aligned}$$

Then the proximal operator for $g(\sigma )$ is,

$$\begin{aligned} \begin{aligned} prox_{g}(v)&= \underset{\sigma }{\text {argmin }} \left( g(\sigma ) + \frac{1}{2\delta }\parallel \sigma - v\parallel _{2}^{2}\right) \\&=\underset{\sigma }{\text {argmin }} \left( \lambda \parallel \sigma \parallel _{1} + \frac{1}{2\delta } \parallel \sigma - v\parallel _{2}^{2}\right) \\&= \underset{\sigma }{\text {argmin }} \left( \lambda \sum _{i=1}^{n} \mid \sigma _{i}\mid + \frac{1}{2\delta }\sum _{i=1}^{n} (\sigma _{i} - v)^{2}\right) \\ \end{aligned} \end{aligned}$$

For $\sigma = (\sigma _1 ,..., \sigma _n)$

$$\begin{aligned} (prox_{\delta g}(v)_{i})_{i}= & {} \underset{\sigma _i}{\text {argmin }} \left( \lambda \mid \sigma _i\mid + \frac{1}{2\delta }(\sigma _i - v_i)^{2}\right) \\= & {} \underset{\sigma _i}{\text {argmin }} {\left\{ \begin{array}{ll} \left( \lambda - \frac{v_i}{\delta }\right) \sigma _i + \frac{1}{2\delta }\sigma _i^{2} , \sigma _i>0\\ -\left( \lambda + \frac{v_i}{\delta }\right) \sigma _i + \frac{1}{2\delta }\sigma _i^{2}, \sigma _i<0 \Bigg \} \end{array}\right. } \end{aligned}$$

Hence,

$$\begin{aligned} prox_{g}(v)_{i} = {\left\{ \begin{array}{ll} 0 , &{}\mid v_{i}\mid \le \lambda \\ v_{i} - \lambda sign(v_{i}), &{}\mid v_{i}\mid >\lambda \end{array}\right. } \end{aligned}$$

with $\delta =1$