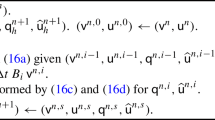Appendix A. Recurrence relations for increasing parameters We derive some useful recurrence relations for generalized Koornwinder polynomials in Appendix 1 –1 . Firstly, we rewrite the Koornwinder polynomials in the collapsed coordinate to simplify the incoming proofs,
$$\begin{aligned} \mathcal {J}_{\varvec{\ell }}^{\varvec{\alpha }}(\varvec{\hat{x}})&= J_{\ell _1}^{\alpha _0,\alpha _1}(\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1} J_{\ell _2}^{2\ell _1+\alpha _0+\alpha _1+1,\alpha _2}(\eta )\nonumber \\&\quad \times \left( \frac{1-\zeta }{2}\right) ^{\ell _1+\ell _2} J_{\ell _3}^{2\ell _1+2\ell _2+\alpha _0+\alpha _1+\alpha _2+2,\alpha _3}(\zeta ), \end{aligned}$$
(A.1)
where
$$\begin{aligned} \xi =\dfrac{2\hat{x}_1}{1-\hat{x}_2-\hat{x}_3}-1,\quad \eta =\dfrac{2\hat{x}_2}{1-\hat{x}_3}-1,\quad \zeta =2\hat{x}_3-1. \end{aligned}$$
(A.2)
We also let
$$\begin{aligned} \begin{aligned}&\dot{\varvec{e}}_0=(1,0,0,0),\quad \dot{\varvec{e}}_1=(0,1,0,0),\quad \dot{\varvec{e}}_2=(0,0,1,0),\quad \dot{\varvec{e}}_3=(0,0,0,1). \end{aligned} \end{aligned}$$
All coefficient functions in appendixes are defined as in Lemma 2.1 –2.4 .
Lemma A.1
For any \(\varvec{\alpha }\in [-1,+\infty )^4\) and \(\varvec{\ell }\in \mathbb {N}_0^3\) , the following recurrence relations hold:
$$\begin{aligned}&{\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }}(\varvec{\hat{x}}) = \sum \limits _{p=0}^1 \sum \limits _{q=0}^1 \sum \limits _{r=0}^1 \mathcal {A}_{p,q,r}^1 (\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( p,\, q-p,\, r-q\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_0} (\varvec{\hat{x}}), \end{aligned}$$
(A.3)
$$\begin{aligned}&{\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})= \sum \limits _{p=0}^1 \sum \limits _{q=0}^1 \sum \limits _{r=0}^1 \mathcal {A}_{p,q,r}^2 (\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( p,\, q-p,\, r-q\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_1} (\varvec{\hat{x}}), \end{aligned}$$
(A.4)
$$\begin{aligned}&{\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})= \sum \limits _{q=0}^1 \sum \limits _{r=0}^1 \mathcal {A}_{q,r}^3 (\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( 0,\,q,\,r-q\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_2}(\varvec{\hat{x}}), \end{aligned}$$
(A.5)
$$\begin{aligned}&{\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }}(\varvec{\hat{x}}) = \sum \limits _{r=0}^1 \mathcal {A}_r^4(\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( 0,0,r\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_3}(\varvec{\hat{x}}), \end{aligned}$$
(A.6)
where the corresponding coefficients are presented in Tables 1 .
Table 1 The values of \(\mathcal {A}^1_{p,q,r},\) \(\mathcal {A}^2_{p,q,r}\) , \(\mathcal {A}^3_{q,r}\) and \(\mathcal {A}^4_{r}\) . Proof
We take the proof of (A.5 ) as an example. Other identities shall be proved in a similar way. According to (2.9 ), (2.8 ) and (2.11 ), one has
$$\begin{aligned} \begin{aligned} \mathcal {J}_{\varvec{\ell }}^{\varvec{\alpha }}(\varvec{\hat{x}})&=J_{\ell _1}^{\alpha _0,\alpha _1}(\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1} \bigg [ b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} J_{\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2+1}(\eta ) \left( \frac{1-\zeta }{2}\right) ^{\ell _1+\ell _2} \\&\qquad \times \left( b_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} J_{\ell _3}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+3,\alpha _3}(\zeta )+ b_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} J_{\ell _3-1}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+3,\alpha _3}(\zeta )\right) \\&\qquad \qquad -b_{2,\ell _2}^{\alpha _2,2\ell _1+|\varvec{\alpha }^1|+1} J_{\ell _2-1}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2+1}(\eta ) \left( \frac{1-\zeta }{2}\right) ^{\ell _1+\ell _2-1} \\&\qquad \times \left( e_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+1,\alpha _3} J_{\ell _3}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+1,\alpha _3}(\zeta )+ e_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+1,\alpha _3} J_{\ell _3+1}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+1,\alpha _3}(\zeta ) \right) \bigg ]. \end{aligned} \end{aligned}$$
This completes the proof. \(\square \)
Appendix B. Recurrence relations for derivatives
Lemma B.1
For any \(\varvec{\alpha }\in [-1,+\infty )^4\) and \(\varvec{\ell }\in \mathbb {N}_0^3\) , the following recurrence relations hold:
$$\begin{aligned}&\partial _{\hat{x}_1}{\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})=2d_{\ell _1}^{\alpha _0,\alpha _1} {\mathcal {J}}_{\varvec{\ell }-(1,0,0)}^{\varvec{\alpha }+\dot{\varvec{e}}_{0}+\dot{\varvec{e}}_1} (\varvec{\hat{x}}), \end{aligned}$$
(B.1)
$$\begin{aligned}&\partial _{\hat{x}_2} {\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})= \sum \limits _{p=0}^1 \mathcal {D}^2_p(\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( p,1-p,0\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_{0}+\dot{\varvec{e}}_2} (\varvec{\hat{x}}), \end{aligned}$$
(B.2)
$$\begin{aligned}&\left( \partial _{\hat{x}_2}- \partial _{\hat{x}_1}\right) {\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})= \sum \limits _{p=0}^1 \mathcal {D}^{21}_p(\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( p,1-p,0\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_{1}+\dot{\varvec{e}}_2} (\varvec{\hat{x}}), \end{aligned}$$
(B.3)
$$\begin{aligned}&\partial _{\hat{x}_3} {\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})=\sum \limits _{p=0}^1 \sum \limits _{q=0}^1\mathcal {D}^3_{p,q}(\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( p,\,q-p,\,1-q\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_{0}+\dot{\varvec{e}}_3} (\varvec{\hat{x}}), \end{aligned}$$
(B.4)
$$\begin{aligned}&\left( \partial _{\hat{x}_1}- \partial _{\hat{x}_3}\right) {\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}}) =\sum \limits _{p=0}^1 \sum \limits _{q=0}^1\mathcal {D}^{13}_{p,q}(\varvec{\ell },\varvec{\alpha }) {\mathcal {J}}_{\varvec{\ell }-\left( p,\,q-p,\,1-q\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_{1}+\dot{\varvec{e}}_3} (\varvec{\hat{x}}), \end{aligned}$$
(B.5)
$$\begin{aligned}&\left( \partial _{\hat{x}_3}- \partial _{\hat{x}_2}\right) {\mathcal {J}}_{\varvec{\ell }}^{\varvec{\alpha }} (\varvec{\hat{x}})=\sum \limits _{q=0}^1 \mathcal {D}_q^{32}(\varvec{\ell },\varvec{\alpha }){\mathcal {J}}_{\varvec{\ell }-\left( 0,q,1-q\right) }^{{\varvec{\alpha }}+\dot{\varvec{e}}_{2}+\dot{\varvec{e}}_3}(\varvec{\hat{x}}). \end{aligned}$$
(B.6)
With the notations
$$\begin{aligned} \begin{aligned}&\rho _{\varvec{\ell }}^{\varvec{\alpha }} := 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1}-\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1},\quad \kappa _{\varvec{\ell }}^{\varvec{\alpha }} := \ell _1 b_{2,\ell _1}^{\alpha _1,\alpha _0}-2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _0,\alpha _1+1},\\&\theta _{\varvec{\ell }}^{\varvec{\alpha }} := 2d_{\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} e_{1,\ell _2-1}^{\alpha _2, 2\ell _1+|\varvec{\alpha }^1|+2} - \ell _2 b_{2,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2}, \end{aligned} \end{aligned}$$
the corresponding coefficients are presented as follows.
$$\begin{aligned}&\mathcal {D}_0^2(\varvec{\ell },\varvec{\alpha })=2d_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{1,\ell _1}^{\alpha _0,\alpha _1}, \\&\mathcal {D}_1^2(\varvec{\ell },\varvec{\alpha }) =\tfrac{ \left( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1} \right) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}}{ b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1}}. \end{aligned}$$
$$\begin{aligned}&\mathcal {D}_0^{21}(\varvec{\ell },\varvec{\alpha }) = \mathcal {D}_0^{2}(\varvec{\ell },\varvec{\alpha }),\\&\mathcal {D}_1^{21}(\varvec{\ell },\varvec{\alpha }) = \tfrac{\left( \ell _1 b_{2,\ell _1}^{\alpha _1,\alpha _0} -2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _0,\alpha _1+1} \right) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} - 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _1,\alpha _0} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}}{ b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1}}. \end{aligned}$$
$$\begin{aligned}&\mathcal {D}^3_{0,0}(\varvec{\ell },\varvec{\alpha }) = 2d_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} b_{1,\ell _1}^{\alpha _0,\alpha _1} b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2},\\&\mathcal {D}^3_{0,1}(\varvec{\ell },\varvec{\alpha }) = \tfrac{ b_{1,\ell _1}^{\alpha _0,\alpha _1} \theta _{\varvec{\ell }}^{\varvec{\alpha }} b_{1,\ell _3}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2| +2,\alpha _3} +2 d_{\ell _3}^{2|\varvec{\ell }^2| + |\varvec{\alpha }^2| +2,\alpha _3} b_{1,\ell _1}^{\alpha _0,\alpha _1} b_{2,\ell _2}^{2\ell _1+|\varvec{\alpha }^1| +1,\alpha _2} e_{2,\ell _3-1}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2| +2,\alpha _3+1} }{b_{1,\ell _3}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+2,\alpha _3+1}},\\&\mathcal {D}^3_{1,0}(\varvec{\ell },\varvec{\alpha }) = 2d_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|,\alpha _2}, \end{aligned}$$
$$\begin{aligned}&\mathcal {D}^3_{1,1}(\varvec{\ell },\varvec{\alpha })\\&= \frac{ \left( \rho _{\varvec{\ell }}^{\varvec{\alpha }} + b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} \theta _{\varvec{\ell }}^{\varvec{\alpha }} \right) b_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} +2b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|,\alpha _2} d_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2| +2,\alpha _3} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^2|,\alpha _2} e_{2,\ell _3-1}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+2,\alpha _3+1}}{b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|,\alpha _2} b_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+1,\alpha _3+1}}. \end{aligned}$$
$$\begin{aligned}&\mathcal {D}^{13}_{0,0}(\varvec{\ell },\varvec{\alpha }) = -\mathcal {D}^{3}_{0,0}(\varvec{\ell },\varvec{\alpha }),\\&\mathcal {D}^{13}_{0,1}(\varvec{\ell },\varvec{\alpha }) = -\mathcal {D}^{3}_{0,1}(\varvec{\ell },\varvec{\alpha }),\\&\mathcal {D}^{13}_{1,0}(\varvec{\ell },\varvec{\alpha }) = 2d_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} b_{2,\ell _1}^{\alpha _1,\alpha _0} e_{2,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|,\alpha _2}, \end{aligned}$$
$$\begin{aligned}&\mathcal {D}^{13}_{1,1}(\varvec{\ell },\varvec{\alpha }) = \tfrac{ \left( b_{2,\ell _1}^{\alpha _1,\alpha _0} e_{2,\ell _2-1}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} \theta _{\varvec{\ell }}^{\varvec{\alpha }}-\kappa _{\varvec{\ell }}^{\varvec{\alpha }} \right) b_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} +2b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|,\alpha _2} d_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2| +2,\alpha _3} b_{2,\ell _1}^{\alpha _1,\alpha _0} e_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^2|,\alpha _2} e_{2,\ell _3-1}^{2|\varvec{\ell }^2| +|\varvec{\alpha }^2|+2,\alpha _3+1}}{b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|,\alpha _2} b_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+1,\alpha _3+1}}. \end{aligned}$$
$$\begin{aligned}&\mathcal {D}^{32}_{0}(\varvec{\ell },\varvec{\alpha }) = 2d_{\ell _3}^{2|\varvec{\ell }^2| + |\varvec{\alpha }^2|+2,\alpha _3} b_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2}, \end{aligned}$$
Proof
It follows from (A.2 ) that
$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{\hat{x}_1} = \dfrac{8}{(1-\eta )(1-\zeta )} \partial _{\xi },\\ \partial _{\hat{x}_2} = \dfrac{4(1+\xi )}{(1-\eta )(1-\zeta )} \partial _{\xi } + \dfrac{4}{1-\zeta } \partial _{\eta },\\ \partial _{\hat{x}_3} = \dfrac{4(1+\xi )}{(1-\eta )(1-\zeta )} \partial _{\xi } + \dfrac{2(1+\eta )}{1-\zeta } \partial _{\eta } +2\partial _{\zeta }. \end{array}\right. } \end{aligned}$$
(B.7)
We take the proof of (B.2 ) as an example. Other identities shall be proved in a similar way. To begin with, when \(\ell _1 = 0,\) one has
$$\begin{aligned} \begin{aligned} \partial _{\hat{x}_2}\mathcal {J}^{\alpha _0,\alpha _1,\alpha _2,\alpha _3}_{0,\ell _2,\ell _3}&= 2 \partial _\eta J_{\ell _2} ^{ |\varvec{\alpha }^1| +1,\alpha _2} (\eta ) \left( \frac{1-\zeta }{2}\right) ^{\ell _2-1} J_{\ell _3}^{2\ell _2+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&=2d_{\ell _2}^{ |\varvec{\alpha }^1| +1,\alpha _2} J_{\ell _2-1} ^{ |\varvec{\alpha }^1| +2,\alpha _2+1} (\eta ) \left( \frac{1-\zeta }{2}\right) ^{\ell _2-1} J_{\ell _3}^{2\ell _2+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&=2d_{\ell _2}^{ |\varvec{\alpha }^1| +1,\alpha _2} \mathcal {J}_{0,\ell _2-1,\ell _3}^{\alpha _0+1,\alpha _1,\alpha _2+1,\alpha _3}. \end{aligned} \end{aligned}$$
When \(\ell _1>1,\) a direct computation yields
$$\begin{aligned} \begin{aligned}&\partial _{\hat{x}_2}\mathcal {J}^{\varvec{\alpha }}_{\varvec{\ell }} = \bigg [ (1+\xi ) \partial _{\xi } J_{\ell _1} ^{\alpha _0,\alpha _1} (\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1-1} J_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} (\eta ) \\&\quad + 2 J_{\ell _1} ^{\alpha _0,\alpha _1} (\xi ) \partial _\eta \big [ \left( \frac{1-\eta }{2}\right) ^{\ell _1} J_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} (\eta ) \big ]\bigg ] \times \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} J_{\ell _3}^{2|\varvec{\ell }^2|+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&= \bigg [ \left( d_{\ell _1}^{\alpha _0,\alpha _1} (1+\xi ) J_{\ell _1-1}^{\alpha _0+1,\alpha _1+1}(\xi )-\ell _1 J_{\ell _1}^{\alpha _0,\alpha _1}(\xi ) \right) \left( \frac{1-\eta }{2}\right) ^{\ell _1-1} J_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} (\eta ) \\&\quad +2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} J_{\ell _1}^{\alpha _0,\alpha _1} (\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1} J_{\ell _2-1} ^{2\ell _1+ |\varvec{\alpha }^1| +2,\alpha _2+1} (\eta ) \bigg ] \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} J_{\ell _3}^{2|\varvec{\ell }^2|+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta ). \end{aligned} \end{aligned}$$
(B.8)
Recalling (2.8 ) and (2.12 ), we have
$$\begin{aligned} \begin{aligned}&d_{\ell _1}^{\alpha _0,\alpha _1} (1+\xi ) J_{\ell _1-1}^{\alpha _0+1,\alpha _1+1}(\xi )-\ell _1 J_{\ell _1}^{\alpha _0,\alpha _1}(\xi ) \\&\quad = 2d_{\ell _1}^{\alpha _0,\alpha _1} \left( e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ) -e_{2,\ell _1-1}^{\alpha _0+1,\alpha _1} J_{\ell _1}^{\alpha _0+1,\alpha _1}(\xi )\right) \\&\qquad -\ell _1 \left( b_{1,\ell _1}^{\alpha _0,\alpha _1} J_{\ell _1}^{\alpha _0+1,\alpha _1}(\xi ) + b_{2,\ell _1}^{\alpha _0,\alpha _1} J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ) \right) \\&\quad = \left( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}\right) J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ).\quad \left( \because -2d_{\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _1-1}^{\alpha _0+1,\alpha _1} -\ell _1 b_{1,\ell _1}^{\alpha _0,\alpha _1} = 0\right) \end{aligned} \end{aligned}$$
Substituting the above formula into (B.8 ) and using (2.8 ), (2.9 ) and (2.11 ), one has
$$\begin{aligned}&\partial _{\hat{x}_2} \mathcal {J}_{\varvec{\ell }}^{\varvec{\alpha }} = \bigg [ \left( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}\right) J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1-1} J_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} (\eta ) \\&\quad +2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} \left( b_{1,\ell _1}^{\alpha _0,\alpha _1} J_{\ell _1}^{\alpha _0+1,\alpha _1}(\xi ) +b_{2,\ell _1}^{\alpha _0,\alpha _1} J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi )\right] \left( \frac{1-\eta }{2}\right) ^{\ell _1} J_{\ell _2-1} ^{2\ell _1+ |\varvec{\alpha }^1| +2,\alpha _2+1} (\eta ) \bigg ] \\&\quad \times \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} J_{\ell _3}^{2|\varvec{\ell }^2|+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&=2d_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{1,\ell _1}^{\alpha _0,\alpha _1} \mathcal {J}_{\ell _1,\ell _2-1,\ell _3}^{\alpha _0+1,\alpha _1,\alpha _2+1,\alpha _3}\\&\quad + J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1-1} \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} J_{\ell _3}^{2|\varvec{\ell }^2|+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&\quad \times \bigg [ \left( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}\right) J_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} (\eta ) \\&\quad +2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} \frac{1-\eta }{2} J_{\ell _2-1} ^{2\ell _1+ |\varvec{\alpha }^1| +2,\alpha _2+1} (\eta ) \bigg ] \\&=2d_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{1,\ell _1}^{\alpha _0,\alpha _1} \mathcal {J}_{\ell _1,\ell _2-1,\ell _3}^{\alpha _0+1,\alpha _1,\alpha _2+1,\alpha _3}\\&\quad + J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1-1} \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} J_{\ell _3}^{2|\varvec{\ell }^2|+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&\quad \times \bigg [ \left( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}\right) \\&\quad \times \left( b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} (\eta ) -b_{2,\ell _2}^{\alpha _2, 2\ell _1+ |\varvec{\alpha }^1| +1} J_{\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} (\eta ) \right) \\&\quad + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} \left( e_{1,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} J_{\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}(\eta )\right. \\&\quad \left. +e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}(\eta ) \right) \bigg ]\\&=2d_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{1,\ell _1}^{\alpha _0,\alpha _1} \mathcal {J}_{\ell _1,\ell _2-1,\ell _3}^{\alpha _0+1,\alpha _1,\alpha _2+1,\alpha _3} + J_{\ell _1-1}^{\alpha _0+1,\alpha _1}(\xi ) \left( \frac{1-\eta }{2}\right) ^{\ell _1-1}\\&\quad \times \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} J_{\ell _3}^{2|\varvec{\ell }^2|+ |\varvec{\alpha }^2| +2,\alpha _3}(\zeta )\\&\quad \times \bigg [ \left( ( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} \right) \\&\quad \times J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}(\eta )\\&\quad + \left( ( \ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1} - 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1}) b_{2,\ell _2}^{\alpha _2,2\ell _1+ |\varvec{\alpha }^1| +1} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} \right) \\&\quad \times J_{\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}(\eta ) \bigg ]. \end{aligned}$$
Note that \(b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1}\ne 0\) when \(\ell _1>0.\) It is readily checked that
$$\begin{aligned} \begin{aligned}&\left( ( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} \right) \\&\quad \times J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}(\eta )\\&\quad \,+ \left( ( \ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1} - 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1}) b_{2,\ell _2}^{\alpha _2,2\ell _1+ |\varvec{\alpha }^1| +1} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} \right) \\&\quad \times J_{\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}(\eta ) \\&=\frac{( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}}{ b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1}}\\&\quad \times \left( b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1} J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} (\eta ) + b_{2,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1} J_{\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1} (\eta ) \right) \\&=\frac{( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}}{ b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1}}\\&\quad \times J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1} (\eta ). \end{aligned} \end{aligned}$$
Thus, it concludes that
$$\begin{aligned} \begin{aligned}&\partial _{\hat{x}_2} \mathcal {J}_{\varvec{\ell }}^{\varvec{\alpha }} = 2d_{\ell _2} ^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{1,\ell _1}^{\alpha _0,\alpha _1} \mathcal {J}_{\ell _1,\ell _2-1,\ell _3}^{\alpha _0+1,\alpha _1,\alpha _2+1,\alpha _3}\\&\quad +\frac{( 2d_{\ell _1}^{\alpha _0,\alpha _1} e_{1,\ell _1-1}^{\alpha _1,\alpha _0+1} -\ell _1 b_{2,\ell _1}^{\alpha _0,\alpha _1}) b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} + 2d_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2} b_{2,\ell _1}^{\alpha _0,\alpha _1} e_{2,\ell _2-1}^{2\ell _1+ |\varvec{\alpha }^1| +1,\alpha _2+1}}{ b_{1,\ell _2}^{2\ell _1+ |\varvec{\alpha }^1| ,\alpha _2+1}}\\&\qquad \mathcal {J}_{\ell _1-1,\ell _2,\ell _3}^{\alpha _0+1,\alpha _1,\alpha _2+1,\alpha _3}. \end{aligned} \end{aligned}$$
This ends the proof. \(\square \)
Appendix C. Coefficients in the three-term recurrence relations By introducing the notations,
$$\begin{aligned}&\tau _{1,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{c_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2},\quad&\tau _{2,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{c_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2},\quad&\tau _{3,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{c_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2},\\&\tau _{4,\varvec{\ell }}^{\varvec{\alpha }} := -\tfrac{a_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2},\quad&\tau _{5,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{(1-a_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3})}{2},\quad&\tau _{6,\varvec{\ell }}^{\varvec{\alpha }} := -\tfrac{a_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2},\\&\tau _{7,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{g_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3}}{2},\quad&\tau _{8,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{g_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3}}{2},\quad&\tau _{9,\varvec{\ell }}^{\varvec{\alpha }} := \tfrac{g_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3}}{2}, \end{aligned}$$
we write the coefficients \(\mathscr {C}_{r}(\varvec{\ell },\varvec{\alpha })\) as
$$\begin{aligned} \left[ \mathscr {C}_{-1}(\varvec{\ell },\varvec{\alpha }), \mathscr {C}_{0}(\varvec{\ell },\varvec{\alpha }), \mathscr {C}_{1}(\varvec{\ell },\varvec{\alpha }) \right] = \bigg [ \frac{a_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2}, \frac{1+a_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2}, \frac{a_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}}{2} \bigg ], \end{aligned}$$
and list in Table 2 the coefficients \(\mathscr {C}_{p,q,r}(\varvec{\ell },\varvec{\alpha })\) , \(\mathscr {C}_{q,r}(\varvec{\ell },\varvec{\alpha })\) used in Theorem 2.1 .
Table 2 The values of \(\mathscr {C}_{p,q,r}(\varvec{\ell },\varvec{\alpha })\) , \(\mathscr {C}_{q,r}(\varvec{\ell },\varvec{\alpha })\) and \(\mathscr {C}_{r}(\varvec{\ell },\varvec{\alpha })\) . Proof
We shall take the proof of (2.20 ) as an example to explain the derivations of these coefficients. From (A.2 ), one obtains
$$\begin{aligned} \hat{x}_2 = \frac{1+\eta }{2} \frac{1-\zeta }{2}. \end{aligned}$$
It then follows from (2.7 ), (2.10 ) and (2.13 ) that
$$\begin{aligned} \hat{x}_2 \mathcal {J}_{\varvec{\ell }}^{\varvec{\alpha }}&= J_{\ell _1}^{\alpha _0,\alpha _1}(\xi ) \left( \frac{1-\eta }{2} \right) ^{\ell _1} \frac{1+\eta }{2} J_{\ell _2}^{2\ell _1+ |\varvec{\alpha }^1|+1,\alpha _2} (\eta )\left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|+1}J_{\ell _3}^{2 |\varvec{\ell }^2| +|\varvec{\alpha }^2|+2,\alpha _3}(\zeta )\\&=J_{\ell _1}^{\alpha _0,\alpha _1}(\xi ) \left( \frac{1-\eta }{2} \right) ^{\ell _1} \bigg [ \frac{a_{1,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2}}{2} J_{\ell _2+1}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} (\eta ) \left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|+1}\\&\quad \times \bigg ( c_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} J_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+4,\alpha _3}(\zeta )+ c_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} J_{\ell _3-1}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+4,\alpha _3}(\zeta )\\&\quad + c_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3} J_{\ell _3-2}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+4,\alpha _3}(\zeta ) \bigg )\\&\quad + \frac{1+a_{2,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2}}{2} J_{\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} (\eta )\left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|} \\&\quad \times \bigg ( -\frac{a_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2| +2,\alpha _3}}{2} J_{\ell _3+1}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}(\zeta )+ \frac{1-a_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2| +2,\alpha _3}}{2} J_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}(\zeta )\\&\quad - \frac{a_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2| +2,\alpha _3}}{2} J_{\ell _3-1}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|+2,\alpha _3}(\zeta ) \bigg )\\&\quad + \frac{a_{3,\ell _2}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2}}{2} J_{\ell _2-1}^{2\ell _1+|\varvec{\alpha }^1|+1,\alpha _2} (\eta )\left( \frac{1-\zeta }{2}\right) ^{|\varvec{\ell }^2|-1} \\&\quad \times \left( g_{1,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3} J_{\ell _3+2}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3}(\zeta )+ g_{2,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3} J_{\ell _3+1}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3}(\zeta )\right. \\&\quad \left. + g_{3,\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3} J_{\ell _3}^{2|\varvec{\ell }^2|+|\varvec{\alpha }^2|,\alpha _3}(\zeta ) \right) \bigg ]. \end{aligned}$$
The proof is completed. \(\square \)
Appendix D. Exact eigenvalues of homogeneous Dirichlet Laplacian on \(\mathcal {T}_F\)
We first claim that the generalized sine functions are eigenfunctions of the Dirichlet Laplacian on \(\mathcal {T}_F\) . Actually, motivated by the study of [23 ], we introduce homogeneous coordinates \(\mathbf {s}\in \mathbb {R}_H^4\) with
$$\begin{aligned} \mathbb {R}_H^4:= \left\{ \mathbf {s}=(s_0,s_1,s_2,s_3)\in \mathbb {R}^4: |\mathbf {s}| = 0 \right\} ,\quad | \mathbf {s}| = \sum \limits _{j=0}^3 s_j. \end{aligned}$$
(D.1)
For convenience, we adopt the convention of using bold letters, such as \(\mathbf {s}\) and \(\mathbf {k}\) , to denote points represented in homogeneous coordinates. The transformation between \(\varvec{x}\in \mathbb {R}^3\) and \(\mathbf {s}\in \mathbb {R}^4_H\) is then defined by [23 , (3.1)],
$$\begin{aligned} {\left\{ \begin{array}{ll} x_1 = s_2+s_3,\\ x_2 = s_3+s_1,\\ x_3 = s_1 + s_2, \end{array}\right. } \end{aligned}$$
(D.2)
and \(s_0=-s_1-s_2-s_3.\)
We further define the function on \(\Omega _H=\left\{ \mathbf {s}\in \mathbb {R}^4_H: -1\le s_i-s_j\le 1, 0\le i,j\le 3\right\} \) that
$$\begin{aligned} \begin{aligned}&\phi _{\mathbf {k}}(\mathbf {s}):=e^{\frac{\pi \mathrm {i}}{2} \mathbf {k}\cdot \mathbf {s}},\quad \mathbf {k}\in \Lambda _0,\\&\Lambda _0:=\left\{ \mathbf {k}\in \mathbb {R}^4_H \cap \mathbb {Z}^4: k_0\equiv k_1\equiv k_2 \equiv k_3 \,\,(\mathrm{{mod}}\, 4), k_0<k_1<k_2<k_3 \right\} . \end{aligned} \end{aligned}$$
(D.3)
Here \(\mathrm {i}\) is the imaginary number satisfying \(\mathrm {i}^2=-1.\) Let \(\mathcal {G}\) be the permutation group of four elements. For \(\mathbf {k}\in \mathbb {R}^4_{H}\) and \(\sigma \in \mathcal {G},\) the permutation of the elements in \(\mathbf {k}\) by \(\sigma \) is denoted by \(\mathbf {k}\sigma .\) The generalized sine functions are then defined as [23 , Definition 4.2]
$$\begin{aligned} \mathrm{TS}_{\mathbf {k}}(\mathbf {s}):= \frac{1}{24} \sum \limits _{\sigma \in \mathcal {G}} (-1)^{|\sigma |} \phi _{\mathbf {k}\sigma }(\mathbf {s}),\quad \mathbf {k}\in \Lambda _0, \end{aligned}$$
(D.4)
where \(|\sigma |\) represents the number of inversions in \(\sigma .\) Thus, we arrive at the following lemma.
Lemma D.1
The generalized sine functions \(\mathrm{TS}_{\mathbf {k}}(\mathbf {s}), \mathbf {k}\in \Lambda _0\) are the eigenfunctions of the Laplacian on \(\mathcal {T}_F\) subject to the homogeneous Dirichlet boundary condition:
$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta \mathrm{TS}_{\mathbf {k}}(\mathbf {s}) = \mu _{\mathbf {k}} \mathrm{TS}_{\mathbf {k}}(\mathbf {s}),\quad &{}\mathrm{{in}}\,\mathcal {T}_F,\\ \mathrm{TS}_{\mathbf {k}}(\mathbf {s})=0,\quad &{}\mathrm{{on}}\,\partial \mathcal {T}_F, \end{array}\right. } \end{aligned}$$
(D.5)
where
$$\begin{aligned} \mu _{\mathbf {k}}=\frac{\pi ^2|\mathbf {k}|^2}{4},\quad |\mathbf {k}|^2=\sum \limits _{j=0}^3 k_j^2. \end{aligned}$$
(D.6)
Proof
Due to the symmetry of \(\mathrm{TS}_{\mathbf {k}}(\mathbf {s})\) , it vanishes on \(\partial \mathcal {T}_F.\) From the transformation (D.2 ), we have
$$\begin{aligned} \begin{aligned}&\partial _{s_1}-\partial _{s_0} = \partial _{x_2}+\partial _{x_3},\quad \partial _{s_2}-\partial _{s_0} = \partial _{x_3}+\partial _{x_1},\quad \partial _{s_3}-\partial _{s_0} = \partial _{x_1}+\partial _{x_2},\\&\partial _{s_1}-\partial _{s_2} = \partial _{x_2}-\partial _{x_1},\quad \partial _{s_2}-\partial _{s_3} = \partial _{x_3}-\partial _{x_2},\quad \partial _{s_3}-\partial _{s_1} = \partial _{x_1}-\partial _{x_3}. \end{aligned} \end{aligned}$$
One easily obtains an equivalent expression of the Laplacian operator in homogenous coordinates that
$$\begin{aligned} \Delta = \frac{1}{4} \sum \limits _{1\le i< m\le 3} \left( \left( \partial _{x_i}+\partial _{x_m}\right) ^2 + \left( \partial _{x_i}-\partial _{x_m}\right) ^2 \right) = \frac{1}{4} \sum \limits _{0\le j< n\le 3} \left( \partial _{s_j} - \partial _{s_n}\right) ^2. \end{aligned}$$
(D.7)
Applying (D.7 ) on \(\phi _{\mathbf {k}}\) yields
$$\begin{aligned} \begin{aligned} -\Delta \phi _{\mathbf {k}}(\mathbf {s})&= -\frac{1}{4} \sum \limits _{0\le j< n\le 3} \left( \partial _{s_j} - \partial _{s_n}\right) ^2 \phi _{\mathbf {k}}(\mathbf {s})= \frac{\pi ^2}{16} \sum \limits _{0\le j< n\le 3} \left( k_j - k_n\right) ^2 \phi _{\mathbf {k}}(\mathbf {s})\\&= \frac{\pi ^2}{32} \sum \limits _{\begin{array}{c} 0\le j, n\le 3 \\ j\ne n \end{array}} \left( k_j - k_n\right) ^2 \phi _{\mathbf {k}}(\mathbf {s})\\&= \frac{\pi ^2}{32} \left( 4\sum \limits _{j=0}^3 k_j^2 + 4\sum \limits _{n=0}^3 k_n^2 -2 \left( \sum \limits _{j=0}^3 k_j \right) \left( \sum \limits _{n=0}^3 k_n \right) \right) \phi _{\mathbf {k}}(\mathbf {s})\\&= \frac{\pi ^2}{4} \sum \limits _{j=0}^3 k_j^2 \phi _{\mathbf {k}}(\mathbf {s})= \frac{\pi ^2}{4} |\mathbf {k}|^2 \phi _{\mathbf {k}}(\mathbf {s}). \end{aligned} \end{aligned}$$
Therefore, by the definition of generalized sine functions (D.4 ), it holds that
$$\begin{aligned} \begin{aligned} -\Delta \mathrm{TS}_{\mathbf {k}}(\mathbf {s})&= \frac{1}{24} \sum \limits _{\sigma \in \mathcal {G}} (-1)^{|\sigma |+1} \Delta \phi _{\mathbf {k}\sigma }(\mathbf {s})= \frac{\pi ^2}{4} \frac{1}{24} \sum \limits _{\sigma \in \mathcal {G}} (-1)^{|\sigma |} |\mathbf {k}\sigma |^2 \phi _{\mathbf {k}\sigma }(\mathbf {s})\\&=\frac{\pi ^2 |\mathbf {k}|^2 }{4} \frac{1}{24} \sum \limits _{\sigma \in \mathcal {G}} (-1)^{|\sigma |} \phi _{\mathbf {k}\sigma }(\mathbf {s})= \frac{\pi ^2 |\mathbf {k}|^2 }{4} \mathrm{TS}_{\mathbf {k}}(\mathbf {s}). \end{aligned} \end{aligned}$$
This completes the proof. \(\square \)