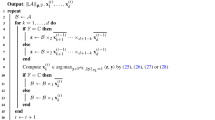Orthogonal Iterations on Companion-Like Pencils

Abstract

We present a class of fast subspace algorithms based on orthogonal iterations for structured matrices/pencils that can be expressed as small rank perturbations of unitary matrices. The representation of the matrix by means of a new data-sparse factorization—named LFR factorization—using orthogonal Hessenberg matrices is at the core of these algorithms. The factorization can be computed at the cost of $O(n k^2)$ arithmetic operations, where n and k are the sizes of the matrix and the small rank perturbation, respectively. At the same cost from the LFR format we can easily obtain suitable QR and RQ factorizations where the orthogonal factor Q is a product of orthogonal Hessenberg matrices and the upper triangular factor R is again given into the LFR format. The orthogonal iteration reduces to a hopping game where Givens plane rotations are moved from one side to the other side of these two factors. The resulting new algorithms approximate an invariant subspace of size s associated with a set of s leading or trailing eigenvalues using only O(nks) operations per iteration. The number of iterations required to reach an invariant subspace depends linearly on the ratio $|\lambda _{s+1}|/|\lambda _s|$. Numerical experiments confirm the effectiveness of our adaptations.

1 Introduction

Subspace methods are an important tool in modern adaptive systems [33]. The goal is the iterative estimation of the s largest or smallest eigenvalues and the associated eigenvectors of a possibly time-varying matrix/pencil. In this paper, we are concerned with the design of fast subspace algorithms for a class of structured matrices (pencils) representable as small rank perturbations of unitary matrices. The paramount example is (block) companion matrices/pencils arising from the linearization of polynomial eigenvalue problems. The companion form linearization of a matrix polynomial $P(\lambda )=\sum _{i=0}^d P_i\lambda ^i$, $P_i\in {\mathbb {C}}^{k\times k}$, is given by

$$\begin{aligned} A=\left[ \begin{array}{cccc} -P_{d-1} &{} \ldots &{}\ldots &{} -P_0 \\ I_k \\ &{} \ddots \\ &{} &{} I_k \end{array} \right] , \quad B=\left[ \begin{array}{cccc} P_d \\ &{} I_k \\ &{} &{} \ddots \\ &{} &{} &{} I_k \end{array} \right] , \end{aligned}$$

(1.1)

with $A, B\in {\mathbb {C}}^{n\times n}$, $n=dk$. It is well known that the eigenvalues of $A -\lambda B$ are identical with the eigenvalues of $P(\lambda )$. Also, observe that $A, B\in {\mathcal {U}}_k$, the set of unitary-plus-rank-k matrices.

The computation of selected eigenspaces of large companion pencils has several applications.

• 1. Subspace tracking is often required in system and signal processing analysis because the characteristics of the possibly time-varying system (signal) can be retrieved from the eigenvalues of some associated parameter-dependent matrix polynomial [22, 23, 30, 34]. Subspace methods are ideally suited for these computations since they can use the approximate eigenspace computed in the previous step as starting guess for the new iteration.

• 2. Adaptations of the block power method as well as its orthogonal generalizations are used to compute the solvents and spectral factors of a matrix polynomial (see [37] for a review and applications of the matrix solvent theory). The unilateral matrix equation $\sum _{i=0}^d P_i X^i=0$ is equivalent to

  $$\begin{aligned} A \left[ \begin{array}{cccc} {X^T}^{d-1}&\ldots&X^T&I_k \end{array}\right] ^T = B \left[ \begin{array}{cccc} {X^T}^{d-1}&\ldots&X^T&I_k \end{array}\right] ^T X. \end{aligned}$$

  The matrix X is called the solvent and its computation reduces to approximate an invariant subspace of (A, B).

• 3. Nonlinear eigenvalue problems of the form $T(z)v=0,$ $v\ne 0$, where $T:\Omega \rightarrow {\mathbb {C}}^{k\times k}$ is a holomorphic matrix-valued function and $\Omega \subseteq {\mathbb {C}}$ is a connected and open set, can be addressed using interpolation techniques [20, 24]. The approach consists first of interpolating T(z) with a matrix polynomial $P_d(z)$ at certain nodes inside a subset $\Delta \subset \Omega$, and then of computing the eigenvalues of $P_d(z)$ to provide numerical approximations of the eigenvalues of T(z) in $\Delta$. Since in general we are interested only in the few eigenvalues of T(z) laying inside the target region $\Delta$, it is convenient to approximate only the eigenvalues of interest rather than approximate the full spectrum of $P_d(z)$.

Subspace methods based on orthogonal iterations can be numerically accurate and backward stable. The method of orthogonal iteration goes back to Bauer (see [32] and the reference given therein). A fast eigenvalue algorithm for $n\times n$ scalar companion matrices based on orthogonal iteration first appeared in [36]. Essentially, that algorithm is a game of orthonormal Givens plane rotations moved from one side to the other side of orthogonal factors at the cost of O(ns) flops, where s is the dimension of the subspace we want to approximate. More recently such schemes have been termed core-chasing algorithms [5].

In this paper we extend the game to more general matrices $A\in {\mathbb {C}}^{n\times n}$ which are unitary plus some low rank-k correction term, $k\ge 1$. This class includes block companion matrices together with some generalizations for matrix polynomial expressed w.r.t. certain interpolation bases [1, 15]. The development follows by exploiting the properties of a suitable LFR factorization [11, 12] of some bordered extension ${\widehat{A}}$ of A, that is, ${\widehat{A}}=LFR$, where L (R) is a unitary k-lower (k-upper) Hessenberg matrix and $F=U+EZ$ is a unitary plus rank-k matrix where U is a block diagonal unitary matrix of the form $\begin{bmatrix}I_k &{}\\ &{} {\hat{U}} \end{bmatrix}$ and $E=[I_k, 0]^T$. The unitary matrix ${\hat{U}}$ can be expressed as product of $\ell <n-k$ unitary Hessenberg matrices.

It is shown that the shape of ${\hat{U}}$ determines the shape of ${\widehat{A}}$. In particular ${\widehat{A}}$ and, a fortiori, A is upper triangular if and only if ${\hat{U}}$ is upper triangular and hence, because of the unitary structure of U, diagonal. This key property makes it possible to design a fast implementation of both direct and inverse orthogonal iteration on A. Specifically, from the LFR format of ${\hat{A}}$, we can easily get suitable QR and RQ factorizations of ${\hat{A}}$ at the cost of $O(nk\ell )$ flops, where the orthogonal factor Q is a product of orthogonal Hessenberg matrices and the upper triangular factor R is again given into the LFR format. It turns out that for the matrices of interest $\ell \le k$. Direct and inverse orthogonal iterations applied to A can be carried out stably and efficiently by using these factorizations. Specifically, we show that both iterations can be implemented by moving the Givens plane rotations which specify the current approximation from one side to the other side of the factorizations. Due to the representation of the two factors R and Q in terms of orthogonal Hessenberg matrices the movement of one single rotation reduces to hop from one Hessenberg matrix to the successive in a chain of k matrices. The overall movement is therefore completed at each step with a cost per iteration of only O(nsk) flops.

The resulting algorithm is backward stable since it involves operations among orthogonal matrices only. The corresponding unstructured implementation performed without any preliminary reduction of A into Hessenberg form would require a quadratic complexity in both s and k per iteration. The linear dependence of our estimate from these two quantities makes the proposed algorithm maximally fast w.r.t. the size of the correction term and the invariant eigenspace. Moreover, it can be easily generalized to deal with both the orthogonal and the inverse orthogonal iteration method for structured pencils (A, B) where A and/or B are perturbed unitary matrices.

The paper is organized as follows. In Sect. 2 we recall the theoretical background concerning the orthogonal iteration methods and the properties of modified unitary matrices. Section 3 presents the derivation of our fast adaptations of the orthogonal iteration methods for modified unitary matrices. In Sect. 4 we show the results of numerical experiments that lend support to the theoretical findings. Finally, Sect. 5 summarizes conclusions and future work.

2 Preliminaries

In this section we recall some preliminary results concerning the formulation of both direct and inverse orthogonal iterations for matrix pencils and the structural properties and data-sparse representations of modified unitary matrices.

2.1 The Method of Orthogonal Iteration for Matrix Pencils

The method of orthogonal iteration (sometimes called subspace iteration or simultaneous iteration) can be easily generalized for matrix pencils. Let $A-\lambda B$, $A,B\in {\mathbb {C}}^{n\times n}$, be a regular matrix pencil with A or B invertible. The orthogonal iteration method can be applied for approximating the largest or smallest magnitude eigenvalues of the matrix pencil by working on the matrices $B^{-1} A$ or $A^{-1}B$.

If B is nonsingular then a generalization of the orthogonal iteration method to compute the s-largest (in magnitude) generalized eigenvalues and corresponding eigenvectors of the matrix pencil $A-\lambda B$ proceeds as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} AQ_i=BZ_{i+1} &{}\quad i=1, 2 \ldots \\ Q_{i+1}R_{i+1}=Z_{i+1} &{}\quad \text {economy size QR factorization of } Z_{i+1}. \end{array} \right. \end{aligned}$$

(2.1)

where $Q_1\in {\mathbb {C}}^{n\times s}$ is a starting orthonormal matrix comprising the initial approximations of the desired eigenvectors. A detailed convergence analysis of this iteration can be found in Chapter 8 of [2]. It is found that the convergence is properly understood in terms of invariant subspaces. Specifically, under mild assumptions it is proved that the angle between the subspace generated by the columns of $Q_i$ and the invariant subspace associated with the s largest-magnitude generalized eigenvalues $\lambda _1, \lambda _2, \ldots , \lambda _s \in {\mathbb {C}}$, with $|\lambda _1|\ge \ldots \ge |\lambda _s|>|\lambda _{s+1}| \ge \ldots \ge |\lambda _{n}|$, tends to zero as $O((|\lambda _{s+1}|/|\lambda _{s}|)^i)$ for i going to infinity. The number of iterations required to reach an invariant subspace depends linearly on the ratio $|\lambda _{s+1}|/|\lambda _s|$. Once the subspace has been approximated projection techniques can be employed to find single eigenvalues and corresponding eigenvectors. An effective stopping criterion is the following

$$\begin{aligned} \Vert E_i\Vert _2=\Vert (I-Q_{i-1}Q_{i-1}^*)Q_i\Vert _2<\tau , \end{aligned}$$

(2.2)

where $\tau$ is a desired tolerance. Observe that this quantity measures the distance between the subspaces ${\mathcal {S}}_{i-1}=\mathrm{span}\{Q_{i-1}\}$ and ${\mathcal {S}}_{i}=\mathrm{span}\{Q_i\}$, in fact $(I-Q_{i-1}Q_{i-1}^*))Q_i$ can be taken as a measure of the angle between ${\mathcal {S}}_{i-1}$ and ${\mathcal {S}}_{i}$. Note moreover that

$$\begin{aligned} E_i^*E_i=Q_i^*(I-Q_{i-1}Q_{i-1}^*)(I-Q_{i-1}Q_{i-1}^*)Q_i=Q_i^*(I-Q_{i-1}Q_{i-1}^*)Q_i=I_s-W^*W, \end{aligned}$$

where $W=Q_{i-1}^*Q_i$. Then $\Vert E_i\Vert _2^2=1-\sigma _{min}^2(W)$. At convergence ${\mathcal {S}}_{i-1}\approx {\mathcal {S}}_{i}$ then $Q_{i}\approx Q_{i-1}U$ for an $s\times s$ unitary matrix U, then $\sigma _i(W)\approx \sigma _i(U)=1$ for $i=1, \ldots , s$.

Assume now we are given a pencil $A-\lambda B$ with A invertible and that we would like to compute the s smallest-magnitude generalized eigenvalues $\lambda _1, \lambda _2, \ldots , \lambda _s \in {\mathbb {C}}$ with $|\lambda _1|\le |\lambda _2|\le \cdots \le |\lambda _s|<|\lambda _{s+1}| \le \ldots \le |\lambda _{n}|$. Inverse orthogonal iterations can be used to approximate the desired eigenvalues. Starting with a set of s orthogonal vectors stored in the matrix $Q_0\in {\mathbb {C}}^{n\times s}$, we compute the sequences

$$\begin{aligned} \left\{ \begin{array}{ll} AZ_i=BQ_{i-1} &{}\quad i=1, 2 \ldots \\ Q_{i}R_{i}=Z_i &{}\quad \text {economy size QR factorization of}\; Z_i. \end{array} \right. \end{aligned}$$

(2.3)

The direct and inverse orthogonal iterations (2.1), (2.3) can be carried out by solving the associated linear systems, but such an approach is prone to numerical instabilities due to the conditioning of the resulting coefficient matrices. A more stable way to perform these schemes is using the QR/RQ factorization of the matrices involved. In particular for the inverse iteration (2.3) one may proceed at each step as:

• 1. Compute the full QR factorization of $Q_R R_R:=BQ_{i-1}$;

• 2. Compute the full RQ factorization of $R_LQ_L:=Q_R^*A$;

• 3. Determine $Q_i$ such that $Z_i=Q_iR_i$ solves $R_LQ_L Z_i=R_R$. The set of orthogonal vectors satisfying the linear system is such that $Q_i^*=Q_L(1:s, :)$.

In the next subsection we introduce a suitable factorization of modified unitary matrices which makes possible to realize this QR-based process in an efficient way. Since (2.1) can be implemented similarly by interchanging the role of the matrices A and B, in the sequel we refer to orthogonal iteration as the scheme (2.3).

2.2 Fast Compressed Representations of Modified Unitary Matrices

In this section we introduce a suitable compressed factorization of unitary plus rank-k matrices which can be exploited for the design of fast orthogonal iterations according to the QR-based process described above. See [11, 12] for additional theoretical results.

We denote by ${\mathcal {U}}_k$ the set of unitary-plus-rank-k matrices, that is, $A \in {\mathcal {U}}_k$ if and only if there exists a unitary matrix V and two skinny matrices $X, Y\in {\mathbb {C}}^{n\times k}$ such that $A = V + XY^*$. A key role is played by generalized Hessenberg factors.

Definition 2.1

A matrix $R\in {\mathbb {C}}^{m\times m}$ is called k-upper Hessenberg if $r_{ij}=0$ when $i>j+k$. Similarly, L is called k-lower Hessenberg if $l_{ij}=0$ when $j>i+k$. In addition, when R is k-upper Hessenberg (L is k-lower Hessenberg) and the outermost entries are non-zero, that is, $r_{j+k,j}\ne 0$ ($l_{j,j+k}\ne 0$), $1\le j\le m-k$, then the matrix is called proper. A matrix which is simultaneously k-lower and k-upper Hessenberg is called k-banded.

Note that for $k=1$ a Hessenberg matrix is proper if and only if it is unreduced. Also, a k-upper Hessenberg matrix $R\in {\mathbb {C}}^{m\times m}$ is proper if and only if $\det (R(k+1:m, 1:m-k))\ne 0$. Similarly a k-lower Hessenberg matrix L is proper if and only if $\det (L(1:m-k, k+1:m))\ne 0$. To make the presentation easier when possible, we use the letter R to denote unitary generalized upper Hessenberg matrices, and the letter L for unitary generalized lower Hessenberg matrices.

Note that k-lower (upper) Hessenberg matrices can be obtained as the product of k matrices with the lower (upper) Hessenberg structure, and that unitary block Hessenberg matrices with blocks of size k are (non-proper) k-Hessenberg matrices.

In the following we will work with Givens rotations acting on two consecutive rows and columns. In particular we will denote by ${{\mathcal {G}}}_i=I_{i-1}\oplus G_i \oplus I_{n-i-1}$ the $n\times n$ unitary matrix where $G_i$ is a $2\times 2$ complex Givens rotation of the form $\left[ \begin{array}{cc} c &{}-s\\ s&{} {\bar{c}} \end{array}\right]$ such that $|c|^2+s^2=1$, with $s\in {\mathbb {R}}, s\ge 0$. The subscript index i indicates the active part of the matrix ${{\mathcal {G}}}_i$. In the case $G_i=I_2$ we say that $G_i$ is a trivial rotation.

Definition 2.2

Given a unitary matrix $U\in {\mathbb {C}}^{n\times n}$, we say that U has a data-sparse representation if it can be expressed as the product of O(n) Givens matrices of the form ${{\mathcal {G}}}_i$ described before, possibly multiplied by a diagonal unitary matrix.

Note that the Definition 2.2 includes unitary (generalized) Hessenberg defined in 2.1, CMV-matrices [17], and other zig–zag patterns [38], as well as the product of a constant number of these structures.

Next lemma shows how the product between data-sparse unitary terms can be factorized swapping the role of the two factors.

Lemma 2.3

Let $R\in {\mathbb {C}}^{n\times n}$ be a unitary k-upper Hessenberg matrix and let U be a unitary matrix. Then there exist two unitary matrices V and S such that $RU=VS$ where S is k-upper Hessenberg and $V=\begin{bmatrix} I_k&{}\\ &{} {\hat{V}}. \end{bmatrix}$ Similarly, let L be a unitary k-lower Hessenberg matrix and let U be a unitary matrix. Then there exist two unitary matrices V and M such that $LU=VM$ where M is k-lower Hessenberg and $V=\begin{bmatrix} {\hat{V}} &{}\\ &{} I_k. \end{bmatrix}$

Proof

Let us partition R and U as follows

$$\begin{aligned} R=\begin{bmatrix} R_{11}&{}R_{12}\\ R_{21} &{} R_{22}, \end{bmatrix}\quad U=\begin{bmatrix} U_{11}&{}U_{12}\\ U_{21} &{} U_{22} \end{bmatrix} \end{aligned}$$

where $R_{21}$ is an upper triangular matrix of size $n-k$, and $U_{11}$ is square of size $n-k$. Multiplying R and U and imposing the conditions on the blocks of the product VS we get $S_{11}=R_{11}U_{11}+R_{12}U_{21}, S_{12}=R_{11}U_{12}+R_{12}U_{22}$. Moreover, since S should be a k-upper Hessenberg matrix, we have that $S_{21}$ should be triangular. Hence ${\hat{V}}$ and $S_{21}$ can be computed as the Q and R factors of the QR factorization of $R_{21} U_{11}+R_{22}U_{21}$. Finally we set $S_{22}={\hat{V}}^*(R_{21}U_{12}+R_{22}U_{22})$. Using the same technique we prove that there exist V and M such that $LU=VM$. $\square$

Definition 2.4

The (lower) staircase of a matrix $A = (a_{i,j} ) \in {\mathbb {C}}^{n\times n}$ is the sequence $m_j(A), 1 \le j \le n$, defined as follows

$$\begin{aligned} m_0(A)=0, \quad m_j(A) =\max \{ m_{j-1}(A), \max _{i>j} \{i : a_{i,j} \ne 0 \}\}. \end{aligned}$$

The sequence $m_j(A)$ allows to represent the zero pattern of a matrix, in particular to identify zero sub-blocks in the matrix, in fact for each $1\le j\le n,$ it holds $A(m_j(A)+1:n, 1:j)=0$. We note that proper k-upper Hessenberg matrices have $m_j(A)=j+k$ for $j=1, \ldots , n-k$, and $m_j(A)=n$, for $j=n-k+1, \ldots , n$.

Lemma 2.5

Let $A\in {\mathbb {C}}^{n\times n}$ be a matrix with staircase described by the sequence $\{m_j(A)\}$, for $1\le j\le n$ and let $T\in {\mathbb {C}}^{n\times n}$ be a non singular upper triangular matrix, we have $m_j(TA)=m_j(AT)=m_j(A)$ for $1\le j\le n$.

Proof

Let $B=TA$. We have $b_{ij}=\sum _{s=i}^n t_{is}a_{sj}$. Because of the staircase profile of A we have $a_{sj}=0$, for $s>m_j(A)$, hence $b_{ij}=0$ for $i>m_j(A)$, implying that $m_j(B)\le m_j(A)$. To prove the equality of the staircase profile of B and A consider the entry $b_{m_j(A), j}=t_{m_j(A), m_j(A)} a_{m_j(A), j}$. If $a_{m_j(A), j}\ne 0$ we conclude that $m_j(B)=m_j(A)$, however it may happen that $a_{m_j(A), j}= 0$, but from the definition of staircase profile we know that there exists an index $s, s<j$ such that $a_{m_j(A), s}\ne 0$, and $m_s(A)=m_j(A)$. Hence $b_{m_j(A), s}= r_{m_j(A), m_j(A)}a_{m_j(A), s}\ne 0$, implying that $m_j(B)=m_s(A)=m_j(A)$. The proof that $m_j(AT)=m_j(A)$ can be carried on with a similar technique. $\square$

Any unitary matrix of size n can be factorized as the product of at most $n-1$ unitary upper Hessenberg matrices,¹ that is $U=R_{n-1}R_{n-2}\ldots R_1\, D$, where each $R_{i}=\prod _{j=i}^{n-1}{{\mathcal {G}}}_j$ and D is a diagonal unitary matrix. To describe the representation and the algorithm we use a pictorial representation already introduced in several papers (compare with [5] and the references given therein). Specifically, the action of a Givens rotation acting on two consecutive rows of the matrix is depicted as . Then a chain of ascending two-pointed arrows as below

represents a unitary upper Hessenberg matrix (in the case of size 8). Some of the rotations may be identities (trivial rotations), and we might omit them in the picture. For example, in the above definition of $H_{i}$ we only have non-trivial rotations ${{\mathcal {G}}}_{j}$ for $j\ge i$, while the representation of $H_3$ is

Givens transformations can also interact with each other by means of the fusion or the turnover operations (see [39], pp. 112–115). The fusion operation will be depicted as and consists of the concatenation of two Givens transformations acting on the same rows. The result is a Givens rotation multiplied by a $2\times 2$ phase matrix. The turnover operation allows to rearrange the order of Givens transformations (see [39]).

Graphically we will depict this rearrangement of Givens transformations as:

Note that if the Givens transformations involved in turnover operations are all non-trivial also the resulting three new matrices are non trivial (see [4]).

In this paper we are interested in the computation of a few eigenvalues of matrices belonging to ${{\mathcal {U}}}_k$ by means of the orthogonal iteration schemes outlined in Sect. 2.1. We will represent these matrices in the so-called LFR format, a factorization introduced in [11, 12].

Definition 2.6

We say that a matrix $A\in {\mathbb {C}}^{n\times n}, A\in {\mathcal {U}}_k$ is represented in the LFR format if (L, F, R) are matrices such that:

• 1. $A=LFR$;

• 2. $L\in {\mathbb {C}}^{n\times n}$ is a unitary k-lower Hessenberg matrix;

• 3. $R\in {\mathbb {C}}^{n\times n}$ is a unitary k-upper Hessenberg matrix;

• 4. $F=U+ E \,Z^*\in {\mathbb {C}}^{n\times n}$ is a unitary plus rank-k matrix, where $U=\begin{bmatrix}I_k &{}\\ &{} {\hat{U}} \end{bmatrix}$, with ${\hat{U}}$ unitary, $E=[I_k, 0]^T$ and $Z\in {\mathbb {C}}^{n\times k}$.

Any matrix in ${\mathcal {U}}_k$ can be brought in the LFR format as follows. Let $A\in {\mathcal {U}}_k$, such that $A=V+XY^*$ , then L is a k-lower unitary Hessenberg such that $L^*X=\begin{bmatrix}T_k\\ 0\end{bmatrix}$, where $T_k$ is upper triangular. Then $A=L(L^*V+\begin{bmatrix}T_k\\ 0\end{bmatrix} Y^*)$. Using Lemma 2.3 we can rewrite $L^*V=UR$, where R is unitary k-upper Hessenberg and $U=\left[ \begin{array}{c|c} I_k &{} \\ \hline &{} {\hat{U}} \end{array}\right]$ with ${\hat{U}}$ unitary. Bringing R on the right we get our factorization, where $F=U+E Z^*$ and $Z=R\,Y\,T_k^*$.

The LFR format of modified unitary matrices is the key tool to develop fast and accurate adaptations of the orthogonal iterations as we will see in the next section.

3 Fast Adaptations of the Orthogonal Iterations

As underlined in Sect. 2.1, to compute the next orthogonal vectors approximating a basis of the invariant subspace we need to compute the QR decomposition of $BQ_i$ and the RQ decomposition of $Q_R^*A$.

3.1 RQ and QR Factorization of Unitary Plus Low Rank Matrices

To recognize the triangular factors from the LFR decomposition of A and B it is useful to embed the matrices of the pencil into larger matrices obtained edging the matrices with k additional rows and columns. Next theorem explains how we can get such a larger matrices still maintaining the unitary plus rank-k structure.

Theorem 3.1

Let $A\in {\mathbb {C}}^{n\times n} , A\in {\mathcal {U}}_k$, then it is always possible to construct a matrix of size $m=n+k$, ${\hat{A}}\in {\mathcal {U}}_k$ of size $m=n+k$ such that

$$\begin{aligned} {\hat{A}}=\begin{bmatrix} A&{} C_A\\ 0_{kn}&{} 0_{kk} \end{bmatrix} \quad \text {for a suitable}\; C_A. \end{aligned}$$

(3.1)

The unitary part of ${\hat{A}}$ can be described with additional nk Givens rotations with respect to the representation of the unitary part of A.

Proof

Let $A=V+XY^*$, with V unitary. We assume that $Y\in {\mathbb {C}}^{n\times n}$ has orthogonal columns, otherwise we compute the economy size QR factorization of Y and then we set $Y=Q$ and $X=XR^*$. Set $C_A=VY$, and consider the matrices

$$\begin{aligned} {\hat{V}}=\begin{bmatrix} V-VYY^*&{} C_A\\ Y^*&{}0_k \end{bmatrix} ,\quad {\hat{X}}=\begin{bmatrix} X+C_A\mathrm{i}_k \end{bmatrix},\quad {\hat{Y}}= \begin{bmatrix} Y\\ 0_k \end{bmatrix}. \end{aligned}$$

(3.2)

We can prove that ${\hat{V}}$ is unitary by direct substitution. The last k rows of ${\hat{A}}={\hat{V}}+{\hat{X}}{\hat{Y}}^*$ are zero. The matrix V can be factorized as product of unitary factors which are related to the original players of A, namely V, X and Y. In particular

$$\begin{aligned} {\hat{V}}=\begin{bmatrix} V&{}\\ &{} I_k \end{bmatrix}S\begin{bmatrix}-I_k&{}\\ &{}I_n\end{bmatrix} S^*, \end{aligned}$$

where S is a k-lower Hessenberg matrix such that

$$\begin{aligned} S^*\begin{bmatrix}Y\mathrm{i}_k\end{bmatrix}=\begin{bmatrix}\sqrt{2} I_k\\ 0\end{bmatrix}. \end{aligned}$$

Such a S always exists and is proper (see Lemma 3 in [12]). $\square$

Note that the LFR format of ${\hat{A}}$ is such that L is proper, since ${\hat{X}}$ has the last k rows equal to $-I_k$ (see [12] Lemma 3).

Theorem 3.2

Let $L, R\in {\mathbb {C}}^{m\times m}$, $m=n+k$, be two unitary matrices, where L is a proper unitary k-lower Hessenberg matrix and R is a proper unitary k-upper Hessenberg matrix. Let U be a block diagonal unitary matrix of the form $U=\left[ \begin{array}{l|l} I_k &{} \\ \hline &{} {\hat{U}} \end{array}\right]$, with ${\hat{U}}$ $n\times n$ unitary. Let F be the unitary plus rank$-k$ matrix defined as $F=U+E\,Z^*$ with $Z\in {\mathbb {C}}^{m\times k}$. Suppose that the matrix ${\hat{A}}=LFR$ satisfies the block structure in (3.1). Then $A={\hat{A}}(1:n, 1:n)$ is nonsingular and has the staircase profile of ${\hat{U}}$.

Proof

Since L is unitary, we have $L^*{\hat{A}}=FR$. Let partition L and R as follows: $L=\begin{bmatrix} L_{11} &{}L_{12}\\ L_{21}&{}L_{22}\end{bmatrix}$, with $L_{12}$ a $n\times n$ lower triangular matrix, and similarly partition R in such a way that $R_{21}$ is $n\times n$ upper triangular. Then we get $L_{12}^* A={\hat{U}} R_{21}.$ For Lemma 2.5 we know that $L_{12}^* A$ has the same staircase profile as A, and ${\hat{U}} R_{21}$ has the same staircase profile as ${\hat{U}}$. $\square$

Next lemma helps us to recognize triangular matrices in the LFR format.

Lemma 3.3

If ${\hat{A}}=L(I+E \,Z^*)R$ satisfies the block structure in (3.1), then ${\hat{A}}$ is upper triangular.

Proof

We have $L_{21}^* A=R_{21}$. Because L is proper, the triangular block $L_{12}^*$ is nonsingular and $A=({L_{12}^{*}})^{-1}R_{21}$. Hence A is upper triangular because is the product of upper triangular factors. ${\hat{A}}$ is upper triangular as well because is obtained padding with zeros (3.1). $\square$

We now give an algorithmic interpretation of Lemma 2.3. A pictorial interpretation of the lemma is given in Fig. 1, where we omit the diagonal unitary factors that are possibly present in the general case.

Fig. 1

An example of the swap Lemma 2.3. Here R is a unitary 2-upper Hessenberg matrix factorized as the product of two descending sequence of Givens rotations. The unitary matrix U is represented in terms of a sparse set of rotations. When applying the rotations of U to R only the rotations in the blue triangle pop out (transformed by the turnover operations) on the left, while the remaining Givens transformations of U are fused with the bottom transformations of R. In the picture we omit to represent a diagonal phase matrix which can be produced by the fusion operations (Color figure online)

Starting from Fig. 1 we can describe an algorithm for the “swap” of two unitary terms. In fact, we can obtain the new Givens rotations in the factors V and S simply applying repeatedly fusion and turnover operations as described by the algorithm in Fig. 2. We formalize the algorithm as if the Givens rotations involved in the swap were all non-trivial. The algorithm has a cost O(nk) only when U admits a data-sparse representation. Matrix U can be generally factorized as the product of at most $\ell \le n-1$ unitary upper or lower Hessenberg matrices. In this case the overall cost is $O(nk\ell )$. In procedure SwapRU we choose to factorize U as the product of lower Hessenberg factors, but we can obtain a similar algorithm expressing U in terms of upper Hessenberg factors, and consider the worst case $\ell =n-1$. At step $i-1$ we have removed the first $i-1$ chains of ascending Givens rotations from U, so the situation is the following

$$\begin{aligned} RU=V^{(1)}V^{(2)}\cdots V^{(i-1)} \, \Sigma _i L^{(i)}\cdots L^{(n-1)}, \end{aligned}$$

where $\Sigma _i$ is an intermediate k-upper Hessenberg which is transformed by the turnover and fusion operations. In particular $\Sigma _1=R$ and $\Sigma _{n-1}=S$.

At the step i we pass the rotations in $L^{(i)}$, from right to left. The bottom k Givens of each $L^{(i)}$ are fused with the Givens in the last rows of $\Sigma _i$, so that the shape of ${\hat{V}}$ reproduces the shape of the Givens rotations in the blue top triangle of U.

Fig. 2

Procedure to swap an upper and a lower generalized Hessenberg matrices

Similarly to the procedure SwapRU we can design a procedure SwapLU to factorize the product between a unitary k-lower Hessenberg matrix L and a unitary matrix U as the product of a unitary factor $V=\begin{bmatrix} {\hat{V}} &{} \\ &{} I_k \end{bmatrix}$ and a unitary k-lower Hessenberg matrix M. Note that from these two swapping procedures we can obtain also new factorizations when multiplying on the left a k-lower or a k-upper Hessenberg unitary matrix, that is $U^*R^*=(RU)^*=(VS)^*=S^* V^*$, and $U^*L^*=(LU)^*=(VM)^*=M^*V^*$. We will denote the analogue procedures as SwapUL and SwapUR keeping in mind that the matrices involved are unitary, and that we denote generalized lower Hessenberg matrices using the letter L and generalized upper Hessenberg matrices using the letter R.

From the LFR format of ${\hat{A}}$ we can easily get the QR and RQ factorization of ${\hat{A}}$. This procedure requires $O(nk\ell )$ flops where $\ell$ is the number of Hessenberg unitary factors in U. Let ${\hat{A}}=L(U+E \, Z^*)R$ as in Definition 2.6. Swapping L and U according with Lemma 2.3, i.e $LU= Q {\tilde{L}}$, we have that ${\tilde{L}}(I+E\, Z^*)R$ is upper triangular for Lemma 3.3. Since Q is unitary, we have a QR decomposition of A. Similarly swapping U and R in such a way that $UR={\hat{R}} \,Q$ we get an RQ decomposition of A where the triangular factor is $L(I+E\,{\hat{Z}}^*){\hat{R}}$, with ${\hat{Z}}= UZ$, and the unitary factor is Q. The proof is straightforward since, again from Lemma 3.3, we have that $L(I+E\,{\hat{Z}}^*){\hat{R}}$ is upper triangular.

3.2 The Algorithm

In this section we describe the orthogonal iterations on a pencil (A, B) where A and B are unitary-plus-low-rank matrices. For the sake of readability we assume $A, B\in {\mathcal {U}}_k$, even if situation where the low-rank part of A and B do not have the same rank is possible: in that case we assume that k is the maximum between the values of the low rank parts in A and B.

We will assume that A and B have been embedded in a larger pencil $({\hat{A}}, {\hat{B}})$ as described in Theorem 3.1. Since $\det ({\hat{A}}-\lambda {\hat{B}})=0$ for all $\lambda$, the pencil is singular and the k new eigenvalues introduced with the embedding are indeterminate: MATLAB returns “NaN” as eigenvalues in these cases. However, thanks to the block triangular structure of ${\hat{A}}$ and ${\hat{B}}$ the other eigenvalues coincide with those of the original pencil (A, B). The LFR formats of ${\hat{A}}$ and ${\hat{B}}$ implicitly reveal these block triangular profiles and although we use the representation of the larger matrices the proposed iterative scheme basically works on the original pencil (A, B) so that its convergence is not affected by indeterminate eigenvalues. In order to understand this crucial point the following properties play a role.

• 1. To guarantee that the orthogonal iterations on $({\hat{A}}, {\hat{B}})$ do not converge to an invariant subspace corresponding to an indeterminate eigenvalue it is necessary to start with a bunch of orthogonal vectors of the kind ${\hat{Q}}_0=\begin{bmatrix} Q_0\\ 0_{k,s} \end{bmatrix}$. The representation of the initial ${\hat{Q}}_0$ by means of Givens rotations has then trivial rotations (i.e. $I_2$) acting on the last k rows. The swap procedures do not destroy this structure, meaning that ${\hat{Q}}_i=\begin{bmatrix} Q_i\\ 0_{k,s} \end{bmatrix}$, $i\ge 0$.

• 2. Among the infinitely many QR and RQ factorizations of ${\hat{A}}$ and ${\hat{B}}$ the procedure described at the end of the previous section computes block triangular factorizations by manipulating the LFR formats of ${\hat{A}}$ and ${\hat{B}}$. To see this let ${\hat{A}}=L(U+E \, Z^*)R$ as in Definition 2.6 with L unitary k-lower Hessenberg and U unitary k-upper Hessenberg. Swapping L and U according with Lemma 2.3, i.e $LU= Q {\tilde{L}}$, consists of moving Givens plane rotations which specify U from the right to the left of L. This process creates bulges in positions (i, j) with $i<n$ which can be removed by applying rotations on the left acting on the i-th and $i+1$-st rows. This means that the factor Q is block triangular and hence block diagonal, i.e. $Q=\begin{bmatrix} {\tilde{Q}}_R &{} 0\\ 0 &{} I_k \end{bmatrix}$. Since ${\hat{A}}$ is also block triangular the same holds for the upper triangular factor implicitly represented by its LFR format as ${\tilde{L}}(I+E\, Z^*)R$, where L and R are proper unitary k-Hessenberg matrices. Similar results are still valid for the RQ factorization and ${\hat{B}}$.

• 3. In the swap procedures Givens plane rotations pass through the QR factorization of ${\hat{A}}$. Suppose we apply such a rotation on the right of ${\hat{A}}$ working on its $j, j+1$ columns. From the structure of ${\hat{Q}}_i$ we find $j<n$. Due to the opposite profiles of L and R the bulge into the upper triangular factor can be removed on the left by a Givens plane rotation acting on the $j, j+1$ rows. In other words, insensitively of the composite form of the upper triangular factor the overall scheme is mathematically equivalent with the one working on the input matrix A.

We are now in position to describe how we can carry out an orthogonal iteration using only the turnover and fusion operations. The key ingredient for the algorithm is the SwapUR procedure and its variants as described in Sect. 3.1. In fact, working with the pencil and with the LFR factorization, the orthogonal iterations can be reformulated as follows. Let

$$\begin{aligned} {\hat{A}}=L_A(U_A+E\,Z_A^*) R_A, \quad {\hat{B}}=L_B(U_B+E\, Z_B^*) R_B \end{aligned}$$

be the LFR decomposition of ${\hat{A}}$ and ${\hat{B}}$. The s starting orthogonal vectors in ${\hat{Q}}_0\in {\mathbb {C}}^{N\times s}, N=n+k$, as well as all the intermediate orthogonal vectors ${\hat{Q}}_i$, can be represented as the product of s sequences of ascending Givens rotations. In fact, the columns of ${\hat{Q}}_0$ can be always be completed to an orthogonal basis $\{q_0, q_1, \ldots , q_N\}$ such that $[q_0, q_1, \ldots , q_N]$ is a k-lower Hessenberg matrix (see [12]). In the description of the algorithm, since we are working with the representation of ${\hat{Q}}_i$ in terms of Givens rotations we will identify with ${\hat{Q}}_i$ either the full square matrix or its first s columns.

As we see in the algorithm in Fig. 3, the procedure starts computing the RQ factorization of ${\hat{A}}$ and the QR factorizarion of ${\hat{B}}$ by means of SwapUR and SwapLU. This is a preprocessing step which simplifies the iterations of the algorithm. Then we have ${\hat{A}}=(L_A(I+E\, {\hat{Z}}_A^*){\hat{R}}_A) Q_A$, and ${\hat{B}}=Q_B({\tilde{L}}_B(I+E\, Z_B^*)R_B)$. The factors $Q_A$ and $Q_B$ obtained with the swap procedures are block diagonal with the tailing diagonal block equal to $I_k$. In terms of Givens rotations this correspond to have trivial rotations at the bottom of each Givens chain. Note that we do not have actually to update either $Z_A$ or $Z_B$ which are not needed for the the computation of the ${\hat{Q}}_i$.

The iterations then boil down to the application of the two procedures MoveSequencesLeft and MoveSequencesRight that can be described in terms of the LFR representation. Note that $Q_R$ and $Q_L$ returned by the procedures MoveSequenceRight and MoveSequenceLeft have the block diagonal structure with a tailing identity block.

Fig. 3

Inverse orthogonal iterations described in terms of the LFR representation of the pencil

3.3 Computational Complexity

Analyzing the cost of the Orthogonal Iterations for companion-like pencils we have to consider the inizialization phase where the LFR decompositions are computed and the initial swaps for the computation of the RQ and QR factorizations of ${\hat{A}}$ and ${\hat{B}}$ are performed. The computation of the initial LFR form of ${\hat{A}}$ and ${\hat{B}}$ requires in general $O(n^2k)$ turnover or fusion operations but reduces to $O(n k^2)$ when the unitary factors in A and B have a data-sparse representation such as in the block-companion-like case (see [12] for more details). The computation of the LFR format does not require a pre-processing step to transform the matrix into scalar Hessenberg form but can directly be applied to the two matrices ${\hat{A}}$ and ${\hat{B}}$.

The cost of the swap procedure depends on the number of chains in which the factors to be swapped are decomposed, as explained in detail in Sect. 2. In the case of interest the cost is O(nks). In fact the representation of the initial ${\hat{Q}}_0$ requires ns rotations and therefore it can be decomposed into the product of s unitary Hessenberg matrices. The cost for each iteration is given by the cost of the two procedures MoveSequenceRight and MoveSequenceLeft each one performing three swaps between k and s chains of rotations. Hence each step requires O(nks) operations.

The number of iterations to reach the invariant subspace depends linearly on the ratio $|\lambda _{s+1}|/|\lambda _s|$, as described in [2], Chapter 8. Denoting by it the number of iterations needed to reach an invariant subspace, the total cost is $O(nk^2+\mathtt{it}\, nks)$ floating point operations.

3.4 A Posteriori Measure of Backward Error

The backward stability of the iterative algorithm in Fig. 3 follows from the observation that it involves operations between unitary factors only. A formal proof using the properties of LFR formats can be obtained as in [12] by relying upon the estimates in [5] for the arithmetic among Givens plane rotations. In this section we are interested to devise some a posteriori computable measure of the backward error which will be used in the next section to illustrate the global behaviour of our proposed algorithm.

Suppose that the orthogonal iterations method has reached a numerically invariant subspace spanned by the s orthogonal columns of the matrix Q. We expect that for the computed ${\tilde{Q}}$, $\sigma _{s+1}([A{\tilde{Q}}, B{\tilde{Q}}])$ is small since in exact arithmetic we should have $AQ=BQ \,\Lambda$, with $\Lambda \in {\mathbb {C}}^{s\times s}$. To evaluate the stability we analyze then the quantity

$$\begin{aligned} \mathrm{back_s}=\frac{\sqrt{2} \sigma _{s+1}([A{\tilde{Q}}, B{\tilde{Q}}])}{\Vert [A, B]\Vert _2}. \end{aligned}$$

The following theorem proves that under mild assumptions we can use $\mathrm{back_s}$ to estimate the backward stability of the method.

Theorem 3.4

Let A be invertible and let ${\tilde{Q}}\in {\mathbb {C}}^{n\times s}$ such that ${\tilde{Q}}^* {\tilde{Q}}=I_s$. Moreover, suppose that $B{\tilde{Q}}$ has full rank s and $\sigma _{s+1}([A{\tilde{Q}}, B{\tilde{Q}}])<\sigma _s(B{\tilde{Q}})$. Then, there exist matrices $\Delta _A$, $\Delta _B$ and ${{\tilde{\Lambda }}}$ satisfying

$$\begin{aligned} (A+\Delta _A){\tilde{Q}}=(B+\Delta _B){\tilde{Q}} \, {{\tilde{\Lambda }}} \end{aligned}$$

with

$$\begin{aligned} \frac{\Vert [\Delta _A, \Delta _B]\Vert _2}{\Vert [A, B]\Vert _2}<\mathrm{back_s}. \end{aligned}$$

Proof

Let us consider the SVD decomposition of $[A{\tilde{Q}}, B{\tilde{Q}}]$.We have

$$\begin{aligned}{}[A{\tilde{Q}}, B{\tilde{Q}}]=[U_1, U_2]\begin{bmatrix} \Sigma _1 &{}\\ {} &{} \Sigma _2\\ \end{bmatrix} \begin{bmatrix} V_{11}^* &{} V_{21}^*\\ V_{12}^* &{}V_{22}^* \end{bmatrix}, \quad \Sigma _1\in {\mathbb {R}}^{s\times s}, \Sigma _2\in {\mathbb {R}}^{(n-s)\times s}. \end{aligned}$$

We find $A{\tilde{Q}}=U_1 \Sigma _1 V_{11}^*+U_2\Sigma _2 V_{12}^*$ and $B{\tilde{Q}}=U_1 \Sigma _1 V_{21}^*+U_2\Sigma _2 V_{22}^*$. Moreover the $s\times s$ matrix ${\tilde{Q}}^*B^*B{\tilde{Q}}=V_{21}\Sigma _1^2 V_{21}^*+V_{22}\Sigma _2^2 V_{22}^*$ is invertible since $B{\tilde{Q}}$ is full rank. Then, we have

$$\begin{aligned} V_{21}\Sigma _1^2 V_{21}^*=Q^*B^*BQ(I-(Q^*(B^*B)Q)^{-1}V_{22}\Sigma _2^2V_{22}^*). \end{aligned}$$

Consider now the matrix $I-({\tilde{Q}}^*(B^*B){\tilde{Q}})^{-1}V_{22}\Sigma _2^2V_{22}^*$, which is invertible since

$$\begin{aligned} \Vert ({\tilde{Q}}^*(B^*B){\tilde{Q}})^{-1}V_{22}\Sigma _2^2V_{22}^*\Vert _2\le \Vert ({\tilde{Q}}^*(B^*B){\tilde{Q}})^{-1}\Vert _2\Vert V_{22}\Sigma _2^2V_{22}^*\Vert _2 \end{aligned}$$

and

$$\begin{aligned} \Vert ({\tilde{Q}}^*(B^*B){\tilde{Q}})^{-1}\Vert _2\Vert V_{22}\Sigma _2^2V_{22}^*\Vert _2 \le \frac{\sigma _{s+1}([A {\tilde{Q}}, B{\tilde{Q}}])^2}{\sigma _s(BQ)^2}\le 1. \end{aligned}$$

This shows that under this assumption $V_{21}$ is invertible as well.

Now we are looking for matrices $\Delta _A$, $\Delta _B$ and ${{\tilde{\Lambda }}}$ such that the equality

$$\begin{aligned} \Delta _A {\tilde{Q}}-\Delta _B {\tilde{Q}} {{\tilde{\Lambda }}}=-A {\tilde{Q}}+B{\tilde{Q}} {{\tilde{\Lambda }}} \end{aligned}$$

is fulfilled. Rewriting the relation in terms of the SVD factors we get

$$\begin{aligned} \Delta _A {\tilde{Q}}-\Delta _B {\tilde{Q}} \, {{\tilde{\Lambda }}}=U_1\Sigma _1(-V_{11}^*+V_{21}^*\Lambda )+U_2\Sigma _2(-V_{12}^*+V_{22}^*{{\tilde{\Lambda }}}). \end{aligned}$$

Since $V_{21}$ is invertible, we can choose ${{\tilde{\Lambda }}}=V_{21}^{-*} V_{11}^*$, so that

$$\begin{aligned} \Delta _A{\tilde{Q}}-\Delta _B {\tilde{Q}} {{\tilde{\Lambda }}}= -U_2\Sigma _2V_{12}^*+ U_2 \Sigma _2 V_{22}^*{{\tilde{\Lambda }}}. \end{aligned}$$

We can then set $\Delta _A=-U_2 \Sigma _2 V_{12}^*{\tilde{Q}}^*$ and $\Delta _B=U_2 \Sigma _2 V_{22}^*{\tilde{Q}}^*$, and it holds $\Vert \Delta _A\Vert _2 \le \sigma _{s+1}([A{\tilde{Q}}, B{\tilde{Q}}])$ and $\Vert \Delta _B\Vert _2\le \sigma _{s+1}([A{\tilde{Q}}, B{\tilde{Q}}])$. Finally, we conclude that

$$\begin{aligned} \Vert [ \Delta _A, \Delta _B]\Vert _2^2= \Vert \Delta _A^* \Delta _A+\Delta _B^* \Delta _B\Vert _2\le (\Vert \Delta _A\Vert _2^2+\Vert \Delta _B\Vert _2^2)\le 2( \sigma _{s+1}([A {\tilde{Q}}, B {\tilde{Q}}]))^2. \end{aligned}$$

$\square$

4 Numerical Results

In this section we provide a few numerical illustrations of the properties of convergence and stability of the proposed methods. We perform several tests using nonlinear matrix functions $T(\lambda )\in {\mathbb {C}}^{k\times k}$. For matrix polynomials $T(\lambda )= P(\lambda )=\sum _{i=0}^d P_i\lambda ^i$ we consider the companion linearization (1.1) with $A, B\in {{\mathcal {U}}}_k$. For non-polynomial matrix functions we first approximate by interpolation the matrix function with polynomials of different degrees, then we linearize the polynomials as companion pencils (A, B), with $A, B\in {{\mathcal {U}}}_k$.

We focus on the problem of computing a selected eigenspace of (A, B). When building the pencil, our method performs the inverse orthogonal iterations as defined in the algorithm Orthogonal Iterations in Fig. 3, until an invariant subspace is revealed. Then the corresponding eigenvalues ${{\tilde{\lambda }}}_i$ are computed applying the MATLAB eig function to the $s\times s$ pencil $(A_s, B_s)$ determined as the restriction of A and B to the subspace spanned by the columns of $Q_i$, i.e. the generalized Rayleigh quotients of A and B.

As an error measure for individual eigenvalues, we consider

$$\begin{aligned} \text {err}_T(i)=\frac{\Vert T({{\tilde{\lambda }}}_i) \mathbf{v}\Vert _2}{\Vert T({{\tilde{\lambda }}}_i)\Vert _2 \Vert \mathbf{v}\Vert _2}, \end{aligned}$$

where $\mathbf{v}$ is the k-th right singular vector of $T({{\tilde{\lambda }}}_i)$. In practice we compute $\text {err}_T(i)= \frac{\sigma _k}{\sigma _1}$ where $\sigma _1\ge \sigma _2\ge \cdots \ge \sigma _k$ are the singular values of $T({{\tilde{\lambda }}}_i)$. Following [24] it can be shown that $\text {err}_T(i)$ is an upper bound on the backward error for the approximate eigenvalue ${{\tilde{\lambda }}}_i$ of $T(\lambda )$. According to the customary rule of thumb, this also measures the forward error for well-conditioned problems.

As a measure of convergence of the orthogonal iterations we consider

$$\begin{aligned} \text{ averr}_P=\frac{1}{s}\sum _{i=1}^s |{{\tilde{\lambda }}}_i-\mu _i|, \end{aligned}$$

where $\mu _i$ are the “exact” eigenvalues of the pencil (A, B) obtained with MATLAB eig. The subscript P specifies that this quantity is calculated for polynomial matrix functions $T(\lambda )=P(\lambda )$ only. If $\Sigma _s=\{{{\tilde{\lambda }}}_1, \ldots , {{\tilde{\lambda }}}_s\}$ and $\Sigma =\{\mu _1, \ldots , \mu _s\}$ are the computed eigenvalues of $(A_s, B_s)$ and (A, B), respectively, then these eigenvalues are paired by means of the following rule:

Note that in the genuinely (nonpolynomial) nonlinear case, where $P(\lambda )$ is a polynomial approximation of $T(\lambda )$, $\text{ averr}_P$ refers to the average error with respect to the eigenvalues of the approximating polynomial while $\text {err}_T(i)$ also depends on the quality of the approximation of the nonlinear function with the matrix polynomial.

4.1 Matrix Polynomials

We tested our method on some matrix polynomials of small and large degrees. The first test suite consists of matrix polynomials of degree 3 and 4 from the NLEVP collection [9] using the companion linearization. Table 1 summarizes the results. We see that all the test give good results in terms of the backward error with respect to the pencil. For the plasma_drift polynomial, the backward errors on the pencil reflect the termination of the algorithm with the adopted criteria, and the invariant subspace is found with an adequate accuracy. The plasma_drift is a very challenging problem for any eigensolver [26], due to several eigenvalues of high multiplicity and/or clustered around zero. In [26] the authors proposed a variation of the Jacobi–Davidson method for computing several eigenpairs of the polynomial eigenvalue problem. For this problem, they ran their algorithm with a residual threshold of 1.0e−2 and within 200 iterations they were able to compute the approximations of the 19 eigenvalues closer to the origin. To compare with those results we repeated the experiment on plasma_drift twice, once by setting the stopping criteria in (2.2) to a tolerance of 1.0e−04, and then performing 250 iterations. With only 6 iterations we get a backward error of 8.12e−06 while the error respect to the eigenvalues is approximately of order 1.0e−09. Performing 250 iterations the error on the eigenvalues reaches machine precision.

Table 1 Matrix polynomials of degree 3 and 4 from the NLEVP collection

Regarding the other experiments, we ran the tests setting the tolerance for the stopping criteria to $tol=1.0$e−14 and the maximum number of iterations to 1000. For the orr_sommerfeld problem, we observe that the condition $\Vert E_i\Vert _2< tol$ is not sufficient to guarantee also a sufficiently small error on the eigenvalues. In fact, the method requires only six iterations to stop because the approximating subspaces spanned by the columns of $Q_i$ are converging very slowly, so that $\Vert E_i\Vert _2$ is small despite the invariant subspace has not been reached yet. For this problem also with the MATLAB command polyeig or with methods which do not use scaling and balancing of the coefficients of the polynomial (see Table 1 in [19]) we have similar bounds on ${\textit{err}}_P$. However, scaling the orr_sommerfeld polynomial as described in [8, 19], the error on the coefficients of the polynomial reaches $O(10^{-14})$ and the number of iterations increases. The result is better than some of the results reported in [19] where a balanced version of the Sakurai–Sugiura method with Rayleigh–Ritz projection is presented. Then, by comparison of our result with that reported in [6], where a structured version of the QZ method is employed, we see that for the orr_sommerfeld problem we get a slightly better backward error on the pencil. However, we are estimating only 2 or 4 eigenvalues while the QZ allows us to approximate the full spectrum and, moreover, differently from [6] our error analysis assumes a uniform bound for the norm of the perturbation of A and B. The accuracy of the computed eigenvalues is in accordance with the conditioning estimates.

For the butterfly problem our method performs similarly to the results reported in [18] and the number of iterations in relative_pose_5pt agrees with the separation ratio of the eigenvalues. For the other tests there are remarkable differences in the number of iterations depending on the sensibility of our stopping criterion (2.2) used in Algorithm Orthogonal Iterations w.r.t. specific features of the considered eigenproblem. Comparisons with other stopping criteria introduced in the literature are ongoing work.

Table 2 Solvent problem from M/G/1 type Markov chains from [16]

Concerning large degree polynomials, we have considered applications arising in Markov chain theory that require the computation of solvents. It is well known that the computation of the steady-state vector of an M/G/1-type Markov chain can be related to the solution of a certain unilateral matrix equation (see [14] and the references given therein). In particular, we are interested in the computation of the minimal nonnegative solution of the matrix equation. As already pointed out in the introduction, the nonlinear problem can be reformulated in a matrix setting as the computation of a certain invariant subspace of a matrix pencil (A, B) corresponding with the generalized eigenvalues of minimum modulus. In our experiments, we have tested several cases of M/G/1-type Markov chains introduced in [16]. We do not describe in detail the construction, as it would take some space, but refer the reader to [16,  Sections 7.1]. The construction of the Markov chain depends on two probability distributions and a parameter $\rho$ which makes it possible to tune the separation ratio $\frac{|\lambda _s|}{|\lambda _{s+1}|}$. In Table 2 we show our results in two settings. In each setting, we have fixed the probability distributions by varying $\rho =0.5,0.7,0.9$. The stopping criterion was set to $tol=10^{-13}$. We see that the backward errors slightly deteriorate as the parameter $\rho$ approaches 1 and the number of iterations increases. This is the same behaviour usually observed in the unshifted QR eigenvalue method.

Fig. 4

This plot shows that each step of the Orthogonal Iterations algorithm requires a time that is linear in s. We ran tests on a matrix from Markov Chain theory of size 80, with $k=20$, for odd values of s ranging from 3 to $k-1$ plus the value 20. For each s, we draw a point reporting the time per iteration. The blue line is the linear fit of the data points (Color figure online)

We used large degree polynomials associated with Markov chains to assess the time complexity of the proposed algorithm. Figure 4 shows the linear dependence on the dimension of the invariant subspace s. For a matrix of size $n=80$ drawn from the M/G/1 type Markov chain model described in [16], we applied our algorithm with increasing values of s. Then, the time-per-iteration required by the method is plotted in correspondence with the values of s used. In Fig. 5, for some $10\times 10$ matrix polynomials with degree ranging from 590 to 2016 (constructed with the technique described in [16]), corresponding to pencils of size $n=5190$ up to $n=20{,}160$, and with $s=2$, we draw a dot corresponding to the coordinates $(n, T/( k \,s))$, where T is the time for an iteration without accounting for computing the LFR factorization. In both the figures, the solid line is the linear fit of these points.

Fig. 5

This plot shows that the time required by Orthogonal Iterations is linear in n and ks. For each experiment, characterized by a particular value of n, k and s, we draw a dot in correspondence of the coordinates (n, T/(ks)) where T is the time in seconds for one iteration. The blue line is the linear fit of the data points (Color figure online)

4.2 Nonlinear Matrix Functions

Another set of experiments have dealt with matrix polynomials generated in the process of solving nonlinear matrix equations $\det T(z)=0$ with $T(\lambda )\in {\mathbb {C}}^{k\times k}$ a nonlinear matrix function. Our test suite includes:

• 1. Shifted Time-delay equation [13]. Applying the transformation $z\rightarrow 6z-1$, the matrix function in [13] becomes $T(z)=6 I_2\, z+{\tilde{T}}_0+T_1 \exp (-6z+1)$ with

  $$\begin{aligned} {\tilde{T}}_0 = \left[ \begin{array}{cc}4 &{} -1\\ -2 &{}5\end{array}\right] ; \quad T_1 = \left[ \begin{array}{cc} -2 &{} 1\\ 4 &{}-1\\ \end{array}\right] . \end{aligned}$$

  This function has three eigenvalues inside the unit circle.

• 2. Model of cancer growth [7]. The matrix function is $T(z)= zI_3 -A_0-A_1\exp (-r z)$, where

  $$\begin{aligned} A_0=\left[ \begin{array}{ccc}-\mu _1&{} 0&{}0\\ 2b1&{} -\mu _2&{} b_Q\\ 0&{} \mu _Q&{} -(b_Q+\mu _G)\end{array}\right] ,\, A_1=\exp (-\mu _2r) \left[ \begin{array}{ccc}2b_1&{} 0&{} b_Q\\ -2b_1&{} 0&{} -b_Q\\ 0&{}0&{}0\end{array}\right] . \end{aligned}$$

  The parameters are chosen as suggested in [7] by setting $r=5; b_1=0.13; b_Q=0.2; \mu _1=0.28; \mu _0=0.11; \mu _Q=0.02; \mu _G=0.0001$, $\mu _2=\mu _0+\mu _Q$. We refer to [7] for the physical meaning of the constants and for the description of the model. This function has three eigenvalues inside the unit circle.

• 3. Neutral functional differential equation [21]. The function is scalar $t(z)= 1+0.5 z+z^2+ h z^2 \exp (-\tau z)$. The case $h=-0.82465048736655, \tau =6.74469732735569$ is analyzed in [28] corresponding to a Hopf bifurcation point. This function has three eigenvalues inside the unit circle.

• 4. Spectral abscissa optimization [29]. The function is $T(z)=zI_3 -A -B \exp (-z \tau )$ with $\tau =5$, $B={\varvec{b}} {\varvec{q}}^T$ and

  $$\begin{aligned} A=\left[ \begin{array}{ccc}-0.08 &{} -0.03&{} 0.2\\ 0.2 &{} -0.04&{} -0.005\\ -0.06 &{} 0.2 &{} -0.07 \end{array}\right] , \ {\varvec{b}}=\left[ \begin{array}{c} -0.1\\ -0.2\\ 0.1 \end{array}\right] , \ {\varvec{q}}=\left[ \begin{array}{c} 0.47121273 \\ 0.50372106 \\ 0.60231834 \end{array}\right] . \end{aligned}$$

  The choice of ${\varvec{q}}$ leads to an eigenvalue problem with multiple eigenvalues that are often defective. This function has 4 eigenvalues inside the unit circle.

• 5. Hadeler problem [9]. The matrix function is $T(z)=(\exp (z)-1)A_2+z^2 A_1-\alpha A_0$ where $A_0, A_1,A_2\in {\mathbb {R}}^{k\times k}$, and $V=\text {ones}(k, 1)*[1:k]$ $A_0=\alpha I_k, A_1= k*I_k + 1./(V+V'), A_2=(k+1 - \max (V,V')) .* ([1:k]*[1:k]')$. In our experiments we set $k=8$ and $\alpha =100$. Ruhe [31] proved that the problem has k real and positive eigenvalues, in particular two of them are in the open interval (0, 1), and hence lie inside the unit circle.

• 6. Vibrating string [9, 35]. The model refers to a string of unit length clamped at one end, while the other one is free but is loaded with a mass m attached by an elastic spring of stiffness $k_p$. Assuming $m=1$, and discretizing the differential equation one gets the nonlinear eigenvalue problem $F(z)v=0$, where $F(z)=A-B z+k_p C \frac{z}{z-k_p}$ is rational, $A, B, C\in {\mathbb {R}}^{k\times k}$, $k_p=0.01, h=1/k$,

  $$\begin{aligned} A=\frac{1}{h} \left[ \begin{array}{ccccc} 2 &{} -1 &{}&{}&{}\\ -1 &{}\ddots &{} \ddots &{}&{}\\ &{} \ddots &{} &{} 2 &{}-1\\ &{} &{} &{} -1 &{}1 \end{array}\right] , \, B=\frac{h}{6} \left[ \begin{array}{ccccc} 4 &{} 1 &{}&{}&{}\\ 1 &{}\ddots &{} \ddots &{}&{}\\ &{} \ddots &{} &{} 4 &{}1\\ &{} &{} &{} 1 &{}2 \end{array}\right] , \, C={\varvec{e}}_k {\varvec{e}}_k^T. \end{aligned}$$

• 7. The function F(z) $: \Omega \rightarrow {\mathbb {C}}^{3\times 3}$ from [3] is defined as follows:

  $$\begin{aligned} {{ F(z)=\left[ \begin{matrix} 2 e^z+cos(z)-14&{} (z^2-1)\sin (z)+(2 e^z+14)\cos (z)&{} 2 e^z-14 \\ (z+3)(e^z-7)&{}\sin (z)+(z+3)(e^z-7)\cos (z)&{} (z+3)(e^z-7) \\ e^z-7&{}(e^z-7)\cos (z)&{} e^z-7 \end{matrix}\right] . }} \end{aligned}$$

  (4.1)

  The function F(z) was transformed using elementary transformations from ${{\,\mathrm{diag}\,}}(\cos (z),\sin (z), e^z-7)$. Hence, it has seven real known eigenvalues given by $\left\{ \pm \pi , \pm \pi /2, 0, \log (7), 3\pi /2 \right\}$. We applied the transformation $z\rightarrow 4z+1$ to bring six of the seven eigenvalues inside the unit disk. With this transformation we do not get an approximation of the eigenvalue $-\pi$ which after the translation is not inside the unit disk.

For all these functions we compute the interpolating polynomial $P_d(z)$ over the roots of unity for different degrees d ranging from 16 to 128. With this choice of the interpolation nodes we have theoretical results [10, 20] about the uniform convergence of the interpolating polynomials to the nonlinear function inside the unit disk which prevents the occurrence of spurious eigenvalues. Furthermore, the coefficients of the interpolating polynomial in the monomial basis are computed by means of an FFT which is very stable. In Table 3 are summarized some results for the nonlinear functions considered. In Table 4 are reported the complete results for the test 7 where we know the exact eigenvalues.

Table 3 Numerical results for the nonlinear non-polynomial matrix functions 1–6

In general, for sufficiently large values of the degree we get a very good approximation of the eigenvalues inside the unit disk. Comparing the results in Table 4 with those reported in paper [3] we see that using the same degree ($\text {d}=64$) as in [3] we get a results with 5 more digits of precision respect to the results reported in [3].

The error results in Table 3 are also comparable with those reported in [10], where a structured QR method was employed to compute all the eigenvalues of the matrix/pencil. In general the number of iterations it does not depend on the size of the problem, but only on the ratio $|\lambda _s|/|\lambda _{s+1}|$, so the cost of the orthogonal iterations can be asymptotically cheaper. In addition, the computation of all eigenvalues of $P_d(\lambda )$ is wasteful since only s of them are reliable because the polynomial is a good approximation of the nonlinear function only inside the unit disk.

Table 4 Function F(z) in (4.1)

5 Conclusions and Future Work

In this paper we have presented a fast and backward stable subspace algorithm for block companion forms using orthogonal iterations. The proposed method exploits the properties of a suitable data-sparse factorization of the matrix involving unitary factors. The method can be extended to more generally perturbed unitary matrices and it can incorporate the acceleration techniques based on the updated computation of Ritz eigenvalues and eigenvectors [2]. The design of fast adaptations using adaptive shifting techniques such as the ones proposed in [27] is an ongoing research project. Another very interesting topic for future work is the comparison of orthogonal subspace iteration algorithms and Krylov subspace methods. A refined implementation of these latter for nonlinear eigenvalue problems can be found in [25]. Our approach would be regarded as a robust alternative once complemented with efficient techniques for choosing the size of the polynomial approximation and of the invariant subspace.