Stability and Functional Superconvergence of Narrow-Stencil Second-Derivative Generalized Summation-By-Parts Discretizations

Abstract

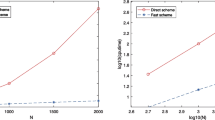
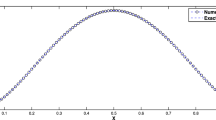
We analyze the stability and functional superconvergence of discretizations of diffusion problems with the narrow-stencil second-derivative generalized summation-by-parts (SBP) operators coupled with simultaneous approximation terms (SATs). Provided that the primal and adjoint solutions are sufficiently smooth and the SBP-SAT discretization is primal and adjoint consistent, we show that linear functionals associated with the steady diffusion problem superconverge at a rate of 2p when a degree $p+1$ narrow-stencil or a degree p wide-stencil generalized SBP operator is used for the spatial discretization. Sufficient conditions for stability of adjoint consistent discretizations with the narrow-stencil generalized SBP operators are presented. The stability analysis assumes nullspace consistency of the second-derivative operator and the invertibility of the matrix approximating the first derivative at the element boundaries. The theoretical results are verified by numerical experiments with the one-dimensional Poisson problem.

Appendices

A Proof of Proposition 2.1

The form of the second derivative we wish to prove, (2.6), corresponds to application of integration by parts twice. Substituting (2.1) and (2.2) into (2.4), we have

$$\begin{aligned} \begin{aligned} \mathsf {D}_{k}^{(2)}(\varLambda )=\mathsf {H}_{k}^{-1}\left[ -\mathsf {M}_k+\mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\right]&=-\mathsf {H}_{k}^{-1}\mathsf {M}_k+\mathsf {H}_{k}^{-1}\left( \mathsf {R}_{r k}^{T}\mathsf {R}_{r k}-\mathsf {R}_{\ell k}^{T}\mathsf {R}_{\ell k}\right) \varLambda _{k}\mathsf {D}_{b,k} \\&=-\mathsf {H}_{k}^{-1}\mathsf {M}_k+\mathsf {H}_{k}^{-1}\mathsf {R}_{r k}^{T}\mathsf {D}_{r k}+\mathsf {H}_{k}^{-1}\mathsf {R}_{\ell k}^{T}\mathsf {D}_{\ell k} \end{aligned} \end{aligned}$$

Adding and subtracting $\mathsf {H}_{k}^{-1}\left( \mathsf {D}_{k}^{(2)}(\varLambda )\right) ^{T}\mathsf {H}_{k}$, we get

$$\begin{aligned} \mathsf {D}_{k}^{(2)}(\varLambda )= & {} -\mathsf {H}_{k}^{-1}\mathsf {M}_{k}+\mathsf {H}_{k}^{-1}\left( \mathsf {D}_{k}^{(2)}(\varLambda )\right) ^{T}\mathsf {H}_{k}-\mathsf {H}_{k}^{-1}\left( \mathsf {D}_{k}^{(2)}(\varLambda )\right) ^{T}\mathsf {H}_{k} \\&+\mathsf {H}_{k}^{-1}\mathsf {R}_{r k}^{T}\mathsf {D}_{r k}+\mathsf {H}_{k}^{-1}\mathsf {R}_{\ell k}^{T}\mathsf {D}_{\ell k} \\= & {} \mathsf {H}_{k}^{-1}\left( \mathsf {D}_{k}^{(2)}(\varLambda )\right) ^{T}\mathsf {H}_{k}-\mathsf {H}_{k}^{-1}\left[ -\mathsf {M}_{k}^{T}+\mathsf {D}_{b,k}^{T}\varLambda _{k}^{T}\mathsf {E}_{k}^{T}\right] \\&+\mathsf {H}_{k}^{-1}\mathsf {R}_{r k}^{T}\mathsf {D}_{r k} +\mathsf {H}_{k}^{-1}\mathsf {R}_{\ell k}^{T}\mathsf {D}_{\ell k}-\mathsf {H}_{k}^{-1}\mathsf {M}_{k} \\= & {} \mathsf {H}_{k}^{-1}\left( \mathsf {D}_{k}^{(2)}(\varLambda )\right) ^{T}\mathsf {H}_k-\mathsf {H}_{k}^{-1}\mathsf {D}_{r k}^{T}\mathsf {R}_{r k}-\mathsf {H}_{k}^{-1}\mathsf {D}_{\ell k}^{T}\mathsf {R}_{\ell k} \\&+\mathsf {H}_{k}^{-1}\mathsf {R}_{r k}^{T}\mathsf {D}_{r k}+\mathsf {H}_{k}^{-1}\mathsf {R}_{\ell k}^{T}\mathsf {D}_{\ell k} -\mathsf {H}_{k}^{-1}\left( \mathsf {M}_{k}-\mathsf {M}_{k}^{T}\right) , \end{aligned}$$

which is the desired result.

B Proof of Theorem 4.1

It is sufficient to show that the result holds for a domain tessellated by two elements, $\varOmega _L$ and $\varOmega _R$, as the interface SATs considered couple immediate neighboring elements only. We let the Dirichlet and Neumann boundary conditions be implemented at the left and right boundaries of the domain. The boundary terms in both forms of the functional, (3.2) and (3.4), involve the products $\psi \lambda {\partial }\mathcal {U}/{\partial }x$ and $\mathcal {U} \lambda {\partial }\psi /{\partial }x$. Using the continuity of $\psi$, $\mathcal {U}$, and $\lambda$, we can approximate $(\psi \lambda {\partial }\mathcal {U}/{\partial }x) \in \mathcal {C}^{2p+1}(\varOmega )$ and ($\mathcal {U} \lambda {\partial }\psi /{\partial }x) \in \mathcal {C}^{2p+1}(\varOmega )$ at the boundary nodes by degree $\le 2p$ polynomials. The integrands in the volume integrals of (3.2) and (3.4) are 2p times differentiable, i.e., $(\mathcal {G}\mathcal {U}), (\psi \mathcal {F}) \in \mathcal {C}^{2p}(\varOmega )$. Since integrals are approximated by quadratures of order $h^{2p}$, replacing $(\mathcal {G}\mathcal {U}), (\psi \mathcal {F}) \in \mathcal {C}^{2p}(\varOmega )$ by $(\widetilde{\mathcal {G}\mathcal {U}}), (\widetilde{\psi \mathcal {F}})\in \mathbb {P}^{2p-1}({\varOmega })$ in the functionals introduces an error of order $h^{2p}$. Therefore, we consider $\widetilde{\mathcal {U}}, (\widetilde{\lambda {\partial }\mathcal {U}/{\partial }x}) \in \mathbb {P}^{p}({\varOmega })$ to be at least order $h^{p+1}$ approximations of $\mathcal {U}$ and $({\lambda {\partial }\mathcal {U}/{\partial }x})$, respectively, and thus $\widetilde{\mathcal {F}} \in \mathbb {P}^{p-1}({\varOmega })$ due to the steady version of the primal PDE, (3.1). Similarly, considering $\widetilde{\psi }, (\widetilde{\lambda {\partial }\psi /{\partial }x}) \in \mathbb {P}^{p}({\varOmega })$ to be at least order $h^{p+1}$ approximations of $\psi$ and $({\lambda {\partial }\psi /{\partial }x})$, respectively, gives $\widetilde{\mathcal {G}} \in \mathbb {P}^{p-1}({\varOmega })$ due to the adjoint PDE, (3.5). For primal and adjoint consistent discretizations, the numerical primal and adjoint solutions are order $h^{\ge p+1}$ accurate despite the polynomial approximations; hence, it is sufficient to show that either (4.21) or (4.22) hold for the polynomial integrands instead of the general continuous functions. Note that compatible functionals satisfy $\mathcal {I}(\mathcal {U}) = \mathcal {I}(\psi )$, and we enforced the condition $I_h(\varvec{u}_h) = I_h(\varvec{\psi }_h)$ to find the discrete adjoint problem; hence, $\mathcal {I}(\mathcal {U})-I_h(\varvec{u}_h) = \mathcal {I}(\psi ) - I_h(\varvec{\psi }_h)$. For the rest of the proof, we drop the tilde sign used to distinguish polynomials from the general continuous functions.

If ${\mathcal {U}}\in \mathbb {P}^{p}({\varOmega })$ and $({\lambda {\partial }\mathcal {U}/{\partial }x}) \in \mathbb {P}^{p}({\varOmega })$, then we discretize (3.2) to find

$$\begin{aligned} \mathcal{I}(\mathcal{U})={\varvec{u}}_{L}^{T}\mathsf {H}_{L}\varvec{g}_{L}+\varvec{g}_{R}^{T}\mathsf {H}_{R}{\varvec{u}}_{R}-\psi _{D}w_{\ell L}+\psi _{N}u_{r R}+\mathcal{O}\left( h^{2p}\right) , \end{aligned}$$

(B.1)

where $w_{\ell L} = [\lambda \frac{\partial {\mathcal{U}}}{\partial x}n_{\ell }]_{\varGamma ^{D}}$ and $u_{r R} = {\mathcal {U}}|_{\varGamma ^N}$. Subtracting (4.3) from (B.1) and rearranging, we have

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \mathcal {U}\right)&=I_h{\varvec{u}_h}-\varvec{g}_{L}^{T}\mathsf {H}_{L}\left( \varvec{u}_{h,L}-{\varvec{u}}_{L}\right) +\psi _{D}\left( \mathsf {D}_{\ell L}\varvec{u}_{h,L}-w_{\ell L}\right) \\&\quad -\psi _{D}\mathsf {T}_{\ell L}^{(D)}\left( \mathsf {R}_{\ell L}\varvec{u}_{h,L}-u_{\ell L}\right) -\varvec{g}_{R}^{T}\mathsf {H}_{R}\left( \varvec{u}_{h,R}-{\varvec{u}}_{R}\right) \\&\quad -\psi _{N}\left( \mathsf {R}_{r R}\varvec{u}_{h,R}-u_{r R}\right) +\mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.2)

Since ${\mathcal {U}}\in \mathbb {P}^{p}({\varOmega })$, the $\mathsf {R}_{\gamma k}$ and $\mathsf {D}_{\gamma k}$ matrices are exact when applied to the restriction of $\mathcal {U}$ to the grid points, e.g., $\mathsf {R}_{r R}{\varvec{u}}_R = u_{r R}$ and $\mathsf {D}_{\ell L}{\varvec{u}}_L = w_{\ell L}$. Applying this property in (B.2) and simplifying we obtain

$$\begin{aligned} \mathcal {I}\left( \mathcal {U}\right) =I_{h}\left( \varvec{u}_{h}\right) -\varvec{g}^{T}\mathbb {H}\left( \varvec{u}_{h}-{\varvec{u}}\right) -\left[ \begin{array}{c} \psi _{D}\mathsf {T}_{\ell L}^{(D)}\mathsf {R}_{\ell L}-\psi _{D}\mathsf {D}_{\ell L}\\ \psi _{N}\mathsf {R}_{r R} \end{array}\right] \left( \varvec{u}_{h}-{\varvec{u}}\right) +\mathcal{O}\left( h^{2p}\right) .\nonumber \\ \end{aligned}$$

(B.3)

Adding $\varvec{\psi }^{T}\mathbb {H}R_{h,u}\left( \varvec{u}_{h}\right) =0$ to the RHS of (B.3) and rearranging terms, we have

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \mathcal {U}\right)&=I_{h}\left( \varvec{u}_{h}\right) -\varvec{\psi }^{T}\mathbb {H}\mathbb {D}^{(2)}{\varvec{u}}-\varvec{\psi }^{T}\mathbb {H}\varvec{f}+\bigg \{-\varvec{g}^{T}-\varvec{\psi }^{T}\mathbb {H}\mathbb {D}^{(2)}\mathbb {H}^{-1} \\&\quad +\varvec{\psi }^{T}\mathbb {A}\mathbb {H}^{-1}-\left[ \begin{array}{c} \psi _{D}\mathsf {T}_{\ell L}^{(D)}\mathsf {R}_{\ell L}-\psi _{D}\mathsf {D}_{\ell L}\\ \psi _{N}\mathsf {R}_{r R} \end{array}\right] \mathbb {H}^{-1} \\&\quad +\varvec{\psi }^{T}\left[ \begin{array}{c} \mathsf {R}_{\ell L}^{T}\mathsf {T}_{\ell L}^{(D)}\mathsf {R}_{\ell L}-\mathsf {D}_{\ell L}^{T}\mathsf {R}_{\ell L}\\ \mathsf {R}_{r R}^{T}\mathsf {D}_{r R} \end{array}\right] \mathbb {H}^{-1}\bigg \}\mathbb {H}\left( \varvec{u}_{h}-{\varvec{u}}\right) +\mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.4)

Using the identity in (2.6) we can write

$$\begin{aligned} \begin{aligned} -\mathbb {H}\mathbb {D}^{(2)}\mathbb {H}^{-1}&=-\left( \mathbb {D}^{(2)}\right) ^{T}+\begin{bmatrix} \mathsf {D}_{\ell L}^{T}\mathsf {R}_{\ell L}-\mathsf {R}_{\ell L}^{T}\mathsf {D}_{\ell L}&{} \varvec{0}\\ \varvec{0} &{} \mathsf {D}_{r R}^{T}\mathsf {R}_{r R}-\mathsf {R}_{r R}^{T}\mathsf {D}_{r R} \end{bmatrix}\mathbb {H}^{-1} \\&\quad +\begin{bmatrix} \mathsf {D}_{r L}^{T}\mathsf {R}_{r L}-\mathsf {R}_{r L}^{T}\mathsf {D}_{r L} &{} \varvec{0}\\ \varvec{0} &{} \mathsf {D}_{\ell R}^{T}\mathsf {R}_{\ell R}-\mathsf {R}_{\ell R}^{T}\mathsf {D}_{\ell R} \end{bmatrix}\mathbb {H}^{-1} + \mathbb {M}\mathbb {H}^{-1}, \end{aligned} \end{aligned}$$

(B.5)

which, after substituting into (B.4) and simplifying, gives

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \mathcal {U}\right)&=I_{h}\left( \varvec{u}_{h}\right) -\varvec{\psi }^{T}\mathbb {H}\left[ \mathbb {D}^{(2)}{\varvec{u}}+\varvec{f}\right] +\bigg \{-\varvec{g}^{T}-\varvec{\psi }^{T}\left( \mathbb {D}^{(2)}\right) ^{T} \\&\quad +\varvec{\psi }^{T}\mathbb {B}^{T}\mathbb {H}^{-1}+\left[ \mathbb {F}\left( \varvec{\psi }\right) \right] ^{T}\mathbb {H}^{-1}-\varvec{\psi }^{T}\mathbb {M}^T\mathbb {H}^{-1}\bigg \}\mathbb {H}\left( \varvec{u}_{h}-{\varvec{u}}\right) +\mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.6)

Since ${\mathcal {U}}\in \mathbb {P}^{p}({\varOmega })$, the second term on the RHS vanishes due to the primal PDE. The third term is $\mathcal {O}(h^{\ge 2p+1})$ due to the consistency of the adjoint discretization, the fact that $\mathbb {H}$ is $\mathcal {O}(h)$, and Assumption 1. Therefore, $\mathcal {I}\left( \mathcal {U}\right) =I_{h}\left( \varvec{u}_{h}\right) +\mathcal{O}\left( h^{2p}\right)$.

Alternatively, if we consider ${\psi }\in \mathbb {P}^{p}({\varOmega })$ and $({\lambda {\partial }\psi /{\partial }x}) \in \mathbb {P}^{p}({\varOmega })$, we start by discretizing the second form of the functional, (3.4),

$$\begin{aligned} \mathcal{I}(\psi )={\varvec{\psi }}_{L}^{T}\mathsf {H}_{L}\varvec{f}_{L}+{\varvec{\psi }}_{R}^{T}\mathsf {H}_{R}\varvec{f}_{R}-u_{D}z_{\ell L}+u_{N}\psi _{r R}+\mathcal{O}\left( h^{2p}\right) , \end{aligned}$$

(B.7)

where $z_{\ell L} = \left[ \lambda \frac{\partial {\psi }}{\partial x}n_{\ell }\right] _{\varGamma ^{D}}$ and $\psi _{r R} = {\psi }|_{\varGamma ^{N}}$. Subtracting (4.4) from (B.7) and rearranging, we obtain

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \psi \right)&= I_h(\varvec{\psi }_h)-\varvec{f}_{L}^{T}\mathsf {H}_{L}\left( \varvec{\psi }_{h,L}-{\varvec{\psi }}_{L}\right) +u_{D}\left( \mathsf {D}_{\ell L}\varvec{\psi }_{h,L}-z_{\ell L}\right) \\&\quad -u_{D}\mathsf {T}_{\ell L}^{(D)}\left( \mathsf {R}_{\ell L}\varvec{\psi }_{h,L}-\psi _{\ell L}\right) -\varvec{f}_{R}^{T}\mathsf {H}_{R}\left( \varvec{\psi }_{h,R}-{\varvec{\psi }}_{R}\right) \\&\quad -u_{N}\left( \mathsf {R}_{r R}\varvec{\psi }_{h,R}-\psi _{r R}\right) +\mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.8)

Using the accuracies of $\mathsf {R}_{\gamma k}$ and $\mathsf {D}_{\gamma k}$ to approximate the boundary terms, adding $\varvec{u}^{T}\mathbb {H}R_{h,\psi }\left( \varvec{\psi }_{h}\right) =0$, and simplifying leads to

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \psi \right)&=I_{h}\left( \varvec{\psi }_{h}\right) -\left[ \varvec{u}^{T}\mathbb {H}\mathbb {D}^{(2)}{\varvec{\psi }}+\varvec{u}^{T}\mathbb {H}\varvec{g}\right] +\bigg \{-\varvec{f}^{T}-\varvec{u}^{T}\mathbb {H}\mathbb {D}^{(2)}\mathbb {H}^{-1} \\&\quad +\varvec{u}^{T}\mathbb {B}\mathbb {H}^{-1}-\left[ \begin{array}{c} u_{D}\mathsf {T}_{\ell L}^{(D)}\mathsf {R}_{\ell L}-u_{D}\mathsf {D}_{\ell L}\\ u_{N}\mathsf {R}_{r R} \end{array}\right] \mathbb {H}^{-1} \\&\quad +\varvec{u}^{T}\left[ \begin{array}{c} \mathsf {R}_{\ell L}^{T}\mathsf {T}_{\ell L}^{(D)}\mathsf {R}_{\ell L}-\mathsf {D}_{\ell L}^{T}\mathsf {R}_{\ell L}\\ \mathsf {R}_{r R}^{T}\mathsf {D}_{r R} \end{array}\right] \mathbb {H}^{-1}\bigg \}\mathbb {H}\left( \varvec{\psi }_{h}-{\varvec{\psi }}\right) - \varvec{u}^T\mathbb {M}\varvec{\psi }_h + \mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.9)

Using the identity (B.5) and simplifying, we find

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \psi \right)&=I_{h}\left( \varvec{\psi }_{h}\right) -\varvec{u}^{T}\mathbb {H}\left[ \mathbb {D}^{(2)}{\varvec{\psi }}+\varvec{g}\right] +\bigg \{-\varvec{f}^{T}-\varvec{u}^{T}\left( \mathbb {D}^{(2)}\right) ^{T} +\varvec{u}^{T}\mathbb {A}^{T}\mathbb {H}^{-1} \\&\quad +\left[ \mathbb {E}\left( \varvec{u}\right) \right] ^{T}\mathbb {H}^{-1} -\varvec{u}^T\mathbb {M}^T\mathbb {H}^{-1}\bigg \}\mathbb {H}\left( \varvec{\psi }_{h}-{\varvec{\psi }}\right) - \varvec{u}^T\mathbb {M}\varvec{\psi }_h+\mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.10)

Noting that $\mathbb {M} + \mathbb {M}^T = \varvec{0}$, we have

$$\begin{aligned} \begin{aligned} \mathcal {I}\left( \psi \right)&=I_{h}\left( \varvec{\psi }_{h}\right) -\varvec{u}^{T}\mathbb {H}\left[ \mathbb {D}^{(2)}{\varvec{\psi }}+\varvec{g}\right] +\bigg \{-\varvec{f}^{T}-\varvec{u}^{T}\left( \mathbb {D}^{(2)}\right) ^{T} +\varvec{u}^{T}\mathbb {A}^{T}\mathbb {H}^{-1} \\&\quad +\left[ \mathbb {E}\left( \varvec{u}\right) \right] ^{T}\mathbb {H}^{-1} \bigg \}\mathbb {H}\left( \varvec{\psi }_{h}-{\varvec{\psi }}\right) - \varvec{u}^T\mathbb {M}\varvec{\psi }+\mathcal{O}\left( h^{2p}\right) . \end{aligned} \end{aligned}$$

(B.11)

The second and fourth terms on the RHS of (B.11) vanish due to the adjoint PDE and the adjoint consistency requirement that $\mathbb {M}=\varvec{0}$, respectively. The third term is $\mathcal {O}(h^{\ge 2p+1})$ due to the consistency of the primal discretization, the scaling of the norm matrix, and Assumption 1. Therefore, the estimates in (4.21) and (4.22) hold.

C Proof of Lemma 4.1

The nullspace consistency of the $\mathsf {D}_{k}^{(2)}(\varLambda )$ in Assumption 3 implies the following:

$$\begin{aligned} \mathsf {H}_{k}\mathsf {D}_{k}^{(2)}(\varLambda ) \varvec{v}_c&= \left( -\mathsf {M}_k + \mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\right) \varvec{v}_c = -\mathsf {M}_k\varvec{v}_c + \mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{v}_c = \varvec{0}, \end{aligned}$$

(C.1)

$$\begin{aligned} \mathsf {H}_{k}\mathsf {D}_{k}^{(2)}(\varLambda ) \varvec{x}_k&= \left( -\mathsf {M}_k + \mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\right) \varvec{x}_k = -\mathsf {M}_k\varvec{x}_k + \mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{x}_k = \varvec{0}. \end{aligned}$$

(C.2)

The second term in the last equality in (C.1) is zero due to the structure of the $\mathsf {E}_{k}$ matrix, i.e., $\mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{v}_c = \varvec{0}$; thus, $\mathsf {M}_k \varvec{v}_c = \varvec{0}$. Furthermore, $\mathsf {M}_k\varvec{x}_k\ne \varvec{0}$ in (C.2) since otherwise we would obtain

$$\begin{aligned} \mathsf {H}_{k}\mathsf {D}_{k}^{(2)}(\varLambda ) \varvec{x}_k = \mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{x}_k = \mathsf {R}_{r k}^T\mathsf {D}_{r k}\varvec{x}_k + \mathsf {R}_{\ell k}^T \mathsf {D}_{\ell k}\varvec{x}_k = \mathsf {R}_{r k}^T\lambda _{r} - \mathsf {R}_{\ell k}^T \lambda _{\ell }= \varvec{0}, \end{aligned}$$

(C.3)

which is not possible as $\mathsf {R}_{r k}$ and $\mathsf {R}_{\ell k}$ do not have nonzero values at the same entries, and $\lambda > 0$. We have used the accuracy of $\mathsf {D}_{r k}$ and $\mathsf {D}_{\ell k}$ in the penultimate equality in (C.3), i.e., $\mathsf {D}_{r k}\varvec{x}_k = \lambda _{r}$ and $\mathsf {D}_{\ell k}\varvec{x}_k = -\lambda _{\ell }$, where $\lambda _{\ell }$ and $\lambda _{r}$ are at least order $h^{p+1}$ approximations of $\lambda$ at the left and right boundaries of $\varOmega _{k}$, respectively. Hence, there is no vector spanned by $\{\varvec{1},\varvec{x}_k\}$ other than $\varvec{v}_c$ that is in the nullspace of $\mathsf {M}_k$. If there exists a nontrivial vector $\varvec{v}$ such that $\varvec{v} \notin \mathrm{span}\{\varvec{1}, \varvec{x}_k\}$ and $\mathsf {M}_k \varvec{v} = \varvec{0}$, then

$$\begin{aligned} \mathsf {H}_k\mathsf {D}_{k}^{(2)}(\varLambda ) \varvec{v}=\mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{v} \ne \varvec{0}, \end{aligned}$$

(C.4)

because $\mathsf {D}_{k}^{(2)}(\varLambda )$ is nullspace consistent and $\mathsf {H}_k$ is SPD. The vector $\mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{v}$ has zero entries at rows corresponding to the zero rows of the $\mathsf {E}_{k}$ matrix. By construction, $\mathsf {D}_{k}^{(2)}(\varLambda )$ has larger dense blocks at the top left and bottom right corners (consisting of more rows and columns) than the $\mathsf {E}_{k}$ matrix; therefore, it follows from the nullspace consistency of the $\mathsf {D}_{k}^{(2)}(\varLambda )$ matrix that $[\mathsf {H}_k\mathsf {D}_{k}^{(2)}(\varLambda ) \varvec{v}]_i \ne 0$ and $[\mathsf {E}_{k}\varLambda _{k}\mathsf {D}_{b,k}\varvec{v}]_i = 0$, at least for one entry, the i-th entry, near the boundaries. This implies that the equality in (C.4) cannot hold for any vector $\varvec{v}\notin \mathrm{span}\{\varvec{1},\varvec{x}_k\}$; hence, we have $\mathcal {N}(\mathsf {M}_k)=\varvec{v}_c$. Since $\mathsf {M}_{k}= \mathsf {M}_{k}^T$, it follows that $\mathcal {N}(\mathsf {M}_{k}^{T})=\varvec{v}_c$. Using the result in (4.27) with the fact that $\mathcal {N}(\mathsf {M}_k) = \mathcal {N}(\mathsf {M}_{k}^T)= \varvec{v}_c$, we obtain

$$\begin{aligned} \mathsf {V}_{k}\varvec{v}_0 = \mathsf {D}_{b,k}^{-T}(\mathsf {M}_k + \mathsf {M}_{k}^T) \mathsf {D}_{b,k}^{-1}\varvec{v}_0 = \mathsf {D}_{b,k}^{-1}(\mathsf {M}_k + \mathsf {M}_{k}^T) \varvec{v}_c = \varvec{0}. \end{aligned}$$

(C.5)

Thus, $\varvec{v}_0$ is the only nontrivial vector in the nullspace of $\mathsf {V}_{k}$. Analogous results hold for $\mathsf {V}_{v}$.

D Proof of Theorem 4.3

We wish to show that the matrices in (4.30) are positive semidefinite. The matrix $\mathsf {A}$, whose components are given in (4.31), is symmetric; thus, we can use Theorem 4.2 to determine the conditions required for it to be positive semidefinite. We have $\mathsf {A}_{22} \succeq 0$ because $\mathsf {V}_{k}$ and $\mathsf {V}_{v}$ are positive semidefinite, $\alpha _{\gamma k}>0$, and $\alpha _{\gamma v} >0$. Therefore, the first condition in Theorem 4.2 is satisfied. The second condition in Theorem 4.2 requires that

$$\begin{aligned} \left( \mathsf {I}_{2n_p}-\mathsf {A}_{22}\mathsf {A}_{22}^{+}\right) \mathsf {A}_{21}= 2 \begin{bmatrix} \mathsf {I}_{n_p}-\mathsf {V}_{k}\mathsf {V}_{k}^{+} &{} \varvec{0}\\ \varvec{0} &{} \mathsf {I}_{n_p}-\mathsf {V}_{v}\mathsf {V}_{v}^{+} \end{bmatrix} \begin{bmatrix} \mathsf {C}_{\gamma k}^{T}\mathsf {T}_{\gamma k}^{(2)} &{} -\mathsf {C}_{\gamma k}^{T}\mathsf {T}_{\gamma k}^{(2)}\\ -\mathsf {C}_{\gamma v}^{T}\mathsf {T}_{\gamma v}^{(2)} &{} \mathsf {C}_{\gamma v}^{T}\mathsf {T}_{\gamma v}^{(2)} \end{bmatrix}=0, \end{aligned}$$

(D.1)

where $\mathsf {I}_{2n_p}$ and $\mathsf {I}_{n_p}$ are identity matrices of size $2n_p \times 2n_p$ and $n_p\times n_p$, respectively. To show that (D.1) holds, we consider the singular value decomposition of $\mathsf {V}_{k}$,

$$\begin{aligned} \mathsf {V}_{k}=\mathsf {X}\varSigma \mathsf {Y}^{T}, \end{aligned}$$

(D.2)

where the columns of $\mathsf {X}$ and $\mathsf {Y}$ contain orthonormal basis vectors of the column and row spaces, respectively, and $\varSigma$ is a diagonal matrix containing the singular values of $\mathsf {V}_{k}$ along its diagonal. Lemma 4.1 and Assumption 4 ensure that the matrix $\mathsf {V}_{k} \in \mathbb {R}^{{n_p}\times {n_p}}$ has only one nontrivial vector in its nullspace; hence, the first $n_p - 1$ columns of $\mathsf {X}$ contain orthonormal basis vectors that span the column space of $\mathsf {V}_{k}$ and the last column contains the vector in the nullspace of $\mathsf {V}_{k}$, which is $\varvec{v}_0$. We also note that

$$\begin{aligned} \mathsf {V}_{k}\mathsf {V}_{k}^{+}=\mathsf {X}\varSigma \mathsf {Y}^{T}\mathsf {Y}\varSigma ^{+}\mathsf {X}^{T}=\mathsf {X}\varSigma \varSigma ^{+}\mathsf {X}^{T}=\mathsf {X}\mathsf {I}_m\mathsf {X}^{T}, \end{aligned}$$

(D.3)

where we have used the orthonormality of $\mathsf {Y}$ in the second equality, i.e., $\mathsf {Y}^{T}\mathsf {Y}=\mathsf {I}_{n_p}$, and $\mathsf {I}_m$ denotes an identity matrix of size $n_p \times n_p$ with the last diagonal entry set to zero (since $\varSigma _{ii} = 0$ for $i>m$, where $m = n_p -1$ is the rank of $\mathsf {V}_{k}$). Therefore, for operators that include the boundary nodes, we have $\mathsf {I}_{n_p}-\mathsf {V}_{k}\mathsf {V}_{k}^{+}=\mathsf {I}_{n_p}-\mathsf {X}\mathsf {I}_m\mathsf {X}^{T}$, which gives

$$\begin{aligned} \mathsf {I}_{n_p}-\mathsf {X}\mathsf {I}_m\mathsf {X}^{T}= & {} \mathsf {I}_{n_p} -\begin{bmatrix} \times &{} \dots &{} &{} \times &{} 0\\ \times &{} \dots &{} &{} \times &{} \times \\ \vdots &{} &{} &{} \vdots &{} \vdots \\ \times &{} \dots &{} &{} \times &{} \times \\ \times &{} \dots &{} &{} \times &{} 0 \end{bmatrix} \begin{bmatrix} 1\\ &{} 1\\ &{} &{} \ddots \\ &{} &{} &{} 1\\ &{} &{} &{} &{} 0 \end{bmatrix} \begin{bmatrix} \times &{} \times &{} \dots &{} \times &{} \times \\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ \\ \times &{} \times &{} \dots &{} \times &{} \times \\ 0 &{} \times &{} \dots &{} \times &{} 0 \end{bmatrix}\nonumber \\= & {} \begin{bmatrix} 0 &{} 0 &{} \dots &{} 0 &{} 0\\ 0 &{} \times &{} \dots &{} \times &{} 0\\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ 0 &{} \times &{} \dots &{} \times &{} 0\\ 0 &{} 0 &{} \dots &{} 0 &{} 0 \end{bmatrix}, \end{aligned}$$

(D.4)

where $\times$ denotes an entry that we do not need to specify for this analysis. Similarly, for operators that do not include boundary nodes, we obtain

$$\begin{aligned} \mathsf {I}_{n_p}-\mathsf {V}_{k}\mathsf {V}_{k}^{+}=\mathsf {I}_{n_p}-\mathsf {X}\mathsf {I}_m\mathsf {X}^{T}= \begin{bmatrix} 0\\ &{} \ddots \\ &{} &{} 0\\ &{} &{} &{} \times &{} \dots &{} \times \\ &{} &{} &{} \vdots &{} &{} \vdots \\ &{} &{} &{} \times &{} \dots &{} \times \\ &{} &{} &{} &{} &{} &{} 0\\ &{} &{} &{} &{} &{} &{} &{} \ddots \\ &{} &{} &{} &{} &{} &{} &{} &{} 0 \end{bmatrix}, \end{aligned}$$

(D.5)

i.e., the first and last s rows are zero, where s is half of the number of zero entries in $\varvec{v}_0$. For operators that have nodes at the boundaries, the LHS of (D.1) can be evaluated using (D.4) as

$$\begin{aligned} \left( \mathsf {I}_{2n_p}-\mathsf {A}_{22}\mathsf {A}_{22}^{+}\right) \mathsf {A}_{21} =\begin{bmatrix} \begin{array}{ccccc} 0 &{} 0 &{} \dots &{} 0 &{} 0\\ 0 &{} \times &{} \dots &{} \times &{} 0\\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ 0 &{} \times &{} \dots &{} \times &{} 0\\ 0 &{} 0 &{} \dots &{} 0 &{} 0 \end{array}\\ &{} \begin{array}{ccccc} 0 &{} 0 &{} \dots &{} 0 &{} 0\\ 0 &{} \times &{} \dots &{} \times &{} 0\\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ 0 &{} \times &{} \dots &{} \times &{} 0\\ 0 &{} 0 &{} \dots &{} 0 &{} 0 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array}{c} 0\\ \vdots \\ \\ 0\\ \mathsf {T}_{\gamma k}^{(2)}\lambda _{\gamma k} \end{array} &{} \begin{array}{c} 0\\ \vdots \\ \\ 0\\ -\mathsf {T}_{\gamma k}^{(2)}\lambda _{\gamma k} \end{array}\\ \begin{array}{c} -\mathsf {T}_{\gamma v}^{(2)}\lambda _{\gamma v}\\ 0\\ \vdots \\ 0\\ 0 \end{array} &{} \begin{array}{c} \mathsf {T}_{\gamma v}^{(2)}\lambda _{\gamma v}\\ 0\\ \vdots \\ 0\\ 0 \end{array} \end{bmatrix}=0.\nonumber \\ \end{aligned}$$

(D.6)

Similarly, substituting (D.5) into (D.1), it is straightforward to show that the condition $\left( \mathsf {I}_{2n_p}-\mathsf {A}_{22}\mathsf {A}_{22}^{+}\right) \mathsf {A}_{21} = 0$ also holds for operators that do not include boundary nodes. For $\mathsf {A}$ to be positive semidefinite, it remains to find sufficient conditions to satisfy the last requirement in Theorem 4.3, i.e., $\mathsf {A}_{11}-\mathsf {A}_{12}\mathsf {A}_{22}^{+}\mathsf {A}_{21} \succeq 0$, which, after some algebra, gives the condition

$$\begin{aligned} \begin{bmatrix} 1 &{} -1\\ -1 &{} 1 \end{bmatrix}\otimes \left[ \mathsf {T}_{1}-\left( \frac{2}{\alpha _{\gamma k}}\mathsf {T}_{\gamma k}^{(2)}\mathsf {C}_{\gamma k}\mathsf {V}_{k}^{+}\mathsf {C}_{\gamma k}^{T}\mathsf {T}_{\gamma k}^{(2)}+\frac{2}{\alpha _{\gamma v}}\mathsf {T}_{\gamma v}^{(2)}\mathsf {C}_{\gamma v}\mathsf {V}_{v}^{+}\mathsf {C}_{\gamma v}^{T}\mathsf {T}_{\gamma v}^{(2)}\right) \right] \succeq 0, \end{aligned}$$

(D.7)

where $\otimes$ denotes the Kronecker product. Since $\big [\begin{matrix} 1 &{} -1 \\ -1 &{} 1 \end{matrix}\big ] \succeq 0$, the inequality in (D.7) is satisfied if

$$\begin{aligned} \mathsf {T}_{\gamma }^{(1)}&\ge \frac{2}{\alpha _{\gamma k}}\mathsf {T}_{\gamma k}^{(2)}\mathsf {C}_{\gamma k}\mathsf {V}_{k}^{+}\mathsf {C}_{\gamma k}^{T}\mathsf {T}_{\gamma k}^{(2)}+ \frac{2}{\alpha _{\gamma v}}\mathsf {T}_{\gamma v}^{(2)}\mathsf {C}_{\gamma v}\mathsf {V}_{v}^{+}\mathsf {C}_{\gamma v}^{T}\mathsf {T}_{\gamma v}^{(2)}, \end{aligned}$$

(D.8)

which is the same as the condition given by (4.32). Note that $\mathsf {C}_{\gamma k}\mathsf {V}_{k}^{+}\mathsf {C}_{\gamma k}^{T} = \mathsf {R}_{\gamma k}\varLambda _{k}\mathsf {V}_{k}^{+}\varLambda _{k}\mathsf {R}_{\gamma k}^{T}$ since $n_{\gamma k}^2 = 1$.

The second matrix in (4.30) can be written as

$$\begin{aligned} \begin{bmatrix} 2\mathsf {T}_{\gamma k}^{(4)} &{} 2\mathsf {T}_{\gamma k}^{(4)}\\ 2\mathsf {T}_{\gamma k}^{(4)} &{} 2\mathsf {T}_{\gamma k}^{(4)} \end{bmatrix} = 2\mathsf {T}_{\gamma k}^{(4)}\begin{bmatrix} 1 &{} 1\\ 1 &{} 1 \end{bmatrix}, \end{aligned}$$

(D.9)

which is positive semidefinite provided $\mathsf {T}_{\gamma k}^{(4)}=\mathsf {T}_{\gamma v}^{(4)} \ge 0$, since $\big [\begin{matrix} 1 &{} 1 \\ 1 &{} 1 \end{matrix}\big ] \succeq 0$ . Finally, we note that the last matrix in (4.30) is symmetric, and $\alpha _{\gamma k}\mathsf {V}_{k} \succeq 0$. Furthermore, using the same approach used to obtain (D.6) it can be shown that

$$\begin{aligned} (\mathsf {I}_{n_p} - \mathsf {V}_{k}\mathsf {V}_{k}^{+})(-2\mathsf {C}_{\gamma k}^T)=0 \end{aligned}$$

(D.10)

irrespective of whether or not the operator includes boundary nodes. The last condition required for positive semidefiniteness of the last matrix in (4.30) is

$$\begin{aligned} 2\mathsf {T}_{\gamma k}^{(D)} - 4\mathsf {C}_{\gamma k}\left( \alpha _{\gamma k}\mathsf {V}_{k}\right) ^{+}\mathsf {C}_{\gamma k}^{T} \ge 0, \end{aligned}$$

(D.11)

which is satisfied if (4.33) holds. Therefore, the conditions in Theorem 4.3 are indeed sufficient for energy stability.