Numerical solution and bifurcation analysis of nonlinear partial differential equations with extreme learning machines

Abstract

We address a new numerical method based on a class of machine learning methods, the so-called Extreme Learning Machines (ELM) with both sigmoidal and radial-basis functions, for the computation of steady-state solutions and the construction of (one-dimensional) bifurcation diagrams of nonlinear partial differential equations (PDEs). For our illustrations, we considered two benchmark problems, namely (a) the one-dimensional viscous Burgers with both homogeneous (Dirichlet) and non-homogeneous boundary conditions, and, (b) the one- and two-dimensional Liouville–Bratu–Gelfand PDEs with homogeneous Dirichlet boundary conditions. For the one-dimensional Burgers and Bratu PDEs, exact analytical solutions are available and used for comparison purposes against the numerical derived solutions. Furthermore, the numerical efficiency (in terms of numerical accuracy, size of the grid and execution times) of the proposed numerical machine-learning method is compared against central finite differences (FD) and Galerkin weighted-residuals finite-element (FEM) methods. We show that the proposed numerical machine learning method outperforms in terms of numerical accuracy both FD and FEM methods for medium to large sized grids, while provides equivalent results with the FEM for low to medium sized grids; both methods (ELM and FEM) outperform the FD scheme. Furthermore, the computational times required with the proposed machine learning scheme were comparable and in particular slightly smaller than the ones required with FEM.

1 Introduction

The solution of partial differential equations (PDEs) with the aid of machine learning as an alternative to conventional numerical analysis methods can been traced back in the early ’90s. For example, Lagaris et al. [42] presented a method based on feedforward neural networks (FNN) that can be used for the numerical solution of linear and nonlinear PDEs. The method is based on the construction of appropriate trial functions, the analytical derivation of the gradient of the error with respect to the network parameters and collocation. The training of the FNN was achieved iteratively with the quasi-Newton BFGS method. Gonzalez-Garcia et al. [24] proposed a multilayer neural network scheme that resembles the Runge-Kutta integrator for the identification of dynamical systems described by nonlinear PDEs.

Nowadays, the exponentially increasing- over the last decades- computational power and recent theoretical advances, have allowed further developments at the intersection between machine learning and numerical analysis. In particular, on the side of the numerical solution of PDEs, the development of systematic and robust machine-learning methodologies targeting at the solution of large scale systems of nonlinear problems with steep gradients constitutes an open and challenging problem in the area. Very recently [51, 52] addressed the use of numerical Gaussian Processes and Deep Neural Networks (DNNs) with collocation to solve time-dependent non-linear PDEs circumventing the need for spatial discretization of the differential operators. The proposed approach is demonstrated through the one-dimensional nonlinear Burgers, the Schrödinger and the Allen-Cahn equations. In [28], DNNs were used to solve high-dimensional nonlinear parabolic PDEs including the Black-Scholes, the Hamilton-Jacobi-Bellman and the Allen-Cahn equation. In [55], DNNs were used to approximate the solution of PDEs arising in engineering problems by exploiting the variational structure that may arise in some of these problems. In [10, 22, 26] DNNs were used to solve high-dimensional semi-linear PDEs; the efficiency of the method was compared against other deep learning schemes. In [62], the authors used FNN to solve modified high-dimensional diffusion equations: the training of the FNN is achieved iteratively using an unsupervised universal machine-learning solver. Most recently, in [21], the authors have used DNN to construct non-linear reduced-order models of time-dependent parametrized PDEs.

Over the last few years, extreme learning machines (ELMs) which belong to the more general family of random projection neural networks (RPNN) together with randomized and random vector functional link network (RVFLN) [35, 47, 57], echo-state neural networks and reservoir computing [37, 38, 45, 48, 54] have been used as an alternative to other machine learning schemes, thus providing a good generalization at a low computational cost [34]. The idea behind ELMs is to randomly set the values of the weights between the input and hidden layer, the biases and the parameters of the activation/transfer functions and determine the weights between the last hidden and output layer by solving a least-squares problem. The solution of such a least-squares problem is the whole “training” procedure; hence, no iterative training is needed for ELMs, in contrast with what happens with the other aforementioned machine learning methods. Extensions to this basic scheme include multilayer ELMs [14, 30, 59] and deep ELMs [60]. As with conventional neural networks, convolutional networks and deep learning, ELMs have been mainly used for classification purposes [4, 11, 12, 32, 59, 61].

On the other hand, the use of ELMs for “traditional” numerical analysis tasks and in particular for the numerical solution of PDEs is still widely unexplored. Very recently in [20], it has been proposed a physics-informed ELM to solve stationary and time dependent linear PDEs, where the authors however report a failure of ELMs to deal, for example, with PDEs which solutions exhibit steep gradients. In [46], the authors used ELMs to solve ordinary and linear PDEs. In [18], the authors proposed a neural network for solving linear and nonlinear partial differential equations, based on the concepts of ELMs, domain decomposition and local neural networks: the domain is tessellated into sub-domains, and the solution on each sub-domain is represented by a local shallow feed-forward neural network (ELMs). The authors solved the linear and the nonlinear 1D Helmotz equation, the 1D diffusion equation and the 1D viscous Burger’s Equation. A comparison with Finite Elements with respect to the maximum error approximation as well as the computational time is also performed. Moreover, in [19], the authors addressed a modified batch intrinsic plasticity method for pre-training the random internal weights of the ELMs and applied the method to solve linear PDEs, namely the 2D Poisson equation and the 1D time-dependent problems of the wave equation and the diffusion equation. In [8], we have proposed an ELM scheme to deal with such steep gradients appearing in linear elliptic PDEs demonstrating through several benchmark problems that the proposed approach is efficient.

Here, we propose a problem-independent numerical scheme based on ELMs for the solution of steady-state problems of nonlinear 1D and 2D PDEs that exhibit sharp gradients. As nonlinear PDEs may also exhibit non-uniqueness and/or non-existence of solutions, we also show how one can use ELMs for the construction of (one-dimensional) bifurcation diagrams of PDEs. The efficiency of the proposed numerical scheme is demonstrated and discussed through two well-studied benchmark problems: the 1D viscous Burgers equation, a representative of the class of advection-diffusion problems and the 1D- and 2D Liouville–Bratu–Gelfand PDE, a representative of the class of reaction-diffusion problems. The numerical accuracy of the proposed scheme is compared against the analytical solutions and the exact locations of the limit points that are known for the one-dimensional PDEs, but also against the corresponding numerical approximations obtained with central Finite Differences (FD) and Galerkin Finite Elements Method (FEM).

2 Extreme Learning Machines

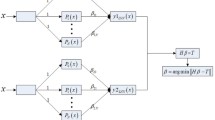
ELMs are a class of machine-learning techniques for defining functions derived by artificial neural networks (ANNs) with fixed internal weights and biases. Thus, ELMs have the same structure of a single hidden layer FNN with N neurons. Next, we report the definition of ELM functions which we denote by ${v}(\varvec{x}):{\mathbb {R}}^d\rightarrow {\mathbb {R}}$.

Definition 1

(ELM network with a single hidden layer) Assuming:

• An infinitely differentiable non polynomial function $\psi$, the activation (transfer) function for the neurons in the hidden layer.

• A randomly-generated matrix $A \in {\mathbb {R}}^{N \times d}$, made up of N rows

  $$\begin{aligned}A=\begin{pmatrix} \varvec{\alpha _1}\\ \varvec{\alpha _2}\\ \dots \\ \varvec{\alpha _N} \end{pmatrix}, \qquad \varvec{\alpha }_{j}=(\alpha _{j,1}, \alpha _{j,2}, \dots , \alpha _{j,d}) \in {\mathbb {R}}^{d}, \end{aligned}$$

  containing the internal weights connecting the input layer and the hidden layer.

• A randomly-generated vector $\varvec{\beta }\in {\mathbb {R}}^{N}$, containing the biases in the hidden layer.

Then, we say that v is an ELM function with a single hidden layer, if there exists a choice of $\varvec{w}\in {\mathbb {R}}^{N}$, (the external weights vector between the hidden layer and the output layer) such that:

$$\begin{aligned} {v}(\varvec{x};A,\varvec{\beta };\varvec{w})=\sum _{j=1}^N w_{j} \psi (\varvec{\alpha }_{j} \cdot \varvec{x} + \beta _{j}), \end{aligned}$$

(1)

where $\varvec{x}\in \mathbb {R}^d$ is the input column vector.

We remark that the regularity assumption in the above definition is not mandatory for the approximation properties, but in our case some regularity is needed to write the collocation method, thus for this case, we also briefly present the necessary theory. It is well-known, that for ANNs, where A and $\varvec{\beta }$ are not a-priori fixed, holds the universal approximation theorem, if $\psi$ is a non-polynomial function: the functional space is spanned by the basis functions $\{\psi (\varvec{\alpha }_j \cdot \varvec{x} + \beta _j) , \varvec{\alpha }_j\in \mathbb {R}^d, \beta _j\in \mathbb {R} \}$ that is dense in $L_2$. Moreover, with some regularity assumptions on the activation function(s), the approximation holds true also for the derivatives (see e.g. Theorem 3.1 and Theorem 4.1 in [49]). Besides, fixing A and $\varvec{\beta }$ a priori is not a limitation, because the universal approximation is still valid in the setting of ELMs (see Theorem 2 in [29]):

Theorem 1

(Universal approximation) Let the coefficients $\varvec{\alpha }_j, \beta _j$ in the function sequence $\{ \psi (\varvec{\alpha }_{j} \cdot \varvec{x} + \beta _{j})\}_{j=1}^N$ be randomly generated according to any continuous sampling distribution and call ${\tilde{v}}^N\in \text {span}\{ \psi (\varvec{\alpha }_{j} \cdot \varvec{x} + \beta _{j}) \,,\ j=1\dots N \}$ the ELM function determined by ordinary least square solution of $\Vert f(\varvec{x})- {\tilde{v}}^N(\varvec{x}) \Vert$, where f is a continuous function.

Then, one has with probability one that $\lim _{N\rightarrow \infty } \Vert f-{\tilde{v}}^N\Vert = 0$.

We remark that in the ANN framework, the classical way is to optimize the parameters of the network (internal and external weights and biases) iteratively, e.g. by stochastic gradient descent algorithms that have a high computational cost and don’t ensure a global but only local convergence. On the other hand, ELM networks are advantageous because the solution of an interpolation problem leads to a system of linear equations, where the only unknowns are the external weights $\varvec{w}$. For example, consider M points $\varvec{x}_i$ such that $y_i=v(\varvec{x}_i)$ for $i=1,\dots ,M$. In the ELM framework (1) the interpolation problem becomes:

$$\begin{aligned} \sum _{j=1}^N w_j \psi _j(\varvec{x}_i)=y_i, \qquad i=1,\dots ,M, \end{aligned}$$

where N is the number of neurons and $\psi _j(\varvec{x})$ is used to denote $\psi (\varvec{\alpha }_j \cdot \varvec{x} + \beta _j)$. Thus, this is a system of M equations and N unknowns that in a matrix form can be we written as:

$$\begin{aligned} S\varvec{w}=\varvec{y}, \end{aligned}$$

(2)

where $\varvec{y}=(y_1,\dots ,y_M) \in {\mathbb {R}}^M$ and $S \in {\mathbb {R}}^{M \times N}$ is the matrix with elements $(S)_{ij}=\psi _j(\varvec{x}_i)$. If the problem is square ($N=M$) and the parameters $\varvec{\alpha }_j$ and $\beta _j$ are chosen randomly, it can be proved that the matrix S is invertible with probability 1 (see i.e. Theorem 1 [29]) and so, there is a unique solution, than can be numerically found; if one has to deal with an ill-conditioned matrix, one can still attempt to find a numerically robust solution by applying established numerical analysis methods suitable for such a case (e.g. by constructing the Moore–Penrose pseudoinverse using QR factorization or SVD). If the problem is under-determined ($N>M$), the linear system has (infinite) many solutions and can be solved by applying regularization in order to pick the solution, with e.g. the minimal $L_2$ norm. Such an approach provides the best solution to the optimization problem related to the magnitude of the calculated weights (see [33]).

Thus, in ELM networks, one has to choose the type of the activation/transfer function and the values of the internal weights and biases. Since the only limitation is that $\psi$ is a non-polynomial function, there are infinitely many choices. The most common choice are the sigmoidal functions (SF) (also referred as ridge functions or plane waves) and the radial basis functions (RBF) [2, 49].

Below, we describe the construction procedure and main features of the proposed ELM scheme, based on these two transfer functions. In the case of the logistic sigmoid transfer function, this investigation was made in our work for one-dimensional linear PDEs [8]. Here, we report the fundamental arguments and address a new numerical scheme for the numerical solution of one and two-dimensional steady-state nonlinear problems. Furthemore, we show how the proposed scheme can be coupled with tools from the numerical bifurcation theory for the construction of bifurcation diagrams.

2.1 ELM with Sigmoidal Functions

For the SF case, we select the logistic sigmoid, that is defined by

$$\begin{aligned} \psi _j(\varvec{x}) \equiv \sigma _j(\varvec{x})=\frac{1}{1+\text {exp}(-\varvec{\alpha }_j\cdot \varvec{x}-\beta _j)}. \end{aligned}$$

(3)

For this function, it is straightforward to compute the derivatives. In particular, the derivatives with respect to the k-th component of $\varvec{x}$, $\varvec{x}(k)$ are given by

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \varvec{x}(k)}\sigma _j(\varvec{x})&= \alpha _{j,k}\frac{\text {exp}(z_j)}{(1+\text {exp}(z_j))^2},\\ \frac{\partial ^2}{\partial x_k^2}\sigma _j(\varvec{x})&= \alpha _{j,k}^2\frac{\text {exp}(z_j) \cdot (\text {exp}(z_j)-1)}{(1+\text {exp}(z_j))^3}, \end{aligned} \end{aligned}$$

(4)

where $z_j=\varvec{\alpha }_j \cdot \varvec{x}+\beta _j$.

A crucial point in the ELM framework is how to fix the values of the internal weights and biases in a proper way. Indeed, despite the fact that theoretically any random choice should be good enough, in practice, it is convenient to define an appropriate range of values for the parameters $\alpha _{j,k}$ and $\beta _{j}$ that are strictly related to the selected activation function. For the one-dimensional case ($d=1$), the logistic sigmoid $\sigma _j$ is a monotonic function such that:

$$\begin{aligned} \begin{aligned} \alpha _{j,1}>0&\Rightarrow \qquad \lim _{x\rightarrow +\infty } \sigma _j(x)=1, \qquad \lim _{x\rightarrow -\infty } \sigma _j(x)=0\\ { \alpha _{j,1}<0}&\Rightarrow \qquad \lim _{x\rightarrow +\infty } \sigma _j(x)=0, \qquad \lim _{x\rightarrow -\infty } \sigma _j(x)=1. \end{aligned} \end{aligned}$$

This function has a inflection point, that we call center $c_j$ defined by the following property:

$$\begin{aligned} \sigma _j(\alpha _{j,1} c_j + \beta _j)=\frac{1}{2}. \end{aligned}$$

(5)

Now since $\sigma (0)=1/2$, the following relation between parameters holds:

$$\begin{aligned} c_j=-\frac{\beta _j}{\alpha _{j,1}}. \end{aligned}$$

Finally, $\sigma _j$ has a steep transition that is governed by the amplitude of $\alpha _{j,1}$: if $|\alpha _{j,1}|\rightarrow +\infty$, then $\sigma _j$ approximates the Heaviside function, while if $|\alpha _{j,1}|\rightarrow 0$, then $\sigma _j$ becomes a constant function. Now, since in the ELM framework, these parameters are fixed a priori, what one needs to avoid is to have some function that can be “useless”¹ in the domain, say $I=[a,b]$.

Therefore, for the one-dimensional case, our suggestion is to chose $\alpha _{j,1}$ uniformly distributed as:

$$\begin{aligned} \alpha _{j,1} \sim {\mathcal {U}}\biggl (-\frac{N-55}{10|I|},\frac{N+35}{10|I|}\biggr ), \end{aligned}$$

where N is the number of neurons in the the hidden layer and $|I|=b-a$ is the domain length. Moreover, we also suggest to avoid too small in module coefficients $a_{j}$ by setting:

$$\begin{aligned} |\alpha _{j,1}|>\frac{1}{2|I|}. \end{aligned}$$

Then, for the centers $c_j$, we select equispaced points in the domain I, that are given by imposing the $\beta _j$s to be:

$$\begin{aligned} \beta _j=-\alpha _{j,1} \cdot c_j. \end{aligned}$$

In the two-dimensional case ($d=2$), we denote as $\varvec{x}=(x,y)^T \in \mathbb {R}^2$ the input and $A \in {\mathbb {R}}^{N \times 2}$ the matrix with rows $\varvec{\alpha }_j=(\alpha _{j,1},\alpha _{j,2})$. Then, the condition (5) becomes:

$$\begin{aligned} \sigma _j(x,y)=\sigma (\alpha _{j,1} x+\alpha _{j,2} y+\beta _j)=\frac{1}{2}. \end{aligned}$$

So, now we have:

$$\begin{aligned} s \equiv y=-\frac{\alpha _{j,1}}{\alpha _{j,2}}x- \frac{\beta _j}{\alpha _{j,2}} \end{aligned}$$

where s is a straight line of inflection points that we call central direction. As the direction parallel to the central direction $\sigma _j$ is constant, while the orthogonal direction to s, the sigmoid $\sigma _j$ is exactly the one-dimensional logistic sigmoid. So considering one point $\varvec{c}_j=(c_{j,1},c_{j,2})$ of the straight line s, we get the following relation between parameters:

$$\begin{aligned} \beta _j=-\alpha _{j,1}\cdot c_{j,1}-\alpha _{j,2}\cdot c_{j,2}. \end{aligned}$$

Now, the difference with the one-dimensional case is the fact that in a domain $I^2 =[a,b]^2$ discretized by a grid of $n \times n$ points, the number of neurons $N=n^2$ grows quadratically, while the distance between two adjacent points decreases linearly, i.e. is given by $|I|/(n-1)$. Thus, for the two-dimensional case, we take $\alpha _{j,k}$ uniformly distributed as:

$$\begin{aligned} \alpha _{j,k} \sim {\mathcal {U}}\biggl (-\frac{\sqrt{N}-60}{20|I|},\frac{\sqrt{N}+40}{20|I|}\biggr ), \qquad k=1,2 \end{aligned}$$

where N is the number of neuron in the network and $|I|=b-a$.

2.2 ELM with Radial Basis Functions

Here, for the RBF case, we select the Gaussian kernel, that is defined as follows:

$$\begin{aligned} \psi _j(\varvec{x}) \equiv \varphi _j(\varvec{x})=\text {exp}(-\varepsilon _j^2||\varvec{x}-\varvec{c}_j||_2^2)=\text {exp}\biggl (-\varepsilon _j^2 \sum _{k=1}^d(\varvec{x}(k)-c_{j,k})^2\biggr ), \end{aligned}$$

(6)

where $\varvec{c}_j \in {\mathbb {R}}^d$ is the center point and $\varepsilon _j \in {\mathbb {R}}$ is the inverse of the standard deviation. For such functions, we have:

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \varvec{x}(k)}\varphi _j(\varvec{x})&=-2 \varepsilon _j^2(x_k-c_{j,k}) \text {exp}(-\varepsilon ^2_j r_j^2),\\ \frac{\partial ^2}{\partial x_k^2}\varphi _j(\varvec{x})&= -2 \varepsilon _j^2 (1-2\varepsilon ^2_j (x_k-c_{j,k})^2)\text {exp}(-\varepsilon ^2_j r_j^2), \end{aligned} \end{aligned}$$

(7)

where $r_j=||\varvec{x}-\varvec{c}_j||_2$. In all the directions, the Gaussian kernel is a classical bell function such that:

$$\begin{aligned} \begin{aligned} \lim _{\Vert \varvec{x}-\varvec{c}_j\Vert \rightarrow + \infty } \phi _j(\varvec{x})=0, \qquad \phi _j(\varvec{c}_j)=1. \end{aligned} \end{aligned}$$

Moreover, the parameter $\varepsilon _j^2$ controls the steepness of the amplitude of the bell function: if $\varepsilon _j\rightarrow + \infty$, then $\phi _j$ approximates the Dirac function, while if $\varepsilon \rightarrow 0$, $\phi _j$ approximates a constant function. Thus, in the case of RBFs one can relate the role of $\varepsilon _j$ to the role of $\alpha _{j,k}$ for the case of SF. For RBFs, it is well known that the center has to be chosen as a point internal to the domain and also more preferable to be exactly a grid point, while the steepness parameter $\varepsilon$ is usually chosen to be the same for each function. Here, since we are embedding RBFs in the ELM framework, we take randomly the steepness parameter $\varepsilon _j$ in order to have more variability in the functional space, while for the centers $\varvec{c}_j$ we select equispaced points in the domain. Thus, as for the SF case, we set the parameters $\varepsilon ^2_j$ random uniformly distributed as:

$$\begin{aligned} \varepsilon _{j}^2 \sim {\mathcal {U}}\biggl (\frac{1}{|I|},\frac{N+65}{15|I|}\biggr ), \end{aligned}$$

where N denotes the number of neurons in the hidden layer and $|I|=b-a$ is the domain length. Besides, note that for the RBF case, it is trivial to extend the above into the multidimensional case, since $\varphi _j$ is already expressed with respect to the center. For the two-dimensional case, we do the same reasoning as for the SF taking:

$$\begin{aligned} \varepsilon _{j}^2 \sim {\mathcal {U}}\biggl (\frac{1}{2|I|},\frac{\sqrt{N}+50}{30|I|}\biggr ). \end{aligned}$$

3 Numerical Bifurcation Analysis of Nonlinear Partial Differential Equations with Extreme Learning Machines

In this section, we introduce the general setting for the numerical solution and bifurcation analysis of nonlinear PDEs with ELMs based on basic numerical analysis concepts and tools (see e.g. [7, 9, 13, 23, 50]). Let’s start from a nonlinear PDE of the general form:

$$\begin{aligned} L u= f(u,\lambda ) \text{ in } \varOmega , \end{aligned}$$

(8)

with boundary conditions:

$$\begin{aligned} B_l u =g_l, \text{ in } \partial \varOmega _l\,,\ l=1,2,\dots ,m \,,\ \end{aligned}$$

(9)

where L is the partial differential operator acting on u, $f(u,\lambda )$ is a nonlinear function of u and ${\lambda } \in {\mathbb {R}}^{p}$ is the vector of model parameters, and $\{\partial \varOmega _l\}_l$ denotes a partition of the boundary.

A numerical solution ${\tilde{u}}={\tilde{u}}(\lambda )$ to the above problem at particular values of the parameters $\lambda$ is typically found iteratively by applying e.g. Newton-Raphson or matrix-free Krylov-subspace methods (Newton-GMRES) (see e.g. [39]) on a finite system of M nonlinear algebraic equations. In general, these equations reflect some zero residual condition, or exactness equation, and thus the numerical solution that is sought is the optimal solution with respect to the condition in the finite dimensional space. Assuming that ${\tilde{u}}$ is fixed via the degrees of freedom $\varvec{w}\in {\mathbf {R}}^N$ - we use the notation ${\tilde{u}}={\tilde{u}}({\mathbf {w}})$ - then these degrees of freedom are sought by solving:

$$\begin{aligned} F_{k} (w_{1},w_{2}, \dots w_{j} \dots w_{N};\lambda ) =0\,,\ k=1,2,...M \ . \end{aligned}$$

(10)

Many methods for the numerical solution of Eq. (8), (9) are written in the above form after the application of an approximation and discretization technique such as Finite Differences (FD), Finite Elements (FEM) and Spectral Expansion (SE), as we detail next.

The system of M algebraic equations (10) is solved iteratively (e.g. by Newton’s method), that is by solving until a convergence criterion is satisfied, the following linearized system:

$$\begin{aligned} \nabla _{\varvec{w}} \varvec{F}(\varvec{w}^{(n)},\lambda ) \cdot d\varvec{w}^{(n)}=-\varvec{F}(\varvec{w}^{(n)},\lambda ), \quad \varvec{w}^{(n+1)}=\varvec{w}^{(n)}+d\varvec{w}^{(n)}. \end{aligned}$$

(11)

$\nabla _{\varvec{w}} \varvec{F}$ is the Jacobian matrix:

$$\begin{aligned} \nabla _{\varvec{w}} \varvec{F} (\varvec{w}^{(n)},\lambda )= \left[ \frac{\partial F_k}{\partial w_j}\right] _{\big |({\varvec{w}^{(n)},\lambda )}}= \begin{bmatrix} \frac{\partial F_1}{\partial w_1} &{} \frac{\partial F_1}{\partial w_2} &{} \dots &{} \frac{\partial F_1}{\partial w_j} &{} \dots &{}\partial \frac{F_1}{\partial w_N}\\ \frac{\partial F_2}{\partial w_1} &{} \frac{\partial F_2}{\partial w_2} &{} \dots &{} \frac{\partial F_2}{\partial w_j} &{} \dots &{}\frac{\partial F_2}{\partial w_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ \frac{\partial F_k}{\partial w_1} &{} \frac{\partial F_k}{\partial w_2} &{} \dots &{} \frac{\partial F_k}{\partial w_j} &{} \dots &{}\frac{\partial F_k}{\partial w_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ \frac{\partial F_M}{\partial w_1} &{} \frac{\partial F_M}{\partial w_2} &{} \dots &{} \frac{\partial F_M}{\partial w_j} &{} \dots &{}\frac{\partial F_M}{\partial w_N} \end{bmatrix}_{\big |{(\varvec{w}^{(n)},\lambda )}} \end{aligned}$$

(12)

If the system is not square (i.e. when $M\ne N$), then at each iteration, one would perform e.g. QR-factorization of the Jacobian matrix

$$\begin{aligned} \nabla _{\varvec{w}} \varvec{F} (\varvec{w}^{(n)},\lambda )=R^T Q^T=\begin{bmatrix} R_{1}^T&0 \end{bmatrix} \begin{bmatrix} Q_1^T \\ Q_2^T \end{bmatrix}, \end{aligned}$$

(13)

where $Q \in {\mathbb {R}}^{N\times N}$ is an orthogonal matrix and $R \in {\mathbb {R}}^{N \times M}$ is an upper triangular matrix. Then, the solution of Eq. (11) is given by:

$$\begin{aligned} d\varvec{w}^{(n)}=-Q_1 R_1^{-1} \cdot \varvec{F} (\varvec{w}^{(n)},\lambda ). \end{aligned}$$

Branches of solutions in the parameter space past critical points on which the Jacobian matrix $\nabla F$ with elements $\dfrac{\partial F_k}{\partial w_{j}}$ becomes singular can be traced with the aid of numerical bifurcation analysis theory (see e.g. [15,16,17, 25, 40, 41, 56]). For example, solution branches past saddle-node bifurcations (limit/turning points) can be traced by applying the so called “pseudo” arc-length continuation method [9]. This involves the parametrization of both ${\tilde{u}}(\varvec{w})$ and $\lambda$ by the arc-length s on the solution branch. The solution is sought in terms of both ${\tilde{u}}(\varvec{w};s)$ and $\lambda (s)$ in an iterative manner, by solving until convergence the following augmented system:

$$\begin{aligned} \begin{bmatrix} \nabla _{\varvec{w}} \varvec{F} &{} \nabla _{\lambda }\varvec{F}\\ \nabla _{\varvec{w}} {N} &{} \nabla _{\lambda } {N} \end{bmatrix} \cdot \begin{bmatrix}d\varvec{w}^{(n)}(s)\\ d\lambda ^{(n)}(s) \end{bmatrix} =-\begin{bmatrix}\varvec{F}(\varvec{w}^{(n)}(s),\lambda (s))\\ N({\tilde{u}}(\varvec{w}^{(n)};s),\lambda ^{(n)}(s))\end{bmatrix}, \end{aligned}$$

(14)

where

$$\begin{aligned} \nabla _{\lambda }\varvec{F}=\begin{bmatrix} \frac{\partial F_1}{\partial \lambda }&\frac{\partial F_2}{\partial \lambda }&\dots&\frac{F_M}{\partial \lambda } \end{bmatrix}^T, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&N({\tilde{u}}(\varvec{w}^{(n)};s),\lambda ^{(n)}(s))\\&\quad = ({\tilde{u}}(\varvec{w}^{(n)};s)-{\tilde{u}}(\varvec{w};s)_{-2})^T\cdot \frac{({\tilde{u}}(\varvec{w})_{-2}-{\tilde{u}}(\varvec{w})_{-1})}{ds}\\&\qquad + (\lambda ^{(n)}(s)-\lambda _{-2})\cdot \frac{(\lambda _{-2}-\lambda _{-1})}{ds}-ds, \end{aligned} \end{aligned}$$

is one of the choices for the so-called “pseudo arc-length condition” (for more details see e.g. [9, 16, 23, 25, 41]); ${\tilde{u}}(\varvec{w})_{-2}$ and ${\tilde{u}}(\varvec{w})_{-1}$ are two already found consequent solutions for $\lambda _{-2}$ and $\lambda _{-1}$, respectively and ds is the arc-length step for which a new solution around the previous solution $({\tilde{u}}(\varvec{w})_{-2},\lambda _{-2})$ along the arc-length of the solution branch is being sought.

3.1 Finite Differences and Finite Elements Cases: The Application of Newton’s Method

In FD methods, one aims to find the values of the solution per se (i.e. $u_{j}= w_{j}$) at a finite number of nodes within the domain. The operator in the differential problem (8) and the boundary conditions (9) are approximated by means of some finite difference operator: $L^h\approx L\,;\ B^h_l\approx B_l$: the finite operator reveals in some linear combination of the function evaluations for the differential part, while keeping non-linear requirement to be satisfied due to the presence of nonlinearities. Then, approximated equations are collocated in internal and boundary points $\varvec{x}_k$ giving equations that can be written as residual equations (10).

With FEM and SE methods, the aim is to find the coefficients of a properly chosen basis function expansion of the solution within the domain such that the boundary conditions are satisfied precisely. In the Galerkin-FEM with Lagrangian basis (see e.g. [44, 50]), the discrete counterpart seeks for a solution of Eq. (8), (9) in N points $x_j$ of the domain $\varOmega$ according to:

$$\begin{aligned} u=\sum _{j=1}^{N} w_{j} \phi _{j}, \end{aligned}$$

(15)

where the basis functions $\phi _{j}$ are defined so that they satisfy the completeness requirement and are such that $\phi _{j}(x_k)=\delta _{jk}$. This, again with the choice of nodal variables to be the function approximation at the points, gives that $u(x_j)=w_j$ are exactly the degrees of freedom for the method. Then, the numerical approximation of the solution is achieved by setting zero the weighted residuals $R_k, k=1,2,\dots N$ defined as:

$$\begin{aligned} R_k=\int _{\varOmega } (L u- f(u,\lambda )) \phi _k\, d\varOmega +\sum _{l=1}^{m} \int _{\partial \varOmega _k} (B_k u -g_l) \phi _l\, d\sigma , \end{aligned}$$

(16)

where the weighting functions $\phi _i$ are the same basis functions used in Eq. (15) for the approximation of u. The above constitutes a nonlinear system of N algebraic equations that for a given set of values for $\lambda$ are solved by Newton-Raphson, thus solving until convergence the following linearized system seen in equation (11), where $R_k$ plays the role of $F_k$.

Note that the border rows and columns of the Jacobian matrix (12) are appropriately changed so that Eq. (11) satisfy the boundary conditions. Due to the construction of the basis functions, the Jacobian matrix is sparse, thus allowing the significant reduction of the computation cost for the solution of (11) at each Newton’s iteration.

3.2 Extreme Learning Machine Collocation: The Application of Newton’s Method

In an analogous manner to FE methods, Extreme Learning Machines aim at solving the problem (8), (9), using an approximation ${\tilde{u}}_N$ of u with N neurons as an ansatz. The difference is that, similarly to FD methods, the equations are constructed by collocating the solution on $M_{\varOmega }$ points $\varvec{x}_i \in \varOmega$ and $M_l$ points $\varvec{x}_k \in \partial \varOmega _l$, where $\varOmega _l$ are the parts of the boundary where boundary conditions are posed, see e.g. [3, 50]:

$$\begin{aligned} \begin{aligned} L{\tilde{u}}_N(\varvec{x}_i;\varvec{w})&=f({\tilde{u}}_N(\varvec{x}_i;\varvec{w}),\lambda ), \quad i=1,\dots ,M_{\varOmega }\\ B_l{\tilde{u}}_N(\varvec{x}_k;\varvec{w})&=g_l(\varvec{x}_k), \quad k=1,\dots ,M_{l}, \quad l=1,\dots ,m. \end{aligned} \end{aligned}$$

Then, if we denote $M=M_{\varOmega }+\sum _{l=1}^m M_l$, we have a system of M nonlinear equations with N unknowns that can be rewritten in a compact way as:

$$\begin{aligned} F_k(\varvec{w},\lambda )=0, \quad k=1,\dots ,M, \end{aligned}$$

where for $k=1,\dots ,M_{\varOmega }$, we have:

$$\begin{aligned} F_k(\varvec{w},\lambda )=L\biggl ( \sum _{i=1}^N w_j \psi (\varvec{\alpha }_j \cdot \varvec{x}_i+\beta _j)\biggr )-f\biggl (\sum _{i=1}^N w_j \psi (\varvec{\alpha }_j \cdot \varvec{x}_i+\beta _j) \biggr )=0, \end{aligned}$$

while for the l-th boundary condition, for $k=1,\dots ,M_l$ we have:

$$\begin{aligned} F_k(\varvec{w},\lambda )=B_l\biggl ( \sum _{i=1}^N w_j \psi (\varvec{\alpha }_j \cdot \varvec{x}_i+\beta _j)\biggr )-g\biggl (\sum _{i=1}^N w_j \psi (\varvec{\alpha }_j \cdot \varvec{x}_i+\beta _j) \biggr )=0. \end{aligned}$$

At this system of non-linear algebraic equations, here we apply Newton’s method (11). Notice that the application of the method requires the explicit knowledge of the derivatives of the functions $\psi$; in the ELM case as described, we have explicit formulae for these (see Eq. (4), (7)).

Remark 1

In our case, Newton’s method is applied to non-squared systems. When the rank of the Jacobian is small, here we have chosen to solve the problem with the use of Moore–Penrose pseudo inverse of $\nabla _{\varvec{w}} F$ computed by the SVD decomposition; as discussed above, another choice would be QR-decomposition (13). This means that we cut off all the eigenvectors correlated to small eigenvalues,² so:

$$\begin{aligned} \nabla _{\varvec{w}}\varvec{F}=U\varSigma V^T, \qquad (\nabla _{\varvec{w}}\varvec{F})^{+}=V\varSigma ^{+}U^T, \end{aligned}$$

where $U \in {\mathbb {R}}^{M\times M}$ and $V \in {\mathbb {R}}^{N\times N}$ are the unitary matrices of left and right eigenvectors respectively, and $\varSigma \in {\mathbb {R}}^{M \times N}$ is the diagonal matrix of singular values. Finally, we can select $q\le rank(\nabla F)$ to get:

$$\begin{aligned} \nabla _{\varvec{w}}\varvec{F}=U_q\varSigma _q V_q^T, \qquad (\nabla _{\varvec{w}}\varvec{F})^{+}=V_q\varSigma _q^{+}U_q^T, \end{aligned}$$

(17)

where $U_q \in {\mathbb {R}}^{M\times q}$ and $V \in {\mathbb {R}}^{N\times q}$ and $\varSigma _q \in {\mathbb {R}}^{q \times q}$. Thus, the solution of Eq. (11) is given by:

$$\begin{aligned} d\varvec{w}^{(n)}=-V_q\varSigma _q^+ U_q^T \cdot \varvec{F} (\varvec{w}^{(n)},\lambda ). \end{aligned}$$

Branches of solutions past turning points can be traced by solving the augmented, with the pseudo-arc-length condition, problem given by Eq. (14). In particular in (14), for the ELM framework (1), the term $\nabla _{\varvec{w}}N$ becomes:

$$\begin{aligned} \nabla _{\varvec{w} }{N}=\varvec{S}^T\frac{({\tilde{u}}(\varvec{w})_{-2}-{\tilde{u}}(\varvec{w})_{-1})}{ds}, \end{aligned}$$

where $\varvec{S}$ is the collocation matrix defined in equation (2).

Remark 2

The three numerical methods (FD, FEM and ELM) are compared with respect to the dimension of the Jacobian matrix J, that in the case of FD and FEM is square and related to the number N of nodes, i.e. $J \in {\mathbb {R}}^{N \times N}$, and in the case ELM is rectangular and related to both the number M of collocation nodes and the number N of neurons, i.e. $J \in {\mathbb {R}}^{M\times N}$. Actually, N is the parameter related to the computational cost, i.e. the inversion of the J for FD and FEM is done by LU factorization that has a computational cost of $O(N^3)$. For the ELM case, which leads to an under-determined system, the computational cost is related to the inversion of the matrix $J^T J \in {\mathbb {R}}^{N\times N}$, that therefore has the same leading computational cost $O(N^3)$. Moreover, if the solution is computed with the Moore–Penrose pseudo–inverse, the computational cost is based on Singular Value Decomposition which has a computational cost of $O(MN^2+M^2N)$. Finally, we make explicit that in all the rest of the paper, we use ELM networks with a number of M of collocation points that is half the number N of neurons in the hidden layer. Such a choice is justified by our previous work [8] that works better for linear PDEs with steep gradients. In general, we pinpoint that by increasing the number M to be $\frac{2N}{3}, \frac{3N}{4}$, etc.³ one gets even better results.

Thus, in the case of collocation methods, such as FD and the proposed machine learning (ELMs) scheme, most of the computational cost is related to the solution of the linear system. In the case of isoparametric Galerkin methods, there is an extra computational cost related with the computation of the quantities of interest, such as the derivatives of the shape functions and the computation of the integrals.

4 Numerical Analysis Results: The Case Studies

The efficiency of the proposed numerical scheme is demonstrated through two benchmark nonlinear PDEs, namely (a) the one dimensional nonlinear Burgers equation with Dirichlet boundary conditions and also mixed boundary conditions, and, (b) the one- and two-dimensional Liouville–Bratu–Gelfand problem. These problems have been widely studied as have been used to model and analyse the behaviour of many physical and chemical systems (see e.g. [1, 6, 9, 23, 27, 36, 53]).

All computations were made with a CPU Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz, RAM 16.0 GB using MATLAB R2020b.

In this section, we present some known properties of the proposed problems and provide details on their numerical solution with FD, FEM and the proposed machine learning (ELM) scheme with both logistic and Gaussian RBF transfer functions.

4.1 The Nonlinear Viscous Burgers Equation

Here, we consider the one-dimensional steady state viscous Burgers problem:

$$\begin{aligned} \nu \frac{\partial ^2u}{\partial x^2}-u \frac{\partial u}{\partial x}=0 \end{aligned}$$

(18)

in the unit interval [0, 1], where $\nu >0$ denotes the viscosity. For our analysis, we considered two different sets of boundary conditions:

• Dirichlet boundary conditions

  $$\begin{aligned} u(0)=\gamma \,,\ u(1)=0\,,\ \gamma >0 \ ; \end{aligned}$$

  (19)

• Mixed boundary conditions: Neumann condition on the left boundary and zero Dirichlet on the right boundary:

  $$\begin{aligned} \frac{\partial u}{\partial x}(0)=-\vartheta \,,\ u(1)=0\,,\ \vartheta >0 \ . \end{aligned}$$

  (20)

The two sets of boundary conditions result to different behaviours (see [1, 5]). We summarize in the next two lemmas some of the main results.

Lemma 1

(Dirichlet case) Consider Eq. (18) with boundary conditions given by (19). Moreover, take (notice that $\gamma \xrightarrow [\nu \rightarrow 0]{}1$):

$$\begin{aligned} \gamma =\frac{2}{1+\text {exp}(\frac{-1}{\nu })}-1 . \end{aligned}$$

Then, the problem (18)–(19) has a unique solution given by:

$$\begin{aligned} u(x)=\frac{2}{1+\text {exp}(\frac{x-1}{\nu })}-1 \ . \end{aligned}$$

(21)

We will use this test problem because the solution has a boundary layer and for this simple case, we can also implement and discuss the efficiency of a fixed point iteration by linearization, while in the mixed-boundaries case, we implement only the Newton’s iterative procedure.

Lemma 2

(Mixed case) Consider Eq. (18) with boundary conditions given by (20). The solution of the problem can be written as [1] :

$$\begin{aligned} u(x)=\sqrt{2c}\tanh {\left( \dfrac{\sqrt{2c}}{2\nu }(1-x)\right) }, \end{aligned}$$

(22)

where c is constant value which can be determined by the imposed Neumann condition.

Then, for $\vartheta$ sufficiently small the viscous Burgers problem with mixed boundary conditions admits two solutions:

• (a) a stable lower solution such that $\forall x \in (0, 1)$:

  $$\begin{aligned} u(x) \xrightarrow [\vartheta \rightarrow 0] {}0,\quad \frac{\partial u(x)}{\partial x} \xrightarrow [\vartheta \rightarrow 0] {}0, \end{aligned}$$

• (b) an unstable upper solution $u(x)>0\, \forall x \in (0, 1)$ such that:

  $$\begin{aligned} \frac{\partial u(0)}{\partial x} \xrightarrow [\vartheta \rightarrow 0] {}0,\quad \frac{\partial u(1)}{\partial x}\xrightarrow [\vartheta \rightarrow 0] {} -\infty \,, \end{aligned}$$

  and

  $$\begin{aligned} \forall x \in (0, 1)\,,\quad u(x) \xrightarrow [\vartheta \rightarrow 0] {}\infty \ . \end{aligned}$$

Proof

The spatial derivative of (22) is given by:

$$\begin{aligned} \frac{\partial u(x)}{\partial x}=-\frac{c}{\nu }{{\,\mathrm{sech}\,}}^2{\left( \dfrac{\sqrt{2c}}{2\nu }(1-x)\right) }. \end{aligned}$$

(23)

(a) When $c\rightarrow 0$ then from Eq. (22), we get asymptotically the zero solution, i.e. $u(x)\rightarrow 0$, $\forall x \in (0, 1)$ and from Eq. (23), we get $\frac{\partial u(x)}{\partial x}\rightarrow 0$, $\forall x \in (0, 1)$. At $x=1$, the Dirichlet boundary condition $u(1)=0$ is satisfied exactly (see Eq. (22)), while at the left boundary $x=0$ the Neumann boundary condition is also satisfied as due to Eq. (23) and our assumption ($\vartheta \rightarrow 0$): $\frac{\partial u(0)}{\partial x}=-\vartheta \rightarrow 0$, when $c\rightarrow 0$.

(b) When $\frac{\partial u(1)}{\partial x}\rightarrow -\infty$, then (23) is satisfied $\forall x \in (0, 1)$ when $c \rightarrow \infty$. In that case, at $x=0$, the Neumann boundary condition is satisfied as due to Eq. (23) is easy to prove that $\frac{\partial u(0)}{\partial x}\rightarrow 0$. Indeed, from Eq. (23):

$$\begin{aligned} \lim _{c\rightarrow \infty } \frac{\partial u(x)}{\partial x}=-\lim _{c\rightarrow \infty } \frac{\nu }{\exp {\frac{\sqrt{2c}}{\nu }}}=0. \end{aligned}$$

(24)

Finally Eq. (22) gives $u(x) \rightarrow \infty$, $\forall x \in (0, 1)$. $\square$

To better understand the behaviour of the unstable solution with respect to the left boundary condition, we can prove the following.

Corollary 1

Consider Eq. (18) with boundary conditions given by (20). For the non-zero solution, when $\vartheta =\epsilon \rightarrow 0$ the solution at $x=0$ goes to infinity with values:

$$\begin{aligned} u(0)=\nu \log \left( \frac{\nu }{\epsilon }\right) \tanh \left( \frac{1}{2}\log \left( \frac{\nu }{\epsilon }\right) \right) . \end{aligned}$$

(25)

Proof

By setting the value of $\vartheta$ in the Neumann boundary condition to be a very small number, i.e. $\vartheta =\epsilon \ll 1$, then from Eq. (24), we get that the slope of the analytical solution given by Eq. (23) is equal to $\epsilon$, when

$$\begin{aligned} c=\frac{1}{2}\nu ^2 \log ^2 \left( \frac{\nu }{\epsilon }\right) . \end{aligned}$$

(26)

Plugging the above into the analytical solution given by Eq. (22), we get Eq. (25). $\square$

The above findings imply also the existence of a limit point bifurcation with respect to $\vartheta$ that depends also on the viscosity. For example, as shown in [1], for $\vartheta >0$ and $\nu =1/10$, there are two equilibria arising due to a turning point at $\vartheta ^*=0.087845767978$.

4.1.1 Numerical Solution of the Burgers Equation with Finite Differences and Finite Elements

The discretization of the one-dimensional viscous Burgers problem in N points with second-order central finite differences in the unit interval $0\le x \le 1$ leads to the following system of $N-2$ algebraic equations $\forall x_j=(j-1)h, j=2,\dots N-1$, $h=\frac{1}{N-1}$:

$$\begin{aligned} F_j( \varvec{u})=\frac{\nu }{h^2}(u_{j+1}-2u_{j}+u_{j-1})-u_{j}\frac{u_{j+1}-u_{j-1}}{2h}=0\ . \end{aligned}$$

At the boundaries $x_1=0, x_N=1$, we have $u_1=\gamma$, $u_N=0$, respectively for the Dirichlet boundary conditions (19) and $u_1=(2h\vartheta +4u_2-u_3)/3$, $u_N=0$, respectively for the mixed boundary conditions (20).

The above $N-2$ nonlinear algebraic equations are the residual equations (10) that are solved iteratively using Newton’s method (11). The Jacobian (12) is now triagonal: at each i-th iteration, the non-null elements are given by:

$$\begin{aligned} \frac{\partial F_j}{\partial u_{j-1}}=\frac{\nu }{h^2}+\frac{u_j}{2h} \, ;\ \frac{\partial F_j}{\partial u_j}=-\nu \frac{2}{h^2}-\frac{u_{j+1}-u_{j-1}}{2h} \, ;\ \frac{\partial F_j}{\partial u_{j+1}}=\frac{\nu }{h^2}-\frac{u_j}{2} \ . \end{aligned}$$

The Galerkin residuals (16) in the case of the one-dimensional Burgers equation read:

$$\begin{aligned} R_k=\int _{0}^{1} \biggl (\nu \frac{\partial ^2u(x)}{\partial x^2}-u \frac{\partial u(x)}{\partial x}\biggr ) \phi _{k}(x) dx. \end{aligned}$$

(27)

By inserting the numerical solution (15) into Eq. (27) and by applying the Green’s formula for integration, we get:

$$\begin{aligned} \begin{aligned} R_k=\,&\nu \phi _{k}(x)\frac{du}{dx}\Big |_{0}^{1}-\nu \sum _{j=1}^{N} u_j \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx\\&-\int _{0}^{1} \sum _{j=1}^{N} u_j \phi _{j}(x) \sum _{j=1}^{N} u_j \frac{d\phi _{j}(x)}{dx}\phi _{k}(x) dx. \end{aligned} \end{aligned}$$

(28)

At the above residuals, we have to impose the boundary conditions. If Dirichlet boundary conditions (19) are imposed, Eq. (28) becomes:

$$\begin{aligned} \begin{aligned} R_k=\,&-\nu \sum _{j=1}^{N} u_j \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx\\&-\,\int _{0}^{1} \sum _{j=1}^{N} u_j \phi _{j}(x) \sum _{j=1}^{N} u_j \frac{d\phi _{j}(x)}{dx}\phi _{k}(x) dx. \end{aligned} \end{aligned}$$

(29)

In the case of the mixed boundary conditions (20), Eq. (28) becomes:

$$\begin{aligned} \begin{aligned} R_k=\,&\nu \vartheta \phi _{k}(0) -\nu \sum _{j=1}^{N} u_j \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx\\&-\,\int _{0}^{1} \sum _{j=1}^{N} u_j \phi _{j}(x) \sum _{j=1}^{N} u_j \frac{d\phi _{j}(x)}{dx}\phi _{k}(x) dx. \end{aligned} \end{aligned}$$

(30)

In this paper, we use a $P^2$ Finite Element space, thus quadratic basis functions using an affine element mapping in the interval $[0, 1]^d$. For the computation of the integrals, we used the Gauss quadrature numerical scheme: for the one-dimensional case, we used the three-points gaussian rule:

$$\begin{aligned} \left\{ \left( \frac{1}{2}-\sqrt{\frac{3}{20}}, \frac{5}{18}\right) , \left( 0.5, \frac{8}{18}\right) , \left( \frac{1}{2}+\sqrt{\frac{3}{20}},\frac{5}{18}\right) \right\} \ . \end{aligned}$$

When writing Newton’s method (11), the elements of the Jacobian matrix for both (29) and (30) are given by:

$$\begin{aligned} \frac{\partial R_k}{\partial u_j}=- \nu \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx-2 \int _{0}^{1} \sum _{j=1}^{N} u_j \phi _{j}(x) \frac{d\phi _{j}(x)}{dx}\phi _{k}(x) dx. \end{aligned}$$

(31)

Finally, with all the above, the Newton’s method (11) involves the iterative solution of a linear system. For the Dirichlet problem this becomes:

$$\begin{aligned} \begin{bmatrix} 1 &{} 0 &{} \dots &{} 0 &{} \dots &{} 0\\ \frac{\partial R_2}{\partial u_1} &{} \frac{\partial R_2}{\partial u_2} &{} \dots &{} \frac{\partial R_2}{\partial u_j} &{} \dots &{}\frac{\partial R_2}{\partial u_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ \frac{\partial R_k}{\partial u_1} &{} \frac{\partial R_k}{\partial u_2} &{} \dots &{} \frac{\partial R_k}{\partial u_j} &{} \dots &{}\frac{\partial R_k}{\partial u_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ 0 &{} 0 &{} \dots &{} 0 &{} \dots &{} 1 \end{bmatrix}_{\big |{u^{(n)}}} \cdot \begin{bmatrix} du^{(n)}_{1}\\ du^{(n)}_{2}\\ \vdots \\ du^{(n)}_{j}\\ \vdots \\ du^{(n)}_{N} \end{bmatrix}=- \begin{bmatrix} 0\\ R_{2}\\ \vdots \\ R_{k}\\ \vdots \\ 0 \end{bmatrix}_{\big |{u^{(n)}}} \ , \end{aligned}$$

(32)

while for the problem with the mixed boundary conditions, at each iteration, we need to solve the following system:

$$\begin{aligned} \begin{bmatrix} \frac{\partial R_1}{\partial u_1} &{} \frac{\partial R_1}{\partial u_2} &{} \dots &{} \frac{\partial R_1}{\partial u{j}} &{} \dots &{} \frac{\partial R_1}{\partial u_N} \\ \frac{\partial R_2}{\partial u_1} &{} \frac{\partial R_2}{\partial u_2} &{} \dots &{} \frac{\partial R_2}{\partial u_j} &{} \dots &{}\frac{\partial R_2}{\partial u_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ \frac{\partial R_k}{\partial u_1} &{} \frac{\partial R_k}{\partial u_2} &{} \dots &{} \frac{\partial R_k}{\partial u_j} &{} \dots &{}\frac{\partial R_k}{\partial u_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ 0 &{} 0 &{} \dots &{} 0 &{} \dots &{} 1 \end{bmatrix}_{\big |{u^{(n)}}} \cdot \begin{bmatrix} du^{(n)}_{1}\\ du^{(n)}_{2}\\ \vdots \\ du^{(n)}_{j}\\ \vdots \\ du^{(n)}_{N} \end{bmatrix}=- \begin{bmatrix} R_{1}\\ R_{2}\\ \vdots \\ R_{k}\\ \vdots \\ 0 \end{bmatrix}_{\big |{u^{(n)}}}\ . \end{aligned}$$

(33)

4.1.2 Numerical Solution of the Burgers Equation with Extreme Learning Machine Collocation

Collocating the ELM network function for the one-dimensional Burgers equation leads to the following nonlinear algebraic system for $i=2,\dots , M-1$:

$$\begin{aligned} F_i(\varvec{w},\nu )=\nu \sum _{j=1}^Nw_j\frac{d^2\psi _j(x_i)}{d x^2}-\biggl (\sum _{j=1}^Nw_j\psi _j(x_i)\biggr )\biggl ( \sum _{j=1}^Nw_j \frac{d\psi _j(x_i)}{d x}\biggr )=0 \ . \end{aligned}$$

(34)

Then, the imposition of the boundary conditions (19) gives:

$$\begin{aligned} F_1(\varvec{w},\nu )=\sum _{j=1}^N w_j \psi _j(0)-\gamma =0, \qquad F_M(\varvec{w},\nu )=\sum _{j=1}^N w_j \psi _j(1)=0 \ , \end{aligned}$$

(35)

while boundary conditions (20) lead to:

$$\begin{aligned} F_1(\varvec{w},\nu )=\sum _{j=1}^N w_j \frac{d \psi _j(0)}{dx}+\vartheta =0, \qquad F_M(\varvec{w},\nu )=\sum _{j=1}^N w_j \psi _j(1)=0 \ . \end{aligned}$$

(36)

These equations are the residual equations (10) that we solve by Newton’s method (11). The elements of the Jacobian matrix $\nabla _{\varvec{w}}\varvec{F}$ are given by:

$$\begin{aligned} \frac{\partial F_i}{\partial w_j}=\nu \frac{d^2\psi _j(x_i)}{d x^2}-\psi _j(x_i) \biggl ( \sum _{j=1}^Nw_j \frac{d\psi _j(x_i)}{d x}\biggr )-\biggl ( \sum _{j=1}^Nw_j \psi _j(x_i)\biggr ) \frac{d\psi _j(x_i)}{d x}. \end{aligned}$$

For $i=2,\dots ,M-1$ and due to the Dirichlet boundary conditions (35), we have:

$$\begin{aligned} \frac{\partial F_1}{\partial w_j}(\varvec{w},\lambda )=\psi _j(0) \qquad \frac{\partial F_M}{\partial w_j}(\varvec{w},\lambda )=\psi _j(1). \end{aligned}$$

On the other hand, due to the mixed boundary conditions given by (36), we get:

$$\begin{aligned} \frac{\partial F_1}{\partial w_j}(\varvec{w},\lambda )=\frac{d\psi _j(0)}{dx} \qquad \frac{\partial F_M}{\partial w_j}(\varvec{w},\lambda )=\psi _j(1). \end{aligned}$$

At this point, the application of Newton’s method (11) using the exact computation of the derivatives of the basis functions is straightforward (see (4) and (7)).

4.1.3 Numerical Results

In all the computations with FD, FEM and the proposed machine learning (ELM) scheme, the convergence criterion for Newton’s iterations was the $L_2$ norm⁴ of the relative error between the solutions resulting from successive iterations; the convergence tolerance was set to $10^{-6}$. In fact, for all methods, Newton’s method converged quadratically also up to the order of $10^{-10}$, when the bifurcation parameter was not close to zero where the solution of both Burgers with mixed boundary conditions and Bratu problems goes asymptotically to infinity. The exact solutions that are available for the one-dimensional Burgers and Bratu problems are derived using Newton’s method with a convergence tolerance of $10^{-12}$.

Fig. 1

Numerical solution and accuracy of the FD, FEM and the proposed machine learning (ELM) schemes for the one-dimensional viscous Burgers problem with Dirichlet boundary conditions (18), (19), (a,b) with viscosity $\nu =0.1$: (a) Solutions for a fixed problem size $N=40$; (b) $L_2$-norm of differences with respect to the exact solution (21) for various problem sizes. (c,d) with viscosity $\nu =0.007$: (c) Solutions for a fixed problem size $N=40$; (d) $L_2$-norm errors with respect to the exact solution for various problem sizes

Table 1 Execution times (s) for the Burgers equation (18) with Dirichlet boundary conditions (19) and $\nu =0.1$

First, we present the numerical results for the Burgers equation (18) with Dirichlet boundary conditions (19). Recall that for this case, the exact solution is available (see Eq.  (21)). For our illustrations, we have selected two different values for the viscosity, namely $\nu =0.1$ and $\nu =0.007$. Results were obtained with Newton’s iterations starting from an initial guess that is a linear segment that satisfies the boundary conditions. Figure 1 shows the corresponding computed solutions for a fixed size $N=40$ as well as the relative errors with respect to the exact solution. As it is shown, the proposed machine learning scheme outperforms both the FD and FEM schemes for medium to large sizes of the grid; from low to medium sizes of the grid, all methods perform equivalently. However, as shown in Fig. 1c, for $\nu =0.007$, and the particular choice of the size ($N=40$), the FD scheme fails to approximate sufficiently the steep-gradient appearing at the right boundary. Table 1, summarizes the execution times of the four methods (ELM SF, ELM RBF, FD and FEM), when applied for the solution of the Burgers equation (18) with Dirichlet conditions (19) and $\nu =0.1$ for various sizes of the grid. The computations are performed 100 times and we also provide the 5% and 95% percentiles. For all practical means, the execution times obtained with ELMS are comparable with the ones obtained with FD and FEM (with the ones obtained with the proposed machine learning scheme to be slightly faster that the ones obtained with FEM), while, as seen, numerical approximation accuracy is better in the ELMs case; the execution times when using the FD are smaller but as shown the FD scheme fails to approximate solutions with steep gradients while its numerical accuracy is generally lower when compared with FEM and the proposed machine learning scheme.

Then, we considered the case of the non-homogeneous Neumann condition on the left boundary (18)- (20); here, we have set $\nu =1/10$. In this case, the solution is not unique and the resulting bifurcation diagram obtained with FD, FEM and the proposed machine learning (ELM) scheme is depicted in Fig. 2. In Table 2, we report the error between the value of the bifurcation point as computed with FD, FEM and the proposed machine learning (ELM) scheme for various problem sizes N, with respect to the exact value of the bifurcation point (occurring for the particular choice of viscosity at $\vartheta ^*=0.087845767978$). The location of the bifurcation point for all numerical methods was estimated by fitting a parabola around the four points (two on the lower and two on the upper branch) of the largest values of $\lambda$ as obtained by the pseudo-arc-length continuation. As shown, the proposed ELM scheme performs equivalently to FEM for low to medium sizes of the grid, thus outperforming FEM for medium to large grid sizes; both methods FEM and the proposed machine learning (ELM) scheme outperform FD for all sizes of the grid.

Fig. 2

a One-dimensional Burgers equation (18) with mixed boundary conditions (20). Bifurcation diagram with respect to the Neumann boundary value $\theta$ as obtained for $\nu =1/10$, with FD, FEM and ELM schemes with a fixed problem size $N=400$; b Zoom near the turning point

Table 2 One-dimensional Burgers equation (18) with mixed boundary conditions (20)

In this case, steep gradients arise at the right boundary related to the presence of the upper unstable solution, as discussed in Lemma 2 and Corollary 1. In Table 3, we report the error between the numerically computed and the exact analytically obtained value (see Eq. (22)) at $x=0$ when the value of boundary condition $\vartheta$ at the left boundary is $\vartheta =10^{-6}$. Again as shown, near the left boundary, the proposed ELM scheme outperforms both FEM and FD for medium to larger sizes of the grid.

Table 3 One-dimensional Burgers equation (18) with mixed boundary conditions (20)

Remark 3

(Linearization of the Burgers equation for its numerical solution.) For the numerical solution of the Burgers equation (18) with boundary conditions given by (19), one can also consider the following simple iterative procedure that linearizes the equation:

$$\begin{aligned} \left\{ \begin{array}{l} \text {Given } u^{(0)}, \text { do until convergence} \\ \text {find } u^{(k)} \text { such that } \nu \dfrac{\partial ^2u^{(k)}}{\partial x^2}-u^{(k-1)} \dfrac{\partial u^{(k)}}{\partial x}=0 \ . \end{array}\right. \end{aligned}$$

In this way, the nonlinear term becomes a linear advection term with a non-constant coefficient given by the evaluation of u at the previous iteration. This results to a fixed point scheme. Such linearized equations can be easily solved, being linear elliptic equations, and thus in this case one can perform the analysis for linear systems presented in [8]. The results of this procedure are depicted in Fig. 3.

We point out that such iterations converge generally very slowly and, what is most important from our point of view, is that convergence is obtained only for a very “good” guess of the solution.

Fig. 3

Numerical accuracy of FD and ELM schemes with respect to the exact solution, for the case of the one-dimensional Burgers equation (18) with Dirichlet boundary conditions given by (19), as obtained by the fixed point scheme described in Remark 3 for a $\nu =0.1$ and b $\nu =0.007$. We depict the $L_2$-norm of the difference between the solutions obtained with FD and the proposed machine learning (ELMs) scheme and the exact solution (21)

4.2 The One- and Two-Dimensional Liouville–Bratu–Gelfand Problem

The Liouville–Bratu–Gelfand model arises in many physical and chemical systems. It is an elliptic partial differential equation which in its general form is given by [6]:

$$\begin{aligned} \varDelta u(\varvec{x}) +\lambda e^{u(\varvec{x})}=0\,\ \varvec{x} \in \varOmega , \end{aligned}$$

(37)

with homogeneous Dirichlet conditions

$$\begin{aligned} u(\varvec{x}) =0\,,\ \varvec{x} \in \partial \varOmega . \end{aligned}$$

(38)

The domain that we consider here is the $\varOmega =[0, 1]^d$ in $R^d\,,\ d=1,2$.

The one-dimensional problem admits an analytical solution given by [43]:

$$\begin{aligned} u(x)=2\ln \frac{\cosh {\theta }}{\cosh {\theta (1-2x)}}, \text { where} \theta \text { is such that } \cosh {\theta } = \frac{4\theta }{\sqrt{2 \lambda }}. \end{aligned}$$

(39)

It can be shown that when $0<\lambda <\lambda _c$, the problem admits two branches of solutions that meet at $\lambda _c \sim 3.513830719$, a limit point (saddle-node bifurcation) that marks the onset of two branches of solutions with different stability, while beyond that point no solutions exist.

For the two-dimensional problem, to the best of our knowledge, no such (as in the one-dimensional case) exact analytical solution exist that is verified by the numerical results that have been reported in the literature (e.g. [9, 27]), in which the authors report the value of the turning at $\lambda _c \sim 6.808124$.

4.2.1 Numerical Solution with Finite Differences and Finite Elements

The discretization of the one-dimensional problem in N points with central finite differences at the unit interval $0\le x \le 1$ leads to the following system of $N-2$ algebraic equations $\forall x_j=(j-1)h, j=2,\dots N-1$, $h=\frac{1}{N-1}$:

$$\begin{aligned} F_j(u)=\frac{1}{h^2}(u_{j+1}-2u_{j}+u_{j-1})+\lambda e^{u_j}=0, \end{aligned}$$

where, at the boundaries $x_1=0, x_N=1$, we have $u_1=u_N=0$.

The solution of the above $N-2$ nonlinear algebraic equations is obtained iteratively using the Newton-Raphson method. The Jacobian is now tridiagonal; at each n-th iteration, the elements at the main diagonal are given by ${\frac{\partial F_j}{\partial u_j}}^{(n)}=-\frac{2}{h^2}+\lambda e^{u_{j}^{(n)}}$ and the elements of the first diagonal above and the first diagonal below are given by ${\frac{\partial F_{j+1}}{\partial u_j}}^{(n)}={\frac{\partial F_{j}}{\partial u_{j+1}}}^{(n)}=\frac{1}{h^2}$, respectively.

The discretization of the two-dimensional Bratu problem in $N\times N$ points with central finite differences on the square grid $0\le x,y\le 1$ with zero boundary conditions leads to the following system of $(N-2)\times (N-2)$ algebraic equations $\forall (x_i=(i-1)h, y_j=(j-1)h), i,j=2,\dots N-1$, $h=\frac{1}{N-1}$:

$$\begin{aligned} F_{i,j}(u)=\frac{1}{h^2}(u_{i+1,j}+u_{i,j+1}-4u_{i,j}+u_{i,j-1}+u_{i-1,j})+\lambda e^{u_{i,j}}=0. \end{aligned}$$

The Jacobian is now a $(N-2)^2 \times (N-2)^2$ block diagonal matrix of the form:

$$\begin{aligned} \nabla F = \frac{1}{h^2} \begin{bmatrix} T_2 &{} I &{} 0 &{} 0 &{} \dots &{} \dots &{} 0\\ I &{} T_3 &{} I &{} 0 &{} \dots &{} \dots &{} 0\\ 0 &{} I &{} T_4 &{} I &{} 0 &{} \dots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \dots &{} \dots &{} \dots &{} \dots &{} I &{} T_{N-1} \end{bmatrix}, \end{aligned}$$

where I is the $(N-2)\times (N-2)$ identity matrix and $T_i$ is the $(N-2)\times (N-2)$ tridiagonal matrix with non null elements on the j-th row:

$$\begin{aligned} 1\,,\quad -4 +h^{2} \lambda e^{u_{i+j,i+j}} \,,\quad 1 \end{aligned}$$

Regarding the FEM solution, for the one-dimensional Bratu problem, Eq. (16) gives:

$$\begin{aligned} R_k=\int _{\varOmega } \left( \frac{\partial ^2u}{\partial x^2} +\lambda e^{u(x)}\right) \phi _{k}(x) dx. \end{aligned}$$

(40)

By inserting Eq. (15) into Eq. (40) and by applying the Green’s formula for integration, we get:

$$\begin{aligned} R_k=\phi _{k}(x)\frac{du}{dx}\Big |_{0}^{1}-\sum _{j=1}^{N} u_j \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx+\lambda \int _{0}^{1} e^{ \sum _{j=1}^{N} u_j \phi _{j}(x)}\phi _{k}(x) dx \end{aligned}$$

(41)

and because of the zero Dirichlet boundary conditions, Eq. (41) becomes:

$$\begin{aligned} R_k=-\sum _{j=1}^{N} u_j \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx+\lambda \int _{0}^{1} e^{\sum _{j=1}^{N} u_j \phi _{j}(x)}\phi _{k}(x)dx. \end{aligned}$$

The elements of the Jacobian matrix are given by:

$$\begin{aligned} \frac{\partial R_k}{\partial u_j}=- \int _{0}^{1} \frac{d \phi _{j}(x)}{dx}\frac{d\phi _{k}(x)}{dx} dx+\lambda \int _{0}^{1} e^{\sum _{j=1}^{N} u_j \phi _{j}(x)} \phi _{j}(x) \phi _{k}(x)dx \end{aligned}$$

(42)

Due to the Dirichlet boundary conditions, Eq. (42) becomes:

$$\begin{aligned} \begin{bmatrix} 1 &{} 0 &{} \dots &{} 0 &{} \dots &{} 0\\ \frac{\partial R_2}{\partial u_1} &{} \frac{\partial R_2}{\partial u_2} &{} \dots &{} \frac{R_2}{\partial u_j} &{} \dots &{}\frac{R_2}{\partial u_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ \frac{\partial R_k}{\partial u_1} &{} \frac{\partial R_k}{\partial u_2} &{} \dots &{} \frac{R_k}{\partial u_j} &{} \dots &{}\frac{R_k}{\partial u_N}\\ \vdots &{}\vdots &{} \ddots &{} \vdots &{} \ddots &{}\vdots \\ 0 &{} 0 &{} \dots &{} 0 &{} \dots &{} 1 \end{bmatrix}_{\big |{u^{(n)}}} \cdot \begin{bmatrix} du^{(n)}_{1}\\ du^{(n)}_{2}\\ \vdots \\ du^{(n)}_{j}\\ \vdots \\ du^{(n)}_{N} \end{bmatrix}=- \begin{bmatrix} 0\\ R_{2}\\ \vdots \\ R_{k}\\ \vdots \\ 0 \end{bmatrix}_{\big |{u^{(n)}}}. \end{aligned}$$

(43)

For the two-dimensional Bratu problem , the residuals are given by:

$$\begin{aligned} R_k=\iint _{\varOmega } \left( \frac{\partial ^2u(x,y)}{\partial x^2}+\frac{\partial ^2u(x,y)}{\partial y^2} +\lambda e^{u(x,y)}\right) \phi _k(x,y) dx dy. \end{aligned}$$

By applying the Green’s formula for integration, we get:

$$\begin{aligned} \begin{aligned} R_k&=\oint _{\partial {\varOmega }} \nabla u(x,y) d\ell -\iint _{\varOmega } \nabla u(x,y) \nabla \phi _{k}(x,y) dx dy\\&\quad +\iint _{\varOmega } \lambda e^{u(x,y)} \phi _k(x,y) dx dy. \end{aligned} \end{aligned}$$

By inserting Eq. (15) and the zero Dirichlet boundary conditions, we get:

$$\begin{aligned} \begin{aligned} R_k&= -\sum _{j=1}^{N} u_j \iint _{\varOmega } \nabla \phi _{j}(x,y) \nabla \phi _{k}(x,y) dx dy\\&\quad +\iint _{\varOmega } \lambda e^{\sum _{j=1}^{N} u_{j} \phi _{j}(x,y)} \phi _k(x,y) dx dy. \end{aligned} \end{aligned}$$

Thus, the elements of the Jacobian matrix for the two-dimensional Bratu problem are given by:

$$\begin{aligned} \begin{aligned} \frac{\partial R_k}{\partial u_j}&=-\iint _{\varOmega } \nabla \phi _{j}(x,y) \nabla \phi _{k}(x,y) dx dy\\&\quad +\iint _{\varOmega } \lambda e^{\sum _{j=1}^{N} u_{j} \phi _{j}(x,y)} \phi _{j}(x,y) \phi _k(x,y) dx dy. \end{aligned} \end{aligned}$$

As before, for our computations we have used quadratic basis functions using an affine element mapping in the domain $[0, 1]^2$.

4.2.2 Numerical Solution with Extreme Learning Machine Collocation

Collocating the ELM network function (1) in the 1D Bratu problem (37) leads to the following system:

$$\begin{aligned} F_i(\varvec{w},\lambda )\!=\!\sum _{j\!=\!1}^N w_j \frac{d^2\psi _j(x_i)}{d x^2}\!+\!\lambda \text {exp}\biggl (\sum _{j=1}^N w_j \psi _j(x_i)\biggr )\!=\!0, \quad i\!=\!2,\dots ,M-1, \end{aligned}$$

with boundary conditions:

$$\begin{aligned} F_1(\varvec{w},\lambda )=\sum _{j=1}^N w_j \psi _j(0)=0, \qquad F_M(\varvec{w},\lambda )=\sum _{j=1}^N w_j \psi _j(1)=0. \end{aligned}$$

Thus, the elements of the Jacobian matrix $\nabla _{\varvec{w}} \varvec{F}$ are given by:

$$\begin{aligned} \frac{\partial F_i}{\partial w_j}=\frac{d^2\psi _j(x_i)}{d x^2}+\lambda \psi _j(x_i)\text {exp}\biggl (\sum _{j=1}^N w_j \psi _j(x_i)\biggr ), \qquad i=2,\dots ,M-1, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial F_1}{\partial w_j}(\varvec{w},\lambda )=\psi _j(0) \qquad \frac{\partial F_M}{\partial w_j}(\varvec{w},\lambda )=\psi _j(1). \end{aligned}$$

The application of Newton’s method (11) is straightforward using the exact computation of derivatives of the basis functions (see (4) and (7)).

For the two-dimensional Bratu problem (37), we have:

$$\begin{aligned} \begin{aligned} F_i(\varvec{w},\lambda )=&\sum _{j=1}^N w_j \frac{\partial ^2\psi _j(x_i,y_i)}{\partial x^2} +\sum _{j=1}^N w_j \frac{\partial ^2\psi _j(x_i,y_i)}{\partial y^2} \\&+\lambda \, \text {exp}\biggl (\sum _{j=1}^N w_j \psi _j(x_i,y_i)\biggr )=0, \quad i=1,\dots ,M_{\varOmega } \end{aligned} \end{aligned}$$

with boundary conditions:

$$\begin{aligned} F_k(\varvec{w},\lambda )= \sum _{j=1}^N w_j \psi _j(x_k,y_k)=0, \quad k=1,\dots ,M_{1}. \end{aligned}$$

Thus, the elements of the Jacobian matrix $\nabla _{\varvec{w}} F$ read:

$$\begin{aligned} \begin{aligned} \frac{\partial F_i}{\partial w_j}&=\frac{\partial ^2\psi _j(x_i,y_i)}{\partial x^2} +\frac{\partial ^2\psi _j(x_i,y_i)}{\partial y^2} \ +\lambda \psi _j(x_i,y_i)\, \text {exp}\biggl (\sum _{j=1}^N w_j \psi _j(x_i,y_i)\biggr ), \qquad i=1,\dots ,M_{\varOmega } \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial F_k}{\partial w_j}(\varvec{w},\lambda )=\psi _j(x_k,y_k)=0, \quad k=1,\dots ,M_{1} \ . \end{aligned}$$

Also in this case, with the above computations the application of Newton’s method (11) is straightforward.

4.2.3 Numerical Results for the One-Dimensional Problem

First, we show the numerical results for the one-dimensional Liouville–Bratu–Gelfand equation (37) with homogeneous Dirichlet boundary conditions (38). Recall that an exact solution, although in implicit form, is available in this case (see equation (39)); thus, as discussed, the exact solutions are derived using Newton’s method with a convergence tolerance of $10^{-12}$. Figure 4 depicts the comparative results between the exact, FD, FEM and ELM solutions on the upper-branch as obtained by applying Newton’s iterations, for two values of the parameter $\lambda$ and a fixed $N=40$, namely for $\lambda =3$ close to the turning point (occurring at $\lambda _c \sim 3.513830719$) and for $\lambda =0.2$. For our illustrations, we have set as initial guess $u_0(x)$ a parabola that satisfies the homogeneous boundary conditions, namely:

$$\begin{aligned} u_0(x)=4l_0(x-x^2), \end{aligned}$$

with a fixed $L_{\infty }$-norm $||u||_{\infty }=l_0$ close to the one obtained from the exact solution.

Fig. 4

Numerical solutions and accuracy of the FD, FEM and the proposed machine learning (ELMs) schemes for the one-dimensional Bratu problem (37). a Computed solutions at the upper-branch unstable solution at $\lambda =3$ for a fixed problem size $N=40$. b $L_2$-norm of differences with respect to the exact unstable solution (39) at $\lambda =3$ for various values of N. c Computed solutions at the upper-branch unstable solution at $\lambda =0.2$ with a fixed problem size $N=40$. d $L_2$-norm of differences with respect to the exact unstable solution (39) at $\lambda =0.2$ for various values of N. The initial guess of the solutions was a parabola satisfying the homogeneous boundary conditions with a fixed $L_{\infty }$-norm $||u||_{\infty }=l_0$ close to the one resulting from the exact solution

In particular, for $\lambda =3$, we used as initial guess a parabola with $l_0=2.2$; in all cases Newton’s iterations converge to the correct unstable upper-branch solution. For $\lambda =0.2$, we used as initial guess a parabola with $l_0=6.4$ (the exact solution has $l_0 \sim 6.5)$; again in all cases, Newton’s iterations converged to the correct unstable upper-branch solution. To clarify more the behaviour of the convergence, in Fig. 5, we report the regimes of convergence for a grid of $L_{\infty }$ norms of the initial guesses (parabolas) and $\lambda$s. In Table 4, we compare the execution times of the four methods when applied for the solution of the Bratu equation (37) with Dirichlet boundary condition (38) and $\lambda =1$. Computations are performed 100 times and we also provide the 5% and 95% percentiles. Again, for all practical means, the execution times obtained with the proposed machine learning scheme are comparable with the ones obtained with FD and FEM (note that the execution times obtained with the proposed machine learning scheme are slightly smaller that the ones obtained with FEM), while, as seen, numerical approximation accuracy is better in the ELMs case; the execution times when using the FD are slightly smaller but as shown the FD scheme results to a lower numerical accuracy compared with FEM and the proposed machine learning (ELMs) scheme.

Fig. 5

Convergence regimes (basin of attraction) of Newton’s method with the a FD, b FEM, and c, d ELM numerical schemes for the one-dimensional Bratu problem (37) for a grid of initial guesses ($L_{\infty }$-norms of parabolas that satisfy the boundary conditions (38)) and $\lambda$s. Green points indicate convergence to the lower-branch solutions; Red points indicate convergence to the upper-branch solutions; Blue points indicate divergence. c ELM with logistic SF (3). d ELM with Gaussian RBF (6) (Color figure online)

Table 4 Execution times (s) for the Bratu equation (37) with Dirichlet boundary condition (38) and $\lambda =1$

Fig. 6

Fixed point iterations: $L_2$-norm of the difference errors for the low and up branch Liouville–Bratu–Gelfand solution (39) for $\lambda =2$: a $L_2$ errors with respect to N of the low branch solution, b $L_2$ errors with respect to N of the upper branch

Remark 4

(Linearization of the equation for the numerical solution of the Liouville–Bratu–Gelfand problem)

For the solution of the equation (37) with boundary conditions given by (38), one can consider the following iterative procedure that linearizes the equation:

$$\begin{aligned} \left\{ \begin{array}{l} \text {Given } u^{(0)}, \text { do until convergence} \\ \text {find } u^{(k)} \text { such that } \varDelta u^{(k)} + \lambda e^{u^{(k-1)}} u^{(k)} = \lambda ( u^{(k-1)}-1) e^{u^{(k-1)}} \ . \end{array}\right. \end{aligned}$$

In this way, the nonlinear term becomes a linear reaction term with a non-constant coefficient given by the evaluation of the nonlinearity at the previous step. Then, we implemented fixed point iterations until convergence. Such a linearization procedure is used, for example, in [36]. In Fig. 6, we report some results on the application of this method. We note that this scheme converges more slowly and it is not so robust compared to the Newton’s method.

4.2.4 Bifurcation Diagram and Numerical Accuracy

In this section, we report the numerical results obtained by the numerical bifurcation analysis of the one-dimensional Bratu problem (37). Figure 7 shows the constructed bifurcation diagram with respect to the parameter $\lambda$ and in Table 5, we report the accuracy of the computed value as obtained with FD, FEM and the proposed machine learning (ELMs) scheme, versus the exact value of the turning point. As shown, our proposed machine learning scheme provides a bigger numerical accuracy for the value of the turning point for medium to large sizes of the grid, and equivalent results (ELM with SF) to FEM, both outperforming the FD scheme.

Table 5 One-dimensional Bratu problem (37)

Fig. 7

a Bifurcation diagram for the one-dimensional Bratu problem (37), with a fixed problem size $N=400$. b Zoom near the turning point

In Figs. 8 and 9, we depict the contour plots of the $L_{\infty }$-norms of the differences between the computed solutions by FD, FEM and the proposed machine learning (ELMs) scheme and the exact solutions for the lower-Fig. 8 and upper-branch Fig. 9, respectively with respect to N and $\lambda$.

Fig. 8

One-dimensional Bratu problem (37). Contour plots of the $L_{\infty }$-norms of the differences between the computed and exact (39) solutions for the lower stable branch: a FD, b FEM, c ELM with logistic SF (3), d ELM with Gaussian RBF (6)

Fig. 9

One-dimensional Bratu problem (37). Contour plots of the $L_{\infty }$-norms of the differences between the computed and exact (39) solutions for the upper unstable branch: a FD, b FEM, c ELM with logistic SF (3), d ELM with Gaussian RBF (6)

As it is shown, the proposed machine learning schemes outperform both FD and FEM methods for medium to large problem sizes N, and provide equivalent results with FEM for low to medium problem sizes, thus both (FEM and the proposed machine learning (ELMs) scheme) outperforming the FD scheme.

4.2.5 Numerical Results for the Two-Dimensional Problem

For the two-dimensional problem (37)–(38), no exact analytical solution is available. Thus, for comparing the numerical accuracy of the FD, FEM and the proposed machine learning (ELM) schemes, we considered the value of the bifurcation point that has been reported in key works as discussed in Sect. 4.2. Figure 10 depicts the computed bifurcation diagram as computed via pseudo-arc-length continuation (see Sect. 3). Table 6, summarizes the computed values of the turning point as estimated with the FD, FEM and ELM schemes for various sizes N of the grid.

Fig. 10

a Computed bifurcation diagram for the two-dimensional Bratu problem (37), with a grid of $40\times 40$ points. b Zoom near the turning point

Table 6 Turning point estimation of the two-dimensional Bratu problem

Remark 5

(The Gelfand–Bratu model) The Liouville–Bratu–Gelfand equation (37) in a unitary ball $B \subset {\mathbb {R}}^d$ with homogeneous Dirichlet boundary conditions is usually refereed as Gelfand–Bratu model. Such equation posses radial solutions u(r) of the one-dimensional non-linear boundary-value problem [58]:

$$\begin{aligned} \left\{ \begin{array}{rl} &{}u''(r)+ \dfrac{d-1}{r}u'(r)+ \lambda e^{u(r)} =0 \quad 0< r < 1 \\ &{}u(1)=u'(0)=0 \end{array} \right. \end{aligned}$$

(44)

In the case $d=2$ this equation gives multiple solutions if $\lambda <\lambda _c=2$. For example, in [53], the authors have used Mathematica to give analytical solutions at various values of $\lambda$; for our tests we consider:

$$\begin{aligned} \begin{array}{ll} \lambda =\frac{1}{2} \,\rightarrow \ &{} u(r)=\log \left( \dfrac{ 16\left( 7+4\sqrt{3}\right) }{\left( 7+4\sqrt{3}+ r^2 \right) ^2 }\right) \\ \lambda =1 \,\rightarrow \ &{} u(r)=\log \left( \dfrac{ 8\left( 3+2\sqrt{2}\right) }{\left( 3+2\sqrt{2}+ r^2 \right) ^2 }\right) \ . \\ \end{array} \end{aligned}$$

(45)

Figure 11 depicts the numerical accuracy of the proposed machine learning (ELM) collocation scheme with respect to the exact solutions for two values of $\lambda$, namely for $\lambda =1/2$ and for $\lambda =1$. Because no meshing procedure is involved, and because the collocation equation seeks no other point, the implementation of the Newton’s method is straightforward when changing the geometry of the domain.

Fig. 11

Numerical accuracy of ELMs for the radial two-dimensional Gelfand–Bratu problem (44). $L_2$-norm of differences of the analytical solutions (45) w.r.t. the number of neurons N in ELMs with both logistic SF (3) and Gaussian RBF (6): a $\lambda =1/2$, b $\lambda =1$

5 Conclusions

We proposed a machine learning numerical method based on Extreme Learning Machines (ELMs) and collocation for the approximation of steady-state solutions of non-linear PDEs. The proposed numerical scheme takes advantage of the property of the ELMs as universal function approximators, bypassing the need of the computational very expensive - and most-of-the times without any guarantee for convergence of-the training phase of other types of machine learning such as single or multilayer ANNs and Deep-learning networks. The base of the approximation subspace on which a solution of the PDE is sought are the randomized transfer functions of the hidden layer which are weighted by the only unknown parameters, that is the weights of the hidden to output layer. For linear PDEs, these can be computed by solving a linear regularization problem in one step. In our previous work [8], we demonstrated that ELMs can provide robust and accurate approximations of the steady-state solution of benchmark linear PDEs with steep gradients, for which analytical solutions were available. Here, we address a new numerical scheme based on ELMs that can be used to solve steady state problems of non-linear PDEs, and by bridging them with numerical continuation methods, we show how one can exploit the arsenal of numerical bifurcation theory to trace branches of solutions past turning points. For our demonstrations, we considered two celebrated classes of nonlinear PDEs whose solutions bifurcate as parameter values change: the one-dimensional viscous Burgers equation (a fundamental representative of advection-diffusion PDEs) and the one- and two-dimensional Liouville–Bratu–Gelfand equation (a fundamental representative of reaction-diffusion PDEs). By coupling the proposed numerical scheme with Newton-Raphson iterations and the “pseudo” arc-length continuation method, we constructed the corresponding bifurcation diagrams past turning points. The efficiency of the proposed numerical machine learning collocation method was compared against two of the most established numerical solution methods, namely central Finite Differences and Galerkin Finite Elements. By doing so, we showed that (for the same problem size) the proposed machine-learning approach outperforms FD and FEM schemes for relatively medium to large sizes of the grid, both with respect to the accuracy of the computed solutions for a wide range of the bifurcation parameter values and the approximation accuracy of the turning points. Thus, we show that the computational times of the proposed machine learning method are comparable with the ones obtained with the other two schemes (actually the computational times obtained with the proposed method are slightly smaller than the ones obtained with FEM; the FD scheme provides slightly smaller times but fails to approximate solutions with steep gradients and in general results to poorer numerical approximations). Hence, the proposed method arises as an alternative and powerful new numerical technique for the approximation of steady-state solutions of non-linear PDEs. Furthermore, its implementation is far simpler than the implementation of FEM, thus providing equivalent or even better numerical accuracy, and in all cases is shown to outperform the simple FD scheme, which fails to approximate steep gradients as here arise near the boundaries. Of course there are many open problems linked to the implementation of the proposed numerical method that ask for further and deeper investigation, such as the theoretical investigation of the impact of the type of transfer functions and the probability distribution of their parameter values functions to the approximation of the solutions. Further directions could be towards the extension of the method for the solution of time-dependent non-linear PDEs as well as the solution of inverse-problems in PDEs. Finally, we should note that the aim of the current work was to show how random projection neural networks and namely, ELMs can be efficiently used for the numerical solution of steady-state problems of nonlinear PDEs, the comparison of the performance of the proposed method with other traditional methods such as FD and FEM and by exploiting the tools of numerical bifurcation theory, the construction of the corresponding bifurcation diagrams. Thus, a comparison with other machine learning approaches such as deep-learning or other schemes that have been used for the numerical solution of time-dependent PDEs (see e.g. [18, 52]) is out of the scope of this work. Such a comparison is still a challenging task that we aim to confront in a future work.