On the Stochastic Magnus Expansion and Its Application to SPDEs

Abstract

We derive the stochastic version of the Magnus expansion for linear systems of stochastic differential equations (SDEs). The main novelty with respect to the related literature is that we consider SDEs in the Itô sense, with progressively measurable coefficients, for which an explicit Itô-Stratonovich conversion is not available. We prove convergence of the Magnus expansion up to a stopping time $\tau$ and provide a novel asymptotic estimate of the cumulative distribution function of $\tau$. As an application, we propose a new method for the numerical solution of stochastic partial differential equations (SPDEs) based on spatial discretization and application of the stochastic Magnus expansion. A notable feature of the method is that it is fully parallelizable. We also present numerical tests in order to asses the accuracy of the numerical schemes.

1 Introduction

The Magnus expansion (hereafter referred to as ME) is a classical tool to solve non-autonomous linear differential equations. Generalizations of the ME to Stratonovich SDEs are well-known and were proposed by several authors (see for instance [2, 3, 5, 32] and the references given in Sect. 1.2). In this paper we derive, for the first time to the best of our knowledge, the ME for Itô SDEs under general assumptions which do not guarantee an explicit Itô-Stratonovich conversion, namely progressively measurable stochastic coefficients. Our main results are the convergence of the stochastic ME up to a stopping time $\tau$ and a novel asymptotic estimate of the cumulative distribution function of $\tau$. The latter improves some previous estimates obtained in purely Markovian settings and is based on an application of Morrey’s inequality. We also explore possible applications to the numerical solution of stochastic partial differential equations (SPDEs).

Let $d,q\in {\mathbb {N}}$ and consider the linear matrix-valued Itô SDE

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t = B_t X_t dt + A^{(j)}_t X_t dW^j_t,\\ X_0 = I_d, \end{array}\right. } \end{aligned}$$

(1)

with $A^{(1)},\ldots ,A^{(q)},B$ being real $(d\times d)$-matrix-valued bounded stochastic processes, $I_d$ the identity $(d\times d)$-matrix and $W=(W^1,\ldots ,W^q)$ a q-dimensional standard Brownian motion. In (1), as well as anywhere throughout the paper, we use Einstein summation convention to imply summation of terms containing $W^{j}$, over the index j from 1 to q.

In the deterministic case, i.e. $A^{(j)}\equiv 0$, $j=1,\ldots ,q$, (1) reduces to the matrix-valued ODE

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d}{dt}X_t =B_t X_t,\\ X_0 = I_d, \end{array}\right. } \end{aligned}$$

(2)

which admits an explicit solution, in terms of matrix exponential, in the time-homoge-neous case. Namely, if $B_t\equiv B$, the unique solution to (2) reads as

$$\begin{aligned} X_t = e^{tB}, \qquad t\ge 0. \end{aligned}$$

However, in the non-autonomous case, the ODE (2) does not admit an explicit solution. In particular, if $B_t$ is not constant, the solution $X_t$ typically differs from $e^{\int _0^t B_s ds}$. This is due to the fact that, in general, $B_t$ and $B_{s}$ do not commute for $t\ne s$. As it turns out, a representation of the solution in terms of a matrix exponential is still possible, at least for short times, i.e.

$$\begin{aligned} X_t = e^{Y_t}, \end{aligned}$$

(3)

for $t\ge 0$ suitably small and $Y_t$ real valued $(d\times d)$-matrix. Moreover, Y admits a semi-explicit expansion as a series of iterated integrals involving nested Lie commutators of the function B at different times. Such representation is known as Magnus expansion [23] and its first terms read as

$$\begin{aligned} Y_t&= \int _0^t B_s ds + \frac{1}{2} \int _0^t ds \int _0^s [B_s,B_u] du \nonumber \\&\quad + \frac{1}{6} \int _0^t ds \int _0^s du \int _0^u \big ( \big [B_s,[B_u,B_r]\big ] +\big [B_r,[B_u,B_s]\big ] \big ) dr + \cdots , \end{aligned}$$

(4)

where $\left[ A,B\right] := AB-BA$ denotes the Lie commutator. The ME has a wide range of physical applications and the related literature has grown increasingly over the last decades (see, for instance, the excellent survey paper [3] and the references given therein).

In the stochastic case, when $j=1$, $B_t\equiv 0$ and A is constant, i.e. $A_t(\omega )\equiv A$, the Itô equation (1) reduces to

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t = A X_t dW_t,\\ X_0 = I_d, \end{array}\right. } \end{aligned}$$

whose explicit solution can be easily proved to be of the form (3), with

$$\begin{aligned} Y_t = -\frac{1}{2} A^2 t + A W_t, \qquad t\ge 0. \end{aligned}$$

In general, when the matrices $A^{(j)}_t, A^{(j)}_{s},B_t,B_{s}$ with $t\ne s$ do not commute, an explicit solution to (1) is not known. For instance, in the non-commutative case, neither the equation

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t = B dt + A X_t dW_t,\\ X_0 = I_d, \end{array}\right. } \end{aligned}$$

(5)

nor the equation

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t = A_t X_t dW_t,\\ X_0 = I_d, \end{array}\right. } \end{aligned}$$

admit an explicit solution, save some particular cases (see for instance the example in Sect. 3.3). Among the approximation tools that were developed in the literature to solve stochastic differential equations, including (1), some Magnus-type expansions that extend (3)–(4) were derived in different contexts. We now go on to describe our contribution to this stream of literature, and then to firm our results within the existing ones. In particular, a detailed comparison with existing stochastic MEs previously derived by other authors will be provided below, in the last subsection.

1.1 Description of the Main Results

In this paper we derive a Magnus-type representation formula for the solution to the Itô SDE (1), which is (3) together with

$$\begin{aligned} Y_t = Y^{(1)}_t + Y^{(2)}_t + Y^{(3)}_t + \cdots \qquad t\in [0,\tau ], \end{aligned}$$

(6)

for $\tau$ suitably small, strictly positive stopping time. In analogy with the deterministic ME, the general term $Y^{(n)}$ can be expressed recursively, and contains iterated stochastic integrals of nested Lie commutators of the processes $B,A^{(j)}$ at different times.

In the case $j=1$, the first two terms of the expansion read as

$$\begin{aligned} Y^{(1)}_t&= \int _0^t B_s ds + \int _0^t A_s dW_s, \\ Y^{(2)}_t&= \frac{1}{2} \int _{0}^{t}{ \bigg ( \Big [ B_s, \int _{0}^s B_u du + \int _{0}^s A_u dW_u \Big ] - A^2_s \bigg ) ds} \\&\quad + \frac{1}{2} \int _{0}^{t}{ \Big [ A_s, \int _{0}^s B_u du + \int _{0}^s A_u dW_u \Big ] dW_s}. \end{aligned}$$

For example, in the case of SDE (5) the latter can be reduced to

$$\begin{aligned} Y^{(1)}_t&= Bt+AW_t, \\ Y^{(2)}_t&= [{A},{B}]\left( \frac{1}{2}tW_t- \int _{0}^{t}{W_s ds} \right) -\frac{1}{2}A^2 t. \end{aligned}$$

Notice that the last expressions do not contain stochastic integrals. In fact, in the general autonomous case, and if $j=1$, all the iterated stochastic integrals in $Y^{(n)}$ can be solved for any n (see Corollary 5.2.4 in [16]). Therefore, in this case the expansion becomes numerically computable by only approximating Lebesgue integrals, as opposed to stochastic Runge–Kutta schemes, which typically require the numerical approximation of stochastic integrals. As we shall see in the numerical tests in Sect. 3, this feature allows us to choose a sparser time-grid in order to save computation time. This feature is also preserved in some non-autonomous cases as illustrated in Sect. 3.

A notable feature of the expansion is the possibility of parallelizing the computation of its terms. In contrast to standard iterative methods, which require the solution at a given time-step in order to go through the next step in the iteration, the discretization of the integrals in the terms $Y^{(n)}$ can be done simultaneously for all the time steps. Conclusively, this entails the possibility of parallelizing over all times in the time-grid and makes the numerical implementation of the stochastic ME perfectly GPU applicable.

As it often happens when deriving convergent (either asymptotically or absolutely) expansions, a formal derivation precedes the rigorous result: that is what we do for (3)–(6) in Sect. 2.2. Just like the derivation of the deterministic ME relies on the possibility of writing the logarithm Y as the solution to an ODE, in the stochastic case the first step consists in representing Y as the solution to an SDE. Such representation of Y will be more involved compared to the deterministic case because of the presence of the second order derivatives of the exponential map coming from the application of Itô’s formula. This is a distinctive feature of our derivation with respect to other analogous results in the Stratonovich setting where the standard chain-rule applies. With the SDE representation for Y at hand, the expansion (6) stems, like in the deterministic case, from applying a Dyson-type perturbation procedure to the SDE solved by Y.

In the deterministic case, the convergence of the ME (4) to the exact logarithm of the solution to (2) was studied by several authors, who proved progressively sharper lower bounds on the maximum ${\bar{t}}$ such that the convergence to the exact solution is assured for any $t\in [0,{\bar{t}}]$. At the best of our knowledge, the sharpest estimate was given in [26], namely

$$\begin{aligned} {\bar{t}} \ge \sup \bigg \{ t\ge 0 \mid \int _{0}^t \left\| { B_s }\right\| ds < \pi \bigg \}, \end{aligned}$$

(7)

where $\left\| { B_s}\right\|$ denotes the spectral norm. Note that the existence of a real logarithm of $X_t$ is an issue that underlies the study of the convergence of the ME. We state here our main result, proved in Sect. 2.3, which deals with these matters in the stochastic case, when the coefficients $B,A^{(j)}$ in (1) are progressively measurable processes. We defer a comparison with previous convergence results for stochastic Magnus-type expansions to the next subsection. We denote by ${\mathscr {M}}^{d\times d}$ the space of the $(d\times d)$-matrices with real entries. Also, for an ${\mathscr {M}}^{d\times d}$-valued stochastic process $M=(M_t)_{t\in [0,T]}$, we set ${\left\| {M}\right\| _{T}:=\left\| {\Vert {M}\Vert _{F}}\right\| _{L^{\infty }([0,T]\times \varOmega )}}$, where $\Vert {\cdot }\Vert _{F}$ denotes the Frobenius (Euclidean entry-wise) norm.

Theorem 1

Let $A^{(1)},\ldots ,A^{(q)}$ and B be bounded, progressively measurable, ${\mathscr {M}}^{d\times d}$-valued processes defined on a filtered probability space $(\varOmega ,{\mathscr {F}},P,({\mathscr {F}}_t)_{t\ge 0})$ equipped with a standard q-dimensional Brownian motion $W=(W^1,\ldots , W^q)$. For $T>0$ let also $X=(X_t)_{t\in [0,T]}$ be the unique strong solution to (1) (see Lemma 5). There exists a strictly positive stopping time $\tau \le T$ such that:

• (i) $X_t$ has a real logarithm $Y_t\in {\mathscr {M}}^{d\times d}$ up to time $\tau$, i.e.

  $$\begin{aligned} X_t = e^{Y_t},\qquad 0\le t<\tau ; \end{aligned}$$

  (8)

• (ii) the following representation holds P-almost surely:

  $$\begin{aligned} Y_t = \sum _{n=0}^{\infty } Y^{(n)}_t,\qquad 0\le t<\tau , \end{aligned}$$

  (9)

  where $Y^{(n)}$ is the nth term in the stochastic ME as defined in (27) and (31)–(33);

• (iii) there exists a positive constant C, only dependent on $\Vert A^{(1)}\Vert _{T},\ldots ,\Vert A^{(q)}\Vert _{T}$, $\Vert B\Vert _{T}$, T and d, such that

  $$\begin{aligned} P (\tau \le t) \le C t,\qquad t\in [0,T]. \end{aligned}$$

  (10)

The proof of (i) relies on the continuity of X together with a standard representation for the matrix logarithm. The key point in the proof of (ii) consists in showing that $X^{\varepsilon ,\delta }_t$ and its logarithm $Y^{\varepsilon ,\delta }_t$ are holomorphic as functions of $(\varepsilon ,\delta )$, where $X^{\varepsilon ,\delta }_t$ represents the solution of (1) when $A^{(j)}$ and B are replaced by $\varepsilon A^{(j)}$ and $\delta B$, respectively. Once this is established, the representation (9) follows from observing that, by construction, the series in (9) is exactly the formal power series of $Y^{\varepsilon ,\delta }_t$ at $(\varepsilon ,\delta )=(1,1)$. To prove the holomorphicity of $X^{\varepsilon ,\delta }_t$ we follow the same approach typically adopted to prove regularity properties of stochastic flows. Namely, in Lemma 5 we state some maximal $L^p$ and Hölder estimates (with respect to the parameters) for solutions to SDEs with random coefficients and combine them with the Kolmogorov continuity theorem. Finally, the proof of (iii) owes one more time to the $L^p$ estimates in Lemma 5 and to a Sobolev embedding theorem to obtain pointwise estimates w.r.t. the parameters $(\varepsilon ,\delta )$ above.

Theorem 1 has been used in the recent paper [34] (cf. Lemma 1) where a semi-linear non-commuative Itô-SDEs is studied and Euler, Milstein and derivative-free numerical schemes are developed, with a convergence analysis for those schemes.

In the last part of the paper we perform numerical tests with the Magnus expansion. In particular, Sect. 3.2 is devoted to the application of the stochastic ME to the numerical solution of parabolic stochastic partial differential equations (SPDEs). The idea is to discretize the SPDE only in space and then approximate the resulting linear matrix-valued SDE by truncating the series in (8)–(9). The goal here is to propose the application of stochastic MEs as novel approximation tools for SPDEs; we study the error of this approximating procedure only numerically, in a case where an explicit benchmark is available, and we defer the theoretical error analysis to further studies.

1.2 Review of the Literature and Comparison

Stochastic generalizations of the MEs were proposed by several authors. To the best of our knowledge, we recognize mainly two streams of research.

The beginning of the first one can be traced back to the work [2], where the author derived exponential stochastic Taylor expansions (see also [1, 16] for general stochastic Taylor series) of the solution of a system of Stratonovich SDEs with values on a manifold ${\mathscr {M}}$, i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t = B(X_t) dt + A^{(j)}(X_t) \circ dW^{j}_t, \\ X_0 = x_0, \end{array}\right. } \end{aligned}$$

(11)

with $B,A^{(j)}$ being smooth, deterministic and autonomous vector fields on ${\mathscr {M}}$. The stochastic flow of (11) is represented in terms of the exponential map of a stochastic vector field Y, i.e.

$$\begin{aligned} X_t (x_0) = \text {exp}\, Y_t (x_0), \end{aligned}$$

the vector field Y being expressed by an infinite series of iterated stochastic integrals multiplying nested commutators of the vector fields $B,A^{(j)}$. This representation is proved up to a strictly positive stopping time and extends some previous results in [11, 31] for the commutative case and in [13, 19, 33] for the nilpotent case. Refinements of [2] were proved in [6] making the expansion of Y more explicit. Later, numerical methods based on these representations were proposed in [7] and [8]. Such techniques, known as Castell-Gaines methods, require the approximation of the solution to a time-dependent ODE besides the approximation of iterated stochastic integrals. Truncating the expansion of Y at a specified order, these schemes turn out to be asymptotically efficient in the sense of Newton [28].

If ${\mathscr {M}}={\mathscr {M}}^{d\times d}$ and the vector fields are linear, then (11) reduces to the Stratono-vich version of (1) with $B,A^{(j)}$ constant matrices, and the representation of X given in [2] can be seen as a stochastic ME, in that the exponential map of Y reduces to the multiplication by a matrix exponential. In fact, in this case the expansion in [2] becomes explicit in terms of iterated stochastic integrals, and can be shown to coincide with the expansion in this paper by applying Itô-Stratonovich conversion formula. In the very interesting paper [22], the authors study several computational aspects of numerical schemes stemming from the truncated ME, in which the iterated stochastic integrals are approximated by their conditional expectation. Besides showing that asymptotic efficiency holds for an arbitrary number of Brownian components, they compare the theoretical accuracy with the one of analogous schemes based on Dyson (or Neumann) series, which are obtained by applying stochastic Taylor expansion directly on the equation. They find that, although the theoretical accuracy of Magnus schemes is not superior, Magnus-based approximations seem more accurate than their Dyson counterparts in practice. They also discuss the computational cost deriving from approximating the iterated stochastic integrals and the matrix exponentiation, in relation to different features of the problem such as the dimension and the number of Brownian motions, as well as to the order of the numerical scheme.

The second stream of literature is explicitly aimed at extending the original Magnus results to stochastic settings and can be traced back to [5] where the ME is derived via formal arguments for a linear system of Stratonovich SDEs with deterministic coefficients. Clearly, in the autonomous case such expansion coincides with the one obtained by Ben Arous [2], whereas in the non-autonomous case, $B\equiv 0$ and $j=1$, it is formally equivalent to the deterministic ME (4) with all the Lebesgue integrals replaced by Stratonovich ones. The authors of [5] do not address the convergence of the ME, but rather study computational aspects of the resulting approximation, in particular in comparison with Runge-Kutta stochastic schemes. The authors of [24] consider the Ito SDE (1) with constant coefficients, and propose to resolve via Euler method the SDE (25) for the logarithm of the solution. In [32] the ME for the Stratonovich version of (1) with deterministic coefficients is applied to solve non-linear SDEs; however, the error analysis of the truncated expansion seems flawed, since the fact that the Magnus series converges only up to a positive stopping time is overlooked. In [27], a general procedure for designing higher strong order methods for Itô SDEs on matrix Lie groups is outlined.

We now go on to discuss the contribution of this paper with respect to the existing literature. In the first place, Theorem 1 on the convergence of the ME requires very weak conditions on the coefficients, which are stochastic processes satisfying the sole assumption of progressive measurability. This is a novel aspect compared to the results in [2, 6], which surely cover a wider class of SDEs, but under the assumption of time-independent deterministic coefficients. We point out that this feature is also relevant in light of the fact that our result is stated for Itô SDEs as opposed to Stratonovich ones. Indeed, while this difference might appear as minor in the Markovian case, where a simple conversion formula exists (cf. [10, 21]), it becomes substantial in the case of progressively measurable coefficients. We also point out that, even in the Markovian non-autonomous case, convergence issues were not discussed in [5, 22].

Another novel aspect of our result concerns the estimate (10) for the cumulative distribution function of the stopping time $\tau$ up to which the Magnus series converges to the real logarithm of the solution: this kind of estimate was unknown even in the autonomous case. Theorem 11 in [2] (see also [6]) provides an asymptotic estimate for the truncation error of the logarithm, which in the linear case studied in this paper would read as

$$\begin{aligned} Y_t = \sum _{n=1}^N Y^{(n)}_t + t^{\frac{N+1}{2}} R_t, \qquad t<T, \end{aligned}$$

with R bounded in probability. Although this type of result holds for the general SDE (11), it is weaker than Theorem 1 in the linear case. In fact, it can be obtained by (10) together with the standard estimate $\left\| { \sup _{0\le s\le t} \Vert {Y^{(n)}_s}\Vert _{F} }\right\| _{L^2(\varOmega )}\le C t^{\frac{N+1}{2}}$, but not the other way around.

A rigorous error analysis of the ME is left for future research, as well as applications to non-linear SDEs (see [32] for a recent attempt in this direction).

The rest of the paper is structured as follows. In Sect. 2 we derive the ME and prove Theorem 1. In particular, Sect. 2.1 contains the key Lemma 1 with a representations for the first and second order differentials through which the terms $Y^{(n)}$ in (8)–(9) will be defined, and some preliminary results that will be used to derive the expansion. Section 2.2 contains a formal derivation of (8)–(9). Section 2.3 is entirely devoted to the proof of Theorem 1.

In Sect. 3 we first introduce a numerical test for an SDE with constant, non-commuting coefficients. The formulas for the first three orders of the ME in this test will also be used in in Sect. 3.2, where we present the application of the ME to the numerical solution of parabolic SPDEs. In particular, in Sect. 3.2.1 we recall some general facts about stochastic Cauchy problems, in Sect. 3.2.2 we introduce the finite-difference–Magnus approximation scheme and we check the effectiveness of the proposed approach through numerical tests. Finally, we provide an additional numerical test to assess the accuracy of the ME in the case of time-dependent coefficients.

2 Itô-Stochastic ME

In this section we define the terms in the expansion (9) and prove Theorem 1.

2.1 Preliminaries

Let ${\mathscr {M}}^{d\times d}$ be the vector space of $(d\times d)$ real-valued matrices. For the readers’ convenience we recall the following notations. Throughout the paper we denote by $[\cdot ,\cdot ]$ the standard Lie commutator, i.e.

$$\begin{aligned}{}[M,N] := MN - NM,\qquad M,N\in {\mathscr {M}}^{d\times d}, \end{aligned}$$

and by $\left\| {\cdot }\right\|$ the spectral norm on ${\mathscr {M}}^{d\times d}$. Also, we denote by $\beta _k$, $k\in {\mathbb {N}}_0$, the Bernoulli numbers defined as the derivatives of the function $x\mapsto x/(e^{x}-1)$ computed at $x=0$. For sake of convenience we report the first three Bernoulli numbers: $\beta _0=1$, $\beta _1=-\frac{1}{2}$, $\beta _2=\frac{1}{6}$. Note also that $\beta _{2m+1}=0$ for any $m\in {\mathbb {N}}$.

We now define the operators that we will use in the sequel. For a fixed $\varSigma \in {\mathscr {M}}^{d\times d}$, we let:

• $\text {ad}^j_{\varSigma } : {\mathscr {M}}^{d\times d}\rightarrow {\mathscr {M}}^{d\times d}$, for $j\in {\mathbb {N}}_0$, be the linear operators defined as

  $$\begin{aligned} \text {ad}^0_{\varSigma }(M)&:= M,\\ \text {ad}^j_{\varSigma }(M)&:= \left[ {\varSigma },\text {ad}^{j-1}_{\varSigma }(M)\right] , \qquad j\in {\mathbb {N}}. \end{aligned}$$

  To ease notation we also set $\text {ad}_{\varSigma } := \text {ad}^1_{\varSigma }$;

• $e^{\text {ad}_{\varSigma }}: {\mathscr {M}}^{d\times d}\rightarrow {\mathscr {M}}^{d\times d}$ be the linear operator defined as

  $$\begin{aligned} e^{\text {ad}_{\varSigma }}(M):= \sum _{n=0}^{\infty }{ \frac{1}{n!} \text {ad}_{\varSigma }^n(M) }= e^{{\varSigma }} M e^{-{\varSigma }}, \end{aligned}$$

  (12)

  where $e^{\varSigma }:= \sum _{j=0}^{\infty }{\frac{{\varSigma }^j}{j!}}$ is the standard matrix exponential;

• ${\mathscr {L}}_{\varSigma }: {\mathscr {M}}^{d\times d}\rightarrow {\mathscr {M}}^{d\times d}$ be the linear operator defined as

  $$\begin{aligned} {\mathscr {L}}_{\varSigma } (M) := \int _{0}^{1}{ e^{\text {ad}_{\tau \! {\varSigma }}}(M) d\tau }= \sum _{n=0}^{\infty } \frac{1}{(n+1)!} \text {ad}^n_{\varSigma }(M); \end{aligned}$$

  (13)

• ${\mathscr {Q}}_{\varSigma }: {\mathscr {M}}^{d\times d}\times {\mathscr {M}}^{d\times d}\rightarrow {\mathscr {M}}^{d\times d}$ be the bi-linear operator defined as

  $$\begin{aligned}&{\mathscr {Q}}_{\varSigma }(M,N):= {\mathscr {L}}_{\varSigma }(M)\, {\mathscr {L}}_{\varSigma }(N) + \int _{0}^{1}{ \tau \left[ {\mathscr {L}}_{\tau \varSigma } (N) ,e^{\text {ad}_{\tau {\varSigma }}}(M)\right] d\tau } \end{aligned}$$

  (14)
  $$\begin{aligned}&= \sum _{n=0}^{\infty }{ \sum _{m=0}^{\infty }{ \frac{ \text {ad}^n_{\varSigma }(M)}{(n+1)!} \frac{ \text {ad}^m_{\varSigma } (N)}{(m+1)!} } } + \sum _{n=0}^{\infty }{ \sum _{m=0}^{\infty }{ \frac{ \left[ \text {ad}^n_{{\varSigma }}(N),\text {ad}^m_{{\varSigma }}(M)\right] }{ (n+m+2)(n+1)!m! } } }. \end{aligned}$$

  (15)

In the next lemma we provide explicit expressions for the first and second order differentials of the exponential map ${\mathscr {M}}^{d\times d}\ni M\mapsto e^M$. We recall that this map is smooth and in particular, it is continuously twice differentiable.

Lemma 1

For any $\varSigma \in {\mathscr {M}}^{d\times d}$, the first and the second order differentials at $\varSigma$ of the exponential map ${\mathscr {M}}^{d\times d}\ni M\mapsto e^M$ are given by

$$\begin{aligned} \begin{aligned} M&\mapsto {\mathscr {L}}_\varSigma (M)\, e^\varSigma = e^\varSigma \, {\mathscr {L}}_{-\varSigma }(M),&M\in {\mathscr {M}}^{d\times d},\\ (M,N)&\mapsto {\mathscr {Q}}_\varSigma (M,N)\, e^\varSigma ,&M,N\in {\mathscr {M}}^{d\times d}, \end{aligned} \end{aligned}$$

(16)

where ${\mathscr {L}}_\varSigma$ and ${\mathscr {Q}}_\varSigma$ are the linear and (symmetric) bi-linear operators as defined in (13)–(14).

We point out that this result, though very basic, is novel and of independent interest (for instance it was recently employed in [14]).

Proof

The first part of the statement, concerning the first order differential, is a classical result; its proof can be found in [3, Lemma 2] among other references.

We prove the second part. Fix $M\in {\mathscr {M}}^{d\times d}$ and denote by $\partial _{M} e^\varSigma$ the first order directional derivative of $e^\varSigma$ w.r.t. M, i.e.

$$\begin{aligned} \partial _{M} e^\varSigma := \frac{d}{dt} e^{\varSigma +t M}\Big |_{t=0} . \end{aligned}$$

By the first part, we have

$$\begin{aligned} \partial _{M} e^\varSigma = {\mathscr {L}}_\varSigma (M)\, e^\varSigma , \qquad \varSigma \in {\mathscr {M}}^{d\times d}. \end{aligned}$$

We now show that, for any $M,N\in {\mathscr {M}}^{d\times d}$, the second order directional derivative

$$\begin{aligned} \partial _{N,M} e^\varSigma : = \frac{d}{dt} \partial _M e^{\varSigma +t N}\Big |_{t=0} \end{aligned}$$

is given by

$$\begin{aligned} \partial _{N,M} e^\varSigma = {\mathscr {Q}}_\varSigma (N,M) \, e^\varSigma , \qquad \varSigma \in {\mathscr {M}}^{d\times d}. \end{aligned}$$

(17)

We have

$$\begin{aligned} \frac{d}{dt} \partial _{M} e^{\varSigma +t N}&= \frac{d}{dt} \Big ( {\mathscr {L}}_{\varSigma +t N} (M)\, e^{\varSigma +t N} \Big )\nonumber \\&= {\mathscr {L}}_{\varSigma +t N} (M) \, {\mathscr {L}}_{\varSigma +t N} (N)\, e^{\varSigma +t N} + \Big ( \frac{d}{dt} {\mathscr {L}}_{\varSigma +t N} (M)\Big )\, e^{\varSigma +t N}. \end{aligned}$$

(18)

We use the definition (13) and exchange the differentiation and integration signs to obtain

$$\begin{aligned}&\frac{d}{dt} {\mathscr {L}}_{\varSigma +t N}(M) = \int _{0}^{1}{ \frac{d}{dt} e^{\text {ad}_{\tau (\varSigma +tN)}}(M) d\tau }\\&(\mathrm{by} (12))\\&\qquad \qquad \qquad \qquad = \int _{0}^{1}{ \frac{d}{dt} \Big ( e^{\tau (\varSigma +tN)} M e^{ - \tau (\varSigma +tN)} \Big ) d\tau }\\&\qquad \qquad \qquad \qquad = \int _{0}^{1}{ \left( \frac{d}{dt} e^{ \tau (\varSigma +tN)} \right) \, M \, e^{ - \tau (\varSigma +tN)} d\tau } + \int _{0}^{1}{ e^{ \tau (\varSigma +tN)} \, M \, \frac{d}{dt} e^{ - \tau (\varSigma +tN)} d\tau } \end{aligned}$$

(by employing the two expressions in (16) for the first-order differential)

$$\begin{aligned}&= \int _{0}^{1}{ \tau {\mathscr {L}}_{ \tau (\varSigma +tN)}(N) \, e^{ \tau (\varSigma +tN)}\, M \, e^{ - \tau (\varSigma +tN)} d\tau } \\&\quad - \int _{0}^{1}{ \tau e^{ \tau (\varSigma +tN)} \, M \, e^{ -\tau (\varSigma +tN)} \, {\mathscr {L}}_{ \tau (\varSigma +tN)}(N) d\tau }\\&= \int _{0}^{1}{ \tau \left[ {\mathscr {L}}_{\tau (\varSigma +tN)} (N) , e^{\text {ad}_{\tau (\varSigma +tN)}}(M) \right] d\tau }. \end{aligned}$$

This, together with (18), proves (17).

To conclude, we prove equality (15). It is enough to observe that

$$\begin{aligned} \int _{0}^{1}{ \tau \, {\mathscr {L}}_{\tau \varSigma } (N) \, e^{\text {ad}_{\tau \varSigma }} (M) d\tau }&= \int _{0}^{1} { \tau \sum _{n=0}^{\infty }{ \sum _{m=0}^{\infty }{ \frac{ \text {ad}^n_{\tau \varSigma }(N)}{(n+1)!} \frac{ \text {ad}^m_{\tau \varSigma } (M)}{m!} } } d\tau }\\ {}&= \int _{0}^{1}{ \sum _{n=0}^{\infty }{ \sum _{m=0}^{\infty }{ \frac{\text {ad}^n_{\varSigma } (N)}{(n+1)!} \frac{ \text {ad}^m_{\varSigma } (M)}{m!} \tau ^{n+m+1} } }d\tau }\\ {}&= \sum _{n=0}^{\infty }{ \sum _{m=0}^{\infty }{ \frac{ \text {ad}^n_{\varSigma } (N) \text {ad}^m_{\varSigma } (M) }{(n+m+2)(n+1)!m!} } }. \end{aligned}$$

$\square$

Proposition 1

(Itô formula) Let Y be an ${\mathscr {M}}^{d\times d}$-valued Itô process of the form

$$\begin{aligned} dY_t = \mu _t dt + {\sigma ^{j}_t dW^{j}_t}. \end{aligned}$$

(19)

Then we have

$$\begin{aligned} de^{Y_t} = \bigg ( {\mathscr {L}}_{Y_t} \left( \mu _t\right) + \frac{1}{2} \sum _{j=1}^{q} { {\mathscr {Q}}_{Y_t}\big ( \sigma ^j_t, \sigma ^j_t \big ) } \bigg ) e^{Y_t} dt + {{\mathscr {L}}_{Y_t} \big ( \sigma ^j_t \big )\, e^{Y_t} dW^j_t }. \end{aligned}$$

Proof

The statement follows from the multi-dimensional Itô formula (see, for instance, [29]) combined with Lemma 1 and applied to the exponential process $e^{Y_t}$. $\square$

We also have the following inversion formula for the operator ${\mathscr {L}}_{\varSigma }$.

Lemma 2

(Baker, 1905) Let ${\varSigma }\in {\mathscr {M}}^{d\times d}$. The operator ${\mathscr {L}}_{\varSigma }$ is invertible if and only if the eigenvalues of the linear operator $\text {ad}_{\varSigma }$ are different from $2m\pi$, $m\in {\mathbb {Z}}\setminus \{0\}$. Furthermore, if $\left\| {{\varSigma }}\right\| <\pi$, then

$$\begin{aligned} {\mathscr {L}}_{\varSigma }^{-1}(M) = \sum _{k=0}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{\varSigma }(M), \qquad M\in {\mathscr {M}}^{d\times d}. \end{aligned}$$

(20)

For a proof to Lemma 2 we refer the reader to [3].

2.2 Formal Derivation

In this section we perform formal computations to derive the terms $Y^{(n)}$ appearing in the ME (9). Although such computations are heuristic at this stage, they are meant to provide the reader with an intuitive understanding of the principles that underlie the expansion procedure. Their validity will be proved a fortiori, in Sect. 2.3, in order to prove Theorem 1.

Let $(\varOmega ,{\mathscr {F}},P,({\mathscr {F}}_t)_{t\ge 0})$ be a filtered probability space. Assume that, for any $\varepsilon ,\delta \in {\mathbb {R}}$, the process $X^{\varepsilon ,\delta }=\big (X^{\varepsilon ,\delta }_t\big )_{t\ge 0}$ solves the Itô SDE

$$\begin{aligned} {\left\{ \begin{array}{ll} dX^{\varepsilon ,\delta }_t =\delta B_t X^{\varepsilon ,\delta }_t dt+\varepsilon A^{(j)}_t X^{\varepsilon ,\delta }_t dW^j_t,\\ X^{\varepsilon ,\delta }_0 = I_d, \end{array}\right. } \end{aligned}$$

(21)

and that it admits the exponential representation

$$\begin{aligned} X^{\varepsilon ,\delta }_t = e^{Y^{\varepsilon ,\delta }_t} \end{aligned}$$

(22)

with $Y^{\varepsilon ,\delta }$ being an ${\mathscr {M}}^{d\times d}$-valued Itô process. Clearly, if $(\varepsilon ,\delta )=(1,1)$, then (21)–(22) reduce to (1)–(3). Assume now that $Y^{\varepsilon ,\delta }$ is of the form (19). Then, Proposition 1 yields

$$\begin{aligned} \varepsilon A^{(j)}_t&= {\mathscr {L}}_{Y^{\varepsilon ,\delta }_t} \big ( \sigma ^j_t \big ), \qquad j=1,\ldots ,q, \end{aligned}$$

(23)

$$\begin{aligned} \delta B_t&= {\mathscr {L}}_{Y^{\varepsilon ,\delta }_t} \left( \mu _t\right) + \frac{1}{2} \sum _{j=1}^{q}{ {\mathscr {Q}}_{Y^{\varepsilon ,\delta }_t}\big ( \sigma ^j_t, \sigma ^j_t \big ) }. \end{aligned}$$

(24)

Inverting now (23)–(24), in accord with (20), one obtains

$$\begin{aligned} \sigma ^j_t&= {\mathscr {L}}_{Y^{\varepsilon ,\delta }_t}^{-1} \big ( \varepsilon A^{(j)}_t \big ) = \varepsilon \sum _{k=0}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{Y^{\varepsilon ,\delta }_t}\big (A^{(j)}_t\big ), \qquad \qquad j=1,\ldots ,q, \\ \mu _t&= {\mathscr {L}}_{Y^{\varepsilon ,\delta }_t}^{-1} \bigg ( \delta B_t - \frac{1}{2} \sum _{j=1}^{q}{ {\mathscr {Q}}_{Y^{\varepsilon ,\delta }_t}\big ( \sigma ^j_t, \sigma ^j_t \big ) } \bigg ) \\&= \sum _{k=0}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{Y^{\varepsilon ,\delta }_t}\biggl ( \delta B_t - \frac{1}{2} \sum _{j=1}^{q} \sum _{n=0}^{\infty } \sum _{m=0}^{\infty } \biggl ( \frac{ \text {ad}^n_{Y^{\varepsilon ,\delta }_t}\big (\sigma ^j_t\big )}{(n+1)!} \frac{ \text {ad}^m_{Y^{\varepsilon ,\delta }_t} \big (\sigma ^j_t\big )}{(m+1)!}\\&\quad +\frac{\big [{\text {ad}^n_{{Y^{\varepsilon ,\delta }_t}}\big (\sigma ^j_t\big )},{\text {ad}^m_{{Y^{\varepsilon ,\delta }_t}}\big (\sigma ^j_t\big )}\big ] }{ (n+m+2)(n+1)!m! } \biggr ) \biggr ). \end{aligned}$$

Equivalently, $Y^{\varepsilon ,\delta }$ solves the Itô SDE

$$\begin{aligned} {\left\{ \begin{array}{ll} dY^{\varepsilon ,\delta }_t = \mu ^{\varepsilon ,\delta }\big (t,Y^{\varepsilon ,\delta }_t\big ) dt + \sigma ^{\varepsilon }_j\big (t,Y^{\varepsilon ,\delta }_t\big ) dW^j_t, \\ Y^{\varepsilon ,\delta }_0 = 0, \end{array}\right. } \end{aligned}$$

(25)

with

$$\begin{aligned} \sigma ^{\varepsilon }_j(t,\cdot )&= \varepsilon \sum _{n=0}^{\infty } \frac{\beta _n}{n!} \text {ad}^n_{\,\cdot }\big (A^{(j)}_t\big ),\qquad {j=1,\ldots ,d,} \\ \mu ^{\varepsilon ,\delta }(t,\cdot )&= \sum _{n=0}^{\infty } \frac{\beta _n}{n!} \text {ad}^n_{\,\cdot } \bigg (\delta B_t - \frac{1}{2} \sum _{j=1}^q {\mathscr {Q}}_{\cdot }\big (\sigma ^{\varepsilon }_j(t,\cdot ),\sigma ^{\varepsilon }_j(t,\cdot )\big )\bigg ). \end{aligned}$$

We now assume that $Y^{\varepsilon ,\delta }$ admits the representation

$$\begin{aligned} Y^{\varepsilon ,\delta }_t = \sum _{n=0}^{\infty } \sum _{r=0}^{n} Y^{(r,n-r)}_t \varepsilon ^{r}\delta ^{n-r}, \end{aligned}$$

(26)

for a certain family $(Y^{(r,n-r)})_{n,r\in {\mathbb {N}}_0}$ of stochastic processes. In particular, setting $(\varepsilon ,\delta )=(1,1)$, (26) would yield

$$\begin{aligned} Y_t = \sum _{n=0}^{\infty } Y^{(n)}_t \quad \text {with}\quad Y^{(n)}_t := \sum _{r=0}^{n} Y^{(r,n-r)}_t. \end{aligned}$$

(27)

Remark 1

Note that it is possible to re-order the double series $\sum \nolimits _{n=0}^{\infty } \sum \nolimits _{r=0}^{n} Y^{(r,n-r)}_t$ according to any arbitrary choice, for the latter will be proved to be absolutely convergent. The above choice for $Y^{(n)}$ contains all the terms of equal order by weighing $\varepsilon$ and $\delta$ in the same way. A different choice, which respects the probabilistic relation $\sqrt{\varDelta t} \approx \varDelta W_t$, corresponds to weighing $\delta$ as $\varepsilon ^2$. This would lead to setting

$$\begin{aligned} Y^{(n)}_t := \sum _{r=0}^{\left\lfloor \frac{n}{2}\right\rfloor } Y^{(n-2 r, r)}_t \end{aligned}$$

in (27).

Remark 2

Observe that, if the function $(\varepsilon ,\delta )\mapsto Y^{\varepsilon ,\delta }_0$ is assumed to be continuous P-almost surely, then the initial condition in (25) implies

$$\begin{aligned} Y^{(i,j)}_0 = 0 \quad P\text {-a.s}., \qquad i,j\in {\mathbb {N}}_0, \end{aligned}$$

and thus

$$\begin{aligned} Y^{(n)}_0 = 0 \quad P\text {-a.s}., \qquad n\in {\mathbb {N}}_0. \end{aligned}$$

We now plug (26) into (25) and collect all terms of equal order in $\varepsilon$ and $\delta$. Up to order 2 we obtain

$$\begin{aligned} \varepsilon ^0\delta ^0:&\quad Y^{(0,0)}_t = 0, \end{aligned}$$

(28)

$$\begin{aligned} \varepsilon ^1\delta ^0:&\quad Y^{(1,0)}_t = \int _0^t A^{(j)}_s dW^j_s, \end{aligned}$$

(29)

$$\begin{aligned} \varepsilon ^0\delta ^1:&\quad Y^{(0,1)}_t = \int _0^t B_s ds, \nonumber \\ \varepsilon ^2\delta ^0:&\quad Y^{(2,0)}_t = - \frac{1}{2} \int _0^t \big (A^{(j)}_s\big )^2 ds + \frac{1}{2} \int _0^t \Big [ A^{(j)}_s , \int _{0}^{s} A^{(i)}_r d{W^{i}_r} \Big ] dW^{j}_s,\qquad \nonumber \\ \varepsilon ^1\delta ^1:&\quad Y^{(1,1)}_t = \frac{1}{2} \int _0^t \Big [ B_s, \int _{0}^{s} A^{(j)}_r dW_r^j \Big ] ds + \frac{1}{2} \int _0^t \Big [ A^{(j)}_s, \int _{0}^{s} B_r dr \Big ] d{W^{j}_s}, \nonumber \\ \varepsilon ^0\delta ^2:&\quad Y^{(0,2)}_t = \frac{1}{2} \int _0^t \Big [ B_s, \int _{0}^{s} B_r dr \Big ] ds, \end{aligned}$$

(30)

for any $t\ge 0$, where we used, one more time, Einstein summation convention to imply summation over the indexes i, j and Remark 2 to set all the initial conditions equal to zero. Proceeding by induction, one can obtain a recursive representation for the general term $Y^{(r,n-r)}$ in (26), namely:

$$\begin{aligned} Y^{(r,n-r)}_t = \int _0^t \mu ^{r,n-r}_s ds + \int _0^t \sigma ^{r,n-r,j}_s dW^j_s, \qquad n\in {\mathbb {N}}_0, \ r=0,\ldots ,n, \end{aligned}$$

(31)

where the terms $\sigma ^{r,n-r,j},\mu ^{r,n-r}$ are defined recursively as

$$\begin{aligned} \sigma ^{r,n-r,j}_s&:= \sum _{i=0}^{n-1}\frac{\beta _i}{i!} S^{r-1,n-r,i}_s\big (A^{(j)}\big ), \end{aligned}$$

(32)

$$\begin{aligned} \mu ^{r,n-r}_s&:= \sum _{i=0}^{n-1}\frac{\beta _i}{i!} S^{r,n-r-1,i}_s(B) - \frac{1}{2} \sum _{j=1}^q \sum _{i=0}^{{ n-2}}\frac{\beta _i}{i!} \sum _{q_1=2}^{{ r }} \sum _{q_2=0}^{{ n-r}} S^{r-q_1,n-r-q_2,i} \big ( Q^{q_1,q_2,j} \big ), \end{aligned}$$

(33)

with

$$\begin{aligned} Q^{q_1,q_2,j}_s :&= \sum _{i_1=2}^{q_1}\sum _{i_2=0}^{q_2} \sum _{h_1=1}^{i_1-1} \sum _{h_2=0}^{i_2} \sum _{p_1=0}^{q_1-i_1} \sum _{{p_2}=0}^{q_2-i_2}\ \sum _{m_1=0}^{p_1+p_2} \ \sum _{{m_2}=0}^{q_1-i_1-p_1+q_2-i_2-p_2} \\&\quad \Bigg ({ \frac{S_s^{p_1,p_2,m_1}\big (\sigma ^{h_1,h_2,j}_s\big )}{({m_1}+1)!} \frac{ S_s^{q_1-i_1-p_1,q_2-i_2-p_2,m_2} \big (\sigma ^{i_1-h_1,i_2-h_2,j}_s\big )}{({m_2}+1)!} } \\&\quad + {\frac{ \left[ S_s^{p_1,p_2,m_1}\big (\sigma ^{i_1-h_1,i_2-h_2,j}_s\big ),S_s^{q_1-i_1-p_1,q_2-i_2-p_2,m_2}\big (\sigma ^{h_1,h_2,j}_s\big )\right] }{ ({m_1}+{m_2}+2)({m_1}+1)!{m_2}! } } \Bigg ), \end{aligned}$$

and with the operators S being defined as

$$\begin{aligned} S^{r-1,n-r,0}_s(A)&:= {\left\{ \begin{array}{ll} A &{} \text {if } r=n=1,\\ 0 &{} \text {otherwise}, \end{array}\right. }\\ S^{r-1,n-r,i}_s(A)&:= \sum _{\begin{array}{c} (j_1,k_1),\ldots ,(j_i,k_i) \in {\mathbb {N}}_0^2 \\ j_1 + \cdots + j_i = r-1 \\ k_1+ \cdots +k_{i} = n-r \end{array}} \big [Y^{(j_1,k_1)}_s, \big [ \ldots , \big [ Y^{(j_i,k_i)}_s, A_s \big ] \dots \big ] \big ] \\&= \sum _{\begin{array}{c} (j_1,k_1),\dots ,(j_i,k_i) \in {\mathbb {N}}_0^2 \\ j_1 + \cdots + j_i = r-1 \\ k_1+ \cdots k_{i} = n-r \end{array}} \text {ad}_{Y^{(j_1,k_1)}_s} \circ \cdots \circ \text {ad}_{Y^{(j_i,k_i)}_s}(A_s), \qquad i\in {\mathbb {N}}. \end{aligned}$$

Remark 3

All the processes $Y^{(r,n-r)}$, with $n\in {\mathbb {N}}$ and $r=0,\ldots ,n$, are well defined according to the recursion (31)–(32)–(33), as long as B and $A^{(1)},\ldots , A^{(q)}$ are bounded and progressively measurable stochastic processes.

Example 1

As we already pointed out in the introduction, in the case $j=1$ and $B\equiv 0$, the SDE (1) admits an explicit solution given by

$$\begin{aligned} Y_t = -\frac{1}{2} A^2 t + A W_t, \qquad t\ge 0, \end{aligned}$$

and the terms in the ME (27) read as

$$\begin{aligned} Y^{(1)}_t = A W_t,\qquad Y^{(2)}_t = -\frac{1}{2} A^2 t,\qquad Y^{(n)}_t=0, \ n\ge 3. \end{aligned}$$

In particular, the ME coincides with the exact solution with the first two terms.

2.3 Convergence Analysis

In this section we prove Theorem 1. To avoid ambiguity, only in this section, we denote by ${\mathscr {M}}^{d\times d}_{{\mathbb {R}}}$ and ${\mathscr {M}}^{d\times d}_{{\mathbb {C}}}$ the spaces of $(d\times d)$-matrices with real and complex entries, respectively; on these spaces we shall make use of the Frobenius norm denoted by $\Vert {\cdot }\Vert _{F}$. We say that a matrix-valued function is holomorphic if all its entries are holomorphic functions. We recall that $W=(W^1,\ldots , W^q)$ is a q-dimensional standard Brownian motion and $A^{(1)},\ldots , A^{(q)},B$ are bounded ${\mathscr {M}}^{d\times d}_{{\mathbb {R}}}$-valued progressively measurable stochastic processes defined on a filtered probability space $(\varOmega ,{\mathscr {F}},P,({\mathscr {F}}_t)_{t\ge 0})$. Also recall that, for any ${\mathscr {M}}^{d\times d}_{{\mathbb {R}}}$-valued process $M=(M_t)_{t\in [0,T]}$, we set ${\left\| {M}\right\| _{T}:=\left\| {\Vert {M}\Vert _{F}}\right\| _{L^{\infty }([0,T]\times \varOmega )}}$.

We start with two preliminary lemmas.

Lemma 3

Assume that $Y=(Y^{\varepsilon ,\delta }_t)_{\varepsilon ,\delta \in {\mathbb {R}},\, t\in {\mathbb {R}}_{\ge 0}}$ is a ${\mathscr {M}}^{d\times d}_{{\mathbb {R}}}$-valued stochastic process that can be represented as a convergent series of the form (26). If Y solves the SDE (25) up to a positive stopping time $\tau$, then $Y^{(r,n-r)}$ in (26) are Itô processes and satisfy (31)–(32)–(33) for any $t<\tau$.

Proof

We prove (31)–(32)–(33) only for $n=0,1$. Namely, we show that (28), (29) and (30) hold up to time $\tau$, P-a.s. The representation for the general term $Y^{(r,n-r)}$ can be proved by induction; we omit the details for brevity.

Since Y is of the form (26) then $Y^{(0,0)}_t = Y^{0,0}_t$ for any $t<\tau$. Moreover, since Y solves the SDE (25) then $Y^{0,0}\equiv 0$ on $[0,\tau [$, P-a.s. Thus (28) holds up to time $\tau$, P-a.s.

Now, (25) yields

$$\begin{aligned} Y^{\varepsilon ,0}_t&= \varepsilon \int _{0}^t A^{(j)}_s dW^{j}_s + \varepsilon R^{\varepsilon }_t, \qquad t\in [0,\tau [, \quad P\text {-a.s.}, \end{aligned}$$

(34)

where

$$\begin{aligned} R^{\varepsilon }_t= & {} \int _{0}^t \bigg ( \sum _{k=1}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{Y^{\varepsilon ,0}_s}\big (A^{(j)}_s\big ) \bigg ) dW^j_s \\&\quad - \frac{\varepsilon }{2} \int _0^t {\mathscr {L}}_{Y^{\varepsilon ,0}_s}^{-1} \Bigg ( {\mathscr {Q}}_{Y^{\varepsilon ,0}_s}\bigg ( \sum _{k=0}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{Y^{\varepsilon ,0}_s}\big (A^{(j)}_s\big ), \sum _{k=0}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{Y^{\varepsilon ,0}_s}\big (A^{(j)}_s\big ) \bigg ) \Bigg ) ds. \end{aligned}$$

Note that, again by (25), $R^{0}\equiv 0$ P-a.s. Moreover, representation (26) implies continuity of $\varepsilon \mapsto Y^{\varepsilon ,0}_t$ near $\varepsilon =0$, which in turn implies the continuity of $\varepsilon \mapsto R^{\varepsilon }_t$. Thus we have $\lim \limits _{\varepsilon \rightarrow 0}R^\varepsilon _t=R^0_t$ P-a.s. This, together with (34) and (26) implies that (29) necessarily holds, up to time $\tau$, P-a.s.

Similarly, (25) yields

$$\begin{aligned} Y^{0,\delta }_t = \delta \int _0^t B_s ds + \delta Q^{\delta }_t, \qquad t\in [0,\tau [, \quad P\text {-a.s.}, \end{aligned}$$

with

$$\begin{aligned} Q^{\delta }_t = \int _0^t \bigg ( \sum _{k=1}^{\infty } \frac{\beta _k}{k!}\text {ad}^k_{Y^{0,\delta }_s} (B_s ) \bigg ) ds \end{aligned}$$

and the same argument employed above yields (30) up to time $\tau$, P-almost surely. $\square$

Lemma 4

Let $M\in {\mathscr {M}}_{{\mathbb {C}}}^{d\times d}$ be nonsingular and such that $\left\| { M - I_d}\right\| < 1$ where $\left\| {\cdot }\right\|$ is the spectral norm. Then M has a unique logarithm, which is

$$\begin{aligned} \log M&= \sum _{n=1}^{\infty } (-1)^{n+1} \frac{(M-I_d)^n}{n} \\&= (M - I_d) \int _0^{\infty } \frac{1}{1+\mu } (\mu I_d + M)^{-1} d\mu . \end{aligned}$$

In particular, we have

$$\begin{aligned} \left\| {\log M}\right\| \le - \log \big ( 1 - \left\| { M - I_d }\right\| \big ). \end{aligned}$$

(35)

Proof

The first representation is a standard result. The second representation stems from the factorization $M=V J V^{-1}$ with J in Jordan form, under the assumption that M has no non-positive real eigenvalues, i.e. $\lambda \in {\mathbb {C}}\setminus ]-\infty ,0]$ for any $\lambda$ eigenvalue of M. This last property, however, is ensured by the assumption $\left\| { M - I_d }\right\| < 1$. Indeed, the latter implies

$$\begin{aligned} \Vert {M v - v}\Vert _{F} < 1, \qquad v\in {\mathbb {R}}^d,\ \left| {v}\right| =1, \end{aligned}$$

which in turn implies that, if $\lambda$ is a real eigenvalue of M and v is one of its normalized eigenvectors, then

$$\begin{aligned} 1>\Vert {M v - v}\Vert _{F}=\left| {\lambda v-v}\right| =\left| \lambda -1\right| . \end{aligned}$$

$\square$

We have one last preliminary lemma, containing some technical results concerning the solutions to (21). These are semi-standard, in that they can be inferred by combining and adapting existing results in the literature.

Lemma 5

For any $T>0$ and $\varepsilon ,\delta \in {\mathbb {C}}$, the SDE (21) has a unique strong solution $(X^{\varepsilon ,\delta }_t)_{t\in [0,T]}$. For any $p\ge 1$ and $h>0$ there exists a positive constant $\kappa$, only dependent on $\Vert A^{(1)}\Vert _{T},\ldots ,\Vert A^{(q)}\Vert _{T}$, $\Vert B\Vert _{T}$, d, T, h and p, such that

$$\begin{aligned} E\Big [ \Vert { X^{\varepsilon ,\delta }_t - X^{\varepsilon ',\delta '}_{s}}\Vert _{F}^{2p} \Big ]&\le \kappa {\big ( \left| t-s\right| ^p +\left( \left| \varepsilon -\varepsilon '\right| +\left| \delta -\delta '\right| \right) ^{2p} \big )}, \end{aligned}$$

(36)

$$\begin{aligned} E\Big [ \sup _{0 \le u\le t} \Vert { X^{\varepsilon ,\delta }_u - X^{\varepsilon ,\delta }_{0} }\Vert _{F}^{2p} \Big ]&\le \kappa t^{p} (\left| \varepsilon \right| + \left| \delta \right| )^{2p}, \end{aligned}$$

(37)

for any $0\le t,s\le T$ and $\varepsilon ,\delta ,\varepsilon ',\delta '\in {\mathbb {C}}$ with $\left| \varepsilon \right| ,\left| \delta \right| ,\left| \varepsilon '\right| ,\left| \delta '\right| \le h$.

Up to modifications, $(X^{\varepsilon ,\delta }_t)_{\varepsilon ,\delta \in {\mathbb {C}},\, t\in [0,T]}$ is a continuous process such that:

• i) for any $t\in [0,T]$, the function $(\varepsilon ,\delta )\mapsto X^{\varepsilon ,\delta }_t$ is holomorphic;

• ii) the functions $(t,\varepsilon ,\delta )\mapsto \partial _{\varepsilon } X^{\varepsilon ,\delta }_t$ and $(t,\varepsilon ,\delta )\mapsto \partial _{\delta } X^{\varepsilon ,\delta }_t$ are continuous;

• iii) for any $p\ge 1$ and $h>0$ there exists a positive constant $\kappa$ only dependent on $\Vert A^{(1)}\Vert _{T},\ldots ,\Vert A^{(q)}\Vert _{T}$, $\Vert B\Vert _{T}$, d, T, h and p, such that

  $$\begin{aligned} E\Big [ \sup _{0 \le s\le t} \Big \{ \Vert { \partial _{\varepsilon } X^{\varepsilon ,\delta }_s }\Vert _{F}^{2p} + \Vert { \partial _{\delta } X^{\varepsilon ,\delta }_s }\Vert _{F}^{2p} \Big \} \Big ] \le \kappa t^p(\left| \varepsilon \right| + \left| \delta \right| )^p, \end{aligned}$$

  (38)

  for any $t\in [0,T]$ and $\left| \varepsilon \right| ,\left| \delta \right| \le h$.

Proof

Existence of the solution and estimates (36)–(37) of the moments follow from the results in Section 5, Chapter 2 in [18] (in particular, see Corollary 5 on page 80 and Theorem 7 on page 82).

The second part of the statement is a refined version of the Kolmogorov continuity theorem in the form that can be found for instance in Sect. 2.3 in [20]: a detailed proof is provided in [15]. $\square$

Remark 4

The existence and uniqueness for the solution to (1) is a particular case of the previous result.

We are now in the position to prove Theorem 1.

Proof of Theorem 1

We fix $h>1$, $T>0$, and let $(X^{\varepsilon ,\delta }_t)_{\varepsilon ,\delta \in {\mathbb {C}},\, t\in [0,T]}$ be the solution of the SDE (21) as defined in Lemma 5. Moreover, for $t\in \,]0,T]$, we set $Q_{t,h}:=\, ]0,t[ \times B_{h}(0)$ where $B_{h}(0)=\{(\varepsilon ,\delta )\in {\mathbb {C}}^{2}\mid |(\varepsilon ,\delta )|<h\}$.

Part (i): as $X^{\varepsilon ,\delta }_0=I_d$, by continuity the random time defined as

$$\begin{aligned} \tau := \sup \left\{ t\in [0,T] \left| \Vert { X^{\varepsilon ,\delta }_s - I_d}\Vert _{F} < 1-e^{-\pi } \text { for any } (s,\varepsilon ,\delta )\in Q_{t,h}\right. \right\} \end{aligned}$$

(39)

is strictly positive. Furthermore, again by continuity,

$$\begin{aligned} (\tau \le t) = \bigcup _{ (s,\varepsilon ,\delta )\in {\tilde{Q}}_{t,h} } \left( \Vert { X^{\varepsilon ,\delta }_s -I_d }\Vert _{F} \ge 1-e^{-\pi }\right) , \qquad t\in [0,T], \end{aligned}$$

where ${\tilde{Q}}_{t,h}$ is a countable, dense subset of $Q_{t,h}$, which implies that $\tau$ is a stopping time.

Let $(t,\varepsilon ,\delta )\in Q_{\tau ,h}$: by Lemma 4 applied to $M=X^{\varepsilon ,\delta }_t$ we have

$$\begin{aligned} Y_t^{\varepsilon ,\delta }&:= \log X_t^{\varepsilon ,\delta } = \sum _{n=1}^{\infty } (-1)^{n+1} \frac{\big (X_t^{\varepsilon ,\delta }-I_d\big )^n}{n} \nonumber \\ {}&= \big (X_t^{\varepsilon ,\delta } - I_d\big ) \int _0^{\infty } \frac{1}{1+\mu } \big (\mu I_d + X_t^{\varepsilon ,\delta }\big )^{-1} d\mu . \end{aligned}$$

(40)

Notice that $X^{\varepsilon ,\delta }_t$ (and therefore also $Y^{\varepsilon ,\delta }_t$) is real for $\varepsilon ,\delta \in {\mathbb {R}}$: in particular, $Y_t = Y_t^{1,1}$ is real and this proves Part (i).

Part (ii): since $(\varepsilon ,\delta )\mapsto X_t^{\varepsilon ,\delta }$ is holomorphic, we can differentiate (40) to infer that $(\varepsilon ,\delta )\mapsto Y_t^{\varepsilon ,\delta }$ is holomorphic as well: indeed, we have for $(t,\varepsilon ,\delta )\in Q_{\tau ,h}$

$$\begin{aligned} \partial _{\varepsilon }Y_t^{\varepsilon ,\delta }&= \partial _{\varepsilon } X_t^{\varepsilon ,\delta } \int _0^{\infty } \frac{1}{1+\mu } \big (\mu I_d + X_t^{\varepsilon ,\delta }\big )^{-1} d\mu \\&\quad + \big (X_t^{\varepsilon ,\delta } - I_d\big ) \int _0^{\infty } \frac{1}{1+\mu } \big (\mu I_d + X_t^{\varepsilon ,\delta }\big )^{-1} \big ( \partial _{\varepsilon }X_t^{\varepsilon ,\delta } \big ) \big (\mu I_d + X_t^{\varepsilon ,\delta }\big )^{-1} d\mu , \end{aligned}$$

and similarly by differentiating w.r.t. to $\delta$. Then the expansion of $Y_t^{\varepsilon ,\delta }$ in power series at $(\varepsilon ,\delta )=(0,0)$ is absolutely convergent on $B_{h}(0)$ and the representation (26) holds on $Q_{\tau ,h}$ for some random coefficients $Y^{(r,n-r)}_t$. To conclude we need to show that the latter are as given by (31)–(32)–(33). Then (9) will stem from (26) by setting $(\varepsilon ,\delta )=(1,1)$.

In light of Lemma 4, the logarithmic map is continuously twice differentiable on the open subset of ${\mathscr {M}}_{{\mathbb {C}}}^{d\times d}$ of the matrices M such that $\left\| { M - I_d }\right\| < 1$: thus $Y_{t}^{\varepsilon ,\delta }$ admits an Itô representation (19) for $(t,\varepsilon ,\delta ) \in Q_{\tau ,h}$. Then Proposition 1 together with (21) yield (23)–(24) P-a.s. up to $\tau$ for any $(\varepsilon ,\delta )\in B_h(0)\cap {\mathbb {R}}^2$. Furthermore, by estimate (35) of Lemma 4 we also have $\left\| {Y_{t}^{\varepsilon ,\delta }}\right\| <\pi$ for $t<\tau$. Therefore, we can apply Baker’s Lemma 2 to invert ${\mathscr {L}}_{Y^{\varepsilon ,\delta }_t}$ in (23)–(24) and obtain that $Y^{\varepsilon ,\delta }$ solves (25) up to $\tau$ for any $(\varepsilon ,\delta )\in B_h(0)\cap {\mathbb {R}}^2$. Part (ii) then follows from Lemma 3.

Part (iii): for $t\le T$ let

$$\begin{aligned} f_t(\varepsilon ,\delta ):= \max _{ s\in [0,t] }\Vert {X^{\varepsilon ,\delta }_{s} - I_d}\Vert _{F},\qquad M_{t}:=\sup _{(\varepsilon ,\delta )\in B_{h}(0)}f_t(\varepsilon ,\delta ). \end{aligned}$$

By definition (39), we have

$$\begin{aligned} P (\tau \le t)\le P\left( M_{t}\ge 1-e^{-\pi }\right) \le \frac{1}{\left( 1-e^{-\pi }\right) ^2}{E\left[ M^2_{t}\right] }, \end{aligned}$$

(41)

and therefore (10) follows by suitably estimating $E\left[ M^2_{t}\right]$. To prove such an estimate we will show in the last part of the proof that $f_t$ belongs to the Sobolev space $W^{1,2 p}(B_{h}(0))$ for any $p\ge 1$ and we have

$$\begin{aligned} E\big [ \Vert f_t \Vert ^{2 p}_{W^{1,2p}(B_{h}(0))} \big ] \le C t^p, \qquad t\in [0,T], \end{aligned}$$

(42)

where the positive constant C depends only on $\Vert A^{(1)}\Vert _{T},\ldots ,\Vert A^{(q)}\Vert _{T}$, $\Vert B\Vert _{T}$, d, T, h and p. Since $f_t\in W^{1,2 p}(B_{h}(0))$ and $B_{h}(0)\subseteq {\mathbb {R}}^{4}$, by Morrey’s inequality (cf., for instance, Corollary 9.14 in [4]) for any $p>2$ we have

$$\begin{aligned} M_{t}\le c_{0} \Vert f_t\Vert _{W^{1,2p}(B_{h}(0))}, \end{aligned}$$

(43)

where $c_{0}$ is a a positive constant, dependent only on p and h (in particular, $c_{0}$ is independent of $\omega$). Combining (42) with (43), for a fixed $p>2$ we have

$$\begin{aligned} E\left[ M^2_{t}\right]&\le c^{2}_{0} E\big [ \Vert f_t\Vert ^{2}_{W^{1,2p}(B_{h}(0))} \big ]\le \end{aligned}$$

(by Hölder inequality)

$$\begin{aligned}&\le c^{2}_{0}C t,\qquad t\in [0,T]. \end{aligned}$$

This last estimate, combined with (41), proves (10).

To conclude, we are left with the proof of (42). First we have

$$\begin{aligned} E\bigg [ \int _{B_{h}(0)} | f_t(\varepsilon ,\delta ) |^{2p} d\varepsilon \, d\delta \bigg ] = \int _{B_{h}(0)} E\big [ | f_t(\varepsilon ,\delta ) |^{2p} \big ] d\varepsilon \, d\delta \le C t^p, \end{aligned}$$

(44)

where we used the estimate (37) of Lemma 5 in the last inequality. Fix now $t\in \,]0,T]$, $(\varepsilon ,\delta ),(\varepsilon ',\delta ')\in B_{h}(0)$ such that $f_t(\varepsilon ',\delta ')\le f_t(\varepsilon ,\delta )$ and set

$$\begin{aligned} {\bar{t}} \in \underset{0\le s\le t}{\arg \max } \Vert {X^{\varepsilon ,\delta }_{s} - I_d}\Vert _{F},\qquad {\tilde{t}} \in \underset{0\le s\le t}{\arg \max } \Vert {X^{\varepsilon ',\delta '}_{s} - I_d}\Vert _{F}. \end{aligned}$$

Note that the $\arg \max$ above do exist in that the process $g_s(\varepsilon ,\delta ):= X^{\varepsilon ,\delta }_{s} - I_d$ is continuous in s and we have

$$\begin{aligned} \left| f_t(\varepsilon ,\delta )-f_t(\varepsilon ',\delta ')\right|&= \left| \Vert {g_{{\bar{t}}}(\varepsilon ,\delta )}\Vert _{F} - \Vert {g_{{\tilde{t}}}(\varepsilon ',\delta ') }\Vert _{F} \right| \le {\left| \Vert {g_{{\bar{t}}}(\varepsilon ,\delta )}\Vert _{F} - \Vert {g_{{\bar{t}}}(\varepsilon ',\delta ')}\Vert _{F} \right| } \\&\le \Vert {g_{{\bar{t}}}(\varepsilon ,\delta ) - g_{{\bar{t}}}(\varepsilon ',\delta ')}\Vert _{F} \le \sup _{0\le s\le t} \Vert {g_{s}(\varepsilon ,\delta ) - g_{s}(\varepsilon ',\delta ')}\Vert _{F} \\&\le \left| {(\varepsilon ,\delta )-(\varepsilon ',\delta ')}\right| \sup _{0\le s\le t} \sup _{\begin{array}{c} |{\bar{\varepsilon }} - \varepsilon | \le | \varepsilon ' - \varepsilon | \\ |{\bar{\delta }} - \delta | \le | \delta ' - \delta | \end{array}} \Vert {\nabla g_{s}({\bar{\varepsilon }},{\bar{\delta }}) }\Vert _{F}, \end{aligned}$$

where $\nabla =\nabla _{\!\varepsilon ,\delta }$. This, as $(s,\varepsilon ,\delta )\mapsto \nabla g_{s}({\varepsilon },{\delta })$ is continuous on $Q_{t,h}$, implies $f_t\in W^{1,2 p}(B_{h}(0))$ and yields the key inequality

$$\begin{aligned} \left| { \nabla f_t(\varepsilon ,\delta ) }\right| \le \sup _{ 0\le s\le t } \Vert { \nabla X^{\varepsilon ,\delta }_{s} }\Vert _{F}, \qquad (\varepsilon ,\delta )\in B_{h}(0). \end{aligned}$$

Therefore, we have

$$\begin{aligned} E\bigg [ \int _{B_{h}(0)} \left| { \nabla f_t(\varepsilon ,\delta ) }\right| ^{2p} d\varepsilon \, d\delta \bigg ]&= \int _{B_{h}(0)} E\big [ \left| { \nabla f_t(\varepsilon ,\delta ) }\right| ^{2p} \big ] d\varepsilon \, d\delta \\&\le \int _{B_{h}(0)} E\bigg [ \sup _{ 0\le s\le t }\Vert {\nabla X^{\varepsilon ,\delta }_{s} }\Vert _{F}^{2p} \bigg ] d\varepsilon \, d\delta \le C t^p, \end{aligned}$$

where we used the estimate (38) of Lemma 5 in the last inequality. This, together with (44), proves (42) and conclude the proof. $\square$

3 Numerical Tests and Applications to SPDEs

We present here some numerical tests in order to confirm the accuracy of the approximate solutions to (1) stemming from the truncation of the series (9). We also show how this approximation can be applied to approximate the solutions to stochastic partial differential equations (SPDEs) of parabolic type.

We consider two examples of SDEs (one in Sect. 3.1 and one in Sect. 3.3), for which we compute the first three terms of the ME given by (27)–(31) and present numerical experiments to test the accuracy of the approximate solutions to (1) stemming from it. In both cases we consider $j=1$ in (1) and replace $A^{(1)}$ with A to shorten notation. The first example will be for constant matrices A and B. In the second one we will consider $B\equiv 0$ and a deterministic upper diagonal $A_t$. For each numerical test we will implement the exponential of the truncated ME up to order $n=1,2$ and 3, i.e.

$$\begin{aligned} X^{(n)}:= e^{\sum _{i=1}^{n}Y^{(i)}}, \qquad n=1,2,3, \end{aligned}$$

(45)

and compare it with a benchmark solution to (1). In Sect. 3.2 we turn our attention to the application of the ME to the numerical resolution of SPDEs. In particular, in the numerical tests we will make use of the ME for constant matrices discussed in Sect. 3.1. Error and notations. Throughout this section we will employ the following tags:

• 1. euler for the solution obtained with Euler-Maruyama scheme, which was implemented with Matlab’s pagefun for the matrix multiplication on a single GPU and vectorized over all samples;

• 2. exact to denote the time-discretization of an explicit solution, if available;

• 3. m1, m2 and m3 for the time-discretization of the Magnus approximations in (45), up to order 1,2 and 3, respectively.

For the numerical error analysis in the SDE examples we will make use of the following norms. Denoting by $X^{\text {ref}}$ and by $X^{{\text {app}}}$ a benchmark and an approximate solution, respectively, to (1) and by $\left( t_k\right) _{k=0,\ldots ,N}$ a homogeneous discretization of [0, t], we consider the random variable

$$\begin{aligned} \text {Err}_t := \frac{\varDelta }{t} \sum _{k=1}^N \frac{\Vert { X^{\text {ref}}_{t_k}- X^{\text {app}}_{t_k}}\Vert _{F} }{\Vert { X^{\text {ref}}_{t_k}}\Vert _{F}}\approx \frac{1}{t} \int _{0}^{t} { \frac{ \Vert { X^{\text {ref}}_s - X^{\text {app}}_s }\Vert _{F}}{\Vert { X^{\text {ref}}_s }\Vert _{F}} } ds \qquad \text {with}\ \varDelta =\frac{t}{N}, \end{aligned}$$

namely a discretization of the time-averaged relative error on the interval [0, t]. This is a way to measure the error on the whole trajectory as opposed to the error at a specific given time. Then we use Monte Carlo simulation, with M independent realizations of the discretized Brownian trajectories, to approximate the distribution of $\text {Err}_t$.

The matrix norm above is the Frobenius norm. In the following tests, m1, m2 and m3 will always play the role of $X^{\text {app}}$, exact always the role of $X^{\text {ref}}$, whereas euler will be either $X^{\text {app}}$ or $X^{\text {ref}}$ depending on whether exact is available or not.

We used for the calculations Matlab R2021a with Parallel Computing Toolbox running on Windows 10 Pro, on a machine with the following specifications: processor Intel(R) Core(TM) i7-8750H @ 2.20 GHz, 2x32 GB (Dual Channel) Samsung SODIMM RAM @ 2667 MHz, and a NVIDIA GeForce RTX 2070 with Max-Q Design (8 GB GDDR6 RAM). Also, we will make use of the Matlab built-in routine expm for the computation of the matrix exponential. As it turns out, this represents the most expensive step in the implementation of the Magnus approximation. However important, the pursue of optimized method for the matrix exponentiation is an extended topic of separate interest, which goes beyond the goals of this paper. Therefore, here we will limit ourselves to pointing out, separately, the computational times for the approximations of the logarithm and of the matrix exponential.

In the implementation we simulate the Brownian motion first and use it as an input for each scheme to be able to compare the trajectories of each scheme amongst each other.

3.1 Example: Constant A and B

With a slight abuse of notation, we consider $A_t\equiv A$ and $B_t\equiv B$. Recall that, if A and B do not commute, there is in general no closed-form solution to (1). The first three terms of the ME read as

$$\begin{aligned} Y_t^{(1)}&=B t + A W_t,\qquad Y_t^{(2)}=\left[ A,B\right] \left( \frac{1}{2}tW_t-\int _{0}^{t}{W_s ds}\right) -\frac{1}{2}A^2 t,\nonumber \\ Y_t^{(3)}&=\left[ \left[ B,A\right] ,A\right] \bigg ( \frac{1}{2} \int _{0}^{t}{W_s^2 ds} -\frac{1}{2} W_t \int _{0}^{t}{W_s ds} +\frac{1}{12} tW_t^2 \bigg ) \nonumber \\&\quad +\left[ \left[ B,A\right] ,B\right] \bigg ( \int _{0}^{t}{sW_s ds} -\frac{1}{2} t\int _{0}^{t}{W_s ds} -\frac{1}{12} t^2 W_t\bigg ). \end{aligned}$$

(46)

We point out that, in this case, all the stochastic integrals appearing in the ME can be solved in terms of Lebesgue integrals by using Itô’s formula. Therefore, in order to discretize $Y^{(n)}$ it is not necessary to approximate stochastic integrals. This allows to use a sparser time grid compared to the Euler method, for which the discretization of stochastic integrals is necessary. In particular, the theoretical speed of convergence with respect to the time-step is of order $\sqrt{\varDelta }$ for Euler-Maruyama scheme and of order $\varDelta$ for deterministic Euler, which is the scheme used to discretize the Lebesgue integrals in the Magnus expansion above. In the following numerical tests, we discretize in time with mesh $\varDelta$ equal to $10^{-4}$ for euler and equal to $\sqrt{\varDelta }=10^{-2}$ for m1, m2 and m3. Note that, as it is confirmed by the results in Table 1, choosing a finer time-discretization for euler (our reference method here) is essential in order to make it comparable with m3. Furthermore, in the example of Sect. 3.3, where an explicit solution is available, we show (see Tables 7 and 9 ) that choosing a sparser time-grid (say $\varDelta =10^{-3}$) the Euler-Maruyama method incurs a sensitive loss of precision.

It is also clear that the implementation is totally parallelizable, in that $Y^{(1)}$, $Y^{(2)}$ and $Y^{(3)}$ do not depend on each other and thus they can be computed in parallel. More importantly, the discretization of the integrals in each $Y^{(n)}$ can be parallelized as the latter are explicit and not implicitly defined through a differential equation.

We choose A and B at random and normalize them by their spectral norms. In particular, the results below refer to

$$\begin{aligned} A= \left( \begin{matrix} 0.335302 &{} -0.645492 \\ -0.264419 &{} 0.634641 \end{matrix}\right) , \qquad B= \left( \begin{matrix} -0.0572262 &{} 0.0493763 \\ -0.665366 &{} 0.742744 \end{matrix}\right) . \end{aligned}$$

In Fig. 1 we plot one realization of the trajectories of the top-left component $(X_t)_{11}$, computed with the methods above, up to time $t=0.75$. In Table 1 we show the expectations $E[\text {Err}_t]$ for different values of t, with euler as benchmark solution, computed via Monte Carlo simulation with $10^{3}$ samples. The same samples are used in Fig. 3 to plot the empirical CDF of $\text {Err}_t$. The computational times for the $10^3$ sampled trajectories of X, up to time $t=1$, computed with m1, m2, m3 and euler are reported in Table 2. For the Magnus methods we separate the time to compute the approximate logarithm from the one to compute the matrix exponential.

Fig. 1

A and B constant. One realization of the trajectories of the top-left component $(X_t)_{11}$, computed with euler, m1, m2, m3

Fig. 2

A and B constant. Empirical CDF of $\text {Err}_t$, at $t=0.75$, for m1, m2, m3, with euler as benchmark solution, obtained with $10^{3}$ samples

Table 1 A and B constant

Table 2 A and B constant

Remark 5

We can see from Table 2 that the Magnus methods m1, m2 and m3 are significanty faster than euler. The reason for this is two-fold: on the one hand, we have the possibility of parallelizing the Magnus methods over both time and samples, while euler is only parallelizable over all samples, and on the other hand, we can discretize the Magnus expansion with a time-step that is the square root of the one used for Euler-Maruyama, due to the different rates of convergence.

In our numerical experiments we already use 6 CPU cores to parallelize the computation of the matrix exponential on the CPU, while we use one GPU to compute the Magnus logarithm. For euler we speed up in each iteration the matrix multiplications by using pagefun on a GPU to parallelize over all samples. As for m1, m2 and m3, if we were to increase the number of CPU cores to, say, 12, we could see an approximate reduction in the computation time of matrix exponentiation by half (plus overhead), making it about 24 times as fast as the Euler method.

Now, the very nature of euler (see Example 2 together with Table 3) as an iterative scheme yields another advantage of the Magnus methods; namely, that the computation of the logarithm is very fast and if one needs only the solution of the SDE at the terminal time then one has to compute the matrix exponential only at a single time. Let us consider Table 2 for the moment. In this particular experiment it would mean that we can divide the computational time of the matrix exponentiation by approximately $\varDelta ^{-1}=10^2$ without increasing the CPU core count. Hence, the Magnus methods would require approximately only 0.04 s plus effects from distributing the memory to the different processors. The euler method, in contrast, does not benefit from this because, as an iterative method, it must fully evaluate the trajectories.

Such situations are not uncommon; for example, in mathematical finance pricing a European call option depends only on the terminal time of the underlying process, giving the Magnus methods a tremendous advantage even without increasing CPUs or GPUs. We will illustrate such a situation in Example 2 together with Table 3. In calibration procedures, such as fitting a model to data at few points in time, the Magnus method also excels for the same reason.

Table 3 A and B constant

Example 2

In this example we want to demonstrate the benefit, explained in Remark 5, of using the Magnus methods compared to iterative schemes, such as the Euler method, when calculating the first, second and third element-wise moments of the terminal value of a matrix-valued SDE.

Precisely, we evaluate $E\big [((X_t)_{ij})^k\big ]$ for $i,j=1,\ldots ,d$ and $k=1,2,3$. We will keep the same parameters as in Table 1.

The results of this example are summarized in Table 3. In this table columns 2–4 contain the values of the element-wise moments at the terminal time of the solution to the SDE with constant coefficients starting with the upper left corner of the solution matrix, then the upper right, lower left and lower right, respectively. In the last column we present the computational times in seconds.

The values of the moments do not differ significantly between euler and m3, and remarkably the Magnus methods are roughly 35 times as fast in this particular example. We stress again at this point that a coarser time-grid for euler would not be comparable to the accuracy of m3.

In the interesting paper [12] a non-linear extension in the case of commuting A and B can be found and applications to SPDEs via space discretizations are discussed, which is the same approach we take in the next subsection with the ME.

3.2 Applications to SPDEs

The aim of this subsection is to apply the previously derived ME for the numerical solution of parabolic stochastic partial differential equations (SPDEs). We derive an approximation scheme for the general case of variable coefficients, which we only test in the case of the stochastic heat-equation (Example 3), for which an exact solution is available.

3.2.1 Stochastic Cauchy Problem and Fundamental Solution

Let $(\varOmega ,{\mathscr {F}},P, ({\mathscr {F}}_t)_{t\ge 0})$ be a filtered probability space endowed with a real Brownian motion W. We consider the stochastic Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} du_t(x) = \mathbf{L}_t u_t (x) dt + \mathbf{G}_t u_t(x) dW_t, \qquad t> 0,\ x\in {\mathbb {R}},\\ u_0 = \varphi , \end{array}\right. } \end{aligned}$$

(47)

where $\mathbf{L}_t$ is the elliptic linear operator acting as

$$\begin{aligned} \mathbf{L}_t u_t(x) = \frac{1}{2} \mathbf{a}_t(x) \partial _{xx}u_t(x) + \mathbf{b}_t(x) \partial _{x}u_t(x) + \mathbf{c}_t(x)u_t(x), \end{aligned}$$

and $\mathbf{G}_t$ is the first-order linear operator acting as

$$\begin{aligned} \mathbf{G}_t u_t(x) = {\varvec{\sigma }}_t (x) \partial _x u_t(x) +\mathbf{g}_t(x) u_t(x). \end{aligned}$$

The coefficients $(\mathbf{a}, \mathbf{b}, \mathbf{c}, \mathbf{g}, {\varvec{\sigma }})$ are random fields indexed by $(t,x)\in [0,\infty [\times {\mathbb {R}}$ and the initial datum $\varphi$ is a random field on ${\mathbb {R}}$. A classical solution to (47) is understood here as a predictable and almost-surely continuous random field $u=u_t(x)$ over $[0,\infty [\times {\mathbb {R}}$, such that $u_t \in C^{2}({\mathbb {R}})$ a.s. for any $t>0$ and

$$\begin{aligned} u_t (x) = \phi (x) + \int _{0}^t \mathbf{L}_{\tau } u_{\tau } (x) d\tau + \int _0^t \mathbf{G}_{\tau } u_{\tau }(x) dW_{\tau }, \qquad t\ge 0,\ x\in {\mathbb {R}}. \end{aligned}$$

There is a vast literature on stochastic SPDEs and problems of the form (47), under suitable measurability, regularity and boundedness assumptions on the coefficients and on the initial datum: see, for instance, [9, 17, 25, 30] and the references therein.

Note that, in analogy with deterministic PDEs, the solution of the Cauchy problem (47) can be written, in some cases, as a convolution of the initial datum with a stochastic fundamental solution $p(t,x;0,\xi )$, i.e.

$$\begin{aligned} u_t(x) = \int _{{\mathbb {R}}} p(t,x;0,\xi ) \phi (\xi ) d\xi , \qquad (t,x)\in \,]0,\infty [\times {\mathbb {R}}, \end{aligned}$$

with $p(t,x;0,\xi )$ being a random field that solves the SPDE in (47) with respect to the variables (t, x) and which approximates a Dirac delta centered at $\xi$ as t approaches 0.

3.2.2 Finite-Difference Magnus Scheme

We employ the stochastic ME to develop an approximation scheme for the Cauchy problem (47). Our goal here is only to hint at the possibility that the stochastic ME is a useful tool for the numerical solution of SPDEs. Therefore, we keep the exposition at a heuristic level and postpone the rigorous study of the problem for further research.

The idea is to apply finite-difference space-discretization for the operators $\mathbf{L}$ and $\mathbf{G}$, and then ME to solve the resulting linear (matrix-valued) Itô SDE. We fix a bounded interval [a, b] and use the following notation: for a given $d\in {\mathbb {N}}$, we denote by $\varsigma _d$ a mesh of $d+2$ equidistant points in [a, b], i.e.

$$\begin{aligned} { \varsigma _d = \{ x^d_i \mid x^d_i = a + i h,\ i=0,\ldots , d+1 \}, \qquad h:=\frac{b-a}{d+1} }, \end{aligned}$$

and for any random field $\mathbf{f}(x)$, $x\in {\mathbb {R}}$, we denote by $\mathbf{f}^{d}= (\mathbf{f}^{{d}}_{0}, \ldots , \mathbf{f}^{{d}}_{{d+1}})$ the random vector whose components correspond to $\mathbf{f}$ evaluated at the points of the mesh, namely

$$\begin{aligned} \mathbf{f}^{{d}}_{i} = \mathbf{f}(x^{{d}}_i), \qquad i=0,\ldots , {d+1}. \end{aligned}$$

Following the classical centered finite-difference discretization, we approximate the spatial derivatives in each point as

$$\begin{aligned} \partial _x u_t (x^{{d}}_i) \approx \frac{u^{{d}}_{t,i} - u^{{d}}_{t,i-1}}{h},\quad \partial _{xx} u_t (x^{{d}}_i) \approx \frac{u^{{d}}_{t,i+1} - 2 u^{{d}}_{t,i} + u^{{d}}_{t,i-1}}{h^2}, \qquad i=1,\ldots , {d}, \end{aligned}$$

to obtain the system of Itô SDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} du^{{d}}_{t,i} = (\mathbf{L}^{{d}}_t u^{{d}}_t)_i dt + (\mathbf{G}^{{d}}_t u^{{d}}_t)_i dW_t,&{} \\ u^{{d}}_{0,i} = \phi ^{{d}}_i,&{} \end{array}\right. } \end{aligned}$$

(48)

for $i=1,\ldots , {d}$, where $\mathbf{L}^{{d}}_t$ and $\mathbf{G}^{{d}}_t$ are now the operators acting as

$$\begin{aligned} (\mathbf{L}^{{d}}_t u^{{d}}_t)_i&= \frac{1}{2} \mathbf{a}^{{d}}_{t,i} \frac{u^{{d}}_{i+1} - 2 u^{{d}}_{i} + u^{{d}}_{i-1}}{h^2} + \mathbf{b}^{{d}}_{t,i} \frac{u^{{d}}_i - u^{{d}}_{i-1}}{h} + \mathbf{c}^{{d}}_{t,i} u^{{d}}_{i}, \\ ( \mathbf{G}^{{d}}_t u^{{d}}_t)_i&= {\varvec{\sigma }}^{{d}}_{t,i} \frac{u^{{d}}_i - u^{{d}}_{i-1}}{h} +\mathbf{g}^{{d}}_{t,i} u^{{d}}_{i}. \end{aligned}$$

By imposing some boundary conditions, for instance

$$\begin{aligned} u^{{d}}_{t,0} = u^{{d}}_{t,{{d+1}}} = 0, \qquad t>0, \end{aligned}$$

(49)

the system of SDEs (48) can be cast in the framework of the previous section. More precisely, under condition (49), system (48) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} d{\bar{u}}^{{d}}_{t} = A^{{d}}_t {\bar{u}}^{{d}}_t dt + B^{{d}}_t {\bar{u}}^{{d}}_t dW_t,&{}\\ {\bar{u}}^{{d}}_{0} = {\bar{\phi }}^{{d}},&{} \end{array}\right. } \end{aligned}$$

(50)

where we set

$$\begin{aligned} {\bar{u}}^{{d}}_t = (u^{{d}}_{t,1},\ldots , u^{{d}}_{t,{{d}}}),\qquad {\bar{\phi }}^{{d}} = (\phi ^{{d}}_{1}, \ldots , \phi ^{{d}}_{{{d}}}), \end{aligned}$$

and $A^{{d}}_t,B^{{d}}_t$ are the random tridiagonal $({{d}}\times {{d}})$-matrices given by

$$\begin{aligned}&A^{{d}}_t = \left( \begin{array}{cccc} -\frac{\mathbf{a}^{{d}}_{t,1}}{h^2} + \frac{ \mathbf{b}^{{d}}_{t,1}}{h} +\mathbf{c}^{{d}}_{t,1} &{} \frac{1}{2} \frac{\mathbf{a}^{{d}}_{t,1}}{h^2} &{} \cdots &{} 0 \\ \frac{1}{2} \frac{\mathbf{a}^{{d}}_{t,2}}{h^2} -\frac{\mathbf{b}^{{d}}_{t,2}}{h} &{} -\frac{\mathbf{a}^{{d}}_{t,2}}{h^2} + \frac{ \mathbf{b}^{{d}}_{t,2}}{h} +\mathbf{c}^{{d}}_{t,2} &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \frac{1}{2} \frac{\mathbf{a}^{{d}}_{t,{{d -1}}}}{h^2} \\ 0&{} \cdots &{} \frac{1}{2} \frac{\mathbf{a}^{{d}}_{t,{{d}}}}{h^2} -\frac{\mathbf{b}^{{d}}_{t,{{d}}}}{h} &{} -\frac{\mathbf{a}^{{d}}_{t,{{d}}}}{h^2} + \frac{ \mathbf{b}^{{d}}_{t,{{d}}}}{h} +\mathbf{c}^{{d}}_{t,{{d}}} \\ \end{array} \right) , \\&B^{{d}}_t =\left( \begin{array}{cccc} \frac{ {\varvec{\sigma }}^{{d}}_{t,1}}{h} +\mathbf{g}^{{d}}_{t,1} &{} 0 &{} \cdots &{} 0 \\ -\frac{{\varvec{\sigma }}^{{d}}_{t,2}}{h} &{} + \frac{ {\varvec{\sigma }}^{{d}}_{t,2}}{h} +\mathbf{g}^{{d}}_{t,2} &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} 0 \\ 0&{} \cdots &{} -\frac{{\varvec{\sigma }}^{{d}}_{t,{{d}}}}{h} &{} + \frac{ {\varvec{\sigma }}^{{d}}_{t,{{d}}}}{h} +\mathbf{g}^{{d}}_{t,{{d}}} \end{array}\right) . \end{aligned}$$

Now, the solution to (50) can be written as

$$\begin{aligned} {\bar{u}}^{{d}}_t = X^{{d}}_t {\bar{u}}^{{d}}_0, \qquad t\ge 0, \end{aligned}$$

where $X^{{d}}$ is in turn the solution to the ${\mathscr {M}}^{{{d}}\times {{d}}}$-valued Itô SDE

$$\begin{aligned} {\left\{ \begin{array}{ll} dX^{{d}}_t = A^{{d}}_t X^{{d}}_t dt + B^{{d}}_t X^{{d}}_t dW_t,\\ X^{{d}}_0=I_{{{d}}}. \end{array}\right. } \end{aligned}$$

(51)

Remark 6

The components of $X^{{d}}$ can be regarded as approximations of the integrals of the fundamental solution of the SPDE in (47), when it exists, on each sub-interval $[\frac{1}{2}(x^{{d}}_{j-1}+x^{{d}}_{j}), \frac{1}{2}(x^{{d}}_{j}+x^{{d}}_{j+1})]$, namely

$$\begin{aligned} (X^{{d}}_t)_{i,j} \approx \int _{\frac{1}{2}(x^{{d}}_{j-1}+x^{{d}}_{j})}^{\frac{1}{2}(x^{{d}}_{j}+x^{{d}}_{j+1})} p\big (t,x^{{d}}_i;0,\xi \big ) d\xi =: ({\mathscr {I}}^{{d}}_t)_{i,j}, \qquad i,j = 1,\ldots ,{{d}}. \end{aligned}$$

(52)

Example 3

We consider a special case of (47) with $\mathbf{a}_t\equiv \mathbf{a}>0$, $\mathbf{b},\mathbf{c},\mathbf{g}\equiv 0$ and ${\varvec{\sigma }}_t\equiv {\varvec{\sigma }}> 0$. Hence, we consider the stochastic heat equation

$$\begin{aligned} du_t = \frac{\mathbf{a}}{2} \partial _{xx}u_t(x) dt + {\varvec{\sigma }}\partial _x u_t(x) dW_t, \qquad t> 0,\ x\in {\mathbb {R}}, \end{aligned}$$

with $\mathbf{a}>{\varvec{\sigma }}^2$, whose stochastic fundamental solution is given explicitly by

$$\begin{aligned} p(t,x;0,\xi ):= \frac{1}{\sqrt{2\pi (\mathbf{a}- {\varvec{\sigma }}^2)t }} \exp \bigg ( - \frac{( x + {\varvec{\sigma }}W_t - \xi )^2}{2 (\mathbf{a}- {\varvec{\sigma }}^2)t } \bigg ), \qquad t>0,\ x,\xi \in {\mathbb {R}}. \end{aligned}$$

(53)

The matrices $A_t^{{d}}$ and $B_t^{{d}}$ in (51) now read as

$$\begin{aligned} A^{{d}}_t \equiv \frac{\mathbf{a}}{h^2}\left( \begin{matrix} -1 &{} \frac{1}{2} &{} \cdots &{} 0 \\ \frac{1}{2}&{} - 1 &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \frac{1}{2} \\ 0&{} \cdots &{} \frac{1}{2} &{} -1 \\ \end{matrix}\right) , \qquad B^{{d}}_t \equiv \frac{{\varvec{\sigma }}}{h}\left( \begin{matrix} 1 &{} 0 &{} \cdots &{} 0 \\ -1&{} 1 &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} 0 \\ 0&{} \cdots &{} -1 &{} 1 \\ \end{matrix}\right) . \end{aligned}$$

In particular, they do not commute and are constant for fixed d.

In the next numerical test we compare the approximate solutions to (51), obtained with the stochastic ME in the special case of constant coefficients (46), with the ${\mathscr {M}}^{{{d}}\times {{d}}}$-valued stochastic process ${\mathscr {I}}^{{d}}$, whose components are given by the integral in (52) with p as in (53). In doing this, we shall keep in mind that the difference between the latter quantities can be decomposed into two errors, namely: the one between $X^{{d}}$ and its approximation, and the one between $X^{{d}}$ and ${{\mathscr {I}}^d}$. In turn, the latter is the result of both space-discretization and the error that stems by imposing null boundary conditions (see (49)). In particular, this last error cannot be reduced by refining the space-grid. Therefore, the analysis should be restricted to the “central" components of ${\mathscr {I}}^{{d}}$, namely those which do not depend on the values of the fundamental solution in the vicinity of the boundary $\{a,b\}$. This motivates the definition that follows. For a given $\kappa \in {\mathbb {N}}$ with $\kappa < {d}$, and a given approximation $X^{{{d}},\text {app}}$ of $X^{{{d}}}$, we define the process

$$\begin{aligned} \text {Err}^{{d}}_t := \frac{\Vert { \tilde{{\mathscr {I}}}^{{{d}},\kappa }_{t}- {\tilde{X}}^{{{d}},\kappa ,{\text {app}}}_{t}}\Vert _{F} }{\Vert { \tilde{{\mathscr {I}}}^{{{d}},\kappa }_{t}}\Vert _{F}}, \qquad t>0, \end{aligned}$$

(54)

where $\tilde{{\mathscr {I}}}^{{{d}},\kappa }_{t}$ and ${\tilde{X}}^{{{d}},\kappa ,{\text {app}}}_{t}$ are the projections on ${\mathscr {M}}^{\kappa \times {{d}}}$ obtained by selecting the central $\kappa$ rows of ${\mathscr {I}}^{{{d}}}_{t}$ and $X^{{{d}},\text {app}}_{t}$, respectively. The matrix norm above is the Frobenius norm. The role of $X^{{{d}},\text {app}}$ will be played by the time-discretization of the truncated ME (8)–(9). In particular, we will denote by m1 and m3 the discretized first and third-order MEs of $X^{{d}}$, respectively. We will not consider the second-order Magnus approximation m2 as it appears less stable than the others. Note that, being $A^{{d}}_t$ and $B^{{d}}_t$ constant matrices, the first three terms of the ME are given explicitly by (46).

In the numerical experiments we set

$$\begin{aligned} a=-2,\ b=2,\quad \mathbf{a}=0.2,\quad {\varvec{\sigma }}=0.15. \end{aligned}$$

(55)

Setting the parameter $\kappa$ in (54), which determines the number of rows that are taken into account to asses the error, as $\kappa = \left\lfloor {{d}}/2 \right\rfloor$, we study the expectation of $\text {Err}^{{{d}}}_t$ up to $t=0.5$. Such choice for $\kappa$ and t allows us to study the error in a region that is suitably away from the boundary. Indeed, choosing $\kappa$ as above implies $x^{{d}}_i$ in (52) ranging roughly from $-1$ to 1. On the other hand, the standard-deviation parameter associated to the Gaussian density (53) at $t=0.5$ is roughly 0.30, while the mean parameter is $0.15\times W_{0.5}$, whose standard deviation is in turn roughly 0.10. Therefore, both $(\tilde{{\mathscr {I}}}^{{{d}},\kappa }_{t})_{i,1}$ and $(\tilde{{\mathscr {I}}}^{{{d}},\kappa }_{t})_{i,{{d}}}$ are likely to be very close to zero, thus meeting the null boundary condition implied by (49).

In Tables 4, 5, 6, we report the approximate values of ${\mathbb {E}}[\text {Err}^{{d}}_t]$ for ${{d}}=50, 100$ and 200, respectively. These were obtained via simulation of 50 trajectories of W with time step-size $\varDelta = 10^{-4}$. Now, let us inspect the Tables 4–6 in more detail. As a reminder, these results were obtained by using the exact solution as a reference, which is available in this particular example. In Table 4 it is noticeable that euler and m3 can exhibit worse results for small times compared to m1. This is due to the coarse space approximation with only 52 space grid points. Increasing the number d of grid points improves the error of euler and m3 for all displayed times, which can be seen in Tables 5 and 6 by comparing each column for the same final time. Finally, notice that the third-order Magnus expansion has the same magnitude of error as the euler scheme for all final times.

Table 4 SPDE

Table 5 SPDE

Table 6 SPDE

3.3 Example: $j=1$, $B=0$ and $A_t$ Upper Triangular

We now test the ME on an SDE with time-dependent coefficients and with known explicit solution.

Set

$$\begin{aligned} A_t= \left( \begin{matrix} 2 &{} t \\ 0 &{} -1 \end{matrix}\right) , \qquad B_t\equiv 0. \end{aligned}$$

(56)

In this case (1) admits an explicit solution, which can be obtained by using Itô’s formula, given by

$$\begin{aligned} X_t= \left( \begin{array}[c]{cc} e^{ 2\left( W_t - t\right) } &{} e^{ 2\left( W_t - t\right) }\left( \int _{0}^{t}{ s\, e^{ -3 W_s + \frac{3}{2} s }\, dW_s }-2 \int _{0}^{t}{ s\, e^{ -3 W_s + \frac{3}{2} s }\, ds } \right) \\ 0 &{} e^{ -(W_t + \frac{1}{2}t) } \end{array} \right) . \end{aligned}$$

The first three terms of the ME read as

$$\begin{aligned} Y_t^{(1)}&= \left( \begin{array}[c]{cc} 2 W_t &{} tW_t-\int _{0}^{t}{W_s ds}\\ 0 &{} - W_t \end{array} \right) , \\ Y_t^{(2)}&= -\frac{1}{2} \left( \begin{array}[c]{cc} 4t &{} \frac{1}{2}t^2\\ 0 &{} t \end{array} \right) -\frac{3}{2} \left( \begin{array}[c]{cc} 0 &{} W_t\int _{0}^{t}{W_u du}- \int _{0}^{t}{W_u^2 du}\\ 0 &{} 0 \end{array} \right) , \\ Y_t^{(3)}&= \left( \begin{array}[c]{cc} 0 &{} \frac{3}{4}( t-W_t^2)\int _{0}^{t} W_u du - \frac{3}{2} \int _{0}^{t}{ W_u u du } \\ 0 &{} 0 \end{array} \right) \\&\qquad + \left( \begin{array}[c]{cc} 0 &{} \frac{9}{4} W_t\int _{0}^{t}{ W_u^2du }-\frac{3}{2} \int _{0}^{t}{ W_u^3 du } + \frac{3}{8} t^2W_t\\ 0 &{} 0 \end{array} \right) . \end{aligned}$$

Again, all the stochastic integrals appearing in the ME can be solved in terms of Lebesgue integrals by using Itô’s formula, which allows us to use one more time a sparser time grid compared to the Euler method and the discretized exact solution. In the following numerical tests, we discretize in time with mesh $\varDelta$ equal to $10^{-4}$ for exact and equal to $10^{-2}$ for m1, m2 and m3. For euler we run two experiments with mesh equal to $10^{-4}$ and $10^{-3}.$ Note that euler serves here as an alternative approximation and that choosing a finer time-discretization for euler and exact (our reference method here) is again essential in order to make them comparable with m3.

In Table 7 we show the expectations $E[\text {Err}_t]$ for different values of t, with exact as benchmark solution, computed via Monte Carlo simulation with $10^{3}$ samples. The same samples are used in Fig. 3 to plot the empirical CDF of $\text {Err}_t$. It is clear from the results that the time-step size $\varDelta =10^{-3}$ is not small enough in order for euler to yield accurate results. Also note that m3 outperforms euler with $\varDelta =10^{-4}$ up to $t=0.75$.

Table 7 $B_t$ and $A_t$ as in (56)

Table 8 Computational times (s) for $10^3$ sampled trajectories of X, up to time $t=1$, choosing $\varDelta = 10^{-2}$ for m1, m2 and m3, and $\varDelta = 10^{-4}$ for euler and exact

Fig. 3

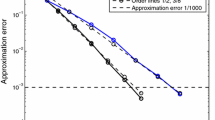
$B\equiv 0$ and $A_t$ as in (56). Empirical CDF of $\text {Err}_t$, at $t=0.75$, for euler, m1, m2, m3, with exact as benchmark solution, obtained with $10^3$ samples

The computational time for $10^3$ sampled trajectories, up to time $t=1$, which is given in Table 8, is approximately 0.7 s for exact, 4.6 s for euler and 0.6 s for either m1, m2 or m3. The latter, however, is divided as follows: nearly 0.05 s to compute the ME and nearly 0.55 s to compute the matrix exponential with the Matlab function expm. Let us recall Remark 5 and note that the computation of the logarithm via ME is very fast thanks to the possibility of parallelizing the computation of the integrals in $Y^{(1)}, Y^{(2)}$ and $Y^{(3)}$.

As it appears in the results above, the accuracy of the ME quickly deteriorates as the time increases. This is largely due the fact that the spectral norm

$$\begin{aligned} \left\| {A_t}\right\| = \sqrt{\frac{1}{2} \left( t^2+\sqrt{t^4+10 t^2+9}+5\right) } \end{aligned}$$

is an increasing function of t. This behavior shall not come as a surprise, since the proof of Theorem 1 already uncovered the relation between the convergence time $\tau$ and the spectral norms of $A_t$ and $B_t$. Such relation is also consistent with the convergence condition (7) that holds in the deterministic case. In order to asses numerically the impact of the spectral norm of $A_t$ on the quality of the Magnus approximation, we now repeat the experiments on the equation obtained by normalizing $A_t$ as in (56) with respect to $\left\| { A_t}\right\|$. As it turns out, the accuracy of m1, m2 and m3 improves considerably with this normalization. Note that, in this case, (1) no longer admits a closed-form solution, while the representation for the terms $Y^{(1)}, Y^{(2)}$ and $Y^{(3)}$ in the ME is omitted for it becomes rather tedious to write. In Fig. 4 we plot one realization of the trajectories of the top-right component $(X_t)_{12}$, computed with all the methods above, up to time $t=10$. In this case we did not plot a diagonal component of the solution because the latter are exact for m2 and m3, up to discretization errors of Lebesgue integrals. Table 9 and Fig. 5 are analogous to Table 7 and Fig. 3 and are obtained again with $10^3$ independent samples. The computational times, reported in Table 8, are comparable with those of the non normalized case. The same can said about the accuracy results reported in Table 9, which are comparable with those in Table 7.

Fig. 4

$B_{t}$ and $A_t$ as in (56) normalized by its spectral norm. One realization of the trajectories of the top-right component $(X_t)_{12}$, computed with exact, euler, m1, m2, m3

Table 9 $B_{t}$ and $A_t$ as in (56) normalized by its spectral norm

Fig. 5

$B_{t}$ and $A_t$ as in (56) normalized by its spectral norm. Empirical CDF of $\text {Err}_t$, at $t=0.75$, for euler, m1, m2, m3, with exact as benchmark solution, obtained with $10^3$ samples