Abstract
The necessity of dealing with uncertainties is growing in many different fields of science and engineering. Due to the constant development of computational capabilities, current solvers must satisfy both statistical accuracy and computational efficiency. The aim of this work is to introduce an asynchronous framework for Monte Carlo and Multilevel Monte Carlo methods to achieve such a result. The proposed approach presents the same reliability of state of the art techniques, and aims at improving the computational efficiency by adding a new level of parallelism with respect to existing algorithms: between batches, where each batch owns its hierarchy and is independent from the others. Two different numerical problems are considered and solved in a supercomputer to show the behavior of the proposed approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The increasing necessity of handling data uncertainties in many different science and engineering scenarios and the development of computational capabilities of supercomputers are leading to the necessity of having a strict integration between Uncertainty Quantification (UQ) techniques and efficient algorithms. UQ studies how uncertainties propagate in the problem of interest, and has already been applied in different engineering fields, spacing from aerodynamics [26, 36] to civil infrastructure [18] and finance [22]. The final aim of these analyses is to perform a statistical study of an output quantity, hereafter called Quantity of Interest (Q).
Nowadays, different UQ approaches exist in literature, such as stochastic Galerkin, stochastic collocation and polynomial chaos, which are efficient when the number of uncertain parameters is small. We refer to [19, 24, 37] for more details. Nevertheless, in this work, we focus on Monte Carlo (MC) methods because we aim at describing the most general scenario, in which the stochastic dimension can be arbitrarily big. For the sake of simplicity, hereafter we will refer to the whole class of Monte Carlo algorithms with the term MC family, which will then include both MC and all the other strategies enhanced from it.
In literature, many applications of MC algorithms already exist. These have been successfully applied to hyperbolic conservation laws with stochastic input data [27, 28], to elliptic Partial Differential Equations [11], in engineering applications [7, 29] and in software [1].
The MC techniques are not affected by the so-called curse of dimensionality, i.e. they do not have a direct proportionality between the number of uncertain parameters and the computational cost, and the convergence rate is independent from the stochastic dimension. Another crucial advantage is that these approaches are non-intrusive, meaning that the physical system can be considered as a black-box. The key idea of the algorithms belonging to the MC family is to draw many independent and identically distributed samples, and to perform a statistical analysis from the results. It is known that the statistics converge to the exact ones as the number of realizations grows. However, considering the standard MC method, its slow convergence rate becomes unfeasible when dealing with complex engineering problems.
As a consequence, different techniques were developed inside the MC family in order to overcome this slow convergence obstacle. An example is the Multilevel Monte Carlo (MLMC) algorithm [20, 21], which is based on a hierarchy of levels of increasing accuracy. The key is to draw many MC samples on the coarsest levels, in order to capture the statistical variability, and only a few on the finest ones, to reduce the discretization error. This way, the computational effort relies mainly on the coarsest levels, while for standard MC the computational effort is performed on the finest. Therefore, this leads to notable computational savings.
A huge potential of the MC family lies in the fact that such algorithms are highly parallelizable. In standard approaches, three different layers of parallelism are available: between levels, between samples per level, and on each realization at solver level. In order to exploit such parallelisms when running in distributed environments, different scheduling strategies can be adopted, depending on the problem under consideration. In [16], the authors propose and discuss different static scheduling approaches for running in supercomputers. The hierarchy, i.e. the number of levels and of samples per level, is defined before the execution starts and optimizes the computational efficiency and the time to solution. Although efficient, this procedure is problem dependent and only allows to run one iteration, without a check of the convergence criteria on the fly. In addition, it does not take into account the fact that the sampling in MC algorithms is always stochastic, so the execution time of each realization is random. Hence, a static planning cannot adapt the scheduling, as the execution goes, in order to optimize the available resources usage. In fact, as discussed in [16], dynamic scheduling suites best for simulations whose run-time may vary, resulting to be faster than their static counterparts.
Therefore, we aim for a dynamic scheduling approach for both MC and MLMC, as problem independent as possible, which optimally adapts to the length of each execution. Our dynamic approach re-evaluates the scheduling each time a task execution finishes, while the static scheduling approach introduced in [16] defines the scheduling once, when all tasks are launched. Even though this last approach can successfully handle heterogeneity in the task duration and adapt the scheduling on it, it cannot react when the actual duration differs with respect to the precomputed estimation. Instead, with our dynamic approach, the scheduling decisions are taken on the fly, providing a higher adaptability. Moreover, a dynamic scheduling is preferred when the workload can vary depending on the partial results of the computation, and therefore not predictable statically.
Knowing that MLMC has more levels and MC just has one, the amount of CPUs used by the solver at each level should be tuned accordingly to the scalability limits of the solver for the considered problem size. As general rule, since scalability improves as the problem grows in size, the amount of assigned resources should be as high as possible, while keeping a reasonable efficiency. In addition, it must be taken into account that the amount of CPUs set for each MLMC level should be defined in such a way that the available memory per processor is enough to perform a typical execution of that level. This way, it is possible to keep a good efficiency while reducing as much as possible the imbalance between the different levels. Concerning the overall performance, the hierarchy size is the most impacting factor, and it needs to be tuned accordingly to the problem under consideration.
Standard algorithms require the presence of synchronization points. Hence, they need to wait until a certain parameter is computed in order to resume the execution. At this exact point, the full machine is idle. This is highly inefficient when running in supercomputers, since it may occur that the machine remains idle for long periods of time. This fact is particularly important in UQ, where the run-time of each realization depends on some random data, and may result in the whole algorithm waiting for a single realization to end before going on.
In order to achieve the desired accuracy, a tuning phase is needed in order to calibrate the hierarchy of the simulation. This set-up takes place before the execution of the main algorithm, and normally few samples per level are run. Nevertheless, the set-up is an expensive and challenging phase, since, if wrongly calibrated, it may lead to oversampling. An improved and verified approach may be to update on the fly the hierarchy of the simulation, exploiting a decreasing sequence of tolerances [12, 32]. However, an initial screening phase is still needed. We will refer to this class of algorithms estimating the hierarchy on the fly based on available statistics as adaptive.
In this work, we propose an asynchronous version of the algorithms belonging to the MC family, together with a reference implementation based on the Kratos Multiphysics software [13, 14] and the XMC library [3], exploiting the PyCOMPSs programming model [2, 25, 34]. We focus on MC and MLMC, but the work can be easily extended to other methods.
The aim of this work is to develop an asynchronous framework, suitable for running in supercomputers. The proposed framework allows to bypass the expensive tuning phase, to preserve statistical reliability and to avoid the presence of classical synchronization points, thus improving computational efficiency. The idea is to add a new level of parallelism, between batches, where each batch is defined by its own hierarchy. This can be interpreted as a sort of pre-fetching, which consists in optimistically performing computational work that may turn out to be useful. Pre-fetching has been already applied with success to other Monte Carlo methods, as shown in [5, 8]. The update of the statistics of Q and the convergence check of the algorithm are performed on the fly. Therefore, the estimation is reliable, because we run until we reach a desired tolerance, and efficient, since the small batch hierarchy avoids oversampling.
The structure of the article is the following. Section 2 introduces the physical problems we are interested in. Section 3 presents an overview of the current state of the art of MC methods, of statistical analysis and of convergence criteria. Section 4 describes our asynchronous proposal. Section 5 reports the numerical tests that were run in order to validate the approach.
2 Physical Problems Overview
In this section we introduce the governing equations describing the physical problems we will consider later in Sect. 5: the steady-state potential equation and the incompressible Navier–Stokes equations.
2.1 Compressible Potential Flow Problem
The first problem is the compressible potential flow around a NACA 0012 airfoil. We are interested in computing the lift coefficient on the body. A sketch of the problem can be observed in Fig. 1. It is known that when the fluid proceeds at high Reynolds number and small angle of attack with respect to the airfoil, the flow can be considered steady-state, compressible and isentropic [15, 17]. Therefore, the analysis of such a two-dimensional flow around a NACA 0012 is governed by the steady-state potential equation

where \( \rho \) is the density, \( {\mathbf {u}} = (u_x,u_y) \) the velocity potential,  the domain and x and y denote the horizontal and vertical directions of the system, respectively. A stochastic inlet boundary condition on \( \varGamma _{D} \) is considered, that is
the domain and x and y denote the horizontal and vertical directions of the system, respectively. A stochastic inlet boundary condition on \( \varGamma _{D} \) is considered, that is
where \( u_\infty = M_\infty a_\infty \). The velocity potential is therefore function of the Mach number \( M_\infty \), of the angle of attack of the airfoil \( \alpha \) and of the sound velocity \(a_\infty =340\,\text {ms}^{-1}\). The Mach number and the angle of attack are random quantities. The probability distribution of the two stochastic variables are \( M_\infty \sim {\mathcal {N}}(0.3,0.003) \) and \( \alpha \sim {\mathcal {N}}(5.0,0.05) \), respectively. \( {\mathcal {N}}(\mu ,\sigma ^2) \) denotes a normal distribution of mean \( \mu \) and variance \( \sigma ^2 \), and the angle of attack measures are expressed in degrees. Moreover, a Neumann condition is defined on \( \varGamma _{N} \) and a wake boundary condition is imposed in order to properly describe the wake generated by the airfoil.
2.2 Wind Engineering Problem
The second problem we consider is the two-dimensional flow past a square building in a domain  and a time interval
and a time interval  . The objective is computing the drag force on the building. The system can be observed in Fig. 2, and is described by the incompressible Navier–Stokes equations [33]:
. The objective is computing the drag force on the building. The system can be observed in Fig. 2, and is described by the incompressible Navier–Stokes equations [33]:

where \( {\mathbf {u}} \) is the velocity field, p the pressure field, \( \nu \) the kinematic viscosity and \( {\mathbf {f}} \) the vector field of body forces. The Reynolds number of the problem is 1. The boundary condition defined in the inlet \( \varGamma _{in} \) is stochastic and constant in time. The flow in the inlet follows the power law
where \( {\mathbf {n}} \) is the unit normal on boundary \( \varGamma _{in} \), \({\overline{u}}\sim {\mathcal {N}}(10,1.0)\), \(\alpha \sim {\mathcal {N}}(0.12,0.012)\), z and \( z_0 \) the vertical coordinate and a reference height, respectively, and \( {\mathcal {N}} \) denotes a normal distribution. Wall boundary conditions are applied to \( \varGamma _{{\textit{surf}}} \), free slip conditions to \( \varGamma _{{\textit{up}}} \), zero flux boundary conditions to \( \varGamma _{{\textit{out}}} \) and no slip conditions to \( \varGamma _{{\textit{down}}} \) [4].
The stochastic nature of both problems requires to solve them using UQ techniques, to analyze and study the propagation of uncertainties across the system and their influence on the quantity of interest of the problem. The hierarchical Monte Carlo methods we use are presented in Sects. 3 and 4.
3 Statistical Overview
We review the current state of the art of UQ, focusing mainly in the features we need to describe the asynchronous framework development. Once more, we remark that with Monte Carlo algorithms we will denote the whole class of schemes descending from Monte Carlo, such as Monte Carlo or Multilevel Monte Carlo [32]. In the following, standard algorithms will be also denoted as non-adaptive, due to the deterministic nature of the hierarchy update.
The above-mentioned UQ schemes allow to study the propagation of uncertainties in stochastic problems through the statistical analysis of an output quantity of interest Q, which can be both a scalar or a field. We are interested in the computation of the expected value of the output quantity of interest  , even though other statistics are computed in order to verify the accuracy of the results.
, even though other statistics are computed in order to verify the accuracy of the results.
Referring to the solution of the problem under consideration with  , we have
, we have  , where
, where  is the random variable (r.v.) of the system. We generically identify the domain of the problem with
is the random variable (r.v.) of the system. We generically identify the domain of the problem with  . The physical problems considered are solved exploiting the Finite Element Method, thus we consider a discretized domain
. The physical problems considered are solved exploiting the Finite Element Method, thus we consider a discretized domain  , where
, where  is the discretization parameter of the domain. The way of choosing
is the discretization parameter of the domain. The way of choosing  depends on the problem under consideration, and an option can be the reciprocal of the minimal size.
depends on the problem under consideration, and an option can be the reciprocal of the minimal size.
We start reviewing two Monte Carlo algorithms (MC, MLMC), and briefly a third one, namely Continuation Multilevel Monte Carlo (CMLMC) [12, 20, 21, 32]. Then, we focus on the computation of the statistics of Q, which is a crucial part for the development of asynchronous algorithms, since these quantities are needed for checking the convergence. Successively, we describe the stopping criteria we consider. Finally, we report the algorithms previously described.
3.1 Monte Carlo Algorithms
3.1.1 Monte Carlo
The MC method is the reference technique in the stochastic analysis of multi-physics problems with uncertainties in the data parameters. As previously mentioned, it gives origin to a wide class of different algorithms, whose main idea is to repeat many times the realization with uncorrelated r.v.  , and to estimate the desired statistics of Q a posteriori.
, and to estimate the desired statistics of Q a posteriori.
The MC potential lies in its basic property of convergence to the exact statistics as the number of samples  tends to infinity, independently from the dimensionality of the stochastic space. It also presents the advantage of considering the solver as a “black box”, since it is non-intrusive and directly applicable to any simulation code, making it suitable for any kind of problem.
tends to infinity, independently from the dimensionality of the stochastic space. It also presents the advantage of considering the solver as a “black box”, since it is non-intrusive and directly applicable to any simulation code, making it suitable for any kind of problem.
Considering  , where
, where  is the approximation on the discretized domain
is the approximation on the discretized domain  , the MC expected value estimator of the output quantity of interest is:
, the MC expected value estimator of the output quantity of interest is:

where  ,
,  , are
, are  independent, identically distributed values computed on
independent, identically distributed values computed on  .
.
The MC estimation accuracy of the expectation can be evaluated through the mean square error, that reads

where  is the true expected value of Q and
is the true expected value of Q and  the variance of Q. The term
the variance of Q. The term  is the discretization error (DE), it is independent from the statistics of Q and only depends on the accuracy of the domain we are exploiting to solve the problem. On the other hand,
is the discretization error (DE), it is independent from the statistics of Q and only depends on the accuracy of the domain we are exploiting to solve the problem. On the other hand,  is the statistical error (SE), which decreases as long as the number of samples grows, and is an indicator of the variance of the expected value estimator.
is the statistical error (SE), which decreases as long as the number of samples grows, and is an indicator of the variance of the expected value estimator.
The main drawback of the MC method is its computational cost, which makes it unaffordable for the stochastic analysis of industrial problems with complex geometries. In fact,  decreases proportionally to
decreases proportionally to  . To try to overcome this limitation, different algorithms have been developed [12, 20, 21, 32], such as MLMC and CMLMC.
. To try to overcome this limitation, different algorithms have been developed [12, 20, 21, 32], such as MLMC and CMLMC.
3.1.2 Multilevel Monte Carlo
The main idea of the MLMC algorithm is to draw MC instances simultaneously on a sequence of levels of increasing accuracy, increasing computational cost and increasingly small difference between outputs on successive levels. When the error is governed by the spatial resolution, the standard procedure to build the hierarchy of levels is to perform uniform refinement in space. This means that the mesh parameter  grows as long as the level increases, i.e.
grows as long as the level increases, i.e.  , where
, where  is the maximum number of levels the current simulation may reach.
is the maximum number of levels the current simulation may reach.
Due to the linearity of the expectation operator, the mean of Q can be written as a telescopic sum of the expectations of Q. Therefore, the MLMC expected value of Q on level  is:
is:

where  and
and  . For the sake of simplicity, the dependence on the random variable
. For the sake of simplicity, the dependence on the random variable  is made explicit only in the last expression, from which we observe that the two Quantities of Interest
is made explicit only in the last expression, from which we observe that the two Quantities of Interest  and
and  are computed using the same random variable realization
are computed using the same random variable realization  .
.
Analogously to the MC algorithm, the mean square error of the MLMC expectation estimator is the sum of a discretization error and a statistical error:

where the first term represents the discretization error and the latter the statistical error. We can observe matching Eqs. (6) and (8) that the only difference in the mean square error evaluation is the statistical contribute. In fact, in Eq. (6) the variance of  is computed, while in Eq. (8) we consider the difference
is computed, while in Eq. (8) we consider the difference  on two consecutive levels, whose variance is consistently smaller with respect to the one of
on two consecutive levels, whose variance is consistently smaller with respect to the one of  .
.
3.1.3 Adaptivity
Three important considerations lie at the basis of both MC and MLMC algorithms:
-
the cost of computing one sample
 grows with the level accuracy
grows with the level accuracy  ,
, -
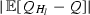 decreases as
decreases as  grows,
grows, -
- \(\bullet \):
-
MC:
 more or less constant with respect to
more or less constant with respect to  ,
, - \(\bullet \):
-
MLMC:
 decreases as the level grows.
decreases as the level grows.
The evaluation of the computational cost, the discretization error and the variance allows to estimate the optimal hierarchy for reaching statistical convergence, i.e. number of levels  and number of samples per level
and number of samples per level  . Adaptive MC and adaptive MLMC require a screening phase to assess properly the hierarchy. This set-up is executed with a predefined number of levels and of samples per level, and may lead to inaccurate predictions in case
. Adaptive MC and adaptive MLMC require a screening phase to assess properly the hierarchy. This set-up is executed with a predefined number of levels and of samples per level, and may lead to inaccurate predictions in case  and
and  are too low, or may be too expensive in the opposite case.
are too low, or may be too expensive in the opposite case.
3.1.4 Continuation Multilevel Monte Carlo
In [12], the authors introduce the Continuation Multilevel Monte Carlo (CMLMC) algorithm, whose idea is to update the optimal hierarchy on the fly, to decrease the risk of oversampling. The idea of CMLMC is to run, after the initial screening phase, a certain number of times \( {\mathcal {I}}\) the MLMC algorithm using a decreasing sequence of tolerances  at each iteration, in order to increase the accuracy of the parameters estimation as the number of iterations performed grows. As a consequence, the optimal hierarchy is updated on the fly. We refer to [12, 32] for further details.
at each iteration, in order to increase the accuracy of the parameters estimation as the number of iterations performed grows. As a consequence, the optimal hierarchy is updated on the fly. We refer to [12, 32] for further details.
The main problem of CMLMC and the other approaches is their intrinsically serial nature. The scope of this work is to propose an asynchronous alternative to the algorithms above described, maximizing the parallelism and avoiding the highly inefficient idle times.
3.2 Computation of Moments
The computation of the statistics of Q is crucial for having high efficiency frameworks. Different techniques are possible, and the two possibilities analyzed in this work are:
As we will see in Sect. 3.3, computing central moments is necessary in order to check the convergence of the algorithm. We define the central moment of order \( p\) as  , where
, where  .
.
3.2.1 Online Update of Central Moments
The first possibility is to directly update with a one-pass formula the central moments, where one-pass means that we update the central moment online, adding one value per time. We refer to [30] as reference, and we report the dependencies of the update formula for an arbitrary order \(P\) and number of samples  :
:

Update formulas with arbitrary set decomposition exist, and the dependencies for an arbitrary order \(P\) read as:

where  are the sizes of the two sets.
are the sizes of the two sets.
3.2.2 Online Update of Power Sums
A second possibility is to update with one-pass algorithms the power sums, where a power sum of order \( p\) is defined as  . From this definition, we can see the dependencies of updating online for an arbitrary order \( P\) and number of samples
. From this definition, we can see the dependencies of updating online for an arbitrary order \( P\) and number of samples  :
:

The power sums allow the computation of the h-statistics, which is an unbiased estimator with minimal variance of central moments. In other words,  . The h-statistics, for an arbitrary order \( P\), is just function of the power sums and of the number of samples
. The h-statistics, for an arbitrary order \( P\), is just function of the power sums and of the number of samples  , therefore
, therefore

3.3 Stopping Criteria
Convergence is said to be accomplished if the estimator of the expected value ( or
or  ) achieves a desired tolerance
) achieves a desired tolerance  , with respect to the true estimator
, with respect to the true estimator  , with a confidence \( (1 - \phi ) \in (0,1)\). Intuitively speaking, the error of the sampled estimator is smaller than the tolerance
, with a confidence \( (1 - \phi ) \in (0,1)\). Intuitively speaking, the error of the sampled estimator is smaller than the tolerance  with probability (confidence) \( (1 - \phi ) \). The higher the confidence, the surer we are about the sampled estimator accuracy.
with probability (confidence) \( (1 - \phi ) \). The higher the confidence, the surer we are about the sampled estimator accuracy.
Then, we define a failure probability, and we want it to be met with a certain level of confidence. The failure probability is defined asFootnote 1

The total error (\(\tau \)) can be bounded, with confidence \( (1 - \phi ) \), by the sum of the discretization and the root square of the statistical errors, multiplied by a confidence factor [12, 32]:

where  and
and  is the Cumulative Distribution Function (CDF) of the standard normal distribution \( {\mathcal {N}}(0,1) \). The variance of the MLMC expected value estimator is
is the Cumulative Distribution Function (CDF) of the standard normal distribution \( {\mathcal {N}}(0,1) \). The variance of the MLMC expected value estimator is

while for MC it simplifies to

For MC, the variance of  can be estimated as
can be estimated as

However, as described above, we approximate  exploiting h-statistics. Therefore
exploiting h-statistics. Therefore

The same considerations apply to MLMC.
Therefore, the estimate of the total error is \( \tau = \text {DE}+ {\mathcal {C}}_{\phi }\sqrt{\hbox {SE}}\), and the convergence criteria is

While for MLMC it is possible to approximate DE as  [32], for MC the same approximation is not possible. Then, in this case, we will consider just the statistical error in the convergence criteria, which will read
[32], for MC the same approximation is not possible. Then, in this case, we will consider just the statistical error in the convergence criteria, which will read

3.4 Algorithms
We report MC and MLMC algorithms. To simplify comparisons with section 4, we exploit the fact that  and Eq. (12).
and Eq. (12).
We define  as the power sum of level \( l\) and power \( p\), where \( p\in [1,P] \) and \( P\) is the maximum order we need. Similarly, the h-statistic of level \( l\) and power \( p\) is defined as
as the power sum of level \( l\) and power \( p\), where \( p\in [1,P] \) and \( P\) is the maximum order we need. Similarly, the h-statistic of level \( l\) and power \( p\) is defined as  . Since for MC there is just one level, the dependency on \( l\) is omitted. The number of iterations \( {\textit{it}}\) is updated each time a convergence check is performed. The number of levels, of samples per level and the mesh parameters are represented by
. Since for MC there is just one level, the dependency on \( l\) is omitted. The number of iterations \( {\textit{it}}\) is updated each time a convergence check is performed. The number of levels, of samples per level and the mesh parameters are represented by  and
and  , respectively. The left horizontal arrow denotes the update or the computation of the left value as a function of the right values.
, respectively. The left horizontal arrow denotes the update or the computation of the left value as a function of the right values.
Non-adaptive and adaptive MC algorithms are described in Algorithm 1, while non-adaptive and adaptive MLMC are reported in Algorithm 2. Concerning the adaptive version, the initial screening phase is represented by the first iteration inside the \({\textit{while}}\) loop. Afterwards, the central moments are computed and then it is possible to estimate the optimal hierarchy. As mentioned in Sect. 5, in both cases upper and lower thresholds are applied in order to be able to control the number of levels and of samples per level estimated. This allows us to better check and compare the results obtained from different algorithms.


We also present the dependency graph of one MC iteration in Fig. 3. The circles denote tasks, that are the execution units that are sent to worker nodes to be executed in parallel. Task executions are uniquely identified through a number, while the arrows mean that the following task needs to wait for the previous one to finish before being launched, since it requires a data produced by the previous task.
Graph connections of synchronous algorithm dependencies. The first iteration is represented. Each gray tonality identifies a different action: ExecuteInstance the simulation task, AddResults and UpdateOnePassPowerSums the power sums update, ComputeHStatistics the h-statistics computation and CheckConvergence the convergence check. Each circle represents a different task and is uniquely identified by a number
It is important to realize how the dependencies shown in Fig. 3 contain a unavoidable synchronization point. In fact, we observe the requirement of waiting for the whole single hierarchy to finish before performing the statistical analysis of Q. Therefore, to compute the convergence (task 18), we need to wait for all the realizations to finish, and this may be highly inefficient if, for example, we are waiting for a single execution to end that is taking longer due to its random variable input value.
Theoretical trace of the synchronous framework. The gray rectangles represent all the different tasks, from the execution of the instances (ExecuteInstance) to the check of the convergence (CheckConvergence), which implies a synchronization point. The black rectangles are the synchronization points. The dashed vertical line denotes the achievement of the algorithm convergence after four iterations
Figure 4 represents the theoretical trace of a synchronous algorithm execution, i.e. shows how well we are filling-up the machine. The bottleneck of synchronous algorithms is clearly visible: at each iteration there is a period in which the machine is empty, therefore not executing any computation, and this moment corresponds to the synchronization point towards which all tasks need to converge at the end of each iteration. In case of Fig. 4 we have four iterations, then four periods in which the computer is not doing any computation. As previously mentioned, these idle times can be very costly, since we cannot know a priori their time length. As a consequence, to gain computational efficiency, the idea is to minimize as much as possible the idle times, by developing an asynchronous framework, introduced in Sect. 4. The dependency graph of MLMC follows as a consequence, and for the sake of simplicity we choose to report only the MC dependency graph.
Graph connections of synchronous algorithm dependencies. Each gray tonality identifies a different action: ExecuteInstance the simulation task, ComputeBatchesPassPowerSums and UpdateBatchesPassPowerSums the in-batch power sums update, UpdateGlobalPowerSums the global power sums update, ComputeHStatistics the h-statistics computation and CheckConvergence the convergence check. Each circle represents a different task and is uniquely identified by a number
Theoretical trace of the asynchronous framework. Different gray colors of the rectangles represent different bacthes. Each batch contains all the tasks from the execution of the instances (ExecuteInstance) to the check of the convergence (CheckConvergence). The black rectangles are the synchronization points. The dashed vertical line denotes the achievement of the algorithm convergence after four iterations. The two types of parallel diagonal lines indicate that the instances of the unfinished batches are discarded (left with respect to the dashed line) or stopped (right with respect to the dashed line)
4 Asynchronous Framework
As we have seen in the previous section, a single slow simulation, for example due to particular random variable values or to system malfunction, can simply lead to a huge hardware usage inefficiency, caused by a high percentage of the available resources being idle during a long time. We present here an asynchronous framework that can be applied to the above algorithms, allowing for a continuous feed of the machine, when running in a distributed environment. The main idea of our approach is to fill the idle resources while finishing a batch computation, just in case the convergence is not achieved. This way, part of the work needed for an hypothetical new batch will be already started when checking the convergence. It is clear that, when converging, we will always be discarding some work already done under the non-convergence hypothesis. Nevertheless, this methodology allows to have a much better usage of the resources.
As shown in Sect. 3.2, the two considered possibilities to compute central moments are Eqs. (9) and (12). The strategy we follow is to update the central moments using the second option, and the advantage of this choice is that in both Eqs. (11) and (12) there is no dependency on the central moment values of previous steps.
Our idea is to work in batches, each one with its own hierarchy, hereafter called batch hierarchy. Each batch updates its local power sums, which afterwards add their contribution to the global power sums. To preserve the correctness of the statistical analysis, it is important to avoid introducing bias, i.e. to consider only the fastest samples of our problem. Then, the update from local (of a single batch) to global takes place only after all the simulations of a single batch have finished, and the batches are considered in the same order that they have been spawned. Therefore, we are able to update the statistics and to check the convergence of the scheme while other batches are running. This approach avoids global synchronization, thus keeping all the available resources busy. Each time convergence is not achieved, a new batch is launched. When convergence is reached, the remaining analyses are stopped and all the executions corresponding to incomplete batches are discarded.
We see the described behavior in Fig. 5. Here we start the simulation by running three batches: tasks 1–10 , 16–25 and 31–40 stand for batch number one, two and three, respectively. Focusing on the first batch, we observe its instances update the local power sums on the fly and all the contributions are taken into account to check the convergence. The synchronization point of the first batch is local, not global, since it runs in parallel with other batches. In fact, the local power sums of the second batch (task 55) is directly updating the global power sums of the successive iteration (task 84), guaranteeing asynchronicity. Therefore, the difference between Figs. 3 and 5 is clear, and we see how this framework allows to have more executions running while the statistical analysis of a single batch hierarchy is being computed.
Observing the trace in Fig. 6, we can appreciate how the machine is being filled-up and the parallelism between the single-batch synchronization point and other batches. Moreover, we acknowledge that all the tasks that would have been executed after the convergence achievement are stopped, while the ones already computed and belonging to unfinished batches are discarded.
The asynchronous approach adds one new level of parallelism to the MC family, which now are:
-
between batches,
-
between levels,
-
between samples per level,
-
on the simulation of each sample.
The advantages of having many small batches running gives efficiency and reliability to the method we propose. The former is guaranteed since the expensive screening phase is no more needed and the number of samples is not exceeding much the optimal hierarchy to achieve convergence, considering it is directly related to the batch size hierarchy, which is non-adaptively updated. Reliability is ensured by the stopping criteria conditions and the fact that unbiased estimators are exploited to estimate central moments.
A final consideration is that power sums are computed from a sum that is both associative and commutative. Therefore, it is possible to compute central moments following a tree scheme, as we see in tasks 11–15, 46–49 of Fig. 5.
4.1 Asynchronous Algorithms
The update of the number of batches \( B\), of the number of levels  and of the number of samples per level
and of the number of samples per level  are only function of the iteration counter \( {\textit{it}}\) and of their previous values. We define
are only function of the iteration counter \( {\textit{it}}\) and of their previous values. We define  as the local power sum of batch \( b\), level \( l\) and power \( p\), where \( p\in [1,P] \) and \( P\) is the maximum order we need. The global power sum of level \( l\) and order \( p\) is defined as
as the local power sum of batch \( b\), level \( l\) and power \( p\), where \( p\in [1,P] \) and \( P\) is the maximum order we need. The global power sum of level \( l\) and order \( p\) is defined as  . Analogously, the h-statistic of level \( l\) and power \( p\) is denoted with
. Analogously, the h-statistic of level \( l\) and power \( p\) is denoted with  . The left horizontal arrow denotes the update or the computation of the left value as a function of the right values.
. The left horizontal arrow denotes the update or the computation of the left value as a function of the right values.
We present in Algorithm 3 the asynchronous MC algorithm, where we omit to specify level \( l= 0 \).

MLMC follows the same idea, as shown in Algorithm 4.

For the development of this work, also other algorithms, such as CMLMC, were developed. At the current state of art, research about asynchronous-adaptive algorithms is still ongoing.
5 Numerical Experiments
In order to verify the accuracy, the efficiency and the computational improvements of the proposed methods, two different test cases have been performed. The first, presented in Sect. 5.1, describes the two-dimensional steady-state compressible flow of the fluid around an airfoil NACA 0012. Successively, in Sect. 5.2, a two-dimensional analysis simulating the wind flow past a square structure is analyzed. Details about the physical systems are given in Sects. 2.1 and 2.2, respectively.
The analysis will be carried out comparing the computational cost and the time to solution needed by each algorithm for satisfying the convergence criteria. The asynchronous framework is compared with two synchronous approaches: the standard non-adaptive method and one replicating the adaptive behavior, which minimizes the number of iterations. For the adaptive approach, the update of the number of levels and realizations per level is controlled by lower and upper thresholds, which balance the hierarchy of the execution to properly compare the computational efforts of all algorithms. For all methods, the initial number of levels  and the amount of samples per level
and the amount of samples per level  is the same, and is the result of an a priori strategy which optimizes the batch execution. For MLMC, this is integrated with a MLMC estimate based on precomputed variance and computational cost estimates.
is the same, and is the result of an a priori strategy which optimizes the batch execution. For MLMC, this is integrated with a MLMC estimate based on precomputed variance and computational cost estimates.
The considered supercomputer for the analyses is the MareNostrum 4 system, with 11.15 Petaflops of peak performance, which consists of 3456 compute nodes equipped with two Intel®Xeon Platinum 8160 (24 cores at 2.1 GHz each) processors. The analyses are performed exploiting 16 worker nodes, which accounts for 768 cores. Moreover, for the latter and more challenging problem, a scalability test is provided.
In the tables presenting the results, \( B\) identifies the initial number of batches, defined by the initial hierarchy, \( {\textit{it}}\) the number of iterations, that is the amount of convergence checks executed,  the total number of realizations computed per level at the end of the of the execution,
the total number of realizations computed per level at the end of the of the execution,  and
and  the expected value estimate, SE the statistical error, time to solution the total time the simulation required to finish, measured in seconds, and
the expected value estimate, SE the statistical error, time to solution the total time the simulation required to finish, measured in seconds, and  the computational cost of the algorithm run, expressed in CPU hours. The considered algorithms are summarized in Table 1.
the computational cost of the algorithm run, expressed in CPU hours. The considered algorithms are summarized in Table 1.
Even though the aim of this work is not to show the superiority of MLMC over MC, some considerations regarding this topic are provided.
5.1 Compressible Potential Flow Benchmark
The two-dimensional flow around a NACA 0012 is described in Sect. 2.1. The output quantity of interest of the problem is the lift coefficient \( C_l \) of the airfoil, and the problem is studied with both MC and MLMC strategies. MC realizations are performed on the finest MLMC level, therefore the two strategies provide the same discretization error.
Even though the physical analysis of the results is outside the scope of this work, we want to remark that in both scenarios the lift coefficient expected value estimation is consistent with literature results.
5.1.1 MC Analysis
The problem is run considering a confidence \( (1 - \phi ) = 0.99 \) and a tolerance  . We exploit Eq. (20) for assessing convergence and results are presented in Table 2.
. We exploit Eq. (20) for assessing convergence and results are presented in Table 2.
The asynchronous algorithm is faster and cheaper compared to the other two synchronous strategies. The reason relies on the fact that asynchronous MC spawns many small batches at the beginning, therefore the machine is continuously fed and the idle time is reduced to the minimum. On the other hand, this is not happening in the other two scenarios, in which the synchronization points leave the machine underutilized for longer times, producing computational inefficiencies.
In addition, considering the synchronous algorithms, we can state that the computational efficiency, for a given amount of samples, grows as the number of iterations \( {\textit{it}}\) decreases. This happens because we reduce the amount of synchronization points. Nevertheless, since the convergence check is done less frequently, we risk to do much more computations than the ones really needed to achieve the desired accuracy, if the hierarchy estimation is not accurate enough.
5.1.2 MLMC Analysis
For running MLMC, the tolerance is set to  and the confidence is \( (1 - \phi ) = 0.99 \). Convergence is assessed with Eq. (19).
and the confidence is \( (1 - \phi ) = 0.99 \). Convergence is assessed with Eq. (19).
We report in Table 3 the results of the analyses for the different strategies. The asynchronous non-adaptive MLMC outperforms the two synchronous algorithms, requiring less than half of their computational cost and time to solution. Therefore, spawning many small batches from the beginning is the best strategy.
Comparing MC and MLMC runs, the two strategies provide comparable discretization errors, since MC analyses were run on the finest MLMC level. On the other hand, the best MLMC strategy provides a smaller SE than the best MC approach, for the same computational cost. Then, for the same computational cost, asynchronous non-adaptive MLMC gives a smaller total error than asynchronous non-adaptive MC.
5.1.3 Traces
Apart from looking at the results of Tables 2 and 3, a computational efficiency comparison can be done also looking at how the algorithms feed the machine.
In Fig. 7a we report the execution trace of the AMC algorithm, run with 16 worker nodes, i.e. 768 cores, and performing 15 iterations. The black spaces denote when the CPU has not received any task to execute. The absence of these spaces in the middle of the execution shows that the algorithm has no apparent synchronization points when analyzing its behavior.
Figure 7c is a timeline that shows the number of CPUs used at each step in the AMC run. We observe that the machine is working at its maximum potential during the whole simulation, thus confirming we obtain the desired behavior. On the other hand, SMC trace and CPU efficiency are reported in Fig. 7b, d. We can observe that at each convergence check, the machine is idle. This fact is the main explanation why synchronous approaches require more time to converge. In Fig. 7 all plots have the same time scale. The black space present at the end of the execution in Fig. 7a shows that the simulation finishes before. Similar traces are obtained for synchronous adaptive MC and the three MLMC executions.
5.2 Wind Engineering Benchmark
The second numerical example studies the two-dimensional flow past a square building, and details are given in Sect. 2.2. The output quantity of interest Q of the system is the drag force \( F_d \) computed on the surface \( \varGamma _{{\textit{surf}}} \). The physical analysis of such a problem is out of the scope of this work, and will be objective of other works. In fact, our goal is to compare the synchronous and asynchronous approaches for both MC and MLMC. MC is run on the finest MLMC level, thus all algorithms will have the same discretization error.
The choice of a case like this is particularly relevant, since it is a realistic and challenging simplification of wind engineering problems, and we aim to show how adopting the asynchronous framework increases the overall computational efficiency.
5.2.1 MC Analysis
The tolerance is set to  , and the confidence is \( (1 - \phi ) = 0.99 \). We remark that
, and the confidence is \( (1 - \phi ) = 0.99 \). We remark that  is a dimensional quantity. Equation (20) is exploited for assessing convergence.
is a dimensional quantity. Equation (20) is exploited for assessing convergence.
In Table 4 the results of the MC algorithms are reported. We can see that the asynchronous algorithm is faster and cheaper than the two synchronous approaches. The reason is the same as before: spawning many small batches at the beginning of the simulation is more convenient than to launch one per iteration, even in the case of reduced number of synchronization points.
5.2.2 MLMC Analysis
For the MLMC analysis, the tolerance is set to  and the confidence is \( (1 - \phi ) = 0.99 \). Convergence is assessed with Eq. (19).
and the confidence is \( (1 - \phi ) = 0.99 \). Convergence is assessed with Eq. (19).
In Table 5 we can observe the results obtained with the three different MLMC strategies. Once more, the asynchronous method is the cheapest and fastest, compared to the synchronous algorithms. Even reducing a lot the number of iterations, the asynchronous strategy is the most efficient.
Similarly to the previous problem, we compare MC and MLMC. We can observe that, for the same computational cost, MLMC presents a smaller statistical error, thus asynchronous MLMC is the preferred strategy. The discretization errors of MC and MLMC are the same, since MC realizations are run on MLMC finest level.
5.2.3 Traces
In Fig. 8a, c, the executing trace of the asynchronous MLMC algorithm and its CPU usage are reported, while in Fig. 8b, d we observe the trace and the CPU usage of the synchronous adaptive MLMC algorithm. The time scale is the same for all plots.
One important observation to be made is that simulations on higher levels are running on multiple threads. On the other hand, the trace only shows the main thread that actually receives the task execution order. The rest of working threads are shown as idle. This means that for each line corresponding to a 2 CPU task, there is one apparently idle CPU that is working. For the tasks running on 4 CPUs, there are 3 CPUs that seem idle but are actually busy. In order to ease the comprehension of this fact, we have included CPU usage graphs, that take into account the real amount of CPU that are working. Looking at both figures at the same time, it can be deduced that the yellow tasks occupy a single CPU, the red tasks 2 and the blue tasks 4. Keeping that in mind, it is possible to state that the resource usage is more efficient in the AMLMC algorithm.
5.2.4 Scalability of Asynchronous Algorithm
In addition to the previous results, a strong scalability test of the asynchronous MLMC algorithm is presented in Fig. 9 and Table 6. The algorithm runs the wind engineering benchmark problem described above. Different settings and batch hierarchies with respect to previous executions are considered, thus results are not comparable.
Figure 9 reports the problem’s speedup, defined as the ratio between the execution time with 2 worker nodes and N worker nodes, \( N=\{2,4,8,16,32,64,128\} \). In Table 6, N indicates the number of worker nodes and T is the execution time of the simulation (measured in seconds).
We can observe that the proposed algorithm implementation scales pretty well up to 128 worker nodes. Indeed, we scale almost linearly until 64 worker nodes, and only at 128 worker nodes we start to observe some parallel efficiency loss.
6 Conclusions
In this work we explored a new way of performing UQ analyses exploiting hierarchical MC algorithms, focusing mainly on Monte Carlo and Multilevel Monte Carlo. The proposed asynchronous strategy is particularly interesting when running in HPC environments with uncertain parameters.
A dependency analysis of the statistical techniques to update on the fly the central moments was carried out, and the h-statistics is the chosen tool to estimate the central moments, since it allows to perform at batch level the main computations, and at global level just one simple operation per each central moment we are interested in. The stopping criteria to check the statistical reliability of the analysis was discussed and then applied in the simulations.
The key feature of the asynchronous framework is the new level of parallelism, between batches, which is added to the existing parallelism between levels, samples per level and on the solver of each instance. The proposed algorithms possess both reliability and efficiency, since desired tolerance and confidence of Q are achieved before stopping the computations, and because the capability of running many batches at once, with small hierarchies, prevents the drawing of big batches, avoiding oversampling. Additionally, the batches parallelism allows to continuously feed the machine, avoiding expensive and useless idle times and increasing the computational efficiency.
We analyzed the behavior of the asynchronous framework, with respect to current state of the art algorithms. In all cases, the asynchronous approach was the one with the best performance for achieving the desired tolerance. When the number of iterations and of convergence checks is similar, the gain in computational time is huge. On the other hand, if the synchronous algorithm minimizes the number of iterations, thus reducing the idle time of the machine to the minimum, the computational efficiency improves, but never reaches the one of the asynchronous approach. Moreover, we would like to remark how solving the problem estimating a priori the number of levels and of samples per level is a challenging task, and requires a screening phase with a reasonable number of samples in order to perform such an estimation. Instead, our asynchronous approach does not require any tune phase in order to run, since the batch hierarchy can be as small as desired.
At the current moment, the update on the fly of the hierarchy, i.e. of the number of batches running, of levels and of samples per level, is non-adaptive. The capability of estimating it on the fly will be addressed in future studies. We focused on the computation of many statistical estimators. It is known that the expected value is not sensitive to high values, while central moments consider oscillations. However, central moments are symmetric with respect to the mean, and high oscillations on one side of the probability density function may be compensated by small variations on the other side. For this reason, other statistical estimators, as the Value at Risk or the Conditional Value at Risk, may be preferred, since they measure the risk in the tail of the probability density function [35]. Update on the fly of such estimators is currently being studied.
Data Availability
The datasets generated and analysed during the current study are available from the corresponding author on request. The software applications used to generate the results are open source and the corresponding author can provide instructions on how to reproduce the analyses.
Notes
For sake of simplicity, we use
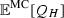 as sampled estimator. The same applies for
as sampled estimator. The same applies for  .
.
References
Adams, B.M., Eldred, M.S., Geraci, G., Hooper R.W., Jakeman, J.D., Maupin, K.A., Monschke, J.A., Rushdi, A.A., Wildey, J.A.S., Swiler, L.P., M.T.: Dakota, a multilevel parallel object-oriented framework for design optimization, parameter estimation, uncertainty quantification, and sensitivity analysis: version 6.10 user’s manual. Tech. rep., SAND2014-4633 Unlimited Release, July 2014. Updated May 15, 2019 (2014)
Amela, R., Ramon-Cortes, C., Ejarque, J., Conejero, J., Badia, R.M.: Executing linear algebra kernels in heterogeneous distributed infrastructures with PyCOMPSs. Oil & Gas Science and Technology-Revue d’IFP Energies nouvelles 73, 47 (2018). https://doi.org/10.2516/ogst/2018047
Amela, R., Ayoul-Guilmard, Q., Badia, R.M., Ganesh, S., Nobile, F., Rossi, R., Tosi, R.: ExaQUte XMC (2019). https://doi.org/10.5281/zenodo.3235833
Andre, M.S.: Aeroelastic modeling and simulation for the assessment of wind effects on a parabolic trough solar collector. Ph.D. thesis, Technische Universität München (2018)
Angelino, E., Kohler, E., Waterland, A., Seltzer, M., Adams, R.P.: Accelerating MCMC via parallel predictive prefetching. In: Uncertainty in Artificial Intelligence—Proceedings of the 30th Conference, UAI 2014 (2014)
Bennett, J., Grout, R., Pébay, P., Roe, D., Thompson, D.: Numerically stable, single-pass, parallel statistics algorithms. In: Proceedings—IEEE International Conference on Cluster Computing, ICCC (2009). https://doi.org/10.1109/CLUSTR.2009.5289161
Blondeel, P., Robbe, P., Van hoorickx, C., Lombaert, G., Vandewalle, S.: Multilevel Monte Carlo for uncertainty quantification in structural engineering. arXiv e-prints p. arXiv:1808.10680 (2018)
Brockwell, A.E.: Parallel Markov Chain Monte Carlo simulation by pre-fetching. J. Comput. Graph. Stat. (2006). https://doi.org/10.1198/106186006X100579
Chan, T.F., Golub, G.H., LeVeque, R.J.: Updating formulae and a pairwise algorithm for computing sample variances. In: Caussinus, H., Ettinger, P., Tomassone, R. (eds.) COMPSTAT 1982 5th Symposium held at Toulouse 1982, pp. 30–41. Physica-Verlag HD, Heidelberg (1982)
Chan, T.F., Golub, G.H., Leveque, R.J.: Statistical computing: algorithms for computing the sample variance: analysis and recommendations. Am. Stat. 37(3), 242–247 (1983). https://doi.org/10.1080/00031305.1983.10483115
Cliffe, K.A., Giles, M.B., Scheichl, R., Teckentrup, A.L.: Multilevel Monte Carlo methods and applications to elliptic PDEs with random coefficients. Comput. Vis. Sci. 14, 3–15 (2011). https://doi.org/10.1007/s00791-011-0160-x
Collier, N., Haji-Ali, A.L., Nobile, F., von Schwerin, E., Tempone, R.: A continuation multilevel Monte Carlo algorithm. BIT Numer. Math. 55(2), 399–432 (2015). https://doi.org/10.1007/s10543-014-0511-3
Dadvand, P., Rossi, R., Gil, M., Martorell, X., Cotela, J., Juanpere, E., Idelsohn, S.R., Oñate, E.: Migration of a generic multi-physics framework to HPC environments. Comput. Fluids 80(1), 301–309 (2013). https://doi.org/10.1016/j.compfluid.2012.02.004
Dadvand, P., Rossi, R., Oñate, E.: An object-oriented environment for developing finite element codes for multi-disciplinary applications. Arch. Comput. Methods Eng. 17(3), 253–297 (2010)
Davari, M., Rossi, R., Dadvand, P., López, I., Wüchner, R.: A cut finite element method for the solution of the full-potential equation with an embedded wake. Comput. Mech. 63(5), 821–833 (2019). https://doi.org/10.1007/s00466-018-1624-3
Drzisga, D., Gmeiner, B., Rüde, U., Scheichl, R., Wohlmuth, B.: Scheduling massively parallel multigrid for multilevel Monte Carlo methods. SIAM J. Sci. Comput. 39(5), S873–S897 (2017). https://doi.org/10.1137/16m1083591
Eller, D.: Fast, unstructured-mesh finite-element method for nonlinear subsonic flow. J. Aircr. (2012). https://doi.org/10.2514/1.C031738
Ellingwood, B.R., Kinali, K.: Quantifying and communicating uncertainty in seismic risk assessment. Struct. Saf. 31(2), 179–187 (2009). https://doi.org/10.1016/j.strusafe.2008.06.001
Ghanem, R.G., Spanos, P.D.: Stochastic Finite Elements: A Spectral Approach. Springer, New York (2011). https://doi.org/10.1007/978-1-4612-3094-6
Giles, M.B.: Multilevel Monte Carlo path simulation. Oper. Res. 56(3), 607–617 (2008). https://doi.org/10.1287/opre.1070.0496
Giles, M.B.: Multilevel Monte Carlo methods. Acta Numer. 24(May), 259–328 (2015). https://doi.org/10.1017/S096249291500001X
Giles, M., Kuo, F.Y., Sloan, I.H., Waterhouse, B.J.: Quasi-Monte Carlo for finance applications. ANZIAM J. 50, 308 (2008). https://doi.org/10.21914/anziamj.v50i0.1440
Halmos, P.R.: The theory of unbiased estimation. Ann. Math. Stat. 17(1), 34–43 (2007). https://doi.org/10.1214/aoms/1177731020
Lord, G.J., Powell, C.E., Shardlow, T.: An Introduction to Computational Stochastic PDEs. Cambridge University Press, New York (2014). https://doi.org/10.1017/CBO9781139017329
Lordan, F., Tejedor, E., Ejarque, J., Rafanell, R., Álvarez, J., Marozzo, F., Lezzi, D., Sirvent, R., Talia, D., Badia, R.M.: ServiceSs: an interoperable programming framework for the cloud. J. Grid Comput. 12(1), 67–91 (2014). https://doi.org/10.1007/s10723-013-9272-5
Mathelin, L., Hussaini, M.Y., Zang, T.A.: Stochastic approaches to uncertainty quantification in CFD simulations. Numer. Algorithms 38, 209–236 (2005). https://doi.org/10.1007/s11075-004-2866-z
Mishra, S., Schwab, C.: Sparse tensor multi-level Monte Carlo finite volume methods for hyperbolic conservation laws with random initial data. Math. Comput. (2012). https://doi.org/10.1090/s0025-5718-2012-02574-9
Mishra, S., Schwab, C., Šukys, J.: Multi-level Monte Carlo finite volume methods for nonlinear systems of conservation laws in multi-dimensions. J. Comput. Phys. (2012). https://doi.org/10.1016/j.jcp.2012.01.011
Mishra, S., Schwab, C., Šukys, J.: Multilevel Monte Carlo finite volume methods for shallow water equations with uncertain topography in multi-dimensions. SIAM J. Sci. Comput. 34(6), B761–B784 (2012). https://doi.org/10.1137/110857295
Pébay, P., Terriberry, T.B., Kolla, H., Bennett, J.: Numerically stable, scalable formulas for parallel and online computation of higher-order multivariate central moments with arbitrary weights. Comput. Stat. 31(4), 1305–1325 (2016). https://doi.org/10.1007/s00180-015-0637-z
Pisaroni, M., Krumscheid, S., Nobile, F.: Quantifying uncertain system outputs via the multilevel Monte Carlo method—Part I: central moment estimation. J. Comput. Phys. (2020). https://doi.org/10.1016/j.jcp.2020.109466
Pisaroni, M., Nobile, F., Leyland, P.: A continuation multi level Monte Carlo (C-MLMC) method for uncertainty quantification in compressible inviscid aerodynamics. Comput. Methods Appl. Mech. Eng. 326, 20–50 (2017). https://doi.org/10.1016/j.cma.2017.07.030
Pope, S.B.: Turbulent Flows. Cambridge University Press (2000). https://doi.org/10.1017/CBO9780511840531. https://www.cambridge.org/core/product/identifier/9780511840531/type/book
Tejedor, E., Becerra, Y., Alomar, G., Queralt, A., Badia, R.M., Torres, J., Cortes, T., Labarta, J.: PyCOMPSs: parallel computational workflows in Python. Int. J. High Perform. Comput. Appl. 31(1), 66–82 (2017). https://doi.org/10.1177/1094342015594678
Tyrrell Rockafellar, R., Royset, J.O.: Engineering decisions under risk averseness. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 1(2), 04015003 (2015). https://doi.org/10.1061/ajrua6.0000816
Walters, R.W., Huyse, L.: Uncertainty Analysis for Fluid Mechanics with Applications. Tech. rep. (2002). NASA CR-2002-211449
Xiu, D., Karniadakis, G.E.: The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 24(2), 619–644 (2003). https://doi.org/10.1137/s1064827501387826
Acknowledgements
The authors would like to thank M. Núñez and B. Keith for their help in defining the numerical problems.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 800898. This work has been supported by the Spanish Government (contracts SEV2015- 0493 and TIN2015-65316-P), by the Generalitat de Catalunya (contract 2014- SGR-1051). The authors thankfully acknowledge the computer resources at MareNostrum and the technical support provided by Barcelona Supercomputing Center (IM-2020-1-0016).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tosi, R., Amela, R., Badia, R.M. et al. A Parallel Dynamic Asynchronous Framework for Uncertainty Quantification by Hierarchical Monte Carlo Algorithms. J Sci Comput 89, 28 (2021). https://doi.org/10.1007/s10915-021-01598-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-021-01598-6
Keywords
- Monte Carlo
- Multilevel Monte Carlo
- Asynchronous Algorithms
- Distributed Computing
- High Performance Computing







 grows with the level accuracy
grows with the level accuracy  ,
,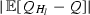 decreases as
decreases as  grows,
grows, more or less constant with respect to
more or less constant with respect to  ,
, decreases as the level grows.
decreases as the level grows.






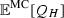 as sampled estimator. The same applies for
as sampled estimator. The same applies for  .
.