1 Introduction

In recent years, with ever increasing computational capacities, space-time methods have received fast growing attention from the scientific community. Space-time approximations of dynamic problems, in contrast to standard time-stepping techniques, enable full space-time parallelism on modern massively parallel architectures [27]. Moreover, they can naturally deal with moving domains [38, 57,58,59, 63] and allow for space-time adaptivity [1, 24, 28, 39, 47, 49, 61]. The main idea of space-time formulations is to consider the temporal dimension as an additional spatial one and assemble a large space-time system to be solved in parallel as in [25]. Space-time methods have been used in combination with various numerical techniques, including finite differences [2, 11, 35], finite elements [4, 26, 37, 40], isogeometric analysis [34, 41], and discontinuous Galerkin methods [1, 16, 32, 37, 38, 48, 57, 63]. Moreover, they have been considered for a variety of applications, such as mechanics [15], fluid dynamics [11, 38, 54], fluid-structure interaction [60], and many others. When dealing with space-time finite elements, the time direction needs special care. To ensure that the information flows in the positive time direction, a particular choice of the basis in time is often used. The discontinuous Galerkin formulation with an “upwind” flow is a common choice in this context; see, for example, [38, 51, 57, 62].

Specialized parallel solvers have been recently developed for the large linear systems arising from space-time discretizations. We mention in particular the space-time parallel multigrid proposed by Gander and Neum\(\ddot{\text{ u }}\)ller [29], the parallel preconditioners for space-time isogeometric analysis proposed by Hofer et al. [34], the fast diagonalization techniques proposed by Langer and Zank [42] and Loli et al. [44], and the parallel proposal by McDonald and Wathen [46]. We also refer the reader to [56] for a recent review on space-time methods for parabolic evolution equations, and to [55] for algebraic multigrid methods.

In the present paper, we focus on the diffusion equation

$$\begin{aligned} \left\{ \begin{aligned}&\partial _t u(t,{\mathbf{x}})-\nabla \cdot K({\mathbf{x}})\nabla u(t,{\mathbf{x}})=f(t,{\mathbf{x}}),&\quad (t,{\mathbf{x}})\in (0,\mathrm{T})\times (0,1)^d,\\&u(t,{\mathbf{x}})=0,&\quad (t,{\mathbf{x}})\in (0,\mathrm{T})\times \partial ((0,1)^d),\\&u(t,{\mathbf{x}})=0,&\quad (t,{\mathbf{x}})\in \{0\}\times (0,1)^d, \end{aligned}\right. \end{aligned}$$
(1.1)

where \(K({\mathbf{x}})\in \mathbb R^{d\times d}\) is the matrix of diffusion coefficients and \(f(t,{\mathbf{x}})\) is a source term. It is assumed that \(K({\mathbf{x}})\) is symmetric positive definite at every point \({\mathbf{x}}\in (0,1)^d\) and each component of \(K({\mathbf{x}})\) is a continuous bounded function on \((0,1)^d\). We impose homogeneous Dirichlet initial/boundary conditions both for simplicity and because the inhomogeneous case reduces to the homogeneous case by considering a lifting of the boundary data [50]. We consider for (1.1) the same space-time approximation as in [10], involving a \({\varvec{p}}\)-degree \(C^{\varvec{k}}\) isogeometric analysis (IgA) discretization in space and a q-degree discontinuous Galerkin (DG) discretization in time. Here, \({\varvec{p}}=(p_1,\ldots ,p_d)\) and \({\varvec{k}}=(k_1,\ldots ,k_d)\), where \(\mathbf{0}\le {\varvec{k}}\le {\varvec{p}}-\mathbf{1}\) (i.e., \(0\le k_i\le p_i-1\) for all \(i=1,\ldots ,d\)) and the parameters \(p_i\) and \(k_i\) represent, respectively, the polynomial degree and the smoothness of the IgA basis functions in direction \(x_i\).

The overall discretization process leads to solving a large space-time linear system. We propose a fast solver for this system in the case of maximal smoothness \({\varvec{k}}={\varvec{p}}-\mathbf{1}\), i.e., the case corresponding to the classical IgA paradigm [3, 9, 17, 36]. The solver is a preconditioned GMRES (PGMRES) method whose preconditioner \(\tilde{P}\) is obtained as an approximation of another preconditioner P inspired by the spectral analysis carried out in [10]. Informally speaking, the preconditioner \(\tilde{P}\) is a standard multigrid, which is applied only in space and not in time, and which involves, at all levels, a single symmetric Gauss–Seidel post-smoothing step and standard bisection for the interpolation and restriction operators (following the Galerkin assembly). The proposed solver is then a multigrid preconditioned GMRES (MG-GMRES). Its performance is illustrated through numerical experiments and turns out to be satisfactory in terms of iteration count and run-time. In addition, the solver is suited for parallel computation as it shows remarkable scaling properties with respect to the number of cores. Comparisons with other benchmark solvers are also presented and reveal the actual competitiveness of our proposal.

The paper is organized as follows. In Sect. 2, we briefly recall the space-time IgA-DG discretization of (1.1) and we report the main result of [10] concerning the spectral distribution of the associated discretization matrix C. In Sect. 3, we present a PGMRES method for the matrix C, which is the root from which the proposed solver originated. In Sect. 4, we describe the proposed solver. In Sect. 5, we describe its parallel version. In Sect. 6, we illustrate its performance in terms of iteration count, run-time and scaling. In Sect. 7, we test it on a generalization of problem (1.1) where \((0,1)^d\) is replaced by a non-rectangular domain and the considered IgA discretization involves a non-trivial geometry. In Sect. 8, we draw conclusions. In order to keep this paper as concise as possible, we borrow notation and terminology from [10]. It is therefore recommended that the reader takes a look at Sects. 1 and 2 of [10].

2 Space-time IgA-DG Discretization of the Diffusion Equation

Let \(N\in \mathbb N\) and \({\varvec{n}}=(n_1,\ldots ,n_d)\in \mathbb N^d\), and define the following uniform partitions in time and space:

$$\begin{aligned} \begin{array}{ll} t_i =i\Delta t, &{}\qquad i = 0,\ldots ,N, \\ {\mathbf{x}}_{\varvec{i}}= {\varvec{i}}\Delta {\mathbf{x}}=(i_1\Delta x_1,\ldots ,i_d \Delta x_d), &{}\qquad \varvec{{ i}} =\mathbf{0},\ldots ,{\varvec{n}},\\ \end{array} \end{aligned}$$

where \(\Delta t =\mathrm{T}/{ N}\, \mathrm{and}\, \Delta {\mathbf{x}}=(\Delta x_1,\ldots ,\Delta x_2) = (1/n_1,\ldots ,1/n_d)\). We consider for the differential problem (1.1) the same space-time discretization as in [10], i.e., we use a \({\varvec{p}}\)-degree \(C^{\varvec{k}}\) IgA approximation in space based on the uniform mesh \(\{{\mathbf{x}}_{\varvec{i}},\ {\varvec{i}}=\mathbf{0},\ldots ,{\varvec{n}}\}\) and a q-degree DG approximation in time based on the uniform mesh \(\{t_i,\ i=0,\ldots ,N\}\). Here, \({\varvec{p}}=(p_1,\ldots ,p_d)\) and \({\varvec{k}}=(k_1,\ldots ,k_d)\) are multi-indices, with \(p_i\) and \(0\le k_i\le p_i-1\) representing, respectively, the polynomial degree and the smoothness of the IgA basis functions in direction \(x_i\). As explained in [10, Sect. 3], the overall discretization process leads to a linear system

$$\begin{aligned} C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K){\mathbf{u}}={\mathbf{f}}, \end{aligned}$$
(2.1)

where:

  • \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) is the \(N\times N\) block matrix given by

    $$\begin{aligned} C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)=\left[ \begin{array}{cccc} A_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K) &{} &{} &{} \\ B_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]} &{} A_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K) &{} &{} \\ &{} \ddots &{} \ddots &{} \\ &{} &{} B_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]} &{} A_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K) \end{array}\right] ; \end{aligned}$$
    (2.2)

  • the blocks \(A_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) and \(B_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}\) are \((q+1)\bar{n}\times (q+1)\bar{n}\) matrices given by

    $$\begin{aligned} A_{\varvec{n}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)&=K_{[q]}\otimes M_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}+\frac{\Delta t}{2}M_{[q]}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K), \end{aligned}$$
    (2.3)
    $$\begin{aligned} B_{\varvec{n}}^{[q,{\varvec{p}},{\varvec{k}}]}&=-J_{[q]}\otimes M_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}, \end{aligned}$$
    (2.4)

    where \(\bar{n}=\prod _{i=1}^d(n_i(p_i-k_i)+k_i-1)\) is the number of degrees of freedom (DoFs) in space (the total number of DoFs is equal to the size \(N(q+1)\bar{n}\) of the matrix \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\)); each block row in the block partition of \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) given by (2.2) is referred to as a time slab;

  • \(M_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}\) and \(K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)\) are the \(\bar{n}\times \bar{n}\) mass and stiffness matrices in space, which are given by

    $$\begin{aligned} M_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}&=\left[ \int _{[0,1]^d}B_{{\varvec{j}}+\mathbf{1},[{\varvec{p}},{\varvec{k}}]}({\mathbf{x}})B_{{\varvec{i}}+\mathbf{1},[{\varvec{p}},{\varvec{k}}]}({\mathbf{x}})\mathrm{d}{\mathbf{x}}\right] _{{\varvec{i}},{\varvec{j}}=\mathbf{1}}^{{\varvec{n}}({\varvec{p}}-{\varvec{k}})+{\varvec{k}}-\mathbf{1}}, \end{aligned}$$
    (2.5)
    $$\begin{aligned} K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)&=\left[ \int _{[0,1]^d}\bigl [K({\mathbf{x}})\nabla B_{{\varvec{j}}+\mathbf{1},[{\varvec{p}},{\varvec{k}}]}({\mathbf{x}})\bigr ]\cdot \nabla B_{{\varvec{i}}+\mathbf{1},[{\varvec{p}},{\varvec{k}}]}({\mathbf{x}})\mathrm{d}{\mathbf{x}}\right] _{{\varvec{i}},{\varvec{j}}=\mathbf{1}}^{{\varvec{n}}({\varvec{p}}-{\varvec{k}})+{\varvec{k}}-\mathbf{1}}, \end{aligned}$$
    (2.6)

    where \(B_{\mathbf{1},[{\varvec{p}},{\varvec{k}}]},\ldots ,B_{{\varvec{n}}({\varvec{p}}-{\varvec{k}})+{\varvec{k}}+{\mathbf{1}},[{\varvec{p}},{\varvec{k}}]}\) are the tensor-product B-splines defined by

    $$\begin{aligned} B_{{\varvec{i}},[{\varvec{p}},{\varvec{k}}]}({\mathbf{x}})=\prod _{r=1}^dB_{i_r,[p_r,k_r]}(x_r),\quad {\varvec{i}}=\mathbf{1},\ldots ,{\varvec{n}}({\varvec{p}}-{\varvec{k}})+{\varvec{k}}+\mathbf{1}, \end{aligned}$$

    and \(B_{1,[p_r,k_r]},\ldots ,B_{n_r(p_r-k_r)+k_r+1,[p_r,k_r]}\) are the B-splines of degree \(p_r\) and smoothness \(C^{k_r}\) defined on the knot sequence

    $$\begin{aligned} \biggl \{\underbrace{0,\ldots ,0}_{p_r+1},\ \underbrace{\frac{1}{n_r},\ldots ,\frac{1}{n_r}}_{p_r-k_r},\ \underbrace{\frac{2}{n_r},\ldots ,\frac{2}{n_r}}_{p_r-k_r},\ \ldots ,\ \underbrace{\frac{n_r-1}{n_r},\ldots ,\frac{n_r-1}{n_r}}_{p_r-k_r},\ \underbrace{1,\ldots ,1}_{p_r+1}\biggr \}. \end{aligned}$$

  • \(M_{[q]}\), \(K_{[q]}\), \(J_{[q]}\) are the \((q+1)\times (q+1)\) blocks given by

    $$\begin{aligned} M_{[q]}&=\left[ \int _{-1}^1\ell _{j,[q]}(\tau )\ell _{i,[q]}(\tau )\mathrm{d}\tau \right] _{i,j=1}^{q+1},\end{aligned}$$
    (2.7)
    $$\begin{aligned} K_{[q]}&=\left[ \ell _{j,[q]}(1)\ell _{i,[q]}(1)-\int _{-1}^1\ell _{j,[q]}(\tau )\ell '_{i,[q]}(\tau )\mathrm{d}\tau \right] _{i,j=1}^{q+1}, \end{aligned}$$
    (2.8)
    $$\begin{aligned} J_{[q]}&=\left[ \ell _{j,[q]}(1)\ell _{i,[q]}(-1)\right] _{i,j=1}^{q+1}, \end{aligned}$$
    (2.9)

    where \(\{\ell _{1,[q]},\ldots ,\ell _{q+1,[q]}\}\) is a fixed basis for the space of polynomials of degree \(\le q\). In the context of (nodal) DG methods [33], \(\ell _{1,[q]},\ldots ,\ell _{q+1,[q]}\) are often chosen as the Lagrange polynomials associated with \(q+1\) fixed points \(\{\tau _1,\ldots ,\tau _{q+1}\}\subseteq [-1,1]\), such as, for example, the Gauss–Lobatto or the right Gauss–Radau nodes in \([-1,1]\).

The solution of system (2.1) yields the approximate solution of problem (1.1); see [10] for details. The main result of [10] is reported in Theorem 2.1 below; see also [8, Sect. 6.2] for a more recent and lucid proof. Before stating Theorem 2.1, let us recall the notion of spectral distribution for a given sequence of matrices. In what follows, we say that a matrix-valued function \({\mathbf{f}}:D\rightarrow \mathbb C^{s\times s}\), defined on a measurable set \(D\subseteq \mathbb R^\ell \), is measurable if its components \(f_{ij}:D\rightarrow \mathbb C\), \(i,j=1,\ldots ,s\), are (Lebesgue) measurable.

Definition 2.1

Let \(\{X_m\}_m\) be a sequence of matrices, with \(X_m\) of size \(d_m\) tending to infinity, and let \({\mathbf{f}}:D\rightarrow \mathbb C^{s\times s}\) be a measurable matrix-valued function defined on a set \(D\subset \mathbb R^\ell \) with \(0<\mathrm{measure}(D)<\infty \). We say that \(\{X_m\}_m\) has a (asymptotic) spectral distribution described by \({\mathbf{f}}\), and we write \(\{X_m\}_m\sim _\lambda {\mathbf{f}}\), if

$$\begin{aligned} \lim _{m\rightarrow \infty }\frac{1}{d_m}\sum _{j=1}^{d_m}F(\lambda _j(X_m))=\frac{1}{\mathrm{measure}(D)}\int _D\frac{\sum _{i=1}^sF\left( \lambda _i({\mathbf{f}}({\mathbf{y}}))\right) }{s}\mathrm{d}{\mathbf{y}}\end{aligned}$$

for all continuous functions \(F:\mathbb C\rightarrow \mathbb C\) with compact support. In this case, \({\mathbf{f}}\) is called the spectral symbol of \(\{X_m\}_m\).

Remark 2.1

The informal meaning behind Definition 2.1 is the following: assuming that \({\mathbf{f}}\) possesses s Riemann-integrable eigenvalue functions \(\lambda _i({\mathbf{f}}({\mathbf{y}}))\), \(i=1,\ldots ,s\), the eigenvalues of \(X_m\), except possibly for \(o(d_m)\) outliers, can be subdivided into s different subsets of approximately the same cardinality; and the eigenvalues belonging to the ith subset are approximately equal to the samples of the ith eigenvalue function \(\lambda _i({\mathbf{f}}({\mathbf{y}}))\) over a uniform grid in the domain D. For instance, if \(\ell =1\), \(d_m=ms\), and \(D=[a,b]\), then, assuming we have no outliers, the eigenvalues of \(X_m\) are approximately equal to

$$\begin{aligned} \lambda _i\Bigl ({\mathbf{f}}\Bigl (a+j\frac{b-a}{m}\Bigr )\Bigr ),\quad j=1,\ldots ,m,\quad i=1,\ldots ,s, \end{aligned}$$

for m large enough; similarly, if \(\ell =2\), \(d_m=m^2s\), and \(D=[a_1,b_1]\times [a_2,b_2]\), then, assuming we have no outliers, the eigenvalues of \(X_m\) are approximately equal to

$$\begin{aligned} \lambda _i\Bigl ({\mathbf{f}}\Bigl (a_1+j_1\frac{b_1-a_1}{m},a_2+j_2\frac{b_2-a_2}{m}\Bigr )\Bigr ),\quad j_1,j_2=1,\ldots ,m,\quad i=1,\ldots ,s, \end{aligned}$$

for m large enough; and so on for \(\ell \ge 3\).

Theorem 2.1

Let \(q\ge 0\) be an integer, let \({\varvec{p}}\in \mathbb N^d\) and \(\mathbf{0}\le {\varvec{k}}\le {\varvec{p}}-\mathbf{1}\). Assume that \(K({\mathbf{x}})\) is symmetric positive definite at every point \({\mathbf{x}}\in (0,1)^d\) and each component of \(K({\mathbf{x}})\) is a continuous bounded function on \((0,1)^d\). Suppose the following two conditions are met:

  • \({\varvec{n}}={\varvec{\alpha }}n\), where \({\varvec{\alpha }}=(\alpha _1,\ldots ,\alpha _d)\) is a vector with positive components in \(\mathbb Q^d\) and n varies in some infinite subset of \(\mathbb N\) such that \({\varvec{n}}={\varvec{\alpha }}n\in \mathbb N^d\);

  • \(N=N(n)\) is such that \(N\rightarrow \infty \) and \(N/n^2\rightarrow 0\) as \(n\rightarrow \infty \).

Then, for the sequence of normalized space-time matrices \(\{2Nn^{d-2}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\}_n\) we have the spectral distribution relation

$$\begin{aligned} \{2Nn^{d-2}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\}_n\sim _\lambda {\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}, \end{aligned}$$

where:

  • the spectral symbol \({\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}:[0,1]^d\times [-\pi ,\pi ]^d\rightarrow \mathbb C^{(q+1)\prod _{i=1}^d(p_i-k_i)\times (q+1)\prod _{i=1}^d(p_i-k_i)}\) is defined as

    $$\begin{aligned}&{\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}({\mathbf{x}},{\varvec{\theta }})={\mathbf{f}}_{[{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}({\mathbf{x}},{\varvec{\theta }})\otimes \mathrm{T}M_{[q]}; \end{aligned}$$
    (2.10)

  • \({\mathbf{f}}_{[{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}:[0,1]^d\times [-\pi ,\pi ]^d\rightarrow \mathbb C^{\prod _{i=1}^d(p_i-k_i)\times \prod _{i=1}^d(p_i-k_i)}\) is defined as

    $$\begin{aligned}&{\mathbf{f}}_{[{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}({\mathbf{x}},{\varvec{\theta }}) =\frac{1}{\prod _{i=1}^d\alpha _i}\sum _{i,j=1}^d\alpha _i\alpha _jK_{ij}({\mathbf{x}})(H_{[{\varvec{p}},{\varvec{k}}]})_{ij}({\varvec{\theta }}); \end{aligned}$$
    (2.11)

  • \(H_{[{\varvec{p}},{\varvec{k}}]}\) is a \(d\times d\) block matrix whose (i, j) entry is a \(\prod _{i=1}^d(p_i-k_i)\times \prod _{i=1}^d(p_i-k_i)\) block defined as in [10, eq. (5.12)];

  • \(\mathrm{T}\) is the final time in (1.1) and \(M_{[q]}\) is given in (2.7).

With the same argument used for proving Theorem 2.1, it not difficult to prove the following result.

Theorem 2.2

Suppose the hypotheses of Theorem 2.1 are satisfied, and let

$$\begin{aligned} Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)=\frac{\Delta t}{2}\,I_N\otimes M_{[q]}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K). \end{aligned}$$

Then,

$$\begin{aligned}\{2Nn^{d-2}(I_N\otimes A_{{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K))\}_n\sim _\lambda {\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]},\qquad \{2Nn^{d-2}Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\}_n\sim _\lambda {\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}.\end{aligned}$$

3 PGMRES for the Space-time IgA-DG System

Suppose the hypotheses of Theorem 2.1 are satisfied. Then, on the basis of Theorem 2.2 and the theory of (block) generalized locally Toeplitz (GLT) sequences [7, 8, 30, 31, 52, 53], we expect that the sequence of preconditioned matrices

$$\begin{aligned} (I_N\otimes A_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K))^{-1}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K), \end{aligned}$$
(3.1)

as well as the sequence of preconditioned matrices

$$\begin{aligned} (Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K))^{-1}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)=\frac{2}{\Delta t}\,(I_N\otimes M_{[q]}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K))^{-1}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K), \end{aligned}$$
(3.2)

has an asymptotic spectral distribution described by the preconditioned symbol

$$\begin{aligned} \bigl ({\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[\varvec{\alpha },K]}\bigr )^{-1}{\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[\varvec{\alpha },K]}=I_{(q+1)\prod _{i=1}^d(p_i-k_i)}. \end{aligned}$$

This means that the eigenvalues of the two sequences of matrices (3.1) and (3.2) are (weakly) clustered at 1; see [7, Sect. 2.4.2]. Therefore, in view of the convergence properties of the GMRES method [13]—see in particular [13, Theorem 2.13] and the original research paper by Bertaccini and Ng [14]—we may expect that the PGMRES with preconditioner \(I_N\otimes A_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) or \(Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) for solving a linear system with coefficient matrix \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) has an optimal convergence rate, i.e., the number of iterations for reaching a preassigned accuracy \(\varepsilon \) is independent of (or only weakly dependent on) the matrix size. We may also expect that the same is true for the PGMRES with preconditioner

$$\begin{aligned} P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)=I_N\otimes I_{q+1}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)=I_{N(q+1)}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K), \end{aligned}$$
(3.3)

because (up to a negligible normalization factor \(\Delta t/2\)) \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) is spectrally equivalent to \(Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\). Indeed, the spectrum of \((P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K))^{-1}(I_N\otimes M_{[q]}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K))\) is contained in \([c_q,C_q]\) for some positive constants \(c_q,C_q>0\) depending only on q. For instance, one can take \(c_q=\lambda _{\min }(M_{[q]})\) and \(C_q=\lambda _{\max }(M_{[q]})\), which are both positive as \(M_{[q]}\) is symmetric positive definite (see (2.7)).

Table 1 Number of iterations GM[p] and PGM[p] needed by, respectively, the GMRES and the PGMRES with preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\), for solving the linear system (2.1), up to a precision \(\varepsilon =10^{-8}\), in the case where \(d=2\), \(K({\mathbf{x}})=I_2\), \(f(t,{\mathbf{x}})=1\), \(\mathrm{T}=1\), \(q=0\), \({\varvec{n}}=(n,n)\), \({\varvec{p}}=(p,p)\), \({\varvec{k}}=(p-1,p-1)\), \(N=n\)
Full size table
Table 2 Number of iterations GM[p, k] and PGM[p, k] needed by, respectively, the GMRES and the PGMRES with preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\), for solving the linear system (2.1), up to a precision \(\varepsilon =10^{-8}\), in the case where \(d=2\), \( K(x_1,x_2) = \begin{bmatrix} \cos (x_1)+ x_2 &{} 0 \\ 0 &{} x_1 + \sin (x_2) \end{bmatrix},\) \(f(t,{\mathbf{x}})=1\), \({\mathrm{T}}=1\), \(q=1\), \({\varvec{n}}=(n,n)\), \({\varvec{p}}=(p,p)\), \({\varvec{k}}=(k,k)\), \(N=20\)
Full size table

To show that our expectation is realized, we solve system (2.1) in two space dimensions (\(d=2\)), up to a precision \(\varepsilon =10^{-8}\), by means of the GMRES and the PGMRES with preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\), using \(f(t,{\mathbf{x}})=1\), \(\mathrm{T}=1\), \({\varvec{\alpha }}= (1,1)\), \({\varvec{n}}= {\varvec{\alpha }}n = (n,n)\), \({\varvec{p}}= (p,p)\), \({\varvec{k}}= (k,k)\), and varying \(K({\mathbf{x}})\), N, n, q, p, k. The resulting number of iterations are collected in Tables 1, 2, 3. We see from the tables that the GMRES solver rapidly deteriorates with increasing n, and it is not robust with respect to p, k. On the other hand, the convergence rate of the proposed PGMRES is robust with respect to all spatial parameters n, p, k, though its performance is clearly better in the case where N is fixed (Tables 2, 3) than in the case where N increases (Table 1). An explanation of this phenomenon based on Theorem 2.1 is the following. In the case where N is fixed, the ratio \(N/n^2\) converges to 0 much more quickly than in the case where \(N=n\). Consequently, when N is fixed, the spectrum of both \(2Nn^{d-2}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) and \(2Nn^{d-2}Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) is better described by the symbol \({\mathbf{f}}_{[q,{\varvec{p}},{\varvec{k}}]}^{[{\varvec{\alpha }},K]}\) than when \(N=n\). Similarly, the spectrum of the preconditioned matrix \((Q_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K))^{-1}C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) is better described by the preconditioned symbol \(I_{(q+1)\prod _{i=1}^d(p_i-k_i)}\). In conclusion, the eigenvalues of the preconditioned matrix are supposed to be more clustered when N is fixed than when \(N=n\).

Table 3 Number of iterations GM[p, k] and PGM[p, k] needed by, respectively, the GMRES and the PGMRES with preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\), for solving the linear system (2.1), up to a precision \(\varepsilon =10^{-8}\), in the case where \(d=2\), \(K(x_1,x_2) = \begin{bmatrix}( 2 + \cos x_1 )(1+x_2) &{} \cos (x_1+x_2)\sin (x_1+x_2) \\ \cos (x_1+x_2)\sin (x_1+x_2) &{} (2+\sin x_2)(1+x_1) \end{bmatrix}, \) \(f(t,{\mathbf{x}})=1\), \(\mathrm{T}=1\), \(q=2\), \({\varvec{n}}=(n,n)\), \({\varvec{p}}=(p,p)\), \({\varvec{k}}=(k,k)\), \(N=20\)
Full size table

In order to investigate the influence of q on the number of PGMRES iterations, we performed a further numerical experiment in Table 4. We observe that the considered PGMRES is not robust with respect to q, but the number of PGMRES iterations grows linearly with q. By comparing Tables 1 and 4, we note that the PGMRES convergence is linear with respect to both N and q. In practice, increasing q is the most convenient way to improve the temporal accuracy of the discrete solution \(\mathbf {u}\); see, e.g., [12]. This is due to the superconvergence property, according to which the order of convergence in time of a q-degree DG method is \(2q+1\) [19, 43]. Tables 1 and 4 show that the strategy of keeping N fixed and increasing q is more convenient even in terms of performance of the proposed PGMRES.

Table 4 Same setting as in Table 1 with \(n=N=20\) and \(q=0,1,2,3,4\)
Full size table

As it is known, each PGMRES iteration requires solving a linear system with coefficient matrix given by the preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\), and this is not required in a GMRES iteration. Thus, if we want to prove that the proposed PGMRES is fast, we have to show that we are able to solve efficiently a linear system with matrix \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\). However, for the reasons explained in Sect. 4, this is not exactly the path we will follow.

Before moving on to Sect. 4, we remark that, thanks to the tensor structure (3.3), the solution of a linear system with coefficient matrix \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\) reduces to the solution of \(N(q+1)\) linear systems with coefficient matrix \(K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)\). Indeed, the solution of the system \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K)\mathbf{x}=\mathbf{y}\) is given by

$$\begin{aligned} \mathbf{x}&=(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{k}}]}(K))^{-1}\mathbf{y}=(I_{N(q+1)}\otimes K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)^{-1})\mathbf{y}=\begin{bmatrix}K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)^{-1}{\mathbf{y}}_1\\ \vdots \\ K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)^{-1}{\mathbf{y}}_{N(q+1)}\end{bmatrix}, \end{aligned}$$
(3.4)

where \({\mathbf{y}}^T=[{\mathbf{y}}_1^T,\ldots ,{\mathbf{y}}_{N(q+1)}^T]\) and each \({\mathbf{y}}_i\) has length \(\bar{n}\). It is then clear that the computation of the solution \(\mathbf{x}\) is equivalent to solving the \(N(q+1)\) linear systems \(K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)\mathbf{x}_i=\mathbf{y}_i\), \(i=1,\ldots ,N(q+1)\). Note that the various \(\mathbf{x}_i\) can be computed in parallel as the computation of \(\mathbf{x}_i\) is independent of the computation of \(\mathbf{x}_j\) whenever \(i\ne j\).

4 Fast Solver for the Space-time IgA-DG System

From here on, we focus on the maximal smoothness case \({\varvec{k}}={\varvec{p}}-\mathbf{1}\), that is, the case corresponding to the classical IgA approach. For notational simplicity, we drop the subscript/superscript \({\varvec{k}}={\varvec{p}}-\mathbf{1}\), so that, for instance, the matrices \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{p}}-{\mathbf{1}}]}(K)\), \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}},{\varvec{p}}-{\mathbf{1}}]}(K)\), \(K_{{\varvec{n}},[{\varvec{p}},{\varvec{p}}-{\mathbf{1}}]}(K)\) will be denoted by \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\), \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\), \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\), respectively.

The solver suggested in Sect. 3 for a linear system with matrix \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\) is a PGMRES with preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\). According to (3.4), the solution of a linear system with matrix \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\), which is required at each PGMRES iteration, is equivalent to solving \(N(q+1)\) linear systems with matrix \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\). Fast solvers for \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\) that have been proposed in recent papers (see [20,21,22] and references therein) might be employed here. However, using an exact solver for \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\) is not what we have in mind. Indeed, it was discovered experimentally that the PGMRES method converges faster if the linear system with matrix \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\) occurring at each PGMRES iteration is solved inexactly. More precisely, when solving the \(N(q+1)\) linear systems with matrix \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\) occurring at each PGMRES iteration, it is enough to approximate their solutions by performing only a few standard multigrid iterations in order to achieve an excellent PGMRES run-time; and, in fact, only one standard multigrid iteration is sufficient. In view of these experimental discoveries, we propose to solve a linear system with matrix \(C_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\) in the following way.

figure a

As we shall see in the numerics of Sect. 6, the choice \(\mu =1\) yields the best performance of Algorithm 4.1. The proposed solver is not the PGMRES with preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\) because, at each iteration, the linear system associated with \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\) is not solved exactly. However, the solver is still a PGMRES with a different preconditioner \(\tilde{P}_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\). To see this, let MG be the iteration matrix of the multigrid method used in step 3 of Algorithm 4.1 for solving a linear system with matrix \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\). Recall that MG depends only on \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\) and not on the specific right-hand side of the system to solve. If the system to solve is \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\mathbf{x}_i=\mathbf{y}_i\), the approximate solution \(\tilde{\mathbf{x}}_i\) obtained after \(\mu \) multigrid iterations starting from the zero initial guess is given by

$$\begin{aligned} \tilde{\mathbf{x}}_i=(I_{\bar{n}}-MG^\mu )K_{{\varvec{n}},[{\varvec{p}}]}(K)^{-1}\mathbf{y}_i. \end{aligned}$$

Hence, the approximation \(\tilde{\mathbf{x}}\) computed by our solver for the exact solution (3.4) of the system \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K){\mathbf{x}}={\mathbf{y}}\) is given by

$$\begin{aligned} \tilde{\mathbf{x}}&=\begin{bmatrix}(I_{\bar{n}}-MG^\mu )K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)^{-1}{\mathbf{y}}_1\\ \vdots \\ (I_{\bar{n}}-MG^\mu )K_{{\varvec{n}},[{\varvec{p}},{\varvec{k}}]}(K)^{-1}{\mathbf{y}}_{N(q+1)}\end{bmatrix}=(I_{N(q+1)}\otimes (I_{\bar{n}}-MG^\mu )K_{{\varvec{n}},[{\varvec{p}}]}(K)^{-1}){\mathbf{y}}\\&=\tilde{P}_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)^{-1}{\mathbf{y}}, \end{aligned}$$

where

$$\begin{aligned} \tilde{P}_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)=I_{N(q+1)}\otimes K_{{\varvec{n}},[{\varvec{p}}]}(K)(I_{\bar{n}}-MG^\mu )^{-1}. \end{aligned}$$
(4.1)

In conclusion, the proposed solver is the PGMRES with preconditioner \(\tilde{P}_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\). From the expression of \(\tilde{P}_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\), we can also say that the proposed solver is a MG-GMRES, that is, a PGMRES with preconditioner given by a standard multigrid applied only in space. A more precise notation for this solver could be \(MG _{space }\)-GMRES, but for simplicity we just write MG-GMRES.

5 Fast Parallel Solver for the Space-time IgA-DG System

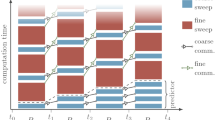
In Sect. 4, we have described the sequential version of the proposed solver. The same version is used also in the case where \(\rho \le N(q+1)\) processors are available, with the only difference that step 3 of Algorithm 4.1 is performed in parallel. In practice, \(s_i\) linear systems are assigned to the ith processor for \(i=1,\ldots ,\rho \), with \(s_1+\ldots +s_\rho =N(q+1)\) and \(s_1,\ldots ,s_\rho \) approximately equal to each other according to a load balancing principle. This is illustrated in Fig. 1 (left), which shows the row-wise partition of \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)=I_{N(q+1)}\otimes K_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\) corresponding to the distribution of the \(N(q+1)\) systems among \(\rho =N(q+1)-1\) processors.

Fig. 1
figure 1

Row-wise partitions of the preconditioner \(P_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)=I_{N(q+1)}\otimes \tilde{K}\) using \(\rho =N(q+1)-1\) processors (left) and \(\rho =N(q+1)+1\) processors (right) with \(N(q+1)=4\). For simplicity, we write “\(\tilde{K}\)” instead of “\(K_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K)\)”

Full size image

If \(\rho >N(q+1)\) processors are available, we use a slight modification of the solver, which is suited for parallel computation. As before, the modification only concerns step 3 of Algorithm 4.1. Since we now have more processors than systems to be solved, after assigning 1 processor to each system, we still have \(\rho -N(q+1)\) unused processors. Following again a load balancing principle, we distribute the unused processors among the \(N(q+1)\) systems, so that now one system can be shared between two or more different processors; see Fig. 1 (right). Suppose that the system \(K_{N,{\varvec{n}}}^{[q,{\varvec{p}}]}(K){\mathbf{x}}={\mathbf{y}}\) is shared between \(\sigma \) processors. The symmetric Gauss–Seidel post-smoothing iteration in step 3 of Algorithm 4.1 cannot be performed in parallel. Therefore, we replace it with its block-wise version. To be precise, we recall that the symmetric Gauss–Seidel iteration for a system with matrix \(E=L+U-D\) is just the preconditioned Richardson iteration with preconditioner \(M=LD^{-1}U\).Footnote 1 Its block-wise version in the case where we consider \(\sigma \) diagonal blocks \(E_1,\ldots ,E_\sigma \) of E is simply the preconditioned Richardson iteration with preconditioner \(M_1\oplus \cdots \oplus M_\sigma \), where \(M_i\) is the symmetric Gauss–Seidel preconditioner for \(E_i\) and \(M_1\oplus \cdots \oplus M_\sigma \) is the block diagonal matrix whose diagonal blocks are \(M_1,\ldots ,M_\sigma \). This block-wise version is suited for parallel computation in the case where \(\sigma \) processors are available.

6 Numerical Experiments: Iteration Count, Timing and Scaling

In this section, we illustrate through numerical experiments the performance of the proposed solver and we compare it to the performance of other benchmark parallel solvers, such as the PGMRES with block-wise ILU(0) preconditioner.

6.1 Implementation Details

For the numerics of this section, as well as throughout this paper, we used the C++ framework PETSc [5, 6] and the domain specific language Utopia [64] for the parallel linear algebra and solvers, and the Cray-MPICH compiler. For the assembly of high order finite elements, we used the PetIGA package [18]. A parallel tensor-product routine was implemented to assemble space-time matrices. Numerical experiments have been performed on the Cray XC40 nodes of the Piz Daint supercomputer of the Swiss national supercomputing centre (CSCS).Footnote 2 The used partition features 1813 computation nodes, each of which holds two 18-core Intel Xeon E5-2695v4 (2.10GHz) processors. We stress that the PETSc default row-wise partition follows a load balancing principle and, except in the trivial case \(\rho =N\), does not correspond to the row-wise partition described in Sect. 5; see Fig. 2. Therefore, the partition must be adjusted by the user. Alternatively, one can use a PETSc built-in class for sparse block matrices and specify the block size \((q+1)\bar{n}\).

Fig. 2
figure 2

The PETSc default row-wise partition does not account for the structure of the space-time problem; compare with Fig. 1

Full size image
Table 5 PGMRES iterations and run-time (using 64 cores) to solve the linear system (2.1) up to a precision of \(10^{-8}\), according to the experimental setting described in Sect. 6.2
Full size table

6.2 Experimental Setting

In the numerics of this section, we solve the linear system (2.1) arising from the choices \(d=2\), \(f(t,{\mathbf{x}})=1\), \(\mathrm{T}=1\), \({\varvec{n}}=(n,n)\), \({\varvec{p}}=(p,p)\), \({\varvec{k}}=(p-1,p-1)\). The basis functions \(\ell _{1,[q]},\ldots ,\ell _{q+1,[q]}\) are chosen as the Lagrange polynomials associated with the right Gauss–Radau nodes in \([-1,1]\). The values of \(K({\mathbf{x}})\), N, n, q, p are specified in each example. For each solver considered herein, we use the tolerance \(\varepsilon =10^{-8}\) and the PETSc default stopping criterion based on the preconditioned relative residual. Moreover, the PGMRES method is always applied with restart after 30 iterations as per PETSc default. Whenever we report the run-time of a solver, the time spent in I/O operations and matrix assembly is ignored. Run-times are always expressed in seconds. In all the tables below, the number of iterations needed by a given solver to converge within the tolerance \(\varepsilon =10^{-8}\) is reported in square brackets next to the corresponding run-time. Throughout this section, we use the following abbreviations for the solvers.

  • \(\boxed {\mathrm{ILU}(0)\text{- }\mathrm{GMRES}}\) PGMRES with preconditioner given by an ILU(0) factorization (ILU factorization with no fill-in) of the system matrix.

  • \(\boxed {\mathrm{MG}_{\mu ,\nu }^L\text{- }\mathrm{GMRES}}\) The proposed solver, as described in Sect. 4, with \(\mu \) multigrid (V-cycle) iterations applied to \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\). Each multigrid iteration involves \(\nu \) symmetric Gauss–Seidel post-smoothing steps at the finest level and 1 symmetric Gauss–Seidel post-smoothing step at the coarse levels. The choice \(\nu =1\) corresponds to our solver proposal. Different values of \(\nu \) are considered for comparison purposes. The superscript L denotes the number of multigrid levels.

  • \(\boxed {\mathrm{TMG}_{\mu ,\nu }^L\text{- }\mathrm{GMRES}}\) The same as MG\(_{\mu ,\nu }^L\)-GMRES, with the only difference that the multigrid iterations are performed with the telescopic option, thus giving rise to the telescopic multigrid (TMG) [23, 45]. This technique consists in reducing the number of processors used on the coarse levels and can be beneficial for the parallel multigrid performance. In the numerics of this section, we only reduced the number of processors used on the coarsest level to one fourth of the number of processors used at all other levels.

6.3 Iteration Count and Timing

Tables 5, 6, 7 illustrate the performance of the proposed solver in terms of number of iterations and run-time. It is clear from the tables that the best performance of the solver is obtained when applying to \(K_{{\varvec{n}},[{\varvec{p}}]}(K)\) a single multigrid iteration (\(\mu =1\)) with only one smoothing step at the finest level (\(\nu =1\)). Moreover, the solver is competitive with respect to the ILU(0)-GMRES. The worst performance of the solver with respect to the ILU(0)-GMRES is attained in Table 6, where the diffusion matrix \(K(x_1,x_2)\) is singular at \((x_1,x_2)=(0,0)\).

Table 6 PGMRES iterations and run-time (using 64 cores) to solve the linear system (2.1) up to a precision of \(10^{-8}\), according to the experimental setting described in Sect. 6.2
Full size table
Table 7 PGMRES iterations and run-time (using 64 cores) to solve the linear system (2.1) up to a precision of \(10^{-8}\), according to the experimental setting described in Sect. 6.2
Full size table
Table 8 Strong scaling: PGMRES iterations and run-time to solve the linear system (2.1) up to a precision of \(10^{-8}\), according to the experimental setting described in Sect. 6.2.
Full size table
Table 9 Space-time weak scaling: PGMRES iterations and run-time to solve the linear system (2.1) up to a precision of \(10^{-8}\), according to the experimental setting described in Sect. 6.2
Full size table

6.4 Scaling

In the scaling experiments, besides the multigrid already considered above, we also employ a TMG for performance reasons. To avoid memory bounds, we use at most 16 cores per node. From Table 8 and Fig. 3 we see that the proposed solver, especially when using the TMG option, shows a nearly optimal strong scaling with respect to the number of cores.Footnote 3 Table 9 and Fig. 4 illustrate the weak scaling properties of the proposed solver, which possesses a superior parallel efficiency with respect to the standard ILU(0) approach in terms of iteration count and run-time. For both solvers, however, the weak scaling is not ideal (constant run-time). This is due to the fact that N grows from 8 to 64 and both solvers are not robust with respect to N.

Fig. 3
figure 3

Graphical representation of the run-times reported in Table 8

Full size image
Fig. 4
figure 4

Graphical representation of the run-times reported in Table 9

Full size image

7 Non-rectangular Domain and Non-trivial Geometry

So far, the performance of the proposed solver has been illustrated for the diffusion problem (1.1) over the hypersquare \((0,1)^d\). However, no special difficulty arises if \((0,1)^d\) is replaced by a non-rectangular domain \(\Omega \) described (exactly) by a geometry map \({\mathbf{G}}:[0,1]^d\rightarrow \overline{\Omega }\) as per IgA paradigm. Indeed, as long as a tensor-product structure between space and time is maintained, the geometry map \({\mathbf{G}}\) acts as a reparameterization of \(\Omega \) through \((0,1)^d\), and the resulting discretization matrix is still given by (2.2)–(2.9) with the only difference that:

  • a factor \(|\mathrm{det}(J_{{\mathbf{G}}}({\mathbf{x}}))|\) should be included in the integrand of (2.5), where \(J_{{\mathbf{G}}}({\mathbf{x}})\) is the Jacobian matrix of \({\mathbf{G}}({\mathbf{x}})\);

  • the matrix \(K({\mathbf{x}})\) in (2.6) should be replaced by \(J_{{\mathbf{G}}}({\mathbf{x}})^{-1}K({\mathbf{G}}({\mathbf{x}}))J_{{\mathbf{G}}}({\mathbf{x}})^{-T}|\mathrm{det}(J_{{\mathbf{G}}}({\mathbf{x}}))|\).

In short, a change of domain from \((0,1)^d\) to \(\Omega \) essentially amounts to a mere change of diffusion matrix from K to \(J_{{\mathbf{G}}}^{-1}K({\mathbf{G}})J_{{\mathbf{G}}}^{-T}|\mathrm{det}(J_{{\mathbf{G}}})|\), which does not affect the performance of the proposed solver.

In Table 10, we validate the previous claim by testing the solver on the linear system arising from the space-time IgA-DG discretization of (1.1) in the case where \((0,1)^d\) is replaced by a non-rectangular domain \(\Omega \) described by a non-trivial geometry map \({\mathbf{G}}:[0,1]^d\rightarrow \overline{\Omega }\). The experimental setting is the same as in Sect. 6.2, with the only difference that \((0,1)^2\) is now replaced by a quarter of an annulus

$$\begin{aligned} \Omega =\{\mathbf{x}\in \mathbb R^2: r^2<x_1^2+x_2^2<R^2,\ x_1>0, \ x_2>0\},\qquad r=1,\qquad R=2, \end{aligned}$$
(7.1)

described by the geometry map \({\mathbf{G}}:[0,1]^2\rightarrow \overline{\Omega }\),

$$\begin{aligned} {\mathbf{G}}(\hat{\mathbf{x}})= {\left\{ \begin{array}{ll} x_1=[r+\hat{x}_1(R-r)]\cos \bigl (\frac{\pi }{2}\hat{x}_2\bigr ),\\ x_2=[r+\hat{x}_1(R-r)]\sin \bigl (\frac{\pi }{2}\hat{x}_2\bigr ), \end{array}\right. }\quad \hat{\mathbf{x}}\in [0,1]^2. \end{aligned}$$
(7.2)

We remark that the geometry map \({\mathbf{G}}\) is a common benchmark example in IgA; see, e.g., [20, 21].

Table 10 PGMRES iterations and run-time (using 64 cores) to solve, up to a precision of \(10^{-8}\), the linear system arising from the space-time IgA-DG discretization of (1.1) in the case where \((0,1)^d\) is replaced by the domain (7.1) described by the geometry map (7.2). The experimental setting is the same as in Sect. 6.2
Full size table

8 Conclusions

We have proposed a MG-GMRES solver for the space-time IgA-DG discretization of the diffusion problem (1.1). Through numerical experiments, we have illustrated the competitiveness of our proposal in terms of iteration count, run-time and parallel scaling. We have also shown its applicability to more general problems than (1.1) involving a non-rectangular domain \(\Omega \) and a non-trivial geometry map \({\mathbf{G}}\). To conclude, we remark that the proposed solver is highly flexible as it does not depend on the domain or the space-time discretization. It could therefore be applied to other space-time discretizations, as long as a tensor-product structure is maintained between space and time.