A High Order Accurate Finite Difference Method for the Drinfel’d–Sokolov–Wilson Equation

Abstract

We analyse numerically the periodic problem and the initial boundary value problem of the Korteweg-de Vries equation and the Drindfeld–Sokolov–Wilson equation using the summation-by-parts simultaneous-approximation-term method. Two sets of boundary conditions are derived for each equation of which stability is shown using the energy method. Numerical analysis is done when the solution interacts with the boundaries. Results show the benefit of higher order SBP operators.

1 Introduction

Solitons (or solitary waves) are special kinds of waves with a distinct set of features. Solitons arise due to a balance between nonlinear effects and dispersive effects. Thus, soliton solutions can be found for nonlinear dispersive partial differential equations (PDEs). Solitons are characterized by the following: (i) when propagating at a constant speed, the shape of the soliton remains unchanged; (ii) when a collision occurs between two solitons, both solitons emerge unchanged. In this paper, we study two different PDEs that both exhibit soliton solutions [7].

Originated in the nineteenth century, but it was not until the sixties when the Korteweg-de Vries (KdV) equation became a fruitful research object for scientists after they realized its apparent benefits in various applications [25]. The early-known soliton solution of the equation mimics an observed phenomenon of water waves induced by boat engines and initially called by its father the “Waves of Translation”. In modern application, the equation is most used to describe the translation of waves with weak dispersion, such as the waves in shallow water which have small amplitude and long wavelength; or the movement of internal flows in some special fluid [13]. It is also helpful in constructing various complex models such as plasma waves, shock waves, tornados, hydrodynamics. Since an exact solution can be derived, the KdV equation is usually useful to verify the accuracy of numerical methods.

An extension of the KdV equation is the coupled Drinfel’d–Sokolov–Wilson (DSW) equation. The DSW equation is a coupled system of two nonlinear dispersive PDEs, independently proposed by Drinfel’d and Sokolov [4] and Wilson [23]. Similarly to the KdV equation, it can be used to model the translation of shallow water waves. Interestingly, in addition to the regular soliton solutions found for the KdV equation, this system exhibits a new class of solutions referred to as “static solitons”, which are shaped differently but behave similarly to regular solitons [6]. In this paper, however, we focus on regular soliton solutions.

Considerable works on numerical approximations have been done for the KdV equation concerning both periodic and non-periodic boundary conditions (e.g., [2, 14]). Several attempts have also been made on the more complicated nonlinear system of DSW equation (e.g., [9, 22, 8, 24]), and its variations (e.g., [17]). However, the non-periodic initial boundary-value problem to this equation, to the best of our knowledge, has not been analysed.

Boundary treatment has long been known to pose a major challenge for time-dependent PDEs. A robust solution approach is to approximate the governing equation using Summation-By-Parts (SBP) operators [10] and impose boundary conditions with the Simultaneous Approximation Term (SAT) method [3], that we refer as the SBP-SAT method. A natural advantage of the SBP-SAT method is that it comes with well-controlled stability and high accuracy orders, which implies computational efficiency and the capability to capture more complex phenomena [1, 15, 21]. In a recent paper on nerve solitons [15], the method reveals its suitability for solving equations of the same type to this work. However, since our objective is a coupled system of nonlinear equations, boundary treatment remains a difficult problem since it is nontrivial to derive stable sets of boundary conditions and the corresponding numerically stable SBP-SAT schemes. Our main tool for the numerical analysis is the energy method (see [5, 21]). It is used to verify well-posedness or stability for continuous problems and discrete stability for numerical approximations. For time integration, the fourth-order explicit Runge–Kutta method is used.

In Sect. 2, we study stability properties of the KdV equation and derive stable SBP-SAT approximations for two sets of boundary conditions. The DSW system is investigated in Sect. 3. For the DSW equations, we propose two sets of boundary conditions and derive the corresponding stable SBP-SAT approximations. Tables containing convergence analysis are presented as well as efficiency plots. Finally, the obtained results are concluded in Sect. 4.

2 The Korteweg-de Vries Equation

We begin by looking at a scalar equation. The initial boundary-value problem to this equation has been analysed in [14]. This section is included to increase readability and to introduce necessary definitions that will be used throughout the paper.

The KdV equation in its most known form can be written as

$$\begin{aligned} u_t+6uu_x+u_{xxx} = 0, \end{aligned}$$

(1)

where the subscript notations denote the partial derivatives. The function u depending on the one-dimensional space variable x and the time variable t characterizes the elongation of the wave at point x and time t [25]. The second and third term on the left hand side of (1) is called the nonlinear term and the dispersion term, respectively.

Fig. 1

The soliton solution (2) of the KdV equation at two different time points with different choices of the wave speed

An exact solution of (1) is given by (cf, [13])

$$\begin{aligned} u_{\text{ exact }}(x,t) = \frac{c}{2} sech^2\left( \frac{\sqrt{c}(x-ct-a)}{2}\right) , \end{aligned}$$

(2)

where c is the wave speed and a is the starting offset. We use the above exact solution to construct the initial condition and calculate the errors for the efficiency analysis.

From (2), it is clear that to have a real-valued solution, the wave speed c must be a non-negative number. Figure 1 illustrates the soliton solution given by (2) for several positive values of c. It can be observed that with those choices of c, the soliton propagates to the right; and its amplitude is proportional to c. In other words, this family of solitary solutions to (1) with higher amplitude move faster than the ones with smaller amplitude.

2.1 Continuous Stability

Definition 1

Given two continuous functions u and v, a continuous inner product is defined as $(u,v) = \displaystyle \int _{x_l}^{x_r} u^Tvdx$ and its corresponding norm is $\left\Vert u\right\Vert ^2 = (u,u)= \displaystyle \int _{x_l}^{x_r} u^Tudx$.

To analyse continuous stability, we use the so-called “energy method”. Given an equation in the form $u_t = f(u, u_x, ...)$, we multiply both sides of the equation by $u^T$ and integrate by parts to obtain $(u,u_t)$. We then add the transpose $(u_t,u)$. For the continuous problem to be stable, it requires that there is no energy growth in time, $\frac{d}{dt} \left\Vert u\right\Vert ^2 < 0$ for homogeneous boundary conditions. In the context of nonlinear problems, no energy growth in time does not lead to well-posedness as existence, uniqueness and continual data dependence of the solution are not straightforwardly followed. However, considering linear or linearised problems, one could formulate this statement more formally as a sufficient condition for well-posedness, see [5, 12]. This property is usually investigated using the relation $\frac{d}{dt} \left\Vert u\right\Vert ^2 = (u_t, u) + (u, u_t)$. To simplify notation, we denote $u_l = u(x_l,t), u_r = u(x_r,t)$.

We write (1) in skew-symmetric form,

$$\begin{aligned} u_t + 3\alpha (u^2)_x + 6(1-\alpha )u u_x + u_{xxx} = 0, \end{aligned}$$

(3)

for some constant $\alpha$. Now we apply the energy method to (3),

$$\begin{aligned} (u,u_t)&= - (u,u_{xxx}) - 3\alpha (u,(u^2)_x) - 6(1 - \alpha )(u,u u_x) \\&= (u_{xxx},u) + 3\alpha (u_x,u^2) + 6(1-\alpha )((u^2)_x,u) + (u^2_x - 2u u_{xx})|^{x_r}_{x_l} \\&- ((3\alpha + 6(1 - \alpha ))u^3)|^{x_r}_{x_l}. \end{aligned}$$

Adding the transpose $(u_t,u)$ yields

$$\begin{aligned} \frac{d}{dt}\left\Vert u\right\Vert ^2&= (u^2_x - 2u u_{xx})|^{x_r}_{x_l} - ((3\alpha + 6(1-\alpha ))u^3)|^{x_r}_{x_l} + (6(1-\alpha ) - 3\alpha )((u^2)_x,u) \\&\qquad + (3\alpha - 6(1-\alpha ))(u_x,u^2). \end{aligned}$$

Setting $\alpha = \frac{2}{3}$ leads to

$$\begin{aligned} \frac{d}{dt}\left\Vert u\right\Vert ^2 = (u^2_x - 2u u_{xx} - 4u^3)|^{x_r}_{x_l}. \end{aligned}$$

(4)

For the periodic problem, RHS in (4) is identically zero, and (3) is thus stable at the continuous level.

2.2 Semi-discrete Stability

Consider a computational domain $[x_l, x_r] \subset {\mathbb {R}}$. We discretise the domain using m grid points $\{x_l \equiv x_1< x_2<\dots <x_m \equiv x_r \}$, where

$$\begin{aligned} x_i = x_l + (i-1)h,\quad h = \frac{x_r-x_l}{m-1},\quad i = 1, 2, ..., m. \end{aligned}$$

Definitions of the SBP operators used in this paper are restated in Definition 2 and 3. See [14] for other details on the SBP-SAT approximation technique. Let $e_1 = (1,0,\dots ,0)^T, e_m = (0,\dots ,0,1)^T$ be column vectors of length m.

Definition 2

A finite difference operator $D_1 = H^{-1}(Q+\frac{1}{2}B),B=-e_1e_1^T+e_me_m^T$ approximating $\frac{\partial }{\partial x}$ is said to be a first derivative SBP operator if the matrix H is symmetric positive definite and $Q + Q^T = 0$.

Definition 3

A finite difference operator $D_3 = H^{-1}(R+\frac{1}{2}d_{1;1}^Td_{1;1}-\frac{1}{2}d_{1;m}^Td_{1;m}-e_1d_{2;1}+e_md_{2;m})$ approximating $\frac{\partial ^3}{\partial x^3}$ is said to be a third derivative SBP operator if the matrix H is symmetric positive definite, $R + R^T = 0$, $d_{1;1},d_{1;m}$ approximate the first derivatives at the left and right boundary points, and $d_{2;1},d_{2;m}$ approximate the second derivatives at the left and right boundary points, respectively.

Definition 4

A discrete diagonal norm corresponding to the continuous norm given in Definition 1 is defined as $\left\Vert v\right\Vert _H^2 = v^THv.$

Analogously to the continuous case, the energy method can also be applied to an approximation in the form $v_t = F(v)$, where v is a discrete solution vector. We multiply both sides of the equation by $v^TH$ to obtain $v^THv_t$ and add the transpose $v_t^THv$. For the approximation to be stable, it requires that there is no energy growth in time, $\frac{d}{dt} \left\Vert v\right\Vert ^2 \le 0$, for homogeneous boundary data. The relation $\frac{d}{dt} \left\Vert v\right\Vert ^2 = v^THv_t + v_t^THv$ is usually utilised.

A consistent finite difference approximation of (1), ignoring the boundary treatment, can be written as

$$\begin{aligned} v_t + 2 D_1 \bar{v} v + 2\bar{v}D_1 v + D_3 v= 0, \end{aligned}$$

(5)

where the discrete function $v=[v_1,v_2,\dots ,v_m]$ approximates u on m grid points; the diagonal matrix

$$\begin{aligned} \bar{v} = \begin{bmatrix}v_1 &{} &{} &{} \\ {} &{} v_2 &{} &{}\\ {} &{} &{} \ddots &{}\\ &{} &{} &{} v_m\end{bmatrix}. \end{aligned}$$

By Definitions 2 and 3, the SBP operators $D_1, D_3$ mimic integration-by-part properties of the corresponding continuous differential operators which leads to the following discrete estimate

$$\begin{aligned} \frac{d}{dt}\left\Vert v\right\Vert _H^2 = -4v_m^3+4v_1^3+(d_{1;m}v)^2-(d_{1;1}v)^2-2v_md_{2;m}v + 2v_1d_{2;1}v, \end{aligned}$$

(6)

which exactly mimics (4).

Let ${\widetilde{D}}_1$ and ${\widetilde{D}}_3$ be periodic operators approximating $\frac{\partial }{\partial x}$ and $\frac{\partial ^3}{\partial x^3}$, respectively. The stencils of ${\widetilde{D}}_1$ and ${\widetilde{D}}_3$ can be constructed in a non-overlapping circular manner. For example, a second order periodic SBP operator approximating the first derivative $\frac{\partial }{\partial x}$ can be constructed as

$$\begin{aligned} {\widetilde{D}}_1 = {\widetilde{H}}^{-1} {\widetilde{Q}}, {\widetilde{H}} = hI, {\widetilde{Q}} = \begin{bmatrix}0&{}1/2&{} &{} &{}-1/2\\ -1/2&{}0&{} 1/2 &{} &{}\\ &{} -1/2 &{} \ddots &{} \ddots &{}\\ &{} &{} \ddots &{} \ddots &{} 1/2\\ 1/2&{} &{} &{} -1/2 &{} 0\end{bmatrix}, \end{aligned}$$

where the matrices ${\widetilde{D}}_1,{\widetilde{H}}, {\widetilde{Q}}$ and the identity matrix I are of size $(m-1)\times (m-1)$, and the solution vector is $v = (v_1, v_2, \dots , v_{m-1})$. The first component $v_1$ approximates v at $x_1 = x_l$ and the final component $x_{m-1}$ approximates v at $x_{m-1} = x_r - h$. A consistent periodic finite difference scheme approximating (1) reads

$$\begin{aligned} v_t + 2 {\widetilde{D}}_1 \bar{v} v + 2\bar{v}{\widetilde{D}}_1 v + {\widetilde{D}}_3 v= 0, \end{aligned}$$

(7)

The approximation (7) is stable due to the pure skew-symmetry of ${\widetilde{D}}_1, {\widetilde{D}}_3$.

Fig. 2

$l_{2}$-error as a function of the runtime. The approximate solution is evaluated at time $t_{\text {end}} = 5.$

An analysis of runtime-error efficiency is performed on the domain $[x_l, x_r] = [-20, 20]$ with $m=51, 101, 201, 301$ grid points, wave speed $c = 2$, time step size $\Delta t = \beta h^3$. The periodic scheme (7) is used . Notice that the time step scaling ${\mathcal {O}}(h^3)$ comes from the third derivative in (1). The result is shown in Fig. 2. For a fair comparison among different orders of accuracy, sharp estimates of the CFL number $\beta$ as shown in Table 1 are used. For each accuracy order, starting from a sufficiently large value, the CFL number $\beta$ is computed by gradually decreasing it until the solution becomes unstable.

Table 1 Sharp estimates of $\beta$ for second-, fourth- and sixth-order operators with $m=201$

A convergence analysis of the periodic scheme (7) is performed on the domain $[x_l, x_r] = [-20, 20]$ with m space grid points, the wave speed $c = 2$ and $\beta = 0.2$. The result is shown in Table 2. Let u be the vector containing nodal values of the exact solution. We denote the error vector as $e = u - v$, and the $l_2$-error as $l_2(e) = \left\Vert e\right\Vert _H = e^THe$. We calculate the convergence rate for two different number of grid points $m_1,m_2$ as

$$\begin{aligned} q = \log _{10}\left( \frac{l_2(e_{m_1})}{l_2(e_{m_2})}\right) /\log _{10}\left( \frac{m_2}{m_1}\right) . \end{aligned}$$

Table 2 $l_2$-norm of the global error and convergence rate for the KdV problem with periodic boundary conditions by different accuracy orders of SBP operators and number of grid points. Solutions are examined at $t=5$

2.2.1 A Set of Stable ‘Dirichlet like’ Boundary Conditions

The following set of boundary conditions yields a stable problem to (1)

$$\begin{aligned} {\left\{ \begin{array}{ll} u_l = g_l(t),\\ u_r = g_r(t),\\ (u_x)_r = {\tilde{g}}_r(t). \end{array}\right. } \end{aligned}$$

(8)

Applying these BCs to (4) leads to,

$$\begin{aligned} \frac{d}{dt}\left\Vert u\right\Vert ^2&= \tilde{g_r}^2(t) - 2g_r((u_{xx})_r + 2g_r^2) - (u_x)_l^2 + 2g_l((u_{xx})_l + 2g_l^2)\\&= \tilde{g_r}^2(t) - 2g_r (u_{xx})_r - 4g_r^3 - (u_x)_l^2 + 2g_l (u_{xx})_l + 4g_l^3. \end{aligned}$$

We see that with zero boundary data, $g_l(t) = g_r(t) = \tilde{g_r} = 0$, the problem (1), (8) is stable with $\dfrac{d}{dt}\left\Vert v\right\Vert _H^2 = 0$. However, since the energy growth is not exclusively bounded by boundary data, (8) is not strongly stable. We refer the readers to [5] for the definition of strong stability.

Lemma 1

A stable SBP-SAT approximation of (1) subjected to (8) reads

$$\begin{aligned} v_t&= -2 D_1 \bar{v} v - 2\bar{v}D_1 v - D_3 v\nonumber \\&\qquad + \tau _1 H^{-1}e_1v_1(v_1 - g_l(t)) + \tau _2 H^{-1}e_mv_m(v_m - g_r(t))\nonumber \\&\qquad + \tau _3H^{-1}d_{2;m}^T(v_m - g_r(t)) + \tau _4 H^{-1}d_{1;m}^T(d_{1;m}v - {{\tilde{g}}}_r(t)) + \tau _5 H^{-1}d_{2,1}^T(v_1 - g_l(t)). \end{aligned}$$

(9)

Proof

The energy method applied to (9) with zero boundary data yields the following energy estimate:

$$\begin{aligned} \frac{d}{dt}\left\Vert v\right\Vert _H^2&= -4v_m^3+4v_1^3+(d_{1;m}v)^2-(d_{1;1}v)^2 -2v_md_{2;m}v + 2v_1d_{2;1}v\\&\qquad + 2\tau _1 v_1^3 + 2\tau _2 v_m^3 + 2\tau _3v_m d_{2;m}v + 2\tau _4(d_{1;m})^2 + 2\tau _5 v_1 d_{2;1}v\\&= (4 + 2\tau _1)v_1^3 + (2\tau _2 - 4)v_m^3 + (2\tau _3 - 2)v_m d_{2;m}v\\&\qquad + (2\tau _4 + 1)(d_{1;m})^2 + (2\tau _5 + 2)v_1d_{2;1}v - (d_{1;1})^2. \end{aligned}$$

We choose the penalty terms $\tau _1 = -2, \tau _2 = 2, \tau _3 = 1, \tau _4 \le -\frac{1}{2}, \tau _5 = -1$ to obtain the final energy estimate

$$\begin{aligned} \frac{d}{dt}\left\Vert v\right\Vert _H^2 = -(d_{1;1})^2 + (2\tau _4 + 1)(d_{1;m})^2, \end{aligned}$$

(10)

which mimics the continuous stability estimate with homogeneous boundary conditions. $\square$

Snapshots at different time points of the boundary interaction with ‘physical’ homogeneous data $g_l(t) = g_r(t) = \tilde{g_r} = 0$ and the total energy over the course of interaction are shown in Fig. 3. The tests are performed with $m = 401$ grid points using 6th order SBP operators. As can be seen from Fig. 3, after hitting the right ‘wall’ at $t=10$, the solution is reflected and bounces back wave-like without losing energy. Not until $t=15$, the left-going waves hit and ‘go out of’ the left wall. For this test problem, we observe that there is no significant difference in the interaction behavior when using operators of different orders.

Fig. 3

Snapshots of a numerical solution to the KdV equation with the first set of boundary conditions during boundary interaction and the total energy over time

To verify the accuracy of the approximation (9), time-dependent analytic data is prescribed for $g_l(t), g_r(t), {{\tilde{g}}}_r(t)$ in (8), where $g_l(t), g_r(t)$ are taken directly from the analytic solution and

$$\begin{aligned} {{\tilde{g}}}_r(t) = \frac{\partial }{\partial x} (u_{\text {exact}}(t))\Big |_{x_r} =\left. -\frac{1}{2}c^{\frac{3}{2}}\tanh \left( \frac{\sqrt{c} (x-ct-a)}{2}\right) {{\,\mathrm{sech}\,}}^2\left( \frac{\sqrt{c} (a-ct-x)}{2}\right) \right| _{x_r}. \end{aligned}$$

The domain is narrowed to $[x_l, x_r] = [-4, 4]$ so that the solution is initialized non-zero at both boundaries, and the right boundary cuts the soliton in the middle at time $t = 2$, see Fig. 4. The free SAT penalty parameter $\tau _4$ is set to be -1. Other problem parameters are chosen same to the convergence study in Table 2. The result is shown in Table 3.

Fig. 4

Solution at final time $t=2$ for the convergence study in Table 3

Table 3 $l_2$-norm of the global error and convergence rate for the KdV problem with the first set of boundary conditions (8) by different accuracy orders of SBP operators and number of grid points. Solutions are examined at $t=2$

2.2.2 A Set of Strongly Stable Boundary Conditions

We show that the following set of boundary conditions yields a strongly stable problem subjected to (1),

$$\begin{aligned} {\left\{ \begin{array}{ll} 2(u_l+\left| u_l\right| ) u_l + (u_{xx})_l = g_l(t),\\ 2(u_r-\left| u_r\right| ) u_r + (u_{xx})_r = g_r(t),\\ (u_x)_r = {\tilde{g}}_r(t). \end{array}\right. } \end{aligned}$$

(11)

Denote $u^{\pm }=\frac{u\pm \left| u\right| }{2}$, hence $u=u^++u^-,u+\left| u\right| = 2u^+,u-\left| u\right| = 2u^-$ and $u^+-u^-=\left| u\right|$. The conditions (11) can then be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} 4u_l^+u_l + (u_{xx})_l = g_l(t),\\ 4u_r^-u_r + (u_{xx})_r = g_r(t),\\ (u_x)_r = {\tilde{g}}_r(t). \end{array}\right. } \end{aligned}$$

Recall that

$$\begin{aligned} \frac{d}{dt} \left\Vert u\right\Vert ^2 =&\, (u_x)_r^2-(u_x)_l^2-2u_r(2u_r^2+(u_{xx})_r)+2u_l(2u_l^2+(u_{xx})_l)\\ =&\;(u_x)_r^2-(u_x)_l^2-2u_r(2u_r(u_r^++u_r^-)+(u_{xx})_r)\\&\,+2u_l(2u_l(u_l^++u_l^-))+(u_{xx})_l). \end{aligned}$$

Inserting (11) and completing the squares leads to

$$\begin{aligned} \frac{d}{dt} \left\Vert u\right\Vert ^2&= {\tilde{g}}_r^2(t)-(u_x)_l^2-2u_r(2u_ru_r^+-2u_ru_r^-+g_r)+2u_l(-2u_lu_l^++2u_lu_l^-+g_l)\\&={\tilde{g}}_r^2(t)-(u_x)_l^2-2u_r(2u_r\left| u_r\right| +g_r)+2u_l(-2u_l\left| u_l\right| +g_l)\\&={\tilde{g}}_r^2(t)-(u_x)_l^2-\left| u_r\right| \left( 4u_r^2+2u_r\frac{g_r}{\left| u_r\right| }\right) -\left| u_l\right| \left( 4u_l^2-2u_l\frac{g_l}{\left| u_l\right| }\right) \\&={\tilde{g}}_r^2(t)-(u_x)_l^2-\left| u_r\right| \left( 2u_r+\frac{g_r}{2\left| u_r\right| }\right) ^2+\frac{g_r^2}{4\left| u_r\right| }\\&-\left| u_l\right| \left( 2u_l-\frac{g_l}{2\left| u_l\right| }\right) ^2+\frac{g_l^2}{4\left| u_l\right| }. \end{aligned}$$

It is clear that all the terms on the right hand side are either bounded or less than or equal to zero when $\left| u_l\right| \gg 0,\left| u_r\right| \gg 0$. However, even if $\left| u_l\right| \longrightarrow 0$ we can still control $\lim _{\left| u_l\right| \longrightarrow 0}-\left| u_l\right| \left( 2u_l-\frac{g_l}{2\left| u_l\right| }\right) ^2+\frac{g_l^2}{4\left| u_l\right| } = 0$. Similar argument can be applied for $u_r$ to deduce that the right hand side is still bounded. Therefore, it is sufficient to conclude that (11) is a set of strongly stable boundary conditions for (1).

We show that there exists real numbers $\tau _l, \tau _r, \sigma _r$ such that the following SBP-SAT approximation of (1) subjected to (11) is stable,

$$\begin{aligned} v_t+2D_1\bar{v}v + 2\bar{v}D_1v + D_3v =&\; \tau _lH^{-1}e_1\big (2(v_1+\left| v_1\right| ) v_1 + d_{2;1}v - g_l\big )\nonumber \\&+\tau _r H^{-1}e_m\big ( 2(v_m-\left| v_m\right| ) v_m + d_{2;m}v - g_r \big )\nonumber \\&+\sigma _r H^{-1}d_{1;m}^T \big (d_{1;m}v - {\tilde{g}}_r\big ). \end{aligned}$$

(12)

Lemma 2

Equation (12) is strongly stable if

$$\begin{aligned} \tau _l = -1; \tau _r = 1; \sigma _r < -\frac{1}{2}. \end{aligned}$$

Proof

The energy method applied to (12) leads to,

$$\begin{aligned} \frac{d}{dt} \left\Vert v\right\Vert _H^2 =&\; -4v_m^3+4v_1^3+(d_{1;m}v)^2-(d_{1;1}v)^2-2v_md_{2;m}v + 2v_1d_{2;1}v.\\&+2\tau _lv_1(4v_1^+v_1+d_{2;1}v-g_l)+2\tau _rv_m(4v_m^-v_m+d_{2;m}v-g_r)\\&+2\sigma _rd_{1;m}v(d_{1;m}v-{\tilde{g}}_r)\\ =&\; -4v_m^2(v_m^++v_m^--2\tau _rv_m^-)+2\tau _lv_1(d_{2;1}v-g_l)\\&+4v_1^2(v_1^++v_1^-+2\tau _lv_1^+)+2\tau _rv_m(d_{2;m}v-g_r)\\&-(d_{1;1}v)^2+(2\sigma _r+1)(d_{1;m}v)^2-2\sigma _rd_{1;m}v{\tilde{g}}_r\\&-2v_md_{2;m}v+2v_1d_{2;1}v. \end{aligned}$$

To cancel the cubic terms and the terms involving second derivatives, we choose $\tau _l=-1,\tau _r=1$. The equation becomes

$$\begin{aligned} \frac{d}{dt} \left\Vert v\right\Vert _H^2 =&\;-4v_m^2\left| v_m\right| -4v_1^2\left| v_1\right| +2v_1g_l-2v_mg_r\\ \nonumber&-(d_{1;1}v)^2+(2\sigma _r+1)(d_{1;m}v)^2-2\sigma _r{\tilde{g}}_rd_{1;m}v. \end{aligned}$$

(13)

If $2\sigma _r+1 = 0$, a desirable estimate cannot be obtained because ${\tilde{g}}_rd_{1;m}v$ is not bounded. When $2\sigma _r+1 \ne 0$, we have

$$\begin{aligned} \frac{d}{dt} \left\Vert v\right\Vert _H^2 =&-\left| v_m\right| \left( 2v_m+\frac{g_r}{2\left| v_m\right| }\right) ^2+\frac{g_r^2}{4\left| v_m\right| }-\left| v_1\right| \left( 2v_1-\frac{g_l}{2\left| v_1\right| }\right) ^2+\frac{g_l^2}{4\left| v_1\right| }\\&-(d_{1;1}v)^2+(2\sigma _r+1)\left( d_{1;m}v-\frac{\sigma _r{\tilde{g}}_r}{2\sigma _r+1}\right) ^2-\frac{\sigma _r^2{\tilde{g}}_r^2}{2\sigma _r+1}. \end{aligned}$$

It can be seen that with $2\sigma _r+1 < 0$, all terms of the above estimate are either bounded or non-positive. $\square$

Snapshots at different time points of the boundary interaction with homogeneous data $g_l(t) = g_r(t) = \tilde{g_r} = 0$ and the total energy over the course of interaction are shown in Fig. 5. The tests are performed with $m = 401$ grid points using 6th order SBP operators. The behavior is fundamentally different from the previously derived boundary conditions (8). Most of the solution is absorbed by the right wall, while the small remaining part is reflected. The energy decreases smoothly in time in contrast to the fluctuating downtrends in Fig. 3 with the boundary conditions (8). There is also no difference in the interaction behaviour between operators of different orders.

Fig. 5

Snapshots of a numerical solution to the KdV equation with the second set of boundary conditions during boundary interaction and the total energy over time

We observe same interior and boundary accuracy properties for this set of boundary conditions as reported in Table 3.

3 The Coupled Drinfeld–Sokolov–Wilson Equation

We consider the following system of nonlinear equations,

$$\begin{aligned}&u_t + 3v v_x = 0,\\ \nonumber&v_t + v u_x + 2u v_x + 2v_{xxx} = 0. \end{aligned}$$

(14)

An exact solution of (14) is given as follows [26],

$$\begin{aligned}&u_{\text{ exact }}(x,t) = \dfrac{3c}{2}{{\,\mathrm{sech}\,}}^2\left( \sqrt{\dfrac{c}{2}}(x-ct-a)\right) ,\\&v_{\text{ exact }}(x,t) = c{{\,\mathrm{sech}\,}}\left( \sqrt{\dfrac{c}{2}}(x-ct-a) \right) , \end{aligned}$$

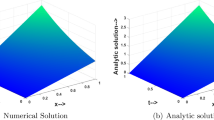
where c is the wave speed and a is the starting offset. An illustration is given in Fig. 6 showing the soliton solution at two different time points.

Fig. 6

Soliton solution at different time points with parameters $c = 2,a=0$

Unlike the Korteweg-de Vries equation, a similar technique to perform a skew-symmetric splitting does not straightforwardly give a nonlinear estimate. Instead, we define a linearised problem to (14) as

$$\begin{aligned}&u_t + 3\bar{v} v_x = 0,\nonumber \\&\quad v_t + \bar{v} u_x + 2\bar{u} v_x + 2v_{xxx} = 0, \end{aligned}$$

(15)

where $\bar{u}$ and $\bar{v}$ are constant fields, or frozen coefficients [20]. Applying the energy method leads to

$$\begin{aligned} (u,u_t) =&-3\bar{v}uv \Big |_{x_l}^{x_r}+3\bar{v}(u_x,v)\\ (u_t,u) =&-3\bar{v}(v_x,u)\\ (v,v_t) =&(-\bar{v}uv-2\bar{u}v^2-4vv_{xx}+2v_x^2)\Big |_{x_l}^{x_r}+\bar{v}(v_x,u)+2\bar{u}(v_x,v)+2(v_{xxx},v)\\ (v_t,v) =&-\bar{v}(u_x,v)-2\bar{u}(v_x,v)-2(v_{xxx},v). \end{aligned}$$

We thus can obtain the energy estimate for each component.

$$\begin{aligned} \dfrac{d}{dt} \left\Vert u\right\Vert ^2 =&-3\bar{v}uv\Big |_{x_l}^{x_r}+3\bar{v}(u_x,v)-3\bar{v}(v_x,u)\\ \dfrac{d}{dt} \left\Vert v\right\Vert ^2 =&(-\bar{v}uv-2\bar{u}v^2-4vv_{xx}+2v_x^2)\Big |_{x_l}^{x_r}+\bar{v}(v_x,u)-\bar{v}(u_x,v) \end{aligned}$$

It can be shown that in the standard norm $\left\Vert u\right\Vert ^2+\left\Vert v\right\Vert ^2$, we cannot obtain an upper bound in the energy since besides the boundary terms, the remainder terms cannot be controlled. However, in the modified norm $\dfrac{1}{3}\left\Vert u\right\Vert ^2+\left\Vert v\right\Vert ^2$, it is possible to obtain an estimate,

$$\begin{aligned} \begin{aligned} \dfrac{d}{dt} \left( \dfrac{1}{3}\left\Vert u\right\Vert ^2+\left\Vert v\right\Vert ^2\right)&= (-2\bar{v}uv-2\bar{u}v^2-4vv_{xx}+2v_x^2)\Big |_{x_l}^{x_r}\\&= \left. \begin{bmatrix}u\\ v\\ v_x\\ v_{xx}\end{bmatrix}^T\begin{bmatrix}0&{}-\bar{v}&{}0&{}0\\ bar{v}&{}-2\bar{u}&{}0&{}-2\\ 0&{}0&{}2&{}0\\ 0&{}-2&{}0&{}0\end{bmatrix}\begin{bmatrix}u\\ v\\ v_x\\ v_{xx}\end{bmatrix}\right| ^{x_r}_{x_l}. \end{aligned} \end{aligned}$$

(16)

At continuous level, (16) shows that the periodic linearised problem (15) is well-posed. In this paper, we refer to this property of the original nonlinear problem (14) as it is “linearly stable”. Considering zero boundary data, the four-by-four matrix in (16) has three eigenvalues. Therefore, the correct number of boundary conditions is three.

A consistent SBP approximation to the linearised problem (15) reads

$$\begin{aligned}&u_t = -3\bar{V}D_1v,\nonumber \\&v_t = -\bar{V}D_1u-2\bar{U}D_1v-2D_3v, \end{aligned}$$

(17)

where u, v are the discrete variables (here we use the same notation as the corresponding continuous variables) and $\bar{U}$, $\bar{V}$ denote the square diagonal constant matrices of which diagonals contain the discrete analogues of frozen coefficients ${\bar{u}}$ and ${\bar{v}}$, respectively. In that case, we call (17) a “linearised scheme” which we utilise to derive a discrete $l_2$ estimate. The corresponding “nonlinear scheme” to the original problem (14) is then obtained by replacing $\bar{U}$, $\bar{V}$ with the discrete variables u, v in the diagonals.

We discuss stability of the nonlinear problem (14) and the linearised scheme (17) in the following remark.

Remark

Assuming smoothness of u, v, [20] shows that discrete stability of the linearised scheme and the nonlinear scheme are equivalent. Because our main focus is to derive provably stable discretisations, we omit the details on nonlinear well-posedness and nonlinear stability and refer the interested readers to [18] and [11]. The main argument to include here is that under the smoothness assumption, studying the linearised scheme can help guide the discrete boundary treatment of the nonlinear scheme (17). It is important to highlight that the approach of deriving nonlinear schemes through analysing the corresponding linearised problem has been successful for systems such as the Navier-Stokes equations, compressible Euler equations, and shallow water equations [12, 16, 19].

Applying the energy method to (17) gives

$$\begin{aligned} u^THu_t =&\;-3u^T\bar{V}\left( Q+\frac{1}{2}B\right) v,\\ u_t^THu =&-3v^T\left( Q^T+\frac{1}{2}B\right) \bar{V}u,\\ v^THv_t =&-v^T\bar{V}\left( Q+\frac{1}{2}B\right) u-2v^T\bar{U}\left( Q+\frac{1}{2}B\right) v-2v^THD_3v,\\ v_t^THv =&-u^T\left( Q^T+\frac{1}{2}B\right) \bar{V}v - 2v^T\left( Q^T+\frac{1}{2}B\right) \bar{U}v - 2(D_3v)^THv, \end{aligned}$$

where the sum of the third derivatives can be simplified as

$$\begin{aligned} v^THD_3v + (D_3v)^THv&= (d_{1;1}v)^2-(d_{1;m}v)^2-2v_1d_{2;1}v+2v_md_{2;m}v. \end{aligned}$$

Analogously to the continuous estimate (16), we have the discrete energy estimate

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\left( \frac{1}{3}\left\Vert u\right\Vert _H^2+\left\Vert v\right\Vert _H^2\right) =&-2\bar{v}_m u_m v_m + 2 \bar{v}_1 u_1 v_1 - 2 \bar{u}_m v_m^2 + 2\bar{u}_1v_1^2\\&+2(d_{1;m}v)^2-2(d_{1;1}v)^2-4v_md_{2;m}v+4v_1d_{2;1}v. \end{aligned} \end{aligned}$$

(18)

This estimate shows that in the modified norm, the linearised scheme (17) approximating the periodic problem (15) is stable.

The discrete error is calculated as $e = \begin{bmatrix}u\\ v\end{bmatrix}-\begin{bmatrix}u_{\text{ exact }}\\ v_{\text{ exact }}\end{bmatrix}.$ A convergence study of the periodic nonlinear version of (17) is performed on the domain $[x_l, x_r] = [-30, 30]$ with m space grid points, the wave speed $c = 2$, time step size $\Delta t = 0.2 h^3$ where $h = (x_r-x_l)/m$. The result is shown in Table 4.

Table 4 $l_2$-norm of the global error and convergence rate for the DSW problem with periodic boundary conditions by different accuracy orders of SBP operators and number of grid points. Solutions are examined at $t=5$

Fig. 7

$l_{2}$-error as a function of the runtime. The approximate solution is evaluated at time $t_{\text {end}} = 5.$

An analysis of runtime-error efficiency is performed on the same domain and problem settings with different number of grid points. The result is shown in Fig. 7. For a fair comparison among different orders of accuracy, sharp estimates of the CFL number $\beta$, as shown in Table 5, are used. For each accuracy order, starting from a sufficiently large value, the CFL number $\beta$ is computed by gradually decreasing it until the solution becomes unstable.

Table 5 Sharp estimates of the CFL condition for $m = 201$

3.1 A Set of Stable ‘Dirichlet like’ Boundary Conditions

A set of linearly well-posed boundary conditions is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} v_l = g_l(t),\\ v_r = g_r(t),\\ (v_{x})_r = {\tilde{g}}_r(t). \end{array}\right. } \end{aligned}$$

(19)

A consistent SBP-SAT approximation of (14) subjected to the boundary conditions (19) reads

$$\begin{aligned} \begin{aligned} u_t =&-3\bar{V}D_1v + \tau _1H^{-1}e_1{\bar{v}}_1(v_1-g_l(t)) + \tau _2H^{-1}e_m{\bar{v}}_m(v_m-g_r(t))\\ v_t =&-\bar{V}D_1u-2\bar{U}D_1v-2D_3v\\&+ \tau _3H^{-1}e_1{\bar{u}}_1(v_1-g_l(t)) + \tau _4H^{-1}e_m{\bar{u}}_m(v_m-g_r(t))\\&+\sigma _1H^{-1}d_{2;m}^T(v_m-g_r(t))+\sigma _2H^{-1}d_{1;m}^T(d_{1;m}v-{\tilde{g}}_r(t))\\&+ \sigma _3H^{-1}d_{2;1}^T(v_1-g_l(t)). \end{aligned} \end{aligned}$$

(20)

We discuss stability of (20) in the following lemma.

Lemma 3

The approximation (20) is stable if

$$\begin{aligned} \tau _1 = -3, \tau _2 = 3, \tau _3 = -1, \tau _4 = 1, \sigma _1 = 2, \sigma _2 \le -1, \sigma _3 = -2. \end{aligned}$$

Proof

Applying the energy method to (20), we have

$$\begin{aligned} u^THu_t =&\;-3u^T\bar{v}\left( Q+\frac{1}{2}B\right) v+\tau _1u_1v_1^2+\tau _2u_mv_m^2; \end{aligned}$$

$$\begin{aligned} u_t^THu&= -3v^T\left( Q^T+\frac{1}{2}B\right) \bar{v}u + \tau _1u_1v_1^2+\tau _2u_mv_m^2; \end{aligned}$$

$$\begin{aligned} v^THv_t =&-v^T\bar{v}\left( Q+\frac{1}{2}B\right) u-2V^T\bar{u}\left( Q+\frac{1}{2}B\right) v-2v^THD_3v\\&+\sigma _1v_md_{2;m}v+\sigma _2(d_mv)^2+\sigma _3v_1d_{2;1}v;\\ v_t^THv =&-u^T\left( Q^T+\frac{1}{2}B\right) \bar{v}v - 2v^T\left( Q^T+\frac{1}{2}B\right) \bar{u}v - 2(D_3v)^THv\\&+\sigma _1v_md_{2;m}v+\sigma _2(d_mv)^2+\sigma _3v_1d_{2;1}v. \end{aligned}$$

Therefore, we have the discrete energy estimate

$$\begin{aligned} \frac{d}{dt}\left( \frac{1}{3}\left\Vert u\right\Vert _H^2+\left\Vert v\right\Vert _H^2\right) =&-2\bar{v}_m u_m v_m + 2 \bar{v}_1 u_1 v_1 - 2 \bar{u}_m v_m^2 + 2\bar{u}_1v_1^2\\&+2(d_{1;m}v)^2-2(d_{1;1}v)^2-4v_md_{2;m}v+4v_1d_{2;1}v\\&+\frac{2}{3}\tau _1{\bar{v}}_1u_1v_1+\frac{2}{3}\tau _2{\bar{v}}_mu_mv_m+2\tau _3{\bar{u}}_1v_1^2+2\tau _4{\bar{u}}_mv_m^2\\&+2\sigma _1v_md_{2;m}v+2\sigma _2(d_mv)^2+2\sigma _3v_1d_{2;1}v. \end{aligned}$$

We choose the penalty parameters $\tau _1 = -3, \tau _2=3, \tau _3 = -1, \tau _4 = 1, \sigma _1=2,\sigma _2 \le -1,\sigma _3=-2$ to obtain the final boundary terms

$$\begin{aligned} \frac{d}{dt}\left( \frac{1}{3}\left\Vert u\right\Vert _H^2+\left\Vert v\right\Vert _H^2\right) = -2(d_{1;1}v)^2+2(1+\sigma _2)(d_{1;m}v)^2 \le 0. \end{aligned}$$

Therefore, with the above choice of parameters, the linear approximation (20) is stable. $\square$

Fig. 8

Snapshot after boundary interaction of a numerical solution to the DSW equations with the boundary conditions (19) and the total energy over time using $m=201$ grid points and SBP operators of different orders

Snapshots at $t=20$ of the boundary interaction and the total energy over the course of interaction are shown in Fig. 8. The numerical experiment is performed on the corresponding nonlinear scheme to (20) with SBP operators of 2nd, 4th and 6th order using the same number of grid points $m=201$. Due to the boundary condition $v_l = v_r = (v_x)_r =0$, a stationary profile after the interaction appears near the right boundary. In Fig. 8, we cut off showing this stationary pulse because the difference in the interior behavior among different orders is more interesting. The less accurate second order operators generate spurious oscillations which are amplified from the error in capturing the boundary interaction. This so-called “$\pi$-mode” pollutes the solution and does not disappear with grid refinement. Though the energy grows after the interaction at around $t=15$, it is still bounded in long time simulation as seen in the energy plot (Fig. 8b). The energy plots (Fig. 8b, d, f) numerically verify that our boundary treatment is stable. Notice that the energy jump for 4th and 6th order operators are of lower magnitude.

Similar convergence study after boundary interaction is performed in $[x_l, x_r] = [-4,4]$. The boundary data $g_l(t), g_r(t)$ in (19) (20) is derived from the exact solution $v_{\text {exact}}$, and

$$\begin{aligned} {{\tilde{g}}}_r(t) =\left. -\frac{1}{2}c^{\frac{3}{2}}\tanh \left( \frac{\sqrt{c} (x-ct-a)}{\sqrt{2}}\right) {{\,\mathrm{sech}\,}}\left( \frac{\sqrt{c} (x-ct-a)}{\sqrt{2}}\right) \right| _{x_r}. \end{aligned}$$

Note again that at the final time $t=2$, the right boundary cuts the soliton profile in the middle, see Fig. 9. The free parameter $\sigma _2$ is set to be $-2$. The convergence rates are reported in Table 6. Because the boundary conditions (19) only specify the analytic solution to v, optimal rates can be seen for the v component, but degraded rates are obtained on the u component.

Fig. 9

Solution at final time $t=2$ for the convergence study in Table 6

Table 6 $l_2$-norm of the global error and convergence rate for the KdV problem with the first set of boundary conditions (19) by different accuracy orders of SBP operators and number of grid points. The upper part shows error on the u component and the lower part shows error on the v component. Solutions are examined at $t=2$

3.2 Characteristic Boundary Conditions

We denote BT the boundary terms given by (16). Recall that $\text{ BT } = w^T M w\Big |_{x_l}^{x_r}$, where

$$\begin{aligned} w = (u,v,v_x,v_{xx})^T, M = \begin{bmatrix}0&{}-{\bar{v}}&{}0&{}0\\ -{\bar{v}}&{}-2\bar{u}&{}0&{}-2\\ 0&{}0&{}2&{}0\\ 0&{}-2&{}0&{}0\end{bmatrix}. \end{aligned}$$

Since M is symmetric, it can be diagonalized as

$$\begin{aligned} M = S \Lambda S^T, \end{aligned}$$

where

$$\begin{aligned} \Lambda =\begin{bmatrix}0&{}0&{}0&{}0\\ 0&{}2&{}0&{}0\\ 0&{}0&{}\sqrt{{\bar{u}}^2+{\bar{v}}^2+4}-{\bar{u}}&{}0\\ 0&{}0&{}0&{}-\sqrt{{\bar{u}}^2+{\bar{v}}^2+4}-{\bar{u}}\end{bmatrix}; \end{aligned}$$

and

$$\begin{aligned} S=\begin{bmatrix}\dfrac{-2}{\bar{v}\sqrt{1+\frac{4}{\bar{v}^2}}}&{}0&{}\dfrac{\bar{v}}{\sqrt{2(\bar{u}^2+\bar{v}^2+4-\bar{u}\sqrt{\bar{u}^2+\bar{v}^2+4})}}&{}\dfrac{\bar{v}}{\sqrt{2(\bar{u}^2+\bar{v}^2+4+\bar{u}\sqrt{\bar{u}^2+\bar{v}^2+4})}}\\ 0&{}0&{}\dfrac{\bar{u}-\sqrt{\bar{u}^2+\bar{v}^2+4}}{\sqrt{2(\bar{u}^2+\bar{v}^2+4-\bar{u}\sqrt{\bar{u}^2+\bar{v}^2+4})}}&{}\dfrac{\bar{u}+\sqrt{\bar{u}^2+\bar{v}^2+4}}{\sqrt{2(\bar{u}^2+\bar{v}^2+4+\bar{u}\sqrt{\bar{u}^2+\bar{v}^2+4})}}\\ 0&{}1&{}0&{}0\\ \dfrac{1}{\sqrt{1+\frac{4}{\bar{v}^2}}}&{}0&{}\dfrac{2}{\sqrt{2(\bar{u}^2+\bar{v}^2+4-\bar{u}\sqrt{\bar{u}^2+\bar{v}^2+4})}}&{}\dfrac{2}{\sqrt{2(\bar{u}^2+\bar{v}^2+4+\bar{u}\sqrt{\bar{u}^2+\bar{v}^2+4})}}\end{bmatrix}, \end{aligned}$$

which satisfies $S^T \equiv S^{-1}$.

Let $\Lambda ^{+} = \dfrac{\Lambda +\left| \Lambda \right| }{2},\Lambda ^{-} = \dfrac{\Lambda -\left| \Lambda \right| }{2},M^+=S \Lambda ^+ S^T,M^-=S \Lambda ^- S^T$. It is clear that $\Lambda = \Lambda ^++\Lambda ^-$,$M = M^++M^-$, and $M^+,M^-$ are symmetric matrices $(M^+)^T=(S\Lambda ^+S^T)^T=S\Lambda ^+S^T=M^+$. A set of characteristic boundary conditions is

$$\begin{aligned} {\left\{ \begin{array}{ll} M^+w = M^+g_r(t), \text{ at } x = x_r\\ M^-w = M^-g_l(t), \text{ at } x = x_l \end{array}\right. } \end{aligned}$$

(21)

where $g_r(t), g_l(t)$ are $4\times 1$ vectors of time-dependent real functions.

We apply (21) to the boundary term given by (18) to obtain the continuous estimate

$$\begin{aligned} \begin{aligned} \text{ BT }&= w^TM^-w \Big |^{x_r}_{x_l} + w^TM^+w \Big |^{x_r}_{x_l}\\&= w^TM^-w\Big |^{x_r} - g_l^TM^-g_l + g_r^TM^+g_r - w^TM^+w \Big |^{x_l} , \end{aligned} \end{aligned}$$

(22)

which contains the terms that are either bounded by given data or non-positive. Therefore, (21) is a set of strongly well-posed boundary conditions for the linearised problem (15).

We prove that the following SBP-SAT approximation of (14) is stable.

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t = -3\bar{V}D_1v\\ -3H^{-1}\begin{bmatrix}e_m&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\end{bmatrix}M_r^+(w_m-g_r)+3H^{-1}\begin{bmatrix}e_1&{}{\mathbf {0}}&{}{\mathbf {0}}&{}{\mathbf {0}}\end{bmatrix}M_l^-(w_1-g_l)\\ v_t = -\bar{V}D_1u-2\bar{U}D_1v-2D_3v\\ -H^{-1}\begin{bmatrix}{\mathbf {0}}&{}e_m&{}d_{1;m}^T&{}d_{2;m}^T\end{bmatrix}M_r^+(w_m-g_r)+H^{-1}\begin{bmatrix}{\mathbf {0}}&e_1&d_{1;1}^T&d_{2;1}^T\end{bmatrix}M_l^-(w_1-g_l), \end{array}\right. } \end{aligned}$$

(23)

where ${\mathbf {0}}$ is an $m\times 1$ vector of zeros; $w_1 = \begin{bmatrix}u_1\\ v_1\\ d_{1;1}v\\ d_{2;1}v\end{bmatrix},w_m = \begin{bmatrix}u_m\\ v_m\\ d_{1;m}v\\ d_{2;m}v\end{bmatrix}$; $M_l^-, M_r^+$ are the frozen coefficient matrices $M^-, M^+$ with the substitution of $(u_1, v_1)$ and $(u_m, v_m)$, respectively.

Using the energy method,

$$\begin{aligned} u^THu_t&= \, -3u^T\bar{V}\left( Q+\frac{1}{2}B\right) v-3[u_m,0,0,0]M_r^+(w_m-g_r)\\&\quad +3[u_1,0,0,0]M_l^-(w_1-g_l). \end{aligned}$$

Because $M^+, M^-$ are symmetric,

$$\begin{aligned} u_t^THu&= -3v^T\left( Q^T+\frac{1}{2}B\right) \bar{V}u-3(w_m-g_r)^TM_r^+\begin{bmatrix}u_m\\ 0\\ 0\\ 0\end{bmatrix}+3(w_1-g_l)^TM_l^-\begin{bmatrix}u_1\\ 0\\ 0\\ 0\end{bmatrix};\\ v^THv_t =&-v^T\bar{V}\left( Q+\frac{1}{2}B\right) u-2v^T\bar{U}\left( Q+\frac{1}{2}B\right) v-2v^THD_3v\\&-[0,v_m,d_{1;m}v,d_{2;m}v]M_r^+(w_m-g_r)+[0,v_1,d_{1;1}v,d_{2;1}v)M_l^-(w_1-g_l);\\ v_t^THv =&-u^T\left( Q^T+\frac{1}{2}B\right) \bar{V}v - 2v^T(Q^T+\frac{1}{2}B)\bar{U}v - 2(D_3v)^THv\\&-(w_m-g_r)^TM_r^+\begin{bmatrix}0\\ v_m\\ d_{1;m}v\\ d_{2;m}v\end{bmatrix}+(w_1-g_l)^TM_l^-\begin{bmatrix}0\\ v_1\\ d_{1;1}v\\ d_{2;1}v\end{bmatrix}. \end{aligned}$$

Therefore, we have the semi-discrete energy estimate

$$\begin{aligned} \frac{d}{dt}\left( \frac{1}{3}\left\Vert u\right\Vert _H^2+\left\Vert v\right\Vert _H^2\right) =&\; w_m^TM_r^-w_m-w_1^TM_l^-w_1+w_m^TM_r^+w_m-w_1^TM_l^+w_1\\&-w_m^TM_r^+(w_m-g_r)+w_1^TM_l^-(w_1-g_l)\\&-(w_m-g_r)^TM_r^+w_m+(w_1-g_l)^TM_l^-w_1\\ =&\; w_m^TM_r^-w_m-w_1^TM_l^+w_1+g_r^TM_r^+g_r-g_l^TM_l^-g_l\\&-(w_m-g_r)^TM_r^+(w_m-g_r)+(w_1-g_l)^TM_l^-(w_1-g_l) \end{aligned}$$

which mimics the continuous energy estimate (22) with additional damping terms.

Fig. 10

Snapshot after boundary interaction of a numerical solution to the DSW equations with the characteristics boundary conditions (21) and the total energy over time using $m=201$ grid points and SBP operators of different orders

Snapshot at $t=15$ of the boundary interaction with the set of characteristics boundary conditions (21) and the total energy over the course of interaction are shown in Fig. 10. The experiment is performed with the corresponding nonlinear scheme to (23). This type of boundary condition makes the problem more stiff. We have used $\beta =0.01$ for the second order case, $\beta =0.001$ for the fourth order case, $\beta =0.0001$ for the 6th order case. We only show the significant part of the solution $x\in [20, 30]$ in Fig. 10a, c, e. The observed behaviour differs from the previous set of boundary conditions (19). As can be compared to the result in Fig. 8, in this case, the left-going reflections are not visible. Although a stationary pulse in variable u is still left on the right boundary, from the energy plots (Fig. 10b, d, f), it can be seen that there is almost no energy growth over time except for a small increase at $t=15$.

4 Conclusion

In this paper, we investigate the numerical properties of solitons by studying two PDE-models, the Korteweg-de Vries equation and the coupled Drinfeld–Sokolov–Wilson equation, that can be used to describe such phenomenon. The SBP operators for finite difference method are applied to solve the periodic problem. We analyse the involvement of boundary conditions by deriving two different sets of stable boundary conditions for each equation. The implementation of those boundary conditions utilizes the SAT technique, of which accuracy and stability is shown in the numerical result by different orders of accuracy. For the KdV equation, we show nonlinear stability using the energy method and skew-symmetric splitting. For the DSW equation, we show linear stability in a modified norm. The numerical solution converges to the exact solution with the expected convergence rate. The boundary interaction is illustrated in figures. The numerical study also strengthens the motivation for higher order accurate SBP operators.

Future work may consist of applying optimized time-stepping to the discrete approximations. One could also investigate the possibility of obtaining a nonlinear energy estimate for the DSW equation.