Entropy Stable Discontinuous Galerkin Methods for Nonlinear Conservation Laws on Networks and Multi-Dimensional Domains

Abstract

We present a high-order entropy stable discontinuous Galerkin method for nonlinear conservation laws on both multi-dimensional domains and on networks constructed from one-dimensional domains. These methods utilize treatments of multi-dimensional interfaces and network junctions which retain entropy stability when coupling together entropy stable discretizations. Numerical experiments verify the stability of the proposed schemes, and comparisons with fully 2D implementations demonstrate the accuracy of each type of junction treatment.

Appendix A

In this appendix, we examine junction treatments for the compressible Euler equations with entropy conservative fluxes. The compressible Euler equations for gas dynamics in two dimensions are given by

$$\begin{aligned} \frac{\partial }{\partial t}\begin{bmatrix} \rho \\ \rho u\\ \rho v\\ E \end{bmatrix}+ \frac{\partial }{\partial x}\begin{bmatrix} \rho u\\ \rho u^2+p\\ \rho uv\\ u(E+p) \end{bmatrix}+ \frac{\partial }{\partial y}\begin{bmatrix} \rho v\\ \rho uv\\ \rho v^2+p\\ v(E+p) \end{bmatrix} = 0. \end{aligned}$$

(A1)

Here, $\rho$ and p denote density and the pressure, respectively. The velocity in the x direction is denoted by u and the velocity in the y direction is denoted by v. The total energy is denoted by E and satisfies the constitutive relation involving the pressure p

$$\begin{aligned} E = \frac{1}{2}\rho \left\| U \right\| ^2 + \frac{p}{\gamma -1}, \end{aligned}$$

(A2)

where $\left\| U \right\| ^2 = u^2+v^2$, and $\gamma = 1.4$ is the ratio of specific heat a diatomic gas. In this example, we have conservative variables $\varvec{u} = [\rho , \rho u, \rho v,E]^T$ and flux functions $\varvec{f}_1 = [\rho u, \rho u^2+p, \rho uv, u(E+p)]^T$ and $\varvec{f}_2 = [\rho v, \rho uv, \rho v^2+p, v(E+p)]^T$.

The one-dimensional compressible Euler equations can also be derived under assumptions similar to those used to derive the one-dimensional shallow water equations from the two-dimensional system. In one dimension, the compressible Euler equations are

$$\begin{aligned} \frac{\partial }{\partial t}\begin{bmatrix} \rho \\ \rho u\\ E \end{bmatrix}+ \frac{\partial }{\partial x}\begin{bmatrix} \rho u\\ \rho u^2+p\\ u(E+p) \end{bmatrix}= 0. \end{aligned}$$

(A3)

where we define $\left\| U \right\| ^2 = u^2$ in one dimension.

The transform matrix $\varvec{R}$ between 1D and 2D for the compressible Euler equations is

$$\begin{aligned} \varvec{R} = \begin{bmatrix} 1 &{}0 &{}0\\ 0 &{}n_1 &{}0\\ 0 &{}n_2 &{}0\\ 0 &{}0 &{}1\\ \end{bmatrix}, \qquad \varvec{R}^T\varvec{R} = \varvec{I}. \end{aligned}$$

(A4)

In this work, the mathematical entropy for the compressible Euler equations is taken to be the unique mathematical entropy for the compressible Navier-Stokes equations [37]

$$\begin{aligned} S(\varvec{u}) = -\rho s, \end{aligned}$$

where $s = \log \left( \frac{p}{\rho ^\gamma } \right)$ is the physical specific entropy. The entropy variables $\varvec{v}$ in d dimensions are

$$\begin{aligned} v_1 = \frac{\rho e (\gamma + 1 - s) - E}{\rho e}, \qquad v_{1+ i}= \frac{\rho {{u}_i}}{\rho e}, \qquad v_{d+2} = -\frac{\rho }{\rho e}, \end{aligned}$$

(A5)

for $i = 1,\ldots , d$. The inverse map from entropy to conservative variables is

$$\begin{aligned} \rho = -(\rho e) v_{d+2}, \qquad \rho {u_i} = (\rho e) v_{1+i}, \qquad E = (\rho e)\left( 1 - \frac{\sum _{j=1}^d{v_{1+j}^2}}{2 v_{d+2}} \right) , \end{aligned}$$

where $i = 1,\ldots ,d$, and $\rho e$ and s in terms of the entropy variables are

$$\begin{aligned} \rho e = \left( \frac{(\gamma -1)}{\left( -v_{d+2} \right) ^{\gamma }} \right) ^{1/(\gamma -1)}e^{\frac{-s}{\gamma -1}}, \qquad s = \gamma - v_1 + \frac{\sum _{j=1}^d{v_{1+j}^2}}{2v_{d+2}}. \end{aligned}$$

To introduce the entropy conservative fluxes for the compressible Euler equations, we start with some notations. Let f denote some piecewise continuous function, and $f^+$ denote the exterior value of f across an element face. The average and logarithmic averages are

$$\begin{aligned} \left\{ \!\{f\}\! \right\} = \frac{f+f^{+}}{2}, \quad \left\{ \!\{f\}\! \right\} ^{\mathrm {log}} = \frac{f^{+}-f}{{\mathrm {log}}(f^{+})-{\mathrm {log}} (f)}. \end{aligned}$$

(A6)

The average and logarithmic average are assumed to act component-wise on vector valued functions.

The entropy conservative numerical fluxes for the 2D compressible Euler equations are given by Chandrashekar [38]:

$$\begin{aligned} \varvec{f}^x_{S}\left( \varvec{u}_L,\varvec{u}_R \right)&= \begin{bmatrix} \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{u\}\! \right\} \\ \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{u\}\! \right\} ^2 + p_\mathrm{{avg}}\\ \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{u\}\! \right\} \left\{ \!\{v\}\! \right\} \\ (E_\mathrm{{avg}} + p_\mathrm{{avg}}) \left\{ \!\{u\}\! \right\} \end{bmatrix}, \qquad \varvec{f}^y_{S}\left( \varvec{u}_L,\varvec{u}_R \right)&= \begin{bmatrix} \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{v\}\! \right\} \\ \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{u\}\! \right\} \left\{ \!\{v\}\! \right\} \\ \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{v\}\! \right\} ^2 + p_\mathrm{{avg}}\\ (E_\mathrm{{avg}} + p_\mathrm{{avg}}) \left\{ \!\{v\}\! \right\} \end{bmatrix}. \end{aligned}$$

(A7)

where we need to introduce the auxiliary quantities $\beta = \frac{\rho }{2p}$ and

$$\begin{aligned} p_\mathrm{{avg}} = \frac{\left\{ \!\{\rho \}\! \right\} }{2 \left\{ \!\{\beta \}\! \right\} } , E_\mathrm{{avg}} = \frac{\left\{ \!\{\rho \}\! \right\} ^\mathrm{{log}}}{2 \left\{ \!\{\beta \}\! \right\} ^\mathrm{{log}} (\gamma -1)} + \frac{u_\mathrm{{avg}}^2}{2}, u_\mathrm{{avg}}^2 = u_Lu_R+v_Lv_R. \end{aligned}$$

(A8)

The entropy conservative fluxes for the compressible Euler equations in 1D are

$$\begin{aligned} \varvec{f}_{S1D}\left( \varvec{u}_L,\varvec{u}_R \right)&= \begin{bmatrix} \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{u\}\! \right\} \\ \left\{ \!\{p\}\! \right\} ^\mathrm{{log}}\left\{ \!\{u\}\! \right\} ^2 + p_\mathrm{{avg}}\\ (E_\mathrm{{avg}} + p_\mathrm{{avg}}) \left\{ \!\{u\}\! \right\} \end{bmatrix}, \end{aligned}$$

(A9)

where we need calculate the term $E_\mathrm{{avg}}$ with $u_\mathrm{{avg}}^2 = u_Lu_R$ in 1D

1.1 A Numerical Experiments for the Compressible Euler Equations

1.1.1 A.1 Parallel Split and Converge (1D-2D and 1D-1D Junction Treatments)

For the compressible Euler equations, we reuse the same mesh and setup in Sect. 5.1.1 (as shown in Fig. 7) with the following initial conditions:

$$\begin{aligned} \rho _0 = \sin (\pi x/2)+2, u_0=2, v_0=0, \gamma = 1.4, p_0 = 2. \end{aligned}$$

(A10)

We also test with different polynomial degree on each domain and list the maximum absolute value of the entropy RHS (5.7) up to time $T=1$. Results for the 1D-2D model are shown in Table 2 and results for the 1D-1D model are shown in Table 3.

Table 2 Maximum of absolute value of entropy RHS (5.7) for compressible Euler 1D-2D coupling

Table 3 Maximum of absolute value of entropy RHS (5.7) for compressible Euler 1D-1D coupling

Fig. 25

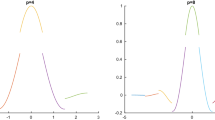
Density $\rho$ in the parallel split problem with initial conditions (A10) at point P1 for the fully 2D, 1D-2D, and 1D-1D junction models. Errors are computed using the fully 2D model as the “exact” solution

To test accuracy of these three models, fully 2D, 1D-2D and 1D-1D junction treatments, for the compressible Euler equations, we plot the results at the midpoints of each channel, as marked in Fig. 7. Coincidentally, because we have the periodic initial conditions and these points are separated by exactly one wavelength, all three points share the same solutions. We notice that with continuous solutions, all three models produce very solutions with small errors as shown in Fig. 25.

From these experiments, we can conclude that our numerical method is entropy conservative for both the shallow water equations and the compressible Euler equations using either 1D-2D or 1D-1D junction treatments. Different models produce different oscillations near the jump, but the their magnitudes are on the same scale. For the solutions that remain continuous, both 1D-2D and 1D-1D junction models generate solutions extremely close to the fully 2D model with absence of vertical flows. However, we expect the 1D-1D junction model to fail where fully 2D motions exist near the junction as in the shallow water experiment in Sect. 5.

1.1.2 A.2 Diamond Split and Converge

For our second experiment with the compressible Euler equations, we reuse the diamond split setup in Sect. 5.1.2 (as shown in Fig. 12) with the following initial conditions:

$$\begin{aligned} \rho _0 = 2, u_0=v_0=0, \gamma = 1.4, p_0 = {\left\{ \begin{array}{ll} 3 &{} \text {in channel 1}\\ 4 &{} \text {otherwise}\\ \end{array}\right. }. \end{aligned}$$

(A11)

We run the test without local Lax-Friedrichs penalization up to time $T=5$ to verify the conservation of entropy. Then, we enable local Lax-Friedrichs penalization for our accuracy test. We plot the values of $\rho$ at midpoints P1 and P2 from both fully 2D and 1D-2D junction treatments in Fig. 26.

Fig. 26

Density $\rho$ in diamond split and converge with initial conditions (A11) at points P1 a and P2 b for the fully 2D model and 1D-2D junction models

We also test the compressible Euler equations with continuous initial conditions:

$$\begin{aligned} \rho _0 = 2, u_0=v_0=0, \gamma = 1.4, p_0 = {\left\{ \begin{array}{ll} 2+\sin (\pi (x+5.5\sqrt{2}+5)/5) &{} \text {in channel 1}\\ 2 &{} \text {otherwise}\\ \end{array}\right. }. \end{aligned}$$

(A12)

We run the test up to time $T=5$ and plot the values of $\rho$ at P1 and P2 from fully 2D and 1D-2D junction models in Fig. 27.

Fig. 27

Density $\rho$ in the diamond split and converge with initial conditions (A12) at points P1 (a and P2 (b) for the fully 2D and 1D-2D junction models

In both shallow water and compressible Euler equations, we observe that the 1D-2D capture the general trend of the flow, but produce slightly different oscillation patterns compared to the fully 2D model.

1.1.3 A.3 Dam Break and Turning Channel

Last, we test the compressible Euler equations on the dam break and turning channel setting in Sect. 5.1.5, as shown in Fig. 22. We first confirm conservation of entropy in the absence of Lax-Friedrichs penalization with the initial conditions:

$$\begin{aligned} \rho _0 = 2, u_0=v_0=0, \gamma = 1.4, p_0 = {\left\{ \begin{array}{ll} 5 &{} \text {in reservoir }\\ 2 &{} \text {in channel}\\ \end{array}\right. }. \end{aligned}$$

(A13)

We test the accuracy of the model with Lax-Friedrichs penalization and plot $\rho$ at midpoints P1 and P2 in the Fig. 28. We run up to time $T=5$ and notice that similar patterns are generated from both the 1D-2D and fully 2D models. At P1, the oscillations from the fully 2D and 1D-2D junction models have noticeable discrepancies from time $T=1.5$ to $T=3.5$. We also find that there is a small bump at point P2 around time $T=2$, which the 1D-2D model does not capture.

Fig. 28

Density $\rho$ in the dam break and turning channel with initial conditions (A13) at points P1 a and P2 b for the fully 2D and 1D-2D junction models