A New Class of A Stable Summation by Parts Time Integration Schemes with Strong Initial Conditions

Abstract

Since integration by parts is an important tool when deriving energy or entropy estimates for differential equations, one may conjecture that some form of summation by parts (SBP) property is involved in provably stable numerical methods. This article contributes to this topic by proposing a novel class of A stable SBP time integration methods which can also be reformulated as implicit Runge-Kutta methods. In contrast to existing SBP time integration methods using simultaneous approximation terms to impose the initial condition weakly, the new schemes use a projection method to impose the initial condition strongly without destroying the SBP property. The new class of methods includes the classical Lobatto IIIA collocation method, not previously formulated as an SBP scheme. Additionally, a related SBP scheme including the classical Lobatto IIIB collocation method is developed.

1 Introduction

Based on the fact that integration by parts plays a major role in the development of energy and entropy estimates for initial boundary value problems, one may conjecture that the summation by parts (SBP) property [8, 47] is a key factor in provably stable schemes. Although it is complicated to formulate such a conjecture mathematically, there are several attempts to unify stable methods in the framework of summation by parts schemes, starting from the origin of SBP operators in finite difference methods [16, 43] and ranging from finite volume [23, 24] and discontinuous Galerkin methods [9] to flux reconstruction schemes [37].

Turning to SBP methods in time [2, 19, 25], a class of linearly and nonlinearly stable SBP schemes has been constructed and studied in this context, see also [18, 41, 42]. If the underlying quadrature is chosen as Radau or Lobatto quadrature, these Runge-Kutta schemes are exactly the classical Radau IA, Radau IIA, and Lobatto IIIC methods [29]. Having the conjecture “stability results require an SBP structure” in mind, this article provides additional insights to this topic by constructing new classes of SBP schemes, which reduce to the classical Lobatto IIIA and Lobatto IIIB methods if that quadrature rule is used. Consequently, all A stable classical Runge-Kutta methods based on Radau and Lobatto quadrature rules can be formulated in the framework of SBP operators. Notably, instead of using simultaneous approximation terms (SATs) [5, 6] to impose initial conditions weakly, these new schemes use a strong imposition of initial conditions in combination with a projection method [22, 26, 27].

By mimicking integration by parts at a discrete level, the stability of SBP methods can be obtained in a straightforward way by mimicking the continuous analysis. All known SBP time integration methods are implicit and their stability does not depend on the size of the time step. In contrast, the stability analysis of explicit time integration methods can use techniques similar to summation by parts, but the analysis is in general more complicated and restricted to sufficiently small time steps [36, 44, 46]. Since there are strict stability limitations for explicit methods, especially for nonlinear problems [30, 31], an alternative to stable fully implicit methods is to modify less expensive (explicit or not fully implicit) time integration schemes to get the desired stability results [10, 15, 32, 33, 39, 45].

This article is structured as follows. At first, the existing class of SBP time integration methods is introduced in Sect. 2, including a description of the related stability properties. Thereafter, the novel SBP time integration methods are proposed in Section 3. Their stability properties are studied and the relation to Runge-Kutta methods is described. In particular, the Lobatto IIIA and Lobatto IIIB methods are shown to be recovered using this framework. Afterwards, results of numerical experiments demonstrating the established stability properties are reported in Sect. 4. Finally, the findings of this article are summed up and discussed in Sect. 5.

2 Known Results for SBP Schemes

Consider an ordinary differential equation (ODE)

$$\begin{aligned} \forall t \in (0,T):\quad u'(t) = f(t, u(t)), \qquad u(0) = u_0, \end{aligned}$$

(1)

with solution u in a Hilbert space. Summation by parts schemes approximate the solution on a finite grid $0 \le \tau _1< \dots < \tau _s \le T$ pointwise as $\pmb {u}_i = u(\tau _i)$ and $\pmb {f}_i = f(\tau _i, \pmb {u}_i)$. Although the grid does not need to be ordered for general SBP schemes, we impose this restriction to simplify the presentation. (An unordered grid can always be transformed into an ordered one by a permutation of the grid indices.) The SBP operators can be defined as follows, cf. [7, 8, 47].

Definition 2.1

A first derivative SBP operator of order p on [0, T] consists of

• a discrete operator D approximating the derivative $D \pmb {u} \approx u'$ with order of accuracy p,

• a symmetric and positive definite discrete quadrature matrix M approximating the $L^2$ scalar product $\pmb {u}^T M \pmb {v} \approx \int _{0}^{T} u(\tau ) v(\tau ) {\mathrm{d}}\tau$,

• and interpolation vectors $\pmb {t}_L, \pmb {t}_R$ approximating the boundary values as $\pmb {t}_L^T \pmb {u} \approx u(0)$, $\pmb {t}_R^T \pmb {u} \approx u(T)$ with order of accuracy at least p, such that the SBP property

  $$\begin{aligned} M D + (M D)^T = \pmb {t}_R \pmb {t}_R^T - \pmb {t}_L \pmb {t}_L^T \end{aligned}$$

  (2)

  holds.

Remark 2.2

There are analogous definitions of SBP operators for second or higher order derivatives [20, 21, 34]. In this article, only first derivative SBP operators are considered.

Remark 2.3

The quadrature matrix M is sometimes called norm matrix (since it induces a norm via a scalar product) or mass matrix (in a finite element context).

Because of the SBP property (2), SBP operators mimic integration by parts discretely via

(3)

However, this mimetic property does not suffice for the derivations to follow. Nullspace consistency will be used as an additional required mimetic property. This novel property was introduced in [48] and has been a key factor in [18, 38].

Definition 2.4

A first derivative SBP operator D is nullspace consistent, if the nullspace (kernel) of D satisfies .

Here, $\pmb {1}$ denotes the discrete grid function with value unity at every node.

Remark 2.5

Every first derivative operator D (which is at least first order accurate) maps constants to zero, i.e. $D \pmb {1} = \pmb {0}$. Hence, the kernel of D always satisfies . Here and in the following, $\le$ denotes the subspace relation of vector spaces. If D is not nullspace consistent, there are more discrete grid functions besides constants which are mapped to zero (which makes it inconsistent with $\partial _t$). Then, and undesired behavior can occur, cf. [18, 29, 48, 49].

An SBP time discretization of (1) using SATs to impose the initial condition weakly is [2, 19, 25]

$$\begin{aligned} D \pmb {u} = \pmb {f} + M^{-1} \pmb {t}_L \bigl ( u_0 - \pmb {t}_L^T \pmb {u} \bigr ). \end{aligned}$$

(4)

The numerical solution $u_+$ at $t=T$ is given by $u_+ = \pmb {t}_R^T \pmb {u}$, where $\pmb {u}$ solves (4).

Remark 2.6

The interval [0, T] can be partitioned into multiple subintervals/blocks such that multiple steps of this procedure can be used sequentially [19].

In order to guarantee that (4) can be solved for a linear scalar problem, $D + \sigma M^{-1} \pmb {t}_L \pmb {t}_L^T$ must be invertible, where $\sigma$ is a real parameter usually chosen as $\sigma = 1$. The following result has been obtained in [18, Lemma 2].

Theorem 2.7

If D is a first derivative SBP operator, $D + M^{-1} \pmb {t}_L \pmb {t}_L^T$ is invertible if and only if D is nullspace consistent.

Remark 2.8

In [41, 42], it was explicitly shown how to prove that $D + M^{-1} \pmb {t}_L \pmb {t}_L^T$ is invertible in the pseudospectral/polynomial and finite difference case.

As many other one-step time integration schemes, SBP-SAT schemes (4) can be characterized as Runge-Kutta methods, given by their Butcher coefficients [4, 11]

$$\begin{aligned} \begin{array}{c | c} c &{} A \\ \hline &{} b^T \end{array}, \end{aligned}$$

(5)

where $A \in {\mathbb {R}}^{s \times s}$ and $b, c \in {\mathbb {R}}^s$. For (1), a step from $u_0$ to $u_+ \approx u(\varDelta t)$ is given by

$$\begin{aligned} u_i = u_0 + \varDelta t\sum _{j=1}^{s} a_{ij} \, f(c_j \varDelta t, u_j), \qquad u_+ = u_0 + \varDelta t\sum _{i=1}^{s} b_{i} \, f(c_i \varDelta t, u_i). \end{aligned}$$

(6)

Here, $u_i$ are the stage values of the Runge-Kutta method. The following characterization of (4) as Runge-Kutta method was given in [2].

Theorem 2.9

Consider a first derivative SBP operator D. If $D + M^{-1} \pmb {t}_L \pmb {t}_L^T$ is invertible, (4) is equivalent to an implicit Runge-Kutta method with the Butcher coefficients

$$\begin{aligned} \begin{aligned} A&= \frac{1}{T} (D + M^{-1} \pmb {t}_L \pmb {t}_L^T)^{-1} = \frac{1}{T} (M D + \pmb {t}_L \pmb {t}_L^T)^{-1} M, \\ b&= \frac{1}{T} M \pmb {1}, c = \frac{1}{T} (\tau _1, \dots , \tau _s)^T. \end{aligned} \end{aligned}$$

(7)

The factor $\frac{1}{T}$ is needed since the Butcher coefficients of a Runge-Kutta method are normalized to the interval [0, 1].

Next, we recall some classical stability properties of Runge-Kutta methods for linear problems, cf. [12, Section IV.3]. The absolute value of solutions of the scalar linear ODE

$$\begin{aligned} u'(t) = \lambda u(t), \quad u(0) = u_0 \in {\mathbb {C}}, \quad \lambda \in {\mathbb {C}}, \end{aligned}$$

(8)

cannot increase if ${\text {Re}}\lambda \le 0$. The numerical solution after one time step of a Runge-Kutta method with Butcher coefficients A, b, c is $u_+ = R(\lambda \, \varDelta t) u_0$, where

$$\begin{aligned} R(z) = 1 + z b^T ({\text {I}}- z A)^{-1} \pmb {1} = \frac{\det ({\text {I}}- z A + z \pmb {1} b^T)}{\det ({\text {I}}- z A)} \end{aligned}$$

(9)

is the stability function of the Runge-Kutta method. The stability property of the ODE is mimicked discretely as $\left| u_+\right| \le \left| u_0\right|$ if $\left| R(\lambda \, \varDelta t)\right| \le 1$.

Definition 2.10

A Runge-Kutta method with stability function $\left| R(z)\right| \le 1$ for all $z \in {\mathbb {C}}$ with ${\text {Re}}(z) \le 0$ is A stable. The method is L stable, if it is A stable and $\lim _{z \rightarrow \infty } R(z) = 0$.

Hence, A stable methods are stable for every time step $\varDelta t > 0$ and L stable methods damp out stiff components as $\left| \lambda \right| \rightarrow \infty$.

The following stability properties have been obtained in [2, 19].

Theorem 2.11

Consider a first derivative SBP operator D. If $D + M^{-1} \pmb {t}_L \pmb {t}_L^T$ is invertible, then the SBP-SAT scheme (4) is both A and L stable.

Corollary 2.12

The SBP-SAT scheme (4) is both A and L stable if D is a nullspace consistent SBP operator.

Proof

This result follows immediately from Theorem 2.7 and Theorem 2.11. $\square$

3 The New Schemes

The idea behind the novel SBP time integration scheme introduced in the following is to mimic the reformulation of the ODE (1) as an integral equation

$$\begin{aligned} u(t) = u_0 + \int _0^t f(\tau , u(\tau )) {\mathrm{d}}\tau . \end{aligned}$$

(10)

Taking the time derivative on both sides yields $u'(t) = f(t, u(t))$. The initial condition $u(0) = u_0$ is satisfied because $\int _0^0 f(\tau , u(\tau )) {\mathrm{d}}\tau = 0$. Hence, the solution u of (1) can be written implicitly as the solution of the integral equation (10). Note that the integral operator $\int _0^t \cdot {\mathrm{d}}\tau$ is the inverse of the derivative operator $\frac{\hbox {d}}{\hbox {d}t}$ with a vanishing initial condition at $t = 0$. Hence, a discrete inverse (an integral operator) of the discrete derivative operator D with a vanishing initial condition will be our target.

Definition 3.1

In the space of discrete grid functions, the scalar product induced by M is used throughout this article. The adjoint operators with respect to this scalar product will be denoted by $\cdot ^*$, i.e. $D^* = M^{-1} D^T M$. The adjoint of a discrete grid function $\pmb {u}$ is denoted by $\pmb {u}^* = \pmb {u}^T M$.

By definition, the adjoint operator $D^*$ of D satisfies

$$\begin{aligned} \left\langle {\pmb {u},\, D^* \pmb {v}}\right\rangle _M = \pmb {u}^T M D^* \pmb {v} = \pmb {u}^T D^T M \pmb {v} = (D \pmb {u})^T M \pmb {v} = \left\langle {D \pmb {u},\, \pmb {v}}\right\rangle \end{aligned}$$

(11)

for all grid functions $\pmb {u}, \pmb {v}$. The adjoint $\pmb {u}^*$ is a discrete representation of the inverse Riesz map applied to a grid function $\pmb {u}$ [40, Theorem 9.18] and satisfies

$$\begin{aligned} \pmb {u}^* \pmb {v} = \pmb {u}^T M \pmb {v} = \left\langle {\pmb {u},\, \pmb {v}}\right\rangle _M. \end{aligned}$$

(12)

The following lemma and definition were introduced in [38].

Lemma 3.2

For a nullspace consistent first derivative SBP operator D, $\dim {\text {ker}}D^* = 1$.

Definition 3.3

A fixed but arbitrarily chosen basis vector of ${\text {ker}}D^*$ for a nullspace consistent SBP operator D is denoted as $\pmb {o}$.

The name $\pmb {o}$ is intended to remind the reader of (grid) oscillations, since the kernel of $D^*$ is orthogonal to the image of D [40, Theorem 10.3] which contains all sufficiently resolved functions. Several examples are given in [38]. To prove ${\text {ker}}D^* \perp {\text {im}}D$, choose any $D \pmb {u} \in {\text {im}}D$ and $\pmb {v} \in {\text {ker}}D^*$ and compute

$$\begin{aligned} \left\langle {D \pmb {u},\, \pmb {v}}\right\rangle _M = \left\langle {\pmb {u},\, D^* \pmb {v}}\right\rangle _M = \left\langle {\pmb {u},\, \pmb {0}}\right\rangle _M = 0. \end{aligned}$$

(13)

Example 3.4

Consider the SBP operator of order $p = 1$ defined by the $p+1 = 2$ Lobatto-Legendre nodes $\tau _1 = 0$ and $\tau _2 = T$ in [0, T]. Then,

$$\begin{aligned} \begin{aligned} D&= \frac{1}{T} \begin{pmatrix} -1 &{} 1 \\ -1 &{} 1 \end{pmatrix},&M&= \frac{T}{2} \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix},&\pmb {t}_L&= \begin{pmatrix} 1 \\ 0 \end{pmatrix},&\pmb {t}_R&= \begin{pmatrix} 0 \\ 1 \end{pmatrix}. \end{aligned} \end{aligned}$$

(14)

Therefore,

$$\begin{aligned} D^* = M^{-1} D^T M = \frac{1}{T} \begin{pmatrix} -1 &{} -1 \\ 1 &{} 1 \end{pmatrix} \end{aligned}$$

(15)

and , where $\pmb {o}= (-1, 1)^T$. Here, $\pmb {o}$ represents the highest resolvable grid oscillation on $[\tau _1, \tau _2]$ and $\pmb {o}$ is orthogonal to ${\text {im}}D$, since $\pmb {o}^T M D = \pmb {0}^T$.

The following technique has been used in [38] to analyze properties of SBP operators in space. Here, it will be used to create new SBP schemes in time. Consider a nullspace consistent first derivative SBP operator D on the interval [0, T] using s grid points and the corresponding subspaces

(16)

Here and in the following, $\pmb {u}(t = 0)$ denotes the value of the discrete function $\pmb {u}$ at the initial time $t = 0$. For example, $\pmb {u}(t = 0) = \pmb {t}_L^T \pmb {u} = \pmb {u}^{(1)}$ is the first coefficient of $\pmb {u}$ if $\tau _1 = 0$ and $\pmb {t}_L = (1, 0, \dots , 0)^T$.

$V_0$ is the vector space of all grid functions which vanish at the left boundary point, i.e. $V_0 = {\text {ker}}\pmb {t}_L^T$. $V_1$ is the vector space of all grid functions which can be represented as derivatives of other grid functions, i.e. $V_1 = {\text {im}}D$ is the image of D.

Remark 3.5

From this point in the paper, D denotes a nullspace consistent first derivative SBP operator.

Lemma 3.6

The mapping $D:V_0 \rightarrow V_1$ is bijective, i.e. one-to-one and onto, and hence invertible.

Proof

Given $\pmb {u} \in V_1$, there is a $\pmb {v} \in {\mathbb {R}}^s$ such that $\pmb {u} = D \pmb {v}$. Hence,

$$\begin{aligned} D (\pmb {v} - (\pmb {t}_L^T \pmb {v}) \pmb {1}) = D \pmb {v} - (\pmb {t}_L^T \pmb {v}) D \pmb {1} = D \pmb {v} = \pmb {u} \end{aligned}$$

(17)

and

$$\begin{aligned} \pmb {t}_L^T (\pmb {v} - (\pmb {t}_L^T \pmb {v}) \pmb {1}) = \pmb {t}_L^T \pmb {v} - \pmb {t}_L^T \pmb {v} = 0, \end{aligned}$$

(18)

since $\pmb {t}_L^T \pmb {v}$ is a scalar. Hence, (18) implies that $\pmb {v} - (\pmb {t}_L^T \pmb {v}) \pmb {1} \in V_0$. Moreover, (17) shows that an arbitrary $\pmb {u} \in V_1$ can be written as the image of a vector in $V_0$ under D. Therefore, $D:V_0 \rightarrow V_1$ is surjective (i.e. onto).

To prove that D is injective (i.e. one-to-one), consider an arbitrary $\pmb {u} \in V_1$ and assume there are $\pmb {v}, \pmb {w} \in V_0$ such that $D \pmb {v} = \pmb {u} = D \pmb {w}$. Then, $D (\pmb {v} - \pmb {w}) = \pmb {0}$. Because of nullspace consistency, $\pmb {v} - \pmb {w} = \alpha \pmb {1}$ for a scalar $\alpha$. Since $\pmb {v}, \pmb {w} \in V_0 = {\text {ker}}\pmb {t}_L^T$,

$$\begin{aligned} 0 = \pmb {t}_L^T (\pmb {v} - \pmb {w}) = \alpha \pmb {t}_L^T \pmb {1} = \alpha . \end{aligned}$$

(19)

Thus, $\pmb {v} = \pmb {w}$. $\square$

Remark 3.7

$V_0$ is isomorphic to the quotient space ${\mathbb {R}}^s / {\text {ker}}D$, since D is nullspace consistent. Hence, Lemma 3.6 basically states that D is a bijective mapping from $V_0 \cong {\mathbb {R}}^s / {\text {ker}}D$ to $V_1 = {\text {im}}D$.

Definition 3.8

The inverse operator of $D:V_0 \rightarrow V_1$ is denoted as $J:V_1 \rightarrow V_0$.

The inverse operator $J$ is a discrete integral operator such that $J\pmb {v} \approx \int _0^t v(\tau ) {\mathrm{d}}\tau$. In general, there is a one-parameter family of integral operators given by $\int _{t_0}^t v(\tau ) {\mathrm{d}}\tau$. Here, we chose the one with $t_0 = 0$ to be consistent with (10).

Example 3.9

Continuing Example 3.4, the vector spaces $V_0$ and $V_1$ are

(20)

This can be seen as follows. For $V_0 = {\text {ker}}\pmb {t}_L^T$, using $\pmb {t}_L^T = (1, 0)$ implies that the first component of $\pmb {u} \in V_0$ is zero and that the second one can be chosen arbitrarily. For $V_1 = {\text {im}}D$, note that both rows of D are identical. Hence, every $\pmb {u} = D \pmb {v} \in V_1$ must have the same first and second component.

At the level of ${\mathbb {R}}^2$, the inverse $J$ of D can be represented as

$$\begin{aligned} J= T \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix}. \end{aligned}$$

(21)

Indeed, if $\pmb {u} = \begin{pmatrix} 0 \\ \pmb {u}_2 \end{pmatrix} \in V_0$, then

$$\begin{aligned} JD \pmb {u} = T \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \frac{1}{T} \begin{pmatrix} -1 &{} 1 \\ -1 &{} 1 \end{pmatrix} \begin{pmatrix} 0 \\ \pmb {u}_2 \end{pmatrix} = \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \begin{pmatrix} \pmb {u}_2 \\ \pmb {u}_2 \end{pmatrix} = \begin{pmatrix} 0 \\ \pmb {u}_2 \end{pmatrix} = \pmb {u}. \end{aligned}$$

(22)

Similarly, if $\pmb {u} = \pmb {u}_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} \in V_1$, then

$$\begin{aligned} D J\pmb {u} = \frac{1}{T} \begin{pmatrix} -1 &{} 1 \\ -1 &{} 1 \end{pmatrix} T \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \begin{pmatrix} \pmb {u}_1 \\ \pmb {u}_1 \end{pmatrix} = \begin{pmatrix} -1 &{} 1 \\ -1 &{} 1 \end{pmatrix} \begin{pmatrix} 0 \\ \pmb {u}_1 \end{pmatrix} = \begin{pmatrix} \pmb {u}_1 \\ \pmb {u}_1 \end{pmatrix} = \pmb {u}. \end{aligned}$$

(23)

Hence, $JD = {\text {id}}_{V_0}$ and $D J= {\text {id}}_{V_1}$, where ${\text {id}}_{V_i}$ is the identity on $V_i$.

Note that the matrix representation of $J$ at the level of ${\mathbb {R}}^s$ is not unique since $J$ is only defined on $V_1 = {\text {ker}}\pmb {o}^* = {\text {im}}D$. In general, a linear mapping from ${\mathbb {R}}^s$ to ${\mathbb {R}}^s$ is determined uniquely by $s^2$ real parameters (the entries of the corresponding matrix representation). Since $J$ is defined as a mapping between the $(s-1)$-dimensional spaces $V_1$ and $V_0$, it is given by $(s-1)^2$ parameters. Requiring that $J$ maps to $V_0$ yields s additional constraints $\pmb {t}_L^T J= \pmb {0}^T$. Hence, $s - 1$ degrees of freedom remain for any matrix representation of $J$ at the level of ${\mathbb {R}}^s$. Indeed, adding $\pmb {v} \pmb {o}^*$ to any matrix representation of $J$ in ${\mathbb {R}}^s$ results in another valid representation if $\pmb {v} \in V_0 = {\text {ker}}\pmb {t}_L^T$. In this example, another valid representation of $J$ at the level of ${\mathbb {R}}^2$ is

$$\begin{aligned} J= T \begin{pmatrix} 0 &{} 0 \\ 1 &{} 0 \end{pmatrix}, \end{aligned}$$

(24)

which still satisfies $JD = {\text {id}}_{V_0}$, $D J= {\text {id}}_{V_1}$, and yields the same results as the previous matrix representation when applied to any $\pmb {v} \in V_1$.

Now, we have introduced the inverse $J$ of $D:V_0 \rightarrow V_1$, which is a discrete integral operator $J:V_1 \rightarrow V_0$. However, the integral operator $J$ is only defined for elements of the space $V_1 = {\text {im}}D$. Hence, one has to make sure that a generic right hand side vector $\pmb {f}$ is in the range of the derivative operator D in order to apply the inverse $J$. To guarantee this, components in the direction of grid oscillations $\pmb {o}$ must be removed. For this, the discrete projection/filter operator

$$\begin{aligned} F= {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \end{aligned}$$

(25)

will be used.

Lemma 3.10

The projection/filter operator $F$ defined in (25) is an orthogonal projection onto the range of D, i.e. onto $V_1 = {\text {im}}D = ({\text {ker}}D^*)^\perp$. It is symmetric and positive semidefinite with respect to the scalar product induced by M.

Proof

Clearly, $\frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2}$ is the usual orthogonal projection onto ${\text {span}}\{ \pmb {o}\}$ [40, Theorems 9.14 and 9.15]. Hence, $F$ is the orthogonal projection onto the orthogonal complement ${\text {span}}\{ \pmb {o}\}^\perp = ({\text {ker}}D^*)^\perp = {\text {im}}D = V_1$. In particular, for a (real or complex valued) discrete grid function $\pmb {u}$,

$$\begin{aligned} \left\langle {\pmb {u},\, F\pmb {u}}\right\rangle _M = \left\langle {\pmb {u},\, \pmb {u}}\right\rangle _M - \frac{|\left\langle {\pmb {u},\, \pmb {o}}\right\rangle _M|^2}{\left| \left| \pmb {o}\right| \right| _M^2} \ge 0 \end{aligned}$$

(26)

because of the Cauchy-Schwarz inequality [40, Theorem 9.3]. $\square$

Now, all ingredients to mimic the integral equation (10) have been provided. Applying at first the discrete projection operator $F$ and second the discrete integral operator J to a generic right hand side $\pmb {f}$ results in $JF\pmb {f}$, which is a discrete analog of the integral $\int _0^t f {\mathrm{d}}\tau$. Additionally, the initial condition has to be imposed, which is done by adding the constant initial value as $u_0 \otimes \pmb {1}$. Putting it all together, a new class of SBP schemes mimicking the integral equation (10) discretely is proposed as

$$\begin{aligned} \pmb {u} = u_0 \otimes \pmb {1} + JF\pmb {f}, \quad u_+ = \pmb {t}_R^T \pmb {u}. \end{aligned}$$

(27)

For a scalar ODE (1), the first term on the right-hand side of the proposed scheme (27) is $u_0 \otimes \pmb {1} = (u_0, \dots , u_0)^T \in {\mathbb {R}}^s$. Note that (27) is an implicit scheme since $f = f(t, u)$.

Example 3.11

Continuing Examples 3.4 and 3.9, the adjoint of $\pmb {o}$ is

$$\begin{aligned} \pmb {o}^* = \pmb {o}^T M = (-1, 1) \frac{T}{2} \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} = \frac{T}{2} (-1, 1). \end{aligned}$$

(28)

Hence, ${\left| \left| \pmb {o}\right| \right| _M^2} = \pmb {o}^* \pmb {o}= T$, and the projection/filter operator (25) is

$$\begin{aligned} F= {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} = \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} - \frac{1}{2} \begin{pmatrix} 1 &{} -1 \\ -1 &{} 1 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix}. \end{aligned}$$

(29)

Thus, $F$ is a smoothing filter operator that removes the highest grid oscillations and maps a grid function into the image of the derivative operator D. Hence, the inverse $J$, the discrete integral operator, can be applied after $F$, resulting in

$$\begin{aligned} JF= J\left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) = T \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1 \end{pmatrix} \frac{1}{2} \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix} = \frac{T}{2} \begin{pmatrix} 0 &{} 0 \\ 1 &{} 1 \end{pmatrix}. \end{aligned}$$

(30)

Finally, for an arbitrary $\pmb {u} \in {\mathbb {R}}^2$,

$$\begin{aligned} JF\pmb {u} = \frac{T}{2} \begin{pmatrix} 0 &{} 0 \\ 1 &{} 1 \end{pmatrix} \begin{pmatrix} \pmb {u}_1 \\ \pmb {u}_2 \end{pmatrix} = \frac{T}{2} \begin{pmatrix} 0 \\ \pmb {u}_1 + \pmb {u}_2 \end{pmatrix} \in V_0. \end{aligned}$$

(31)

A more involved example of the development presented here is given in Appendix B.

3.1 Summarizing the Development

As stated earlier, the SBP time integration scheme (27) mimics the integral reformulation (10) of the ODE (1). Instead of using $J$ as discrete analog of the integral operator $\int _0^t \cdot {\mathrm{d}}\tau$ directly, the projection/filter operator $F$ defined in (25) must be applied first in order to guarantee that the generic vector $\pmb {f}$ is in the image of D. Finally, the initial condition is imposed strongly.

Note that

$$\begin{aligned} \pmb {t}_L^T \pmb {u} = \pmb {t}_L^T (u_0 \otimes \pmb {1}) + \pmb {t}_L^T J\left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) \pmb {f} = u_0. \end{aligned}$$

(32)

The second summand vanishes because $J$ returns a vanishing value at $t = 0$, i.e. $\pmb {t}_L^T J= \pmb {0}^T$, since $J:V_1 \rightarrow V_0$ maps onto $V_0 = {\text {ker}}\pmb {t}_L^T$.

Note that the projection/filter operator $F$ is required in (27), since the discrete integral operator $J$ only operates on objects in $V_1$. Note also that the matrix representations of $J$ in ${\mathbb {R}}^s$ given in the examples above are constructed such that they should be applied only to vectors $\pmb {v} \in V_1$. As explained in Example 3.9, the matrix representation of $J$ in ${\mathbb {R}}^s$ is not unique. Thus, choosing any of these representations without applying the filter/projection operator $F$ would result in undefined/unpredictable behavior. The projection/filter operator $F$ is necessary to make (27) well-defined. Indeed, the product $JF$ is well-defined, i.e. it is the same for any matrix representation of $J$, since $F$ maps to $V_1 = {\text {im}}D$ and the action of $J$ is defined uniquely on this space. In particular, $JF$ itself is a valid matrix representation of $J$ in ${\mathbb {R}}^{s}$. As an example, $JF$ in (30) is a linear combination of the possible representations (21) and (24) of $J$ in ${\mathbb {R}}^{s}$ and thus also a representation of $J$ in $R^{s}$.

Another argument for the necessity of the filter/projection operator $F$ can be derived using the following result.

Lemma 3.12

Let D be a nullspace consistent first derivative SBP operator. Then, $D JF= F$ and the solution $\pmb {u}$ of (27) satisfies

$$\begin{aligned} D \pmb {u} = F\pmb {f}. \end{aligned}$$

(33)

Before proving Lemma 3.12, we discuss its meaning here. In general, it is not possible to find a solution $\pmb {u}$ of $D \pmb {u} = \pmb {f}$ for an arbitrary right-hand side $\pmb {f}$, since D is not invertible on ${\mathbb {R}}^s$. Multiplying $\pmb {f}$ by the orthogonal projection operator $F$ ensures that the new right-hand side $F\pmb {f}$ of (33) is in the image of D and hence that (33) can be solved for any given $\pmb {f}$. This projection $F$ onto $V_1 = {\text {im}}D$ is necessary in the discrete case because of the finite dimensions.

Proof of Lemma 3.12

Taking the discrete derivative on both sides of (27) results in

$$\begin{aligned} D \pmb {u} = D JF\pmb {f}, \end{aligned}$$

(34)

since $D (u_0 \otimes \pmb {1}) = u_0 \otimes (D \pmb {1}) = \pmb {0}$. Hence, (33) holds if $D JF= F$. To show $D JF= F$, it suffices to show $D JF\pmb {f} = F \pmb {f}$ for arbitrary $\pmb {f}$. Write $\pmb {f}$ as $\pmb {f} = D \pmb {v} + \alpha \pmb {o}$, where $\pmb {t}_L^T \pmb {v} = 0$ and $\alpha \in {\mathbb {R}}$. This is always possible since D is nullspace consistent. Then,

$$\begin{aligned} D JF\pmb {f} = D JFD \pmb {v} + \alpha D JF\pmb {o}= D JD \pmb {v} = D \pmb {v}, \end{aligned}$$

(35)

where we used $FD = D$, $F\pmb {o}= \pmb {0}$, $JD = {\text {id}}_{V_0}$, and $\pmb {v} \in V_0 = {\text {ker}}\pmb {t}_L^T$. Using again $FD = D$ and $F\pmb {o}= \pmb {0}$, we get

$$\begin{aligned} D \pmb {v} = FD \pmb {v} + \pmb {0} = F(D \pmb {v} + \alpha \pmb {o}) = F\pmb {f}. \end{aligned}$$

(36)

Hence, $D JF\pmb {f} = F \pmb {f}$. $\square$

Remark 3.13

In the context of SBP operators, two essentially different interpretations of integrals arise. Firstly, the integral $\int _0^T \cdot {\mathrm{d}}\tau$ gives the $L^2$ scalar product, approximated by the mass matrix M which maps discrete functions to scalar values. Secondly, the integral $\int _0^t \cdot {\mathrm{d}}\tau$ is the inverse of the derivative with vanishing values at $t = 0$. This operator is discretized as $J$ on its domain of definition $V_1 = {\text {im}}D$ and maps a discrete grid function in $V_1 = {\text {im}}D$ to a discrete grid function in $V_0 = {\text {ker}}\pmb {t}_L^T$.

3.2 Linear Stability

In this section, linear stability properties of the new scheme (27) are established.

Theorem 3.14

For nullspace consistent SBP operators, the scheme (27) is A stable.

Proof

For the scalar linear ODE (8) with ${\text {Re}}\lambda \le 0$, the energy method will be applied to the scheme (27). We write ${\overline{\cdot }}$ to denote the complex conjugate. Using $\pmb {t}_L^T \pmb {u} = u_0$ from (32) and $u_+ = \pmb {t}_R^T \pmb {u}$ from the definition of the scheme (27), the difference of the energy at the final and initial time is

$$\begin{aligned} \begin{aligned} \left| u_+\right| ^2 - \left| u_0\right| ^2&= \left| \pmb {t}_R^T \pmb {u}\right| ^2 - \left| \pmb {t}_L^T \pmb {u}\right| ^2 = \overline{\pmb {u}}^T \pmb {t}_R \pmb {t}_R^T \pmb {u} - \overline{\pmb {u}}^T \pmb {t}_L \pmb {t}_L^T \pmb {u} \\&= \overline{\pmb {u}}^T \bigl ( M D + (M D)^T \bigr ) \pmb {u}, \end{aligned} \end{aligned}$$

(37)

where the SBP property (2) has been used in the last equality. As shown in Lemma 3.12, the scheme (27) yields $D \pmb {u} = F\pmb {f}$. For the scalar linear ODE (8), $\pmb {f} = \lambda \pmb {u}$. Hence, we can replace $D \pmb {u}$ by $F\pmb {f} = \lambda F\pmb {u}$ in (37), resulting in

$$\begin{aligned} \begin{aligned} \left| u_+\right| ^2 - \left| u_0\right| ^2&= 2 {\text {Re}}\bigl ( \overline{\pmb {u}}^T M D \pmb {u} \bigr ) \\&= 2 {\text {Re}}\bigl ( \lambda \overline{\pmb {u}}^T M F\pmb {u} \bigr ) = 2 \underbrace{{\text {Re}}(\lambda )}_{\le 0} \underbrace{\overline{\pmb {u}}^T M F\pmb {u}}_{\ge 0} \le 0. \end{aligned} \end{aligned}$$

(38)

The second factor is non-negative because $F$ is positive semidefinite with respect to the scalar product induced by M, cf. Lemma 3.10. Therefore, $\left| u_+\right| ^2 \le \left| u_0\right| ^2$, implying that the scheme is A stable. $\square$

In general, the novel SBP scheme (27) is not L stable, cf. Remark 3.19.

3.3 Characterization as a Runge-Kutta Method

Unsurprisingly, the new method (27) can be characterized as a Runge-Kutta method.

Theorem 3.15

For nullspace consistent SBP operators that are at least first order accurate, the method (27) is a Runge-Kutta method with Butcher coefficients

$$\begin{aligned} A = \frac{1}{T} JF= \frac{1}{T} J\left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) , \quad b = \frac{1}{T} M \pmb {1}, \quad c = \frac{1}{T} (\tau _1, \dots , \tau _s)^T. \end{aligned}$$

(39)

Proof

First, note that one step (6) from zero to T of a Runge-Kutta method with coefficients A, b, c can be written as

$$\begin{aligned} \pmb {u} = u_0 \otimes \pmb {1} + T A \pmb {f}, \quad u_+ = u_0 + T b^T \pmb {f}, \end{aligned}$$

(40)

where the right hand side vector $\pmb {f}$ is given by $\pmb {f}_i = f(c_i T, \pmb {u}_i)$. Comparing this expression with

$$\begin{aligned} \pmb {u} = u_0 \otimes \pmb {1} + JF\pmb {f}, \quad u_+ = \pmb {t}_R^T \pmb {u}, \end{aligned}$$

(27)

where the right hand side is given by $\pmb {f}_i = f(\tau _i, \pmb {u}_i)$, the form of A and c is immediately clear. The new value $u_+$ of the new SBP method (27) is

$$\begin{aligned} u_+ = \pmb {t}_R^T \pmb {u} = \pmb {1}^T \pmb {t}_R \pmb {t}_R^T \pmb {u}. \end{aligned}$$

(41)

Using the SBP property (2) and $D \pmb {1} = \pmb {0}$,

$$\begin{aligned} u_+ = \pmb {1}^T \pmb {t}_L \pmb {t}_L^T \pmb {u} + \pmb {1}^T M D \pmb {u} + \pmb {1}^T D^T M \pmb {u} = \pmb {t}_L^T \pmb {u} + \pmb {1}^T M D \pmb {u}. \end{aligned}$$

(42)

Inserting $\pmb {t}_L^T \pmb {u} = u_0$ and $D \pmb {u}$ from (33) results in

$$\begin{aligned} u_+ = u_0 + \pmb {1}^T M \left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) \pmb {f} = u_0 + \pmb {1}^T M \pmb {f} - \frac{\left\langle {\pmb {1},\, \pmb {o}}\right\rangle _M \left\langle {\pmb {o},\, \pmb {f}}\right\rangle _M}{\left| \left| \pmb {o}\right| \right| _M^2}. \end{aligned}$$

(43)

Because of $\pmb {1} \in {\text {im}}D \perp {\text {ker}}D^* \ni \pmb {o}$, we have $\left\langle {\pmb {1},\, \pmb {o}}\right\rangle _M = 0$. Hence,

$$\begin{aligned} u_+ = u_0 + \pmb {1}^T M \pmb {f}. \end{aligned}$$

(44)

Comparing this expression with (40) yields the final assertion for b. $\square$

Lemma 3.16

For nullspace consistent SBP operators, the first row of the Butcher coefficient matrix A in (39) of the method (27) is zero if $\pmb {t}_L = (1, 0, \dots , 0)^T$.

Proof

By definition, $J$ yields a vector with vanishing initial condition at the left endpoint, i.e. $\pmb {t}_L^T J= \pmb {0}^T$. Because of $\pmb {t}_L = (1, 0, \dots , 0)^T$, we have $\pmb {0}^T = \pmb {t}_L^T J= J[1,:]$, which is the first row of $J$, where a notation as in Julia [1] has been used. $\square$

3.4 Operator Construction

To implement the SBP scheme (27), the product $JF$ has to be computed, which is (except for a scaling by $T^{-1}$) the matrix A of the corresponding Runge-Kutta method, cf. Theorem 3.15. Since the projection operator $F$ maps vectors into $V_1 = {\text {im}}D$, the columns of $F$ are in the image of the nullspace consistent SBP derivative operator D. Hence, the matrix equation $D X = F$ can be solved for X, which is a matrix of the same size as D, e.g. via a QR factorization, yielding the least norm solution. Then, we have to ensure that the columns of $JF$ are in $V_0 = {\text {ker}}\pmb {t}_L^T$, since $J$ maps $V_1$ into $V_0$. This can be achieved by subtracting $\pmb {t}_L^T X[:,j]$ from each column X[ : , j] of X, $j \in \{1, \dots , s\}$, where a notation as in Julia [1] has been used. After this correction, we have $X = JF$. Finally, we need to solve (27) for $\pmb {u}$ for each step, using the operator $JF$ constructed as described above.

3.5 Lobatto IIIA Schemes

General characterizations of the SBP-SAT scheme (4) on Radau and Lobatto nodes as classical collocation Runge-Kutta methods (Radau IA and IIA or Lobatto IIIC, respectively) have been obtained in [29]. A similar characterization will be obtained in this section.

Theorem 3.17

If the SBP operator D is given by the nodal polynomial collocation scheme on Lobatto-Legendre nodes, the SBP method (27) is the classical Lobatto IIIA method.

Proof

The Lobatto IIIA methods are given by the nodes c and weights b of the Lobatto-Legendre quadrature, just as the SBP method (27). Hence, it remains to prove that the classical condition C(s) is satisfied [4, Section 344], where

(45)

In other words, all polynomials of degree $\le p = s - 1$ must be integrated exactly by A with vanishing initial value at $t = 0$. By construction of A, see (39), this is satisfied for all polynomials of degree $\le p-1$, since the grid oscillations are given by $\pmb {o}= \pmb {\varphi }_p$, where $\pmb {\varphi }_p$ is the Legendre polynomial of degree p, cf. [38, Example 3.6].

Finally, it suffices to check whether $\pmb {\varphi }_p$ is integrated exactly by A. The left hand side of (45) yields

$$\begin{aligned} A \pmb {\varphi }_p = \frac{1}{T} J\left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) \pmb {\varphi }_p = 0, \end{aligned}$$

(46)

since $\pmb {o}= \pmb {\varphi }_p$. On the right hand side, transforming the time domain to the standard interval $[-1,1]$, the analytical integrand of ${\varphi }_p$ is

$$\begin{aligned} \int _{-1}^x {\varphi }_p(s) {\mathrm{d}}s = \frac{1}{p (p+1)} \int _{-1}^x \partial _s \left[ (s^2 - 1) {\varphi }_p'(s) \right] {\mathrm{d}}s = \frac{1}{p (p+1)} (x^2 - 1) {\varphi }_p'(x), \end{aligned}$$

(47)

since the Legendre polynomials satisfy Legendre’s differential equation

$$\begin{aligned} \partial _x \bigl ( (1 - x^2) \partial _x {\varphi }_p(x) \bigr ) + p (p+1) {\varphi }_p(x) = 0. \end{aligned}$$

(48)

Hence, $\int _{-1}^x {\varphi }_p(s) {\mathrm{d}}s$ vanishes exactly at the $s = p+1$ Legendre nodes for polynomials of degree p, which are $\pm 1$ and the roots of ${\varphi }_p'$. Thus, the analytical integral of ${\varphi }_p$ vanishes at all grid nodes. $\square$

Example 3.18

Continuing Examples 3.4 and 3.11, the nodes $c = \frac{1}{T} (\tau _1, \tau _2)^T = (0, 1)^T$ are the nodes of the Lobatto-Legendre quadrature with two nodes in [0, 1]. Moreover, the corresponding weights are given by

$$\begin{aligned} b = \frac{1}{T} M \pmb {1} = \frac{1}{2} \begin{pmatrix} 1 \\ 1 \end{pmatrix}. \end{aligned}$$

(49)

Finally, the remaining Butcher coefficients are given by

$$\begin{aligned} A = \frac{1}{T} JF= \frac{1}{T} J\left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) = \frac{1}{2} \begin{pmatrix} 0 &{} 0 \\ 1 &{} 1 \end{pmatrix}, \end{aligned}$$

(50)

which are exactly the coefficients of the Lobatto IIIA method with $s = 2$ stages.

Remark 3.19

Since the Lobatto IIIA methods are neither L nor B stable, the new SBP method (27) is in general not L or B stable, too.

Remark 3.20

Because of Lemma 3.16, the classical Gauss, Radau IA, Lobatto IIIB, and Lobatto IIIC methods cannot be expressed in the form (27). The classical Radau I, Radau II, and Radau IIA methods are also not included in the class (27). For example, for two nodes, these methods have the A matrices

$$\begin{aligned} \begin{pmatrix} 0 &{} 0 \\ \nicefrac {1}{3} &{} \nicefrac {1}{3} \end{pmatrix}, \qquad \begin{pmatrix} \nicefrac {1}{3} &{} 0 \\ 1 &{} 0 \end{pmatrix}, \qquad \begin{pmatrix} \nicefrac {5}{12} &{} \nicefrac {-1}{12} \\ \nicefrac {3}{4} &{} \nicefrac {1}{4} \end{pmatrix} \end{aligned}$$

(51)

while the methods (27) on the left and right Radau nodes yield the matrices

$$\begin{aligned} \begin{pmatrix} 0 &{} 0 \\ \nicefrac {1}{6} &{} \nicefrac {1}{2} \end{pmatrix}, \qquad \begin{pmatrix} \nicefrac {1}{4} &{} \nicefrac {1}{12} \\ \nicefrac {3}{4} &{} \nicefrac {1}{4} \end{pmatrix}. \end{aligned}$$

(52)

We develop a related SBP time integration scheme that includes the classical Lobatto IIIB collocation method in the appendix. Additionally, we mention why it seems to be difficult to describe Gauss collocation methods in a general SBP setting, cf. Appendix C.

3.6 Order of Accuracy

Next, we establish results on the order of accuracy of the new class of SBP time integration methods.

Theorem 3.21

For nullspace consistent SBP operators that are pth order accurate with $p \ge 1$, the Runge-Kutta method (39) associated to the SBP time integration scheme (27) has an order of accuracy of

• a) at least p for general mass matrices M.

• b) at least 2p for diagonal mass matrices M.

The technical proof of Theorem 3.21 is given in Appendix A.

Remark 3.22

The result on the order of accuracy given in Theorem 3.21 may appear counterintuitive at first when looking from the perspective of classical finite difference SBP operators, since diagonal norm matrices are usually less accurate in this context. Indeed, finite difference SBP operators for the first derivative with a diagonal norm matrix have an order of accuracy of 2q in the interior and $r \le q$ at the boundaries [17], where usually $r = q$. In contrast, the corresponding dense norm operators have an order of accuracy 2q in the interior and $2q-1$ at the boundaries. Hence, the total order of accuracy $p = q$ for diagonal mass matrices is smaller than the order of accuracy $p = 2q-1$ for dense norms. However, dense norms are not guaranteed to result in the same high order of accuracy when used as a quadrature rule. Thus, the total order of accuracy can be smaller even if the pointwise accuracy as a derivative operator is higher (which basically corresponds to the stage order in the context of Runge-Kutta methods).

4 Numerical Experiments

Numerical experiments corresponding to the ones in [19] will be conducted. The novel SBP methods (27) have been implemented in Julia v1.5 [1] and Matplotlib [14] has been used to generate the plots. The source code for all numerical examples is available online [35]. After computing the operators $A = \frac{1}{T} JF$ as described in Section 3.4 and inserting the right-hand sides f of the ODEs considered in the following into the scheme (27), the resulting linear systems are solved using the backslash operator in Julia.

Numerical experiments are shown only for new SBP methods (27) based on finite difference SBP operators and not for methods based on Lobatto quadrature, since the classical Lobatto IIIA and IIIB schemes are already well-known in the literature. The diagonal norm finite difference SBP operators of [21] use central finite difference stencils in the interior of the domain and adapted boundary closures to satisfy the SBP property (2). The Butcher coefficients of some of these methods are given in Appendix D.

4.1 Non-stiff Problem

The non-stiff test problem

$$\begin{aligned} u'(t) = - u(t), \quad u(0) = 1, \end{aligned}$$

(53)

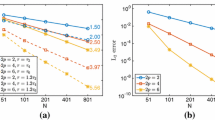
with analytical solution $u(t) = \exp (-t)$ is solved in the time interval [0, 1] using the SBP method (27) with the diagonal norm operators of [21]. The errors of the numerical solutions at the final time are shown in Fig.  1. As can be seen, they converge with an order of accuracy equal to the interior approximation order of the diagonal norm operators. For the operator with interior order eight, the error reaches machine precision for $N = 50$ nodes and does not decrease further. These results are comparable to the ones obtained by SBP-SAT schemes in [19] and match the order of accuracy of the corresponding Runge-Kutta methods guaranteed by Theorem 3.21.

Fig. 1

Convergence behavior of the SBP scheme (27) using the diagonal norm operators of [21] for the non-stiff test problem (53)

4.2 Stiff Problem

The stiff test problem

$$\begin{aligned} u'(t) = \lambda \bigl ( u(t) - \exp (-t) \bigr ) - \exp (-t), \quad u(0) = 1, \end{aligned}$$

(54)

with analytical solution $u(t) = \exp (-t)$ and parameter $\lambda = 1000$ is solved in the time interval [0, 1]. The importance of such test problems for stiff equations has been established in [28]. Using the diagonal norm operators of [21] for the method (27) yields the convergence behavior shown in Fig.  2. Again, the results are comparable to the ones obtained by SBP-SAT schemes in [19]. In particular, the order of convergence is reduced to the approximation order at the boundaries, exactly as for the SBP-SAT schemes of [25]. Such an order reduction for stiff problems is well-known in the literature on time integration methods, see [28] and [12, Chapter IV.15].

Fig. 2

Convergence behavior of the SBP scheme (27) using the diagonal norm operators of [21] for the stiff test problem (54)

5 Summary and Discussion

A novel class of A stable summation by parts time integration methods has been proposed. Instead of using simultaneous approximation terms to impose the initial condition weakly, the initial condition is imposed strongly. Similarly to previous SBP time integration methods, the new schemes can be reformulated as implicit Runge-Kutta methods.

Compared to the SAT approach, some linear and nonlinear stability properties such as L and B stability are lost in general. On the other hand, well-known A stable methods such as the Lobatto IIIA schemes are included in this new SBP framework. Additionally, a related SBP time integration method has been proposed which includes the classical Lobatto IIIB schemes.

This article provides new insights into the relations of numerical methods and contributes to the discussion of whether SBP properties are necessarily involved in numerical schemes for differential equations which are provably stable.

5.1 Final Reflections on Obtained Results

We have concentrated on classical collocation Runge-Kutta methods when looking for known schemes in the new class of SBP time integration methods, since these have direct connections to quadrature rules, which are closely connected to the SBP property [13]. We are not aware of other classical Runge-Kutta methods that are contained in the new class of SBP methods proposed and analyzed in this article besides Lobatto IIIA and IIIB schemes. The implicit equations that need to be solved per time step for the new methods can be easier to solve than the ones occurring in SBP-SAT methods, e.g. since the first stage does not require an implicit solution at all for some methods (Lemma 3.16). On the other hand, the new classes of methods do not necessarily have the same kind of nonlinear stability properties as previous SBP-SAT methods. Hence, a thorough parameter search and comparison of the methods would be necessary for a detailed comparison, which is beyond the scope of this initial article.

In general, methods constructed using SBP operators often imply certain stability properties automatically, which are usually more difficult to guarantee when numerical methods are constructed without these restrictions. On the other hand, not imposing SBP restrictions can possibly result in more degrees of freedom which can be used to construct more flexible and possibly a larger number of numerical methods. From a practical point of view, the availability of numerical algorithms in standard software packages and the efficiency of the implementations are also very important. In this respect, established time integration methods have definitely many advantages, since they are widespread and considerable efforts went into the available implementations. Additionally, a practitioner can choose to make a trade-off between guaranteed stability properties and the efficiency of schemes that “just work” in practice, although only weaker stability results might be available. For example, linearly implicit time integration schemes such as Rosenbrock methods can be very efficient for certain problems.

Having said all that, it is important to note that the process of discretizing differential equations is filled with pitfalls. Potentially unstable schemes may lead to results that seem correct but are in fact erroneous. A provably stable scheme can be seen as a quality stamp.

Appendices

A Proof of Theorem 3.21

Here, we present the technical proof of Theorem 3.21.

Proof of Theorem 3.21

Consider the classical simplifying assumptions

(55)

(56)

(57)

where $B = \mathrm {diag}(\pmb {b})$ is a diagonal matrix. To prove Theorem 3.21, we will use the following result of Butcher [3] for Runge-Kutta methods.

If $B(\xi )$, $C(\eta )$, $D(\zeta )$, $\xi \le 1 + \eta + \zeta$, and $\xi \le 2 + 2\eta$, then the Runge-Kutta method has an order of accuracy at least $\xi$.

• (a) General mass matrices M

  • Proving B(p)

    The quadrature rule given by the weights $\pmb {b} = \frac{1}{T} M \pmb {1}$ of the pth order accurate SBP operator is exact for polynomials of degree $p-1$ for a general norm matrix M [7, Theorem 1]. Hence, B(p) is satisfied.

  • Proving C(p)

    As in the proof of Theorem 3.17, C(p) is satisfied by construction of $A = \frac{1}{T} JF$, since all polynomials of degree $\le p-1$ are integrated exactly by A with vanishing initial value at $t = 0$.

  • Concluding

    Since only B(p) is satisfied in general, the order of the Runge-Kutta method is limited to p and we do not need further conditions on the simplifying assumption $D(\zeta )$. Hence, it suffices to consider the empty condition D(0). Since B(p), $C(p-1)$, and D(0) are satisfied, the result of Butcher cited above implies that the Runge-Kutta method has at least an order of accuracy at least p.

• (b) Diagonal mass matrices M

  • Proving B(2p)

    For a diagonal norm matrix M, the quadrature rule given by the weights $\pmb {b} = \frac{1}{T} M \pmb {1}$ of the pth order accurate SBP operator is exact for polynomials of degree $2p-1$ [7, Theorem 2]. Hence, B(2p) is satisfied.

  • Proving C(p)

    The proof of C(p) is exactly the same as for general mass matrices M.

  • Proving $D(p-1)$

    It suffices to consider a scaled SBP operator such that $T = 1$, $\pmb {t}_L^T \pmb {\tau } = 0$, $\pmb {t}_R^T \pmb {\tau } = 1$. Then, inserting the Runge-Kutta coefficients (39), $D(p-1)$ is satisfied if for all

    $$\begin{aligned} F^T J^T M \pmb {\tau }^{q-1} = \frac{1}{q} M (\pmb {1} - \pmb {\tau }^q). \end{aligned}$$

    (58)

    This equation is satisfied if and only if for all $\pmb {u} \in {\mathbb {R}}^s$

    $$\begin{aligned} \pmb {u}^T F^T J^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {u}^T M (\pmb {1} - \pmb {\tau }^q) = 0. \end{aligned}$$

    (59)

    Every $\pmb {u}$ can be written as $\pmb {u} = D \pmb {v} + \alpha \pmb {o}$, where $\pmb {t}_L^T \pmb {v} = 0$ and $\alpha \in {\mathbb {R}}$, since D is nullspace consistent. Hence, it suffices to consider

    $$\begin{aligned} \begin{aligned}&\quad \pmb {v}^T D^T F^T J^T M \pmb {\tau }^{q-1} + \alpha \pmb {o}^T F^T J^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {v}^T D^T M \pmb {1} - \frac{1}{q} \alpha \pmb {o}^T M \pmb {1} \\&\quad + \frac{1}{q} \pmb {v}^T D^T M \pmb {\tau }^q + \frac{1}{q} \alpha \pmb {o}^T M \pmb {\tau }^q \\&= \pmb {v}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {v}^T D^T M \pmb {1} + \frac{1}{q} \pmb {v}^T D^T M \pmb {\tau }^q. \end{aligned} \end{aligned}$$

    (60)

    Here, we used that $JFD \pmb {v} = \pmb {v}$ by definition of $\pmb {v} \in V_0 = {\text {ker}}\pmb {t}_L^T$. The filter $F$ removes grid oscillations, i.e. $F\pmb {o}= \pmb {0}$. Additionally, grid oscillations are orthogonal to the constant $\pmb {1}$ for SBP operators that are at least first-order accurate and orthogonal to $\pmb {\tau }^q$ for $q \le p-1$ in general (since $D \pmb {\tau }^p = p \pmb {\tau }^{p-1}$).

    Using the SBP property (2), the expression above can be rewritten as

    $$\begin{aligned} \begin{aligned}&\quad \pmb {v}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {v}^T D^T M \pmb {1} + \frac{1}{q} \pmb {v}^T D^T M \pmb {\tau }^q \\&= \pmb {v}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {t}_R^T \pmb {v} + \frac{1}{q} \pmb {v}^T \pmb {t}_R - \frac{1}{q} \pmb {v}^T M D \pmb {\tau }^q = 0, \end{aligned} \end{aligned}$$

    (61)

    where we used $\pmb {t}_L^T \pmb {v} = 0$, $\pmb {t}_R^T \pmb {\tau }^q = 1$, and the accuracy of D. This proves $D(p-1)$.

  • Concluding

    Since B(2p), C(p), and $D(p-1)$ are satisfied, the result of Butcher cited above guarantees an order of accuracy of at least 2p.

$\square$

Remark A.1

The simplifying assumptions used in the proof of Theorem 3.21 can be satisfied to higher order of accuracy. For example, the Lobatto IIIA methods satisfy $C(p+1)$ instead of only C(p), cf. the proof of Theorem 3.17. In that case, the order of the associated quadrature still limits the order of the corresponding Runge-Kutta method to 2p.

Similarly, the method based on left Radau quadrature mentioned in Example 3.20 has Butcher coefficients

$$\begin{aligned} A = \begin{pmatrix} 0 &{} 0 \\ \nicefrac {1}{6} &{} \nicefrac {1}{2} \end{pmatrix}, \quad b = \begin{pmatrix} \nicefrac {1}{4} \\ \nicefrac {3}{4} \end{pmatrix}, \quad c = \begin{pmatrix} 0 \\ \nicefrac {2}{3} \end{pmatrix}. \end{aligned}$$

(62)

Thus, the quadrature condition is satisfied to higher order of accuracy, i.e. B(3) holds instead of only B(2) for $p = 1$. Nevertheless, the Runge-Kutta method is only second-order accurate, i.e. it satisfies the order conditions

$$\begin{aligned} b^T \pmb {1} = 1, \quad b^T A \pmb {1} = \frac{1}{2}, \end{aligned}$$

(63)

but violates one of the additional conditions for a third-order accurate method, i.e.

$$\begin{aligned} b^T (A \pmb {1})^2 = \frac{1}{3}, \quad b^T A^2 \pmb {1} = \frac{1}{4} \ne \frac{1}{6}, \end{aligned}$$

(64)

since neither $C(p+1)$ nor D(p) is satisfied.

B An Example Using Gauss Quadrature

Here, we follow the derivation of the scheme presented in Sect. 3 using a more complicated SBP operator that does not include any boundary node. Consider the SBP operator of order $p = 2$ induced by classical Gauss-Legendre quadrature on [0, T], using the nodes

$$\begin{aligned} \tau _1 = \frac{T}{10} (5 - \sqrt{15}), \quad \tau _2 = \frac{T}{2}, \quad \tau _3 = \frac{T}{10} (5 + \sqrt{15}). \end{aligned}$$

(65)

The associated SBP operator exactly differentiating polynomials of degree $p = 2$ is given by

$$\begin{aligned} D = \frac{\sqrt{15}}{3 T} \begin{pmatrix} -3 &{} 4 &{} -1 \\ -1 &{} 0 &{} 1 \\ 1 &{} -4 &{} 3 \end{pmatrix}, \quad M = \frac{T}{18} \begin{pmatrix} 5 \\ &{} 8 \\ &{}&{} 5 \end{pmatrix}, \quad \pmb {t}_L = \frac{1}{6} \begin{pmatrix} 5 + \sqrt{15} \\ -4 \\ 5 - \sqrt{15} \end{pmatrix}, \quad \pmb {t}_R = \frac{1}{6} \begin{pmatrix} 5 - \sqrt{15} \\ -4 \\ 5 + \sqrt{15} \end{pmatrix}.\nonumber \\ \end{aligned}$$

(66)

Therefore,

$$\begin{aligned} D^* = M^{-1} D^T M = \frac{\sqrt{15}}{30 T} \begin{pmatrix} -30 &{} -16 &{} 10 \\ 25 &{} 0 &{} -25 \\ -10 &{} 16 &{} 30 \end{pmatrix} \end{aligned}$$

(67)

and ${\text {ker}}D^* = {\text {span}}\{ \pmb {o}\}$, where $\pmb {o}= (4, -5, 4)^T$ represents the highest resolvable grid oscillation; $\pmb {o}$ is orthogonal to ${\text {im}}D$, since $\pmb {o}^T M D = \pmb {0}^T$. The adjoint of $\pmb {o}$ is

$$\begin{aligned} \pmb {o}^* = \pmb {o}^T M = \frac{10 T}{9} (1, -2, 1). \end{aligned}$$

(68)

Thus, the filter/projection operator (25) is

$$\begin{aligned} F= {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} = \frac{1}{18} \begin{pmatrix} 14 &{} 8 &{} -4 \\ 5 &{} 8 &{} 5 \\ -4 &{} 8 &{} 14 \end{pmatrix}. \end{aligned}$$

(69)

The vector spaces $V_0$, $V_1$ associated to the given SBP operator are

(70)

To verify this, observe that both vector spaces are two-dimensional, $V_0$ is the nullspace of $\pmb {t}_L^T$, and $V_1$ is the nullspace of $\pmb {o}^*$.

At the level of ${\mathbb {R}}^3$, the inverse J of D can be represented as

$$\begin{aligned} J = \frac{3 T}{24 \sqrt{15}} \begin{pmatrix} 2 &{} 4 (\sqrt{15} - 3) &{} -2 \\ 5 &{} 4 \sqrt{15} &{} -5 \\ 2 &{} 4 (\sqrt{15} + 3) &{} -2 \end{pmatrix}. \end{aligned}$$

(71)

Indeed, for $\pmb {u} = ( \alpha _1, \alpha _2, -(4 + \sqrt{15}) \alpha _1 + 2 (5 + \sqrt{15}) \alpha _2 / 5 )^T$, $\alpha _1, \alpha _2 \in {\mathbb {R}}$,

$$\begin{aligned} J D \pmb {u} = \frac{1}{6} \begin{pmatrix} 1 - \sqrt{15} &{} 4 &{} -5 + \sqrt{15} \\ -5 - \sqrt{15} &{} 10 &{} -5 + \sqrt{15} \\ -5 - \sqrt{15} &{} 4 &{} 1 + \sqrt{15} \end{pmatrix} \begin{pmatrix} \alpha _1 \\ \alpha _2 \\ -(4 + \sqrt{15}) \alpha _1 + 2 (5 + \sqrt{15}) \alpha _2 / 5 \end{pmatrix} = \pmb {u}\nonumber \\ \end{aligned}$$

(72)

and similarly for $\pmb {u} = ( \beta _1, \beta _2, -\beta _1 + 2 \beta _2 )^T$, $\beta _1, \beta _2 \in {\mathbb {R}}$,

$$\begin{aligned} D J \pmb {u} = \frac{1}{2} \begin{pmatrix} 1 &{} 2 &{} -1 \\ - &{} 2 &{} 0 \\ -1 &{} 2 &{} 1 \end{pmatrix} \begin{pmatrix} \beta _1 \\ \beta _2 \\ -\beta _1 + 2 \beta _2 \end{pmatrix} = \pmb {u}. \end{aligned}$$

(73)

Hence, $J D = {\text {id}}_{V_0}$ and $D J = {\text {id}}_{V_1}$, where ${\text {id}}_{V_i}$ is the identity on $V_i$.

Since the filter $F$ removes the highest grid oscillations and maps a grid function into the image of the derivative operator D, the inverse J can be applied after $F$, resulting in

$$\begin{aligned} J F = \frac{T}{72 \sqrt{15}} \begin{pmatrix} -12 + 10 \sqrt{15} &{} -48 + 16 \sqrt{15} &{} -48 + 10 \sqrt{15} \\ 45 + 10 \sqrt{15} &{} 16 \sqrt{15} &{} -45 + 10 \sqrt{15} \\ 48 + 10 \sqrt{15} &{} 48 + 16 \sqrt{15} &{} 12 + 10 \sqrt{15} \end{pmatrix}. \end{aligned}$$

(74)

Thus, the Butcher coefficients associated to the new SBP projection method given by Theorem 3.15 are

$$\begin{aligned} \begin{aligned} A&= \frac{1}{T} J F= \frac{1}{72 \sqrt{15}} \begin{pmatrix} -12 + 10 \sqrt{15} &{} -48 + 16 \sqrt{15} &{} -48 + 10 \sqrt{15} \\ 45 + 10 \sqrt{15} &{} 16 \sqrt{15} &{} -45 + 10 \sqrt{15} \\ 48 + 10 \sqrt{15} &{} 48 + 16 \sqrt{15} &{} 12 + 10 \sqrt{15} \end{pmatrix}, \\ b&= \frac{1}{T} M \pmb {1} = \frac{1}{18} \begin{pmatrix} 5 \\ 8 \\ 5 \end{pmatrix}, \qquad c = \frac{1}{T} (\tau _1, \tau _2, \tau _3)^T = \frac{1}{10} \begin{pmatrix} 5 - \sqrt{15} \\ 5 \\ 5 + \sqrt{15} \end{pmatrix}. \end{aligned} \end{aligned}$$

(75)

Note that the coefficients in A are different from those of the classical Runge-Kutta Gauss-Legendre collocation method (while b and c are the same by construction), see also Remark C.4 below. In particular, this method is fourth-order accurate while the classical Gauss-Legendre collocation method with the same number of stages is of order six.

C Lobatto IIIB Schemes

Another scheme similar to (27) can be constructed by considering $-D$ as bijective operator acting on functions that vanish at the right endpoint. The equivalent of J, the inverse of D mapping ${\text {im}}D$ to the space of grid functions vanishing at the left endpoint, in this context is written as ${\tilde{J}}$, which is the inverse of $-D$ mapping ${\text {im}}(-D)$ to the space of grid functions vanishing at the right endpoint. The corresponding matrix A of the Runge-Kutta method becomes

$$\begin{aligned} A = A^{**} = M^{-1} \bigl ( A^* \bigr )^T M, \quad A^* = \frac{1}{T} {\tilde{J}}\left( {\text {I}}- \frac{\pmb {o}\pmb {o}^*}{\left| \left| \pmb {o}\right| \right| _M^2} \right) . \end{aligned}$$

(76)

Using A of (76) and b, c as in (39), the scheme is defined as the Runge-Kutta method (6) with these Butcher coefficients A, b, c.

Theorem C.1

If the SBP derivative operator D is given by the nodal polynomial collocation scheme on Lobatto-Legendre nodes, the Runge-Kutta method (6) with A as in (76) and b, c as in (39) is the classical Lobatto IIIB method.

Proof

The Lobatto IIIB methods are given by the nodes c and weights b of the Lobatto-Legendre quadrature, just as the SBP method. Hence, it remains to prove that the classical condition D(s) is satisfied [4, Section 344], where

(77)

In matrix vector notation, this can be written as

$$\begin{aligned} A^T M \pmb {c}^{q-1} = \frac{1}{q} M (\pmb {1} - \pmb {c}^q) \iff \underbrace{M^{-1} A^T M}_{=A^*} \pmb {c}^{q-1} = \frac{1}{q} (\pmb {1} - \pmb {c}^q), \end{aligned}$$

(78)

where the exponentiation $\pmb {c}^q$ is performed pointwise.

In other words, all polynomials of degree $\le p$ must be integrated exactly by $A^*$ with vanishing final value at $t = 1$. By construction of A, this is satisfied for all polynomials of degree $\le p-1$, and the proof can be continued as the one of Theorem 3.17. $\square$

Remark C.2

Remarks 3.19 and 3.20 hold analogously: Schemes based on (76) are also in general not L or B stable and other classical schemes on Gauss, Radau, or Lobatto nodes are not included in this class.

Similarly to Theorem 3.21, we present some results on the order of accuracy of the new SBP methods. Since this class of methods is made to satisfy the simplifying condition $D(\zeta )$ instead of $C(\eta )$ and stronger results on $C(\eta )$ are necessary to apply the results of Butcher [3], we concentrate on diagonal norms.

Theorem C.3

For nullspace consistent SBP operators that are pth order accurate with $p \ge 1$ and a diagonal norm matrix M, the Runge-Kutta method associated to the SBP time integration scheme (76) has an order of accuracy of at least 2p.

Proof

This proof is very similar to the one of Theorem 3.21. By construction, the simplifying conditions B(2p) and D(p) are satisfied. Hence, the order of accuracy is at least 2p if $C(p-1)$ is satisfied.

Again, suffices to consider a scaled SBP operator such that $T = 1$, $\pmb {t}_L^T \pmb {\tau } = 0$, $\pmb {t}_R^T \pmb {\tau } = 1$. Then, inserting the Runge-Kutta coefficients (76), $C(p-1)$ is satisfied if for all

$$\begin{aligned} M^{-1} F^T {\tilde{J}}M \pmb {\tau }^{q-1} = \frac{1}{q} \pmb {\tau }^q. \end{aligned}$$

(79)

This equation is satisfied if and only if for all $\pmb {u} \in {\mathbb {R}}^s$

$$\begin{aligned} \pmb {u}^T F^T {\tilde{J}}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {u}^T M \pmb {\tau }^q = 0. \end{aligned}$$

(80)

Every $\pmb {u}$ can be written as $\pmb {u} = D \pmb {v} + \alpha \pmb {o}$, where $\pmb {t}_R^T \pmb {v} = 0$ and $\alpha \in {\mathbb {R}}$, since D is nullspace consistent. Hence, it suffices to consider

$$\begin{aligned} \begin{aligned}&\quad \pmb {v}^T D^T F^T {\tilde{J}}^T M \pmb {\tau }^{q-1} \alpha \pmb {o}^T F^T {\tilde{J}}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {v}^T D^T M \pmb {\tau }^q - \frac{1}{q} \alpha \pmb {o}^T M \pmb {\tau }^q \\&= - \pmb {v}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {v}^T D^T M \pmb {\tau }^q \\&= - \pmb {v}^T M \pmb {\tau }^{q-1} - \frac{1}{q} \pmb {v}^T (\pmb {t}_R \pmb {t}_R^T - \pmb {t}_L \pmb {t}_L^T - M D) \pmb {\tau }^q \\&= - \pmb {v}^T M \pmb {\tau }^{q-1} _ \frac{1}{q} \pmb {v}^T - M D \pmb {\tau }^q - 0. \end{aligned} \end{aligned}$$

(81)

This proves $C(p-1)$. $\square$

Remark C.4

Up to now, it is unclear whether the classical collocation Runge-Kutta schemes on Gauss nodes can be constructed as special members of a family of schemes that can be formulated for (more) general SBP operators. The problem seems to be that SBP schemes rely on differentiation, while the conditions C(s) and D(s) describing the Runge-Kutta methods rely on integration. Thus, special compatibility conditions as in the proof of Theorem 3.17 are necessary. To the authors’ knowledge, no insights in this direction have been achieved for Gauss methods.

D Butcher Coefficients of some Finite Difference SBP Methods

Here, we provide the Butcher coefficients given by Theorem 3.15 for some of the finite difference SBP methods used in the numerical experiments in Sect. 4.

• Interior order 2, $N = 3$ nodes

  $$\begin{aligned} A = \begin{pmatrix} 0 &{} 0 &{} 0 \\ \nicefrac {3}{8} &{} \nicefrac {1}{4} &{} \nicefrac {-1}{8} \\ \nicefrac {1}{4} &{} \nicefrac {1}{2} &{} \nicefrac {1}{4} \\ \end{pmatrix}, \quad b = \begin{pmatrix} \nicefrac {1}{4} \\ \nicefrac {1}{2} \\ \nicefrac {1}{4} \\ \end{pmatrix}, \quad c = \begin{pmatrix} 0 \\ \nicefrac {1}{2} \\ 1 \\ \end{pmatrix} \end{aligned}$$

  (82)

• Interior order 2, $N = 9$ nodes

  $$\begin{aligned} A = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \nicefrac {15}{128} &{} \nicefrac {1}{64} &{} \nicefrac {-1}{64} &{} \nicefrac {1}{64} &{} \nicefrac {-1}{64} &{} \nicefrac {1}{64} &{} \nicefrac {-1}{64} &{} \nicefrac {1}{64} &{} \nicefrac {-1}{128} \\ \nicefrac {1}{64} &{} \nicefrac {7}{32} &{} \nicefrac {1}{32} &{} \nicefrac {-1}{32} &{} \nicefrac {1}{32} &{} \nicefrac {-1}{32} &{} \nicefrac {1}{32} &{} \nicefrac {-1}{32} &{} \nicefrac {1}{64} \\ \nicefrac {13}{128} &{} \nicefrac {3}{64} &{} \nicefrac {13}{64} &{} \nicefrac {3}{64} &{} \nicefrac {-3}{64} &{} \nicefrac {3}{64} &{} \nicefrac {-3}{64} &{} \nicefrac {3}{64} &{} \nicefrac {-3}{128} \\ \nicefrac {1}{32} &{} \nicefrac {3}{16} &{} \nicefrac {1}{16} &{} \nicefrac {3}{16} &{} \nicefrac {1}{16} &{} \nicefrac {-1}{16} &{} \nicefrac {1}{16} &{} \nicefrac {-1}{16} &{} \nicefrac {1}{32} \\ \nicefrac {11}{128} &{} \nicefrac {5}{64} &{} \nicefrac {11}{64} &{} \nicefrac {5}{64} &{} \nicefrac {11}{64} &{} \nicefrac {5}{64} &{} \nicefrac {-5}{64} &{} \nicefrac {5}{64} &{} \nicefrac {-5}{128} \\ \nicefrac {3}{64} &{} \nicefrac {5}{32} &{} \nicefrac {3}{32} &{} \nicefrac {5}{32} &{} \nicefrac {3}{32} &{} \nicefrac {5}{32} &{} \nicefrac {3}{32} &{} \nicefrac {-3}{32} &{} \nicefrac {3}{64} \\ \nicefrac {9}{128} &{} \nicefrac {7}{64} &{} \nicefrac {9}{64} &{} \nicefrac {7}{64} &{} \nicefrac {9}{64} &{} \nicefrac {7}{64} &{} \nicefrac {9}{64} &{} \nicefrac {7}{64} &{} \nicefrac {-7}{128} \\ \nicefrac {1}{16} &{} \nicefrac {1}{8} &{} \nicefrac {1}{8} &{} \nicefrac {1}{8} &{} \nicefrac {1}{8} &{} \nicefrac {1}{8} &{} \nicefrac {1}{8} &{} \nicefrac {1}{8} &{} \nicefrac {1}{16} \\ \end{pmatrix}, \quad b = \begin{pmatrix} \nicefrac {1}{16} \\ \nicefrac {1}{8} \\ \nicefrac {1}{8} \\ \nicefrac {1}{8} \\ \nicefrac {1}{8} \\ \nicefrac {1}{8} \\ \nicefrac {1}{8} \\ \nicefrac {1}{8} \\ \nicefrac {1}{16} \\ \end{pmatrix}, \quad c = \begin{pmatrix} 0 \\ \nicefrac {1}{8} \\ \nicefrac {1}{4} \\ \nicefrac {3}{8} \\ \nicefrac {1}{2} \\ \nicefrac {5}{8} \\ \nicefrac {3}{4} \\ \nicefrac {7}{8} \\ 1 \\ \end{pmatrix}\nonumber \\ \end{aligned}$$

  (83)

• Interior order 4, $N = 9$ nodes

  $$\begin{aligned} A= & {} \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \nicefrac {13}{180} &{} \nicefrac {18}{385} &{} \nicefrac {1}{2044} &{} \nicefrac {2}{211} &{} \nicefrac {-3}{371} &{} \nicefrac {1}{124} &{} \nicefrac {-3}{317} &{} \nicefrac {2}{215} &{} \nicefrac {-1}{267} \\ \nicefrac {5}{434} &{} \nicefrac {60}{271} &{} \nicefrac {3}{103} &{} \nicefrac {-7}{283} &{} \nicefrac {3}{118} &{} \nicefrac {-7}{283} &{} \nicefrac {3}{103} &{} \nicefrac {-20}{699} &{} \nicefrac {5}{434} \\ \nicefrac {17}{265} &{} \nicefrac {37}{361} &{} \nicefrac {37}{228} &{} \nicefrac {13}{230} &{} \nicefrac {-4}{157} &{} \nicefrac {7}{244} &{} \nicefrac {-7}{211} &{} \nicefrac {3}{92} &{} \nicefrac {-4}{305} \\ \nicefrac {11}{408} &{} \nicefrac {11}{56} &{} \nicefrac {47}{689} &{} \nicefrac {99}{614} &{} \nicefrac {1}{16} &{} \nicefrac {-11}{327} &{} \nicefrac {13}{297} &{} \nicefrac {-8}{187} &{} \nicefrac {5}{289} \\ \nicefrac {7}{122} &{} \nicefrac {42}{347} &{} \nicefrac {109}{751} &{} \nicefrac {37}{374} &{} \nicefrac {31}{206} &{} \nicefrac {29}{408} &{} \nicefrac {-8}{159} &{} \nicefrac {20}{391} &{} \nicefrac {-7}{352} \\ \nicefrac {15}{458} &{} \nicefrac {39}{214} &{} \nicefrac {29}{350} &{} \nicefrac {39}{256} &{} \nicefrac {24}{241} &{} \nicefrac {39}{256} &{} \nicefrac {29}{350} &{} \nicefrac {-21}{310} &{} \nicefrac {15}{458} \\ \nicefrac {23}{479} &{} \nicefrac {55}{381} &{} \nicefrac {17}{140} &{} \nicefrac {41}{343} &{} \nicefrac {35}{263} &{} \nicefrac {43}{364} &{} \nicefrac {32}{287} &{} \nicefrac {31}{290} &{} \nicefrac {-9}{322} \\ \nicefrac {12}{271} &{} \nicefrac {57}{371} &{} \nicefrac {43}{384} &{} \nicefrac {43}{337} &{} \nicefrac {1}{8} &{} \nicefrac {43}{337} &{} \nicefrac {43}{384} &{} \nicefrac {57}{371} &{} \nicefrac {12}{271} \\ \end{pmatrix},\nonumber \\ b= & {} \begin{pmatrix} \nicefrac {17}{384} \\ \nicefrac {59}{384} \\ \nicefrac {43}{384} \\ \nicefrac {49}{384} \\ \nicefrac {1}{8} \\ \nicefrac {49}{384} \\ \nicefrac {43}{384} \\ \nicefrac {59}{384} \\ \nicefrac {17}{384} \\ \end{pmatrix}, \; c = \begin{pmatrix} 0 \\ \nicefrac {1}{8} \\ \nicefrac {1}{4} \\ \nicefrac {3}{8} \\ \nicefrac {1}{2} \\ \nicefrac {5}{8} \\ \nicefrac {3}{4} \\ \nicefrac {7}{8} \\ 1 \\ \end{pmatrix}\nonumber \\ \end{aligned}$$

  (84)