Optimization Modeling and Simulating of the Stationary Wigner Inflow Boundary Value Problem

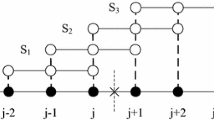
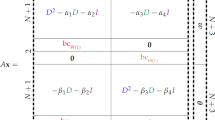Abstract

The stationary Wigner inflow boundary value problem (SWIBVP) is modeled as an optimization problem by using the idea of shooting method in this paper. To remove the singularity at $v=0$, we consider a regularized SWIBVP, where a regularization constraint is considered along with the original SWIBVP, and a modified optimization problem is established for it. A shooting algorithm is proposed to solve the two optimization problems, involving the limited-memory BFGS (L-BFGS) algorithm as the optimization solver. Numerical results show that solving the optimization problems with respect to the SWIBVP with the shooting algorithm is as effective as solving the SWIBVP with Frensley’s numerical method (Frensley in Phys Rev B 36:1570–1580, 1987). Furthermore, the modified optimization problem gets rid of the singularity at $v=0$, and preserves symmetry of the Wigner function, which implies the optimization modeling with respect to the regularized SWIBVP is successful.

Appendices

Proof of Lemma 1

Proof

By the Whittaker–Shannon interpolation formula, P(v) can be reformulated as the series

$$\begin{aligned} P(v)= \sum _{n=-\infty }^{\infty } P(v_n) \frac{\sin (B(v-v_n))}{B(v-v_n)} , \end{aligned}$$

(41)

where $\{v_n: v_n=n\varDelta v+s,\varDelta v= \pi /B, n\in {\mathbb {Z}}\}$ are uniform discrete points with a shift s.

Let ${\mathcal {F}}[\cdot ]$ and ${\mathcal {F}}^{-1}[\cdot ]$ stand for the Fourier transform and the corresponding inverse Fourier transform respectively. Define $g(v)= P(v)\mathbin {*} Q(v)$, then it can be written as

$$\begin{aligned} \begin{aligned} g(v)&= {\mathcal {F}}^{-1} [{\widehat{P}}(y)] \mathbin {*} {\mathcal {F}}^{-1} [{\widehat{Q}}(y)] \\&= {\mathcal {F}}^{-1}[{\widehat{P}}(y) {\widehat{Q}}(y)] \\&= {\mathcal {F}}^{-1}_{y\rightarrow v} [{\widehat{P}}(y) {\widehat{Q}}(y) \chi _{[-B,B]}(y)], \end{aligned} \end{aligned}$$

(42)

where ${\widehat{P}}(y)={\mathcal {F}}[P(v)]$, ${\widehat{Q}}(y)={\mathcal {F}}[Q(v)]$ and

$$\begin{aligned} \chi _{[-B,B]}(y)=\left\{ \begin{array}{cl} 1, &{} y\in [-B,B], \\ 0, &{} others. \end{array} \right. \end{aligned}$$

It is easy to see that ${\widehat{g}}(y)={\mathcal {F}}[g(v)]$ also has compact support on $[-B,B]$ and by the Whittaker–Shannon interpolation formula, we have

$$\begin{aligned} g(v) = \sum _{n=-\infty }^\infty g(v_n) \frac{\sin (B(v-v_n))}{B(v-v_n)}, \end{aligned}$$

(43)

Denote Q(v; B) as the inverse Fourier transform of ${\widehat{Q}}(y)\chi _{[-B,B]}(y)$, i.e.,

$$\begin{aligned} Q(v;B) = \frac{1}{2\pi } \int _{-B}^{B} {\widehat{Q}}(y) e^{ivy} \,\mathrm {d}y. \end{aligned}$$

Recalling the Whittaker–Shannon interpolation formula, Q(v; B) is reformulated as

$$\begin{aligned} Q(v;B) =\sum _{n=-\infty }^\infty Q({\widetilde{v}}_n;L_y) \frac{\sin (B(v-{{\widetilde{v}}}_n))}{B(v-{{\widetilde{v}}}_n)} \end{aligned}$$

(44)

where ${\widetilde{v}}_n= n\varDelta v$ and $\varDelta v =\pi /B$.

Next, we give the value of $g(v_n)$. Substituting (41) and (44) into the definition of $g(v_n)$, we obtain

$$\begin{aligned} \begin{aligned} g(v_n)&= \int _{-\infty }^\infty Q(v_n-v')P(v') \,\mathrm {d}v' = \int _{-\infty }^\infty Q(v_n-v';B)P(v') \,\mathrm {d}v'\\&= \int _{-\infty }^\infty \sum _{m=-\infty }^\infty Q({\widetilde{v}}_m;B) \frac{\sin (B(v_n-v'-\widetilde{v}_m))}{B(v_n-v'-{{\widetilde{v}}}_m)} \sum _{n=-\infty }^{\infty } P(v_k) \frac{\sin (B(v'-v_k))}{B(v'-v_k)} \,\mathrm {d}v' \\&= \sum _{m=-\infty }^\infty \sum _{n=-\infty }^{\infty } Q({\widetilde{v}}_m;B) P(v_k) \int _{-\infty }^\infty \frac{\sin (B(v_{n-m}-v'))}{B(v_{n-m}-v')} \frac{\sin (B(v'-v_k))}{B(v'-v_k)} \,\mathrm {d}v' \\&= \sum _{m=-\infty }^\infty \sum _{n=-\infty }^{\infty } Q({\widetilde{v}}_m;B) P(v_k) \varDelta v \delta _{n-m,k} \\&= \sum _{k=-\infty }^\infty Q({\widetilde{v}}_{n-k};B) P(v_k) \varDelta v , \end{aligned} \end{aligned}$$

where $\delta _{m,k}$ is the Kronecker delta function. $\square$

Proof of Theorem 1

Proof

If $V(\frac{L}{2}+x) = V(\frac{L}{2}-x)$, then we have

$$\begin{aligned} V_w\left( \frac{L}{2}+x,{\widetilde{v}}_k;L_y\right) =-V_w(\frac{L}{2}-x,{\widetilde{v}}_k;L_y), \end{aligned}$$

that is to say,

$$\begin{aligned} {\varvec{W}}\left( \frac{L}{2}+x\right) = -{\varvec{W}}\left( \frac{L}{2}-x\right) . \end{aligned}$$

(45)

Now we consider a final value problem

$$\begin{aligned} \text {(FVP)}\qquad \left\{ \begin{array}{ll} {\varvec{f}}_x-{\varvec{T}}^{-1}{\varvec{W}}(x){\varvec{f}} =0, &{} 0\leqslant x\leqslant \frac{L}{2} ,\\ {\varvec{f}}(\frac{L}{2})={\varvec{h}},&{} \end{array} \right. \end{aligned}$$

(46)

and an initial value problem

$$\begin{aligned} \text {(IVP)}\qquad \left\{ \begin{array}{ll} {\varvec{f}}_x-{\varvec{T}}^{-1}{\varvec{W}}(x){\varvec{f}} =0, &{} \frac{L}{2}\leqslant x \leqslant L ,\\ {\varvec{f}}(\frac{L}{2})={\varvec{h}} .&{} \end{array} \right. \end{aligned}$$

(47)

Introduce ${\varvec{z}}(x)={\varvec{f}}(\frac{L}{2}-x)$ , and the (FVP) (46) can be transformed into an initial value problem for ${\varvec{z}}(x)$ ,

$$\begin{aligned} \left\{ \begin{array}{ll} -{\varvec{z}}_x-{\varvec{T}}^{-1}{\varvec{W}}(\frac{L}{2}-x){\varvec{z}} =0, &{} 0\leqslant x \leqslant \frac{L}{2} ,\\ {\varvec{z}}(0)={\varvec{h}} .&{} \end{array} \right. \end{aligned}$$

(48)

which is equivalent to

$$\begin{aligned} \text {(IVP*)}\qquad \left\{ \begin{array}{ll} {\varvec{z}}_x-{\varvec{T}}^{-1}{\varvec{W}}(\frac{L}{2}+x){\varvec{z}} =0, &{} 0\leqslant x \leqslant \frac{L}{2} ,\\ {\varvec{z}}(0)={\varvec{h}} .&{} \end{array} \right. \end{aligned}$$

(49)

by using the relation (45). Therefore, the (FVP) is equivalent to the (IVP*) if setting ${\varvec{z}}(x)={\varvec{f}}(\frac{L}{2}-x)$ in (46). Similarly, the (IVP) is also equivalent to the (IVP*) if setting ${\varvec{z}}(x)={\varvec{f}}(x-\frac{L}{2})$ in (47). In other word, if $\varvec{\psi }(x)$ is a solution of the (IVP*), then the solution of the (FVP) is

$$\begin{aligned} {\varvec{f}}(x) = \varvec{\psi }\left( \frac{L}{2}-x\right) ,\qquad 0 \leqslant x \leqslant \frac{L}{2} \end{aligned}$$

and the solution of the (IVP) is

$$\begin{aligned} {\varvec{f}}(x) = \varvec{\psi }\left( \frac{L}{2}+x\right) ,\qquad \frac{L}{2} \leqslant x \leqslant L. \end{aligned}$$

It is then concluded that ${\varvec{f}}(\frac{L}{2}-x) = {\varvec{f}}(\frac{L}{2}+x)$ for all $x\in [0,L]$. $\square$