Abstract
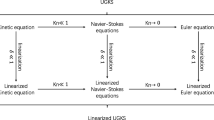
This paper aims at the simulation of multiple scale physics for the system of radiation hydrodynamics. The system couples the fluid dynamic equations with the radiative heat transfer. The coupled system is solved by the gas-kinetic scheme (GKS) for the compressible inviscid Euler flow and the unified gas-kinetic scheme (UGKS) for the non-equilibrium radiative transfer, together with the momentum and energy exchange between these two phases. For the radiative transfer, due to the possible large variation of fluid opacity in different regions, the transport of photons through the flow system is simulated by the multiscale UGKS, which is capable of naturally capturing the transport process from the photon’s free streaming to the diffusive wave propagation. Since both GKS and UGKS are finite volume methods, all unknowns are defined inside each control volume and are discretized consistently in the updates of hydrodynamic and radiative variables. For the coupled system, the scheme has the asymptotic preserving property, such as recovering the equilibrium diffusion limit for the radiation hydrodynamic system in the optically thick region, where the cell size is not limited by photon’s mean free path. A few test cases, such as radiative shock wave problems, are used to validate the current approach.





Similar content being viewed by others
References
Mihala, D., Mihala, B.W.: Foundations of Radiation Hydrodynamics. Oxford University Press, New York (1984)
Lowrie, R.B., Morel, J.E., Hittinger, J.A.: The coupling of radiation and hydrodynamics. Astrophys. J. 521, 432–450 (1999)
Lowrie, R.B., Wollaber, A.B.: Simple material-motion corrections for thermal radiactive transport. In: 23rd International Conference on Transport Theory, Santa Fe, NM, USA, 15–20 September 2013
McClarren, R.G., Evans, T.M., Lowrie, R.B., Densmore, J.D.: Semi-implicit time integration for Pn thermal radiative transfer. J. Comput. Phys. 227, 7561–7586 (2008)
Lowrie, R.B.: A comparison of implicit time integration methods for nonlinear relaxation and diffusion. J. Comput. Phys. 196, 566–590 (2004)
Knoll, D.A., Lowrie, R.B., Morel, J.E.: Numerical analysis of time integration errors for nonequilibrium radiation diffusion. J. Comput. Phys. 226, 1332–1347 (2007)
Olson, G.L.: Second-order time evolution of Pn equations for radiation transport. J. Comput. Phys. 228, 3027–3083 (2009)
Axelrod, T.S., Dubois, P.F., Rhoades Jr., C.E.: An implicit scheme for calculating time- and fequency-dependent flux limited radiation diffusion in one dimension. J. Comput. Phys. 54, 205–220 (1984)
Stone, J.M., Mihalas, D.: Upwind monotonic interpolation methods for the solution of the time dependent radiative transfer equation. J. Comput. Phys. 100, 402–408 (1992)
Brown, P.N., Shumaker, D.E., Woodward, C.S.: Fully implicit solution of large-scale non-equilibrium radiation diffusion with high order time integration. J. Comput. Phys. 204, 760–783 (2005)
Sun, W.J., Jiang, S., Xu, K.: An asymptotic preserving unified gas kinetic scheme for gray radiative transfer equations. J. Comput. Phys. 285, 265–279 (2015)
Sun, W.J., Jiang, S., Xu, K., Li, S.: An asymptotic preserving unified gas kinetic scheme for frequency-dependent radiative transfer equations. J. Comput. Phys. 302, 222–238 (2015)
Sun, W.J., Jiang, S., Xu, K.: An implicit unified gas kinetic scheme for radiative transfer with equilibrium and non-equilibrium diffusive limits. Commun. Comput. Phys. 22, 899–912 (2017)
Toro, E.: Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer, New York (1999)
Xu, K.: A gas-kinetic BGK scheme for the Navier–Stokes equations and its connection with artifical dissipation and Godunov method. J. Comput. Phys. 171, 289–335 (2001)
Kadioglu, S.Y., Knoll, D.A., Lowrie, R.B., Rauenzahn, R.M.: A second order self-consistent IMEX method for radiation hydrodynamics. J. Comput. Phys. 229, 8313–8332 (2010)
Bolding, S., Hansel, J., Edwards, J.D., Morel, J.E., Lowrie, R.B.: Second-order discretization in space and time for radiation-hydrodynamics. J. Comput. Phys. 32, 101–136 (2017)
Lowrie, R.B., Edwards, J.D.: Radiative shock solutions with grey non-equillibrium diffusion. Shock Waves 18, 129–143 (2008)
Dai, W., Woodward, P.R.: Numerical simulations for radiation hydrodynamics. I. Diffusion limit. J. Comput. Phys. 142, 182–207 (1998)
Bates, J.W., Knoll, D.A., Rider, W.J., Lowrie, R.B., Mousseau, V.A.: On consistent time-integration methods for radiation hydrodynamics in the equilibrium diffusion limit: low-energy-density regime. J. Comput. Phys. 167, 99–130 (2001)
Sun, W.J., Jiang, S., Xu, K.: A multidimensional unified gas-kinetic scheme for radiative transfer equations on unstructured mesh. J. Comput. Phys. 351, 455–472 (2017)
Xu, K.: Direct Modeling for Computational Fluid Dynamics: Construction and Application of Unified Gas Kinetic Schemes. World Scientific, Singapore (2015)
Xu, K.: A gas-kinetic BGK scheme for the Navier–Stokes equations and its connection with artificial dissipation and Godunov method. J. Comput. Phys. 171, 289–335 (2001)
Sekora, M., Stone, J.: A higher order godunov method for radiation hydrodynamics: radiation subsystem. Commun. Appl. Comput. Math. 4, 135–152 (2009)
Bhatnagar, P.L., Gross, E.P., Krook, M.: A model for collision processes in gases I: small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525 (1954)
van Leer, B.: Towards the ultimate conservative difference schemes V. A second-order sequal to Godunov’s method. J. Comput. Phys. 32, 101–136 (1979)
Chandrasekhar, S.: Radiative Transfer. Dover Publications, Mineola (1960)
Xu, K., Huang, J.C.: A unified gas-kinetic scheme for continuum and rarefied flows. J. Comput. Phys. 229, 7747–7764 (2010)
Acknowledgements
The current research is supported by NSFC (No. 11671048), CAEP foundation (No. CX20200026), National key project (GJXM92579) and Science Challenge Project (No. TZ2016002) for Sun; by NSFC (Grant Nos. 11631008, GZ1465, 11571046) for Jiang; and by Hong Kong research grant council (16206617) and NSFC (Grant Nos. 11772281, 91852114) for Xu.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Sun, W., Jiang, S., Xu, K. et al. Multiscale Simulation for the System of Radiation Hydrodynamics. J Sci Comput 85, 25 (2020). https://doi.org/10.1007/s10915-020-01337-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-020-01337-3