Abstract
Two higher order time stepping methods for solving subdiffusion problems are studied in this paper. The Caputo time fractional derivatives are approximated by using the weighted and shifted Grünwald–Letnikov formulae introduced in Tian et al. (Math Comput 84:2703–2727, 2015). After correcting a few starting steps, the proposed time stepping methods have the optimal convergence orders \(O(k^2)\) and \( O(k^3)\), respectively for any fixed time t for both smooth and nonsmooth data. The error estimates are proved by directly bounding the approximation errors of the kernel functions. Moreover, we also present briefly the applicabilities of our time stepping schemes to various other fractional evolution equations. Finally, some numerical examples are given to show that the numerical results are consistent with the proven theoretical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Two higher order time stepping methods based on the weighted and shifted Grünwald-Letnikov formulae in Tian et al. [34] are introduced and analyzed for the following subdiffusion problem, with \(0< \alpha <1\),
where \(A=-\varDelta \) and \(\varDelta \) denotes the Laplacian defined on a regular domain \(\varOmega \subset {\mathbb {R}}^{d},d=1,2,3\) with smooth boundary \(\partial \varOmega \) and \(D(A)=H_{0}^{1}(\varOmega ) \cap H^{2}(\varOmega )\). Here the initial value \(u_{0} \in L_{2}(\varOmega )\) and the smoothness of the source term f is described in Theorems 1, 2 in Sect. 2 and 3, respectively. The time fractional derivative \(\, _{0}^{C} D_{t}^{\alpha } u(t), \, 0< \alpha <1 \) is defined in the sense of Caputo, see, e.g., Diethelm [10],
More generally the operator A in (1) could be any linear, selfadjoint, positive definite operator with compact inverse, defined in \(D(A) \subset L_{2}(\varOmega )\), and satisfies the following resolvent estimates, with \(\pi /2< \theta _{0} < \pi \), see, e.g., Lubich et al. [23] and Thomée [33],
It is easy to see that for any \( z \in \varSigma _{\theta } \) with \( \theta \in (\pi /2, \theta _{0})\), we have \(z^{\alpha } \in \varSigma _{\theta _{0}}\) since, with \(0< \alpha <1\),
which implies that, by (2), see, e.g., Jin et al. [14, (2.3)],
In Sects. 2 and 3, with some suitable approximation \(z_{k}\) of z, we shall choose \(\theta \in (\pi /2, \theta _{0}) \) sufficiently close to \(\pi /2\) such that \(z_{k}^{\alpha } \in \varSigma _{\theta _{0}}\) which guarantees that \((z_{k}^{\alpha } I + A)^{-1}\) exists.
Recently, Meerschaert et al. [27] and Tian et al. [34] introduced the weighted and shifted Gr\(\ddot{u}\)nwald-Letnikov difference operators to approximate the Riemann-Liouville fractional derivative and applied such difference operators to solve space fractional partial differential equations under the assumptions that the solution is sufficiently smooth and satisfies the homogeneous boundary conditions. To our knowledge, we have not seen any works in literature to apply such weighted and shifted Grünwald-Letnikov difference operator to construct higher order time discretization schemes for solving the subdiffusion equation (1). One of the possible reasons for lacking such works may be that the solution of (1) is not sufficiently smooth and it has the singularity near \(t=0\). For example, in the homogeneous case of (1) with \(f=0\), one has the following stability estimate, [29], with \(\Vert \cdot \Vert \) the norm in \(L_{2}(\varOmega )\),
which shows that the \(\alpha \)-th order Caputo derivative of the solution of (1) becomes unbounded as \(t\rightarrow 0\). Hence, the \(C^{2}\)-regularity assumption, generally, does not hold for the exact solution of (1). Numerical experiments indicate that the convergence orders of some numerical methods for solving (1) actually do not hold uniformly in t even for the smooth data \(u_{0},\) see, e.g., Jin et al. [15], Stynes et al. [31] and Stynes [30]. Therefore, an attempt has been made in this paper to consider the higher order time discretization schemes for (1), based on the weighted and shifted Grünwald-Letnikov schemes developed in Tian et al. [34] and prove the optimal convergence orders of the proposed schemes with both smooth and nonsmooth data.
There are several approaches to improve the convergence orders of the numerical methods for solving (1), when the solution is not sufficiently smooth. One approach is to correct some weights of the numerical methods in order to capture the singularity of the solution. This idea was first introduced by Lubich et al. [23] for second order time stepping scheme applied to an evolution equation with positive memory term. After correcting some weights of the numerical methods, Lubich et al. [23] proved optimal convergence of the corrected numerical method for both smooth and nonsmooth data. Jin et al. [16] derived some higher order numerical methods in time for the problem (1), where the fractional derivatives are approximated by using the convolution quadrature generated by using the backward difference formulae. By correcting some starting steps of the numerical methods, Jin et al. [16] established that the corrected numerical methods have optimal order of convergence for any fixed time t for both smooth and nonsmooth data, see also [14, 17]. Subsequently, Yan et al. [36] corrected the starting steps of the L1 scheme for solving (1) and proved that the modified L1 scheme has the optimal convergence order \(O (k^{2-\alpha }), 0< \alpha <1\). More recently, Xing and Yan [35] analyzed a numerical method for solving (1), where the Caputo fractional derivative is expressed by using the Hadamard finite-part integral which is then approximated by using the quadratic interpolation polynomials. After correcting some starting steps and some weights of the high-order numerical methods, Xing and Yan [35] derived the optimal convergence order \(O(k^{3- \alpha }), 0< \alpha <1\) of the corrected numerical methods for both smooth and nonsmooth data. For the recent development of the corrections of numerical methods for (1), we refer the readers to the survey paper [12], see also [37]. For other numerical methods for solving time fractional diffusion equation, we refer to [3, 5,6,7,8, 11, 15, 18,19,20,21,22, 24, 25, 28, 32, 38,39,40], etc.
The aim of this paper is to prove that the proposed numerical methods have the optimal convergence orders \(O(k^{2})\) and \(O(k^{3})\), respectively, by correcting a few starting steps of the numerical methods for both smooth and nonsmooth datas. Compared to other higher order time stepping methods in the literature for solving time diffusion problem (1), the proposed methods have two advantages: (i) The weights of our numerical methods are much simpler than those obtained by approximating the fractional derivative with the quadratic interpolating polynomials, see, e.g., in Xing and Yan [35] and further, these weights have a special structure as mentioned in Tian et al. [34], which may be useful for constructing some fast algorithms and also for proving their stability and error analyses; (ii) The weights of the proposed numerical schemes are related not only to the order of the fractional derivative, but also to the shifted numbers, which imply that our methods are more related to the equation itself, see, e.g., Tian et al. [34].
The main contributions of this paper are as follows.
- 1.
Based on the weighted and shifted Gr\(\ddot{u}\)nwald -Letnikov schemes proposed in Tian et al. [34], two new corrected higher order time discretization methods are introduced and the convergence orders are shown to be of \(O(k^2)\) and \(O(k^3),\) respectively for both smooth and nonsmooth data.
- 2.
The error estimates of the corrected numerical methods are proved in both homogeneous and inhomogeneous cases.
- 3.
With the help of Laplace transform techniques, it is shown that the error estimates are even suitable for more general elliptic operator A, which satisfies the resolvent estimate (2).
The paper is organized as follows. In Sect. 2, we consider the error estimates of the time discretization scheme for (1) with the convergence order \(O(k^{2})\) for both smooth and nonsmooth data. In Sect. 3, we derive the error estimates of the time discretization scheme with the convergence order \(O(k^{3})\) again for both smooth and nonsmooth data. Finally in Sect. 4, numerical examples are presented to show that numerical results are consistent with the theoretical results.
By C, we denote a positive constant independent of discretization parameter k, but not necessarily the same at different occurrences.
2 Second Order Time Stepping Scheme
In this section, we analyze a second order time discretization scheme for approximating the solution of the problem (1). After correcting some starting steps of the scheme, the optimal order of convergence is derived for the problem with both smooth and nonsmooth data.
Based on Tian et al. [34], we shall introduce a scheme to approximate the Riemann-Liouville fractional derivative \(_{0} ^{R}D^{\alpha }_{t}\phi (t)\). Let \(0=t_{0}<t_{1}<\cdots <t_{N}=T\) be a time partition of [0, T] and k be the step size. We define the following numerical scheme to approximate \(_{0} ^{R}D^{\alpha }_{t} \phi (t)\) at \(t=t_{n},n\ge 1\)
where
Here \(g_{j}^{(\alpha )},j=0,1,2,\ldots ,\) are generated by the generating function \(\delta _{1}(\zeta )=(1-\zeta )\), that is,
When \( p=0, \, q=-1\) or \(q=0, \, p=-1\), the equation (5) leads to
where
In Table 1, we show the differences numerically between the weights generated by (9) and by BDF2, i.e., backward difference formula with convergence order 2, in Jin et al. [16] with \(n=5\). Here \(w_{j}^{(\alpha )}\) and \(b_{j}^{(\alpha )}, 0< \alpha <1, \, j=0, 1, 2, \ldots , n\) denote the weights generated by (9) and by BDF2, respectively with respect to the different \(0<\alpha <1\).
The corresponding generating function \(\delta (\zeta )\) of the weights \(w^{(\alpha )}_{j}, j=0, 1, 2, \ldots \) in (9) satisfies
As in Lubich et al. [23], we denote the discrete Laplace transform of the sequence \(w_{j}^{(\alpha )}, j=0, 1, 2, \ldots \) by \({\tilde{w}} (\zeta ) = \sum _{j=0}^{\infty } w_{j}^{(\alpha )} \zeta ^{j}\). We then have, by (10),
The following lemma gives the series expansion of \({\tilde{w}} (\zeta )\) in (11) in terms of \((1- \zeta )\), see, the similar argument used in [16, (16)].
Lemma 1
Let \({\tilde{w}} (\zeta )\) be defined by (11). Then, the following expansion holds:
Proof
From (10), we observe that
where we have used the following binomial expansion, with \(\beta \in {\mathbb {R}}\),
This completes the proof of the Lemma 1. \(\square \)
We now introduce a fully discrete scheme for solving (1). Let \({\mathcal {T}}_{h}\) denote a triangulation of \(\varOmega \) with h the maximal length of the sides on \({\mathcal {T}}_{h}\). Let \(S_{h}\subset H^{1}_0(\varOmega )\) denote the piecewise continuous linear finite element space.
For any fixed \(t \in (0, T]\), the finite element method of (1) is to find \(u_{h} (t) \in S_{h}\) such that
where \(A_{h}:S_{h}\rightarrow S_{h}\) denotes the discrete analogue of A defined with some suitable bilinear form \(a(\cdot ,\cdot )\) defined on \(H^1_0(\varOmega ) \times H^1_0(\varOmega )\) associated with the operator A, by
and \(f_{h}=P_{h} f\), where \(P_{h}:L_{2}(\varOmega )\rightarrow S_{h}\) denotes the \(L_{2}\) project operator given by
Here \(u_{0h} \in S_{h} \) denotes some approximation of \(u_{0}\in L_{2}(\varOmega )\). When \(u_{0}\) is nonsmooth, we choose \(u_{0h}=P_{h}u_{0}\) and when \(u_{0}\) is smooth, that is \(u_{0} \in D(A)\), we may choose \(u_{0h}=\mathbf{{R}}_{h}u_{0}\), where \(\mathbf{{R}}_{h}:H_{0}^{1}(\varOmega )\rightarrow S_{h}\) denotes the Ritz projection or elliptic projection defined by
Let \(V_{h}(t)=u_{h}(t)-u_{0h}.\) Then, the equation (14) is equivalent to
Since \(\, _{0} ^{C}D^{\alpha }_{t} V_{h}(t)=\, _{0} ^{R}D^{\alpha }_{t}( V_{h}(t)-V_{h}(0)),0<\alpha <1\), now (15) is rewritten as
An application of Taylor’s expansion as in Jin et al. [17] yields
where \(g*h\) denotes the convolution of g and h.
By the Laplace transform method, we obtain, with \({\hat{g}} (z)\) denoting the Laplace transform of g(t),
A use of the inverse Laplace transform shows at \(t=t_{n}\)
where \( \varGamma \) is defined by, see, e.g., Lubich et al. [23], with some \(\theta \in (\pi /2, \theta _{0})\),
Now we shall consider the time discretization scheme of (1). To improve the accuracy near \(t=0\), we follow the approach in Lubich et al. [23] to correct the values of the first step in the time discretization.
Let \(V^{n}\approx V_{h}(t_{n})\) be the approximation of \(V_{h} (t_{n})\). We define the following time discretization scheme for approximating (1)
where, with \(c_{0}=1/2\),
Applying the discrete Laplace transform in both sides of (19), we obtain
It is easy to see with \({\tilde{V}} (\zeta ) = \sum _{j=0}^{\infty } V^{j} \zeta ^{j}\)
which implies by (20) that
Further, with \({\tilde{w}} (\zeta )\) given in (11), we set
and
By the inverse discrete Laplace transform, it follows for \(n \ge 1\) and using the variable change \(\zeta = e^{-zk}\) that
where, see Lubich et al. [23], with \(\varGamma \) defined in (18),
Below, we state our main result in this section whose proof will be provided subsequently.
Theorem 1
Let \(V_{h}(t_{n})\) and \(V^{n}\) be defined in (17) and (23), respectively. Assume that \(u_{0} \in L_{2}(\varOmega )\) and \(f\in C^{1}([0,T]; L_{2}(\varOmega ))\) and \(\int _{0}^{t_{n}} (t_{n}-s)^{ \alpha -1} \Vert f^{\prime \prime } (s) \Vert \, ds<\infty \) for \(t_{n} \in (0,T]\). Then, there is a positive constant C, independent of k, such that for \(0< \alpha <1\)
To prove Theorem 1, the following two lemmas will be useful.
Lemma 2
Let \( z_{k}\) and \(\mu (\zeta )\) with \( \zeta = e^{-zk}\) be defined by(21) and (22), respectively. Assume that
Then with \(\varGamma _{k}\) defined by (24), the following estimates hold:
Proof
We first show (26). Now, zk is uniformly bounded for any \(z \in \varGamma _{k}\) since, with \(\theta \in (\pi /2, \theta _{0})\),
Further we note that, by (22) and Lemma 1 with \(c_{0}=1/2\),
and this implies that
Hence, there exists \(\delta _{0}>0\) with \( 0< \delta _{0} \le \frac{\pi }{\sin \theta }\) such that (26) holds for \(0 \le |zk| \le \delta _{0}, \, z \in \varGamma _{k}\).
For large zk with \(\delta _{0} \le |zk| \le \frac{\pi }{\sin \theta }\), we now note by (22) that
This is continuous at any \(\zeta \ne 1\), which implies that \( \mu (e^{-zk}) -1\) is continuous at any \( z \ne 0\). Since every continuous function is bounded on the closed and bounded domain, therefore, \( \mu (e^{-zk})-1\) is bounded on \( \delta _{0} \le |zk| \le \frac{\pi }{\sin \theta }, z \in \varGamma _{k}\). Then,
Hence, (26) also holds for \(\delta _{0} \le |zk| \le \frac{\pi }{\sin \theta }, \, z \in \varGamma _{k}\) which completes the estimate (26).
In order to prove the estimate (27), it suffices to show \(|\frac{z}{z_{k}}|\) is bounded for any \(z \in \varGamma _{k}\). Now, a use of (21) yields
To show \(|\frac{z}{z_{k}}|\) is bounded for any \(z \in \varGamma _{k}\), we consider two cases: one for the small zk and the other for the large zk.
For the small zk, observe that
which implies that \(\frac{|z|}{|z_{k}|}\) is bounded for \(0\le |zk| \le \delta _{0},z\in \varGamma _{k}\) with some suitable \(\delta _{0}>0, \; 0< \delta _{0} \le \frac{\pi }{\sin \theta }\).
For the large zk, we note that \(\frac{|z|}{|z_{k}|}\) is continuous at any \(w=zk\ne 0,z\in \varGamma _{k}\) which implies the boundedness of \(\frac{|z|}{|z_{k}|}\) for large |zk| with \(\delta _{0}\le |zk|\le \frac{\pi }{\sin \theta },z\in \varGamma _{k}\). Thus, we complete the estimate (27). Similarly, it is easy to show that \(|\frac{z_{k}}{z}|\) is also bounded for any \(z \in \varGamma _{k}\).
For (28), we first observe with \(\zeta =e^{-zk}\) that
This implies that there exists \(0<\delta _{0} \le \frac{\pi }{\sin \theta }\) such that
For large |zk| with \(\delta _{0}\le |zk|\le \frac{\pi }{\sin \theta },z\in \varGamma _{k}\), an application of (27) shows
Hence,
Following the idea of the proof in Lubich et al. [23, (4.6)] and noting that \(\Vert K_{1}^{\prime } (z) \Vert \le C |z|^{-2}\) in [23, (3.12)], we obtain by mean value theorem and using (31),
As in the proof of [36, Lemma 3.12], and noting that \( | K_{1}(z_{k}) | \le C |z_{k}|^{-1} \le C |z|^{-1}, \, z \in \varGamma _{k}\), we now arrive by (32) and (26) at
which completes the proof of (28).
Finally in order to estimate (29), a use of the mean value theorem, (31) with \(K_{2}(z)=z^{-1}(z^{\alpha }+A_{h})^{-1}\) and \(\Vert K_{2}^{\prime } (z) \Vert \le C |z|^{-2-\alpha }\) yields
Further, noting that \( | K_{2}(z_{k}) | \le C |z_{k}|^{-1-\alpha } \le C |z|^{-1-\alpha }, \, z \in \varGamma _{k}\), we obtain, by (33) and (26),
which shows (29).
Altogether, it concludes the proof of the Lemma 2. \(\square \)
In the following lemma, with \(z_{k}\) defined in (21), we claim that \(z_{k}^{\alpha } \in \varSigma _{\theta _{0}}\) for some \(\theta _{0}\in (\frac{\pi }{2},\pi )\).
Lemma 3
Let \(\theta >\pi /2\) be sufficiently close to \(\pi /2\). Let \(z_{k}\) be defined by (21). Then we have, for some \(\theta _{0} \in (\pi /2, \pi )\), with \(\varGamma _{k}\) defined by (24),
Proof
By the definition of \(z_{k}\) in (21) and the expression of \({\tilde{w}} (\zeta )\) in Lemma 1, we obtain
It suffices to show that both \(\frac{\alpha }{2}(1-\zeta )^{\alpha +1}\) and \((1-\zeta )^{\alpha }\) lie in \(\varSigma _{\theta _{0}}\) for all \(z\in \varGamma _{k}\). Recall that \(z\in \varGamma _{k}\) satisfies \(\mathfrak {I}(zk)\in (0,\pi ]\) and \(\arg (z)=\theta \) with \(\theta >\frac{\pi }{2}\). Note that \(z_{k}^{\alpha }\) depends on z continuously [14, proof of Lemma 3.6]. It suffices to consider the case for z with \(\arg (z)=\frac{\pi }{2}\) and \(\mathfrak {I}(zk)\in (0,\pi ]\). In other words, suppose that we can prove \(\frac{\alpha }{2}(1-\zeta )^{\alpha +1}\in \varSigma _{\theta _{0}}\) for all z with \(\arg (z)=\frac{\pi }{2}\) and \(\mathfrak {I}(zk)\in (0,\pi ]\), then since \(z_{k}\) depends on z continuously, there exist \(\theta _{0}\in (0,\pi )\) such that \(\frac{\alpha }{2}(1-\zeta )^{\alpha +1}\in \varSigma _{\theta _{0}}\). Note that \(\arg (z)=\frac{\pi }{2}\) with \(\mathfrak {I}(zk)\in (0,\pi ]\) implies that \(\zeta =e^{-zk}=e^{-i\varphi },\varphi \in (0,\pi ]\). We next show \(\frac{\alpha }{2}(1-\zeta )^{\alpha +1}\in \varSigma _{\theta _{0}}\) and \((1-\zeta )^{\alpha }\in \varSigma _{\theta _{0}}\) for \(\zeta =e^{-i\varphi },\varphi \in (0,\pi ]\). Write
then, \(0<\mathfrak {R}(1-\zeta )=1-\cos \varphi <1\) and \(0<\mathfrak {I}(1-\zeta )=\sin \varphi <1\) for \(\varphi \in (0,\pi ]\). Thus, we arrive at \(\arg \frac{\alpha }{2}(1-\zeta )^{\alpha +1}\in (0,\pi )\) with \(0<\alpha <1\) and \(\arg (1-\zeta )^{\alpha }\in (0,\frac{\pi }{2})\) with \(0<\alpha <1\). Then, there exists \(\theta _{0}\in (\frac{\pi }{2},\pi )\) such that \(z_{k}^{\alpha }\in \varSigma _{\theta _{0}}\) and this completes the proof. \(\square \)
Remark 1
In Jin et al. [14, Lemma 3.7], the authors have proved that for all \( -\pi \le \theta < \pi \), there exists \(\theta _{0} \in (\pi /2, \pi )\) such that \(z_{k}^{\alpha } \in \varSigma _{\theta _{0}}\) for all \( z \in \varSigma _{\theta }\). Actually in our analysis, we only need to show \(z_{k}^{\alpha } \in \varSigma _{\theta _{0}}\) for all \( z \in \varGamma _{k}\) for some \(\theta >\pi /2 \) sufficiently close to \(\pi /2\).
Lemma 4
Let \(z_{k}\) be defined as in (21), then, there is a positive constant C independent of k such that
Proof
Apply Lemmas 2, 3 to arrive at
This completes the rest of the proof. \(\square \)
Now we turn to the proof of Theorem 1.
Proof
(Proof of Theorem 1) Subtracting (17) from (23), we arrive at
where, with \(K_{2}(z)\) defined by (25),
For \(I_{1}\), apply the bound \(\Vert (z^{\alpha }+A_h)^{-1}A_h\Vert \le C\), (3), (28) and (29) to obtain
For \(I_{2}\), we note that
where
For \(I_{21}\), we easily bound it as
An application of Lemma 4 yields
For \(I_{22}\), following the arguments as in Jin et al. [14, 17], we arrive at
Together these estimates complete the proof of Theorem 1. \(\square \)
3 Third Order Time Discretization Method
In this section, we introduce a third order time discretization scheme for solving (1) based on the weighted and shifted Grünwald-Letnikov difference operator introduced in Tian et al. [34].
Let us define the following weighted and shifted Grünwald-Letnikov difference operator \(\, _{L} D^{\alpha }_{k,p,q,r}\) to approximate the Riemann-Liouville fractional derivative operator \(\, _{0}^{R}D_{t}^{\alpha }\) by
where p, q, r are integers and mutually nonequal, and \(B_{k,p}^{\alpha } \phi (t_{n})\) are defined by (6) and
When \(p=0, \, q=-1, \, r=-2\), we obtain
and we then arrive for \(n\ge 2\) at
Thus, we obtain
where
The discrete Laplace transform of \(w_{j}^{(\alpha )}, j=0, 1, 2, \ldots \) is given by
Below, following the idea in Lemma 1, we consider the series expansion of the function \({\tilde{w}}(\zeta )\) in (41).
Lemma 5
Let \({\tilde{w}} (\zeta )\) be defined by (41). Then,
Proof
From (41), the binomial expansion (13) and \(\lambda _{1} + \lambda _{2} + \lambda _{3}=1\), it now follows that
This concludes the rest of the proof. \(\square \)
Next, we turn to the solution of (16) when \(f_{h}(t)\) is written as
where \(g*h\) denotes the convolution of g and h.
An application of the Laplace transform to (16) with respect to the time variable t yields
By the inverse Laplace transform, the solution of (16) takes the following form at \(t=t_{n}\),
Let \(V^{n}\approx V_{h}(t_{n}),n=0,1,2,\ldots ,N\) denote the approximate solution of the following time discretization scheme for solving (16), with \(V^{0}=0\),
where \(w_{j}^{(\alpha )},j=0,1,2,\ldots \) are defined by (40) and the coefficients \(a_{1}, a_{2}, b_{1}, b_{2}\) satisfy
and
Now we come to the following main theorem in this section
Theorem 2
Let \(V_{h}(t_{n})\) and \(V^{n}\) be the solutions of (16) and (47)–(49), respectively. Assume that \(u_{0} \in L_{2} (\varOmega )\) and \(f\in C^{2}([0,T]; L_{2}(\varOmega ))\) and \(\int _{0}^{t_{n}} (t_{n}-s)^{ \alpha -1} \Vert f^{\prime \prime \prime } (s) \Vert \, ds<\infty \) for \(t_{n} \in (0,T]\). Let \(u_{0h}=P_{h}u_{0}\), then there exists a positive constant C independent of k such that
To prove Theorem 2, we need the following lemmas.
Lemma 6
With \({\tilde{w}} (\zeta )\) given by (41), let \( z_{k}\) and \(\mu (\zeta )\) with \( \zeta = e^{-zk}\) be defined by
and
Further, let \(K_{1}(z)\) and \(K_{2} (z)\) be given by (25). Then, with \(\varGamma _{k}\) as in (24), the following estimates hold:
Proof
The proof is similar to the proof of Lemma 2. For each inequality, again two cases such as the small zk and the large zk are considered.
For (54), a use of Lemma 5 yields, with \(a_{1}= 11/12, \, a_{2}=-5/12 \) by (50),
and then this implies that
Hence (54) holds for small zk with \(0 \le |zk| \le \delta _{0}\) with some positive \(\delta _{0} >0, \, 0 \le \delta _{0} < \frac{\pi }{\sin (\theta )}, \, \theta \in (\pi /2, \theta _{0})\). Note that \(\mu (\zeta )\) is continuous at any point except \(\zeta \ne 1\), which implies that, following the argument as in (30), \(\mu (e^{-zk})-1\) is bounded for large zk with \( \delta _{0} \le |zk| \le \frac{\pi }{\sin (\theta )}\). Hence (54) follows.
We next estimate (55). With \({\tilde{w}} (\zeta )\) defined by (41), we arrive at
Hence,
which implies that \(\frac{|z|}{|z_{k}|}\) is bounded for small |zk| with \(0\le |zk| \le \delta _{0}, z\in \varGamma _{k}\) for some suitable \(0< \delta _{0} \le \frac{\pi }{\sin \theta }\). Note also that \(\frac{|z|}{|z_{k}|}\) is continuous at any \(w=zk\ne 0, z\in \varGamma _{k}\), which implies that \(\frac{|z|}{|z_{k}|}\) is also bounded for large |zk| with \(\delta _{0}\le |zk|\le \frac{\pi }{\sin \theta },z\in \varGamma _{k}\). Hence, we proved the boundedness of \(\frac{|z|}{|z_{k}|}\) for any \(z \in \varGamma _{k}\). Similarly, we may show that \(\frac{|z_{k}|}{|z|}\) is also bounded for any \(z \in \varGamma _{k}\). Thus, we derive the estimate (55).
To estimate (56), we observe that
which implies that there exists \(0<\delta _{0} \le \frac{\pi }{\sin \theta }\) such that
For large |zk|, with \(\delta _{0}\le |zk|\le \frac{\pi }{\sin \theta }, \, z\in \varGamma _{k}\), we have, by (55),
Thus, we obtain
Then an application of the mean-value theorem with (58) and \(\Vert K_{1}^{\prime } (z) \Vert \le C |z|^{-2}\) shows
Following the same line of proof of (28), we arrive from (54), (59), and \( | K_{1}(z_{k}) | \le C |z_{k}|^{-1} \le C |z|^{-1}, z \in \varGamma _{k}\) at
which shows (56).
Finally in order to show (57), we note that \(K_{2}(z)=z^{-1}(z^{\alpha }+A_{h})^{-1}\) and \(\Vert K_{2}^{\prime } (z) \Vert \le C |z|^{-2-\alpha }\). Then, by mean-value theorem and (58), we obtain
Following the same arguments as the proof of (29), a use of \( |K_{2}(z_{k}) | \le C |z_{k}|^{-1-\alpha } \le C |z|^{-1-\alpha }\) yields
Hence, we prove (57).
Together with these estimates, we complete the proof of Lemma 6. \(\square \)
In the following lemma, with \(z_{k}\) defined by (52), we will show that \(z_{k}^{\alpha } \in \varSigma _{\theta _{0}}\) for some \(\theta _{0} \in (\pi /2, \pi )\).
Lemma 7
Let \(\theta >\pi /2\) be sufficiently close to \(\pi /2\). Let \(z_{k}\) be defined by (52). Then, there exists \(\theta _{0} \in (\pi /2, \pi )\) such that
where \(\varGamma _{k}\) is defined by (24).
Proof
By the definition of \(z_{k}\) in (52) and the expression of \({\tilde{w}}(\zeta )\) in Lemma 5, we rewrite
where \(\lambda _{1}=\frac{24+17\alpha +3\alpha ^{2}}{24}\), \(\lambda _{2}=\frac{-22\alpha -6\alpha ^{2}}{24}\), \(\lambda _{3}=\frac{5\alpha +3\alpha ^{2}}{24}\). It suffices to show both \(\lambda _{1}+\lambda _{2}\zeta +\lambda _{3}\zeta ^{2}\) and \((1-\zeta )^{\alpha }\) lie in \(\varSigma _{\theta _{0}}\) for all \(z\in \varGamma _{k}\). Recall that \(z\in \varGamma _{k}\) satisfies \(\mathfrak {I}(zk)\in (0,\pi ]\) and \(\arg (z)=\theta \) with \(\theta >\frac{\pi }{2}.\) Note that \(z_{k}^{\alpha }\) depends on z continuously [14, proof of Lemma 3.6], and \(\arg (z)=\frac{\pi }{2}\) with \(\mathfrak {I}(zk)\in (0,\pi ]\) implies that \(\zeta =e^{-zk}=e^{-i\varphi },\varphi \in (0,\pi ]\). Hence, we only need to show \((\lambda _{1}+\lambda _{2}\zeta +\lambda _{3}\zeta ^{2})\in \varSigma _{\theta _{0}}\) for \(\zeta =e^{-i\varphi },\varphi \in (0,\pi ].\) Observe that
and therefore, we arrive at
Then, \(\mathfrak {R}(\lambda _{1}+\lambda _{2}\zeta +\lambda _{3}\zeta ^{2})>0\) for \(\varphi \in (0,\pi )\) and \(0<\alpha <1\).
Similarly,
Thus, \(\arg (\lambda _{1}+\lambda _{2}\zeta +\lambda _{3}\zeta ^{2}) \in (0,\frac{\pi }{2})\) for \(\varphi \in (0,\pi )\) and \(\arg (1-\zeta )^{\alpha } \in (\frac{\pi }{2},\pi )\) with \(0<\alpha <1\) in Lemma 3. Then, we can infer the existence of \(\theta _{0}\in (0,\frac{\pi }{2})\) such that \(z_{k}^{\alpha }\in \varSigma _{\theta _{0}}\) and this concludes the rest of the proof. \(\square \)
Lemma 8
Let \(z_{k}\) be defined as in (52). Let \(b_{1},b_{2}\) be defined as in (51). Then, the following estimate with \(\zeta = e^{-zk}\), holds:
Proof
Let \(\zeta =e^{-zk}\) and \(x=zk\), then by Lemma 5, we have
for some suitable positive constants \(d_{1}, d_{2}\).
Combining this with (51), we obtain
This completes the proof of Lemma 8. \(\square \)
Remark 2
Observe that following the arguments as in Jin et al. [16], we can choose suitable coefficients \(b_{1}=\frac{1}{12},b_{2}=0.\)
Lemma 9
Let \(z_{k}\) be defined as in (52). Let \(b_{1},b_{2}\) be defined as in (51). Then, there holds
Proof
The proof is similar to the proof of Jin et al. [16, Lemma C.1.] and hence, we omit the proof here. \(\square \)
Lemma 10
Let \(z_{k}\) be defined as in (52), then, there exists a positive constant C independent of k such that
Proof
From Lemma 6, it follows that
This concludes the proof. \(\square \)
We are now ready to prove the main theorem of this section.
Proof
(Proof of Theorem2) We now calculate the approximate solution \(V^{n}\) defined in (47)–(49). Taking the discrete Laplace transform in (47)–(49), we arrive at
Note that
and hence
A use of the inverse discrete Laplace transform yields, with \(\mu (\zeta )\) defined by (53), and \(\varGamma _{k}\) as in (24).
Now, subtracting (46) from (63), we arrive at
where, with \(K_{2}(z)\) defined by (25),
and
and
For \(I_{1}\), apply the bound \(\Vert (z^{\alpha }+A_h)^{-1}A_h\Vert \le C\), (3), (56) and (57) to obtain
For \(I_{21}\), by (3), it follows that
For \(I_{22}\), a use of the Lemma 9 shows
Thus, we obtain
For \(I_{3}\), we observe that
and
where
For \(I_{31}\), we easily bound it as
An application of Lemma 10 yields
For \(I_{32}\), following the arguments as in Jin et al. [14, 17], we now arrive at
Together these estimates complete the proof of Theorem 2. \(\square \)
In order to prove the error analysis in the completely discrete schemes, we now recall the error estimates of the semidiscrete scheme as is developed in [13] for the problem with \(f=0\),
Denote \(U^{n}= V^{n} + P_{h} u_{0}\) with \(V^{n}\) defined by (19) or (47)–(49), respectively. Using (65), we then have the following fully discrete error estimate
where \(m=2\) or 3, respectively, for second order and third order time stepping schemes.
Since our main objective in this article is to derive higher order time stepping schemes, therefore, we may generalize our present results to include mass lumping scheme as discussed in [13].
4 Some Generalizations
This section is devoted to some generalization of the present methods to various other problems, which includes evolution equations with positive memory.
For instance, our generalizations include the following type of problems:
- 1.
Evolution equations with positive memory called time diffusion-wave equation, as in [23],
$$\begin{aligned} u'(x,t)+ \, _{0}^{R}D^{-\alpha }_{t} A u(x,t)=0, \quad \alpha \in (0,1), \end{aligned}$$(66)where \( \, _{0}^{R}D^{-\alpha }_{t}\) denotes the Riemann-Liouville fractional integral operator.
- 2.
The parabolic integro-differential equation with singular kernel, see, [26]
$$\begin{aligned} u'(x,t)+\big (I + \, _{0}^{R}D^{-\alpha }_{t} \big ) A u(x,t)=0, \quad \alpha \in (0,1). \end{aligned}$$(67) - 3.
The Rayleigh-Stokes problem described by the time-fractional differential equation as in [4]
$$\begin{aligned} u'(x,t)+ \big (I+\gamma \, _{0}^{R}D^{-\alpha }_{t} \big ) A u(x,t)=0,\quad \alpha \in (0,1), \end{aligned}$$(68)where \(\gamma \) is a positive constant. In order to unify problems (66)–(68), we define \({\mathcal {J}}^\alpha \) denoting a time integral/differential operator and consider the unified problem by
$$\begin{aligned} u'(x,t)+{\mathcal {J}}^\alpha A u(x,t)=0. \end{aligned}$$(69)
Now, a use of Laplace transforms in (69) yields
with some function h(z) depending on \(\alpha \). Hence, with \(\beta (z)=h(z)^{-1}\) we formally write the representation of solution as \({\hat{u}}=\beta (z) (z \beta (z) I+ A)^{-1} v =: {\hat{E}}_h(z)v.\) Here, for the problem (66), note that \(\beta (z)=z^{\alpha },\) for the problem (67), \(\beta (z)= z^\alpha /(1+z^{\alpha }),\) and for (68), \(\beta (z)=1/(1+\gamma z^\alpha )\).
Assume that one can properly choose \(\theta \) in \((\pi /2,\theta _0)\) with \(\theta _0 \in (\pi /2,\pi )\) such that \(z_k\beta (z_k)\in \varSigma _{\theta _0}\), where \(z_k\) is an approximation of \(z\in \varSigma _{\theta }.\) This is indeed possible in all given examples. With this, the resolvent estimate yields
where \(M_{\theta _0}=1/\sin (\pi -\theta _0)\).
With corresponding \({A}_h\) as semidiscrete approximation of A ( as in Sect. 2), the semidiscrete method becomes: find \({\bar{u}}_h(t)\in V_h\) such that
Following the arguments of [9, 23], one easily deduces property (70), when A is replaced by \(A_h\).
Therefore, our two time stepping methods can be appropriately applied and the desired estimates can be easily derived.
Other generalizations also include the fractional cable equations with mass lumping by Al-Maskari and Karaa [2] and references therein. Further, it may include Fokker-Plank spatial discretization as our analysis does not depend on selfadjointness of the operator A and for complete discrete scheme, we may use the proposed time stepping schemes.
Finally, the present schemes can be applied to the Eq. (1), when A is a fractional Laplacian like \(A= (-\varDelta )^{s},\;s\in (0,1)\), that is, with \( 0< \alpha , \beta <1\) and some positive constant \(\delta >0\),
An appropriate modification of the arguments in [1], we obtain the semidiscrete error estimate as:
with \(\epsilon > 0\) small. Therefore, when it is combined with our proposed time stepping schemes, the final error estimate reads as: with \(U^{n} \approx u_{h} (t_{n})\),
5 Numerical Simulations
In this section, we present five numerical examples to show that the numerical results are consistent with the theoretical results obtained in this paper. The first three examples are solved by using the numerical method (19) for both homogeneous and inhomogeneous problems in one- and two-dimensional cases. The last two examples are computed by using the numerical method (47)–(49) for both homogeneous and inhomogeneous problems in one-dimensional case.
Example 1
Consider, with \(0<\alpha <1\),
where (a) \(u_{0}(x) = x(1-x)\) (smooth data) and (b) \(u_{0}(x)= \chi _{[0, 1/2]}\) (nonsmooth data).
Let \(N_{h}\) be a positive integer. Let \(0=x_{0}< x_{1}< x_{2}< \cdots < x_{N_{h}} =1\) be the space partition and h the space step size. We shall use the piecewise linear finite element method to consider the space discretization.
Let \(0<t_{0}< t_{1}< \cdots < t_{N} =T\) be the time partition and k the time step size. To observe the convergence order of the numerical method, we first need to calculate the reference solution \(u_{ref}(t)\) at some fixed time T with very small step sizes \( h_{ref} = 2^{-6}\) and \( k_{ref} = 2^{-10}\).
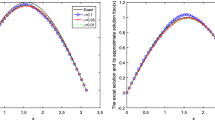
By Theorem 1, we see that the numerical method (19) has the second order convergence. To see this convergence order, we shall calculate the approximate solution of u(T) at \(T=1\) with the space step size \(h=2^{-6}\) and the different time step sizes \( k =\kappa * k_{ref} \) with \(\kappa = [2^2, 2^3, 2^4,2^5, 2^6]\). In Table 2, we observe the convergence orders \(O(k^{2})\) of the corrected scheme (19), where the rows with (a) denote the errors and the experimentally determined convergence orders in the smooth data case and the rows with (b) denote the errors and the orders in the nonsmooth data case. For each \(\alpha \), we choose the average convergence order of the computed orders obtained by using the different time step sizes.
For the numerical method (19) with \(c_{0}=0\), that is, for the uncorrected scheme, we observe that, in Table 3, the experimentally determined convergence order is only O(k) with both smooth and nonsmooth data.
The second example is an inhomogeneous problem with zero initial value and the source term f which is smooth in time.
Example 2
Consider, with \(0<\alpha <1\),
where \(f(x, t)= (\cos (t)+\sin (t)) ( 1 + \chi _{(0, 1/2)}(x))\).
We use the same parameters as in the numerical simulations in Example 1. In Table 4, we observe that the experimentally determined convergence order of the corrected scheme (19) indeed is \(O(k^{2})\) for all \( 0< \alpha <1\) (Table 5).
The third example is a two-dimensional example and we shall consider an inhomogeneous problem with nonsmooth initial data and the source term f which is smooth in time.
Example 3
Consider
where \(\varOmega = (0, 1) \times (0, 1)\), \(u_{0}(x, y)= \chi _{[0, 1/2]}(x) \chi _{[0, 1/2]}(y) \) and \(f(x, y, t)= (\cos (t)+\sin (t)) ( 1 + \chi _{(0, 1/2)}(x)) ( 1 + \chi _{(0, 1/2)}(y))\). Note that f is smooth with respect to the time variable t.
Let \(N_{h}\) be a positive integer. Let \(0=x_{0}< x_{1}< x_{2}< \cdots < x_{N_{h}} =1\) and \(0=y_{0}< y_{1}< y_{2}< \cdots < y_{N_{h}} =1\) be the partition of \(\varOmega \). We divide \(\varOmega \) into some triangles with the same sizes and let h be the maximal length of the sides of the triangle. We shall use the piecewise linear finite element method to consider the space discretization on the triangulation of \(\varOmega \).
Let \(0<t_{0}< t_{1}< \cdots < t_{N} =T\) be the time partition and k the time step size. We shall use the very small space step size \( h_{ref} = 2^{-6}\) and the time step size \( k_{ref} = 2^{-10}\) to calculate the reference solution at time T.
We shall choose \(T=1\) in our simulation. We calculate the approximate solutions with the space step size \(h=2^{-6}\) and the time step sizes \( k =\kappa * k_{ref} \) with \(\kappa = [2^2, 2^3, 2^4,2^5, 2^6]\). In Table 6, the experimentally determined convergence orders \(O(k^{2})\) are observed as we expected.
In Table 7, we observe the experimentally determined convergence orders O(k) for the uncorrected scheme (19) with \(c_{0}=0\) as we expected.
In the next two examples, we shall consider the experimentally determined convergence orders of the numerical method (47)–(49).
Example 4
In this example, we shall use the numerical method (47)–(49) to solve Example 1. We use the same parameters as in the numerical simulation in Example 1. In Table 8, we observe that the corrected scheme (47)–(49) has the convergence orders \(O(k^{3})\) with both smooth and nonsmooth data as expected.
For the uncorrected scheme (47)–(49), that is, \(a_{1}=a_{2}=b_{1}=b_{2}=0\) in (47)–(49), we observe that, in Table 9, the experimentally determined convergence order is only O(k) with both smooth and nonsmooth data.
Example 5
In this example, we shall use the numerical method (47)–(49) to solve Example 2. We use the same parameters as in the numerical simulation in Example 1. In Table 10, we also observe the convergence orders \(O(k^{3})\) of the corrected scheme (47)–(49) in the inhomogeneous case.
In Table 11, the experimentally determined convergence order of the uncorrected scheme (47)–(49) with \(a_{1}=a_{2}=b_{1}=b_{2}=0\) has only convergence order O(k).
Remark 3
In Tables 8 and 10, we observe that the experimentally determined convergence orders are slightly better than the theoretical orders. The possible reason may be that the proposed numerical methods involve both fractional orders and the shifted numbers. These combinations which are more related to the equation may be instrumental in helping us to provide possibly more accurate computational results. But, we do not have a theory yet to establish it. Therefore, in future, we shall continue to investigate this interesting observation.
6 Declarations
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Acosta, G., Bersetche, F.M., Borthagaray, J.P.: Finite element approximations for fractional evolution problems. Fract. Calc. Appl. Anal. 22, 767–794 (2019)
Al-Maskari, M., Karaa, S.: The lumped mass FEM for a time-fractional cable equation. Appl. Numer. Math. 132, 73–90 (2018)
Asl, M.S., Javidi, M., Yan, Y.: A novel high-order algorithm for the numerical estimation of fractional differential equations. J. Comput. Appl. Math. 342, 180–201 (2018)
Bazhlekova, E., Jin, B., Lazarov, R., Zhou, Z.: An analysis of the Rayleigh–Stokes problem for a generalized second-grade fluid. Numer. Math. 131, 1–31 (2016)
Cao, J., Li, C., Chen, Y.: High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equation (II). Fract. Calc. Appl. Anal. 18, 735–761 (2015)
Chen, F., Xu, Q., Hesthaven, J.S.: A multi-domain spectral method for time-fractional differential equations. J. Comput. Phys. 293, 157–172 (2015)
Chen, S., Shen, J., Wang, L.-L.: Generalized Jacobi functions and their applications to fractional differential equations. Math. Comput. 85, 1603–1638 (2016)
Chen, X., Zeng, F., Karniadakis, G.E.: A tunable finite difference method for fractional differential equations with non-smooth solutions. Comput. Methods Appl. Mech. Eng. 318, 193–214 (2017)
Cuesta, E., Lubich, C., Palencia, C.: Convolution quadrature time discretization of fractional diffusion-wave equations. Math. Comput. 75, 673–696 (2006)
Diethelm, K.: The Analysis of Fractional Differential Equations. Volume 2004 of Lecture Notes in Mathematics. Springer, Berlin (2010)
Du, R., Yan, Y., Liang, Z.: A high-order scheme to approximate the Caputo fractional derivative and its application to solve the fractional diffusion wave equation. J. Comput. Phys. 376, 1312–1330 (2019)
Ford, N.J., Yan, Y.: An approach to construct higher order time discretization schemes for time fractional partial differential equations with nonsmooth data. Fract. Calc. Appl. Anal. 20, 1076–1105 (2017)
Jin, B., Lazarov, R., Zhou, Z.: Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM J. Numer. Anal. 51, 445–466 (2013)
Jin, B., Lazarov, R., Zhou, Z.: An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J. Numer. Anal. 36, 197–221 (2016)
Jin, B., Lazarov, R., Zhou, Z.: Two fully discrete schemes for the fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM J. Sci. Comput. 38, A146–A170 (2016)
Jin, B., Li, B., Zhou, Z.: Correction of high-order BDF convolution quadrature for fractional evolution equations. SIAM J. Sci. Comput. 39, A3129–A3152 (2017)
Jin, B., Li, B., Zhou, Z.: An analysis of the Crank–Nicolson method for subdiffusion. IMA J. Numer. Anal. 38, 518–541 (2018)
Jin, B., Yan, Y., Zhou, Z.: Numerical approximation of stochastic time-fractional diffusion. ESAIM: M2AN 53, 1245–1268 (2019)
Karaa, S., Pani, A.K.: Error analysis of a FVEM for fractional order evolution equations with nonsmooth initial data. ESAIM: M2AN 52, 773–801 (2018)
Karaa, S., Mustapha, K., Pani, A.K.: Optimal error analysis of a FEM for fractional diffusion problems by energy arguments. J. Sci. Comput. 74, 519–535 (2018)
Li, Z., Yan, Y.: Error estimates of high-order numerical methods for solving time fractional partial differential equations. Fract. Calc. Appl. Anal. 21, 746–774 (2018)
Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)
Lubich, C., Sloan, I.H., Thomée, V.: Nonsmooth data error estimate for approximations of an evolution equation with a positive-type memory term. Math. Comput. 65, 1–17 (1996)
Lv, C., Xu, C.: Error analysis of a high order method for time-fractional diffusion equations. SIAM J. Sci. Comput. 38, A2699–A2724 (2006)
McLean, W., Mustapha, K.: Time-stepping error bounds for fractional diffusion problems with non-smooth initial data. J. Comput. Phys. 293, 201–217 (2015)
McLean, W., Sloan, I.H., Thomée, V.: Time discretization via Laplace transformation of an integro-differential equation of parabolic type. Numer. Math. 102, 497–522 (2006)
Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)
Mustapha, K., McLean, W.: Uniform convergence for a discontinuous Galerkin, time-stepping method applied to a fractional diffusion equation. IMA J. Numer. Anal. 32, 906–925 (2012)
Sakamoto, K., Yamamoto, M.: Initial/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl 382, 426–447 (2011)
Stynes, M.: Too much regularity may force too much uniqueness. Fract. Calc. Appl. Anal. 19, 1554–1562 (2016)
Stynes, M., O’riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal 55, 1057–1079 (2017)
Sun, Z.-Z., Wu, X.: A fully discrete scheme for a diffusion wave system. Appl. Numer. Math. 56, 193–209 (2011)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer, Berlin (2007)
Tian, W.Y., Zhou, H., Deng, W.H.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84, 1703–1727 (2015)
Xing, Y., Yan, Y.: A higher order numerical method for time fractional partial differential equations with nonsmooth data. J. Comput. Phys. 357, 305–323 (2018)
Yan, Y., Khan, M., Ford, N.J.: An analysis of the modified scheme for the time-fractional partial differential equations with nonsmooth data. SIAM J. Numer. Anal. 56, 210–227 (2016)
Yang, Y., Yan, Y., Ford, N.J.: Some time stepping methods for fractional diffusion problems with nonsmooth data. Comput. Methods Appl. Math. 18, 129–146 (2018)
Yuste, S.B., Acedo, L.: An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equation. SIAM J. Numer. Anal. 42, 1862–1874 (2005)
Zayernouri, M., Karniadakis, G.E.: Fractional spectral collocation method. SIAM J. Sci. Comput. 36, A40–A62 (2014)
Zeng, F., Li, C., Liu, F., Turner, I.: The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J. Sci. Comput. 35, A2976–A3000 (2013)
Acknowledgements
We express our gratitude to the referees for their valuable suggestions that improved this article. The authors would like to thank Professor Zongqi Liang for many valuable discussions and comments for this research topic. The second author (Yuyuan Yan) acknowledges the support from National Natural Science Foundation of China (11801214). The fourth author (AKP) acknowledges the support from SERB, Govt. India via MATRIX Grant No. MTR/201S/000309.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Yan, Y., Yan, Y. et al. Higher Order Time Stepping Methods for Subdiffusion Problems Based on Weighted and Shifted Grünwald–Letnikov Formulae with Nonsmooth Data. J Sci Comput 83, 40 (2020). https://doi.org/10.1007/s10915-020-01223-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-020-01223-y
Keywords
- Weighted and shifted Gr\(\ddot{u}\)nwald–Letnikov formulae
- Subdiffusion equation
- Caputo derivative
- Laplace transform
- Higher order time stepping schemes