Effect of Mesh Quality on Flux Reconstruction in Multi-dimensions

Abstract

Theoretical methods are developed to understand the effect of non-uniform grids on Flux Reconstruction (FR) in multi-dimensions. A better theoretical understanding of the effect of wave angle and grid deformation is established. FR is shown to have a smaller variation in properties than some finite difference counterparts. Subsequent numerical experiments on the Taylor–Green Vortex with jittered elements show the effect of localised regions of expansion and contraction. The effect this had on Nodal DG-like schemes was to increase the dissipation, whereas for more typical FR schemes the effect was to increase the dispersion. Some comparison is made between second-order FR and a second-order finite volume (FV) scheme. FR is found to be more resilient to mesh deformation, however, FV is found to be more resolved when operated at second order on the same mesh.

1 Introduction

Since the inception of the discontinuous spectral element methods of Quarteroni [34], staggered grid methods of Kopriva and Kolias [28], and spectral volume methods of Wang [56], the trajectory of high order methods has trended towards the Flux Reconstruction (FR) method of Huynh [24] and Vincent et al. [52]. This approach draws on the work of Finite Elements, (see Brenner and Ridgway-Scott [10]), enabling the high performance of Flux Reconstruction on heterogeneous computing—as can be seen in the highly efficient use of vast computing resources by Vincent et al. [55]. However, the move towards high order was not born out of a need for more efficient use of modern HPC environments. For example, Brandvik and Pullan [9] showed that high throughput could be obtained using second order Finite Volume (FV) methods. Instead, the main motivating factor has been the increased uptake by industry of turbulence resolving methods, such as Large Eddy Simulation (LES), as this allows for far better exploration of flow physics and moves towards the long term goal of computational wind tunnels. The main feature of LES is the modelling of the very smallest scales of motion, which reduces the need for the extremely high resolution required for Direct Numerical Simulation (DNS). However, Chow and Moin [14] and Ghosal [21] showed that, for LES, the need to keep the truncation error small to enable the sensible use of sub-grid scale models meant that the grid requirements are still demanding. A move to higher order would mean that the scaling of the truncation error with grid spacing occurs with a higher exponent—thus lowering the grid requirements and decoupling the scaling of aliasing error and truncation error. Hence, for wall resolved LES, calculations are often impractical unless the more benign mesh resolution requirements of high order methods are considered.

The analytical understanding of Flux Reconstruction has been explored to a large extent in the work of Vincent et al. [53], Jameson et al. [27], and Castonguay et al. [13], where the stability of linear advection, advection–diffusion, and non-linear problems has been presented. The key findings were the energy stability of FR on linear problems, and the condition for energy stability on non-linear problems. In addition, by investigating the dispersion and dissipation characteristics of FR, the existence of superconvergence after temporal integration and the corresponding CFL limits were found. This work was limited to one dimension—although still applicable, the investigation of the exact behaviour of FR in higher dimensions has been limited, such as that of Williams and Jameson [58] and Sheshadri and Jameson [39]. This work focused primarily on the proof of the Sobolev-type energy stability in 2D similar to that of Hesthaven and Warburton [23], alongside some numerical studies performed for validation.

The advantage of FR—that leads to high performance on heterogeneous and massively parallel architectures—is its unstructured and sub-domain nature. Unstructured grids also allow far more complex geometries to be considered, but the resulting meshes experience deformation, expansion, and contraction of the elements. We wish to characterise the performance of FR under these conditions, and so far the effect of linear mesh deformation on FR has been considered in one dimension by Trojak et al. [45]. Therefore, we make use of the seminal work of Lele [31], in which the dispersion and dissipation of finite difference methods were considered in both one and two dimensions. We wish to repeat this process for FR, and then extend it to also consider deformed grids.

In this paper, we present an extension to the one-dimensional analytical work of Vincent et al. [53] and Trojak et al. [45]. This extension will be shown for a two-dimensional case on quadrilaterals with rectilinear mesh stretching, but could also be performed on higher dimensional hypercubes. From the basis of this more general von Neumann analysis, the behaviour of FR on linearly mapped meshes can be explored. The investigation has been restricted to linear transformations as these are of key importance for complex industrial simulations due to their fundamental nature. For example, they occur in meshes where automated mesh generators have simply tessellated elements to fill the domain. Understanding their character is key, however, we should point to some recent work that has numerically investigated curved meshes [32, 59].

The aim of this work is to understand the effect of moving to higher dimensionality on key metrics governing scheme performance, such as CFL limit, dispersion, and dissipation. Finally, the Taylor–Green vortex will be used to understand how deformed meshes affect full Navier–Stokes calculations, with reference calculations performed by an industrial second order finite volume method.

2 Flux Reconstruction

Flux Reconstruction [12, 24] applied to the linear advection equation will form the basis of the initial investigation to be carried out, and for the reader’s convenience, an overview of the scheme is presented here. For a more detailed understanding, the reader should consult Huynh [24] or Castonguay [12]. The 1D scheme presented can be readily converted to two and three dimensions for quadrilaterals and hexahedrals, respectively. First, let us consider the one-dimensional advection equation:

$$\begin{aligned} {\frac{\partial u}{\partial t}} + {\frac{\partial f}{\partial x}} = 0 \end{aligned}$$

(1)

The FR method is related to the staggered grid approach of Kopriva and Kolias [28] and Discontinuous Galerkin (DG) [35], and as such it makes use of the same subdivision of the domain into discontinuous sub-domains:

$$\begin{aligned} {\varvec{\Omega }} = \bigcup _{n=1}^{N}{{\varvec{\Omega }}_n} \end{aligned}$$

(2)

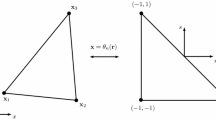
Within the standardised sub-domain, $\hat{\varvec{\Omega }} \in {\mathbb {R}}^d$, computational spatial variables are defined. When $d=1$, $\hat{\varvec{\Omega }} = [-1,1]$, using $\xi$ to denote the value taken. This computational space is discretised with $(p+1)^d$ solution points, and $2d(p+1)^{d-1}$ flux points, placed at the edges of the sub-domain. The solution and flux point locations are typically determined using a tensor grid of a 1D quadrature. Figure 1a shows a 1D example of this. To transform from ${\varvec{\Omega }}_n \rightarrow \hat{\varvec{\Omega }}$, a Jacobian $J_n$ is defined such that:

$$\begin{aligned} {\hat{u}}^{\delta }= {\hat{u}}^{\delta }(\xi ;t) = J_n u^{\delta }(x;t) \end{aligned}$$

(3)

With this domain set up, we now proceed with defining the steps to construct a continuous flux polynomial from the discontinuous segments. The first stage is to define a local solution polynomial in $\hat{{\varvec{\Omega }}}$ using Lagrange interpolation.

$$\begin{aligned} l_k(\xi )&= \prod _{i=0,i\ne k}^{p}{\frac{\xi - \xi _i}{\xi _k - \xi _i}} \end{aligned}$$

(4)

$$\begin{aligned} {\hat{u}}^{\delta }(\xi )&= \sum _{i=0}^{p}{{\hat{u}}^{\delta }_il_i(\xi )} \end{aligned}$$

(5)

Repeating the interpolation for the discontinuous flux in $\hat{{\varvec{\Omega }}}$:

$$\begin{aligned} {\hat{f}}^{\delta D}= {\hat{f}}^{\delta D}(\xi ,t) = \sum _{i=0}^{p}{{\hat{f}}^{\delta D}_il_i(\xi )} \end{aligned}$$

(6)

Here we define ${\hat{f}}^{\delta D}$ as the transformed discontinuous flux polynomial. Now using the Jacobian and the solution polynomials, the primitive values can be calculated in the physical domain ${\varvec{\Omega }}_n$:

$$\begin{aligned} {\overline{u}}^{\delta }(x) = \frac{{\hat{u}}^{\delta }(\xi )}{J_n} = \sum _{i=0}^{p}{u^{\delta }_i l_i(\xi )} \end{aligned}$$

(7)

Fig. 1

Point layout in $\hat{\varvec{\Omega }}$ for $p=3$ and cell interface topology

The primitive polynomial can then be interpolated to the interface and defined as ${\hat{u}}^{\delta }_l = {\hat{u}}^{\delta }(-1)$ and ${\hat{u}}^{\delta }_r = {\hat{u}}^{\delta }(1)$. The values at the interface, I, then allow for a common interface flux, $f^{\delta I}_{I}$, to be calculated in the physical domain. This is shown graphically in Fig. 1b. For a general case, this is done using an approximate Riemann solver on the primitives at the interface, such as: Roe [36]; flux vector splitting [49]; or HLL [22]. In order to get a spatially continuous flux over ${\varvec{\Omega }}$, the common interface flux has to be incorporated into the flux polynomial interior of the element. For FR this is done by using a correction function to propagate the corrected flux into ${\varvec{\Omega }}_n$. The exact definition of the correction function was shown to be important in the determination of the characteristics of FR, by Vincent et al. [53]. Primarily, the correction function is a polynomial which, in one dimension, has the boundary conditions:

$$\begin{aligned} h_L(-1)&= h_R(1) = 1 \end{aligned}$$

(8)

$$\begin{aligned} h_R(-1)&= h_L(1) = 0 \end{aligned}$$

(9)

Beyond this, several sets of stable correction functions have been defined, firstly unified by Vincent et al. [52] and later expanded [43, 44, 48, 54]. However, in this paper we will focus on the correction functions defined by Huynh [24], in particular the Huynh $g_2$ correction function, which is shown in Fig. 1a. We will also consider the correction that can recover Nodal Discontinuous Galerkin (NDG) [23] as it provides a good point of comparison, due to the wide use and maturity of DG. It should be noted that the NDG correction function will only recover NDG in FR for homogeneous linear flux functions, due to the different mechanisms of aliasing.

The correction to the flux function is then calculated using the difference between the discontinuous and common interface values and a correction function. The correction is defined as:

$$\begin{aligned} {\hat{f}}^{\delta C}= \left( {\hat{f}}^{\delta I}_L - {\hat{f}}^{\delta D}_L\right) h_L(\xi ) + \left( {\hat{f}}^{\delta I}_R - {\hat{f}}^{\delta D}_R\right) h_R(\xi ) \end{aligned}$$

(10)

and hence the corrected continuous gradient of the flux is then:

$$\begin{aligned} {\frac{\partial {\hat{f}}^{\delta }}{\partial \xi }}&= \frac{\mathrm {d} {\hat{f}}^{\delta D}}{\mathrm {d} \xi } + \frac{\mathrm {d} {\hat{f}}^{\delta C}}{\mathrm {d} \xi } \end{aligned}$$

(11)

$$\begin{aligned}&= \sum _{j=0}^{p}{\hat{f}}^{\delta D}_j\frac{\mathrm {d} l_j(\xi )}{\mathrm {d} \xi } + \left( {\hat{f}}^{\delta I}_L - {\hat{f}}^{\delta D}_L\right) \frac{\mathrm {d} h_L(\xi )}{\mathrm {d} \xi } + \left( {\hat{f}}^{\delta I}_R - {\hat{f}}^{\delta D}_R\right) \frac{\mathrm {d} h_R(\xi )}{\mathrm {d} \xi } \end{aligned}$$

(12)

Finally, the solution is advanced in time following Eq. (13)—this can be performed via a sensible choice of temporal integration.

$$\begin{aligned} {\frac{\partial {\hat{u}}^{\delta }}{\partial t}} = - {\frac{\partial {\hat{f}}^{\delta }}{\partial \xi }} \end{aligned}$$

(13)

The method detailed here was shown in one dimension for simplicity, but this will be extended to higher dimensionality in subsequent sections. We will briefly state here that, to increase the dimensionality of the method, a tensor product is used. This is the same method as is used in the analysis as well as in the formal implementation of a solver for hypercube elements.

3 Two-Dimensional von Neumann Analysis

The procedure for investigating the dispersion and dissipation properties of finite element methods has been laid out in some detail by Huynh [24], Hesthaven and Warburton [23], and Vincent et al. [53]. It is broadly classified as a von Neumann analysis. The procedure was, however, mainly performed in 1D, with critical insight into the analytical performance of FR when applied to more realistic problems overlooked. Extension of the analysis to higher dimension domains was performed by Lele [31] for various finite difference schemes. This did, however, avoid the increased complexity of finite element von Neumann analysis. To begin our extension we introduce the 2D linear advection equation:

$$\begin{aligned} {\frac{\partial u}{\partial t}} + \nabla \cdot {\mathbf {F}}&= 0 \end{aligned}$$

(14)

$$\begin{aligned} {\mathbf {F}} = \begin{bmatrix} f\\ g \end{bmatrix}&= u{\mathbf {a}} = \begin{bmatrix} au \\ bu \end{bmatrix} \end{aligned}$$

(15)

Flux reconstruction then uses the superposition of the discontinuous flux divergence and flux divergence correction, meaning Eq. (15) can be rewritten as:

$$\begin{aligned} {\frac{\partial {\mathbf {u}}_{i,j}}{\partial t}} = - \nabla \cdot {\mathbf {F}}^{\delta D}_{i,j} - \nabla \cdot {\mathbf {F}}^{\delta C}_{i,j} \end{aligned}$$

(16)

Taking the following definition of the Jacobian, the computational-physical domain transformation can be defined:

$$\begin{aligned} {\mathbf {G}}&= \begin{bmatrix} {\frac{\partial x}{\partial \xi }} \, {\frac{\partial y}{\partial \xi }} \\ {\frac{\partial x}{\partial \eta }} \, {\frac{\partial y}{\partial \eta }} \end{bmatrix} = \begin{bmatrix} G_1 \, G_2 \\ G_3 \, G_4 \end{bmatrix} ~ \quad \mathrm {and} \quad J = |{\mathbf {G}}| \end{aligned}$$

(17)

$$\begin{aligned} u&= J^{-1} {\hat{u}}, \quad {\mathbf {F}} = J^{-1} {\mathbf {G}} \hat{\varvec{F}}, \quad \nabla \cdot {\mathbf {F}} = J^{-1}{\hat{\nabla }}\cdot \hat{\varvec{F}} \end{aligned}$$

(18)

where we use ${\hat{\nabla }}$ to mean $[{\frac{\partial }{\partial \xi }},{\frac{\partial }{\partial \eta }}]^T$ in 2D. We will then impose that grid transformations are purely rectilinear, i.e.$G_2 = G_3 = 0$. This is to reduce the number of dependent variables, while still allowing an important form of grid deformation to be investigated. From the work of Huynh [24], Castonguay [12], and Sheshadri et al. [40], Eq. (15) is written in two dimensions as:

$$\begin{aligned}&{\hat{\nabla }}\cdot \hat{\varvec{F}}^{\delta D} = \sum ^p_{i=0}\sum ^p_{j=0} {\hat{f}}^{\delta D}_{i,j}\frac{\mathrm {d} l_i(\xi )}{\mathrm {d} \xi }l_j(\eta ) + \sum ^p_{i=0}\sum ^p_{j=0} {\hat{g}}^{\delta D}_{i,j}\frac{\mathrm {d} l_j(\eta )}{\mathrm {d} \eta }l_i(\xi ) \end{aligned}$$

(19)

$$\begin{aligned} {\hat{\nabla }}\cdot \hat{\varvec{F}}^{\delta C}&= \sum ^p_{i=0}\Bigg ( \Bigg ({\hat{f}}^{\delta I}_{L,i} - {\hat{f}}^{\delta D}_{L,i}\Bigg )\frac{\mathrm {d} h_{L,i}}{\mathrm {d} \xi } + \Bigg ({\hat{f}}^{\delta I}_{R,i} - {\hat{f}}^{\delta D}_{R,i}\Bigg )\frac{\mathrm {d} h_{R,i}}{\mathrm {d} \xi } \nonumber \\&\quad \, +\Bigg ({\hat{g}}^{\delta I}_{B,i} - {\hat{g}}^{\delta D}_{B,i}\Bigg )\frac{\mathrm {d} h_{B,i}}{\mathrm {d} \eta } + \Bigg ({\hat{g}}^{\delta I}_{T,i} - {\hat{g}}^{\delta D}_{T,i}\Bigg )\frac{\mathrm {d} h_{T,i}}{\mathrm {d} \eta }\Bigg ) \end{aligned}$$

(20)

where we use L, R, B, and T subscripts to mean left, right, bottom, and top respectively. We may now use Eq. (19) and convert it into a matrix form:

$$\begin{aligned} {\hat{\nabla }}\cdot \hat{\varvec{F}}^{\delta D}&= {\mathbf {D}}_{\xi }\hat{\varvec{f}}^{\delta }_{i,j} + {\mathbf {D}}_{\eta }\hat{\varvec{g}}^{\delta }_{i,j} \end{aligned}$$

(21)

$$\begin{aligned} \nabla \cdot {\mathbf {F}}^{\delta D}&= G^{-1}_{1,i,j}{\mathbf {D}}_{\xi }\varvec{f}^{\delta }_{i,j} + G^{-1}_{4,i,j}{\mathbf {D}}_{\eta }\varvec{g}^{\delta }_{i,j} \end{aligned}$$

(22)

To apply the correction function, we need to calculate the interface values around the element. For the case of generalised central/upwinding with upwinding ratio $\alpha$, the common interface fluxes may be written as:

$$\begin{aligned}&G^{-1}_{4,i,j}{\hat{f}}^{\delta I}_L = a\big (\alpha G^{-1}_{4,i-1,j}{\hat{u}}^{\delta }_{i-1,j,R} + (1-\alpha )G^{-1}_{4,i ,j}{\hat{u}}^{\delta }_{i ,j,L}\big ) \end{aligned}$$

(23)

$$\begin{aligned}&G^{-1}_{4,i,j}{\hat{f}}^{\delta I}_R = a\big (\alpha G^{-1}_{4,i,j}{\hat{u}}^{\delta }_{i,j,R} + (1-\alpha )G^{-1}_{4,i+1,j}{\hat{u}}^{\delta }_{i+1,j,L}\big ) \end{aligned}$$

(24)

$$\begin{aligned}&G^{-1}_{1,i,j}{\hat{g}}^{\delta I}_B = b\big (\alpha G^{-1}_{1,i,j-1}{\hat{u}}^{\delta }_{i,j-1,T} + (1-\alpha )G^{-1}_{1,i ,j}{\hat{u}}^{\delta }_{i ,j,B} \big ) \end{aligned}$$

(25)

$$\begin{aligned}&G^{-1}_{1,i,j}{\hat{g}}^{\delta I}_T = b\big (\alpha G^{-1}_{1,i,j}{\hat{u}}^{\delta }_{i,j,T} + (1-\alpha )G^{-1}_{1,i,j+1}{\hat{u}}^{\delta }_{i,j+1,B}\big ) \end{aligned}$$

(26)

where $\alpha = 1$ gives rise to upwinding and $\alpha =0.5$ produces central difference. Hence, the divergence correction can be written as:

$$\begin{aligned} {\hat{\nabla }}\cdot \hat{\varvec{F}}^{\delta C}_{i,j}&= \frac{a\alpha }{G_{4,i,j}^{-1}} \bigg (G^{-1}_{4,i-1,j}\mathbf {h_L}\mathbf {l_R}^T\hat{{\mathbf {u}}}^{\delta }_{i-1,j} - G^{-1}_{4,i,j}\mathbf {h_L}\mathbf {l_L}^T\hat{{\mathbf {u}}}^{\delta }_{i,j}\bigg ) \nonumber \\&\quad + \frac{a(1-\alpha )}{G_{4,i,j}^{-1}} \bigg (G^{-1}_{4,i+1,j}\mathbf {h_R}\mathbf {l_L}^T\hat{{\mathbf {u}}}^{\delta }_{i+1,j} - G^{-1}_{4,i,j}\mathbf {h_R}\mathbf {l_R}^T\hat{{\mathbf {u}}}^{\delta }_{i,j}\bigg )\nonumber \\&\quad + \frac{b\alpha }{G_{1,i,j}^{-1}} \bigg (G^{-1}_{1,i,j-1}\mathbf {h_B}\mathbf {l_T}^T\hat{{\mathbf {u}}}^{\delta }_{i,j-1} - G^{-1}_{1,i,j}\mathbf {h_B}\mathbf {l_B}^T\hat{{\mathbf {u}}}^{\delta }_{i,j}\bigg ) \nonumber \\&\quad +\frac{b(1-\alpha )}{G_{1,i,j}^{-1}} \bigg (G^{-1}_{1,i,j+1}\mathbf {h_T}\mathbf {l_B}^T\hat{{\mathbf {u}}}^{\delta }_{i,j+1} - G^{-1}_{1,i,j}\mathbf {h_T}\mathbf {l_T}^T\hat{{\mathbf {u}}}^{\delta }_{i,j}\bigg ) \end{aligned}$$

(27)

where $\mathbf {h_L}$ now represents the gradient of the left correction function at the solution points and again $\mathbf {l_L}$ are the values of the polynomial basis at the left interface and so on for R, T, and B. Therefore, by grouping terms by their cell indexing and transforming each term into the physical domain:

$$\begin{aligned} \begin{aligned} {\frac{\partial {\mathbf {u}}_{i,j}}{\partial t}} =&- aG_{1,i,j}^{-1}\Big ({\mathbf {C}}_L \varvec{u}^{\delta }_{i-1,j} + {\mathbf {C}}_{0\xi } \varvec{u}^{\delta }_{i,j} + {\mathbf {C}}_R \varvec{u}^{\delta }_{i+1,j} \Big ) \\&- b G_{4,i,j}^{-1}\Big ({\mathbf {C}}_B \varvec{u}^{\delta }_{i,j-1} + {\mathbf {C}}_{0\eta } \varvec{u}^{\delta }_{i,j} + {\mathbf {C}}_T \varvec{u}^{\delta }_{i,j+1} \Big ) \end{aligned} \end{aligned}$$

(28)

where

$$\begin{aligned}&{\mathbf {C}}_{L} = \alpha \mathbf {h}_{\mathbf{L}}\mathbf {l}_{\mathbf{R}}^T \quad {\mathbf {C}}_R = (1-\alpha )\mathbf {h}_{\mathbf{R}}\mathbf {l}_{\mathbf{L}}^T \quad {\mathbf {C}}_{0\xi } = {\mathbf {D}}_{\xi } - \alpha \mathbf {h}_{\mathbf{L}}\mathbf {l}_{ + }^T - (1-\alpha )\mathbf {h}_{\mathbf{R}}\mathbf {l}_{\mathbf{R}}^T \end{aligned}$$

(29)

$$\begin{aligned}&{\mathbf {C}}_B = \alpha \mathbf {h}_{\mathbf{B}}\mathbf {l}_{\mathbf{T}}^T\quad {\mathbf {C}}_T = (1-\alpha )\mathbf {h}_{\mathbf{T}}\mathbf {l}_{\mathbf{B}}^T\quad {\mathbf {C}}_{0\eta } = {\mathbf {D}}_{\eta } - \alpha \mathbf {h}_{\mathbf{B}}\mathbf {l}_{\mathbf{B}}^T - (1-\alpha )\mathbf {h}_{\mathbf{T}}\mathbf {l}_{\mathbf{T}}^T \end{aligned}$$

(30)

Finally, as we are interested in the frequency response of the system, and, importantly to engineers and technicians, how the cell’s orientation relative to an oncoming wave affects performance. Therefore, we impose a trial solution of the form:

$$\begin{aligned} u(x,y;t) = \exp {(ik(x\cos \theta + y\sin \theta - ct))} \end{aligned}$$

(31)

and by substitution into Eq. (15), the advection velocity, ${\mathbf {a}}$, can be found, which is shown schematically in Fig. 2a.

$$\begin{aligned} {\mathbf {a}} = \begin{bmatrix} a\\ b \end{bmatrix} = \begin{bmatrix} \cos \theta \\ \sin \theta \end{bmatrix} \end{aligned}$$

(32)

Fig. 2

Linear advection schematic for two and three dimensions

The plane wave can then be projected into the computational domain and discretised as:

$$\begin{aligned} {\mathbf {u}}_{i,j} = {\mathbf {v}}\exp {\bigg (ik\Big (\big (0.5(\xi +1)\delta _{i} + x_i\big )\cos \theta + \big (0.5(\eta +1)\delta _{j} + y_j\big )\sin \theta -ct\Big )\bigg )} \end{aligned}$$

(33)

where, for brevity, $\delta _i = x_i-x_{i-1}$ and $\delta _j = y_j - y_{j-1}$ are defined. Inserting Eq. (33) into Eq. (28), an eigenvalue problem can be obtained as:

$$\begin{aligned} -ikc(k){\mathbf {v}}&= - G_{1,i,j}^{-1}\cos \theta \Big ({\mathbf {C}}_L\exp {\big (-ik\delta _{i-1}\cos \theta \big )} + {\mathbf {C}}_{0\xi } + {\mathbf {C}}_R\exp {\big (ik\delta _{i}\cos \theta \big )} \Big ){\mathbf {v}} \nonumber \\&\quad \,\, - G_{4,i,j}^{-1}\sin \theta \Big ({\mathbf {C}}_B\exp {\big (-ik\delta _{j-1}\sin \theta \big )} + {\mathbf {C}}_{0\eta } + {\mathbf {C}}_T\exp {\big (ik\delta _j\sin \theta \big )} \Big ){\mathbf {v}} \end{aligned}$$

(34)

where $\mathfrak {R}{k(c(k))}=\mathfrak {R}{(\omega )}$ and $\mathfrak {I}{(kc(k))}=\mathfrak {I}{(\omega )}$ are the dispersion and dissipation, respectively, and $\omega$ is the modified angular frequency response of the system. By studying the trial solution of Eq. (31) it can be understood that if $\mathfrak {I}{(\omega )} > 0$ then the amplitude of the wave will increase and vice versa. Furthermore, if $\mathfrak {R}{(\omega )}\ne k$ then a wave will move at a different speed compared to the other waves inside the packet. This causes the quality of the interpolation to be affected as the solution is advanced in time. An important point is the difference between phase velocity $\omega /k$ and group velocity $\mathrm {d}\omega /\mathrm {d}k$. Phase velocity is the speed of a wave in a packet of waves. Group velocity is the speed of the packet. Therefore, changes to $\mathrm {d}\omega /\mathrm {d}k$ can be thought of as changes to the physics due to the numerical method.

Equation (34) can alternatively be cast in the form of an update equation. If initially Eq. (28) is combined with Eq. (33), then a new matrix, ${\mathbf {Q}}_{i,j}$, can be defined:

$$\begin{aligned} {\frac{\partial {\mathbf {u}}_{i,j}}{\partial t}}&= {\mathbf {Q}}_{i,j}{\mathbf {u}}_{i,j} \end{aligned}$$

(35)

$$\begin{aligned} {\mathbf {Q}}_{i,j}&= - G_{1,i,j}^{-1}\cos \theta \Big ({\mathbf {C}}_L \exp {\big (-ik\delta _{i-1}\cos \theta \big )} + {\mathbf {C}}_{0\xi } + {\mathbf {C}}_R\exp {\big (ik\delta _{i}\cos \theta \big )} \Big )\nonumber \\&\quad \,\, - G_{4,i,j}^{-1}\sin \theta \Big ({\mathbf {C}}_B \exp {\big (-ik\delta _{j-1}\sin \theta \big )} +{\mathbf {C}}_{0\eta } +{\mathbf {C}}_T \exp {\big (ik\delta _j\sin \theta \big )} \Big ) \end{aligned}$$

(36)

This definition of the semi-discrete FR operator, ${\mathbf {Q}}$, can then be used to form what is called the update equation by imposing some temporal discretisation. As such we may write:

$$\begin{aligned} {\mathbf {u}}^{n+1}_{i,j}&= {\mathbf {R}}({\mathbf {Q}}_{i,j}){\mathbf {u}}^n_{i,j} \end{aligned}$$

(37)

$$\begin{aligned} {\mathbf {R}}_{33}&= {\mathbf {I}} + \frac{\tau {\mathbf {Q}}_{i,j}}{1!} + \frac{(\tau {\mathbf {Q}}_{i,j})^2}{2!} + \frac{(\tau {\mathbf {Q}}_{i,j})^3}{3!} \end{aligned}$$

(38)

where the superscript denotes the time level, and our update matrix is ${\mathbf {R}}$. Shown here is also an example definition for ${\mathbf {R}}$ for a 3-step $3^{\mathrm {rd}}$-order Runge–Kutta time integration scheme. Finally, in keeping with von Neumann’s theorems [25, 30] and Banach’s fixed point theorem [29], the spectral radius of ${\mathbf {R}}$ has to be less than or equal to 1 for stability. $\rho ({\mathbf {R}}) \leqslant 1 \, \forall \, k \in {\mathbb {R}}$.

In recent works by Vermeire et al. [51] and Trojak et al. [46], the Fourier analysis was extended by fully discretising the equation. This is performed by taking Eq. (37) and again applying Eq. (31). This results in:

$$\begin{aligned} \exp {(-ik(c-1)\tau )}{\mathbf {v}} = \lambda {\mathbf {v}} = \exp {(ik\tau )}{\mathbf {R}}(k,\tau ){\mathbf {v}} \end{aligned}$$

(39)

where the time step from n to $n+1$ is $\tau$. Hence, we rearrange for the modified wave speed:

$$\begin{aligned} c = \frac{i\log {(\lambda )}}{k\tau } + 1 \end{aligned}$$

(40)

where $\lambda$ are the eigenvalues of $\exp {(ik\tau )}{\mathbf {R}}$. The advantage of this further analysis is that it gives the dispersion and dissipation relations of the full scheme as would be experienced when applied as implicit LES.

The results of this section can then be extended to n-dimensions. The analysis can broadly be repeated but is beyond the scope of this work. But, we give the example for 3D Bloch wave as:

$$\begin{aligned} u = \exp {\big (ik(x\cos \phi \cos \theta + y\cos \phi \sin \theta + z\sin \phi - ct)\big )} \end{aligned}$$

(41)

where the angles are as shown in Fig. 2b, and hence the 3D convective velocities for linear advection are:

$$\begin{aligned} {\mathbf {a}} = \begin{bmatrix} \cos \phi \cos \theta \\ \cos \phi \sin \theta \\ \sin \phi \end{bmatrix} \end{aligned}$$

(42)

4 Two-Dimensional Error and Convergence Analysis

The techniques applied to the linear advection equation of Sect. 3 can be further extended to examine the effects of the grid and wave angle upon the error convergence. This method was initially presented for a 1D uniform grid in FR by Astana et al. [4], and for fully-discrete equations by Trojak et al. [46]. Here we will extend the analysis to include stretched grids in two dimensions with $(p+1)^2$ solution points. To begin, we will diagonalise the semi-discrete FR operator matrix as:

$$\begin{aligned} {\mathbf {Q}} = {\mathbf {W}}{\varvec{\Gamma }}{\mathbf {W}}^{-1} ={\mathbf {W}}ik{\varvec{\Lambda }}{\mathbf {W}}^{-1} \end{aligned}$$

(43)

Here ${\mathbf {W}}$ is an eigenvector matrix and ${\varvec{\Gamma }}$ is the diagonal eigenvalue matrix. The matrix ${\varvec{\Lambda }}$ is then a normalised form of the eigenvalue matrix, used to simplify later notation. This diagonalisation may then be exponentially integrated in order to advance the solution continuously in time such that:

$$\begin{aligned} {\mathbf {u}}_{i,j}^{\delta }(t) = \exp {(ct{\mathbf {Q}})}{\mathbf {u}}(0) = {\mathbf {W}}\exp {(ikct{\varvec{\Lambda }})}{\mathbf {W}}^{-1}{\mathbf {u}}_j(0) \end{aligned}$$

(44)

Here the definition of a matrix exponential has been used with ${\mathbf {W}}^{-1}{\mathbf {W}}={\mathbf {I}}$ to simplify the form. The initial condition is then required and is defined as:

$$\begin{aligned} {\mathbf {u}}_{i,j}(0) = \exp {(ik(x_j\cos {(\theta )} + y_j\sin {(\theta )})}{\mathbf {W}}\pmb {\beta } \end{aligned}$$

(45)

For convenience we will define the solution shift based on the cell location as:

$$\begin{aligned} u_{c,i,j} = \exp {\big (ik(x_i\cos {(\theta )} + y_j\sin {(\theta )}\big )} \end{aligned}$$

(46)

The initial condition may then be substituted into Eq. (44), leading to:

$$\begin{aligned} {\mathbf {u}}_{i,j}^{\delta }(t) = u_{c,i,j}{\mathbf {W}}\exp {(-ikct{\varvec{\Lambda }})}\pmb {\beta } = u_{c,i,j}\sum _{n=1}^{(p+1)^2}\exp {(-ikct\lambda _n)}\beta _n{\mathbf {w}}_{n} \end{aligned}$$

(47)

Here ${\mathbf {w}}_n$ is the $n^\mathrm {th}$ eigenvector taken from ${\mathbf {W}}$ and $\beta _n$ is the $n^\mathrm {th}$ coefficient taken from $\pmb {\beta }$. The semi-discrete error may then be calculated by analytically evolving the discrete solution using exponential integration. Hence, the analytical solution in time is:

$$\begin{aligned} {\mathbf {u}}_{i,j}(t) = u_{c,i,j}\exp {(-ikct)}{\mathbf {u}}_{i,j}(0) = u_{c,i,j}\exp {(-ikct)}\sum ^{(p+1)^2}_{n=1}\beta _n{\mathbf {w}}_{Q,n} \end{aligned}$$

(48)

Therefore, the semi-discrete error can be formed by subtracting Eq. (48) from Eq. (47) as:

$$\begin{aligned} \begin{aligned} {\mathbf {e}}_{i,j}(t,k)&= {\mathbf {u}}_{i,j}^{\delta }(t,k) - {\mathbf {u}}_{i,j}(t,k) \\&= u_{c,i,j}\exp {(-ikct)} \sum ^{(p+1)^2}_{n=1}\Big (\exp {\big (ikct(\lambda _n+1)\big )}-1\Big )\beta _n{\mathbf {w}}_{Q,n} \end{aligned} \end{aligned}$$

(49)

This measure of the semi-discrete error can then inform how the error changes with grid and wavenumber, some results of which were investigated for 1D NDG via FR by Astana et al. [4]. Subsequently, the error may form a rate of convergence, which for grid spacing is then:

$$\begin{aligned} r_h(t,k) = \frac{\log {(\Vert {\mathbf {e}}_{i,j}(t,k,J_1))\Vert _2)} - \log {(\Vert {\mathbf {e}}_{i,j}(t,k,J_2))\Vert _2)}}{\log {(J_1)} - \log {(J_2)}} \end{aligned}$$

(50)

Here $J_1$ and $J_2$ are the Jacobians for two different grid spacings. The rate of convergence with wavenumber is similarly defined as:

$$\begin{aligned} r_k(t,J) = \frac{\log {(\Vert {\mathbf {e}}_{i,j}(t,k_1,J))\Vert _2)} - \log {(\Vert {\mathbf {e}}_{i,j}(t,k_1,J))\Vert _2)}}{\log {(k_1)} - \log {(k_2)}}. \end{aligned}$$

(51)

5 Analytical Findings

The analytical methods presented in Sects. 3 and 4 allow us to investigate many properties of FR, however from Eqs. (36–38) it can be seen that the functional space of ${\mathbf {Q}}$ is 8 dimensional, leading to the functional space of $\rho ({\mathbf {R}})$ being 9 dimensional ($\tau ,\gamma _x,\gamma _y,\varDelta _x,\varDelta _y,k,\theta ,\iota ,p$). Therefore, we need to restrict our investigation to some key results relating to grid deformation. Firstly, understanding the dispersion and dissipation ($\mathfrak {R}{(\omega )}$ and $\mathfrak {I}{(\omega )}$) in 2D for both uniform and stretched grids will be important. Secondly, we wish to briefly understand how higher dimensionality and grid deformations affect the temporal stability of FR through evaluation of the CFL limits [16]. Then we will go on to study the effect of grid deformation and incident angle on the rate of convergence. We will finish the analytic study with the evaluation of the fully-discrete dispersion and dissipation relations. Throughout this investigation we will also look to understand the effect of the correction functions on these properties.

5.1 Review of 1D Grid Expansion

Before commencing with the Fourier/von Neumann analysis in 2D, we will give a brief review of the behaviour exhibited in one dimension. Figure 3 shows the results for upwinded NDG correction functions at various order.

Fig. 3

Upwinded 1D FR, for various orders with NDG correction functions

The results are separated into the real and imaginary parts of ${\hat{\omega }}$, where they represent dispersion and dissipation respectively. Ideally $\mathfrak {R}{({\hat{\omega }})}=1$ and $\mathfrak {I}{({\hat{\omega }})}=0$. However, the numerical discretisation will cause deviation from the ideal dispersion, while the interface upwinding here will cause dissipation. In [47] a non-conservative Jacobian definition was used that resulted in variation of the numerical characteristics as the grid was deformed. However, if a conservative Jacobian is properly applied, then grid stretching has no impact upon dispersion and dissipation of FR other than a change in the Nyquist wavenumber. For a geometrically deformed grid the Nyquist wavenumber will be:

$$\begin{aligned} k_\mathrm {nq} = \frac{1}{2\gamma (p+1)} \end{aligned}$$

(52)

This raises the question, of what is the impact—for this linear system in 2D—of stretching the grid in x and y? And what implications will these effects have for the practical application of the scheme? Additionally, what implications will any effects have on the practical application of the scheme?

5.2 Effect of Grid on Dispersion and Dissipation

For the higher dimensional case, we begin by considering the dispersion and dissipation on a uniform grid in two dimensions as order is varied. We are concerned here with the primary mode—as FR has multiple modes, this is the one that physically represents the wave. Although, as was found by Asthana et al. [4], this may not be how the energy distributes itself. We identify the physical mode as that which has the largest contribution to the energy at very low, well resolved, wavenumbers.

For this investigation into the dispersion and dissipation characteristics of FR, we wish to make a note of the Nyquist frequency of the elements. The Nyquist frequency has a dependency on the expansion ratio. This is found from the harmonic mean of the 1D Nyquist frequencies, then normalised by the adjacent element size at that angle. Hence, the normalised wavenumber is then:

$$\begin{aligned} {\hat{k}} = k/k_\mathrm {nq} = \frac{1}{2}k\max {\big \{\cos {(\theta )},\sin {(\theta )}\big \}}\bigg (\frac{1}{p+1}\bigg )\sqrt{\bigg (\frac{\cos {(\theta )}}{\gamma _x}\bigg )^2 + \bigg (\frac{\sin {(\theta )}}{\gamma _y}\bigg )^2} \end{aligned}$$

(53)

Fig. 4

Primary mode dispersion for 2D upwinded FR, with Huynh $g_2$ corrections, at various orders. Normalised wavenumber as radial distance (markers at $\pi /4$ intervals), and element angle of incidence as azimuthal distance

Fig. 5

Primary mode dissipation for 2D upwinded FR, with Huynh $g_2$ corrections, at various orders. Normalised wavenumber as radial distance (markers at $\pi /4$ intervals), and element angle of incidence as azimuthal distance

The dispersion and dissipation relations are then shown in Figs. 4 and 5 . It is clear that for all orders FR becomes dispersive as the incidence angle is increased to $\theta =45^{\circ }$, but then returns to a dispersion similar to that of $\theta =0^\circ$ close to $\theta =45^\circ$. This can be seen by the bowing out of the contour as the angle approaches $45^\circ$ before receding at $\theta =45^\circ$. In the case of dissipation for uniform grids, the dissipation decreases as the angle increases towards a minimum at $\theta \approx 30^\circ$. Once again at $\theta =45^\circ$, the dissipation returns to that of a wave at $0^\circ$. This behaviour, where both the dispersion and dissipation at $\theta =0^\circ$ and $45^\circ$ are the same, is due to the projection of the wave in y being zero in the $\theta =0^\circ$ case and the projections in x and y being the same in the $\theta =45^\circ$ case.

Looking at the trends shown as order is varied, order seems to only have a minor impact on the angular spread over which the dispersion and dissipation changes. By comparison with the results of Lele [31], where a similar test is performed for finite and compact difference schemes, FR shows a comparatively smaller change in performance as the angle is varied. It is thought that this is due to the method of polynomial fitting used by FR, namely that this implementation of FR used a tensor grid of monomials i.e., the number of solution points is $(p+1)^d$ and hence the monomials in the interpolation go from $(\xi ^0\eta ^0,\xi ^1\eta ^0\dots \xi ^p\eta ^p)$. By contrast, finite differences do not include the cross product terms, which will become increasingly dominant as the angle is increased.

Fig. 6

Two dimensional upwinded FR, $p=3$ with Huynh $g_2$ corrections, for different grid expansion factors. Normalised wavenumber as radial distance (markers at $\pi /4$ intervals), and element angle of incidence as azimuthal distance

Moving on, we then consider the impact of non-uniform grids on the character of the dispersion and dissipation. In particular, we explore the effect of grid expansion and contraction and how they interact, if there is expansion orthogonal to contraction. Initially we will focus on Huynh’s $g_2$ correction function, the results of which are summmarised in Fig. 6.

Let us first focus on the case of $\gamma _x=1$ and $\gamma _y=1.1$, as is presented in Fig. 6a, b. In the region of $0^\circ<\theta <45^\circ$, the impact of the perpendicular grid expansion has been to reduce $\mathfrak {R}{({\hat{\omega }})}$—most notably near $\theta =45^\circ$—as is exemplified in Fig. 7a. Conversely, in the range $45^\circ<\theta <90^\circ$ the grid expansion has caused an increase in dispersion. For the case of $p=3$ explored here, this action is beneficial, however, as order is increased further this may cause a detrimental dispersion overshoot to develop. Studying the impact on dissipation for $\gamma _x=1$, $\gamma _y=1.1$ case, associated with the increase in dispersion, there is additional dissipation over the central wavenumbers. This is preceded by a reduction in dissipation near the Nyquist wavenumber. This behaviour is reversed for dissipation in $45^\circ<\theta <90^\circ$.

We may now apply a contraction perpendicular to an expansion, shown in Fig. 6c, d. The trends that were discussed for $\gamma _x=1$, $\gamma _y=1.1$ seem to continue when an additional contraction is applied. However, the contraction has served to amplify the effect seen previously, which is more clearly visible in Fig. 7. It should also be remarked that the dispersion and dissipation at $\theta =45^\circ$ is no longer the same as the $\theta =0^\circ$ case. This is due to the projection into x and y no longer being the same, which can be understood from Eq. 53. This equation also indicates the origin of the differences with angle and deformation: that, after projection into x and y, the wave components will have different normalised wavenumbers in the element they are advecting from, and hence different properties.

To understand this further we can think about a given wave decomposed into x and y components initially at $\theta =45^\circ$. For $\gamma _x=1$ and $\gamma _y=1.1$ we may calculate the normalised wavenumber of the projections in the adjacent upwind elements, this will aid in understanding how the incoming solution is affected. Although they should be equal, the projection in y will have a lower wavenumber due to the smaller size of the element from which it is advecting. At low wavenumbers this difference will have a small impact on the 2D result as in both x and y we have $c\approx 1$. However at higher wavenumbers the effect will become more pronounced. Larger variations are then seen at other angles due to the projections, even for a uniform grid, having different wavenumbers and hence properties. This also explains why, in Fig. 7, we see the effect of grid deformation being approximately symmetric about the uniform case. Furthermore, this explains why coupling an expansion and contraction causes the effect to become more pronounced.

Fig. 7

Two dimensional upwinded FR, $p=3$, with Huynh $g_2$ corrections at selected incident angles and stretching

We will now vary the correction function and investigate the effect of grid stretching. Here we will apply the NDG correction function, the results of which are presented in Fig. 8. When applied to a uniform grid, it is evident that NDG exhibits similar changes compared to Huynh’s $g_2$ as the incidence angle is varied. Nonetheless, the variation of dispersion and dissipation with $\theta$ appears to be smaller for NDG. As the grid is then deformed, the same changes in the properties take place. Yet, due to the dispersion overshoot of NDG in the uniform case, stretching has led to the changes in dispersion becoming more significant.

Fig. 8

Two dimensional upwinded FR, $p=3$ with NDG corrections, for different grid expansion factors. Normalised wavenumber as radial distance (markers at $\pi /4$ intervals), and element angle of incidence as azimuthal distance

5.3 Effect of Grid on Error and Convergence

The dispersion and dissipation relations explored show that grid expansion, contraction and incidence angle can have an appreciable impact on the numerical characteristics of FR. A means of measuring the impact of these variations is through calculating analytically the error of the method.

Beginning with a uniform grid, the error with wavenumber for a uniform grid can be seen in Fig. 9. Here, time has been normalised by the wave’s time period. Figure 9a shows that we may separate the error into three regions. Low wavenumbers, where the well resolved waves have low levels of error. High wavenumbers, where the lower dissipation of Huynh’s $g_2$ correction function leads to some high amplitude oscillations. Previous works [4, 46] found that these oscillations were due to the solution being formed from secondary, erroneous, modes. Lastly, there is a central range of wavenumbers where the solution is still mainly composed of the primary mode, however, the primary mode’s dissipation is increasing. Therefore, waves here quickly become damped and the error grows.

Comparison may be made to the error evolution for NDG, shown in Fig. 9b. It is evident that NDG has lower error and a wider range of wavenumbers over which waves are well resolved. At higher wavenumbers NDG also produces lower amplitude spurious waves. This is due to the higher dissipation of NDG compared to $g_2$. In the intermediate range of wavenumbers, transients in the error early on are visible for both NDG and $g_2$. However they appear smaller for NDG, again associated with the higher dissipation and reduced half-life of the spurious modes.

Fig. 9

Semi-discrete error of FR, $p=3$, with upwinded interfaces on a uniform grid for $\theta =45^\circ$

The error results presented here were for a wave at $45^\circ$. To understand the effect of incidence angle, the error calculated may then be used to produce a rate of convergence with grid spacing via Eq. (50). A rate of convergence with wavenumber is similarly defined, Eq. (51). However, this gives much the same insight as $r_h$ and is left out for brevity. The results for $r_h$ on a uniform grid, at an absolute wavenumber of $k=2$ and $J_1/J_2 = 2$ are then shown in Fig. 10. For NDG, Fig. 10a, the initial rate of convergence is 4 and, after the dissipation of spurious modes, the rate can be seen to be increasing towards 7. This is the expected behaviour explored by Asthana et al. [4]. As the angle is varied, however, the time for the scheme to reach the convergence-rate-limit increases. This indicates that as the incidence angle is increased towards $\theta =45^\circ$, the half-life of the secondary modes may also increase. This is rooted in the use of an anisotropic quadrature to form the polynomial approximation. In particular, we use a tensor grid, which has higher resolution on the diagonal. Hence, although the primary mode is unaffected at $\theta =45^\circ$, we have shown here that the resolution of the secondary mode is increased. Consequently, this could mean that when the method is applied practically, grid alignment could impact results.

Again, investigating the effect of changing to Huynh’s $g_2$ correction function (Fig. 10b) we see that the initial rate is the expected value of 4, which then asymptotes to a value of 6. The decrease relative to NDG is due to the well know super-convergence of DG [3, 15], and in FR is rooted in the $g_2$ correction function having lower order, $p-1$, terms. For $g_2$ correction functions, the reduction in the dissipation for $\theta \approx 30^\circ$ and $\theta \approx 60^\circ$ coincides with an increase in the time to reach the convergence limit, similar to that observed for NDG. However, the $g_2$ correction functions goes on to have a slight increase in the convergence limit around $\theta =45^\circ$. In a more general sense, it may be remarked that $g_2$ correction functions may be more resilient in higher dimensions due to smaller variation in properties that this rate investigation shows.

Fig. 10

Grid spacing rate of convergence of FR, $p=3$, with upwinded interfaces on a uniform grid

Fig. 11

Semi-discrete error of FR, $p=3$, upwinded interfaces with: $\gamma _x=1$, $\gamma _y=1.1$, and $\theta =30^\circ$. Here Huynh’s $g_2$ correction function has been applied

Now applying a grid expansion in the y direction, we obtain the error results presented in Fig. 11. Here we have extended the time window of the analysis to demonstrate a key result. For the range of wavenumbers that would be expected to be well resolved, the error steadily increases with time. This is not due to excess dissipation. It is clear from Fig. 6b the change in dissipation in this range is negligible, and is in fact reduced. Inspection of the values of ${\varvec{\Lambda }}$ instead show there is a small reduction in the phase velocity ($\omega /k$), which will have an associated reduction in the group velocity ($\partial \omega /\partial k$). Therefore, the speed at which the wave is propagating is incorrect and manifests itself as a gradually oscillating error. Due to this behaviour of the error, it has not been possible to calculate the rate of convergence on stretched grids.

5.4 Effect of Grid on CFL Limit

We add here a brief note on the temporal stability limits on non-uniform grids. The definition of CFL limit, extended to higher dimension, that we will apply is:

$$\begin{aligned} \mathrm {CFL}_d = \tau \sum ^d_{i=1}\frac{a_i}{\varDelta _i} \end{aligned}$$

(54)

where d is the dimensionality, $\tau$ is the time step and, $a_i$ and $\varDelta _i$ are the characteristic velocity and grid spacing in the $i^{\mathrm {th}}$ dimension, respectively. The CFL limit is then the maximum value of CFL at which the scheme is stable in a von Neumann sense.

We undertook an analysis in which the angle, x to y ratio ($\varDelta x/\varDelta y$), and stretching factors ($\gamma _x$ and $\gamma _y$) were varied. It was found that there is no dependence between these factors and the CFL limit when the CFL number is defined as in Eq. (54). This means that when applied to a 2D plane wave the CFL number based on $\tau$ is:

$$\begin{aligned} \mathrm {CFL} = \tau \bigg (\frac{\cos {(\theta )}}{\varDelta x} + \frac{\sin {(\theta )}}{\varDelta y}\bigg ) \end{aligned}$$

(55)

This is clearly an implication of solving a linear equation that could be decomposed into an x and y direction. Moreover, as the correction function was varied the CFL limit in 2D was found to be the same as those presented for 1D by Vincent et al. [53].

5.5 Effect of Grid on Fully Discrete Dispersion and Dissipation

Following on from the exploration of grid expansion on temporal stability limits, we will present the fully discretised Fourier analysis in 2D. In this investigation, we again focus on the Huynh $g_2$ and NDG correction functions, and the effect of angle and grid on the dispersion and dissipation relations. Throughout this investigation as the angle is swept through $0^\circ {-}90^\circ$, the CFL number will be held constant.

Fig. 12

Dispersion and dissipation of upwinded FR, $p=3$, with Huynh $g_2$ corrections, explicit RK44 temporal integration, and $\mathrm {CFL} = 0.8\mathrm {CFL}_\mathrm {max}$. The radial distance is the normalised wavenumber (including the effect of angle), and the azimuthal distance is the angle of incidence to the element

Figure 12 shows the results when using the Huynh $g_2$ correction function, with RK44 explicit temporal integration and $\mathrm {CFL} = 0.8\mathrm {CFL}_\mathrm {max}$. As the angle and wavelength are swept there are some clear anomalous regions, most notably in the dissipation. This is due to difficulties in selecting the primary mode due to large gradients in these regions.

Focusing initially on $\theta =0^\circ$, a large amount of error in the dispersion relation is encountered. Notably, at high wavenumbers, there are regions with rapid changes in $\mathfrak {R}{({\hat{\omega }})}$ and hence a large group velocity ($\partial \omega /\partial k$). This result was also encountered in the 1D work of Vermeire et al. [51], and can result in spurious waves travelling rapidly through the solution, particularly when the method is applied as implicit LES (ILES). What the 2D analysis shows is that as the angle of incidence is increased there is an angle at which the group switches from positive to negative. This occurs here at $\theta \approx 10^\circ$ and then back again at $\theta \approx 35^\circ$. This could have a significant impact on the solution when the method is applied as multidimensional ILES. In this case, spurious high frequency waves will propagate rapidly in different directions depending on the angle of incidence.

For brevity of the main text, results for fully discrete grid stretching have been included in “Appendix A”. They show that grid stretching causes similar changes in behaviour as was observed in the semi-discrete case. The added impact here is that the angle at which the sign of the group velocity changes has been impacted by the grid deformation.

Fig. 13

Dispersion and dissipation of upwinded FR, $p=3$, with NDG corrections, explicit RK44 temporal integration, and $\mathrm {CFL} = 0.8\mathrm {CFL}_\mathrm {max}$. The radial distance is the normalised wavenumber (including the effect of angle), and the azimuthal distance is the angle of incidence to the element

Changing the correction function to use NDG and again maintaining $\mathrm {CFL} = 0.8\mathrm {CFL}_\mathrm {max}$, we obtain the results shown in Fig. 13. When $\theta =0^\circ$, we again see large variations in the dispersion. However, for NDG at high wavenumbers, there is initially an increase in $\mathfrak {R}{({\hat{\omega }})}$ followed by a sharp decrease. This will bring about very high values of group velocity. Sweeping the incidence angle shows somewhat different behaviour to $g_2$ correction functions. There is still a form of change that occurs at $\theta \approx 10^\circ$ and $\theta \approx 35^\circ$, but it has a different character. Now after the switch, the initial increase in dispersion is reduced, and, by inspection, the group velocity at the extreme end of the frequency range seems to have reduced. Throughout the range of wavenumbers with high group velocities, Fig. 13b shows that there is a large amount of dissipation that may reduce the effect of the dispersion. Therefore, it seems that the NDG correction function for ILES with explicit temporal integration may cause smaller dispersion errors for waves that are not grid aligned.

Again, for brevity of the main text, results of grid deformation with the NDG correction function are shown in Appendix A. They indicate the effect of grid deformation is to cause a similar change as to that of the semi-discrete case.

6 Non-linear Navier–Stokes Equations with Deformed Grids

It is common within the CFD community to use the canonical Taylor–Green Vortex (TGV) [41] test case to assess the numerics of a solver applied to the Navier–Stokes equations with turbulence—and to that end, there is a plethora of DNS data available for comparison [19, 50]. However, this case is quite contrived and ultimately will favour spectral or structured methods due to the Cartesian and periodic domain, whilst also being unrepresentative of engineering flows that are often wall bounded and/or have complex geometries. Hence, we propose deforming the elements, initially linearly by jittering the corner nodes to be more representative of real mesh conditions. Importantly, these deformations will introduce cross multiplication into the Jacobian, as well as local regions of expansion and contraction.

The initial conditions of the TGV applied here are those of DeBonis [19], where the character of the flow is controlled by the non-dimensional parameters defined as:

$$\begin{aligned} R_e = \frac{\rho _0U_0L}{\mu }, \quad \quad P_r = 0.71 = \frac{\mu \gamma R}{\kappa (\gamma -1)}, \quad \quad M_a = 0.08 = \frac{U_0}{\sqrt{\gamma R T_0}} \end{aligned}$$

(56)

where we will use the standard set of free-variables for the velocity, density, pressure, and gas characteristics:

$$\begin{aligned} U_0 = 1, \quad \quad \rho _0 = 1, \quad \quad p_0 = 100, \quad \quad R = 1, \quad \quad \gamma = 1.4, \quad \quad L = 1 \end{aligned}$$

(57)

Here, due to the solver implementation, we use a specific gas constant of unity and hence, to achieve the required Reynolds and Prandtl numbers, the dynamic viscosity and thermal conductivity are set appropriately. The statistics that will be studied here are the decay of the kinetic energy and the enstrophy scaled by viscosity, which are defined respectively as:

$$\begin{aligned} -\frac{\mathrm {d} E_k}{\mathrm {d} t}&= -\frac{1}{2U_0^2\rho _0|{\varvec{\Omega }}|}\frac{\mathrm {d} }{\mathrm {d} t}\int _{{\varvec{\Omega }}} \rho (u^2+v^2+w^2)\mathrm {d}{\mathbf {x}} \end{aligned}$$

(58)

$$\begin{aligned} \epsilon&= \frac{\mu }{U_0^2\rho _0^2|{\varvec{\Omega }}|}\int _{{\varvec{\Omega }}}\rho (\pmb {\omega }\cdot \pmb {\omega })\mathrm {d}{\mathbf {x}} \end{aligned}$$

(59)

where $\pmb {\omega }=\nabla \times [u,v,w]^T$ is vorticity and $|{\varvec{\Omega }}|$ is the domain volume. The enstrophy is scaled in such a manner as it is known that in the incompressible case enstrophy and kinetic energy dissipation can be directly related this way. Throughout, a reference DNS solution—labelled ref—is provided from van Rees et al. [50].

The FR method is extended to 3D hexahedrals—from 2D quadrilaterals—by the same tensor product formulation of Huynh [24]. The invisicid common interface calculation was performed using a Rusanov flux [37] with a Davis [17] wave speed. The viscous common interface calculation was the BR1 method of Bassi and Rebay [5, 6]. Here, the gradients of the $C_0$ continuous solution is required at the flux points. These are calculated by first correcting the gradient at the solution points, then interpolating this to the flux points. From here the gradient can be transformed from the computational space to the physical space. The alternative would be to interpolate the solution point gradient after transforming it to the physical space. The two methods will give different results on complex element transformations, however due to the small scale of the viscous terms in the forthcoming cases, investigation of this difference will be deferred.

6.1 Randomised Grids

As has been stated, we begin by taking a uniform periodic mesh on the domain ${\varvec{\Omega }}\in [-\pi ,\pi ]^3$, and jittering corner nodes of the elements that are interior to the domain. The degree of jitter is calculated using a time seeded random number shifted to be centred about zero and scaled by a global factor, $j_f$, between zero and unity. The scaling factor is such that zero gives a uniform mesh and unity could lead to edges of zero length. This transformation is defined as:

$$\begin{aligned} x^\prime&= x + j_f\frac{l({\hat{x}} - 0.5)}{n_x} \end{aligned}$$

(60a)

$$\begin{aligned} y^\prime&= y + j_f\frac{l({\hat{y}} - 0.5)}{n_y} \end{aligned}$$

(60b)

$$\begin{aligned} z^\prime&= z + j_f\frac{l({\hat{z}} - 0.5)}{n_z} \end{aligned}$$

(60c)

where $x^\prime$ etc. are the new points, x etc. are a uniform base grid, and ${\hat{x}}_j\in (0,1]$ etc. are random numbers. To assess the grid quality, we seek a single a metric to describe the relative quality of the meshes produced. We opted for a volume ratio shape factor, slightly redefined as:

$$\begin{aligned} q_h = \frac{6\sqrt{\pi }V_h}{S_h^{3/2}} \end{aligned}$$

(61)

where $S_h$ is the surface area of the hexahedral element and $V_h$ is its volume. The quality metric, $q_h$, is then defined as the ratio of the volume of the element to the volume of a sphere with the same surface area, with $q_h=\sqrt{\pi /6}$ for a perfect cube. To put this parameter into context, some example meshes are shown in Fig. 14.

Fig. 14

Example slices through a 3D hexahedral mesh to illustrate the mesh quality metric

As part of the jittering process, only the four vertices of each element were moved. It remains to propagate these distortions through to the solution and flux points required by the Flux Reconstruction approach. The distortions considered as part of this work were purely linear, and thus the effect of jittering the element vertices could have been carried through to the internal solution points and flux points by use of bilinear interpolation. However, with a view to future work in which non-linear distortions will be applied to the elements, a Radial Basis Function based approach was used to perform the interpolation.

Radial Basis Functions are well known in computational physics for mesh distortion and generalised interpolation (see, for example, [7, 11, 18]). They allow for the easy and smooth interpolation of scattered data, and, in this specific case, for the interpolation of volume distortion from prescribed boundary distortions. A wider discussion of the use of RBFs is outside the scope of this paper, but they take the general form:

$$\begin{aligned} f(x) = \sum _{i=1}^n \lambda _i \phi \left( \left| \left| x - x_i \right| \right| \right) \end{aligned}$$

(62)

where $\lambda _i$ are weights, and $\phi$ is the basis function. The thin plate spline is a widely used radial basis function for mesh warping, and is defined as [20]:

$$\begin{aligned} \phi _{TPS} = \left| \left| x - x_i \right| \right| ^ 2 \ln {\left| \left| x - x_i \right| \right| } \end{aligned}$$

(63)

Once the vertex distortion has been propagated through the solution and flux points of the cell, the Jacobian of the transformation can be defined. Initially, this will be done using the non-conservative formulation ($\xi _x = y_\eta x_\zeta - y_\zeta x_\eta$). This might be expected to be sufficient for the linear distortions to the elements which are being applied here.

Fig. 15

Effect of jitter on turbulent kinetic energy dissipation of the TGV ($R_e=1600$) for FR, $p=2$, with Huynh $g_2$ correction functions on a $120^3$ DoF mesh. Explicit time step size is $\varDelta t = 1\times 10^{-3}$

Fig. 16

Effect of jitter on turbulent kinetic energy dissipation of the TGV ($R_e=1600$) for FR, $p=4$, with Huynh $g_2$ correction functions on a $120^3$ DoF mesh. Explicit time step is $\varDelta t = 1\times 10^{-3}$

Figures 15 and 16 show the first of these results. First looking at Figs. 15a and 16a, which show two specific dissipation curves for a uniform and jittered mesh. At the beginning of the simulation, there is a clear time at which the global energy increases. Extending these runs to cover multiple grid qualities, Figs. 15b and 16b, it is observed that as the grid quality decreases a region where turbulent kinetic energy increases soon emerges. As time progresses, energy dissipation is again seen and the point of peak dissipation arrives early, moving from $t\approx 8.5$ to $t\approx 7.5$. The same behaviour is seen for both $p=2$ and $p=4$. From comparison of $p=2$ and $p=4$, it seems that $p=4$ is slightly more robust to grid deformation, as $p=4$ was able to run at $q_h\approx 0.7$, whereas for $p=2$, $q_h$ could not be reduced much below 0.717 for $120^3$ DoF without completely diverging.

The explanation of this is believed to be due to two interacting components. The first is that, although the randomised grid transformation applied here is linear, the thin plate spline RBF method will not recover an exactly linear model of the transformation. Hence, the second factor is that the non-conservative method for defining the Jacobian is no longer sufficient to accurately define what is now essentially a non-linear transformation. Remedial actions will be presented shortly.

Fig. 17

Comparison of TGV ($R_e=1600$) enstrophy for $120^3$ degree of freedom grid with similar $q_h$

Studying the effect of jittered grids on enstrophy, shown in Fig. 17, it is clear that as the grid is stretched the enstrophy increases. This is indicative of an increase in the vorticity, with the rise occurring within $t=0-1$. This is consistent with energy being added at the large scales, as at this time there are only large scales present. After the initial increase, the enstrophy returns to following the trend of the uniform case. However, in the case of $p=2$, Fig. 17a, a larger initial increase is seen followed by a wider peak. The wider peak is similar in character to that of the uniform case and is due to the grid being mildly under-resolved in the $p=2$ case relative to the DNS. This aims to show that RBF grid transformation can result in non-linearities in the grid and, when coupled to a non-conservative Jacobian, this manifests itself in the energy of the largest scales increasing.

We will investigate further the effect of mesh jittering by instead using the symmetric conservative method similar to that of Thomas et al. [42] ($\xi _x = [(y_\eta z - z_\eta y)_\zeta - (y_\zeta z - z_\zeta y)_\eta ]/2$). Further to this we will also use the grid interpolation methodology of Abe [1]. This combined methodology was shown to satisfy the surface conservation law [2, 60] and hence ensure freestream preservation.

Fig. 18

Comparison of polynomial and RBF methods for point placement on jittered meshes. This is for a TGV, $R_e=1600$, $p=4$, $120^3$ DoF, RK44, and $\varDelta t=10^{-3}$. A jitter factor of $j_f=0.3$ and 0.2 gives $q_h = 0.7157$ and 0.7199 respectively

The results comparing the symmetric conservative Jacobian with RBF and polynomial interpolation methods of point placement are shown in Fig. 18. Here Huynh $g_2$ correction functions are used. Foremost is that in both cases the issue of non-conservation appear to have been removed. Secondly, the methods of point placement appear to give wholly similar results. The most notable difference is shown in the enstrophy based dissipation of the polynomial method at $j_f=0.3$, see Fig. 18b, where the peak value is slightly increased. Coupled to the slight over dissipation in the kinetic energy measure that is unchanged between methods, this may indicate that the polynomial method introduces additional dispersion. However, this difference is small.

Fig. 19

Comparison of Huynh $g_2$ correction functions with NDG for jittered meshes. This is for a TGV, $R_e=1600$, $p=4$, $120^3$ DoF, RK44, and $\varDelta t=10^{-3}$. A jitter factor of $j_f=0.3$ gives $q_h = 0.7157$

Now, varying the correction function with polynomial point placement and the symmetric conservative Jacobian definition, we obtain the results presented in Fig. 19. From Fig. 19b it is clear the lower dissipation of $g_2$ corrections over NDG has led to a more accurate approximation. We may infer this as increased dissipation, particularly at the smallest scales. This will cause the vorticity to be reduced and hence the enstrophy will be reduced. This somewhat confirms the prediction of the convergence rate study of Sect. 4.

As the mesh is then randomised, $g_2$ corrections show an increased enstrophy peak, likely to be dispersion. This is then followed by a dissipation deficit due to the energy deficit. The additional dispersion error is in accordance with the predictions of Sect. 5.5 and Appendix A. Here, the fully discrete analysis showed that on both uniform grid and amplified on non-uniform grids, the scheme suffered from dispersion error without accompanying dissipation to reduce them. When looking at the NDG results, the opposite is true. Although larger error in the dispersion was found analytically, the scheme also has a large amount of accompanying dissipation. This is reflected in the TGV results, where peak enstrophy is reduced.

For both correction functions there are additional errors in the dissipation after the peak for the jittered grids, as the solution tend towards homogeneous decaying turbulence. Initially, the TGV is anisotropic, however for $R_e<\approx 500$, the flow will become isotropic with time [8]. Therefore, as time goes on, waves will go from largely grid aligned to range over all angles. These waves will then be affected by the anisotropic properties shown in Sect. 5. As could also be predicted from the results of Sect. 5, these inaccuracies are made worse by a randomised grid.

To provide some reference as to how FR performs relative to an established method we will use an edge-based Finite Volume (FV) method for comparison. The FV method is a standard central second order method with L2Roe smoothing [33] for stabilisation, which has been validated previously [38]. The particular FR scheme used in this comparison is $p=1$, giving second order, the same as the FV scheme. However, this puts FR at a significant disadvantage as its numeric characteristics at low order are particularly poor. For example, consider the dispersion and dissipation relations in Fig. 20, which, by comparison to the result of Lele [31], show that FR has noticeably lower resolving abilities when compared against a second order FD scheme.

Fig. 20

Dispersion and dissipation relation for 1D upwinded FR, $p=1$, with DG correction function

With this in mind, we present the results of tests on various jittered grids with a total of $170^3$ degrees of freedom in Fig. 21. For the uniform case, the enstrophy clearly shows that FR is under-resolved compared to FV, which is also shown by a slightly increased rate of dissipation earlier—indicating that the implicit filter is too narrow. If we now consider the effect of jittering, several things may be concluded.

For $-dE_k/dt$ it seems that the peak value is less sensitive with FR than with FV, with central FV seeing some large amplitude oscillations in $-dE_k/dt$. This is likely to be rooted in the central differencing at the interfaces. If we change to a kinetic energy preserving formulation [26, 57], as is displayed in Fig. 22, these oscillations are removed. The sensitivity to jitter is then reduced to a similar level as FR. The enstrophy (Fig. 22b) seems to indicate that a large amount of what seemed to be resolved energy may have in fact been dispersion induced fluctuations. However, in both cases FV was able to run with grids up to $j_f=0.9$ and $q_h=0.6382$ (not shown). It appears that in these cases the added stability of the smoothing has greatly helped FV. This is especially so in the central difference case where running without smoothing caused the case to fail even at low levels of jitter. Comparatively, FR was only able to run with $j_f\approx 0.6$, before becoming unstable.

Fig. 21

Comparison of FR, $p=1$ with DG correction functions with a second order central FV scheme with L2 Roe smoothing both with $170^3$ degrees of freedom and $\varDelta t\approx 5\times 10^{-4}$. A reference DNS solution is provided by Brachet et al. [8]

Fig. 22

Comparison of FR, $p=1$ with DG correction functions with a second order KEP FV scheme with L2 Roe smoothing both with $170^3$ degrees of freedom and $\varDelta t\approx 5\times 10^{-4}$. A reference DNS solution is provided by Brachet et al. [8]

Before moving on, it must be noted that for both FR and FV we see a dip in $dE_k/dt$. This is only present in the kinetic energy dissipation and no change in the enstrophy is observed. Therefore, the decrease must be due to an energy increase in the zeroth mode. The reason for this is not currently known. The results presented here show that, even for second order, FR is more resilient to mesh deformation than FV with traditional smoothing. A similar result was reported in [47], but solely for Euler’s equations. Hence, this resilience seems to carry over to the Navier–Stokes equations. However, when FV with a kinetic energy preserving (KEP) [57] scheme is used the mesh sensitivity is greatly reduced and so this should be considered as important for FV solvers. FR and KEP together may also improve further the mesh resilience of FR.

6.2 Curved Grids

To end, we will briefly present some results on curved grids. A more complete numerical study was presented by Mengaldo et al. [32]. However, we seek to understand if the behaviour of the stretched and jittered grids carries over. We will employ a similar curved grid transformation to that used by Abe et al. [1]. To remove some issues of point placement we will initially form a uniform grid and then deform the solution and flux points by the following:

$$\begin{aligned} x^\prime&= x + \frac{l}{n_x}A\sin {\bigg (\frac{k_g\pi y}{l}\bigg )}\sin {\bigg (\frac{k_g\pi z}{l}\bigg )} \end{aligned}$$

(64a)

$$\begin{aligned} y^\prime&= y + \frac{l}{n_y}A\sin {\bigg (\frac{k_g\pi x}{l}\bigg )}\sin {\bigg (\frac{k_g\pi z}{l}\bigg )} \end{aligned}$$

(64b)

$$\begin{aligned} z^\prime&= z + \frac{l}{n_z}A\sin {\bigg (\frac{k_g\pi x}{l}\bigg )}\sin {\bigg (\frac{k_g\pi y}{l}\bigg )} \end{aligned}$$

(64c)

Symbols take the same meaning as before, with the added definition of $k_g$—the grid wavenumber, and A, the grid wave amplitude. In keeping with Abe et al. [1] we will use $k_g=4$ and $A=0.4$.

Fig. 23

Example $120^3$ DoF curved grid for $p=4$, $A = 0.4$, and $k_g=4$. Here a sub-sample of every 10th point is shown

Fig. 24

TGV results for FR, $p=4$, on a curved grid with $120^3$ DoF. RK44 explicit time stepping is used with $\varDelta t =10^{-3}$

Applying this transformation to a $120^3$ DoF $p=4$ mesh, results in $q_h = 0.7128$ and $\varDelta {\mathbf {x}}_\mathrm {max}/\varDelta {\mathbf {x}}_\mathrm {min} = 1.5$—see Fig. 23. The result of applying a TGV to this grid are displayed in Fig. 24. This shows that for both NDG and $g_2$ the curved grid causes a larger variation in the enstrophy, mostly manifesting as over dissipation—and hence dispersion—at $t\approx 10$. This error is less for NDG but due to its presence in both correction functions, it may be concluded that this grid deformation results in the increase in high frequency dispersion with FR.

7 Conclusions

Through this work, a theoretical extension of the FR von Neumann analysis to higher dimensions has been presented. This allowed us to understand the character of the dispersion and dissipation relations of FR as the incident angle of a wave was varied. Differences were noted between the behaviours of FR and finite differencing methods, primarily that FR saw a lower variation in character with the angle of incidence.

Investigations were then performed on deformed meshes. The same mechanism that caused the variation of properties with angle on a uniform grid meant that deformed grids saw a greater variation. For expanding grids this led to dispersion overshoot for waves more aligned with the expansion. Associated with the increase in dispersion was a decrease in dissipation. Application of an expansion and contraction led to this variation being amplified. Investigation of the fully discretised system found large angular variations in the dispersion and dissipation. In some instances, a small perturbation of the angle could cause a complete reversal of the group velocity. Here it was found that for CFL numbers close to the CFL limit, DG may be more resilient due to large levels of dissipation that would reduce the effect of high group velocity induced dispersion errors. The last theoretical investigation into the semi-discrete error and convergence found that Huynh’s $g_2$ correction function suffered less from anisotropy with wave angle, suggesting it may be more suitable for ILES at a lower percentage of the CFL limit.

Numerical experiments were then undertaken to explore the link and impact of the theoretical findings. Some remarks were made about the effect of using RBF projection for grid definition, which highlighted the importance of a symmetric conservative Jacobian definition. Then, by using the Taylor–Green vortex case on randomised grids, it was observed that Huynh’s $g_2$ correction function did indeed show signs of increased dispersion on randomised grids. However, they were better able to resolve the flow thanks, in part, to lower dissipation at high wavenumbers. Conversely, NDG correction functions showed signs of increased dissipation on randomised grids. Finally, some comparison was made between second order FR and an industrial second order finite volume method. It was found if more traditional L2Roe smoothing was used, FV was less resilient to mesh deformation than FR. However, if KEP was employed for the FV method, then both methods were comparably robust. Yet, in both cases FV was better able to resolve the flow. Hence, if a second order method is sought for practical applications, then FV with KEP is recommended. The use of a KEP form of FR remains an open question, and an avenue which may lead to further improvements in FR.

Additional Dispersion and Dissipation Figures

We include some additional figures that explore the effect of grid stretching in 2D, for the fully discretised Fourier analysis.

See Figs. 25 and 26.

Fig. 25

Dispersion and dissipation of upwinded FR, $p=3$, with Huynh $g_2$ corrections, explicit RK44 temporal integration, and $\mathrm {CFL}= 0.8\mathrm {CFL}_\mathrm {max}$. The radial distance is the normalised wavenumber (including the effect of angle), and the azimuthal distance is the angle of incidence to the element

Fig. 26

Dispersion and dissipation of upwinded FR, $p=3$, with NDG corrections, explicit RK44 temporal integration, and $\mathrm {CFL}= 0.8\mathrm {CFL}_\mathrm {max}$. The radial distance is the normalised wavenumber (including the effect of angle), and the azimuthal distance is the angle of incidence to the element