Abstract
A posteriori error estimates in the \(L_\infty (\mathcal {H})\)- and \(L_2(\mathcal {V})\)-norms are derived for fully-discrete space–time methods discretising semilinear parabolic problems; here \( \mathcal {V}\hookrightarrow \mathcal {H}\hookrightarrow \mathcal {V}^*\) denotes a Gelfand triple for an evolution partial differential equation problem. In particular, an implicit–explicit variable order (hp-version) discontinuous Galerkin timestepping scheme is employed, in conjunction with conforming finite element discretisation in space. The nonlinear reaction is treated explicitly, while the linear spatial operator is treated implicitly, allowing for time-marching without the need to solve a nonlinear system per timestep. The main tool in obtaining these error estimates is a recent space–time reconstruction proposed in Georgoulis et al. (A posteriori error bounds for fully-discrete hp-discontinuous Galerkin timestepping methods for parabolic problems, Submitted for publication) for linear parabolic problems, which is now extended to semilinear problems via a non-standard continuation argument. Some numerical investigations are also included highlighting the optimality of the proposed a posteriori bounds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Galerkin finite element methods are popular for the numerical solution of various classes of partial differential equations (PDEs) and related initial/boundary value problems due to their flexibility and accuracy in dealing with various challenging solution properties and computational domain geometries. Owing to their variational structure, Galerkin methods are known to be suitable for mesh adaptivity in an effort to provide sufficient resolution for localised solution features without the introduction of excessive overhead of numerical degrees of freedom. Indeed, adaptive finite element methods for complex nonlinear problems is an active area of research. In their more mathematically justified settings, adaptive algorithms are driven by rigorous, computable bounds on the error residual, the so-called a posteriori error bounds.
Nevertheless, the study of nonlinear time-dependent PDE problems continues to necessitate further research, as a number of important challenges are yet still to be addressed. A central such challenge, in our view, is the development of a posteriori bounds for arbitrary order explicit and implicit–explicit time-stepping methods for nonlinear evolution PDEs, especially treating fully-discrete numerical schemes, in an effort to drive adaptive algorithms. Adaptivity is crucial for computational complexity reduction in this context due to the wealth of potential non-linear features that may appear in the solutions of such PDE problems (interfaces, pattern formation, travelling waves, etc); we refer to [12] for a recent directly related application. Indeed, we are aware of an extremely limited number of works discussing rigorous a posteriori error bounds for explicit time-stepping methods for linear evolution problems [25, 26]. The challenge posed by explicit (or implicit-explicit) timestepping methods in the context of rigorous a posteriori error control is the careful construction of an “implicit perturbation” of the explicit scheme for which we can construct suitable, optimal order, reconstructions that, in turn, can be naturally inserted into the original PDE to construct residuals.
A posteriori error analysis for stationary and evolution problems has been widely investigated over the last 30 years or so, and significant developments have been achieved, see, e.g., the treatises [1, 51] and the references therein for elliptic problems, the works [11, 17,18,19, 22, 27, 29, 35, 36, 38, 40, 42, 43, 50] for space–discrete or fully-discrete parabolic problems, or [2, 4,5,6, 26, 34, 41, 46] for a posteriori error bounds for time semi-discretisations of evolution PDEs; the above lists contain the results most relevant to this work from the growing literature in the area and are, of course, far from constituting a complete bibliographical account.
Discontinuous Galerkin (dG) timestepping for parabolic problems is classical [15, 16, 23, 31, 37, 39, 45, 48]. These methods have received considerable interest in the context of space–time adaptivity throughout the years, as they offer a variational, arbitrary order timestepping framework and, crucially, allow for locally variable timestep sizes in different spatial regions of the computational domain. This is an important attribute towards the aim of full space–time adaptive numerical methods, which was already recognised in [18, 19]. During the last 10 years or so, there has been a revived interest in the derivation of rigorous a posteriori error bounds for dG timestepping schemes [20, 21, 24, 28, 41, 46].
Nonlinear reaction–diffusion parabolic problems are abundant in the literature, especially in the modelling of biological processes and of population dynamics. In such applications, a variety of norms is often required, especially in the context of model parameter calibration from real data. Therefore, the availability of a posteriori bounds of the error in various norms, with different rates of convergence, is desirable to drive space–time adaptive algorithms. To the best of our knowledge, however, there are no previous results on a posteriori error bounds for implicit-explicit high order fully-discrete methods involving dG-timestepping for nonlinear evolution PDEs. This is in contrast with the increasing number of interesting works on a posteriori error analyses for low order time-stepping schemes for nonlinear evolution problems; see, e.g., [8, 10, 12, 17, 36, 52] and the references therein. At the same time, there exist only few works on the a posteriori error analysis of high order time-stepping schemes for time-discrete nonlinear parabolic problems [30, 33, 34, 41, 46].
This work is concerned with the derivation of conditional a posteriori error bounds in the \(L_\infty (\mathcal {H})\)- and \(L_2(\mathcal {V})\)-norms for fully discrete implicit–explicit (IMEX) methods of variable order for semilinear parabolic problems; here \( \mathcal {V}\hookrightarrow \mathcal {H}\hookrightarrow \mathcal {V}^*\) denotes a Gelfand triple setting for an evolution PDE. Typical examples for which the results presented hold are \(\mathcal {H}=L_2(\Omega )\) and \(\mathcal {V}=H^1_0(\Omega )\) or \(\mathcal {V}=H^2_0(\Omega )\). The nonlinear reaction term is assumed to be locally Lipschitz and satisfying a growth condition in the spirit of [49]. Such growth conditions allow for the unified treated also of PDE systems of reaction–diffusion–convection type [9, 12]. The time discretisation consists of an hp-version discontinuous Galerkin method treating implicitly the linear spatial operator, and of an explicit multistep method for the nonlinear reaction term. This is combined with the standard conforming finite element method used for the spatial discretisation. The dG-multistep IMEX time discretisation we consider in this work was introduced in [23], whereby a priori error bounds were proven for the case of globally Lipschitz nonlinear reactions. To reduce the computational overhead, the nonlinear reactions are treated explicitly via sufficiently high-order interpolation of solution values from previous timesteps [23]. Therefore, the solution of one linear system per timestep is required. The proof combines the recent space–time reconstruction proposed in [28] for the implicit dG discretisation, along with a suitable implicit perturbation of the explicitly discretised nonlinear reaction part in the spirit of [25, 26]. The treatment of the non-Lipschitz nonlinearity involves a continuation argument in the spirit of [8,9,10] along with suitable Sobolev imbeddings. The resulting a posteriori error bound is of conditional type, i.e., it is valid subject to an a posteriori smallness condition being satisfied. Such conditional estimates are typical for strongly nonlinear problems [8,9,10, 12, 33], i.e., problems whose nonlinearities do not satisfy strong monotonicity and/or global Lipschitz conditions. In this work, we use energy arguments for the proof a posteriori error bounds, as Sobolev imbeddings are sufficient for control of the nonlinear terms. For the case of blow-up problems an alternative technique based on Duhamel’s principle combined with \(L_\infty \)-control bootstrapping arguments in the time variable is also available; we refer to [30, 33, 34] for time-discrete results in this vein.
Crucially, noa priori Courant-Friedrichs-Lewy (CFL) type conditions (with the respective often obscure constants involved) will be required for the validity of our a posteriori error bounds for explicit timestepping methods (cf., also [25, 26]). Indeed, for unstable combinations of local spatial and temporal meshsizes, the a posteriori estimator remains reliable. In fact, this remarkable property motivates the study of a posteriori estimation of CFL constants as a non-standard potential use of rigorous a posteriori error upper bounds for (implicit–)explicit methods; this will be discussed elsewhere.
The remainder of this work is organised as follows. In Sect. 2 we introduce some notation and define the space–time scheme. In Sect. 3 we introduce the space–time reconstruction operators and state the corresponding error bounds. The a posteriori error analysis for fully-discrete semilinear parabolic equations in \(L_\infty (\mathcal {H})\) and \(L_2(\mathcal {V})\) norms is presented in Sect. 4. In Sect. 5 we present a set of numerical examples for both linear and semilinear test problems investigating the performance of the a posteriori error bounds, while, in the last section, we draw some conclusions.
2 Problem Setup and the Numerical Method
2.1 Abstract Setting
For \(\mathcal {H}\) a real Hilbert space and \(\mathcal {I}=[a,b]\subset {\mathbb {R}}\), the Bochner space \(L_p(\mathcal {I};\mathcal {H})\) is defined by \( L_p(\mathcal {I};\mathcal {H}):=\{v:\mathcal {I}\rightarrow \mathcal {H}\text { such that } \Vert v\Vert _{L_p(\mathcal {I};\mathcal {H})}<\infty \}, \) with the respective norm given by
Upon denoting by \(v'\) the (weak) derivative of v with respect to the “time”-variable \(t\in \mathcal {I}\), we can also define the Sobolev-Bochner spaces
and \(\Vert v\Vert _{W_p^1(\mathcal {I};\mathcal {H})}:=\big (\Vert v\Vert _{L_p(\mathcal {I};\mathcal {H})}^p+\Vert v'\Vert _{L_p(\mathcal {I};\mathcal {H})}^p\big )^{1/p}\). When \(\big (\mathcal {H},(\cdot ,\cdot )_\mathcal {H}\big )\) is a Hilbert space with respective inner product, \(L_2(\mathcal {I};\mathcal {H})\) and \( H^1(\mathcal {I};\mathcal {H})\equiv W_2^1(\mathcal {I};\mathcal {H})\) are also Hilbert spaces endowed with the inner products \( \int _\mathcal {I}(w(t),v(t))_\mathcal {H}\,\mathrm{d}t \) and \( \int _\mathcal {I}(w(t),v(t))_\mathcal {H}+(w'(t),v'(t))_\mathcal {H}\,\mathrm{d}t\), respectively. We may also write \(Z(\alpha ,\beta ;\mathcal {H})\) instead of \(Z(\mathcal {I};\mathcal {H})\) for \(Z\in \{L_p, W^1_p\}\).
Let \(\mathcal {V}\subset \mathcal {H}\) another Hilbert space with norm \(\Vert \cdot \Vert _\mathcal {V}\) and let \(\mathcal {V}^*\) denote its the dual space defined by the functions z for which the norm
is finite; the spaces \(\mathcal {V}\), \(\mathcal {H}\) and \(\mathcal {V}^*\) form a, so-called, Gelfand triple
with the duality pairing \(( \cdot , \cdot )_{\mathcal {V}^* \times \mathcal {V}}\) extending the inner product \((\cdot ,\cdot )_\mathcal {H}\), in the sense that, for all \(u \in \mathcal {H}\) and \(v \in \mathcal {V}\) holds \( ( u , v )_{\mathcal {V}^* \times \mathcal {V}} = (u,v)_\mathcal {H}\). The subscript \({\mathcal {V}^* \times \mathcal {V}}\) in the duality pairing will be omitted whenever no confusion is likely to occur. Although we shall work within the above abstract setting, typical cases include \(\mathcal {H}=L_2(\Omega )\), \(\mathcal {V}=H_0^1(\Omega )\), giving \(\mathcal {V}^*=H^{-1}(\Omega )\), or \(\mathcal {V}=H_0^2(\Omega )\), giving \(\mathcal {V}^*=H^{-2}(\Omega )\).
We consider the semilinear parabolic initial value problem: find \(u \in H^1(0,T;\mathcal {V}^*) \cap L_2(0,T;\mathcal {V})\) such that
for some known function \(u_0\in \mathcal {H}\), where \(\mathcal {A}: \mathcal {V}\longrightarrow \mathcal {V}^*\) is a linear elliptic operator, which is continuous and coercive with respect to the norm of \(\mathcal {V}\). We also define the bilinear form \(a:\mathcal {V}\times \mathcal {V}\longrightarrow {\mathbb {R}}\) associated with \(\mathcal {A}\) by
which inherits the continuity and coercivity properties of \(\mathcal {A}\), viz.,
with \(C_\mathrm{cont},\ C_\mathrm{coer}\) positive constants independent of w, v.
The function \(f:\mathcal {I}\times {\mathbb {R}}^d\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is smooth and locally Lipschitz-continuous, bounded in the first two arguments and satisfying the growth condition for the third argument:
for all \(z_1,z_2\in {\mathbb {R}}\) with \(|\cdot |\) denoting the Euclidean distance, for a positive constant C, uniform with respect to the first two arguments. In what follows, we shall often suppress for brevity the dependence of f on its first two arguments writing, therefore, \(f(t,x,w)= f(w)\). Generalisations of the above assumptions in the first two arguments are possible in the context of certain Caratheodory-type conditions, but we refrain from discussing these in the interest of simplicity of the presentation. Such growth conditions allow for the unified treatment of PDE systems of reaction–diffusion–convection type [9, 12], as in such cases it is either very difficult or, even impossible to deduce positivity/monotonicity properties from complicated reaction patterns. We stress, however, that the results proven below hold subject to restrictions on the range of the exponent \(r\ge 0\), depending on the particular choices of the triple (1) and on the dimension of the spatial computational domain \(\Omega \subset {\mathbb {R}}^d\).
2.2 Space–Time Galerkin Spaces
Let \(\mathcal {I}=[0,T]\) be the time interval with final time \(T > 0\) and, for \(0=t_0< t_1< \cdots < t_N=T\), consider the partition \(\{\mathcal {I}_n, n=0,\ldots ,N\}\) of I into subintervals \( \mathcal {I}_n:=(t_{n-1},t_n]\) for \(n=1,\ldots ,N\), and \(I_0:=\{0\}, \) with corresponding timesteps \(k_n:=t_n-t_{n-1}\), \(n=1,2,\ldots ,N\). We also consider a finite sequence \(\{\mathcal {V}_n\}_{n=0}^N\) of conforming finite element subspaces of \(\mathcal {V}\), each associated with the time subintervals \(\mathcal {I}_n\). To account for mesh-change effects, we also define the largest common subspace \(\mathcal {V}^\ominus _n:=\mathcal {V}_{n-1}\cap \mathcal {V}_n,\) for all \(n=1,\dots ,N\).
Let \(\mathcal {H}\) be a Hilbert space. We define
as the space of \(\mathcal {H}\)-valued polynomials on \(\mathcal {I}\) of degree at most r.
We also consider the space-time finite element subspace
for all \(n =0,1\dots ,N\) with \(r_n\) denoting the local temporal polynomial degree, which may vary from one timestep to another.
Collecting the latter for all time-steps, we define the space–time Galerkin space
often suppressing the dependence on the polynomial degree vector \(\mathbf{r}:=(r_1,r_2,\dots ,r_N)\) for brevity.
Moreover, for a piecewise continuous function \(v:I\subset {\mathbb {R}} \rightarrow \mathcal {H}\), with the time nodes \(t_n\) as possible points of discontinuity, we define the time-jump:
where \(v_n^{\pm }:=\lim _{\delta \rightarrow 0^+} v(t_n \pm \delta ),\) the respective one-sided (right and left) limits for \(n=0,1,\dots ,N\).
For every \(n=0,1,\dots ,N\), we introduce the \(\mathcal {V}^*\)-projection operator \(P_n:{\mathcal {V}}^* \rightarrow \mathcal {V}_n\) defined by
and the corresponding projection operator \(P_n^\ominus \) defined by \( ( P_n^\ominus v,\chi )_\mathcal {H}= {( v,\chi )_{\mathcal {V}^* \times \mathcal {V}} } \) for all \( \chi \in \mathcal {V}_n^\ominus \), respectively. Also, we define the elliptic projection operator \({\tilde{P}}_n:\mathcal {V}\rightarrow \mathcal {V}_n\) by
with \({\tilde{P}}_n^{\ominus }\) the respective elliptic projection onto \(\mathcal {V}_n^{\ominus }\).
For \(w \in \mathcal {H}\), we define the time lifting operator\( L_n : \mathcal {H}\rightarrow \mathcal {P}^{r_n}(\mathcal {I}_n;\mathcal {H}) \), by
If \(\mathcal {W}\subset \mathcal {H}\) is a linear subspace of \(\mathcal {H}\), we have the property
for more details, we refer to [46].
2.3 Space–Time Finite Element Methods
Set \(U_0^-:={\tilde{P}}_0u_0\). Then, the fully-discrete implicit time discontinuous and spatially conforming Galerkin approximation of the exact solution u of (2) reads: find \(U \in \mathcal {X}\) such that
for all \(V\in \mathcal {X}_n\) and for \(n=1,\ldots ,N\), where we recall that \([U]_n=U_n^+-U_n^-\).
The space-time method (10) is fully implicit in the sense that a nonlinear system of equations for the numerical degrees of freedom has to be solved to advance one time interval.
Aiming for a linearly implicit method, we follow [23] and we replace f(U) in (10) by its linear interpolant in time \(\Pi f(U)\), defined so that \(\Pi f(U) |_{\mathcal {I}_n} \in \mathcal {P}^{2r_n}(\mathcal {I}_n,\mathcal {V}_n)\), for all \(n=1,\dots ,N\), using values of U from previous time intervals \(\mathcal {I}_m, m < n\) only and extrapolating the resulting interpolant into \(\mathcal {I}_n\). In this case, the solution process will result in a linear system for U per time-step, giving rise to an implicit–explicit (IMEX) method. Of course, one can also interpolate on the previous and the current time intervals \(\mathcal {I}_m, m \le n\). This case will lead to a nonlinear system of equations for U, although it can be potentially more easy to implement for certain nonlinearities f. In both cases, the time interpolant \(\Pi f(U)\) can be represented on each \(\mathcal {I}_n\) as
where \(\Pi _{n-j}^\lambda \), \(j=0,1\), is the interpolation operator for polynomials of degree \(\lambda \) at the nodes \(t_{n-j-\lambda },\dots , t_{n-j}\) and \(\chi _l\) the respective Lagrange basis functions. The corresponding IMEX space–time scheme reads: set \(U_0^-:={\tilde{P}}_0u_0\) and find \(U \in \mathcal {X}\) such that
for all \(V\in \mathcal {X}_n\), for \(n=2r_1+j,\ldots ,N\). Of course, as this is a multistep method, we can only use it after a certain number of time-steps, depending on the order of the method. Without potential loss of convergence rate, however, we can consider a few (very small in size) timesteps with the zeroth order method, i.e., the implicit Euler method with explicit treatment of the nonlinear reaction, before using (12) with higher order than zero. The interpolant degree \(\lambda = 2r_n\) is required to represent exactly the integrand \( (f(U),V)_\mathcal {H}= (P f(U),V)_\mathcal {H}\) which is a product of two polynomials of degree \(r_n\) each with respect to the time variable. Finally, for \(j=1\), we arrive at the IMEX method, while, for \(j=0\), we retrieve the fully implicit scheme; for further details we refer to [23]. Note that the values \(U_l^-\) are known to be points of superconvergence for the respective time-discrete problem [3, 32].
Despite the specific choices discussed above, in what follows, we shall endeavour to be general with respect to the particular approximation of the nonlinear term. To that end, we shall refrain from using specific properties of any particular interpolant/extrapolant used in the proof of the a posteriori error bounds below, in an effort to be versatile in the choice of linearisation. Indeed, the a posteriori error bounds given below will involve the computable quantity \(\Pi f(U)-f(U)\).
3 Reconstructions
We now discuss the space-time reconstruction technique proposed in [28] for the respective linear problem, which is a modification of the concepts of elliptic reconstruction for the spatial discretisation [35, 40] and of the dG-timestepping reconstruction presented first in [41], and further analysed in the hp-setting in [46].
3.1 Time Reconstruction
The time reconstruction \({\hat{W}}\in H^1(0,T;\mathcal {H})\) of a time-discrete function \(W\in \mathcal {P}^r({\mathcal {I}};\mathcal {H})\) is defined for each \(\mathcal {I}_n\), \(n=1,\dots , N\), by the conditions
and
The time reconstruction \({\hat{W}}\) is well-defined: we have \(r_n+2\) unknowns per time interval \(\mathcal {I}_n\) and \(r_n+1\) conditions from (14) and one more condition from (15). It is also unique; we refer to [41, Lemma 2.1] for a proof of the uniqueness, which also shows that the time reconstruction is also globally continuous with respect to the time variable.
Equivalently, using the lifting operator (8), we can define \({\hat{W}} |_{\mathcal {I}_n} \in \mathcal {P}^{r_{n+1}}(\mathcal {I}_n;\mathcal {H})\) on each time interval \(\mathcal {I}_n\), \(n=1,\dots ,N\), by
where we recall that \( W^-_0 := u_0\).
Proposition 3.1
(Time reconstruction error bounds) Let \(S \subseteq \mathcal {H}\) with \( S \in \{\mathcal {H},\mathcal {V},\mathcal {V}^*\}\), and \(\Psi \in P^{r_n}(\mathcal {I}_n;S)\), for \(n = 1,\ldots ,N\). Then, we have the identities:
with
and
where \({\hat{\Psi }}\) is defined from \(\Psi \) by (13) and (14).
Proof
The proof of (17) first appeared in [41, Lemma 2.2]; the formula for \({K}_n\) was further refined to be explicit in the dependence on \(r_n\) in [46, Theorem 2]. \(\square \)
3.2 Elliptic Reconstruction
For each conforming finite element space \(\mathcal {V}_n \subset \mathcal {V}\), we define the respective discrete elliptic operator \( {\mathbf {A}}_n : \mathcal {V}_n\rightarrow \mathcal {V}_n\) to be the unique linear operator such that \( ( {\mathbf {A}}_n W,V)_\mathcal {H}= a(W,V)\), for all \(V,W \in \mathcal {V}_n.\)
Given \(U\in \mathcal {X}_n\), \(n=0,\ldots ,N\), for \(t \in \mathcal {I}_n \), the elliptic reconstruction\({\tilde{U}}\in {\mathcal {P}^{r_n}(\mathcal {I}_n;\mathcal {V})}\) of U is defined as
with \(\hat{U}\) denoting the time reconstruction of the numerical solution U. The relation (19) can be written in point-wise form as \(\mathcal {A}{\tilde{U}}(\cdot ,t)={\mathbf {A}}_nU(\cdot ,t) {+P_n \hat{U}'(\cdot ,t)-\hat{U}'(\cdot ,t)},\) for all \( t \in \mathcal {I}_n\).
From the definition of \({\mathbf {A}}_n\) and from (19), we have
and, hence, we have
at each \(t\in \mathcal {I}_n\). That is, U is the elliptic projection of the elliptic reconstruction \({\tilde{U}}\). In other words, U is the approximate solution of the elliptic problem whose exact solution is the elliptic reconstruction function \({\tilde{U}}\). Therefore, a crucial consequence of this construction is the ability to estimate the difference \({\tilde{U}} - U\) by a posteriori error estimators for elliptic problems in various norms available in the literature. As we prefer to keep the exposition independent of specific choices of a posteriori error bounds for elliptic problems, we opt for merely postulating their existence.
Assumption 3.2
(Elliptic a posteriori error bounds) Let \(w\in \mathcal {V}\) be the exact solution of the elliptic problem \(\mathcal {A}w = g\), with respective boundary conditions, and let \(W \in \mathcal {V}_{h} \subset \mathcal {V}\) be the finite element solution of this problem in a finite element space \(\mathcal {V}_h\). We assume that there exist a posteriori error bounds
for \(S \in \{\mathcal {H},\mathcal {V},\mathcal {V}^*\}.\)
The literature for such elliptic a posteriori error bounds is vast; see, e.g., [1, 51] and the references therein.
In particular, Assumption 3.2 will imply the validity of the estimates
among other things; see Proposition 4.4 below for details.
Using (14) and (20), the IMEX method (12) can be re-written on \(\mathcal {I}_n\) as
for all \(V \in \mathcal {X}_n\), for \(n=1,\dots ,N\) or, equivalently, in strong form as
noting carefully the cancellation of the terms \(P_n \hat{U}'\) in the course of the calculation.
Remark 3.3
(mesh change error via elliptic reconstruction) The elliptic reconstruction (19) includes the mesh-change type term \(P_n\hat{U}'-\hat{U}'\), in contrast to the (standard) elliptic reconstruction proposed in [35]. In fact, it is the high order counterpart of the elliptic reconstruction presented in [11, Definition 6.1] for backward Euler timestepping. Indeed, on each \(\mathcal {I}_n\) we have, respectively,
By construction [41, 46] there exists a polynomial \(\varkappa _n\) of degree \(r_n\) on \(\mathcal {I}_n\) such that
with
4 A Posteriori Error Bounds
Upon defining the space-time reconstruction\(w:=\hat{\tilde{U}}\), i.e., the time-reconstructed elliptic reconstruction, we begin by decomposing the error as
Note that \(\sigma \) is the time reconstruction error which can be estimated using Proposition 3.1. Similarly, \(\epsilon \) is the elliptic reconstruction error and, therefore, can be estimated using Assumption 3.2. Thus, it remains to estimate \(\rho \) by quantities involving the problem data and/or \(\sigma \) and \(\epsilon \). To do so, we shall work with energy estimates, in conjunction with a continuation argument to treat the non-Lipschitzian nonlinear reactions.
4.1 Error Equation
Subtracting (25) from (2), we obtain after elementary manipulations
on \(\mathcal {I}_n\), for \(n=1,\dots ,N\). For brevity, we set \(\mathrm {P}:[0,T]\rightarrow \mathcal {V}\), defined as \(\mathrm {P}|_{\mathcal {I}_n}=P_n\), \(n=0,\dots ,N\).
Testing (27) against \(\rho \), integrating in space and in time between 0 to \(t\in \mathcal {I}_m\), for some \(m=1,\dots ,N\), we deduce
noticing that \(\rho (0)=0\) by construction, and upon defining Dz to be the time-wise broken derivative of a piecewise smooth function z subordinate to the temporal subdivision. Employing the coercivity (5) and continuity (4) of a, along with standard inequalities, the last estimate implies
for any \(\gamma >0\). Selecting now \(\gamma =1/2\) in (29), we arrive at
We shall now estimate each term on the right-hand side of (30) separately.
4.2 Estimating the Nonlinear Term
We decompose the integrand in the nonlinear term in (30) as
with \(\Vert f(U)-\mathrm {P}\Pi f(U)\Vert _{\mathcal {V}^*}\) measuring how well \(\mathrm {P}\Pi f(U)\) approximates f(U).
As we shall make use of the Sobolev Imbedding Theorem, we first discuss the specific choice \(\mathcal {H}=L_2(\Omega )\) and \(\mathcal {V}=H^1_0(\Omega )\); the case of non-essential boundary conditions also follows without any technical challenge, although it is omitted here for brevity.
Lemma 4.1
(Estimation of the nonlinear term) If the nonlinear reaction fas in Sect. 2, satisfying the growth condition (6) with \(0\le r<2\) for \(d=2\), and with \(0\le r\le 4/3\) for \(d=3\), we have the bound
Proof
Using the growth condition (6), we have, respectively,
For the first term on the right-hand side of (33) we use the inequality
thereby, deducing
Recalling the assumption \(0\le r <2\), Hölder’s inequality with exponent \(p=2/r\), (and, thus, \(q=2/(2-r)\),) we have
using the Sobolev Imbedding Theorem \( \Vert \rho \Vert _{L^{4/(2-r)}(\Omega )} \le C_S \Vert \nabla \rho \Vert _{L_2(\Omega )}, \) with \(0\le r <2\) for \(d=2\) and \(0\le r\le 4/3\) for \(d=3\). Similarly, we have the same estimate (36), with \(\rho \) replaced by \(\sigma \) and \(\epsilon \).
Now, the second term of (33) can be dealt with as follows
Combining the above estimates, we arrive at the required bound.
\(\square \)
To retain the abstract and more compact notation from the previous section, we write (32) as follows
for some known positive scalar function G and and constant \(C_\mathrm{nl}\) and we assume its validity henceforth for any suitable \(\mathcal {H}\) and \(\mathcal {V}\) for the given range of exponents \(r\in [0,r_{\max }]\).
4.3 Continuation Argument
The bound of the nonlinear term (38) still contains norms of \(\rho \) on the right-hand side. To eliminate these, we shall employ a continuation argument in the spirit of [8,9,10].
To this end, assuming (38), or using Lemma 4.1, to bound the respective term on the right-hand side of (30), we arrive at
where
Upon observing that
we deduce
for \(C_1:=C_\mathrm{nl}\max \{1,(2C_\mathrm{coer}^{-1})^{1+r/2}\}\). For each \(n=1,\dots ,N\), consider the interval
where we set \(F(t_n, U):=\exp \big ({C_\mathrm{nl}}\int _0^{t_n} \!\!G(U)\,\mathrm{d}t\big )\), for brevity. We observe that \(J_n\ne \emptyset \) as \(\Vert \rho \Vert _{L_{\infty }(0,t;\mathcal {H})}^2 + \frac{C_\mathrm{coer}}{2}\int _0^t \Vert \rho \Vert _{\mathcal {V}}^2\,\mathrm{d}\tau \) is continuous with respect to t and that it is equal to zero for \(t=0\), owing to the property \(\rho (0)=0\); also, \(J_n\) is closed.
Assuming, without loss of generality, that \(r>0\), (for, otherwise, f in (2) is globally Lipschitz continuous and, thus, the a posteriori bounds follow by combining the results from [28] along with a standard Grönwall inequality; see Corollary 4.11 below for details) we set \(t^\sharp :=\max J_n>0\).
Suppose that \(t_n>t^\sharp \), i.e., \(t_n\notin J_n\). Hence, \( E_1(t_n)\ge E_1(t^\sharp )\). Therefore, (42) with \(t=t^\sharp \) yields
and Grönwall inequality, thus, implies
since \(F(t_n,U)\ge F(t^\sharp ,U)\). Upon assuming that \({E_1(t_n)} \) is such that
the estimate (44) becomes
this is a contradiction, as \(t^\sharp \) was assumed to be the maximum element of \(J_n\). Hence, \(t_n=t^\sharp \) and, thus, we have already proven the following result.
Lemma 4.2
Assuming the validity of estimate (38), (or, in the special case of \(\mathcal {H}=L_2(\Omega )\) and \(\mathcal {V}=H^1_0(\Omega )\), assuming the hypotheses of Lemma 4.1,) the following conditional estimate holds: provided that
with \(E_1(t_n)\) as in (40), we have the bound
We observe that the condition (46) in the estimate above is computable, provided that \({E_1(t_n)}\) is computable. With this in mind, we shall bound the norms of \(\sigma \) and \(\epsilon \) in \(E_1\) by computable quantities below. Assuming that \(\sigma \) and \(\epsilon \) are available, we note that all the remaining constants involved in \({E_1(t_n)}\) are either computable or estimable from above. For instance, the Poincaré/Sobolev imbedding constants for which upper bounds are available for very general spatial domains \(\Omega \); we refer to [47] and the references therein for explicit formulas and a detailed discussion.
If \({E_1(t_n)} \) is computable, then (47) becomes an a posteriori bound for \(\rho \). Triangle inequality, then, would already yield an a posteriori bound for the error e. Of course, we expect that \({E_1(t_n)} \) decreases arbitrarily as the maximum timestep and spatial meshsize decay and/or the order of the dG-timestepping increases. We note, finally, that such conditional estimates are the “a posteriori equivalents” to the standard smallness assumptions on timestep and meshsize appearing in a priori error bounds for finite element methods for nonlinear evolution problems.
Remark 4.3
Crucially, there is no explicit CLF-type restriction in the statement of Lemma 4.2, despite this being concerned with an IMEX discretisation. Indeed, for unstable combinations of timesteps and spatial meshsizes, the bound (47) remains valid, provided the condition (60) is satisfied. It is, therefore, conceivable that (60) holds for CFL-unstable scenarios also; in such cases, (47) will remain valid, resulting to arbitrarily large right-hand sides, c.f., also [26].
4.4 Estimating the Norms of \(\sigma \) and of \(\epsilon \)
Proposition 4.4
(Bounds on norms of \(\epsilon =\tilde{U}-U\)) Given Assumption 3.2, for \(t\in \mathcal {I}_n\), \(n=0,1\dots , N\), we have the bound
and
with
Proof
The first estimate is obvious from Assumption 3.2.
For the second, we work as follows. The definition of time reconstruction (16) implies
Now, observing the identity,
which is valid for all \(v\in \mathcal {V}\), we have the Galerkin orthogonality property
Thus, we can estimate \(\tilde{U}'-U' \) using Assumption (3.2) to deduce
Next, working as in Remark 3.3, we have
The result already follows by resorting once more to Assumption 3.2. \(\square \)
Proposition 4.5
(Bounds on norms of \(\sigma {:=w-\tilde{U}}\)) Given Assumption 3.2, for each \( \mathcal {I}_n\), \(n=0,1\dots , N\), we have the bounds
where
for \(S\in \{\mathcal {H},\mathcal {V}\}\), and
Proof
From Proposition 3.1, we have
Triangle inequality implies \(\Vert [{\tilde{U}}]_{n-1}\Vert _\mathcal {V}\le \Vert [\epsilon ]_{n-1} \Vert _\mathcal {V}+ \Vert [ U]_{n-1}\Vert _\mathcal {V}\). To estimate \(\Vert [\epsilon ]_{n-1} \Vert _\mathcal {V}\) we work completely analogously to the proof of Proposition 4.4: we observe the Galerkin orthogonality
which, together with Assumption 3.2 give rise to the estimate
From (18) in Proposition 3.1, we also have
which, working as above, gives the second estimate. \(\square \)
For an alternative bound, we refer to [28, Lemma 4.4].
Remark 4.6
If no mesh modification takes place, i.e., when \(\mathcal {V}_{n-1}=\mathcal {V}_n\), the above estimates simplify considerably, since we then have
It is possible to avoid invoking to known a posteriori error bounds for elliptic problems as per Assumption 3.2 for the estimation of norms of \(\sigma \). Instead, we can prove directly alternative bounds upon assuming the existence of standard (possibly rough) approximation (e.g., Clément, Scott-Zhang or standard interpolation estimates, depending on the choice of \(\mathcal {H},\mathcal {V}\),) or smoothness estimates (necessary for a duality argument) for lower order norms. Crucially, the estimates below do not require the computation of \(\tilde{P}_n^\ominus \).
Proposition 4.7
(Direct bounds on norms of \(\sigma =w-\tilde{U}\)) Let \( t\in \mathcal {I}_n\), \(n=0,1\dots , N\), and assume that for every \(v\in \mathcal {V}\), there exists an approximant \(V\in \mathcal {V}_n^\ominus \), such that \( \Vert h_{\mathcal {V}_n^\ominus }^{-s}(v-V)\Vert _\mathcal {H}\le C_\mathrm{ap}\Vert v\Vert _\mathcal {V}, \) for some \(s>0\) with \(h_{\mathcal {V}_n^\ominus }\) a (smooth enough) positive scalar function representing the local spatial mesh-size of the approximation space \(\mathcal {V}_n^\ominus \). Then, we have the estimates
with
Let further a subspace of \(\tilde{V}\) of \(\mathcal {V}\) so that \(\mathcal {A}z\in \mathcal {H}\) for \(z\in \tilde{V}\) and such that it contains \(\mathcal {V}_n^\ominus \). Assume the existence of \(z\in {\tilde{\mathcal {V}}}\), so that z is the solution to the problem \(a(w,z)=([\tilde{U}-U]_{n-1},w)\) for all \(w\in \mathcal {V}\) and that \(\Vert z\Vert _{{\tilde{\mathcal {V}}}}\le C_\mathrm{sm} \Vert [\tilde{U}-U]_{n-1}\Vert _{\mathcal {H}}\). Moreover, assume that for every \(v\in \mathcal {V}\), there exists an approximant \(V\in \mathcal {V}_n^\ominus \), such that \( \Vert h_{\mathcal {V}_n^\ominus }^{-\tilde{s}}(v-V)\Vert _\mathcal {H}\le \tilde{C}_\mathrm{ap}\Vert v\Vert _{{\tilde{\mathcal {V}}}}, \) for some \(\tilde{s}>0\). Then, for \(p\in \{2,\infty \}\), we have the estimate
with
Proof
We observe
since both \(((P_n \hat{U}'-\hat{U}')(t_{n-1}^+), V)=0\) and \(((P_{n-1} \hat{U}'-\hat{U}')(t_{n-1}^-), V)=0\) for all \(V\in \mathcal {V}_n^{\ominus }\). Also, we have
for any \(V\in \mathcal {V}_n^{\ominus }\), upon observing that \(P_n \hat{U}'(t_{n-1}^+)- \hat{U}'(t_{n-1}^+)= P_n[U]_{n-1}-[U]_{n-1}\) and \(P_{n-1} \hat{U}'(t_{n-1}^-)- \hat{U}'(t_{n-1}^-)= \varkappa (t_{n-1}^-)(P_{n-1}[U]_{n-2}-[U]_{n-2})\), and using the simultaneous orthogonality of the \(L_2\)-projection errors against \(\mathcal {V}_n^{\ominus }\), respectively. Thus, we conclude the identity
for any \(v\in \mathcal {V}\) and \(V\in \mathcal {V}_n^\ominus \), by invoking to (55).
Upon observing the (trivial) inequalities \(C_\mathrm{coer} \Vert w\Vert _{\mathcal {V}}\le \Vert \mathcal {A}w\Vert _{\mathcal {V}^*}\le C_\mathrm{cont}\Vert w\Vert _{\mathcal {V}}\), for all \(w\in \mathcal {V}\), and using Proposition 3.1, we deduce
Selecting now \(v=[\tilde{U}]_{n-1}\), in (56), and using the coercivity of a along with standard arguments, we deduce
from which (53) already follows.
We continue by proving an upper bound for \(\Vert \sigma \Vert _{L_p(\mathcal {I}_n;\mathcal {H})}\), for \(p=\{2,\infty \}\). Proposition 3.1 implies
Employing now the dual problem as per the statement, we have from (56)
with \({\mathbf {A}}|_{\mathcal {I}_n}:={\mathbf {A}}_n\), \(n=1,\dots ,N\). The result already follows upon invoking to the approximation and smoothness estimates postulated in the statement:
and by the triangle inequality \(\Vert [\tilde{U}]_{n-1}\Vert _\mathcal {H}\le \Vert [\tilde{U}-U]_{n-1}\Vert _\mathcal {H}.+\Vert [U]_{n-1}\Vert _\mathcal {H}\). \(\square \)
The constants appearing in the bounds in Propositions 4.4 and 4.5 (or 4.7) are standard in the a posteriori error analysis literature, and depend typically on the shape-regularity of each mesh and on the spatial geometry. It is possible to estimate these constants from above in typical settings, e.g., when \(\mathcal {V}\equiv H^1_0(\Omega )\) and \(\mathcal {H}\equiv L_2(\Omega )\) or \(\mathcal {V}\equiv H^2_0(\Omega )\) and \(\mathcal {H}\equiv L_2(\Omega )\). We refer, e.g., to [13, 14, 47] for some results in this direction.
Using Propositions 4.4 and 4.5 we can bound the term \({E_1(t_n)} \) given in (40) by \({\mathbb {E}}_1(t_n,U)\) defined as
with \(K|_{\mathcal {I}_n}:=K_n\), \(\zeta _{S}|_{\mathcal {I}_n}:=\zeta _{S,n}\), and \(\theta _{S}|_{\mathcal {I}_n}:=\theta _{S,n}\), for \(n=1,\dots ,N\) and \(S\in \{\mathcal {H},\mathcal {V},\mathcal {V}^* \}\). We can also use instead the direct bounds on norm of \(\sigma \) from Proposition 4.7, by replacing \(\theta _S\) by \({\tilde{\theta }}_{S}\).
Remark 4.8
We note that an alternative and somewhat simpler a posteriori error analysis for the \(L_2(\mathcal {V})\)-norm error only is possible by modifying the space-time reconstruction discussed above, by considering simply the time-reconstruction for the time-derivative and the elliptic reconstruction for the spatial terms. This would result to simpler bounds for the \(L_2(\mathcal {V})\)-norm and avoids completely the need to introduce the \(\ominus \)-projections. The details can be found in [28]. Crucially, however, this approach would lead to suboptimal bounds in the \(L_\infty (\mathcal {H})\)-norm. Thus, we have opted for not presenting this additional error analysis here for \(L_\infty (\mathcal {H})\)-norm error is typically a quantity of practical interest in this context of semilinear PDEs with non-Lipschitz growth.
We are now in a position to finalise the a posteriori error analysis.
4.5 Completing the a Posteriori Error Bounds
We are now ready to complete the a posteriori error analysis.
Theorem 4.9
(\(L_\infty (\mathcal {I};\mathcal {H})\)-norm estimate) Assuming the validity of estimate (38), (or, in the special case of \(\mathcal {H}=L_2(\Omega )\) and \(\mathcal {V}=H^1_0(\Omega )\), assuming the hypotheses of Lemma 4.1,) the following conditional estimate holds: provided that
for \(n=1,\ldots ,N\), with \({\mathbb {E}}_1(t_n,U)\) given in (59), we have the a posteriori error bound
Proof
We begin by observing that the proof and the statement of Lemma 4.2 holds with \(E_1(t_n,U,\sigma ,\epsilon )\) replaced by \({\mathbb {E}}_1(t_n,U)\). Then, triangle inequality implies
Propositions 4.4 and 4.5 now already imply the result. \(\square \)
Similarly, we have an a posteriori bound in the \(L_2(\mathcal {I};\mathcal {V})\)-norm.
Theorem 4.10
(\(L_2(\mathcal {I};\mathcal {V})\)-norm estimate) Assuming the validity of estimate (38), (or, in the special case of \(\mathcal {H}=L_2(\Omega )\) and \(\mathcal {V}=H^1_0(\Omega )\), assuming the hypotheses of Lemma 4.1,) the following conditional estimate holds: provided that (60) holds for \(n=1,\ldots ,N\), we have the a posteriori error bound
with \({\mathbb {E}}_1(t_n,U)\) given in (59).
Proof
The proof follows, again, by triangle inequality, Lemma 4.2 and Propositions 4.4 and 4.5 (or 4.7). \(\square \)
We now briefly discuss the practical relevance and applicability of the derived conditional-type a posteriori error estimates. As noted above the constants involved in the condition (60) are either available or estimable from above. This renders the numerical verification of (60) practical. A second question is the realisability of the condition (60) within a space-time adaptive algorithm. Assuming that the algorithm is able to modify the local time-stepping, (60) will be satisfied if the norms involved in \(E_1(t_n)\) are shown to simply converge to zero upon spatial and/or temporal refinement. A simple inspection of the terms involved shows that this is, indeed, the case upon additional regularity assumptions on the exact solution and on f; we refer to [23, 44] for such a priori error bounds.
The algorithmic details on how one can implement such conditional estimates within adaptive algorithms is a rich subject in itself and will not be covered here. For instance, for nonlinearities with sufficiently strong growth, it may be necessary to restart the adaptive algorithm with smaller space and time discetisation resolutions for the condition to be satisfied. We refer to [10, 12], where a number of such algorithms using conditional estimates and related challenges in their design are presented and discussed in detail.
Finally, we provide the respective result for the simpler case of a globally Lipschitz nonlinearity, i.e., when \(r=0\), for completeness. Note that in this case, no smallness condition is required. The proof follows by inspection of the arguments presented above for \(r=0\), upon noting that, in this case, we can simply take \(C_1=0\) in (42).
Corollary 4.11
(Case \(r=0\)) Assuming the validity of estimate (38), for \(r=0\), we have the a posteriori error bounds
and
5 Numerical Experiments
We present a series of numerical experiments aimed at testing the reliability and efficiency of the a posteriori error bounds derived above. The numerical implementation is based on the deal.II finite element library [7] and the tests run in the high performance computing facility ALICE at the University of Leicester.
In the examples below we consider both linear and semilinear parabolic problems. In all cases, \(\mathcal {A}=\Delta \), i.e., the Dirichlet Laplacian, yielding the heat equation with either linear or nonlinear source terms and \(\mathcal {H}=L_2(\Omega )\), \(\mathcal {V}=H^1_0(\Omega )\), giving \(\mathcal {H}^*=H^{-1}(\Omega )\).
We study the asymptotic behaviour in the \(L_\infty (L_2)\)- and \(L_2(H^1)\)-norms of the error and of the respective estimators by monitoring the evolution of the experimental order of convergence (EOC) over time on a sequence of uniformly refined space meshes indexed by the mesh size h. In each instance, we fix a constant time step k as some power of h and we also use fixed polynomial degrees in both space and time. The resulting errors and estimators are plotted against the corresponding space mesh size h. The EOC of a given sequence of positive quantities \(a_i\) defined on a sequence of meshes of step size \(h_i\) is defined by
We report the EOC relative to the last computed quantities in all figures as an indication of the asymptotic rate of convergence. We also report the respective effectivity indices, i.e., the ratio between estimator and error for each instance. The estimator is deemed reliable if the effectivity is greater than or equal to one and it is most efficient when the effectivity is close to one.
5.1 Example 1: A Linear Problem
We test the IMEX fully discrete scheme analysed in this work on (2) with \(\mathcal {I}\times \Omega := [0,1]\times [0,1]^2\), f independent of the exact solution u and initial and boundary conditions such that the exact solution is given by
The respective a posteriori error bounds when the PDE is linear are given in Corollary 4.11.
We report the results of two tests using different combinations of polynomial orders q and p in time and space, respectively, denoted as dG(q)–cG(p) scheme.
5.1.1 Example 1A: dG(1)–cG(2) Scheme
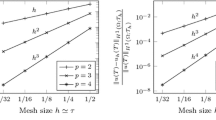
Here, we employ quasiuniform biquadratic elements in space (\(p=2\)) and uniform linear elements in time (\(q=1\)), i.e., the dG(1)–cG(2) scheme. Figure 1 shows the convergence history with \(k=h\) (left plot) and with \(k=h^{3/2}\) (right plot) for both the \(L_\infty (L_2)\)- and \(L_2(H^1)\)-norms. In the case \(k=h\), we observe that the \(L_2(H^1)\) estimator provide the required order of convergence as \(\text {EOC} \approx 2\), in close agreement with the corresponding error; the effectivity is in between 2.90 and 8.93. Also the \(L_\infty (L_2)\) estimator yields the correct rate as \(\text {EOC} \approx 3\), with effectivity between 47.41 and 63.41.
For the case \(k=h^{3/2}\), we again observe the expected order of convergence of the \(L_2(H^1)\)-norm error and estimator, while for the \(L_\infty (L_2)\)-norm we have an EOC of 4.64 and 4.72, respectively, corresponding to the convergence rate expected in time, thus indicating that the time discretisation error dominates in this case. The effectivity is approximately 5.28 and 7.16 for the \(L_2(H^1)\)- and \(L_\infty (L_2)\)-norm estimators, respectively.
5.1.2 Example 1B: dG(2)–cG(2) Scheme
Here, we consider two different timestep and space meshsize relationships \(k=h\) and \(k=h^{4/3}\), respectively, for quasiuniform biquadratic elements in space (\(p=2\)) and uniform quadratic elements in time (\(q=2\)).
The numerical results corresponding to \(k=h\) are shown in the left plot of Fig. 2. We observe that our error estimators provide the expected order of convergence in both the \(L_2(H^1)\)- and \(L_\infty (L_2)\)-norms.
The results obtained with the choice \(k=h^{4/3}\) are reported on the right plot of Fig. 2. Again we observe an optimal experimental order of convergence as \(\text {EOC} \approx 2 \) for both the \(L_2(H^1)\)-norm estimator and error. The respective experimental order of convergence of the \(L_\infty (L_2)\)-norm estimator and error are \(\text {EOC} \approx 4\), corresponding to the optimal convergence rate with respect to the timestep size. In both cases, the estimators’ effectivities show little differences with the corresponding values obtained in Example 1A and are, therefore omitted for brevity.
5.2 Example 2: A Nonlinear Problem
On \(\mathcal {I}\times \Omega := [0,1]\times [0,1]^2\) we consider the semilinear problem (2) with \(f= -u^2 + {\tilde{f}}(x,y,t)\), with \({\tilde{f}}\) such that the exact solution is given by
note that we have \(r=1\) in this case. We test the respective a posteriori error bounds from Theorems 4.9 and 4.10. We test the dG(1)–cG(2) scheme, by considering the two choices \(k=h\) and \(k=h^{3/2}\) with corresponding numerical results in the left and right plots of Fig. 3, respectively.
This results are in line with those of the linear example above. In particular, for \(k=h\) we again observe good agreement between the estimators and the corresponding errors, with \(\text {EOC} \approx 2 \) and \(\text {EOC} \approx 3\) for the \(L_2(H^1)\)- and \(L_\infty (L_2)\)- quantities, respectively. The results corresponding to \(k=h^{4/3}\) are also confirming the theoretical asymptotic rate of convergence. For the \(L_2(H^1)\)-norm estimator and error we have \(\text {EOC} \approx 2\) and, similarly to the linear problem considered earlier, for the \(L_\infty (L_2)\)-norm estimator and error we have \(\text {EOC} \approx 4.5\). The effectivity index was found to be between 1.07 and 12.18 in all computations.
6 Conclusions
A posteriori error bounds in the \(L_\infty (\mathcal {H})\)- and \(L_2(\mathcal {V})\)-norms for the hp-version dG timestepping scheme coupled with conforming finite elements in space for semilinear evolution problems have been derived and tested numerically. The numerical experiments show that the a posteriori error estimators are optimal, reliable, and efficient. An interesting aspect of the a posteriori analysis concerning implicit–explicit time stepping methods, is that no a priori CFL type conditions are required for the validity of the conditional a posteriori error bounds. Hence, the a posteriori estimators remain reliable even for unstable combinations of local spatial and temporal mesh sizes.
References
Ainsworth, M., Oden, J.T.: A Posteriori Error Estimation in Finite Element Analysis. Pure and Applied Mathematics (New York). Wiley, New York (2000)
Akrivis, G., Chatzipantelidis, P.: A posteriori error estimates for the two-step backward differentiation formula method for parabolic equations. SIAM J. Numer. Anal. 48, 109–132 (2010)
Akrivis, G., Makridakis, C.: Galerkin time-stepping methods for nonlinear parabolic equations, M2AN Math. Model. Numer. Anal. 38, 261–289 (2004)
Akrivis, G., Makridakis, C., Nochetto, R.H.: A posteriori error estimates for the Crank–Nicolson method for parabolic equations. Math. Comput. 75, 511–531 (2006)
Akrivis, G., Makridakis, C., Nochetto, R.H.: Optimal order a posteriori error estimates for a class of Runge–Kutta and Galerkin methods. Numer. Math. 114, 133–160 (2009)
Akrivis, G., Makridakis, C., Nochetto, R.H.: Galerkin and Runge–Kutta methods: unified formulation, a posteriori error estimates and nodal superconvergence. Numer. Math. 118, 429–456 (2011)
Bangerth, W., Hartmann, R., Kanschat, G.: deal. ii’a general-purpose object-oriented finite element library. ACM Trans. Math. Softw. (TOMS) 33, 24 (2007)
Bartels, S.: A posteriori error analysis for time-dependent Ginzburg–Landau type equations. Numer. Math. 99, 557–583 (2005)
Cangiani, A., Georgoulis, E.H., Jensen, M.: Discontinuous Galerkin methods for mass transfer through semipermeable membranes. SIAM J. Numer. Anal. 51, 2911–2934 (2013)
Cangiani, A., Georgoulis, E.H., Kyza, I., Metcalfe, S.: Adaptivity and blow-up detection for nonlinear evolution problems. SIAM J. Sci. Comput. 38, A3833–A3856 (2016)
Cangiani, A., Georgoulis, E.H., Metcalfe, S.: Adaptive discontinuous Galerkin methods for nonstationary convection–diffusion problems. IMA J. Numer. Anal. 34, 1578–1597 (2014)
Cangiani, A., Georgoulis, E.H., Morozov, A.M., Sutton, O.J.: Revealing new dynamical patterns in a reaction-diffusion model with cyclic competition via a novel computational framework. Proc. R. Soc. A 474, 20170608 (2018)
Carstensen, C., Funken, S.A.: Constants in Clément-interpolation error and residual based a posteriori error estimates in finite element methods. East-West J. Numer. Math. 8, 153–175 (2000)
Carstensen, C., Hellwig, F.: Constants in discrete Poincaré and Friedrichs inequalities and discrete quasi-interpolation. Comput. Methods Appl. Math. 18, 433–450 (2018)
Chrysafinos, K., Walkington, N.J.: Error estimates for the discontinuous Galerkin methods for parabolic equations. SIAM J. Numer. Anal. 44, 349–366 (2006)
Delfour, M., Hager, W., Trochu, F.: Discontinuous Galerkin methods for ordinary differential equations. Math. Comput. 36, 455–473 (1981)
Dolejší, Vt, Ern, A., Vohralík, M.: A framework for robust a posteriori error control in unsteady nonlinear advection–diffusion problems. SIAM J. Numer. Anal. 51, 773–793 (2013)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems. II. Optimal error estimates in \(L_\infty L_2\) and \(L_\infty L_\infty \). SIAM J. Numer. Anal. 32, 706–740 (1995)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems iv: nonlinear problems. SIAM J. Numer. Anal. 32, 1729–1749 (1995)
Ern, A., Smears, I., Vohralík, M.: Guaranteed, locally space-time efficient, and polynomial-degree robust a posteriori error estimates for high-order discretizations of parabolic problems, Tech. rep. (2016)
Ern, A., Smears, I., Vohralík, M.: Equilibrated flux a posteriori error estimates in \(L^2(H^1)\)-norms for high-order discretizations of parabolic problems, Tech. rep. (2017)
Ern, A., Vohralík, M.: A posteriori error estimation based on potential and flux reconstruction for the heat equation. SIAM J. Numer. Anal. 48, 198–223 (2010)
Estep, D., Larsson, S.: The discontinuous Galerkin method for semilinear parabolic problems. RAIRO Modél. Math. Anal. Numér. 27, 35–54 (1993)
Gaspoz, F.D., Kreuzer, C., Siebert, K.G., Ziegler, D.A.: A convergent time–space adaptive DG(s) finite element method for parabolic problems motivated by equal error distribution. https://arxiv.org/abs/1610.06814, (2017)
Georgoulis, E.H., Hall, E., Makridakis, C.G.: A posteriori error estimates for Runge–Kutta discontinuous Galerkin methods for hyperbolic problems, In preparation
Georgoulis, E.H., Lakkis, O., Makridakis, C.G., Virtanen, J.M.: A posteriori error estimates for leap-frog and cosine methods for second order evolution problems. SIAM J. Numer. Anal. 54, 120–136 (2016)
Georgoulis, E.H., Lakkis, O., Virtanen, J.M.: A posteriori error control for discontinuous Galerkin methods for parabolic problems. SIAM J. Numer. Anal. 49, 427–458 (2011)
Georgoulis, E.H., Lakkis, O., Wihler, T.P.: A posteriori error bounds for fully–discrete \(hp\)-discontinuous Galerkin timestepping methods for parabolic problems, Submitted for publication
Georgoulis, E.H., Virtanen, J.M.: Adaptive discontinuous Galerkin approximations to fourth order parabolic problems. Math. Comput. 84, 2163–2190 (2015)
Holm, B., Wihler, T.P.: Continuous and discontinuous Galerkin time stepping methods for nonlinear initial value problems with application to finite time blow-up. Numer. Math. 138, 767–799 (2018)
Jamet, P.: Galerkin-type approximations which are discontinuous in time for parabolic equations in a variable domain. SIAM J. Numer. Anal. 15, 912–928 (1978)
Karakashian, O., Makridakis, C.: A space-time finite element method for the nonlinear Schrödinger equation: the discontinuous Galerkin method. Math. Comput. 67, 479–499 (1998)
Kyza, I., Makridakis, C.: Analysis for time discrete approximations of blow-up solutions of semilinear parabolic equations. SIAM J. Numer. Anal. 49, 405–426 (2011)
Kyza, I., Metcalfe, S., Wihler, T.P.: \(hp\)-adaptive Galerkin time stepping methods for nonlinear initial value problems. J. Sci. Comput. 75, 111–127 (2018)
Lakkis, O., Makridakis, C.: Elliptic reconstruction and a posteriori error estimates for fully discrete linear parabolic problems. Math. Comput. 75, 1627–1658 (2006)
Lakkis, O., Nochetto, R.H.: A posteriori error analysis for the mean curvature flow of graphs. SIAM J. Numer. Anal. 42, 1875–1898 (2005). (electronic)
Lasaint, P., Raviart, P.-A.: On a finite element method for solving the neutron transport equation, pp. 89–123. Publication No. 33 (1974)
Lozinski, A., Picasso, M., Prachittham, V.: An anisotropic error estimator for the Crank–Nicolson method: application to a parabolic problem. SIAM J. Sci. Comput. 31, 2757–2783 (2009)
Makridakis, C., Babuška, I.: On the stability of the discontinuous Galerkin method for the heat equation. SIAM J. Numer. Anal. 34, 389–401 (1997)
Makridakis, C., Nochetto, R.H.: Elliptic reconstruction and a posteriori error estimates for parabolic problems. SIAM J. Numer. Anal. 41, 1585–1594 (2003)
Makridakis, C., Nochetto, R.H.: A posteriori error analysis for higher order dissipative methods for evolution problems. Numer. Math. 104, 489–514 (2006)
Nicaise, S., Soualem, N.: A posteriori error estimates for a nonconforming finite element discretization of the heat equation, M2AN Math. Model. Numer. Anal. 39, 319–348 (2005)
Picasso, M.: Adaptive finite elements for a linear parabolic problem. Comput. Methods Appl. Mech. Eng. 167, 223–237 (1998)
Sabawi, M.: Discontinuous Galerkin timestepping for nonlinear parabolic problems. Ph.D. Thesis, University of Leicester (2018)
Schötzau, D., Schwab, C.: Time discretization of parabolic problems by the \(hp\)-version of the discontinuous Galerkin finite element method. SIAM J. Numer. Anal. 38, 837–875 (2000)
Schötzau, D., Wihler, T.P.: A posteriori error estimation for \(hp\)-version time-stepping methods for parabolic partial differential equations. Numer. Math. 115, 475–509 (2010)
Tanaka, K., Sekine, K., Mizuguchi, M., Oishi, S.: Estimation of Sobolev-type embedding constant on domains with minimally smooth boundary using extension operator. J. Inequal. Appl. 2015(389), 23 (2015)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Lecture Notes in Mathematics, vol. 1054. Springer, Berlin (1984)
Thomée, V., Wahlbin, L.: On Galerkin methods in semilinear parabolic problems. SIAM J. Numer. Anal. 12, 378–389 (1975)
Verfürth, R.: A posteriori error estimates for finite element discretizations of the heat equation. Calcolo 40, 195–212 (2003)
Verfürth, R.: A Posteriori Error Estimation Techniques for Finite Element Methods. Numerical Mathematics and Scientific Computation. Oxford University Press, Oxford (2013)
Verfürth, R.: A posteriori error estimates for non-stationary non-linear convection–diffusion equations. Calcolo 55, Art. 20, 18 (2018)
Acknowledgements
EHG acknowledges the support of The Leverhulme Trust (Grant RPG-2015-306). MS thanks The Higher Committee for Education Development (HCED) in Iraq for their partial support during the time of preparing this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cangiani, A., Georgoulis, E.H. & Sabawi, M. A Posteriori Error Analysis for Implicit–Explicit hp-Discontinuous Galerkin Timestepping Methods for Semilinear Parabolic Problems. J Sci Comput 82, 26 (2020). https://doi.org/10.1007/s10915-020-01130-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-020-01130-2