Skip to main content
SpringerLink
Log in

Optimal Order Error Estimates for Discontinuous Galerkin Methods for the Wave Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

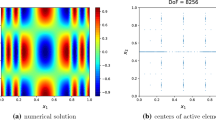
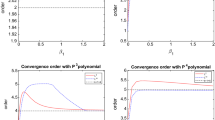
Abstract

In this paper, we derive optimal order error estimates for spatially semi-discrete and fully discrete schemes to numerically solve the second-order wave equation. The numerical schemes are constructed with the discontinuous Galerkin (DG) discretization for the spatial variable and the centered second-order finite difference approximation for the temporal variable. Under appropriate regularity assumptions on the solution, the schemes are shown to enjoy the optimal order error bounds in terms of both the spatial mesh-size and the time-step. In Grote and Schötzau (J Sci Comput 40:257–272, 2009), a fully discrete DG scheme is studied with an explicit finite difference temporal discretization where a CFL condition is required on the mesh-size and the time-step, and optimal order error estimates are derived in the \(L^2(\Omega )\)-norm. In comparison, for our fully discrete DG schemes, we do not require a CFL condition on the mesh-size and the time-step, and our optimal order error estimates are derived for the \(H^1(\Omega )\)-like norm and the \(L^2(\Omega )\) norm. Numerical simulation results are reported to illustrate theoretically predicted convergence orders in the \(H^1(\Omega )\) and \(L^2(\Omega )\) norms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Abraham, D.S., Marques, A.N., Nave, J.-C.: A correction function method for the wave equation with interface jump conditions. J. Comput. Phys. 353, 281–299 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arnold, D.N.: An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 19, 742–760 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  3. Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39, 1749–1779 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  4. Baker, G.A.: Error estimates for finite element methods for second-order hyperbolic equations. SIAM J. Numer. Anal. 13, 564–576 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bassi, F., Rebay, S.: A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier–Stokes equations. J. Comput. Phys. 131, 267–279 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bassi, F., Rebay, S., Mariotti, G., Pedinotti, S., Savini, M.: A high-order accurate discontinuous finite element method for inviscid and viscous turbomachinery flows. In: Decuypere, R., Dibelius, G. (eds.) Proceedings of 2nd European Conference on Turbomachinery, Fluid Dynamics and Thermodynamics, pp. 99–108. Technologisch Instituut, Antwerpen (1997)

    Google Scholar 

  7. Bécache, E., Joly, P., Tsogka, C.: An analysis of new mixed finite elements for the approximation of wave propagation problems. SIAM J. Numer. Anal. 37, 1053–1084 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bey, K., Oden, J.: \(hp\)-Version discontinuous Galerkin methods for hyperbolic conservation laws. Comput. Methods Appl. Mech. Eng. 133, 259–286 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  9. Britt, S., Tsynkov, S., Turkel, E.: Numerical solution of the wave equation with variable wave speed on nonconforming domains by high-order difference potentials. J. Comput. Phys. 354, 26–42 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  10. Brezzi, F., Manzini, G., Marini, D., Pietra, P., Russo, A.: Discontinuous finite elements for diffusion problems. In: Atti Convegno in onore di F. Brioschi (Milan, 1999), Istituto Lombardo. Accademia di Scienze e Lettere, Milan, Italy, pp. 197–217 (1999)

  11. Castillo, P., Cockburn, B., Schötzau, D., Schwab, C.: Optimal a priori error estimates for the \(hp\)-version of the local discontinuous Galerkin method for convection–diffusion problems. Math. Comput. 71, 455–478 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cockburn, B., Kanschat, G., Schötzau, D.: A locally conservative LDG method for the incompressible Navier–Stokes equations. Math. Comput. 74, 1067–1095 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cockburn, B., Karniadakis, G.E., Shu, C.-W. (eds.): Discontinuous Galerkin Methods Theory, Computation and Applications, Lecture Notes in Computational Science and Engineering, vol. 11. Springer, New York (2000)

    Google Scholar 

  14. Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection–diffusion systems. SIAM J. Numer. Anal. 35, 2440–2463 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  15. Cowsar, L.C., Dupont, T.F., Wheeler, M.F.: A-priori estimates for mixed finite element methods for the wave equations. Comput. Methods Appl. Mech. Eng. 82, 205–222 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  16. Douglas Jr., J., Dupont, T.: Interior Penalty Procedures for Elliptic and Parabolic Galerkin Methods. Lecture Notes in Physics, vol. 58. Springer, Berlin (1976)

    Google Scholar 

  17. Dupont, T.: \(L^2\)-estimates for Galerkin methods for second-order hyperbolic equations. SIAM J. Numer. Anal. 10, 880–889 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  18. Grote, M., Schneebeli, A., Schötzau, D.: Discontinuous Galerkin finite element method for the wave equation. SIAM J. Numer. Anal. 44, 2408–2431 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  19. Grote, M., Schötzau, D.: Optimal error estimates for the fully discrete interior penalty DG method for the wave equation. J. Sci. Comput. 40, 257–272 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Han, W., Huang, J., Eichholz, J.: Discrete-ordinate discontinuous Galerkin methods for solving the radiative transfer equation. SIAM J. Sci. Comput. 32, 477–497 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Han, W., Sofonea, M.: Quasistatic Contact Problems in Viscoelasticity and Viscoplasticity, Studies in Advanced Mathematics, vol. 30. Americal Mathematical Society/International Press, Providence/Somerville (2002)

    Book  MATH  Google Scholar 

  22. Houston, P., Schwab, C., Süli, E.: Stabilized \(hp\)-finite element methods for hyperbolic problems. SIAM J. Numer. Anal. 37, 1618–1643 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  23. Hu, C., Shu, C.-W.: A discontinuous Galerkin finite element method for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 666–690 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  24. Kornhuber, R., Lepsky, O., Hu, C., Shu, C.-W.: The analysis of the discontinuous Galerkin method for Hamilton–Jacobi equations. Appl. Numer. Math. 33, 423–434 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  25. Lions, J.-L., Magenes, E.: Non-Homogeneous Boundary Value Problems and Applications, vol. I. Springer, New York (1972)

    Book  MATH  Google Scholar 

  26. Perugia, I., Schötzau, D.: An \(hp\)-analysis of the local discontinuous Galerkin method for diffusion problems. J. Sci. Comput. 17, 561–571 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang, F., Han, W., Cheng, X.: Discontinuous Galerkin methods for solving elliptic variational inequalities. SIAM J. Numer. Anal. 48, 708–733 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, F., Han, W., Cheng, X.: Discontinuous Galerkin methods for solving Signorini problem. IMA J. Numer. Anal. 31, 1754–1772 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wang, F., Han, W., Cheng, X.: Discontinuous Galerkin methods for solving a quasistatic contact problem. Numer. Math. 126, 771–800 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Wang, F., Han, W., Eichholz, J., Cheng, X.: A posteriori error estimates of discontinuous Galerkin methods for obstacle problems. Nonlinear Anal. Real World Appl. 22, 664–679 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  31. Wang, F., Zhang, T., Han, W.: \(C^0\) discontinuous Galerkin methods for a Kirchhoff plate contact problem. J. Comput. Math. (to appear)

  32. Wheeler, M.F.: An elliptic collocation finite element method with interior penalties. SIAM J. Numer. Anal. 15, 152–161 (1978)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, 710049, Shaanxi, China

    Weimin Han, Limin He & Fei Wang

  2. Department of Mathematics and Program in Applied Mathematical and Computational Sciences, University of Iowa, Iowa City, IA, 52242, USA

    Weimin Han

  3. School of Science, Inner Mongolia University of Science and Technology, Baotou, 014010, Inner Mongolia, China

    Limin He

Authors
  1. Weimin Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Limin He
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fei Wang.

Additional information

The work of Weimin Han was partially supported by NSF under Grant DMS-1521684. The work of Limin He, Fei Wang was partially supported by the National Natural Science Foundation of China (Grant Nos. 61663035, 11771350).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, W., He, L. & Wang, F. Optimal Order Error Estimates for Discontinuous Galerkin Methods for the Wave Equation. J Sci Comput 78, 121–144 (2019). https://doi.org/10.1007/s10915-018-0755-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0755-1

Keywords

Mathematics Subject Classification

Search

Navigation