Abstract
In this article, we address the numerical solution of the Dirichlet problem for the three-dimensional elliptic Monge–Ampère equation using a least-squares/relaxation approach. The relaxation algorithm allows the decoupling of the differential operators from the nonlinearities. Dedicated numerical solvers are derived for the efficient solution of the local optimization problems with cubicly nonlinear equality constraints. The approximation relies on mixed low order finite element methods with regularization techniques. The results of numerical experiments show the convergence of our relaxation method to a convex classical solution if such a solution exists; otherwise they show convergence to a generalized solution in a least-squares sense. These results show also the robustness of our methodology and its ability at handling curved boundaries and non-convex domains.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Monge–Ampère equation can be considered as the prototypical example of fully nonlinear elliptic equations [11, 21, 29]. Theoretical investigations of fully nonlinear equations started many years ago [6, 39] and have received a lot of attention lately [4, 5, 8, 14, 16, 19, 35,36,37,38], due to the many applications involving this type of equations, for instance in finance [41], in seismic wave propagation [13], in geostrophic flows [15], in differential geometry [2, 18], and in mechanics and physics. However, the Monge–Ampère equation in three space dimensions is a complicated problem, which is still lacking a full theoretical understanding, particularly when the domain of interest is not strictly convex.
From a computational point of view, various approaches have been identified, relying in particular on finite difference [5, 13] or finite element [3, 9, 17, 27] approximations.
Since the Monge–Ampère equation may not have smooth classical solutions, even for smooth data (see [11]), notions of generalized solutions have been introduced, such as Aleksandrov solutions [1], and viscosity solutions [31, 38]. Actually, another notion of generalized solution for fully nonlinear elliptic equations has been introduced relatively recently, namely generalized solutions in a least-squares sense. These least-squares generalized solutions have been obtained via augmented Lagrangian or least-squares/relaxation approaches [9, 12, 24]. The least-squares approach will be the one used in this article.
We consider in this article three-dimensional bounded domains \({\varOmega }\) with a Lipschitz continuous boundary \(\partial {\varOmega }\). For data f and g sufficiently smooth, it makes sense from the existence, uniqueness and regularity results reported in, e.g., [10], to look for \(\psi \) belonging to \(H^2({\varOmega })\) and convex, solution to the following Dirichlet problem for the Monge–Ampère equation
Indeed, note that, if \({\varOmega }\) is a bounded strictly convex domain of \({\mathbb {R}}^3\) with a \(C^{\infty }\) boundary \(\partial {\varOmega }\), this problem has a unique convex solution belonging to \(C^{\infty }(\bar{{\varOmega }})\) (see, e.g., [10]). On the other hand, if \({\varOmega }\) is a bounded strictly convex domain of \({\mathbb {R}}^3\), the Dirichlet problem for the Monge–Ampère equation has a unique convex generalized solution belonging to \(C^{0}(\bar{{\varOmega }})\cap W^{2,\infty }_{loc}({\varOmega })\) (see, e.g., [29]). Therefore, \(H^2({\varOmega })\) is a reasonable choice to look for a solution to the Monge–Ampère equation in three space dimensions.
The chosen least-squares formulation we used here consists in minimizing the \(L^2\)-distance between \({\mathbf {D}}^2 \psi \) and a matrix-valued function \(\mathbf {p}\in (L^{2}({\varOmega }))^{3\times 3}\), where \(\psi \) satisfies the boundary conditions of the problem (but not the Monge–Ampère equation) and \(\mathbf {p}\) satisfies \(\det \mathbf {p}= f\). Using a relaxation algorithm to minimize such a distance, we obtained a solution method where one solves alternatively, until convergence, a sequence of linear variational problems (to be approximated by mixed finite element methods) and a sequence of cubicly constrained algebraic optimization problems. Using a similar approach, we have been able to compute generalized solutions of the Monge–Ampère equation when this problem has no classical solutions in two dimensions of space [9]. In this article, the methods discussed in [9] have been generalized to three-dimensional problems.
In this article, the linear variational problems we mentioned above are solved by a preconditioned conjugate gradient algorithm, whose computer implementation relies on low order (\({\mathbb {P}}_1\) or \({\mathbb {Q}}_1\)) mixed finite element approximations. The local cubicly constrained optimization problems are solved by Newton-like methods [42] or time-stepping methods associated with a dynamical flow (see, e.g., [30]). The main difference between the two-dimensional case discussed in [9] , and the present article is the cubic nature (vs quadratic) of the equality constraints.
The structure of this article is as follows. In Sect. 2, we describe the proposed methodology, while the relaxation algorithm is described in Sect. 3. Sections 4 and 5 detail the algebraic and differential solvers respectively. The mixed finite element discretization is discussed in Sect. 6. The method is applied in Sect. 7 to the solution of several numerical examples, including examples without a classical exact solution. Finally, in Sect. 8, some numerical results are presented where \({\mathbb {P}}_1\) finite elements have been replaced with \({\mathbb {Q}}_1\) ones.
The numerical solution of the 3D elliptic Monge–Ampère equation has been discussed in [8] using piecewise \({\mathbb {P}}_3\) continuous finite element approximations. A fast multigrid scheme has been presented in [34], while smooth cases on structured meshes have been considered in [3] (with numerical results that are consistent with [9]). However, to the best of our knowledge, the method discussed in the present article is one of the very few able to solve the 3D elliptic Monge–Ampère equation on domains with curved boundaries, using piecewise \({\mathbb {P}}_1\) continuous finite element approximations associated with unstructured meshes, while preserving optimal, or nearly optimal, orders of convergence for the approximation errors, including situations where the solution does not have the \(C^2(\bar{{\varOmega }})\) regularity.
2 Mathematical Formulation and Least-Squares Approach
Let \({\varOmega }\) be a bounded convex domain of \({\mathbb {R}}^3\); we denote by \({\varGamma }\) the boundary of \({\varOmega }\). The Dirichlet problem for the elliptic Monge–Ampère equation reads as follows:
where \({\mathbf {D}}^2 \psi = \left( \frac{\partial ^2 \psi }{\partial x_i\partial x_j} \right) _{1\le i,j\le 3}\) is the Hessian of the unknown function \(\psi \).
Among the various methods available for the solution of (1) discussed in the introduction, we advocate a nonlinear least-squares method that relies on the introduction of an additional auxiliary variable. Namely, we look for:
where:
using the Fröbenius norm and inner product defined by \(\left| \mathbf {T}\right| = \sqrt{ \mathbf {T}: \mathbf {T}}\), \(\mathbf {S}~:~\mathbf {T}= \sum _{i,j=1}^3 s_{ij} t_{ij}\), for all \(\mathbf {S}=(s_{ij}),\mathbf {T}=(t_{ij}) \in {\mathbb {R}}^{3\times 3}\). The functional spaces in (2) are respectively defined by:
We assume that \(f\in L^{2/3}({\varOmega })\) and \(g\in H^{3/2}({\varGamma })\), so that \(V_g\) and \(\mathbf {Q}_f\) are both non-empty. Note that the space \(\mathbf {Q}\) is a Hilbert space for the inner product \((\mathbf {q},\mathbf {q}') \rightarrow \int _{{\varOmega }} \mathbf {q}: \mathbf {q}' d\mathbf {x}\), and the associated norm.
3 Relaxation Algorithm
In order to decouple differential operators from the nonlinearity, we suggest using a relaxation algorithm of the Gauss–Seidel-type. Furthermore, we wish to compute a convex solution to problem (2) (or at least to force the convexity of the solution), and thus advocate the following approach. First, the initialization is performed by solving:
Then, for \(n\ge 0\) and assuming that \(\psi ^n\) is known, one computes \(\mathbf {p}^n, \psi ^{n+1/2}\) and \(\psi ^{n+1}\) as follows:
with \(1\le \omega \le \omega _{\mathrm{max}} < 2\). For the numerical experiments presented in Sect. 7, we used \(\omega \equiv 1\) (unless otherwise specified).
The rationale behind the initialization procedure (4) is based on the above isotropic assumption. If we denote the eigenvalues of \({\mathbf {D}}^2\psi \) by \(\lambda _i\), \(i=1,2,3\), the Monge–Ampère equation reads \(\lambda _1\lambda _2\lambda _3 = f\). If \(\lambda _1, \lambda _2 \) and \(\lambda _3\) are “close” from each other (and thus all equal to, let’s say, \(\lambda \)), we have \(\lambda ^3 = f\), and thus \(\lambda = \root 3 \of {f}\). Therefore:
Since the initialization procedure is based on an isotropic assumption, the case when the eigenvalues are very different from each other has to be put under scrutiny in the numerical experiments. In the sequel, the numerical algorithms used for the solution of problems (5) and (6) will be discussed in details. Despite several investigations, note that the question of the uniqueness of the solution to the local problem (5) still remains an open question.
4 Numerical Approximation of the Local Nonlinear Problems
4.1 Explicit Formulation of the Local Nonlinear Problems
An explicit formulation of problem (5) reads as
Since the objective function in (8) does not contain derivatives of \(\mathbf {q}\), this minimization problem can be solved point-wise (in practice at the vertices of a finite element or finite difference grid). This leads, a.e. in \({\varOmega }\), to the solution of the following finite dimensional minimization problem:
where
In the case of the 2D Monge–Ampère equation, this step led to a class of quadratically constrained minimization problems, whose solution was addressed in [9, 28] using a dedicated algorithm. This dedicated approach does not apply when the constraint is a cubic equation as here, implying that other approaches have to be considered. The two approaches below rely on an appropriate re-parameterization of the problem in order to transform the constrained minimization problem into an unconstrained one; both ending up with some kind of Newton-related methods.
4.2 A Reduced Newton Method
For a. e. \(\mathbf {x}\in {\varOmega }\), (9) is an algebraic optimization problem. Using a Cholesky decomposition of \(\mathbf {q}\), we write \(\mathbf {q}= \mathbf {L}\mathbf {D}\mathbf {L}^t\), where
This re-parameterization is arbitrary but serves two purposes: first, it guarantees that all eigenvalues are strictly positive (convexity of the local solution). Second, the constraint \(\mathrm {det}\mathbf {q}=f(\mathbf {x})\) is automatically satisfied. It thus allows one to replace (9) by an unconstrained minimization problem in the variable \(\mathbf {X}:= (a,b,c,\rho _1,\rho _2)\). For the sake of simplicity, we do not write the dependency on \(\mathbf {x}\in {\varOmega }\) anymore. The problem becomes:
The first order optimality conditions corresponding to (11) can formally be written as
This nonlinear system can be solved with a safeguarded Newton method for the variable \(\mathbf {X}\). Namely, given \(\mathbf {X}^0 \in {\mathbb {R}}^5\), solve, for \(k \ge 0\):
followed by
where \(\lambda ^k \in \mathbb {R}_+\) is a step-length to be adapted according to some Armijo rule (see, e.g., [7]). Typically, we update the step-length if \(\left| \left| \nabla G(\mathbf {X}^{k+1}) \right| \right| > (1-\alpha \lambda ^k) \left| \left| \nabla G(\mathbf {X}^{k}) \right| \right| \), where \(\alpha = 10^{-4}\) and \(\left| \left| \cdot \right| \right| \) denotes the canonical Euclidian norm of \({\mathbb {R}}^5\), and set in that case \(\lambda ^{k+1} = \frac{1}{2} \lambda ^k\).
The stopping criterion is based on the residual value \(\left| \left| \nabla G(\mathbf {X}^{k}) \right| \right| \), and the iterations are stopped if \(\left| \left| \nabla G(\mathbf {X}^{k}) \right| \right| < \varepsilon _{\mathrm{Newton}}\), where \(\varepsilon _{\mathrm{Newton}}\) is a given tolerance.
4.3 A Runge–Kutta Method for the Dynamical Flow Problem
An alternative re-parameterization of the nonlinear problem (9) can be considered, based on a eigenvalues-eigenvectors decomposition, in the spirit of the approach in [28]. Namely, consider \(\mathbf {q}= \mathbf {Q}{\varvec{\Lambda }}\mathbf {Q}^t\), where \(\mathbf {Q}\in O(3) \subset {\mathbb {R}}^{3\times 3}\) is the orthogonal matrix whose columns represent the eigenvectors of \(\mathbf {q}\) (O(3) being the group of the \(3\times 3\) orthogonal matrices), and \({\varvec{\Lambda }}\in {\mathbb {R}}^{3\times 3}\) is the diagonal matrix whose diagonal elements are the corresponding eigenvalues. We can denote
Again, this parameterization is not unique; it ensures that the relation \(\mathrm {det}{\mathbf {q}}=f(\mathbf {x})\) is automatically satisfied and that the eigenvalues are positive in order to enforce convexity of the local solutions. The property \(\mathbf {Q}\in O(3)\) implies the following constraints for its column vectors \(\mathbf {T}_i,i=1,2,3\) (where \(\mathbf {T}_i\cdot \mathbf {T}_j\) denotes the dot product of vectors \(\mathbf {T}_i\) and \(\mathbf {T}_ j\)):
Let us define the variables \(\mathbf {Y}= (\rho _1,\ \rho _2,\ \mathbf {T}_1,\ \mathbf {T}_2, \mathbf {T}_3) \in {\mathbb {R}}^{11}\). Problem (9) can be rewritten as
Below, for \(i = 1, 2, 3\), we will denote by \(|\mathbf {T}_i|\) the quantity \((\mathbf {T}_i \cdot \mathbf {T}_i)^{1/2}\). We penalize the equality constraints in order to obtain an unconstrained problem that can be solved by a Newton approach. Let \(\varepsilon _1,\varepsilon _2>0\) be two given (small) parameters. The constraints are taken into account by penalization, leading to the following unconstrained minimization problem:
where
Similarly to the solution of (11), the first order optimality conditions associated with (12) can be written as
In order to smoothen the transition to critical point(s), we favor an evolutive formulation of the first order optimality conditions (in the sense of a flow problem in the dynamical systems terminology), which read as follows: find \(\mathbf {Y}: (0,+\infty ) \rightarrow {\mathbb {R}}^{11}\) such that
The steady state solution of (13) (14) corresponds to the desired critical point. In order to increase the stability of the numerical scheme and allow larger time steps and therefore a faster convergence to the steady state solution, it is customary to modify (13) into a modified flow problem [32], namely: find \(\mathbf {Y}: (0,+\infty ) \rightarrow {\mathbb {R}}^{11}\) such that
with the same initial condition. The stability of the scheme is important here since we are aiming at solving such a flow problem for a.e. \(\mathbf {x}\in {\varOmega }\), which requires an efficient numerical algorithm. The additional computational cost induced by the introduction of the term \(\left( \nabla ^2 G_{\varepsilon _1,\varepsilon _2}(\mathbf {Y})\right) ^{-1}\) is estimated in the sequel.
System (15) is solved by a two-stage (second order explicit) Runge–Kutta method (see, e.g., [30]) in order to capture steady state solutions. Let \({\varDelta }t\) be a given time step, \(t_n=n {\varDelta }t\) and \(\mathbf {Y}_n \simeq \mathbf {Y}(t_n)\), \(n=0,1,\ldots \). Let us define \(\mathbf {Y}_0=\mathbf {Y}^0\); then, at each time step, solve
An adaptive time stepping strategy for Runge–Kutta methods is incorporated to the numerical algorithm; numerical experiments will show that the adaptive time step is particularly useful at the beginning of the outer iterations loop, when the initial solution is not close to the final steady state solution.
It is worth noticing that, if we treat the modified flow problem with a first order Euler explicit scheme, it leads to solving at each time step
this problem corresponds actually to a classical safeguarded Newton method, reminiscent to the one we presented in Sect. 4.2, with \({\varDelta }t\) playing the role of the step-length \(\lambda \). With this remark, the adaptive time stepping algorithm for Runge–Kutta schemes can be seen as an adaptive Armijo-like rule, with \({\varDelta }t = \lambda \). Furthermore, one can see that the Runge–Kutta approach is slower than the reduced Newton strategy (since it corresponds to solving two Newton-type systems at each time step), but it is more accurate since the two-step Runge–Kutta scheme is a higher order method than the Euler scheme. Finally, a study of the stability of Runge–Kutta schemes [30] shows that its stability properties are better than those of the Euler scheme.
5 Numerical Solution of the Linear Variational Problems
Written in variational form the Euler–Lagrange equation of the sub-problem (6) reads as follows: find \(\psi ^{n+1/2} \in V_g\) satisfying:
where \(V_0 = H^2({\varOmega }) \cap H_0^1({\varOmega })\). The linear variational problem (16) is well-posed and belongs to the following family of linear variational problems:
with the functional \(L(\cdot )\) linear and continuous over \(H^2({\varOmega })\); problem (17) is a bi-harmonic type problem, which can be solved by a conjugate gradient algorithm operating in well-chosen Hilbert spaces (see, e.g., [22, Chapter 3]). Here, our conjugate gradient algorithm operates in the spaces \(V_0\) and \(V_g\), both spaces being equipped with the inner product defined by \((v,w) \rightarrow \int _{{\varOmega }} {\varDelta }v {\varDelta }w d\mathbf {x}\), and the corresponding norm. It reads as follows:
- Step 1 :
-
$$\begin{aligned} u^0 \in V_g \text { given. } \end{aligned}$$(18)
- Step 2 :
-
Solve: find \(g^0 \in V_g\) satisfying
$$\begin{aligned} \int _{{\varOmega }} {\varDelta }g^0 {\varDelta }v d\mathbf {x}= \int _{{\varOmega }} {\mathbf {D}}^2 u^0: {\mathbf {D}}^2 v d\mathbf {x}-L(v), \quad \forall v \in V_0, \end{aligned}$$(19)and set
$$\begin{aligned} w^0 = g^0. \end{aligned}$$(20)Then, for \(k\ge 0\), \(u^k, g^k\) and \(w^k\) being known, the last two different from zero, we compute \(u^{k+1}, g^{k+1}\) and, if necessary, \(w^{k+1}\) as follows.
- Step 3 :
-
Solve: find \(\bar{g}^k \in V_0\) satisfying
$$\begin{aligned} \int _{{\varOmega }} {\varDelta }\bar{g}^k {\varDelta }v d\mathbf {x}= \int _{{\varOmega }} {\mathbf {D}}^2 w^k: {\mathbf {D}}^2 v d\mathbf {x}, \quad \forall v \in V_0, \end{aligned}$$(21)and compute
$$\begin{aligned}&\rho _k = \frac{ \int _{{\varOmega }} \left| {\varDelta }g^k \right| ^2 d\mathbf {x}}{ \int _{{\varOmega }} {\varDelta }\bar{g}^k {\varDelta }w^k d\mathbf {x}}, \end{aligned}$$(22)$$\begin{aligned}&u^{k+1} = u^k - \rho _k w^k, \end{aligned}$$(23)$$\begin{aligned}&g^{k+1} = g^k - \rho _k \bar{g}^k. \end{aligned}$$(24) - Step 4 :
-
Compute
$$\begin{aligned} \delta _k = \frac{ \int _{{\varOmega }} \left| {\varDelta }g^{k+1} \right| ^2 d\mathbf {x}}{ \int _{{\varOmega }} \left| {\varDelta }g^{0} \right| ^2 d\mathbf {x}}. \end{aligned}$$(25)If \(\delta _k < \varepsilon \), take \(u = u^{k+1}\); otherwise, compute:
$$\begin{aligned} \gamma _k = \frac{ \int _{{\varOmega }} \left| {\varDelta }g^{k+1} \right| ^2 d\mathbf {x}}{ \int _{{\varOmega }} \left| {\varDelta }g^k\right| ^2 d\mathbf {x}}; \end{aligned}$$(26)and
$$\begin{aligned} w^{k+1} = g^{k+1} + \gamma _k w^k. \end{aligned}$$(27) - Step 5 :
-
Do \(k+1 \rightarrow k\) and return to Step 3.
6 Mixed Finite Element Approximation
Considering the highly variational flavor of the methodology discussed in the preceding sections, it makes sense to look for finite element methods for the solution of (1). We will use a mixed finite element approximation (closely related to those discussed in, e.g., [25] for the solution of linear and nonlinear bi-harmonic problems) with low order (piecewise linear and globally continuous) finite elements on a partition of \({\varOmega }\) made of tetrahedra. The modification of the numerical approximation method obtained when replacing the \({\mathbb {P}}_1\) based finite element spaces on tetrahedra by the \({\mathbb {Q}}_1\) based finite element spaces associated with partitions of \({\varOmega }\) made of hexahedra is discussed in Sect. 8 with some numerical experiments.
6.1 Finite Element Spaces
For simplicity, let us assume that \({\varOmega }\) is a bounded polyhedral domain of \({\mathbb {R}}^3\), and define \(\mathcal {T}_h\) as a finite element partition of \({\varOmega }\) made out of tetrahedra (see, e.g., [23, Appendix 1]). Let \({\varSigma }_h\) be the set of the vertices of \(\mathcal {T}_h\), \({\varSigma }_{0h} = \left\{ P \in {\varSigma }_h , P \notin {\varGamma }\right\} \), \(N_h = \mathrm {Card}({\varSigma }_h)\), and \(N_{0h} = \mathrm {Card}({\varSigma }_{0h})\). We suppose that \({\varSigma }_{0h} =\left\{ P_j \right\} _{j=1}^{N_{0h}}\) and \({\varSigma }_h = {\varSigma }_{0h} \cup \left\{ P_j \right\} _{j=N_{0h}+ 1}^{N_{h}}\).
From \(\mathcal {T}_h\), we approximate the spaces \(L^2({\varOmega })\), \(H^1({\varOmega })\) and \(H^2({\varOmega })\) by the finite dimensional space \(V_h\) defined by:
with \({\mathbb {P}}_1\) the space of the three-variable polynomials of degree \(\le 1\). We define also \(V_{0h}\) as
In the sequel, \(V_{0h}\) will be used to approximate both \(H_0^1({\varOmega })\) and \(H^2({\varOmega }) \cap H_0^1({\varOmega })\).
6.2 Finite Element Approximation of the Monge–Ampère Equation
When solving (17) by the conjugate gradient algorithm (18)–(27), one has to (i) compute the discrete analogues of the second order derivatives, e.g., \({\mathbf {D}}^2 w^k\) and \({\mathbf {D}}^2 u^0\), and (ii) solve biharmonic problems such as (19) and (21).
Concerning (i) we will approximate the second order derivatives by functions belonging to \(V_{0h}\), but this has to be handled carefully. For a function \(\varphi \) belonging to \(H^2({\varOmega })\), it follows from Green’s formula that, for \(i,j=1,2,3\):
Consider now \(\varphi \in V_h\). We define the discrete analogue \(D^2_{hij} \varphi \in V_{0h}\) of the second derivative \(\frac{\partial ^2 \varphi }{\partial x_i\partial x_j}\) by : for all i, j, \(1\le i,j, \le 3\), \(D^2_{hij}\varphi \in V_{0h}\) and verifies
The functions \(D^2_{hij}\varphi \) are thus uniquely defined; in order to simplify the computation of the above discrete second order partial derivatives, we could use the trapezoidal rule to evaluate the integrals in the left hand sides (mass lumping). Since the Hessian matrix \({\mathbf {D}}^2\psi \) is in \((L^2({\varOmega }))^{3\times 3}\), and since \(H_0^1({\varOmega })\) is dense in \(L^2({\varOmega })\), the approximation \({\mathbf {D}}_h^2\psi \) is considered to be in \(V_{0h}\). Indeed, the underlying method being a collocation method, the Monge–Ampère equation is approximated and imposed at the internal vertices of \({\varOmega }\) only.
As emphasized in [9, 40], when using piecewise linear mixed finite elements, the approximation of the error on the second derivatives of the solution \(\psi \) is, in general, \(\mathcal {O}(1)\) in the \(L^2\)-norm. Therefore, the convergence properties of the global algorithm strongly depends on the type of partition of \({\varOmega }\) one employs, and could be completely jeopardized in some situations. One way to improve the approximation properties of the discrete second order derivatives \(D^2_{hij}\varphi \) is to use, as in [9], a Tychonoff-like regularization [43]. Let us introduce a stabilization constant C (to be calibrated in the numerical experiments), and replace the previous variational problem by: for all i, j, \(1\le i,j \le 3\), \(D^2_{hij}\varphi \in V_{0h}\) and verifies
The rationale behind (30) is to correct the approximation errors of (29), which deteriorate when \(h \rightarrow 0\). This behavior being associated with the high modes of the approximate solutions. Similar ideas have been used for approximations of the Stokes problem in incompressible fluid mechanics when using essentially the same finite element spaces for the velocity components and the pressure (see, e.g., [23, Chapter 5]). Among the possible cures of this unwanted behavior, let us mention the use of higher degree polynomials to define the finite element spaces. However since piecewise affine approximations are optimal for handling domains of (almost) arbitrary shape and with curved boundaries, we will try to rescue them following the approach in [9]. The first step is to approximate (28) by : for all i, j, \(1\le i,j \le 3\), \(\left( \frac{\partial ^2 \psi }{\partial x_i \partial x_j} \right) _{\varepsilon } \in H^1_0({\varOmega })\) and verifies
with \(\varepsilon >0\) a “small” positive number (of the order of \(h^2\) in practice). Problem (31) is well-posed and one can easily show that
In this article, we approximate both (28) and (31) by (30). Numerical experiments show that this regularization procedure provides approximations of optimal or nearly optimal orders.
Defining \({\mathbf {D}}_h^2 \psi _h(P_k) = \left( D^2_{hij} \psi _h(P_k) \right) _{i,j=1}^3\), and assuming that the boundary function g is continuous over \({\varGamma }\), the affine space \(V_g\) can be approximated by
and the discrete Monge–Ampère equation reads: find \(\psi _h \in V_{gh}\) such that
Concerning issue (ii), that is the solution of the bi-harmonic problems encountered in the conjugate gradient algorithm (18)–(27), after space discretization the resulting discrete bi-harmonic problems are all particular cases of
with \({\varLambda }_h \in \mathcal {L}(V_{0h}, \mathbb {R})\) and \({\varDelta }_h \in \mathcal {L}(V_{0h},V_{0h})\) defined by
It follows from this definition that the discrete bi-harmonic problem (33) is equivalent to the following system of easy to solve discrete Poisson–Dirichlet problems:
6.3 Discrete Formulation of the Least-Squares Method
We define the discrete analogues of spaces \(\mathbf {Q}\) and \(\mathbf {Q}_f\) as follows:
We associate with \(V_h\) (or \(V_{0h}\) and \(V_{gh}\)) and \(\mathbf {Q}_h\), the discrete inner products: \((v,w)_{0h} = \frac{1}{4} \sum _{k=1}^{N_h} A_k v(P_k) w(P_k)\) (with corresponding norm \(\left| \left| v \right| \right| _{0h} = \sqrt{ (v,v)_h } \)), for all \(v,w\in V_{0h}\), and \(((\mathbf {S},\mathbf {T}))_{0h} = \frac{1}{4} \sum _{k=1}^{N_h} A_k \mathbf {S}(P_k): \mathbf {T}(P_k)\) (with corresponding norm \(\left| \left| \left| \mathbf {S} \right| \right| \right| _{0h} = \sqrt{ ((\mathbf {S},\mathbf {S}))_{0h} }\)) for all \(\mathbf {S},\mathbf {T}\in \mathbf {Q}_h\), where \(A_k\) is the volume of the polyhedral domain which is the union of those tetrahedra of \(\mathcal {T}_h\) which have \(P_k\) as a common vertex.
The solution of (32) is then addressed via a nonlinear least-squares method, namely find \((\psi _h,\mathbf {p}_h) \in V_{gh} \times \mathbf {Q}_{fh}\) such that
where:
6.4 A Discrete Relaxation Algorithm
The discrete relaxation algorithm we employ reads as follows: First find
For \(n\ge 0\), assuming that \(\psi _h^n\) is known, compute \(\mathbf {p}_h^n, \psi _h^{n+1/2}\) and \(\psi _h^{n+1}\) as follows:
with \(1\le \omega \le \omega _{\max } < 2\).
6.5 Finite Element Approximation of the Local Nonlinear Problems
The finite dimensional minimization problems, discrete analogues of (9), are approximated, at each grid point \(P_k\in {\varSigma }_{0h}\), by:
The methods discussed in Sect. 4 still apply.
6.6 Finite Element Approximation of the Linear Variational Problems
The variational problems arising in the discrete version of the relaxation algorithm can be solved similarly as in the continuous case using a conjugate gradient algorithm. Let us point out however a particularity that arises in the discrete case. The discrete version of (16) reads as follows: find \(\psi _h^{n+1/2} \in V_{gh}\) satisfying:
The linear problem (36) leads to excessive computer resource requirements, which could be acceptable for two-dimensional problems, but become prohibitive for three dimensional ones. (Indeed, to derive the linear system equivalent to (36), we need to compute-via the solution of (30)-the matrix-valued functions \({\mathbf {D}}_h^2w^j\), where the functions \(w^j\) form a basis of \(V_{0h}\).) To avoid this difficulty, we are going to employ, as previously discussed in [9], an adjoint equation approach (see, e,g., [26]) to derive an equivalent formulation of (36), well-suited to a solution by a conjugate gradient algorithm. This adjoint approach reads as
where \(\left\langle \frac{\partial J_h}{\partial \varphi } (\varphi , \mathbf {q}), \theta \right\rangle \) denotes the action of the partial derivative \(\frac{\partial J_h}{\partial \varphi } (\varphi , \mathbf {q})\) on the test function \(\theta \). In order to solve (37), we first determine \(D_{hij}^2 \varphi \) via (30). Then, we find \(\lambda _{hij} \in V_{0h}\), \(1\le i , j \le 3\), by solving the (adjoint) systems:
and we can show (see, e.g., [26]) that, for all \((\varphi _h,\mathbf {p}_h) \in V_{gh} \times \mathbf {Q}_h\):
This last relation can be used directly in the conjugate gradient algorithm (18)–(27), to solve (19) and (21). For instance, the discrete equivalent of (21) consists in finding \(\bar{g}_h^k \in V_{0h}\) such that (with obvious notation):
7 Numerical Results
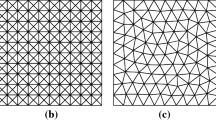
The first numerical results we are going to report, in order to validate our methodology, are associated with the unit cube \({\varOmega }= (0,1)^3\). Two types of partitions of the unit cube are considered, in order to study the mesh-dependence of our methods. These partitions have been constructed by using either advancing front 3D procedures, or successive extrusions [20], and are visualized in Fig. 1. All experiments were performed on a desktop computer with Intel\(^{\tiny {\textregistered }}\) Xeon(R) CPU E5-1650 v3 @ 3.50 GHz \(\times \) 12.
In the numerical examples presented hereafter, we consider \(C=0\) for the structured mesh (i.e. no Tychonoff regularization) and \(C=1\) for the isotropic mesh. The local nonlinear problems are solved with a stopping criterion of \(\varepsilon _{\mathrm{Newton}}=10^{-9}\) on the residual for the Newton method, with a maximal number of iterations equal to 1000. When using the Runge–Kutta method for the dynamical flow approach, the time step is set to \({\varDelta }t = 0.1\), and is reduced only if needed (only for the first 2–3 times steps usually); the maximal number of iterations is 20,000 and the stopping criterion is \(\varepsilon =10^{-7}\) on two successive iterates.
Unless otherwise specified, the relaxation parameter is set to \(\omega =1\) at the beginning of the outer iterations, and gradually increased to 2 to speed up convergence. The conjugate gradient algorithm for the solution of the variational problems has a stopping criterion of \(\varepsilon =10^{-8}\) on successive iterates, with a maximal number of iterations equal to 100. Actually, numerical experiments show that the number of conjugate gradient iterations is never larger than 35. The outer relaxation algorithm has a stopping criterion of \(\varepsilon =5\times 10^{-4}\) on the residual \(\left| \left| \left| {\mathbf {D}}^2_h\psi _h^{n}-\mathbf {p}_h^n \right| \right| \right| _{0h}\), or on successive iterates if the problem does not admit a classical solution (see Sect. 7.3), with a maximal number of iterations equal to 5000.
7.1 Polynomial Examples
Let us consider a first example involving a smooth, “reasonably” isotropic, exact solution. More precisely, let us consider as exact solution
By a direct calculation, one obtains \(\lambda _1 = 1, \lambda _2 = 5, \lambda _3 = 15\), and, therefore the data for the Monge–Ampère problem correspond to
Figure 2 visualizes the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) computed approximation errors obtained by using both approaches for the solution of the local nonlinear problems (Newton stands for the reduced Newton approach presented in Sect. 4.2, while RK stands for the dynamical flow approach presented in Sect. 4.3). Both Newton and Runge–Kutta algorithms provide exactly the same results. For the structured mesh, the method is globally second-order, resp. first-order, convergent for the \(L^2\) (resp. \(H^1\)) norm of the approximation error. Table 1 confirms those convergence results, for both structured and isotropic meshes and for the approach based on the Runge–Kutta approximation for the dynamical flow problem in \({\mathbb {R}}^{11}\). We observe that, for the structured meshes, we have text-book second and first order convergence, while the orders of convergence deteriorate for the isotropic unstructured meshes.
Table 2 provides CPU times versus the number of degrees of freedom involved in the numerical approximation. Comparing mainly with [8, 34] (who also performed CPU times investigations), this test case is more stringent since the eigenvalues of the Hessian are not close from each other, which makes the problem less isotropic than examples used in the literature (typically the example presented in Sect. 7.2).
The second test problem that we consider still has a polynomial exact solution, but this solution is much more anisotropic than the one in (38), since it is given by
Here \(\lambda _1 = 1, \lambda _2 = 10, \lambda _3 = 100\), and the data for the Monge–Ampère problem are given by \(f(x,y) = \displaystyle 1000\) and \(g(x,y,z) =\frac{1}{2}(x^2+10y^2+100z^2)\). This time, the initialisation (4) of the relaxation algorithm is not close to the solution, implying, as expected, that more iterations are needed to achieve convergence. Figure 3 illustrates the convergence orders for the computed approximation error for both types of meshes. Despite the anisotropy of the solution of this second test problem, the approximation errors are similar to those associated with the first test problem, that is perfect second and first orders with the structured meshes and slightly lower convergence orders for the anisotropic unstructured meshes. Note that here we have to choose \(\omega =0.5\) initially (under-relaxation), and increase it gradually to 2, to ensure convergence of the relaxation algorithm, and \(C=2.5\) for the isotropic mesh.
The least-squares approach never enforces directly the solution \(\psi \) to be convex. However, it enforces explicitly the additional matrix-valued variable \(\mathbf {p}\) to be symmetric positive definite. It is thus remarkable that the positive definiteness property of \(\mathbf {p}\) translates automatically to the Hessian of the main variable \(\psi \). More precisely, when the Monge–Ampère problem has a smooth classical solution, the converged iterate satisfy \({\mathbf {D}}^2 \psi = \mathbf {p}\), and thus the convexity of \(\psi \) is automatically verified. For this test problem, and for both types of meshes, \({\mathbf {D}}^2 \psi \) is indeed symmetric positive definite for all grid points.
7.2 A Smooth Exponential Example
The third test problem we consider has a smooth exponential exact solution, namely the radial function \(\psi \) defined by
This test problem generalizes to three dimensions a two-dimensional one commonly used in the community for Monge–Ampère solver benchmarking (see, e.g., [9, 16]). Let us denote \(\sqrt{x^2 + y^2 + z^2 }\) by r. Taking advantage of the fact that, if \(\phi \) is a radial function, one has (with obvious notation) \(\det {\mathbf {D}}^2 \phi = \phi '' (\phi '/r)^2\), the data for the Monge–Ampère–Dirichlet problem (1) associated with the above function \(\psi \) are \(f(x,y,z) = (1+r^2)e^{3r^2/2}\), and \(g(x,y,z) = e^{r^2/2}\). The stopping criterion for the relaxation algorithm is \(\left| \left| \left| {\mathbf {D}}^2_h\psi _h^{n}-\mathbf {p}_h^n \right| \right| \right| _{0h} < 5 \times 10^{-4}\), and \(C=1\) for the isotropic unstructured mesh (as for the first test problem).
Figure 4 visualizes the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) computed approximation errors for both approaches for the solution of the local nonlinear problems. The conclusions are similar: both Newton and Runge–Kutta methods provide exactly the same results, and the method is globally second-order convergent for the \(L^2\) norm. Table 3 confirms these convergence results, showing in particular no loss of convergence orders for the unstructured isotropic mesh.
Table 4 provides CPU times versus the number of degrees of freedom involved in the numerical approximation for both structured and unstructured discretizations of the unit cube. When using a structured mesh of the unit cube, the performance of the algorithm is comparable to the other algorithms from the literature, albeit slightly less efficient. Using an unstructured isotropic mesh degrades the performance of the algorithm; computational performance for the algebraic part is identical, the difference solely coming from the increased number of conjugate gradient iterations. Note that, for this test case, the Hessian matrix \({\mathbf {D}}^2 \psi \) admits the eigenvalues \(\lambda _1 = e^{r^2/2}\), \(\lambda _2 = e^{r^2/2}\) and \(\lambda _3 = (1+r^2)e^{r^2/2}\). This example is thus rather isotropic (the eigenvalues of the Hessian are close to each other).
7.3 Non-smooth Test Problems
Some of the test problems we are going to consider in this section do not have exact solution with the \(H^2({\varOmega })\)-regularity or may have no solution at all (but may have generalized solutions). These non-smooth problems are therefore ideally suited to test the robustness of our methodology, and its ability at capturing generalized solutions when no exact solution does exist.
With \({\varOmega }\) still being the unit cube \((0,1)^3\), the first problem that we consider is the particular case of problem (1) which has the convex function \(\psi \) defined, for \(R \ge \sqrt{3}\), by
When \(R > \sqrt{3}\), this function \(\psi \) belongs to \(C^{\infty }(\bar{{\varOmega }})\), while \(\psi \in C^0(\bar{{\varOmega }}) \cap W^{1,s} ({\varOmega })\), with \(1\le s < 2\), if \(R = \sqrt{3}\). It is therefore interesting to see how our methodology can handle the possible non-smoothness of the particular problem (1) associated with f and g defined by \(f(x,y,z) = \displaystyle \frac{R^2}{(R^2-r^2)^{5/2}}\) and \(g(x,y,z) = - \sqrt{R^2 - (x^2 + y^2 + z^2)}\), with, as earlier, \(r = \sqrt{x^2 + y^2 + z^2}\). (a simple way to compute f is to use, as before, the relation \(\det {\mathbf {D}}^2 \phi = \phi '' (\phi '/r)^2\) if \(\phi \) is a radial function). Of particular interest will be the behavior of our methodology when \(R \rightarrow \sqrt{3}\) from above (or even when \(R=\sqrt{3}\)).
On Tables 5 and 6, we have reported, for \(R = \sqrt{6}\) and \(R=\sqrt{3}\), computed approximation errors and orders of convergence as h varies, together with the number of iterations necessary to achieve convergence of the relaxation algorithm. For \(R=\sqrt{6}\), the convergence orders of the approximation errors are the ones we expect, namely second order (resp., first order) for the \(L^2\)-norm (resp., \(H^1\)-norm), the number of iterations being pretty low. The case \(R=\sqrt{3}\) is more interesting; indeed despite the solution singularity at point (1, 1, 1), the \(L^2({\varOmega })\)-norm of the computed approximation error \(\psi _h - \psi \) still decreases super-linearly with respect to h (for both mesh families), while the related \(H^1({\varOmega })\)-norm stays stable around 0.62 for the same values of h.
Visualization of the numerical solution \(\psi _h\) for \(f(x,y,z) = 1\), \(g(x,y,z) = 0\) on the unit cube; top left: along cuts for \(x=1/2\) and \(y=1/2\) (\(h \simeq 0.0625\)); top right: number of iterations needed for the convergence of the relaxation method for the stopping criterion \(\left| \left| \psi _h^{n+1} - \psi _h^n \right| \right| _{0,h} < 10^{-5}\); bottom left: graphs of the computed solutions restricted to the line \(y = z = 1/2\); bottom right: graphs of the computed solutions restricted to the lines \(x = y\), \(z =1/2\)
To conclude this section, we will consider the particular problem (1) associated with \({\varOmega }= (0,1)^3\), \(f=1\) and \(g = 0\). For these particular data, problem (1) has no smooth solution (the arguments developed in [9, 23] for the related two-dimensional problem still apply here).
Figure 5 shows different features of the approximated solution inside the unit cube. The stopping criterion for this particular case without a classical solution is \(\left| \left| \psi _h^{n+1} - \psi _h^n \right| \right| _{0,h} < 10^{-5}\). When studying the number of outer iterations of the relaxation algorithm, we observe that the number of iterations is larger for structured meshes than isotropic ones, and that it increases as expected when \(h\rightarrow 0\). Figure 5 (bottom row) visualizes graphs of the computed solutions restricted to the lines \(y=z=1/2\) and \(x=y, z=1/2\) for \(x\in (0,1)\), and shows little influence of the type of partition on the solution.
We can also observe that \({\mathbf {D}}^2 \psi \) is symmetric positive definite for 100% of the grid points, independently of the nature of the discretization when \(h \simeq 0.04\), even though the Monge–Ampère equations does not have a classical solution, that is \({\mathbf {D}}^2 \psi \ne \mathbf {p}\). The (necessary) loss of convexity of the solution is thus located (near the corners) in a region smaller than the mesh size. When arbitrarily refining the mesh in a corner of the domain, we observe that the Hessian \({\mathbf {D}}^2 \psi \) is not symmetric positive definite when evaluated in some grid points in a neighborhood of size \(10^{-3}\) around that corner. This effect is highlighted when calculating \(\left| \left| {\mathbf {D}}^2 \psi _h - \mathbf {p}_h \right| \right| _{L^2}\), using a structured mesh of the unit cube, both on \({\varOmega }\), but also on \({\varOmega }' \subset {\varOmega }\), as illustrated in Table 7 for \({\varOmega }' = (0.2,0.8)^3\). These results show that the error inside the domain \({\varOmega }' = (0.2 , 0.8)^3\) is significantly smaller than the error on \({\varOmega }\), implying that the error is mainly committed near the boundary.
7.4 Curved Boundaries and Non Convex Domains
In order to further validate the robustness and flexibility of our methodology, we are going to consider test problems where \({\varOmega }\) has a curved boundary and/or is non-convex. The first domain with a curved boundary we consider is the unit ball \(B_1 = \left\{ (x,y,z) \in {\mathbb {R}}^3 , x^2 + y^2 + z^2 < 1 \right\} \). Assuming that \({\varOmega }= B_1\), \(f= \frac{1}{3\sqrt{3}}\) and \(g = 0\), the unique convex solution \(\psi \) of the related Monge–Ampère–Dirichlet problem (1) is given by
On Fig. 6 (left) we have visualized a typical finite element mesh used for computation and some cuts of the computed solution. On Fig. 6 (right) and Table 8 we have provided information on the \(L^2({\varOmega })\) and \(H^1({\varOmega })\)-norms of the approximation error \(\psi _h - \psi \) and of the related rates of convergence, and on the number of relaxation iterations necessary to achieve convergence. Albeit the \(L^2({\varOmega })\)-approximation error is \(\mathcal {O}(h^{1.8})\), approximately, these numerical results show that our methodology can handle rather accurately domains \({\varOmega }\) with curved boundaries. Table 9 provides CPU times versus the number of degrees of freedom involved in the numerical approximation of the solution on the unit sphere. Results are comparable to those obtained when using unstructured meshes on the unit cube, and thus show that the curved boundaries are handled appropriately.
Left: visualization of the finite element mesh and of computed solution cuts (\(h \simeq 0.1610\)). Right: visualization of the variations with respect to h of the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) norms of the computed approximation error \(\psi _h - \psi \), with \(\psi (x,y,z) = -\frac{1}{2\sqrt{3}} \left( 1 -{x}^{2}-{y}^{2}-{z}^{2}\right) \) (\({\varOmega }= B_1\))
First row: visualization of the variations with respect to h of the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) norms of the computed approximation error \(\psi _h - \psi \), with \(\psi \) defined by (41), \({\varOmega }\) being the truncated unit ball (left: \(\theta = \pi /2\), right: \(\theta = \pi /9\)). Second row: visualization of the truncated balls (left: \(\theta = \pi /2\), right: \(\theta = \pi /9\)). Third row: visualization of the restrictions of the computed solutions to the plane \(z = 0\) (left: \(\theta = \pi /2\), right: \(\theta = \pi /9\))
The non-convexity of \({\varOmega }\) may prevent problem (1) to have solutions (see, e.g., [11]). However, it makes sense to assess the capabilities of our methodology at handling problems having smooth solutions despite the non-convexity of \({\varOmega }\). To do so, we consider the particular problem (1) where: (i) \({\varOmega }\) is the subset of \(B_1\) obtained by removing from this ball a part of angular size \(\theta \), symmetric about Ox and oriented along the Oz axis (as shown on Fig. 7 for \(\theta = \pi /2\) and \(\theta = \pi /9\)), (ii) \(f=1/(3\sqrt{3})\), g being the restriction to \(\partial {\varOmega }\) of the function \(\psi \) defined by (41). The function \(\psi \) defined by (41) is clearly a convex solution of the above problem (1). The solution methodology discussed in Sects. 3–6 still applies for this case where an exact smooth solution does exist, some of the numerical results we obtained being reported in Fig. 7. We observe in particular that the convergence orders are essentially independent of the value of the re-entrant angle \(\theta \).
8 An Alternative Discretization Method Based on \({\mathbb {Q}}_1\) Finite Elements
We finally report some numerical results that were obtained using \({\mathbb {Q}}_1\) finite elements for the space discretization instead of the \({\mathbb {P}}_1\) finite elements used earlier. The finite element library libmesh [33] has been used for implementation. The discretization of the unit cube \({\varOmega }= (0,1)^3\) is based on a structured mesh of elementary cubes, as visualized in Fig. 8. The least-squares/relaxation methodology is still applicable. The nonlinear problems (9) are solved for each vertex of the hexahedral mesh with the Newton and Runge–Kutta methods discussed in Sects. 4.2 and 4.3, respectively. The variational problem (17) is solved by a conjugate gradient algorithm, using Gauss quadrature rules (of order up to 4) for the numerical computation of integrals; all other techniques and approaches remain the same.
All the numerical results reported below are related to \({\varOmega }= (0,1)^3\). On Table 10 we have reported the variations with respect to h of the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) norms of the computed approximation error \(\psi _h - \psi \), for \(\psi \) defined by \(\psi (x,y,z) =e^{\frac{1}{2}(x^2 + y^2 + z^2)}\) and \(\psi (x,y,z) =\frac{1}{2}\left( x^2+5y^2+15z^2 \right) \), the related convergence orders, and the number of relaxation iterations necessary to achieve convergence. The local optimization problems are solved using the Newton method described in Sect. 4.2. As expected, nearly optimal orders of convergence are obtained for both the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) norms of the computed approximation error. Both solutions exhibit comparable orders of convergence, however, the larger anisotropy of the second one implies a larger number of iterations for the relaxation algorithm to achieve its convergence. Approximation errors and iteration numbers are consistent with those reported in Sect. 7.2 for the same test problems.
The next test problem we consider, is the one, already investigated in Sect. 7.3, whose exact solution \(\psi \) is given by \(\psi (x,y,z) = - \sqrt{R^2 - (x^2 + y^2 + z^2)}\), with \(R\ge \sqrt{3}\), \({\varOmega }\) still being the unit cube \((0,1)^3\). Tables 11 and 12 show that, for \(R = \sqrt{6}\) and \(R = \sqrt{3}\), the \(L^2({\varOmega })\) and \(H^1({\varOmega })\)-norms of the approximation error \(\psi _h - \psi \) are nearly of optimal order; moreover, the above tables show that \(||{\mathbf {D}}^2_h\psi _h^{n}-{\mathbf {D}}^2\psi ||_{L^2({\varOmega })} \simeq \mathcal {O}(h^{3/2})\) if \(R = \sqrt{6}\), while \(||{\mathbf {D}}^2_h\psi _h^{n}-{\mathbf {D}}^2\psi ||_{L^2({\varOmega })} \simeq \mathcal {O}(1)\) if \(R = \sqrt{3}\).
The numerical results we have just reported show that, as long as accuracy and number of iterations are concerned, \({\mathbb {Q}}_1\) based finite element approximations of problem (1) compared well with \({\mathbb {P}}_1\) based ones if \({\varOmega }\) is a cube and uniform structured partitions of \({\varOmega }\) are used to define the finite element spaces. However the \({\mathbb {P}}_1\) based methods can easily handle domains \({\varOmega }\) of arbitrary shapes and unstructured finite element partitions, properties that the \({\mathbb {Q}}_1\) based methods do not share.
9 Further Comments and Conclusions
In this article, we have discussed a least-squares/relaxation/mixed finite element methodology for the numerical solution of the Dirichlet problem for the three-dimensional elliptic Monge–Ampère equation \(\det {\mathbf {D}}^2 \psi = f (>0)\) in \({\varOmega }\). The results reported in Sects. 7 and 8 show the robustness and flexibility of this methodology and its ability at approximating smooth convex solutions (if such solutions do exist) with nearly optimal orders of accuracy for the \(L^2({\varOmega })\) and \(H^1({\varOmega })\) norms of the approximation error \(\psi _h - \psi \). To the best of our knowledge, the above methodology is one of the very few which can solve, with nearly optimal orders of accuracy, the three-dimensional Monge–Ampère equation on domains \({\varOmega }\) with curved boundaries using \({\mathbb {P}}_1\) based finite element approximations.
References
Aleksandrov, A.D.: Uniqueness conditions and estimates for the solution of the Dirichlet problem. Am. Math. Soc. Trans. 68, 89–119 (1968)
Aubin, T.: Some Nonlinear Problems in Riemannian Geometry. Springer, Berlin (1998)
Awanou, G., Li, H.: Error analysis of a mixed finite element method for the Monge–Ampère equation. Int. J. Numer. Anal. Model. 11(4), 745–761 (2014)
Benamou, J.D., Froese, B.D., Oberman, A.M.: Two numerical methods for the elliptic Monge–Ampère equation. ESAIM Math. Model. Numer. Anal. 44(4), 737–758 (2010)
Benamou, J.D., Froese, B.D., Oberman, A.M.: Numerical solution of the optimal transportation problem using the Monge–Ampère equation. J. Comput. Phys. 49(4), 107–126 (2014)
Boehmer, K.: On finite element methods for fully nonlinear elliptic equations of second order. SIAM J. Numer. Anal. 46(3), 1212–1249 (2008)
Botsaris, C.A.: A class of methods for unconstrained minimization based on stable numerical integration techniques. J. Math. Anal. Appl. 63(3), 729–749 (1978)
Brenner, S.C., Neilan, M.: Finite element approximations of the three dimensional Monge–Ampère equation. ESAIM Math. Model. Numer. Anal. 46(5), 979–1001 (2012)
Caboussat, A., Glowinski, R., Sorensen, D.C.: A least-squares method for the numerical solution of the Dirichlet problem for the elliptic Monge–Ampère equation in dimension two. ESAIM Control Optim. Calculus Var. 19(3), 780–810 (2013)
Caffarelli, L., Nirenberg, L., Spruck, J.: The Dirichlet problem for nonlinear second-order elliptic equations I. Monge–Ampère equation. Commun. Pure Appl. Math. 37, 369–402 (2014)
Caffarelli, L.A., Cabré, X.: Fully Nonlinear Elliptic Equations. American Mathematical Society, Providence (1995)
Dean, E.J., Glowinski, R.: On the numerical solution of the elliptic Monge–Ampère equation in dimension two: a least-square approach. In: Glowinski, R., Neittaanmäki, P. (eds.) Partial Differ. Equ. Model. Numer. Simul. Comput. Methods Appl. Sci., vol. 16, pp. 43–63. Springer, Berlin (2008)
Engquist, B., Froese, B.D., Yang, Y.: Optimal transport for seismic full waveform inversion. Commun. Math. Sci. 14(8), 2309–2330 (2016)
Feng, X., Neilan, M.: Error analysis for mixed finite element approximations of the fully nonlinear Monge–Ampère equation based on the vanishing moment method. SIAM J. Numer. Anal. 47(2), 1226–1250 (2009)
Feng, X., Neilan, M.: A modified characteristic finite element method for a fully nonlinear formulation of the semigeostrophic flow equations. SIAM J. Numer. Anal. 47(4), 2952–2981 (2009)
Feng, X., Neilan, M.: Vanishing moment method and moment solutions of second order fully nonlinear partial differential equations. J. Sci. Comput. 38(1), 74–98 (2009)
Feng, X., Neilan, M., Glowinski, R.: Recent developments in numerical methods for fully nonlinear 2nd order PDEs. SIAM Rev. 55, 1–64 (2013)
Feng, X., Neilan, M., Prohl, A.: Error analysis of finite element approximations of the inverse mean curvature flow arising from the general relativity. Numer. Math. 108, 93–119 (2007)
Froese, B.D., Oberman, A.M.: Convergent filtered schemes for the Monge–Ampère partial differential equation. SIAM J. Numer. Anal. 51(1), 423–444 (2013)
Geuzaine, C., Remacle, J.F.: Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 79(11), 1309–1331 (2009)
Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations. Springer, New York (1983)
Glowinski, R.: Finite element method for incompressible viscous flow. In: Ciarlet, P.G., Lions, J.L. (eds.) Handbook of Numerical Analysis, vol. IX, pp. 3–1176. Elsevier, Amsterdam (2003)
Glowinski, R.: Numerical Methods for Nonlinear Variational Problems, 2nd edn. Springer, New York (2008)
Glowinski, R.: Numerical methods for fully nonlinear elliptic equations. In: Proceedings of the International Congress on Industrial and Applied Mathematics, 16–20 July 2007, Zürich. EMS Publishing House (2009)
Glowinski, R.: Variational Methods for the Numerical Solution of Nonlinear Elliptic Problem. CBMS-NSF Regional Conference Series in Applied Mathematics. Society for Industrial and Applied Mathematics, Philadelphia (2015)
Glowinski, R., Lions, J.L., He, J.W.: Exact and Approximate Controllability for Distributed Parameter Systems: A Numerical Approach. Encyclopedia of Mathematics and Its Applications. Cambridge University Press, Cambridge (2008)
Glowinski, R., Lueng, T., Liu, H., Qian, J.: A novel method for the numerical solution of the Monge–Ampère equation. Private communication (2017)
Glowinski, R., Sorensen, D.C.: A quadratically constrained minimization problem arising from PDE of Monge–Ampère type. Numer. Algorithms 53(1), 53–66 (2009)
Gutiérrez, C.E.: The Monge–Ampère Equation. Birkhaüser, Boston (2001)
Hairer, E., Norsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I. Nonstiff Problems, Springer Series in Computational Mathematics, vol. 8. Springer, Berlin (1993)
Ishii, H., Lions, P.L.: Viscosity solutions of fully nonlinear second-order elliptic partial differential equations. J. Differ. Equ. 83(1), 26–78 (1990)
Kelley, C.: Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics, Philadelphia (1995)
Kirk, B.S., Peterson, J.W., Stogner, R.H., Carey, G.F.: libMesh: a C++ library for parallel adaptive mesh refinement/coarsening simulations. Eng. Comput. 22(3–4), 237–254 (2006)
Liu, J., Froese, B.D., Oberman, A.M., Xiao, M.: A multigrid scheme for 3D Monge–Ampère equations. Int. J. Comput. Math. 94(9), 1850–1866 (2017)
Nochetto, R.H., Ntogkas, D., Zhang, W.: Two-scale method for the Monge–Ampère equation: convergence to the viscosity solution. arXiv:1706.06193 (2017)
Nochetto, R.H., Ntogkas, D., Zhang, W.: Two-scale method for the Monge–Ampère equation: pointwise error estimates. ArXiv:1706.09113 (2017)
Oberman, A.: The convex envelope is the solution of a nonlinear obstacle problem. Proc. Am. Math. Soc. 135, 1689–1694 (2007)
Oberman, A.: Wide stencil finite difference schemes for the elliptic Monge–Ampère equations and functions of the eigenvalues of the Hessian. Discrete Continuous Dyn. Syst. B 10(1), 221–238 (2008)
Oliker, V.I., Prussner, L.D.: On the numerical solution of the equation \(z_{xx} z_{yy} - z_{xy}^2 = f\) and its discretization. I. Numer. Math. 54, 271–293 (1988)
Picasso, M., Alauzet, F., Borouchaki, H., George, P.L.: A numerical study of some hessian recovery techniques on isotropic and anisotropic meshes. SIAM J. Sci. Comput. 33, 1058–1076 (2011)
Stojanovic, S.: Optimal momentum hedging via Monge–Ampère PDEs and a new paradigm for pricing options. SIAM J. Control Optim. 43, 1151–1173 (2004)
Tapia, R.A., Dennis, J.E., Schaefermeyer, J.P.: Inverse, shifted inverse, and Rayleigh quotient iteration as Newton’s method. SIAM Rev. 60(1), 3–55 (2018)
Tychonoff, A.N.: The regularization of incorrectly posed problems. Dokl. Akad. Nauk. SSSR 153, 42–52 (1963)
Acknowledgements
The authors thank Prof. Marco Picasso (EPFL), the participants of the SCPDE 2017 conference (Hong Kong, June 5–8, 2017) for fruitful discussions, and the anonymous referees for their constructive comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has been supported by the Swiss National Science Foundation (Grant SNF 165785), and the US National Science Foundation (Grant NSF DMS-0913982).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Caboussat, A., Glowinski, R. & Gourzoulidis, D. A Least-Squares/Relaxation Method for the Numerical Solution of the Three-Dimensional Elliptic Monge–Ampère Equation. J Sci Comput 77, 53–78 (2018). https://doi.org/10.1007/s10915-018-0698-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0698-6
Keywords
- Monge–Ampère equation
- Least-squares method
- Nonlinear constrained minimization
- Newton methods
- Mixed finite element method