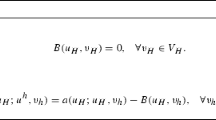Abstract
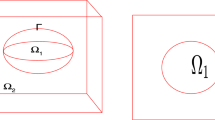
New hybridized discontinuous Galerkin (HDG) methods for the interface problem for elliptic equations are proposed. Unknown functions of our schemes are \(u_h\) in elements and \(\hat{u}_h\) on inter-element edges. That is, we formulate our schemes without introducing the flux variable. We assume that subdomains \(\Omega _1\) and \(\Omega _2\) are polyhedral domains and that the interface \(\Gamma =\partial \Omega _1\cap \partial \Omega _2\) is polyhedral surface or polygon. Moreover, \(\Gamma \) is assumed to be expressed as the union of edges of some elements. We deal with the case where the interface is transversely connected with the boundary of the whole domain \(\overline{\Omega }=\overline{\Omega _1\cap \Omega _2}\). Consequently, the solution u of the interface problem may not have a sufficient regularity, say \(u\in H^2(\Omega )\) or \(u|_{\Omega _1}\in H^2(\Omega _1)\), \(u|_{\Omega _2}\in H^2(\Omega _2)\). We succeed in deriving optimal order error estimates in an HDG norm and the \(L^2\) norm under low regularity assumptions of solutions, say \(u|_{\Omega _1}\in H^{1+s}(\Omega _1)\) and \(u|_{\Omega _2}\in H^{1+s}(\Omega _2)\) for some \(s\in (1/2,1]\), where \(H^{1+s}\) denotes the fractional order Sobolev space. Numerical examples to validate our results are also presented.



Similar content being viewed by others
References
Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2002)
Bernardi, C., Verfürth, R.: Adaptive finite element methods for elliptic equations with non-smooth coefficients. Numer. Math. 85(4), 579–608 (2000)
Bramble, J.H., King, J.T.: A finite element method for interface problems in domains with smooth boundaries and interfaces. Adv. Comput. Math. 6(2), 109–138 (1997), 1996
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15, 3rd edn. Springer, New York (2008)
Cai, Z., Ye, X., Zhang, S.: Discontinuous Galerkin finite element methods for interface problems: a priori and a posteriori error estimations. SIAM J. Numer. Anal. 49(5), 1761–1787 (2011)
Chen, Z., Zou, J.: Finite element methods and their convergence for elliptic and parabolic interface problems. Numer. Math. 79(2), 175–202 (1998)
Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)
Feistauer, M.: On the finite element approximation of functions with noninteger derivatives. Numer. Funct. Anal. Optim. 10(1–2), 91–110 (1989)
Grapperhaus, M.J., Kushner, M.J.: A semianalytic radio frequency sheath model integrated into a two-dimensional hybrid model for plasma processing reactors. J. Appl. Phys. 81(2), 569–577 (1997)
Grisvard.: Behavior of the solutions of an elliptic boundary value problem in a polygonal or polyhedral domain. In: Numerical Solution of P.D.E’s III, Proc. Third Sympos. (SYNSPADE), pp. 207–274 (1976)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Pitman (Advanced Publishing Program), Boston (1985)
Huynh, L.N.T., Nguyen, N.C., Peraire, J., Khoo, B.C.: A high-order hybridizable discontinuous Galerkin method for elliptic interface problems. Int. J. Numer. Methods Eng. 93(2), 183–200 (2013)
Jonsson, A., Wallin, H.: Function spaces on subsets of \(R^n\). Math. Rep. 2(1), xiv+221 (1984)
Kikuchi, F., Ando, Y.: A new variational functional for the finite-element method and its application to plate and shell problems. Nucl. Eng. Des. 21, 95–113 (1972)
Kikuchi, F., Ando, Y.: Some finite element solutions for plate bending problems by simplified hybrid displacement method. Nucl. Eng. Des. 23, 155–178 (1972)
Lions, J.L., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications (Translated from the French by Kenneth, P., Die Grundlehren der mathematischen Wissenschaften, Band 181), vol. I. Springer, New York-Heidelberg (1972)
Massjung, R.: An unfitted discontinuous Galerkin method applied to elliptic interface problems. SIAM J. Numer. Anal. 50(6), 3134–3162 (2012)
Miyashita, M.: Discontinuous model with semi analytical sheath interface for radio frequency plasma. In: The 69th Annual Gaseous Electronics Conference, Session MW6-00077, vol. 61 (2016)
Mu, L., Wang, J., Wei, G., Ye, X., Zhao, S.: Weak Galerkin methods for second order elliptic interface problems. J. Comput. Phys. 250, 106–125 (2013)
Oikawa, I.: Hybridized discontinuous Galerkin method with lifting operator. JSIAM Lett. 2, 99–102 (2010)
Oikawa, I., Kikuchi, F.: Discontinuous Galerkin FEM of hybrid type. JSIAM Lett. 2, 49–52 (2010)
Petzoldt, M.: Regularity results for Laplace interface problems in two dimensions. Z. Anal. Anwendungen 20(2), 431–455 (2001)
Petzoldt, M.: A posteriori error estimators for elliptic equations with discontinuous coefficients. Adv. Comput. Math. 16(1), 47–75 (2002)
Saito, N., Fujita, H.: Remarks on traces of \(H^1\)-functions defined in a domain with corners. J. Math. Sci. Univ. Tokyo 7, 325–345 (2000)
Acknowledgements
We thank the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper. NS is supported by JST CREST Grant Number JPMJCR15D1, Japan and JSPS KAKENHI Grant Numbers 15H03635, 15K13454 Japan.
Author information
Authors and Affiliations
Corresponding author
Proof of Lemma 9
Proof of Lemma 9
Let \(s\in (1/2,1)\). Let \(K\in \mathcal {T}_h\) and \(e\subset \partial K\).
The fractional order Sobolev space \(H^s(K)\) is defined as
where
It suffices to prove
since the desired inequality (20) is a direct consequence of (27).
Suppose that \(\tilde{K}\) is the reference element in \(\mathbb {R}^d\) with \({\text {diam}}(\tilde{K})=1\). Moreover, let \(\tilde{e}\subset \partial \tilde{K}\) be a face (\(d=3\))/edge (\(d=2\)) of \(\tilde{K}\). Trace theorem implies
where \(\tilde{C}\) denotes an absolute positive constant. See [13, Theorem 1, §V.1.1] for example.
Suppose that \(\Phi (\xi )=B\xi +c\), \(B\in \mathbb {R}^{d\times d}\), \(c\in \mathbb {R}^d\), is the affine mapping which maps \(\tilde{K}\) onto K; \(K=\Phi (\tilde{K})\). We know
where \(\tilde{h}={h}_{\tilde{K}}\), \(\tilde{\rho }={\rho }_{\tilde{K}}\) and \({\text {meas}}_d(K)\) denotes the \(\mathbb {R}^d\)-Lebesgue measure of K. Moreover,
We recall that there exists a positive constant \(\nu _2\) that independent of h such that \(h_K/\rho _K\le \nu _2\) (\(\forall K\in \forall \mathcal {T}_h\in \{\mathcal {T}_h\}_h\)) by the shape-regularity of the family of triangulations.
Now we can state the proof of (27). By the density, it suffices to consider (27) for \(v\in C^1(K)\). Set \(\tilde{v}=v\circ \Phi \in C^1(\tilde{K})\). Then,
and
Using those inequalities, we have
which completes the proof.
Rights and permissions
About this article
Cite this article
Miyashita, M., Saito, N. Hybridized Discontinuous Galerkin Method for Elliptic Interface Problems: Error Estimates Under Low Regularity Assumptions of Solutions. J Sci Comput 76, 1657–1673 (2018). https://doi.org/10.1007/s10915-018-0678-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0678-x
Keywords
- Discontinuous Galerkin method
- Elliptic interface problems
- Error estimate
- Fractional order Sobolev space