A Lagrangian Scheme for the Solution of Nonlinear Diffusion Equations Using Moving Simplex Meshes

Abstract

A Lagrangian numerical scheme for solving nonlinear degenerate Fokker–Planck equations in space dimensions $d\ge 2$ is presented. It applies to a large class of nonlinear diffusion equations, whose dynamics are driven by internal energies and given external potentials, e.g. the porous medium equation and the fast diffusion equation. The key ingredient in our approach is the gradient flow structure of the dynamics. For discretization of the Lagrangian map, we use a finite subspace of linear maps in space and a variational form of the implicit Euler method in time. Thanks to that time discretisation, the fully discrete solution inherits energy estimates from the original gradient flow, and these lead to weak compactness of the trajectories in the continuous limit. Consistency is analyzed in the planar situation, $d=2$. A variety of numerical experiments for the porous medium equation indicates that the scheme is well-adapted to track the growth of the solution’s support.

Introduction

Nonlinear Fokker–Planck Equations

We study a variational Lagrangian discretization of the following type of initial value problem:

$$\begin{aligned} \partial _{t} \rho&= \Delta P(\rho ) + \nabla \cdot (\rho \,\nabla V)&\text {on } {\mathbb {R}}_{>0}\times {\mathbb {R}}^d, \end{aligned}$$

(1.1a)

$$\begin{aligned} \rho (\cdot ,0)&= \rho ^0&\text {on }{\mathbb {R}}^d. \end{aligned}$$

(1.1b)

This problem is posed for the time-dependent probability density function $\rho :{\mathbb {R}}_{\ge 0}\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}_{\ge 0}$, with a given initial density $\rho ^0$. We assume that the pressure $P :{\mathbb {R}}_{\ge 0}\rightarrow {\mathbb {R}}_{\ge 0}$ can be written in the form

$$\begin{aligned} P(r) = rh'(r)-h(r) \quad \text {for all }r \ge 0, \end{aligned}$$

(1.2)

for some non-negative and convex $h \in C^1({\mathbb {R}}_{\ge 0})\cap C^\infty ({\mathbb {R}}_{>0})$, and that $V\in C^2({\mathbb {R}}^d)$ is a non-negative potential without loss of generality. Problem (1.1) encompasses a large class of diffusion equations, such as—for power-type nonlinearities $P(r)=r^m$ and vanishing potential $V\equiv 0$—the heat equation ($m=1$), porous medium equations ($m>1$) and fast diffusion equations ($m<1$). By a slight abuse of notation, we refer to (1.1) with more general P and non-vanishing V as nonlinear Fokker–Planck equations. In this paper, we assume a degenerate diffusion, that is $h(0)=h'(0)=0$, and a confining potential, that is V is convex, not necessarily strict. For technical reasons, we further need to assume that

$$\begin{aligned} \lim _{s\rightarrow \infty }sh''(s)=+\infty . \end{aligned}$$

(1.3)

Since our particular spatio-temporal discretization of the initial value problem (1.1) is based on the Lagrangian representation of its dynamics, and on its variational formulation, we briefly recall both of them now.

Lagrangian Formulation

Equation (1.1) can be written as a transport equation,

$$\begin{aligned} \partial _t\rho + \nabla \cdot \big (\rho \,\mathbf {v}[\rho ]\big ) = 0, \end{aligned}$$

(1.4a)

with a velocity field $\mathbf {v}$ that depends on the solution $\rho$ itself,

$$\begin{aligned} \mathbf {v}[\rho ] = -\nabla \big (h' (\rho )+V\big ). \end{aligned}$$

(1.4b)

Various further evolution equations can be written in the form (1.4a), such as non-local aggregation equations (see, e.g., Ambrosio et al. [1]); Keller–Segel type models (see, e.g., Blanchet et al. [5]); and also fourth order thin film equations (see, e.g., Otto [34]) or quantum equations (see, e.g., Gianazza et al. [21]). To simplify the presentation, we stick to equations of nonlinear Fokker–Planck type (1.1a).

The system (1.4) naturally induces a Lagrangian representation of the dynamics, which can be summarized as follows. Below, the reference density ${\overline{\rho }}$ is a probability density supported on some compact set $K\subset {\mathbb {R}}^d$, and we use the notation $G_\#{\overline{\rho }}$ for the push-forward of ${\overline{\rho }}$ under a map $G :K\rightarrow {\mathbb {R}}^d$; the definition is recalled in (2.1).

Lemma 1.1

Assume that $\rho :[0,T]\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}_{\ge 0}$ is a smooth positive solution of (1.1). Let $G^0 :K\rightarrow {\mathbb {R}}^d$ be a given map such that $G^0_\#{\overline{\rho }}=\rho ^0$. Further, let $G :[0,T]\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$ be the flow map associated to (1.4b), satisfying

$$\begin{aligned} \partial _tG_t = \mathbf {v}[\rho _t]\circ G_t, \quad G(0,\cdot )=G^0, \end{aligned}$$

(1.5)

where $\rho _t:=\rho (t,\cdot )$ and $G_t:=G(t,\cdot ) :{\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$. Then, at any $t\in [0,T]$,

$$\begin{aligned} \rho _t = (G_t)_{\#} {\overline{\rho }}. \end{aligned}$$

(1.6)

In short, the solution G to (1.5) is a Lagrangian map for the solution $\rho$ to (1.1). This fact is an immediate consequence of (1.4a); for convenience of the reader, we recall the proof in “Appendix A”. Subsequently, (1.6) can be substituted for $\rho$ in the expression (1.4b) for the velocity, which makes (1.5) an autonomous evolution equation for G:

$$\begin{aligned} \partial _tG_t = -\nabla \left[ h'\left( \frac{{\overline{\rho }}}{\det \mathrm {D}G_t}\right) \right] \circ G_t-\nabla V\circ G_t. \end{aligned}$$

(1.7)

A more explicit form of (1.7) is derived in (5.2).

Variational Structure

It is well-known (see Otto [35] or Ambrosio et al. [1]) that (1.1) is a gradient flow for the relative Renyi entropy functional

$$\begin{aligned} {\mathcal {E}}(\rho ) = \int _{{\mathbb {R}}^d}\big [ h(\rho (x))+V(x)\rho (x)\big ]\,\mathrm {d}x, \end{aligned}$$

(1.8)

with respect to the $L^2$-Wasserstein metric on the space ${\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ of probability densities on ${{\mathbb {R}}^d}$ with finite second moment. It appears to be less well known (see Evans et al. [20], Carrillo and Moll [13], or Carrillo and Lisini [12]) that also (1.7) is a gradient flow, namely for the functional

$$\begin{aligned} {\mathbf {E}}(G|{\overline{\rho }}) := {\mathcal {E}}(G_\#{\overline{\rho }}) = \int _K \left[ \widetilde{h}\left( \frac{\det \mathrm {D}G}{{\overline{\rho }}}\right) + V\circ G\right] {\overline{\rho }}\,\mathrm {d}\omega , \quad \widetilde{h}(s):=s\,h(s^{-1}), \end{aligned}$$

(1.9)

on the Hilbert space $L^2(K\rightarrow {{\mathbb {R}}^d};{\overline{\rho }})$ of square integrable maps from K to ${{\mathbb {R}}^d}$. We shall discuss these gradient flow structures in more detail in Sect. 2 below.

Discretization and Approximation Results

Our discretization in space is based on the Lagrangian formulation. Instead of numerically integrating (1.1a) to obtain the density $\rho$ directly, we approximate the associated Lagrangian maps G that satisfy (1.7): specifically, we assume that a simplicial decomposition ${\mathscr {T}}$ of K is given, and we restrict G to the finite dimensional subspace ${\mathcal {A}}_{\mathscr {T}}$ of continuous maps from K to ${\mathbb {R}}^d$ that are piecewise linear with respect to ${\mathscr {T}}$. A posteriori, we recover an approximation of $\rho$ via (1.6). That ansatz for the Lagrangian maps corresponds to a simple geometric picture: the induced densities are piecewise constant on triangles whose vertices move in time.

For the discretization in time, we exploit the aforementioned variational structure of (1.7): namely, we adopt the celebrated minimizing movement scheme that is known to provide a robust approximation of gradient flows. In the context at hand, this scheme reads as follows: let a time step $\tau >0$ and an initial condition $G_\boxplus ^0\in {\mathcal {A}}_{\mathscr {T}}$ be given. (Here and below, $\boxplus$ symbolizes the space-time mesh generated by ${\mathscr {T}}$ on K and $\tau$ on ${\mathbb {R}}_{>0}$.) Then the nth time iterate $G_\boxplus ^n\in {\mathcal {A}}_{\mathscr {T}}$—that serves as our approximation of $G(n\tau ;\cdot )$—is chosen inductively for $n=1,2,\ldots$ as the minimizer in the respective problem

$$\begin{aligned} \frac{1}{2\tau }\Vert G-G_\boxplus ^n\Vert _{L^2(K\rightarrow {\mathbb {R}}^d;{\overline{\rho }})}^2+{\mathbf {E}}(G|{\overline{\rho }}) \quad \longrightarrow \quad \min , \end{aligned}$$

(1.10)

where the minimization is carried out over the finite dimensional space ${\mathcal {A}}_{\mathscr {T}}$. With the sequence $(G_\boxplus ^n)_{n=0,1,\ldots }$ of approximating Lagrangian maps at hand, we define piecewise-constant-in-time interpolations for the derived density ${\widetilde{\rho }}_\boxplus$ and velocity ${\widetilde{\mathbf {v}}}_\boxplus$ as usual via

$$\begin{aligned} {\widetilde{\rho }}_\boxplus (t) = (G_\boxplus ^n)_{\#}{\overline{\rho }}, \quad {\widetilde{\mathbf {v}}}_\boxplus (t) = \frac{G_\boxplus ^n-G_\boxplus ^{n-1}}{\tau }\quad \text {with }n \text { such that } t\in ((n-1)\tau ,n\tau ]. \end{aligned}$$

Our analytical results on the scheme can be summarized as follows.

• The sequence of fully discrete minimization problems (1.10) is well-posed: see Lemma 3.1. We thus obtain a sequence $(G_\boxplus ^n)_{n=0,1,\ldots }$ for each sufficiently fine discretization $\boxplus$.

• The $G_\boxplus ^n$ are entropy-diminishing and are $\boxplus$-uniformly Hölder continuous: see Lemma 4.1.

• Consequently, the induced densities ${\widetilde{\rho }}_\boxplus$ converge weakly to an absolutely continuous limit trajectory $\rho$, and the fluxes ${\widetilde{\rho }}_\boxplus {\widetilde{\mathbf {v}}}_\boxplus$ converge weakly to a limit of the form $\rho \mathbf {v}$: see Theorem 4.2. The identification of the limit velocity $\mathbf {v}$, however, is only possible under strong additional hypotheses: see Corollary 4.5.

• In $d=2$ dimensions, we prove numerical consistency in the sense that, if G is a smooth solution to (1.7), then its restriction to the mesh $\boxplus$ satisfies the fully discrete Euler–Lagrange equations associated to (1.10), with a quantifiable error that vanishes in a suitable continuous limit: see Theorem 5.2.

• Our previously mentioned consistency results requires that the triangulation ${\mathscr {T}}$ of K is almost ideally hexagonal: see Eq. (5.7). We discuss why consistency cannot be expected if that condition is violated: see Remark 5.4.

Comparison with Results in the Literature

The approach presented in this paper is an alternative to the one developed by Carrillo et al. [13, 15], where G is obtained by directly solving the PDE (1.7) numerically with finite differences or Galerkin approximation via finite element methods. In other words, while Carrillo et al. [13, 15] follows the strategy minimize first then discretize, our present approach is to discretize first then minimize. In the former approach, the minimization (1.10) is performed on the spatially continuous level, yielding Euler–Lagrange equations that are then discretized in space; in the present approach, the space of Lagrangian maps is approximated by the finite dimensional subspace ${\mathcal {A}}_{\mathscr {T}}$, and the minimization problem (1.10) on ${\mathcal {A}}_{\mathscr {T}}$ yields a nonlinear system of Euler–Lagrange equations that are directly solvable numerically.

Let us mention that other numerical methods have been developed to conserve particular properties of solutions of the gradient flow (1.1). Finite volume methods preserving the decay of energy at the semi-discrete level, along with other important properties like non-negativity and mass conservation, were proposed in the papers [4, 8, 10]. Particle methods based on suitable regularizations of the flux of the continuity Eq. (1.1) have been proposed in the papers [18, 27, 28, 37]. A particle method based on the steepest descent of a regularized internal part of the energy ${\mathcal {E}}$ in (1.8) by substituting particles by non-overlapping blobs was proposed and analysed in Carrillo et al. [11, 14]. Deterministic particle methods for diffusions have been recently explored, see [9] and the references therein. High-order relaxation schemes for nonlinear diffusion problems have been proposed in Cavalli et al. [16], while high-resolution schemes for nonlinear convection-diffusion problems are introduced in Kurganov et al. [26]. Moreover, the numerical approximation of the JKO variational scheme has already been tackled by different methods using pseudo-inverse distributions in one dimension (see [5, 7, 23, 40]) or solving for the optimal map in a JKO step (see [3, 25]). Finally, note that gradient-flow-based Lagrangian methods in one dimension for higher-order, drift diffusion and Fokker–Planck equations have recently been proposed in the papers [19, 31,32,33].

There are two main arguments in favour of our taking this indirect approach of solving (1.7) instead of solving (1.1). The first is our interest in structure-preserving discretizations: the scheme that we present builds on the non-obvious “secondary” gradient flow representation of (1.1) in terms of Lagrangian maps. The benefits include monotonicity of the transformed entropy functional ${\mathbf {E}}$ and $L^2$ control on the metric velocity for our fully discrete solutions, that eventually lead to weak compactness of the trajectories in the continuous limit. We remark that our long-term goal is to design a numerical scheme that makes full use of the much richer “primary” variational structure of (1.1) in the Wasserstein distance, which is reviewed in Sect. 2 below. However, despite significant effort in the recent past—see, e.g., the references [3, 5, 14, 15, 19, 22, 25, 29, 36, 40]—it has not been possible so far to preserve features like metric contractivity of the flow under the discretization, except in the rather special situation of one space dimension (see Matthes and Osberger [29]). This is mainly due to the non-existence of finite-dimensional submanifolds of ${\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ that are complete with respect to generalized geodesics.

The second motivation is that Lagrangian schemes are a natural choice for numerical front tracking, see, e.g., Budd [6] for first results on the numerical approximation of self-similar solutions to the porous medium equation. We recall that, due to the assumed degeneracy $P'(0)=0$ of the diffusion in (1.1), solutions that are compactly supported initially remain compactly supported for all times. A numerically accurate calculation of the moving edge of support is challenging, since the solution can have a very complex behavior near that edge, like the waiting time phenomenon (see Vazquez [38]). Our simulation results for $\partial _t\rho =\Delta (\rho ^3)$ — which possesses an analytically known, compactly supported, self-similar Barenblatt solution — indicate that our discretization is indeed able to track the edge of support quite accurately.

The expected convergence of our scheme, with implicit Euler stepping in time and piecewise linear approximation of the Lagrangian maps, is of first order in both space and time. This is confirmed in our experiments. For an improved approximation, particularly of the moving fronts, numerical schemes with a higher order of consistency would be desirable. In principle, such schemes could be constructed along the same lines, for example, by replacing the implicit Euler method by a Runge–Kutta method in time, and the piecewise constant ansatz space ${\mathcal {A}}_{\mathscr {T}}$ by finite elements with functions of higher global regularity in space. However, it is unclear if a similar degree of structure preservation can be achieved for these schemes, and their analysis would be very different from the one presented here.

Structure of the Paper

This work is organized as follows. In Sect. 2, we present an overview of previous results in gradient flows pertaining our work. Section 3 is devoted to the introduction of the linear set of Lagragian maps and the derivation of the numerical scheme. Section 4 shows the compactness of the approximated sequences of discretizations and we give conditions leading to the eventual convergence of the scheme towards (1.1). Section 5 deals with the consistency of the scheme in two dimensions, while Sect. 6 gives several numerical tests showing the performance of this scheme.

Gradient Flow Structures

Notations from Probability Theory

${\mathcal {P}}(X)$ is the space of probability measures on a given base set X. We say that a sequence $(\mu _n)$ of measures in ${\mathcal {P}}(X)$ converges narrowly to a limit $\mu$ in that space if

$$\begin{aligned} \int _Xf(x)\,\mathrm {d}\mu _n(x)\rightarrow \int _Xf(x)\,\mathrm {d}\mu (x) \end{aligned}$$

for all bounded and continuous functions $f\in C^0_b(X)$. The push-forward $T_\#\mu$ of a measure $\mu \in {\mathcal {P}}(X)$ under a measurable map $T :X\rightarrow Y$ is the uniquely determined measure $\nu \in {\mathcal {P}}(Y)$ such that, for all $g\in C^0_b(Y)$,

$$\begin{aligned} \int _Xg\circ T(x)\,\mathrm {d}\mu (x) = \int _Yg(y)\,\mathrm {d}\nu (y). \end{aligned}$$

With a slight abuse of notation — identifying absolutely continuous measures with their densities—we denote the space of probability densities on ${{\mathbb {R}}^d}$ of finite second moment by

$$\begin{aligned} {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)= \left\{ \rho \in L^1({{\mathbb {R}}^d})\,;\,\rho \ge 0,\,\int _{{\mathbb {R}}^d}\rho (x)\,\mathrm {d}x=1,\,\int _{{\mathbb {R}}^d}\Vert x\Vert ^2\rho (x)\,\mathrm {d}x<\infty \right\} . \end{aligned}$$

Clearly, the reference density ${\overline{\rho }}$, which is supported on the compact set $K\subset {\mathbb {R}}^d$, belongs to ${\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$. If $G :K\rightarrow {\mathbb {R}}^d$ is a diffeomorphism onto its image (which is again compact), then the push-forward of ${\overline{\rho }}$’s measure produces again a density $G_\#{\overline{\rho }}\in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$, given by

$$\begin{aligned} G_\#{\overline{\rho }}= \frac{{\overline{\rho }}}{\det \mathrm {D}G}\circ G^{-1}. \end{aligned}$$

(2.1)

Gradient Flow in the Wasserstein Metric

Below, some basic facts about the Wasserstein metric and the formulation of (1.1) as gradient flow in that metric are briefly reviewed. For more detailed information, we refer the reader to the monographs of Ambrosio et al. [1] and Villani [39].

One of the many equivalent ways to define the $L^2$-Wasserstein distance between $\rho _0,\rho _1\in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ is as follows:

$$\begin{aligned} \mathrm {W}_2(\rho _0,\rho _1) := \inf \left\{ \int _{{\mathbb {R}}^d} \Vert T(x)-x\Vert ^2\rho _0(x)\,\mathrm {d}x\,;\,T:{{\mathbb {R}}^d}\rightarrow {{\mathbb {R}}^d}\ \text {measurable},\,T_\#\rho _0=\rho _1\right\} ^{\frac{1}{2}}. \end{aligned}$$

(2.2)

The infimum above is in fact a minimum, and the — essentially unique — optimal map $T^*$ is characterized by Brenier’s criterion; see, e.g., Villani [39, Section 2.1]. A trivial but essential observation is that if ${\overline{\rho }}\in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ is a reference density with support $K\subset {{\mathbb {R}}^d}$, and $\rho _0=(G_0)_\#{\overline{\rho }}$ with a measurable $G_0 :K\rightarrow {{\mathbb {R}}^d}$, then (2.2) can be re-written as follows:

$$\begin{aligned} \mathrm {W}_2(\rho _0,\rho _1) = \inf \left\{ \int _K \Vert G(\omega )-G_0(\omega )\Vert ^2{\overline{\rho }}(\omega )\,\mathrm {d}\omega \,;\,G :K\rightarrow {{\mathbb {R}}^d}\ \text {measurable},\,G_\#{\overline{\rho }}=\rho _1\right\} ^{\frac{1}{2}}, \end{aligned}$$

(2.3)

and the essentially unique minimizer $G^*$ in (2.3) is related to the optimal map $T^*$ in (2.2) via $G^*=T^*\circ G_0$.

$\mathrm {W}_2$ is a metric on ${\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$; convergence in $\mathrm {W}_2$ is equivalent to weak-$\star$ convergence in $L^1({{\mathbb {R}}^d})$ and convergence of the second moment. Since P and hence also h are of super-linear growth at infinity, each sublevel set ${\mathcal {E}}$ is weak-$\star$ closed and thus complete with respect to $\mathrm {W}_2$.

As already mentioned above, solutions $\rho$ to (1.1) constitute a gradient flow for the functional ${\mathcal {E}}$ from (1.8) in the metric space $({\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d);\mathrm {W}_2)$. In fact, assuming that the potential V is $\lambda$-convex (i.e., $\nabla ^2V\ge \lambda \mathbb {1}$), the flow is even $\lambda$-contractive as a semi-group, thanks to the $\lambda$-uniform displacement convexity of ${\mathcal {E}}$ (see McCann [30], or Daneri and Savaré [17]), which is a strengthened form of $\lambda$-uniform convexity along geodesics. The $\lambda$-contractivity of the flow implies various properties (see Ambrosio et al. [1, Section 11.2]) like global existence, uniqueness and regularity of the flow, monotonicity of ${\mathcal {E}}$ and its sub-differential, uniform exponential estimates on the convergence (if $\lambda >0$) or divergence (if $\lambda \le 0$) of trajectories, quantified exponential rates for the approach to equilibrium (if $\lambda >0$) and the like.

An important further consequence is that the unique flow can be obtained as the limit for $\tau \searrow 0$ of the time-discrete minimizing movement scheme (see Ambrosio et al. [1] and Jordan, Kinderlehrer and Otto [24]):

$$\begin{aligned} \rho _\tau ^{n} := \mathop {{{\mathrm{argmin}}}}\limits _{\rho \in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)}{\mathcal {E}}_\tau (\rho ;\rho _\tau ^{n-1}), \quad {\mathcal {E}}_\tau (\rho ,\hat{\rho }):=\frac{1}{2\tau }\mathrm {W}_2(\rho ,\hat{\rho })^{2} + {\mathcal {E}}(\rho ). \end{aligned}$$

(2.4)

This time discretization is well-adapted to approximate $\lambda$-contractive gradient flows. All of the properties of mentioned above are already reflected on the level of these time-discrete solutions.

Gradient Flow in $L^2$

Equation (1.7) is the gradient flow of ${\mathbf {E}}$ on the space $L^2(K\rightarrow {{\mathbb {R}}^d};{\overline{\rho }})$ of square integrable (with respect to ${\overline{\rho }}$) maps $G :K\rightarrow {{\mathbb {R}}^d}$ (see Evans et al. [20] or Jordan et al. [25]). However, the variational structure behind this gradient flow is much weaker than above: most notably, ${\mathbf {E}}$ is only poly-convex, but not $\lambda$-uniformly convex. Therefore, the abstract machinery for $\lambda$-contractive gradient flows in Ambrosio et al. [1] does not apply here. Clearly, by equivalence of (1.1) and (1.7) at least for sufficiently smooth solutions, certain properties of the primary gradient flow are necessarily inherited by this secondary flow, but for instance $\lambda$-contractivity of the flow in the $L^2$-norm seems to fail.

Nevertheless, it can be proven (see Ambrosio, Lisini and Savaré [2]) that the gradient flow is globally well-defined, and it can again be approximated by the minimizing movement scheme:

$$\begin{aligned} G_\tau ^n:=\mathop {{{\mathrm{argmin}}}}\limits _{G\in L^2(K\rightarrow {{\mathbb {R}}^d};{\overline{\rho }})}{\mathbf {E}}_\tau \big (G;G_\tau ^{n-1}\big ), \quad {\mathbf {E}}_\tau (G;\hat{G})= \frac{1}{2\tau }\int _K\Vert G-\hat{G}\Vert ^2\,\,\mathrm {d}{\overline{\rho }}+ {\mathbf {E}}(G|{\overline{\rho }}). \end{aligned}$$

(2.5)

In fact, there is an equivalence between (2.5) and (2.4): simply substitute $(G_\tau ^{n-1})_\#{\overline{\rho }}$ for $\rho _\tau ^{n-1}$ and $G_\#{\overline{\rho }}$ for $\rho$ in (2.4); notice that any $\rho \in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ can be written as $G_\#{\overline{\rho }}$ with a suitable (highly non-unique) choice of $G\in L^2(K\rightarrow {{\mathbb {R}}^d};{\overline{\rho }})$. This equivalence was already exploited in Carrillo et al. [13, 15]. Thanks to the equality (2.3), the minimization with respect to $\rho =G_\#{\overline{\rho }}$ can be relaxed to a minimization with respect to G. Consequently, if $(G_\tau ^0)_\#{\overline{\rho }}=\rho _\tau ^0$, then $(G_\tau ^n)_\#{\overline{\rho }}=\rho _\tau ^n$ at all discrete times $n=1,2,\ldots$. However, while the functional ${\mathcal {E}}_\tau (\cdot ;\rho _\tau ^{n-1})$ in (2.4) is $(\lambda +\tau ^{-1})$-uniformly convex in $\rho$ along geodesics in $\mathrm {W}_2$, the functional ${\mathbf {E}}_\tau (\cdot ;G_\tau ^{n-1})$ in (2.5) has apparently no useful convexity properties in G on $L^2(K\rightarrow {{\mathbb {R}}^d};{\overline{\rho }})$.

Definition of the Numerical Scheme

Recall the Lagrangian formulation of (1.1) that has been given in Lemma 1.1. For definiteness, fix a reference density ${\overline{\rho }}\in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$, whose support $K\subset {{\mathbb {R}}^d}$ is a compact, convex polytope.

Discretization in Space

Our spatial discretization is performed using a finite subspace of linear maps for the Lagrangian maps G. More specifically: let ${\mathscr {T}}$ be some (finite) simplicial decomposition of K with nodes $\omega _{1}$ to $\omega _{L}$ and n-simplices $\Delta _{1}$ to $\Delta _{M}$. In the case $d=2$, which is of primary interest here, ${\mathscr {T}}$ is a triangulation, with triangles $\Delta _m$. The reference density ${\overline{\rho }}$ is approximated by a density ${\overline{\rho }}_{\mathscr {T}}\in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ that is piecewise constant on the simplices of ${\mathscr {T}}$, with respective values

$$\begin{aligned} {\overline{\rho }}_{\mathscr {T}}^m := \frac{\mu _{\mathscr {T}}^m}{|\Delta _m|} \quad \text {for the simplex masses}\quad \mu _{\mathscr {T}}^m:=\int _{\Delta _m}{\overline{\rho }}(\omega )\,\mathrm {d}\omega . \end{aligned}$$

(3.1)

The finite dimensional ansatz space ${\mathcal {A}}_{\mathscr {T}}$ is now defined as the set of maps $G:K\rightarrow {{\mathbb {R}}^d}$ that are globally continous, affine on each of the simplices $\Delta _m\in {\mathscr {T}}$, and orientation preserving. That is, on each $\Delta _m\subset {\mathscr {T}}$, the map $G\in {\mathcal {A}}_{\mathscr {T}}$ can be written as follows:

$$\begin{aligned} G(\omega ) = A_{m} \omega + b_{m} \qquad \text {for all } \omega \in \Delta _{m}, \end{aligned}$$

(3.2)

with a suitable matrix $A_{m} \in {\mathbb {R}}^{d\times d}$ of positive determinant and a vector $b_{m} \in {\mathbb {R}}^d$.

For the calculations that follow, we shall use a more geometric way to describe the maps $G\in {\mathcal {A}}_{\mathscr {T}}$, namely by the positions $G_\ell =G(\omega _\ell )$ of the images of each node $\omega _\ell$. Denote by $({\mathbb {R}}^d)_{\mathscr {T}}^L\subset {\mathbb {R}}^{L\cdot d}$ the space of L-tuples $\mathbf {G}=(G_\ell )_{\ell =1}^L$ of points $G_\ell \in {{\mathbb {R}}^d}$ with the same simplicial combinatorics (including orientation) as the $\omega _\ell$ in ${\mathscr {T}}$. Clearly, any $G\in {\mathcal {A}}_{\mathscr {T}}$ is uniquely characterized by the L-tuple $\mathbf {G}$ of its values, and moreover, any $\mathbf {G}\in ({\mathbb {R}}^d)_{\mathscr {T}}^L$ defines a $G\in {\mathcal {A}}_{\mathscr {T}}$.

Fig. 1

A schematic representation of the spatial discretization for the case $d=2$. Note that the upper-left triangle $\Delta _m$ is part of the reference triangulation ${\mathscr {T}}$, and is fixed in time. In contrast, the upper-right triangulation given by $G_m$ will change with time; see Sect. 3.2

More explicitly, fix a $\Delta _m\in {\mathscr {T}}$, with nodes labelled $\omega _{m,0}$ to $\omega _{m,d}$ in some orientation preserving order, and respective image points $G_{m,0}$ to $G_{m,d}$. With the standard d-simplex given by

$$\begin{aligned} \mathord {\bigtriangleup }^d:= \left\{ \xi =(\xi _1,\ldots ,\xi _d)\in {\mathbb {R}}_{\ge 0}^d\,;\,\sum _{j=1}^d\xi _j\le 1\right\} , \end{aligned}$$

introduce the linear interpolation maps $r_m :\mathord {\bigtriangleup }^d\rightarrow K$ and $q_m :\mathord {\bigtriangleup }^d\rightarrow {{\mathbb {R}}^d}$ by

$$\begin{aligned} r_m(\xi )&= \omega _{m,0} + \sum _{j=1}^d(\omega _{m,j}-\omega _{m,0})\xi _j, \\ q_m(\xi )&= G_{m,0} + \sum _{j=1}^d(G_{m,j}-G_{m,0})\xi _j. \end{aligned}$$

Then the affine map (3.2) equals to $q_m\circ r_m^{-1}$; this is shown schematically in Fig. 1 for the case $d=2$. In particular, we obtain that

$$\begin{aligned} \det A_m = \frac{\det \mathrm {D}q_m}{\det \mathrm {D}r_m} = \frac{\det Q_{\mathscr {T}}^m[G]}{2|\Delta _m|} \quad \text {where}\quad Q_{\mathscr {T}}^m[G]:=\big (G_{m,1}-G_{m,0}\big |\cdots \big |G_{m,d}-G_{m,0}\big ). \end{aligned}$$

(3.3)

For later reference, we give a more explicit representation for the transformed entropy ${\mathbf {E}}$ for $G\in {\mathcal {A}}_{\mathscr {T}}$, and for the $L^2$-distance between two maps $G,\hat{G}\in {\mathcal {A}}_{\mathscr {T}}$. Substitution of the special form (3.2) into (1.9) produces

$$\begin{aligned} {\mathbf {E}}(G|{\overline{\rho }}_{\mathscr {T}}) =\sum _{\Delta _m\in {\mathscr {T}}}\mu _{\mathscr {T}}^m \big [{\mathbb {H}}_{\mathscr {T}}^m(G)+{\mathbb {V}}_{\mathscr {T}}^m(G)\big ] \end{aligned}$$

(3.4)

with the internal energy [recall the definition of $\widetilde{h}$ from (1.9)]

$$\begin{aligned} {\mathbb {H}}_{\mathscr {T}}^m(G) :=\widetilde{h} \left( \frac{\det A_m}{{\overline{\rho }}_{\mathscr {T}}^m} \right) = \widetilde{h}\left( \frac{\det Q_{\mathscr {T}}^m[G]}{2\mu _{\mathscr {T}}^m}\right) \end{aligned}$$

and the potential energy

For the $L^2$-difference of G and $G^*$, we have

$$\begin{aligned} \Vert G-G^*\Vert _{L^2(K;{\overline{\rho }}_{\mathscr {T}})}^2 =\int _K\Vert G-G^*\Vert ^2{\overline{\rho }}_{\mathscr {T}}\,\mathrm {d}\omega = \sum _{\Delta _m\in {\mathscr {T}}}\mu _{\mathscr {T}}^m {\mathbb {L}}_{\mathscr {T}}^m(G,G^*). \end{aligned}$$

(3.5)

Using Lemma B.1, we obtain on each simplex $\Delta _m$:

(3.6)

Discretization in Time

Let a time step $\tau >0$ be given; in the following, we symbolize the spatio-temporal discretization by $\boxplus$, and we write $\boxplus \rightarrow 0$ for the joint limit of $\tau \rightarrow 0$ and vanishing mesh size in ${\mathscr {T}}$.

The discretization in time is performed in accordance with (2.5): we modify ${\mathbf {E}}_\tau$ from (2.5) by restriction to the ansatz space ${\mathcal {A}}_{\mathscr {T}}$. This leads to the minimization problem

$$\begin{aligned} G_\boxplus ^n:&=\mathop {{{\mathrm{argmin}}}}\limits _{G\in {\mathcal {A}}_{\mathscr {T}}}{\mathbf {E}}_\boxplus \big (G;G_\boxplus ^{n-1}\big ) \quad \text {where}\quad {\mathbf {E}}_\boxplus (G;G^*)\nonumber \\&= \frac{1}{2\tau }\Vert G-G^*\Vert _{L^2(K;{\overline{\rho }}_{\mathscr {T}})}^2 + {\mathbf {E}}(G|{\overline{\rho }}_{\mathscr {T}}). \end{aligned}$$

(3.7)

For a fixed discretization $\boxplus$, the fully discrete scheme is well-posed in the sense that for a given initial map $G_\boxplus ^0\in {\mathcal {A}}_{\mathscr {T}}$, an associated sequence $(G_\boxplus ^n)_{n\ge 0}$ can be determined by successive solution of the minimization problems (3.7). One only needs to verify:

Lemma 3.1

For each given $G^*\in {\mathcal {A}}_{\mathscr {T}}$, there exists at least one global minimizer $G\in {\mathcal {A}}_{\mathscr {T}}$ of ${\mathbf {E}}_\boxplus (\cdot ;G^*)$.

Remark 3.2

We do not claim uniqueness of the minimizers. Unfortunately, the minimization problem (3.7) inherits the lack of convexity from (2.5), whereas the correspondence between (2.5) and the convex problem (2.4) is lost under spatial discretization. A detailed discussion of ${\mathbf {E}}_\boxplus$’s (non-)convexity is provided in “Appendix C”.

Proof of Lemma 3.1

We only sketch the main arguments. For definiteness, let us choose (just for this proof) one of the infinitely many equivalent norm-induced metrics on the dL-dimensional vector space $V_{\mathscr {T}}$ of all continuous maps $G :K\rightarrow {\mathbb {R}}^d$ that are piecewise affine with respect to the fixed simplicial decomposition ${\mathscr {T}}$: given $G,G'\in V_{\mathscr {T}}$ with their respective point locations $\mathbf {G},\mathbf {G}'\in {\mathbb {R}}^{dL}$, i.e., $\mathbf {G}=(G_\ell )_{\ell =1}^L$ for $G_\ell =G(\omega _\ell )$, define the distance between these maps as the maximal ${\mathbb {R}}^d$-distance $\Vert G_\ell -G'_\ell \Vert$ of corresponding points $G_\ell \in \mathbf {G}$, $G'_\ell \in \mathbf {G}'$. Clearly, this metric makes $V_{\mathscr {T}}$ a complete space.

It is easily seen that the subset ${\mathcal {A}}_{\mathscr {T}}$ — which is singled out by requiring orientation preservation of the G’s—is an open subset of $V_{\mathscr {T}}$. It is further obvious that the map $G\mapsto {\mathbf {E}}_\boxplus (G;G^*)$ is continuous with respect to the metric. The claim of the lemma thus follows if we can show that the sub-level

$$\begin{aligned} S_c:=\left\{ G\in {\mathcal {A}}_{\mathscr {T}}\,;\,{\mathbf {E}}_\boxplus (G;G^*)\le c\right\} \quad \text {with}\quad c:={\mathbf {E}}(G^*|{\overline{\rho }}_{\mathscr {T}}) \end{aligned}$$

is a non-empty compact subset of $V_{\mathscr {T}}$. Clearly, $G^*\in S_c$, so it suffices to verify compactness.

$S_c$ is bounded. We are going to show that there is a radius $R>0$ such that no $G\in S_c$ has a distance larger than R to $G^*$. From non-negativity of ${\mathbf {E}}$, and from the representations (3.5) and (3.6), it follows that

$$\begin{aligned} c\ge \frac{1}{2\tau }\Vert G-G^*\Vert _{L^2(K;{\overline{\rho }}_{\mathscr {T}})}^2&\ge \frac{\underline{\mu }_{\mathscr {T}}}{2\tau }\sum _{\Delta _m\in {\mathscr {T}}}{\mathbb {L}}_{\mathscr {T}}^m(G,G^*)\\&= \frac{\underline{\mu }_{\mathscr {T}}}{(d+1)(d+2) \tau }\sum _{0\le i\le j\le d}(G_{m,i}-G^*_{m,i})\cdot (G_{m,j}-G^*_{m,j})\\&\ge \frac{\underline{\mu }_{\mathscr {T}}}{2(d+1)(d+2) \tau }\sum _{\ell =1}^L\Vert G_\ell -G_\ell ^*\Vert ^2, \end{aligned}$$

where $\underline{\mu }_{\mathscr {T}}=\min _{\Delta _m}\mu _{\mathscr {T}}^m$. It is now easy to compute a suitable value for the radius R.

$S_c$ is a closed subset of $V_{\mathscr {T}}$. It suffices to show that the limit $\overline{G}\in V_{\mathscr {T}}$ of any sequence $(G^{(k)})_{k=1}^\infty$ of maps $G^{(k)}\in S_c$ belongs to ${\mathcal {A}}_{\mathscr {T}}$. By definition of our metric on $V_{\mathscr {T}}$, global continuity and piecewise linearity of the $G^{(k)}$ trivially pass to the limit $\overline{G}$. We still need to verify that $\overline{G}$ is orientation-preserving. Fix a simplex $\Delta _m$ and consider the corresponding matrices $A_m^{(k)}$ and $\overline{A}_m$ from (3.2). Since the $G^{(k)}$ converge to $\overline{G}$ in the metric, also $A_m^{(k)}\rightarrow \overline{A}_m$ entry-wise. Now, by non-negativity of $\widetilde{h}$, we have for all k that

$$\begin{aligned} c\ge {\mathbf {E}}(G^{(k)}|{\overline{\rho }}_{\mathscr {T}}) \ge \mu _{\mathscr {T}}^m\widetilde{h}\left( \frac{\det A^{(k)}_m}{{\overline{\rho }}_{\mathscr {T}}^m}\right) , \end{aligned}$$

and since $\widetilde{h}(s)\rightarrow +\infty$ as $s\downarrow 0$, it follows that $\det A^{(k)}_m>0$ is bounded away from zero, uniformly in k. But then also $\det \overline{A}_m>0$, i.e., the mth linear map piece of the limit $\overline{G}$ preserves orientation. $\square$

Fully Discrete Equations

We shall now derive the Euler–Lagrange equations associated to the minimization problem (3.7), i.e., for each given $G^*:=G_\boxplus ^{n-1}\in {\mathcal {A}}_{\mathscr {T}}$, we calculate the variations of ${\mathbf {E}}_\boxplus (G;G^*)$ with respect to the degrees of freedom of $G\in {\mathcal {A}}_{\mathscr {T}}$. Since that function is a weighted sum over the triangles $\Delta _m\in {\mathscr {T}}$, it suffices to perform the calculations for one fixed triangle $\Delta _m$, with respective nodes $\omega _{m,0}$ to $\omega _{m,d}$, in positive orientation. The associated image points are $G_{m,0}$ to $G_{m,d}$. Since we may choose any vertex to be labelled $\omega _{m,0}$, it will suffice to perform the calculations at one fixed image point $G_{m,0}$.

• mass term:

  $$\begin{aligned} \frac{\partial }{\partial G_{m,0}}{\mathbb {L}}_{\mathscr {T}}^m(G,G^*)&=\frac{2}{(d+1)(d+2)}\frac{\partial }{\partial G_{m,0}}\sum _{0\le i\le j\le d}(G_{m,i}-G^*_{m,i})\cdot (G_{m,j}-G^*_{m,j}) \\&=\frac{2}{(d+1)(d+2)}\left( 2(G_{m,0}-G^*_{m,0})+\sum _{j=1}^d(G_{m,j}-G^*_{m,j})\right) \end{aligned}$$

• internal energy: observing that—recall (1.2) —

  $$\begin{aligned} \widetilde{h}'(s) = \frac{\mathrm {d}}{\,\mathrm {d}s}\big [sh(s^{-1})\big ] = h(s^{-1})-s^{-1}h'(s^{-1}) = -P(s^{-1}), \end{aligned}$$

  (3.8)

  we obtain

  $$\begin{aligned} \frac{\partial }{\partial G_{m,0}}{\mathbb {H}}_{\mathscr {T}}^m(G) = \frac{\partial }{\partial G_{m,0}} \widetilde{h}\left( \frac{\det Q_{\mathscr {T}}^m[G]}{2\mu _{\mathscr {T}}^m}\right) = \frac{1}{2\mu _{\mathscr {T}}^m}P\left( \frac{2\mu _{\mathscr {T}}^m}{\det Q_{\mathscr {T}}^m[G]}\right) \nu _{\mathscr {T}}^m[G], \end{aligned}$$

  where

  $$\begin{aligned} \nu _{\mathscr {T}}^m[G] := - \frac{\partial }{\partial G_{m,0}} \det Q_{\mathscr {T}}^m[G] = (\det Q_{\mathscr {T}}^m[G])\, (Q_{\mathscr {T}}^m[G])^{-T}\sum _{j=1}^d\mathrm {e}_j \end{aligned}$$

  (3.9)

  is the uniquely determined vector in ${\mathbb {R}}^d$ that is orthogonal to the $(d-1)$-simplex with corners $G_{m,1}$ to $G_{m,d}$ (pointing away from $G_{m,0}$) and whose length equals the $(d-1)$-volume of that simplex.

• potential energy:

  

Now let $\omega _\ell$ be a fixed vertex of ${\mathscr {T}}$. Summing over all simplices $\Delta _m$ that have $\omega _\ell$ as a vertex, and choosing vertex labels in accordance with above, i.e., such that $\omega _{m,0}=\omega _\ell$ in $\Delta _m$, produces the following Euler–Lagrange equation:

(3.10)

Approximation of the Initial Condition

For the approximation $\rho ^0_\boxplus =(G^0_\boxplus )_\#{\overline{\rho }}_{\mathscr {T}}$ of the initial datum $\rho ^0=G^0_\#{\overline{\rho }}$, we require:

• $\rho ^0_\boxplus$ converges to $\rho ^0$ narrowly;

• ${\mathcal {E}}(\rho ^0_\boxplus )$ is $\boxplus$-uniformly bounded, i.e.,

  $$\begin{aligned} \overline{{\mathcal {E}}}:=\sup {\mathcal {E}}(\rho _\boxplus ^0) < \infty . \end{aligned}$$

  (3.11)

In our numerical experiments, we always choose ${\overline{\rho }}:=\rho ^0$, in which case $G^0 :K\rightarrow {\mathbb {R}}^d$ can be taken as the identity on K, and we choose accordingly $G^0_\boxplus$ as the identity as well. Hence $\rho ^0_\boxplus ={\overline{\rho }}_{\mathscr {T}}$, which converges to $\rho ^0={\overline{\rho }}$ even strongly in $L^1(K)$. Moreover, since h is convex, it easily follows from Jensen’s inequality that

$$\begin{aligned} \int _{\Delta _m} h\big ({\overline{\rho }}(x)\big )\,\mathrm {d}x \ge |\Delta _m|h({\overline{\rho }}_{\mathscr {T}}^m), \end{aligned}$$

and therefore,

$$\begin{aligned} {\mathcal {E}}(\rho _\boxplus ^0) \le {\mathcal {E}}(\rho ^0). \end{aligned}$$

In more general situations, in which $G^0$ is not the identity, a sequence of approximations $G^0_\boxplus$ of $G^0$ is needed. Pointwise convergence $G^0_\boxplus \rightarrow G^0$ is more than sufficient to guarantee narrow convergence of $\rho _\boxplus ^0$ to $\rho ^0$, but the uniform bound (3.11) might require a well-adapted approximation, especially for non-smooth $G^0$’s.

Limit Trajectory

In this section, we assume that a sequence of vanishing discretizations $\boxplus \rightarrow 0$ is given, and we study the respective limit of the fully discrete solutions $(G_\boxplus ^n)_{n\ge 0}$ that are produced by the inductive minimization procedure (3.7). For the analysis of that limit trajectory, it is more natural to work with the induced densities and velocities,

$$\begin{aligned} \rho _\boxplus ^n:=(G_\boxplus ^n)_\#{\overline{\rho }}, \quad \mathbf {v}_\boxplus ^n:=\frac{{\mathrm {id}}-G_\boxplus ^{n-1}\circ (G_\boxplus ^n)^{-1}}{\tau }, \end{aligned}$$

instead of the Lagrangian maps $G_\boxplus ^n$ themselves. Note that $\mathbf {v}_\boxplus ^n$ is only well-defined on the support of $\rho _\boxplus ^n$—that is, on the image of $G_\boxplus ^n$—and can be assigned arbitrary values outside. Let us introduce the piecewise constant in time interpolations ${\widetilde{\rho }}_\boxplus :[0,T]\times {{\mathbb {R}}^d}\rightarrow {\mathbb {R}}_{\ge 0}$, and ${\widetilde{\mathbf {v}}}_\boxplus :[0,T]\times {{\mathbb {R}}^d}\rightarrow {\mathbb {R}}^d$ as usual,

$$\begin{aligned} {\widetilde{\rho }}_\boxplus (t) = \rho _\boxplus ^n, \quad {\widetilde{\mathbf {v}}}_\boxplus (t) = \mathbf {v}_\boxplus ^n \quad \text {with }n \text { such that }t\in ((n-1)\tau ,n\tau ]. \end{aligned}$$

Note that ${\widetilde{\rho }}(t,\cdot )\in {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ and ${\widetilde{\mathbf {v}}}_\boxplus (t,\cdot )\in L^2({{\mathbb {R}}^d}\rightarrow {\mathbb {R}}^d;{\widetilde{\rho }}_\boxplus (t,\cdot ))$ at each $t\ge 0$.

Energy Estimates

We start by proving the classical energy estimates on minimizing movements for our fully discrete scheme.

Lemma 4.1

For each discretization $\boxplus$ and for any indices $\overline{n}>\underline{n}\ge 0$, one has the a priori estimate

$$\begin{aligned} {\mathcal {E}}(\rho _\boxplus ^{\overline{n}}) +\frac{\tau }{2}\sum _{n=\underline{n}+1}^{\overline{n}}\left( \frac{\mathrm {W}_2(\rho _\boxplus ^n,\rho _\boxplus ^{n-1})}{\tau }\right) ^2 \le {\mathcal {E}}(\rho ^{\underline{n}}). \end{aligned}$$

(4.1)

Consequently:

• (1) ${\mathbf {E}}$ is monotonically decreasing, i.e., ${\mathcal {E}}({\widetilde{\rho }}_\boxplus (t))\le {\mathcal {E}}({\widetilde{\rho }}_\boxplus (s))$ for all $t\ge s\ge 0$;

• (2) ${\widetilde{\rho }}_\boxplus$ is Hölder-$\frac{1}{2}$-continuous in $\mathrm {W}_2$, up to an error $\tau$,

  $$\begin{aligned} \mathrm {W}_2\big ({\widetilde{\rho }}_\boxplus (t),{\widetilde{\rho }}_\boxplus (s)\big ) \le \sqrt{2{\mathcal {E}}(\rho _\boxplus ^0)}\big (|t-s|^{\frac{1}{2}}+\tau ^{\frac{1}{2}}\big ) \quad \text { for all }t\ge s\ge 0. \end{aligned}$$

  (4.2)

• (3) ${\widetilde{\mathbf {v}}}_\boxplus$ is square integrable with respect to ${\widetilde{\rho }}_\boxplus$,

  $$\begin{aligned} \int _0^T\int _{{\mathbb {R}}^d}\Vert {\widetilde{\mathbf {v}}}_\boxplus \Vert ^2{\widetilde{\rho }}_\boxplus \,\mathrm {d}x\,\mathrm {d}t \le 2{\mathcal {E}}(\rho _\boxplus ^0). \end{aligned}$$

  (4.3)

Proof

By the definition of $G_\boxplus ^n$ as a minimizer, we know that ${\mathbf {E}}_\boxplus (G_\boxplus ^n;G_\boxplus ^{n-1})\le {\mathbf {E}}_\boxplus (G;G_\boxplus ^{n-1})$ for any $G\in {\mathcal {A}}_{\mathscr {T}}$, and in particular for the choice $G:=G_\boxplus ^{n-1}$, which yields:

$$\begin{aligned} \frac{1}{2\tau }\int _K\Vert G_\boxplus ^n-G_\boxplus ^{n-1}\Vert ^2{\overline{\rho }}_{\mathscr {T}}\,\mathrm {d}\omega +{\mathbf {E}}(G_\boxplus ^n|{\overline{\rho }}_{\mathscr {T}}) \le {\mathbf {E}}(G_\boxplus ^{n-1}|{\overline{\rho }}_{\mathscr {T}}). \end{aligned}$$

(4.4)

Summing these inequalies for $n=\underline{n}+1,\ldots ,\overline{n}$, recalling that ${\mathcal {E}}(\rho _\boxplus ^n)={\mathbf {E}}(G_\boxplus ^n|{\overline{\rho }}_{\mathscr {T}})$ by (1.9) and that $\mathrm {W}_2(\rho _\boxplus ^n,\rho _\boxplus ^{n-1})^2\le \int _K|G_\boxplus ^n-G_\boxplus ^{n-1}|^2{\overline{\rho }}\,\mathrm {d}\omega$ by (2.3), produces (4.1).

Monotonicity of ${\mathcal {E}}$ in time is obvious.

To prove (4.2), choose $\underline{n}\le \overline{n}$ such that $s\in ((\underline{n}-1)\tau ,\underline{n}\tau ]$ and $t\in ((\overline{n}-1)\tau ,\overline{n}\tau ]$. Notice that $\tau (\overline{n}-\underline{n})\le t-s+\tau$. If $\underline{n}=\overline{n}$, the claim (4.2) is obviously true; let $\underline{n}<\overline{n}$ in the following. Combining the triangle inequality for the metric $\mathrm {W}_2$, estimate (4.1) above and Hölder’s inequality for sums, we arrive at

$$\begin{aligned} \mathrm {W}_2\big ({\widetilde{\rho }}_\boxplus (t),{\widetilde{\rho }}_\boxplus (s)\big )&= \mathrm {W}_2(\rho _\boxplus ^{\overline{n}},\rho _\boxplus ^{\underline{n}}) \le \sum _{n=\underline{n}+1}^{\overline{n}}\mathrm {W}_2(\rho _\boxplus ^n,\rho _\boxplus ^{n-1}) \\&\le \left[ \sum _{n=\underline{n}+1}^{\overline{n}}\tau \right] ^{\frac{1}{2}} \left[ \sum _{n=\underline{n}+1}^{\overline{n}}\frac{\mathrm {W}_2(\rho _\boxplus ^n,\rho _\boxplus ^{n-1})^2}{\tau }\right] ^{\frac{1}{2}}\\&= \big [\tau (\overline{n}-\underline{n}) \big ]^{\frac{1}{2}} \left[ \tau \sum _{n=\underline{n}+1}^{\overline{n}}\left( \frac{\mathrm {W}_2(\rho _\boxplus ^n,\rho _\boxplus ^{n-1})}{\tau }\right) ^2\right] ^{\frac{1}{2}}\\&\le [t-s+\tau ]^{\frac{1}{2}} \left[ 2\big ({\mathcal {E}}(\rho _\boxplus ^{\underline{n}}) - {\mathcal {E}}(\rho _\boxplus ^{\overline{n}})\big )\right] ^{\frac{1}{2}} \\&\le \big [|t-s|^{\frac{1}{2}}+\tau ^{\frac{1}{2}}\big ]{\mathcal {E}}(\rho _\boxplus ^0)^{\frac{1}{2}}. \end{aligned}$$

Finally, changing variables using $x=G_\boxplus ^n(\omega )$ in (4.4) yields

$$\begin{aligned} \frac{\tau }{2}\int _{{\mathbb {R}}^d}\Vert \mathbf {v}_\boxplus ^n\Vert ^2\rho _\boxplus ^n\,\mathrm {d}x + {\mathbf {E}}(G_\boxplus ^n) \le {\mathbf {E}}(G_\boxplus ^{n-1}), \end{aligned}$$

and summing these inequalities from $n=1$ to $n=N_\tau$ yields (4.3). $\square$

Compactness of the Trajectories and Weak Formulation

Our main result on the weak limit of ${\widetilde{\rho }}_\boxplus$ is the following.

Theorem 4.2

Along a suitable sequence $\boxplus \rightarrow 0$, the curves ${\widetilde{\rho }}_\boxplus :{\mathbb {R}}_{\ge 0}\rightarrow {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$ convergence pointwise in time, i.e., ${\widetilde{\rho }}_\boxplus (t)\rightarrow \rho _*(t)$ narrowly for each $t>0$, towards a Hölder-$\frac{1}{2}$-continuous limit trajectory $\rho _* :{\mathbb {R}}_{\ge 0}\rightarrow {\mathcal {P}}_2^\text {ac}({\mathbb {R}}^d)$.

Moreover, the discrete velocities ${\widetilde{\mathbf {v}}}_\boxplus$ possess a limit $\mathbf {v}_*\in L^2({\mathbb {R}}_{\ge 0}\times {{\mathbb {R}}^d};\rho _*)$ such that ${\widetilde{\mathbf {v}}}_\boxplus {\widetilde{\rho }}_\boxplus \overset{*}{\rightharpoonup }\mathbf {v}_*\rho _*$ in $L^1({\mathbb {R}}_{\ge 0}\times {{\mathbb {R}}^d})$, and the continuity equation

$$\begin{aligned} \partial _t\rho _* + \nabla \cdot (\rho _*\mathbf {v}_*) = 0 \end{aligned}$$

(4.5)

holds in the sense of distributions.

Remark 4.3

The Hölder continuity of $\rho _*$ implies that $\rho _*$ satisfies the initial condition (1.1b) in the sense that $\rho _*(t)\rightarrow \rho ^0$ narrowly as $t\downarrow 0$.

Proof of Theorem 4.2

We closely follow an argument that is part of the general convergence proof for the minimizing movement scheme as given in Ambrosio et al. [1, Section 11.1.3]. Below, convergence is shown for some arbitrary but fixed time horizon $T>0$; a standard diagonal argument implies convergence at arbitrary times.

First observe that by estimate (4.2)—applied with $0=s\le t\le T$—it follows that $\mathrm {W}_2({\widetilde{\rho }}_\boxplus (t),\rho _\boxplus ^0)$ is bounded, uniformly in $t\in [0,T]$ and in $\boxplus$. Since further $\rho ^0_\boxplus$ converges narrowly to $\rho ^0$ by our hypotheses on the initial approximation, we conclude that all densities ${\widetilde{\rho }}_\boxplus (t)$ belong to a sequentially compact subset for the narrow convergence. The second observation is that the term on the right hand side of (4.2) simplifies to $(2\overline{{\mathcal {E}}})^\frac{1}{2}|t-s|^\frac{1}{2}$ in the limit $\boxplus \rightarrow 0$. A straightforward application of the “refined version” of the Ascoli-Arzelà theorem (Proposition 3.3.1 in Ambrosio et al. [1]) yields the first part of the claim, namely the pointwise narrow convergence of ${\widetilde{\rho }}_\boxplus$ towards a Hölder continuous limit curve $\rho _*$.

It remains to pass to the limit with the velocity ${\widetilde{\mathbf {v}}}_\boxplus$. Towards that end, we define a probability measure $\widetilde{\gamma }_\boxplus \in {\mathcal {P}}(Z_T)$ on the set $Z_T:=[0,T]\times {\mathbb {R}}^d\times {\mathbb {R}}^d$ as follows:

$$\begin{aligned} \int _{Z_T}\varphi (t,x,v)\,\mathrm {d}\widetilde{\gamma }_\boxplus (t,x,v) = \int _0^T\int _{{\mathbb {R}}^d} \varphi \big (t,x,{\widetilde{\mathbf {v}}}_\boxplus (t,x)\big )\,{\widetilde{\rho }}_\boxplus (t,x)\,\mathrm {d}x\frac{\mathrm {d}t}{T}, \end{aligned}$$

for every bounded and continuous function $\varphi \in C^0_b(Z_T)$. For brevity, let $\widetilde{M}_\boxplus \in {\mathcal {P}}([0,T]\times {\mathbb {R}}^d)$ be the (t, x)-marginals of $\widetilde{\gamma }_\boxplus$, that have respective Lebesgue densities $\frac{\rho _\boxplus (t,x)}{T}$ on $[0,T]\times {\mathbb {R}}^d$. Thanks to the result from the first part of the proof, $\widetilde{M}_\boxplus$ converges narrowly to a limit $M_*$, which has density $\frac{\rho _*(t,x)}{T}$. On the other hand, the estimate (4.3) implies that

$$\begin{aligned} \int _{Z_T} |v|^2\,\mathrm {d}\widetilde{\gamma }_\boxplus (t,x,v) = \int _{[0,T]\times {\mathbb {R}}^d}|{\widetilde{\mathbf {v}}}_\boxplus (t,x)|^2\,\mathrm {d}\widetilde{M}_\boxplus (t,x) \le 2\overline{{\mathcal {E}}}. \end{aligned}$$

We are thus in the position to apply Theorem 5.4.4 in Ambrosio et al. [1], which yields the narrow convergence of $\widetilde{\gamma }_\boxplus$ towards a limit $\gamma _*$. Clearly, the (t, x)-marginal of $\gamma _*$ is $M_*$. Accordingly, we introduce the disintegration $\gamma _{(t,x)}$ of $\gamma _*$ with respect to $M_*$, which is well-defined $M_*$-a.e.. Below, it will turn out that $\gamma _*$’s v-barycenter,

$$\begin{aligned} \mathbf {v}_*(t,x) := \int _{{\mathbb {R}}^d} v \,\mathrm {d}\gamma _{(t,x)}(v), \end{aligned}$$

(4.6)

is the sought-for weak limit of ${\widetilde{\mathbf {v}}}_\boxplus$. The convergence ${\widetilde{\mathbf {v}}}_\boxplus {\widetilde{\rho }}_\boxplus \overset{*}{\rightharpoonup }\mathbf {v}_*\rho _*$ and the inheritance of the uniform $L^2$-bound (4.3) to the limit $\mathbf {v}_*$ are further direct consequences of Theorem 5.4.4 in Ambrosio et al. [1].

The key step to establish the continuity equation for the just-defined $\mathbf {v}_*$ is to evaluate the limit as $\boxplus \rightarrow 0$ of

$$\begin{aligned} J_\boxplus [\phi ] := \frac{1}{\tau }\left[ \int _0^T\int _{{\mathbb {R}}^d}\phi (t,x){\widetilde{\rho }}_\boxplus (t,x)\,\mathrm {d}x\,\mathrm {d}t - \int _0^T\int _{{\mathbb {R}}^d}\phi (t,x){\widetilde{\rho }}_\boxplus (t-\tau ,x)\,\mathrm {d}x\,\mathrm {d}t \right] \end{aligned}$$

for any given test function $\phi \in C^\infty _c((0,T)\times {\mathbb {R}}^d)$ in two different ways. First, we change variables $t\mapsto t+\tau$ in the second integral, which gives

$$\begin{aligned} J_\boxplus [\phi ]&= \int _0^T\int _{{\mathbb {R}}^d} \frac{\phi (t,x)-\phi (t+\tau ,x)}{\tau }{\widetilde{\rho }}_\boxplus (t,x)\,\mathrm {d}x\,\mathrm {d}t {\mathop {\longrightarrow }\limits ^{\boxplus \rightarrow 0}}\\&\quad -\int _0^T\int _{{\mathbb {R}}^d} \partial _t\phi (t,x)\,\rho _*(t,x)\,\mathrm {d}x\,\mathrm {d}t. \end{aligned}$$

For the second evaluation, we write

$$\begin{aligned} \rho _\boxplus ^{n-1} = \big (G_\boxplus ^{n-1}\circ (G_\boxplus ^n)^{-1}\big )_\#\rho _\boxplus ^n = \big ({\mathrm {id}}-\tau \mathbf {v}_\boxplus ^n\big )_\#\rho _\boxplus ^n, \end{aligned}$$

and substitute accordingly $x\mapsto x-\tau {\widetilde{\mathbf {v}}}_\boxplus (t,x)$ in the second integral, leading to

$$\begin{aligned} J_\boxplus [\phi ]&= \int _0^T\int _{{\mathbb {R}}^d} \frac{\phi (t,x)-\phi \big (t,x-\tau {\widetilde{\mathbf {v}}}_\boxplus (t,x)\big )}{\tau }{\widetilde{\rho }}_\boxplus (t,x)\,\mathrm {d}x\,\mathrm {d}t \\&= \int _0^T\int _{{\mathbb {R}}^d} \nabla \phi (t,x)\cdot {\widetilde{\mathbf {v}}}_\boxplus (t,x){\widetilde{\rho }}_\boxplus (t,x)\,\mathrm {d}x\,\mathrm {d}t + \mathfrak {e}_\boxplus [\phi ]\\&= \int _{Z_T} \nabla \phi (t,x)\cdot v\,\mathrm {d}\widetilde{\gamma }_\boxplus (t,x,v) + \mathfrak {e}_\boxplus [\phi ] \\&\quad {\mathop {\longrightarrow }\limits ^{\boxplus \rightarrow 0}} \int _{Z_T} \nabla \phi (t,x)\cdot v\,\mathrm {d}\gamma _*(t,x,v) \\&= \int _{[0,T]\times {\mathbb {R}}^d}\nabla \phi (t,x)\cdot \left[ \int _{{\mathbb {R}}^d}v\,\mathrm {d}\gamma _{(t,x)}(v)\right] \,\mathrm {d}M_*(t,x) \\&= \int _0^T\int _{{\mathbb {R}}^d}\nabla \phi (t,x)\cdot \mathbf {v}_*(t,x)\rho _*(t,x)\,\mathrm {d}x\,\mathrm {d}t. \end{aligned}$$

The error term $\mathfrak {e}_\boxplus [\phi ]$ above is controlled via Taylor expansion of $\phi$ and by using (4.3),

$$\begin{aligned} \big |\mathfrak {e}_\boxplus [\phi ]\big | \le \int _0^T\int _{{\mathbb {R}}^d}\frac{\tau }{2}\Vert \phi \Vert _{C^2}\big \Vert {\widetilde{\mathbf {v}}}_\boxplus (t,x)\big \Vert ^2{\widetilde{\rho }}_\boxplus (t,x)\,\mathrm {d}x\,\mathrm {d}t \le \overline{{\mathcal {E}}}\Vert \phi \Vert _{C^2}T\;\tau . \end{aligned}$$

Equality of the limits for both evaluations of $J_\boxplus [\phi ]$ for arbitrary test functions $\phi$ shows the continuity Eq. (4.5). $\square$

Unfortunately, the convergence provided by Theorem 4.2 is generally not sufficient to conclude that $\rho _*$ is a weak solution to (1.1), since we are not able to identify $\mathbf {v}_*$ as $\mathbf {v}[\rho _*]$ from (1.4b). The problem is two-fold: first, weak-$\star$ convergence of ${\widetilde{\rho }}_\boxplus$ is insufficient to pass to the limit inside the nonlinear function P. Second, even if we would know that, for instance, $P({\widetilde{\rho }}_\boxplus )\overset{*}{\rightharpoonup }P(\rho _*)$, we would still need a $\boxplus$-independent a priori control on the regularity (e.g., maximal diameter of triangles) of the meshes generated by the $G_\boxplus ^n$ to justify the passage to limit in the weak formulation below.

The main difficulty in the weak formulation that we derive now is that we can only use “test functions” that are piecewise affine with respect to the changing meshes generated by the $G_\boxplus ^n$. For definiteness, we introduce the space

$$\begin{aligned} \mathcal {D}({\mathscr {T}}):=\left\{ \Gamma :K\rightarrow {\mathbb {R}}^d\,;\,\Gamma \text { is globally continuous, and is piecewise affine w.r.t. }\Delta _m\right\} . \end{aligned}$$

Lemma 4.4

Assume $S :{{\mathbb {R}}^d}\rightarrow {\mathbb {R}}^d$ is such that $S\circ G_\boxplus ^n\in \mathcal {D}({\mathscr {T}})$. Then:

$$\begin{aligned} \int _{{{\mathbb {R}}^d}} P(\rho _\boxplus ^{n}) \, \nabla \cdot S \,\mathrm {d}x - \int _{{{\mathbb {R}}^d}} \nabla V \cdot S\, \rho _\boxplus ^{n} \,\mathrm {d}x = \int _{{{\mathbb {R}}^d}} S\cdot \mathbf {v}_\boxplus ^n \rho _\boxplus ^{n} \,\mathrm {d}x. \end{aligned}$$

(4.7)

Proof

For all sufficiently small $\varepsilon >0$, let $G_\varepsilon = ({\mathrm {id}}+S)\circ G_\boxplus ^n$. By definition of $G_\boxplus ^n$ as a minimizer, we have that ${\mathbf {E}}_\boxplus (G_\varepsilon ;G_\boxplus ^{n-1})\ge {\mathbf {E}}_\boxplus (G_\boxplus ^n;G_\boxplus ^{n-1})$. This implies that

$$\begin{aligned} 0&\le \frac{1}{\varepsilon }\int _K\bigg (\frac{1}{2\tau }\big [\Vert G_\varepsilon -G_\boxplus ^{n-1}\Vert ^2-\Vert G_\boxplus ^n-G_\boxplus ^{n-1}\Vert ^2\big ] \nonumber \\&\qquad + \left[ \widetilde{h}\left( \frac{\det \mathrm {D}G_\varepsilon }{{\overline{\rho }}_{\mathscr {T}}}\right) -\widetilde{h}\left( \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\right) \right] + \big [V\circ G_\varepsilon -V\big ]\bigg ) {\overline{\rho }}_{\mathscr {T}}\,\mathrm {d}\omega . \end{aligned}$$

(4.8)

We discuss limits of the three terms under the integral for $\varepsilon \searrow 0$. For the metric term:

$$\begin{aligned} \frac{1}{2\tau \varepsilon }\left[ \Vert G_\varepsilon -G_\boxplus ^{n-1}\Vert ^2-\Vert G_\boxplus ^n-G_\boxplus ^{n-1}\Vert ^2\right]&= \frac{G_\boxplus ^n-G_\boxplus ^{n-1}}{\tau }\cdot \frac{G_\varepsilon -G_\boxplus ^n}{\varepsilon }+ \frac{1}{2\tau \varepsilon }\Vert G_\varepsilon -G_\boxplus ^n\Vert ^2 \\&= \left[ \left( \frac{{\mathrm {id}}-T_\boxplus ^n}{\tau }\right) \cdot S\right] \circ G_\boxplus ^n + \frac{\varepsilon }{2\tau }\Vert S\Vert ^2\circ G_\boxplus ^n, \end{aligned}$$

and since S is bounded, the last term vanishes uniformly on K for $\varepsilon \searrow 0$. For the internal energy, since $\mathrm {D}G_\varepsilon =\mathrm {D}({\mathrm {id}}+\varepsilon S)\circ G_\boxplus ^n\cdot \mathrm {D}G_\boxplus ^n$, and recalling (3.8),

$$\begin{aligned}&\frac{1}{\varepsilon }\left[ \widetilde{h}\left( \frac{\det \mathrm {D}G_\varepsilon }{{\overline{\rho }}_{\mathscr {T}}}\right) -\widetilde{h}\left( \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\right) \right] \\&\quad = \frac{1}{\varepsilon }\left[ \widetilde{h}\left( \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\det ({\mathbb {1}}+\varepsilon \mathrm {D}S)\circ G_\boxplus ^n\right) -\widetilde{h}\left( \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\right) \right] \\&\quad {\mathop {\longrightarrow }\limits ^{\varepsilon \searrow 0}} \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\widetilde{h}'\left( \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\right) \left( \lim _{\varepsilon \searrow 0}\frac{\det ({\mathbb {1}}+\varepsilon \mathrm {D}S)}{\varepsilon }\right) \circ G_\boxplus ^n \\&\quad = -\frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}} P\left( \frac{{\overline{\rho }}_{\mathscr {T}}}{\det \mathrm {D}G_\boxplus ^n}\right) {{\mathrm{tr}}}[\mathrm {D}S]\circ G_\boxplus ^n \\&\quad = - \frac{\det \mathrm {D}G_\boxplus ^n}{{\overline{\rho }}_{\mathscr {T}}}\big [P(\rho ^n)\,\nabla \cdot S\big ]\circ G_\boxplus ^n. \end{aligned}$$

Since the piecewise constant function $\det \mathrm {D}G_\boxplus ^n$ has a positive lower bound, the convergence as $\varepsilon \searrow 0$ is uniform on K. Finally, for the potential energy,

$$\begin{aligned} \frac{1}{\varepsilon }\big [V\circ ({\mathrm {id}}+\varepsilon S)\circ G_\boxplus ^n-V\circ G_\boxplus ^n\big ] {\mathop {\longrightarrow }\limits ^{\varepsilon \searrow 0}} \big [\nabla V\cdot S\big ]\circ G_\boxplus ^n. \end{aligned}$$

Again, the convergence is uniform on K. Passing to the limit in the integral (4.8) yields

$$\begin{aligned} 0&\le \int _K \left[ \left( \frac{{\mathrm {id}}-T_\boxplus ^n}{\tau }\right) \cdot S\right] \circ G_\boxplus ^n{\overline{\rho }}_{\mathscr {T}}\,\mathrm {d}\omega \\&\qquad - \int _K \big [P(\rho ^n)\,\nabla \cdot S\big ]\circ G_\boxplus ^n \det \mathrm {D}G_\boxplus ^n\,\mathrm {d}\omega + \int _K \big [\nabla V\cdot S\big ]\circ G_\boxplus ^n{\overline{\rho }}_{\mathscr {T}}\,\mathrm {d}\omega . \end{aligned}$$

The same inequality is true with $-S$ in place of S, hence this inequality is actually an equality. Since $\rho _\boxplus ^n=(G_\boxplus ^n)_\#{\overline{\rho }}_{\mathscr {T}}$, a change of variables $x=S_\boxplus ^n(\omega )$ produces (4.7). $\square$

Corollary 4.5

In addition to the hypotheses of Theorem 4.2, assume that

• (1) $P({\widetilde{\rho }}_\boxplus )\overset{*}{\rightharpoonup }p_*$ in $L^1([0,T]\times \Omega )$;

• (2) each $G_\boxplus ^n$ is injective;

• (3) as $\boxplus \rightarrow 0$, all simplices in the images of ${\mathscr {T}}$ under $G_\boxplus ^n$ have non-degenerate interior angles and tend to zero in diameter, uniformly w.r.t. n.

Then $\rho _*$ satisfies the PDE

$$\begin{aligned} \partial _t\rho _* = \Delta p_* + \nabla \cdot (\rho _*\nabla V) \end{aligned}$$

(4.9)

in the sense of distributions.

Proof

Let a smooth test function $\zeta \in C^\infty _c({\mathbb {R}}^d\rightarrow {\mathbb {R}}^d)$ be given. For each $\boxplus$ and each n, a $\zeta _\boxplus ^n :{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$ with $\zeta _\boxplus ^n\circ G_\boxplus ^n\in \mathcal {D}({\mathscr {T}})$ can be constructed in such a way that

$$\begin{aligned} \zeta _\boxplus ^n\rightarrow \zeta , \quad \nabla \cdot \zeta _\boxplus ^n\rightarrow \nabla \cdot \zeta \end{aligned}$$

(4.10)

uniformly on ${\mathbb {R}}^d$, and uniformly in n as $\boxplus \rightarrow 0$. This follows from our hypotheses on the $\boxplus$-uniform regularity of the Lagrangian meshes: inside the image of $G_\boxplus ^n$, one can simply choose $\zeta _\boxplus ^n$ as the affine interpolation of the values of $\zeta$ at the points $G_\boxplus ^n(\omega _\ell )$. Outside, one can take an arbitrary approximation of $\zeta$ that is compatible with the piecewise-affine approximation on the boundary of $G_\boxplus ^n$’s image; one may even choose $\zeta _\boxplus ^n\equiv \zeta$ at sufficient distance to that boundary. The uniform convergences (4.10) then follow by standard finite element analysis.

Further, let $\eta \in C^\infty _c(0,T)$ be given. For each $t\in ((n-1)\tau ,n\tau ]$, substitute $S(t,x):=\eta (t)\zeta _\boxplus ^n(x)$ into (4.7). Integration of these equalities with respect to $t\in (0,T)$ yields

$$\begin{aligned} \int _0^T\int _{{\mathbb {R}}^d} P({\widetilde{\rho }}_\boxplus )\nabla \cdot S\,\mathrm {d}x\,\mathrm {d}t - \int _0^T\int _{{\mathbb {R}}^d} \nabla V\cdot S\,\mathrm {d}x\,\mathrm {d}t = \int _0^T\int _{{\mathbb {R}}^d} S\cdot {\widetilde{\mathbf {v}}}_\boxplus {\widetilde{\rho }}_\boxplus \,\mathrm {d}x\,\mathrm {d}t. \end{aligned}$$

We pass to the limit $\boxplus \rightarrow 0$ in these integrals. For the first, we use that $P({\widetilde{\rho }})\overset{*}{\rightharpoonup }p_*$ by hypothesis, for the last, we use Theorem 4.2 above. Since any test function $S\in C^\infty _c((0,T)\times \Omega )$ can be approximated in $C^1$ by linear combinations of products $\eta (t)\zeta (x)$ as above, we thus obtain the weak formulation of

$$\begin{aligned} \rho _*\mathbf {v}_* = \nabla p_* + \rho _*\nabla V. \end{aligned}$$

In combination with the continuity Eq. (4.5), we arrive at (4.9). $\square$

Remark 4.6

In principle, our discretization can also be applied to the linear Fokker–Planck equation with $P(r)=r$ and $h(r)=r\log r$. In that case, one automatically has $P({\widetilde{\rho }})\overset{*}{\rightharpoonup }p_*\equiv P(\rho _*)$ thanks to Theorem 4.2. Corollary 4.5 above then provides an a posteriori criterion for convergence: if the Lagrangian mesh does not deform too wildly under the dynamics as the discretization is refined, then the discrete solutions converge to the genuine solution.

Consistency in 2D

In this section, we prove consistency of our discretization in the following sense. Under certain conditions on the spatial discretization ${\mathscr {T}}$, any smooth and positive solution $\rho$ to the initial value problem (1.1) projects to a discrete solution that satisfies the Euler–Lagrange equations up to a controlled error. We restrict ourselves to $d=2$ dimensions.

Smooth Lagrangian Evolution

First, we derive an alternative form of the velocity field $\mathbf {v}$ from (1.4b) in terms of G.

Lemma 5.1

For $\rho =G_\#{\overline{\rho }}$ with a smooth diffemorphism $G :K\rightarrow {{\mathbb {R}}^d}$, we have

$$\begin{aligned} \mathbf {v}[\rho ]\circ G=\mathbf {V}[G] := P'\left( \frac{{\overline{\rho }}}{\det \mathrm {D}G}\right) \, (\mathrm {D}G)^{-T}\left( {{\mathrm{tr}}}_{12}\big [(\mathrm {D}G)^{-1}\mathrm {D}^2G\big ]^T-\frac{\nabla {\overline{\rho }}}{{\overline{\rho }}}\right) - \nabla V \circ G. \end{aligned}$$

(5.1)

Consequently, the Lagrangian map G—relative to the reference density ${\overline{\rho }}$ — for a smooth solution $\rho$ to (1.1) satisfies

$$\begin{aligned} \partial _t G = \mathbf {V}[G]. \end{aligned}$$

(5.2)

Proof

On the one hand,

$$\begin{aligned} \mathrm {D}\big [h'(\rho )\circ G\big ] = \big [\mathrm {D}h'(\rho )\big ]\circ G\,\mathrm {D}G, \end{aligned}$$

and on the other hand, by definition of the push forward,

$$\begin{aligned} \mathrm {D}\big [h'(\rho )\circ G\big ]&= \mathrm {D}h'\left( \frac{{\overline{\rho }}}{\det \mathrm {D}G}\right) \\&= h''\left( \frac{{\overline{\rho }}}{\det \mathrm {D}G}\right) \,\left( \frac{{\overline{\rho }}}{\det \mathrm {D}G}\right) \,\left( \frac{\mathrm {D}{\overline{\rho }}}{{\overline{\rho }}}-{{\mathrm{tr}}}_{12}\big [(\mathrm {D}G)^{-1}\mathrm {D}^2G \big ]\right) \\&= \big [\rho h''(\rho )\big ]\circ G \,\left( \frac{\mathrm {D}{\overline{\rho }}}{{\overline{\rho }}}-{{\mathrm{tr}}}_{12}\big [(\mathrm {D}G)^{-1}\mathrm {D}^2G \big ]\right) . \end{aligned}$$

Hence

$$\begin{aligned} \nabla h'(\rho ) \circ G = \big [\rho h''(\rho )\big ]\circ G \,(\mathrm {D}G)^{-T}\left( \frac{\nabla {\overline{\rho }}}{{\overline{\rho }}}-{{\mathrm{tr}}}_{12}\big [(\mathrm {D}G)^{-1}\mathrm {D}^2G \big ]^T\right) . \end{aligned}$$

Observing that (1.2) implies that $rh''(r)=P'(r)$, we conclude (5.2) directly from (1.4b). $\square$

Discrete Euler–Lagrange Equations in Dimension $d=2$

In the planar case $d=2$, the Euler–Lagrange equation (3.10) above can be rewritten in a more convenient way.

In the following, fix some vertex $\omega _\times$ of the triangulation, which is incident to precisely six triangles. For convenience, we assume that these are labelled $\Delta _0$ to $\Delta _5$ in counter-clockwise order. Similarly, the six neighboring vertices are labeled $\omega _0$ to $\omega _5$ in counter-clockwise order, so that $\Delta _k$ has vertices $\omega _{k}$ and $\omega _{k+1}$, where we set $\omega _6:=\omega _0$.

Using these conventions and recalling Lemma B.2, the expression for the vector $\nu$ in (3.9) simplifies to

$$\begin{aligned} \nu _{\mathscr {T}}^k = - {\mathbb {J}}(G_{k+1}-G_{k}), \quad \text {where}\quad {\mathbb {J}}= \begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$

Summing the Euler–Lagrange equation (3.10) over $\Delta _0$ to $\Delta _5$, we obtain

$$\begin{aligned} {\mathbf {p}}_\times = {\mathbf {J}}_\times , \end{aligned}$$

(5.3)

where the momentum term ${\mathbf {p}}_\times$ and the impulse ${\mathbf {J}}_\times$, respectively, are given by

$$\begin{aligned} {\mathbf {p}}_\times&= \frac{1}{12}\sum _{k=0}^5\mu _{\mathscr {T}}^k \left[ 2\left( \frac{G_\times -G^*_\times }{\tau }\right) +\left( \frac{G_k-G^*_k}{\tau }\right) +\left( \frac{G_{k+1}-G^*_{k+1}}{\tau }\right) \right] \end{aligned}$$

(5.4)

$$\begin{aligned} {\mathbf {J}}_\times&= \sum _{k=0}^5 \mu _{\mathscr {T}}^{k}\bigg [ \frac{1}{2 \mu _{\mathscr {T}}^{k}}P\left( \frac{2\mu _{\mathscr {T}}^k}{\det (G_k-G_\times |G_{k+1}-G_\times )}\right) {\mathbb {J}}(G_{k+1}-G_k) \end{aligned}$$

(5.5)

(5.6)

We shall now prove our main result on consistency. The setup is the following: a sequence of triangulations ${\mathscr {T}}_\varepsilon$ on K, parametrized by $\varepsilon >0$, and a sequence of time steps $\tau _\varepsilon ={\mathcal {O}}(\varepsilon )$ are given. We assume that there is an $\varepsilon$-independent region $K'\subset K$ on which the ${\mathscr {T}}_\varepsilon$ are almost hexagonal in the following sense: each node $\omega _\times \in K'$ of ${\mathscr {T}}_\varepsilon$ has precisely six neighbors—labelled $\omega _0$ to $\omega _5$ in counter-clockwise order—and there exists a rotation $R\in \mathrm {SO}(2)$ such that

$$\begin{aligned} R(\omega _k-\omega _\times ) = \varepsilon \sigma _k + {\mathcal {O}}(\varepsilon ^2) \quad \text {with}\quad \sigma _k = \begin{pmatrix} \cos \frac{\pi }{3}k \\ \sin \frac{\pi }{3}k \end{pmatrix} \end{aligned}$$

(5.7)

for $k=0,1,\ldots ,5$.

Now, let $G :[0,T]\times K\rightarrow {{\mathbb {R}}^d}$ be a given smooth solution to the Lagrangian evolution Eq. (5.2), and fix a time $t\in (0,T)$. For all sufficiently small $\varepsilon >0$, we define maps $G_\varepsilon ,G_\varepsilon ^*\in {\mathcal {A}}_{{\mathscr {T}}_\varepsilon }$ by linear interpolation of the values of $G(t;\cdot )$ and $G(t-\tau ;\cdot )$, respectively, on ${\mathscr {T}}_\varepsilon$. That is, $G_\varepsilon (\omega _\ell )=G(t;\omega _\ell )$ and $G^*_\varepsilon (\omega _\ell )=G(t-\tau ;\omega _\ell )$, at all nodes $\omega _\ell$ in ${\mathscr {T}}_\varepsilon$. Theorem 5.2 below states that the pair $G_\varepsilon ,G_\varepsilon ^*$ is an approximate solution to the discrete Euler–Lagrange equations (5.3) at all nodes $\omega _\times$ of the respective triangulation ${\mathscr {T}}_\varepsilon$ that lie in $K'$.

The hexagonality hypothesis on the ${\mathscr {T}}_\varepsilon$ is strong, but some very strong restriction of ${\mathcal {A}}_{{\mathscr {T}}_\varepsilon }$’s geometry is apparently necessary. See Remark 5.4 following the proof for further discussion.

Theorem 5.2

Under the hypotheses and with the notations introduced above, the Euler–Lagrange equation (5.3) admits the following asymptotic expansion:

$$\begin{aligned} {\mathbf {p}}_\times&= \frac{\sqrt{3}}{2}\varepsilon ^2\,{\overline{\rho }}(\omega _\times )\partial _tG(t;\omega _\times )+{\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

(5.8a)

$$\begin{aligned} {\mathbf {J}}_\times&= \frac{\sqrt{3}}{2}\varepsilon ^2\,{\overline{\rho }}(\omega _\times )\mathbf {V}[G](t;\omega _\times )+{\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

(5.8b)

as $\varepsilon \rightarrow 0$, uniformly at the nodes $\omega _\times \in K'$ of the respective ${\mathscr {T}}_\varepsilon$.

Remark 5.3

Up to an error ${\mathcal {O}}(\varepsilon ^3)$, the geometric pre-factor $\frac{\sqrt{3}}{2}\varepsilon ^2$ equals to one third of the total area of the hexagon with vertices $\omega _0$ to $\omega _5$, and is thus equal to the integral of the piecewise affine hat function with peak at $\omega _\times$.

Proof of Theorem 5.2

Throughout the proof, let $\varepsilon >0$ be fixed; we shall omit the $\varepsilon$-index for ${\mathscr {T}}_\varepsilon$ and $\tau _\varepsilon$. First, we fix a node $\omega _\times$ of ${\mathscr {T}}\cap K'$. Thanks to the equivariance of both (5.2) and (5.3) under rigid motions of the domain, we may assume that R in (5.7) is the identity, and that $\omega _\times =0$.

We collect some relations that are helpful for the calculations that follow. Trivially,

$$\begin{aligned} \sum _{k=0}^5\sigma _k=0, \quad \sum _{k=0}^5\omega _k={\mathcal {O}}(\varepsilon ^2). \end{aligned}$$

(5.9)

Moreover, we have that

$$\begin{aligned} |\Delta _k| = \det (\omega _k|\omega _{k+1}) = \varepsilon ^2\det (\sigma _k|\sigma _{k+1}) + {\mathcal {O}}(\varepsilon ^3) = \frac{\sqrt{3}}{4}\varepsilon ^2+{\mathcal {O}}(\varepsilon ^3). \end{aligned}$$

(5.10)

On the other hand, by definition of $\mu _{\mathscr {T}}^k$ in (3.1), it follows that

(5.11)

Combining (5.10) and (5.11) yields

$$\begin{aligned} \mu _{\mathscr {T}}^k = \varepsilon ^2\left( \frac{\sqrt{3}}{4}{\overline{\rho }}_\times +{\mathcal {O}}(\varepsilon )\right) . \end{aligned}$$

(5.12)

In accordance with the definition of $G_\varepsilon$ and $G_\varepsilon ^*$ from G detailed above, let $G_\times :=G(t,\omega _\times )$ and $G^*_\times =G(t-\tau ,\omega _\times )$, and define $G_k$, $G_k^*$ for $k=0,\ldots ,5$ in the analogous way. Further, we introduce $\mathrm {D}G_\times =\mathrm {D}G(t,\omega _\times )$, $\mathrm {D}^2G_\times =\mathrm {D}^2G(t,\omega _\times )$, $\partial _tG_\times =\partial _tG(t,\omega _\times )$.

To perform an expansion in the momentum term, first observe that

$$\begin{aligned} G(t-\tau ;\omega _k) = G(t;\omega _k) - \tau \partial _t G(t;\omega _k) + {\mathcal {O}}(\tau ^2), \end{aligned}$$

for each $k=0,1,\ldots ,5$, and so, using that $\tau ={\mathcal {O}}(\varepsilon )$ by hypothesis,

$$\begin{aligned} \frac{G_k-G_k^*}{\tau }= \partial _tG(t;\omega _k) + {\mathcal {O}}(\tau ) = \partial _tG_\times + {\mathcal {O}}(\varepsilon ) + {\mathcal {O}}(\tau ) = \partial _tG_\times + {\mathcal {O}}(\varepsilon ). \end{aligned}$$

Using (5.12) and then (5.9) yields

$$\begin{aligned} {\mathbf {p}}_\times&=\frac{1}{12\tau }\sum _{k=0}^5 \varepsilon ^2\left( \frac{\sqrt{3}}{4}{\overline{\rho }}_\times +{\mathcal {O}}(\varepsilon )\right) \big [4\partial _tG_\times +{\mathcal {O}}(\varepsilon )\big ] \\&=\frac{\sqrt{3}}{2}\varepsilon ^2\,{\overline{\rho }}_\times \partial _tG_\times + {\mathcal {O}}(\varepsilon ^3). \end{aligned}$$

This is (5.8a).

For the impulse term, we start with a Taylor expansion to second order in space:

$$\begin{aligned} G_k = G_\times + \mathrm {D}G_\times \omega _k + \frac{1}{2} \mathrm {D}^2G_\times :[\omega _k]^2 + {\mathcal {O}}(\varepsilon ^3). \end{aligned}$$

We combine this with the observation that $(\omega _k|\omega _{k+1})^{-1}={\mathcal {O}}(\varepsilon ^{-1})$ to obtain:

$$\begin{aligned}&\frac{\mu _{\mathscr {T}}^k}{\det (G_k-G_\times |G_{k+1}-G_\times )} \\&\quad = \frac{\det (\omega _k|\omega _{k+1})}{\det \mathrm {D}G_\times } \frac{{\overline{\rho }}_\times +\varepsilon \nabla {\overline{\rho }}_\times \cdot \frac{\sigma _k+\sigma _{k+1}}{3}+{\mathcal {O}}(\varepsilon ^2)}{\det \big [(\omega _k|\omega _{k+1})+\frac{1}{2}(\mathrm {D}G_\times )^{-1}\big (\mathrm {D}^2G_\times :[\omega _k]^2\big |\mathrm {D}^2G_\times :[\omega _{k+1}]^2\big )+{\mathcal {O}}(\varepsilon ^3)\big ]} \\&\quad = \frac{{\overline{\rho }}_\times }{\det \mathrm {D}G_\times } \frac{1+\displaystyle {\varepsilon \frac{\nabla {\overline{\rho }}_\times }{{\overline{\rho }}_\times }\cdot \frac{\sigma _k+\sigma _{k+1}}{3}}+{\mathcal {O}}(\varepsilon ^2)}{\det \big [{\mathbb {1}}+\frac{1}{2}(\mathrm {D}G_\times )^{-1}\big (\mathrm {D}^2G_\times :[\omega _k]^2\big |\mathrm {D}^2G_\times :[\omega _{k-1}]^2\big ) \,(\omega _k|\omega _{k+1})^{-1}+{\mathcal {O}}(\varepsilon ^2) \big ]} \\&\quad =\frac{{\overline{\rho }}_\times }{\det \mathrm {D}G_\times }\left( 1+\varepsilon \left\{ \chi _k-\frac{1}{2}\vartheta _k\right\} +{\mathcal {O}}(\varepsilon ^2)\right) , \end{aligned}$$

where

$$\begin{aligned} \chi _k&= \frac{\nabla {\overline{\rho }}_\times }{{\overline{\rho }}_\times }\cdot \frac{\sigma _k+\sigma _{k+1}}{3}, \\ \vartheta _k&= {{\mathrm{tr}}}\left[ \big ((\mathrm {D}G_\times )^{-1}\mathrm {D}^2G_\times :[\sigma _k]^2\big |(\mathrm {D}G_\times )^{-1}\mathrm {D}^2G_\times :[\sigma _{k+1}]^2\big )\,(\sigma _k|\sigma _{k+1})^{-1}\right] . \end{aligned}$$

Plugging this in leads to

$$\begin{aligned}&\sum _{k=0}^5\left\{ \frac{1}{2} P\left( \frac{{\overline{\rho }}_\times }{\det \mathrm {D}G_\times }\right) + \frac{\varepsilon }{2}P'\left( \frac{{\overline{\rho }}_\times }{\det \mathrm {D}G_\times }\right) \left\{ \chi _k-\frac{1}{2}\vartheta _k\right\} + {\mathcal {O}}(\varepsilon ^2) \right\} {\mathbb {J}}\mathrm {D}G_\times (\omega _{k+1}-\omega _{k}) \\&=\frac{1}{2} P\left( \frac{{\overline{\rho }}_0}{\det \mathrm {D}G_\times }\right) {\mathbb {J}}\mathrm {D}G_\times \left( \sum _{k=0}^5 (\omega _{k+1}-\omega _{k})\right) \\&\quad + \frac{\varepsilon ^2}{4}P'\left( \frac{{\overline{\rho }}_\times }{\det \mathrm {D}G_\times }\right) {\mathbb {J}}\mathrm {D}G_\times {\mathbb {J}}^T\left( \sum _{k=0}^5 \left\{ 2\chi _k-\vartheta _k\right\} {\mathbb {J}}(\sigma _{k+1}-\sigma _{k})\right) + {\mathcal {O}}(\varepsilon ^3) \\&= 0 + \frac{\sqrt{3}}{2}\varepsilon ^2P'\left( \frac{{\overline{\rho }}_\times }{\det \mathrm {D}G_\times }\right) \, (\mathrm {D}G_\times )^{-T}\left\{ {{\mathrm{tr}}}_{12}\big [(\mathrm {D}G_\times )^{-1}\mathrm {D}^2G_\times \big ]^T-\frac{\nabla \rho _\times }{\rho _\times }\right\} + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

where we have use the auxiliary algebraic results from Lemmas B.2, B.3 and B.4.

For the remaining part of the impulse term, a very rough approximation is sufficient:

$$\begin{aligned} \nabla V(g) = \nabla V(G_\times ) + {\mathcal {O}}(\varepsilon ) \end{aligned}$$

holds for any g that is a convex combination of $G_\times ,G_0,\ldots ,G_5$, where the implicit constant is controlled in terms of the supremum of $\mathrm {D}^2V$ and $\mathrm {D}G$ on $K'$. With that, we simply have, using again (5.12):

Together, this yields (5.8b). $\square$

Remark 5.4

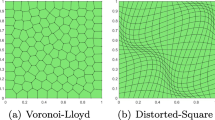
The hypotheses of Theorem (5.2) require that the ${\mathscr {T}}_\varepsilon$ are almost hexagonal on $K'$. This seems like a technical hypothesis that simplifies calculations, but apparently, some strong symmetry property of the ${\mathscr {T}}_\varepsilon$ is necessary for the validity of the result.

To illustrate the failure of consistency—at least in the specific form considered here—assume that $V\equiv 0$ and ${\overline{\rho }}\equiv 1$, and consider a sequence of triangulations ${\mathscr {T}}_\varepsilon$ for which there is a node $\omega _\times$ such that (5.7) holds with the $\sigma _k$ being replaced by a different six-tuple of vectors $\sigma '_k$. Repeating the steps of the proof above, it is easily seen that ${\mathbf {p}}_\times =a\varepsilon ^2\,\partial _tG(t;\omega _\times )+{\mathcal {O}}(\varepsilon ^3)$, with an $\varepsilon$-independent constant $a>0$ in place of $\sqrt{3}/2$, and that

$$\begin{aligned} {\mathbf {J}}_\times =-\frac{\varepsilon ^2}{4} P'\left( \frac{1}{\det \mathrm {D}G_\times }\right) \,(\mathrm {D}G_\times )^{-T} \sum _{k=0}^5\vartheta '_k{\mathbb {J}}(\sigma _{k+1}'-\sigma _k')+{\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

with

$$\begin{aligned} \vartheta _k' = {{\mathrm{tr}}}\left[ \big ((\mathrm {D}G_\times )^{-1}\mathrm {D}^2G_\times :[\sigma _k']^2\big |(\mathrm {D}G_\times )^{-1}\mathrm {D}^2G_\times :[\sigma _{k+1}']^2\big )\,(\sigma _k'|\sigma _{k+1}')^{-1}\right] . \end{aligned}$$

If a result of the form (5.8b)—with $\sqrt{3}/2$ replaced by a—was true, then this implies in particular that

$$\begin{aligned} \sum _{k=0}^5\vartheta '_k{\mathbb {J}}(\sigma _{k+1}'-\sigma _k') = a'{{\mathrm{tr}}}_{12}\big [(\mathrm {D}G_\times )^{-1}\mathrm {D}^2G_\times \big ] \end{aligned}$$

(5.13)

holds with some constant $a'>0$ for arbitrary matrices $\mathrm {D}G_\times \in {\mathbb {R}}^{2\times 2}$ of positive determinant and tensors $\mathrm {D}^2 G_\times \in {\mathbb {R}}^{2\times 2\times 2}$ that are symmetric in the second and third component. A specific example for which (5.13) is not true is given by

$$\begin{aligned} \sigma _0' = {1\atopwithdelims ()0} = -\sigma _3',\quad \sigma _1' = {\frac{1}{2}\atopwithdelims ()\frac{1}{2}} = -\sigma _4',\quad \sigma _2' = {0\atopwithdelims ()1} = -\sigma _5', \end{aligned}$$

(5.14)

in combination with $\mathrm {D}G_\times ={\mathbb {1}}$, and a $\mathrm {D}^2G_\times$ that is zero except for two ones, at the positions (1, 2, 2) and (2, 1, 1). In Lemma B.5, we show that the left-hand side in (5.13) equals to $1\atopwithdelims ()1$; on the other hand, the right-hand side is clearly zero.

Note that this counter-example is significant, insofar as the skew (in fact, degenerate) hexagon described by the $\sigma _k'$ in (5.14) corresponds to a popular method for triangulation of the plane.

Numerical Simulations in $d=2$

Implementation

The Euler–Lagrange equations for the $d=2$-dimensional case have been derived in (5.3). We perfom a small modification in the potential term in order to simplify calculations with presumably minimal loss in accuracy:

$$\begin{aligned} \mathbf {Z}_\times [G;G^*]&= \sum _{k=0}^5\frac{\mu _{\mathscr {T}}^k}{12} \left[ 2\left( \frac{G_\times -G^*_\times }{\tau }\right) +\left( \frac{G_k-G^*_k}{\tau }\right) +\left( \frac{G_{k+1}-G^*_{k+1}}{\tau }\right) \right] \\&\quad + \sum _{k=0}^5 \bigg [ \frac{1}{2}\widetilde{h}'\left( \frac{\det (G_k-G_\times |G_{k+1}-G_\times )}{2\mu _{\mathscr {T}}^k}\right) {\mathbb {J}}(G_{k+1}-G_k)\\&\quad + \frac{\mu _{\mathscr {T}}^{k}}{6}\nabla V(G_{k+\frac{1}{2}})\bigg ], \end{aligned}$$

with the short-hand notation

$$\begin{aligned} G_{k+\frac{1}{2}} = \frac{1}{3}(G_\times +G_k+G_{k+1}). \end{aligned}$$

On the main diagonal, the Hessian amounts to

$$\begin{aligned} \mathbf {H}_{\times \times }[G]&= \left( \sum _{k=0}^5\frac{\mu _{\mathscr {T}}^k}{6\tau }\right) \mathbb {1}_2 \\&\quad + \sum _{k=0}^5\frac{1}{4\mu _{\mathscr {T}}^k}\widetilde{h}''\left( \frac{\det (G_k-G_\times |G_{k+1}-G_\times )}{2\mu _{\mathscr {T}}^k}\right) \big [{\mathbb {J}}(G_{k+1}-G_k)\big ]\big [{\mathbb {J}}(G_{k+1}-G_k)\big ]^\top \!\\&\quad + \sum _{k=0}^5 \frac{\mu _{\mathscr {T}}^{k}}{18}\nabla ^2 V(G_{k+\frac{1}{2}}) \end{aligned}$$

Off the main diagonal, the entries of the Hessian are given by

$$\begin{aligned} \mathbf {H}_{\times k}[G]&= \frac{\mu _{\mathscr {T}}^k+\mu _{\mathscr {T}}^{k-1}}{12\tau }\mathbb {1}_2 \\&\quad + \frac{1}{4\mu _{\mathscr {T}}^k}\widetilde{h}''\left( \frac{\det (G_k-G_\times |G_{k+1}-G_\times )}{2\mu _{\mathscr {T}}^k}\right) \big [{\mathbb {J}}(G_{k+1}-G_k)\big ]\big [{\mathbb {J}}(G_{k+1}-G_\times )\big ]^\top \!\\&\quad - \frac{1}{4\mu _{\mathscr {T}}^{k-1}}\widetilde{h}''\left( \frac{\det (G_{k-1}-G_\times |G_{k}-G_\times )}{2\mu _{\mathscr {T}}^{k-1}}\right) \big [{\mathbb {J}}(G_{k}-G_{k-1})\big ]\big [{\mathbb {J}}(G_{k-1}-G_\times )\big ]^\top \!\\&\quad + \frac{\mu _{\mathscr {T}}^{k}}{18}\nabla ^2 V(G_{k+\frac{1}{2}}) + \frac{\mu _{\mathscr {T}}^{k-1}}{18}\nabla ^2 V(G_{k-\frac{1}{2}}). \end{aligned}$$

The scheme consists of an inner (Newton) and an outer (time stepping) iteration. We start from a given initial density $\rho _0$ and define the solution at the next time step inductively by applying Newton’s method in the inner iteration. To this end we initialise $G^{(0)}:=G^n$ with $G^n$, the solution at the nth time step, and define inductively

$$\begin{aligned} G^{(s+1)} := G^{(s)} + \delta G^{(s+1)} , \end{aligned}$$

where the update $\delta G^{(s+1)}$ is the solution to the linear system

$$\begin{aligned} \mathbf {H}[G^{(s)}] \delta G^{(s+1)} = -\mathbf {Z}[G^{(s)};G^n] . \end{aligned}$$

The effort of each inner iteration step is essentially determined by the effort to invert the sparse matrix $\mathbf {H}[G^{(s)}]$. As soon as the norm of $\delta G^{(s+1)}$ drops below a given stopping threshold, define $G^{n+1}:=G^{(s+1)}$ as approximate solution in the $n+1$st time step.

In all experiments the stopping criterion in the Newton iteration is set to $10^{-9}$.

Numerical Experiments

In this section we present results of our numerical experiments for (1.1) with a cubic porous-medium nonlinearity $P(r)=r^3$ and different choices for the external potential V,

$$\begin{aligned} \partial _t\rho = \Delta (u^3) + \nabla \cdot (u\nabla V). \end{aligned}$$

(6.1)

Numerical experiment 1: unconfined evolution of Barenblatt profile

As a first example, we consider the “free” cubic porous medium equation, that is (6.1) with $V\equiv 0$. It is well-known (see, e.g., Vazquez [38]) that in the long-time limit $t\rightarrow \infty$, arbitrary solutions approach a self-similar one,

$$\begin{aligned} \rho ^*(t,x) = t^{-d\alpha }{\mathcal {B}}_3\big (t^{-\alpha }x\big ) \quad \text {with}\quad \alpha =\frac{1}{6}, \end{aligned}$$

(6.2)

where ${\mathcal {B}}_3$ is the associated Barenblatt profile

$$\begin{aligned} {\mathcal {B}}_3(z) = \left( C_3-\frac{1}{3}\Vert z\Vert ^2\right) _+^{\frac{1}{2}}, \end{aligned}$$

(6.3)

where $C_3=(2\pi )^{-\frac{2}{3}}\approx 0.29$ is chosen to normalize ${\mathcal {B}}_3$’s mass to unity.

Fig. 2

Numerical experiment 1: fully discrete evolution of our approximation for the self-similar solution to the free porous medium equation. Snapshots are taken at times $t=0.02$, $t=0.1$, $t=0.25$, and $t=2.0$

In this experiment, we are only interested in the quality of the numerical approximation for the self-similar solution (6.2). To reduce numerical effort, we impose a four-fold symmetry of the approximation: we use the quarter circle as computational domain K, and interprete the discrete function thereon as one of four symmetric pieces of the full discrete solution. To preserve reflection symmetry over time, homogeneous Neumann conditions are imposed on the artificial boundaries. This is implemented by reducing the degrees of freedom of the nodes along the x- and y-axes to tangential motion. We initialize our simulation with a piecewise constant approximation of the profile of $\rho ^*$ from (6.3) at time $t=0.01$. We choose a time step $\tau =0.001$ and the final time $T=2$. In Fig. 2, we have collected snapshots of the approximated density at different instances of time. The Barenblatt profile of the solution is very well pertained over time.

Remark 6.1

It takes less than 2 min to complete this simulation on standard laptop (Matlab code on a mid-2013 MacBook Air 11” with 1.7 GHz Intel Core i7 processor).

Fig. 3

Numerical experiment 1: comparison of the discrete solution (interpolated surface plots with triangulation) with the Barenblatt profile (solid and dashed black lines along the identity) at different times

Fig. 4

Numerical experiment 1: decay of the energy of the discrete solution in comparison with the analytical decay $t^{-2/3}$ of the Barenblatt solution (left). Numerical convergence for fixed ratio $\tau /h_\mathrm{max}^2=0.4$ (right)

Figure 3 shows surface plots of the discrete solution at different times in comparison with the Barenblatt profile at the respective time. By construction of the scheme, the initial mass is exactly conserved in time as the discrete solution propagates. The left plot in Fig. 4 shows the decay in the energy and gives quantitative information about the difference of the discrete solution to the analytical Barenblatt solution. The numerical solution shows good agreement with the analytical energy decay rate $c=2/3$.

We also compute the $l_1$-error of the discrete solution to the exact Barenblatt profile and observe that it remains within the order of the fineness of the triangulation. The mass of the discrete solution is perfectly conserved, as guaranteed by the construction of our method.

To estimate the convergence order of our method, we run several experiments with the above initial data on different meshes. We fix the ratio $\tau /h_\mathrm{max}^2=0.4$ and compute the $l_1$-error at time $T=0.2$ on triangulations with $h_\mathrm{max}=0.2,\,0.1,\,0.05,\,0.025.$ We expect the error to decay as a power of $h_\mathrm{max}$. The double logarithmic plot should reveal a line with its slope indicating the numerical convergence order. The right plot in Fig. 4 shows the result, the estimated numerical convergence order which is obtained from a least-squares fitted line through the points is equal to 1.18. This indicates first order convergence of the scheme with respect to the spatial discretisation parameter $h_\mathrm{max}$.

Numerical experiment 2: Asymptotic self-similarity

In our second example, we are still concerned with the free cubic porous medium Eq. (6.1) with $V\equiv 0$. This time, we wish to give an indication that the discrete approximation of the self-similar solution from (6.2) from the previous experiment might inherit the global attractivity of its continuous counterpart. More specifically, we track the discrete evolution for the initial datum

$$\begin{aligned} \rho _0(x,y)= 3000(x^2+y^2)\exp [-5(|x|+|y|)]+0.1 \end{aligned}$$

(6.4)

until time $T=0.1$ and observe that it appears to approach the self-similar solution from above. Snapshots of the simulation are collected in Fig. 5.

Fig. 5

Numerical experiment 2: fully discrete evolution for the initial density from (6.4) under the free porous medium equation. Snapshots are taken at times $t=0.001$, $t=0.005$, $t=0.01$, $t=0.025$, and $t=0.1$

Numerical experiment 3: two peaks merging into one under the influence of a confining potential

In this example we consider as initial condition two peaks, connected by a thin layer of mass, given by

$$\begin{aligned} \rho _0(x,y)= & {} \exp [-\,20((x\,-\,0.35)^2\,+\,(y\,-\,0.35)^2)]\,+\,\exp [-\,20((x\,+\,0.35)^2\nonumber \\&+\,(y\,+\,0.35)^2 )]\,+\,0.001. \end{aligned}$$

(6.5)

We choose a triangulation of the square $[-1.5,1.5]^2$ and initialise the discrete solution piecewise constant in each triangle, with a value corresponding to (6.5), evaluated in the centre of mass of each triangle. We solve the porous medium equation with a confining potential, i.e. (1.1) with $P(r)=r^m$ and $V(x,y)=5(x^2+y^2)/2$. The time step is $\tau =0.001$ and the final time is $T=0.2.$

Fig. 6

Numerical experiment 3: evolution of two peaks merging under the porous medium equation with a confining potential

Figure 6 shows the evolution from the initial density. As time increases the peaks smoothly merge into each other. As the thin layer around the peaks is also subject to the potential the triangulated domain shrinks in time. Even if we do not know how to prevent theoretically the intersection of the images of the discrete Lagrangian maps, this seems not to be a problem in practice. As time evolves, the discrete solution approaches the steady state Barenblatt profile given by

$$\begin{aligned} {\mathcal {B}}(z) = \left( C-\frac{5}{3} ||z||^2 \right) _+^{\frac{1}{2}}, \end{aligned}$$

(6.6)

where C is chosen as the mass of the density. The plot in Fig. 7 shows the exponential decay of the $l_1$-distance of the discrete solution to the steady state Barenblatt profile (6.6). We observe that the decay agrees very well with the analytically predicted decay $\exp (-5t)$ until $t=0.08$. For larger times, one would monitor triangle quality numerically, and re-mesh, locally coarsening the triangulation where necessary.

Fig. 7

Numerical experiment 3: two merging peaks: plot of the $l_1$-distance of the discrete solution to the steady state Barenblatt profile in comparison with the analytical decay $c\exp (-5t)$

Numerical experiment 4: one peak splitting under the influence of a quartic potential

We consider as the initial condition

$$\begin{aligned} \rho _0(x,y)=1-(x^2+y^2). \end{aligned}$$

(6.7)

We choose a triangulation of the unit circle and initialise the discrete solution piecewise constant in each triangle, with a value corresponding to (6.7), evaluated in the centre of mass of each triangle. We solve the porous medium equation with a quartic potential, i.e. (1.1) with $P(r)=r^m$ and $V(x)=5(x^2+(1-y^2)^2)/2$. The time step is $\tau =0.005$ and the final time is $T=0.02.$

Figure 8 shows the evolution of the initial density. As time increases the initial density is progressively split, until two new maxima emerge which are connected by a thin layer. For larger times, when certain triangles become excessively distorted, one would monitor triangle quality numerically, and re-mesh, locally refining the triangulation where necessary.

Fig. 8

Numerical experiment 4: evolution of the initial density under the porous medium equation with a quartic potential

Appendices

Appendix A: Proof of the Lagrangian representation

Proof of Lemma 1.1

We verify that the density function given by $(G_t^{-1})_{\#}\rho _t$ on $K\subset {{\mathbb {R}}^d}$ is constant with respect to time t; the identity (1.6) then follows since

$$\begin{aligned} \rho _t = (G_t\circ G_t^{-1})_\#\rho _t = (G_t)_\#\big [(G_t^{-1})_{\#}\rho _t\big ] = (G_t)_\#\big [(G_0^{-1})_\#\rho ^0\big ] = (G_t)_\#{\overline{\rho }}. \end{aligned}$$

Firstly, from the definition of the inverse,

$$\begin{aligned} G_t^{-1}\circ G_t = {\mathrm {id}}\end{aligned}$$

for all t, differentiating with respect to time yields

$$\begin{aligned} \mathrm {D}(G_t^{-1}) \circ G_t\, \partial _{t} G_t + \partial _{t} (G_t^{-1}) \circ G_t = 0, \end{aligned}$$

and so, using (1.5) and (1.4b),

$$\begin{aligned} \partial _{t} (G_t^{-1}) = - \mathrm {D}(G_t^{-1}) (\partial _{t} G_t \circ G_t^{-1}) = - \mathrm {D}(G_t^{-1})\mathbf {v}[\rho _t]. \end{aligned}$$

(A.1)

Now, let $\varphi$ be a smooth test function, and consider

$$\begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}t} \int \varphi \,(G_t^{-1})_{\#} \rho _t = \frac{\mathrm {d}}{\mathrm {d}t} \int (\varphi \circ G_t^{-1}) \rho _t \\&\qquad = \int (\varphi \circ G_t^{-1}) \partial _{t} \rho _t + \int \mathrm {D}\varphi \circ G_t^{-1} \partial _{t} (G_t^{-1}) \rho _t \\&\qquad = -\int (\varphi \circ G_t^{-1}) [\nabla \cdot (\rho _t v(\rho _t))] \\&\qquad \quad - \int (\mathrm {D}\varphi \circ G_t^{-1})\,\mathrm {D}(G_t^{-1})\,v(\rho _t) \rho _t&\text {by }(1.1) \text { and }(1.5) \\&\qquad = \int (\mathrm {D}\varphi \circ G_t^{-1}) \mathrm {D}(G_t^{-1}) \,[v(\rho _t) - v(\rho _t)] \rho _t&\text {integrating by parts} \\&\qquad = 0. \end{aligned}$$

As $\varphi$ was arbitrary, $(G_t^{-1})_{\#}\rho _t$ is constant with respect to time. $\square$

Appendix B: Technical lemmas

Lemma B.1

Given $g_0,g_1,\ldots ,g_d\in {\mathbb {R}}^d$, then

(B.1)

Proof

Thanks to the symmetry of the integral with respect to the exchange of the components $\omega _j$, the left-hand side of (B.1) equals to

(B.2)

We calculate the integrals, using Fubini’s theorem. First integral:

Second integral:

Third integral:

Substitute this into (B.2):

$$\begin{aligned}&\left( 1-\frac{2}{d+1}+\frac{d^2+d}{(d+1)(d+2)}\right) \Vert g_0\Vert ^2 +\left( \frac{2}{d+1}-\frac{2d+2}{(d+1)(d+2)}\right) \sum _{1\le j\le d}g_0\cdot g_j \\&\qquad +\frac{2}{(d+1)(d+2)}\sum _{1\le j\le d}\Vert g_j\Vert ^2 +\frac{2}{(d+1)(d+2)}\sum _{1\le i<j\le d}g_i\cdot g_j\\&\quad =\frac{2}{(d+1)(d+2)}\left( \Vert g_0\Vert ^2 + \sum _{1\le j\le d}g_0\cdot g_j + \sum _{1\le j\le d}\Vert g_j\Vert ^2 + \sum _{1\le i<j\le d}g_i\cdot g_j \right) . \end{aligned}$$

Collecting terms yields the right-hand side of (B.1). $\square$

Lemma B.2

For each $A\in {\mathbb {R}}^{2\times 2}$, we have ${\mathbb {J}}A{\mathbb {J}}^T=(\det A)\,A^{-T}$.

Proof

This is verified by direct calculation:

$$\begin{aligned} {\mathbb {J}}A{\mathbb {J}}^T = \begin{pmatrix} 0 &{} -1 \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{pmatrix} \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix} = \begin{pmatrix} a_{22} &{} -a_{21} \\ -a_{12} &{} a_{11} \end{pmatrix} = (\det A)\, A^{-T}. \end{aligned}$$

$\square$

Lemma B.3

With $\sigma _k\in {\mathbb {R}}^2$ defined as in (5.7), we have that

$$\begin{aligned} \sum _{k=0}^5{\mathbb {J}}(\sigma _{k}-\sigma _{k+1}) \left( \frac{\sigma _k+\sigma _{k+1}}{3}\right) ^T = \sqrt{3}\ {\mathbb {1}}. \end{aligned}$$

Proof

With the abbreviations $\phi _x=\frac{\pi }{3}x$ and $\psi =\frac{\pi }{3}$:

$$\begin{aligned} \sum _{k=0}^5{\mathbb {J}}(\sigma _{k}-\sigma _{k+1}) \left( \frac{\sigma _k+\sigma _{k+1}}{3}\right) ^T&= \frac{1}{3}\sum _{k=0}^5 {\sin \phi _{k+1}-\sin \phi _k\atopwithdelims ()\cos \phi _k-\cos \phi _{k+1}}{\cos \phi _k+\cos \phi _{k+1}\atopwithdelims ()\sin \phi _k+\sin \phi _{k+1}}^T \\&= \frac{1}{3}\sum _{k=0}^5\left( 2\sin \frac{\psi }{2}\right) {\cos \phi _{k+\frac{1}{2}}\atopwithdelims ()\sin \phi _{k+\frac{1}{2}}} \,\left( 2\cos \frac{\psi }{2}\right) {\cos \phi _{k+\frac{1}{2}}\atopwithdelims ()\sin \phi _{k+\frac{1}{2}}}^T \\&= \frac{\sin \psi }{3}\sum _{k=0}^5 \begin{pmatrix} 2\cos ^2\phi _{k+\frac{1}{2}} &{} 2\cos \phi _{k+\frac{1}{2}}\sin \phi _{k+\frac{1}{2}} \\ 2\cos \phi _{k+\frac{1}{2}}\sin \phi _{k+\frac{1}{2}} &{} 2\sin ^2\phi _{k+\frac{1}{2}} \end{pmatrix}\\&= \frac{\sqrt{3}}{6} \sum _{k=0}^5\left[ {\mathbb {1}}+ \begin{pmatrix} \cos \phi _{2k+1} &{} \sin \phi _{2k+1} \\ \sin \phi _{2k+1} &{} -\cos \phi _{2k+1} \end{pmatrix} \right] = \sqrt{3}\ {\mathbb {1}}. \end{aligned}$$

$\square$

Lemma B.4

Let the scheme $B:=(b_{pqr})_{p,q,r\in \{1,2\}}\in {\mathbb {R}}^{2\times 2\times 2}$ of eight numbers $b_{pqr}\in {\mathbb {R}}$ be symmetric in the last two indices, $b_{pqr}=b_{prq}$. With $\sigma _k\in {\mathbb {R}}^2$ defined as in (5.7), we have that

$$\begin{aligned} \sum _{k=0}^5 {{\mathrm{tr}}}\big [\big (\sigma _k\big |\sigma _{k+1}\big )^{-1}\big (B:[\sigma _k]^2\big |B:[\sigma _{k+1}]^2\big )\big ]\,{\mathbb {J}}(\sigma _{k}-\sigma _{k+1}) =2\sqrt{3}{{\mathrm{tr}}}_{12}[B]^T. \end{aligned}$$

(B.3)

Proof

In principle, this lemma can be verified by a direct calculation, by writing out the six terms in the sum explicitly and using trigonometric identities. Below, we give a slightly more conceptual proof, in which we use symmetry arguments to reduce the number of expressions significantly.

For the matrix involving B, we obtain

$$\begin{aligned}&\big (B:[\sigma _k]^2\big |B:[\sigma _{k+1}]^2\big ) \\&= \begin{pmatrix} b_{111}\sigma _{k,1}^2+b_{122}\sigma _{k,2}^2+2b_{112}\sigma _{k,1}\sigma _{k,2} &{} b_{111}\sigma _{k+1,1}^2+b_{122}\sigma _{k+1,2}^2+2b_{112}\sigma _{k+1,1}\sigma _{k+1,2} \\ b_{211}\sigma _{k,1}^2+b_{222}\sigma _{k,2}^2+2b_{212}\sigma _{k,1}\sigma _{k,2} &{} b_{211}\sigma _{k+1,1}^2+b_{222}\sigma _{k+1,2}^2+2b_{212}\sigma _{k+1,1}\sigma _{k+1,2} \end{pmatrix}, \end{aligned}$$

while clearly

$$\begin{aligned} \big (\sigma _k\big |\sigma _{k+1}\big )^{-1} = \frac{2}{\sqrt{3}} \begin{pmatrix} \sigma _{k+1,2} &{} -\sigma _{k+1,1} \\ -\sigma _{k,2} &{} \sigma _{k,1} \end{pmatrix}. \end{aligned}$$

The sum of the diagonal entries of the matrix product are easily calculated,

$$\begin{aligned} T_k:={{\mathrm{tr}}}\big [\big (\sigma _k\big |\sigma _{k+1}\big )^{-1}\big (B:[\sigma _k]^2\big |B:[\sigma _{k+1}]^2\big )\big ] = \frac{2}{\sqrt{3}}\sum _{p,q,r=1}^2 b_{pqr}\gamma _{pqr,k}, \end{aligned}$$

with the trigonometric expressions

$$\begin{aligned}&\gamma _{111,k}=\sigma _{k,1}^2\sigma _{k+1,2}-\sigma _{k+1,1}^2\sigma _{k,2},\quad \gamma _{122,k}=\sigma _{k,2}^2\sigma _{k+1,2}-\sigma _{k+1,2}^2\sigma _{k,2}, \\&\gamma _{112,k}=\gamma _{121,k}=\sigma _{k,1}\sigma _{k,2}\sigma _{k+1,2}-\sigma _{k+1,1}\sigma _{k+1,2}\sigma _{k,2}, \\&\gamma _{211,k}=\sigma _{k+1,1}^2\sigma _{k,1}-\sigma _{k,1}^2\sigma _{k+1,1},\quad \gamma _{222,k}=\sigma _{k+1,2}^2\sigma _{k,1}-\sigma _{k,2}^2\sigma _{k+1,1},\\&\gamma _{212,k}=\gamma _{221,k}=\sigma _{k+1,1}\sigma _{k+1,2}\sigma _{k,1}-\sigma _{k,1}\sigma _{k,2}\sigma _{k+1,1}. \end{aligned}$$

To key step is to calculate the sum over $k=0,1,\ldots ,5$ of the products of $T_k$ with the respective vector

$$\begin{aligned} \eta _k ={\mathbb {J}}(\sigma _{k}-\sigma _{k+1})= \begin{pmatrix} \sigma _{k+1,2}-\sigma _{k,2}\\ \sigma _{k,1}-\sigma _{k+1,1} \end{pmatrix}. \end{aligned}$$

Several simplifications of this sum can be performed, thanks to the particular form of the $\gamma _{pqr,k}$ and elementary trigonometric identities. First, observe that $\sigma _{k+3}=-\sigma _k$, and hence that $\gamma _{pqr,k+3}=-\gamma _{pqr,k}$. Since further $\eta _{k+3}=-\eta _k$, it follows that

$$\begin{aligned} \gamma _{pqr,k+3}\eta _{k+3}=\gamma _{pqr,k}\eta _k. \end{aligned}$$

(B.4)

Second, $\eta$ can be evaluated explicitly for $k=1,2,3$:

$$\begin{aligned} \eta _0 =\frac{1}{2} \begin{pmatrix} \sqrt{3} \\ 1 \end{pmatrix}, \quad \eta _1 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \quad \eta _2 =\frac{1}{2} \begin{pmatrix} -\sqrt{3} \\ 1 \end{pmatrix}. \end{aligned}$$

(B.5)

Third, since $\sigma _{0,1}=-\sigma _{3,1}$ and $\sigma _{1,1}=-\sigma _{2,1}$, as well as $\sigma _{0,2}=\sigma _{3,2}$ and $\sigma _{1,2}=\sigma _{2,2}$, we obtain that

$$\begin{aligned} \gamma _{pqr,1} = 0 \quad \text {if }p+q+r\text { is odd}, \quad \text {and}\quad \gamma _{pqr,2} = (-1)^{p+q+r}\gamma _{pqr,0}. \end{aligned}$$

(B.6)

By putting this together, we arrive at

$$\begin{aligned} \sum _{k=0}^5\gamma _{pqr,k}\eta _k&{\mathop {=}\limits ^{\mathrm{B.4}}}2\sum _{k=0}^2\gamma _{pqr,k}\eta _k \\&{\mathop {=}\limits ^{\mathrm{B.5}}} \begin{pmatrix} \sqrt{3}\big (\gamma _{pqr,0}-\gamma _{pqr,2}\big ) \\ \gamma _{pqr,0}+2\gamma _{pqr,1}+\gamma _{pqr,2} \end{pmatrix} \\&{\mathop {=}\limits ^{\mathrm{B.6}}} \begin{pmatrix} \sqrt{3}\big (1-(-1)^{p+q+r}\big )\gamma _{pqr,0}\\ \big (1+(-1)^{p+q+r}\big )\big (\gamma _{pqr,0}+\gamma _{pqr,1}\big ) \end{pmatrix} = \begin{pmatrix} 2\sqrt{3}\,\gamma _{pqr,0}\,(1-\mathfrak {e}_{pqr})\\ 2\big (\gamma _{pqr,0}+\gamma _{pqr,1}\big )\,\mathfrak {e}_{pqr} \end{pmatrix}, \end{aligned}$$

where $\mathfrak {e}_{pqr}=1$ if $p+q+r$ is even, and $\mathfrak {e}_{pqr}=0$ if $p+q+r$ is odd. By elementary computations,

$$\begin{aligned} \begin{array}{llll} p+q+r\text { odd, }k=0: &{}\gamma _{111,0}=\frac{\sqrt{3}}{2}, &{}\gamma _{122,0}=0, &{}\gamma _{212,0}=\gamma _{221,0}=\frac{\sqrt{3}}{4};\\ p+q+r\text { even, }k=0: &{}\gamma _{211,0}=-\frac{1}{4}, &{}\gamma _{222,0}=\frac{3}{4}, &{}\gamma _{112,0}=\gamma _{121,0}=0;\\ p+q+r\text { even, }k=1: &{}\gamma _{211,1}=\frac{1}{4}, &{}\gamma _{222,1}=\frac{3}{4}, &{}\gamma _{112,1}=\gamma _{121,1}=\frac{3}{4}, \end{array} \end{aligned}$$

and so the final result is:

$$\begin{aligned}&\sum _{k=0}^5 {{\mathrm{tr}}}\big [\big (\sigma _k\big |\sigma _{k+1}\big )^{-1}\big (B:[\sigma _k]^2\big |B:[\sigma _{k+1}]^2\big )\big ]\,{\mathbb {J}}(\sigma _{k}-\sigma _{k+1}) \\&\quad =\sum _{k=0}^5T_k\eta _k =\frac{2}{\sqrt{3}}\sum _{p,q,r=1}^2\left( b_{pqr}\sum _{k=0}^5\gamma _{pqr,k}\eta _k\right) =2\sqrt{3} \begin{pmatrix} b_{111}+b_{212} \\ b_{222}+b_{112} \end{pmatrix}, \end{aligned}$$

which is (B.3). $\square$

Lemma B.5

With $\sigma _k'\in {\mathbb {R}}^2$ defined as in (5.14), and with $B=(b_{pqr})_{p,q,r\in \{1,2\}}\in {\mathbb {R}}^{2\times 2\times 2}$ such that $b_{pqr}=0$ except for $b_{122}=b_{211}=1$, we have that

$$\begin{aligned} \sum _{k=0}^5 {{\mathrm{tr}}}\big [\big (\sigma _k'\big |\sigma _{k+1}'\big )^{-1}\big (B:[\sigma _k']^2\big |B:[\sigma _{k+1}']^2\big )\big ]\,{\mathbb {J}}(\sigma _{k}-\sigma _{k+1}) =-{1\atopwithdelims ()1}. \end{aligned}$$

(B.7)

Proof

This is a slightly tedious, but straightforward calculation. First, by the choice of B,

$$\begin{aligned} \beta _k:=\big (B:[\sigma _k']^2\big |B:[\sigma _{k+1}']^2\big ) = \begin{pmatrix} (\sigma _{k,2}')^2 &{} (\sigma _{k+1,2}')^2 \\ (\sigma _{k,1}')^2 &{} (\sigma _{k+1,1}')^2 \end{pmatrix}, \end{aligned}$$

and so, by definition of the $\sigma _k'$ in (5.14),

$$\begin{aligned} \beta _0 =\beta _3 = \begin{pmatrix} 0 &{} \frac{1}{4} \\ 1 &{} \frac{1}{4} \end{pmatrix}, \quad \beta _0=\beta _3 = \begin{pmatrix} \frac{1}{4} &{} 1 \\ \frac{1}{4} &{} 0 \end{pmatrix}, \quad \beta _0=\beta _3 = \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}. \end{aligned}$$

For the inverse matrices $S_k:=\big (\sigma _k'\big |\sigma _{k+1}'\big )^{-1}$, we obtain

$$\begin{aligned} S_0 = \begin{pmatrix} 1&{}-1 \\ 0 &{} 2 \end{pmatrix} = -S_3, \quad S_1 = \begin{pmatrix} 2&{}0 \\ -1&{}1 \end{pmatrix} = -S_4, S_2 = \begin{pmatrix} 0&{}1 \\ -1&{}0 \end{pmatrix} = -S_5. \end{aligned}$$

For the traces $T_k:={{\mathrm{tr}}}\big [S_k\beta _k\big ]$, we thus obtain the values:

$$\begin{aligned} T_0=T_1=-\frac{1}{2},\quad T_3=T_4=\frac{1}{2}, \quad T_2=T_5=0. \end{aligned}$$

In conclusion,

$$\begin{aligned} \sum _{k=0}^5 T_k\,{\mathbb {J}}(\sigma _{k}-\sigma _{k+1}) = {\mathbb {J}}\left[ -\frac{1}{2} (\sigma _0-\sigma _2) +\frac{1}{2} (\sigma _3-\sigma _5) \right] = {\mathbb {J}}{-1\atopwithdelims ()1} = -{1\atopwithdelims ()1}, \end{aligned}$$

which is (B.7). $\square$

Appendix C: Lack of convexity

Below, we discuss why the minimization problem (3.7) is not convex. More precisely, we show that $G\mapsto {\mathbf {E}}_\boxplus (G;\hat{G})$ is not convex as a function of G on the affine ansatz space ${\mathcal {A}}_{\mathscr {T}}$. Since ${\mathbf {E}}_\boxplus (G;\hat{G})$ is a convex combination of the expressions ${\mathbb {H}}_m\big ((A_m|b_m);(\hat{A}_m|\hat{b}_m)\big )$, it clearly suffices to discuss the convexity of the latter.

We consider a curve $s\mapsto (A_m+s\alpha _m|b_m+s\beta _m)$ and evaluate the second derivatives of the components of the functional at $s=0$. First,

Second,

If we assume that $\nabla ^{2} V \ge \lambda {\mathbb {1}}$, then we obtain for the sum of these two contributions that

For the remaining term, however, we obtain — using the abbreviations $\widetilde{g}(s)=s\widetilde{h}'(s)$ and $\widetilde{f}(s)=s\widetilde{g}'(s)$ — that

$$\begin{aligned} \frac{\mathrm {d}^2}{\mathrm {d}^2 s}\bigg |_{s=0}&\widetilde{h}\left( \frac{\det (A_{m} + s \alpha _{m})}{{\overline{\rho }}_m}\right) \\&=\frac{\mathrm {d}}{\mathrm {d}s}\bigg |_{s=0} \left\{ \widetilde{g}\left( \frac{\det (A_{m} + s \alpha _{m})}{{\overline{\rho }}_m}\right) \,{{\mathrm{tr}}}\big [(A_{m} + s \alpha _{m})^{-1} \alpha _{m}\big ] \right\} \\&=\widetilde{f}\left( \frac{\det A_{m}}{{\overline{\rho }}_m}\right) \,\big ({{\mathrm{tr}}}\big [A_m^{-1}\alpha _m\big ]\big )^2 - \widetilde{g}\left( \frac{\det A_{m}}{{\overline{\rho }}_m}\right) \,{{\mathrm{tr}}}\big [\big ( A_m^{-1}\alpha _m \big )^2\big ] . \end{aligned}$$

Now observe that $\widetilde{f}(s)=P'(1/s)-sP(1/s)$ is a non-negative, and $\widetilde{g}(s) = -sP(1/s)$ is a non-positive function. Thus, from the two terms in the final sum, the first one is generally non-negative whereas the second one is of indefinite sign. Choosing

$$\begin{aligned} \alpha _m:=A_m \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix}, \quad \text {such that}\quad \big ({{\mathrm{tr}}}\big [A_m^{-1}\alpha _m\big ]\big )^2=0, \, {{\mathrm{tr}}}\big [\big ( A_m^{-1}\alpha _m \big )^2\big ]=2, \end{aligned}$$

the sum is obviously negative.