Skip to main content
SpringerLink
Log in

Interior Penalties for Summation-by-Parts Discretizations of Linear Second-Order Differential Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

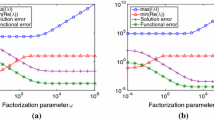
Abstract

This work focuses on simultaneous approximation terms (SATs) for multidimensional summation-by-parts (SBP) discretizations of linear second-order partial differential equations with variable coefficients. Through the analysis of adjoint consistency and stability, we present several conditions on the SAT penalties for general operators, including those operators that do not have nodes on their boundary or do not correspond with a collocation discontinuous Galerkin method. Based on these conditions, we generalize the modified scheme of Bassi and Rebay and the symmetric interior penalty Galerkin method to SBP-SAT discretizations. Numerical experiments are carried out on unstructured grids with triangular elements to verify the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. Equivalently, we can consider the generalized eigenvalue problem \(\mathsf {A} \varvec{v}_{i,j} = \mu _{i,j}\mathsf {H} \varvec{v}_{i,j}\); see, for example, [38, Chapter 8]

References

  1. Fisher, T.C., Carpenter, M.H.: High-order entropy stable finite difference schemes for nonlinear conservation laws: finite domains. J. Comput. Phys. 252(1), 518–557 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Fisher, T.C.: High-order L2 stable multi-domain finite difference method for compressible flows. Ph.D. thesis, Purdue University (2012)

  3. Kreiss, H.-O., Scherer, G.: Finite element and finite difference methods for hyperbolic partial differential equations. In: Mathematical Aspects of Finite Elements in Partial Differential Equations, pp. 195–212. Academic Press, New York (1974)

  4. Strand, B.: Summation by parts for finite difference approximations for d/dx. J. Comput. Phys. 110(1), 47–67 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  5. Carpenter, M.H., Fisher, T.C., Nielsen, E.J., Frankel, S.H.: Entropy stable spectral collocation schemes for the Navier–Stokes equations: discontinuous interfaces. SIAM J. Sci. Comput. 36(5), B835–B867 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Parsani, M., Carpenter, M .H., Nielsen, E .J.: Entropy stable wall boundary conditions for the three-dimensional compressible Navier–Stokes equations. J. Comput. Phys. 292(C), 88–113 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Gassner, G .J., Winters, A .R., Kopriva, D .A.: Split form nodal discontinuous Galerkin Schemes with summation-by-parts property for the compressible Euler equations. J. Comput. Phys. 327(C), 39–66 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chen, T., Shu, C.-W.: Entropy stable high order discontinuous Galerkin methods with suitable quadrature rules for hyperbolic conservation laws. J. Comput. Phys. 345, 427–461 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  9. Crean, J., Hicken, J.E., Del Rey Fernández, D.C., Zingg, D.W., Carpenter, M.H.: Entropy-stable summation-by-parts discretization of the Euler equations on general curved elements. J. Comput. Phys. (in revision) (2017)

  10. Hicken, J.E., Del Rey Fernández, D.C., Zingg, D.W.: Multi-dimensional summation-by-parts operators: general theory and application to simplex elements. SIAM J. Sci. Comput. 38(4), A1935–A1958 (2016)

    Article  MATH  Google Scholar 

  11. Carpenter, M.H., Nordström, J., Gottlieb, D.: A stable and conservative interface treatment of arbitrary spatial accuracy. J. Comput. Phys. 148(2), 341–365 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  12. Carpenter, M.H., Nordström, J., Gottlieb, D.: Revisiting and extending interface penalties for multi-domain summation-by-parts operators. J. Sci. Comput. 45(1), 118–150 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  13. Mattsson, K., Carpenter, M.H.: Stable and accurate interpolation operators for high-order multiblock finite difference methods. SIAM J. Sci. Comput. 32(4), 2298–2320 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Gong, J., Nordström, J.: Interface procedures for finite difference approximations of the advection–diffusion equation. J. Comput. Appl. Math. 236(5), 602–620 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Del Rey Fernández, D.C., Zingg, D .W.: Generalized summation-by-parts operators for the second derivative with a variable coefficient. SIAM J. Sci. Comput 37(6), A2840–A2864 (2015)

    Article  MATH  Google Scholar 

  16. Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Warburton, T., Hesthaven, J.: On the constants in hp-finite element trace inverse inequalities. Comput. Methods Appl. Mech. Eng. 192(25), 2765–2773 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  18. Baumann, C.E., Oden, J.T.: A discontinuous hp finite element method for convection–diffusion problems. Comput. Methods Appl. Mech. Eng. 175(3), 311–341 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  19. Bassi, F., Crivellini, A., Rebay, S., Savini, M.: Discontinuous Galerkin solution of the Reynolds-averaged Navier–Stokes and k turbulence model equations. Comput. Fluids 34(45), 507–540 (2005)

    Article  MATH  Google Scholar 

  20. Douglas, J., Dupont, T.: Interior penalty procedures for elliptic and parabolic Galerkin methods computing methods in applied sciences. In: Glowinski, R., Lions, J.L. (ed), Computing Methods in Applied Sciences, Volume 58 of Lecture Notes in Physics, Chap. 6, pp. 207–216. Springer, Berlin (1976)

  21. Hartmann, R.: Adjoint consistency analysis of discontinuous Galerkin discretizations. SIAM J. Numer. Anal. 45(6), 2671–2696 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Hicken, J.E., Del Rey Fernández, D.C., Zingg, D.W.: Simultaneous approximation terms for multi-dimensional summation-by-parts operators. In: 46th AIAA Fluid Dynamics Conference, Washington, DC, AIAA-2016-3971 (June 2016)

  23. Del Rey Fernández, D.C., Hicken, J.E., Zingg, D.W.: Simultaneous approximation terms for multi-dimensional summation-by-parts operators. J. Sci. Comput. 1–28 (2017). https://doi.org/10.1007/s10915-017-0523-7

  24. Mattsson, K.: Summation by parts operators for finite difference approximations of second-derivatives with variable coefficients. J. Sci. Comput. 51(3), 650–682 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  25. Lipnikov, K., Manzini, G., Shashkov, M.: Mimetic finite difference method. J. Comput. Phys. 257, 1163–1227 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  26. Babuška, I., Miller, A.: The post-processing approach in the finite element methodpart 1: calculation of displacements, stresses and other higher derivatives of the displacements. Int. J. Numer. Methods Eng. 20(6), 1085–1109 (1984)

    Article  MATH  Google Scholar 

  27. Babuška, I., Miller, A.: The post-processing approach in the finite element methodPart 2: the calculation of stress intensity factors. Int. J. Numer. Methods Eng. 20(6), 1111–1129 (1984)

    Article  MATH  Google Scholar 

  28. Pierce, N.A., Giles, M.B.: Adjoint recovery of superconvergent functionals from PDE approximations. SIAM Rev. 42(2), 247–264 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  29. Giles, M.B., Süli, E.: Adjoint methods for PDEs: a posteriori error analysis and postprocessing by duality. Acta Numer. 11, 145–236 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  30. Lu, J.C.: An a posteriori error control framework for adaptive precision optimization using discontinuous Galerkin finite element method, Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, MA (2005)

  31. Fidkowski, K.J., Darmofal, D.L.: Review of output-based error estimation and mesh adaptation in computational fluid dynamics. AIAA J. 49(4), 673–694 (2011)

    Article  Google Scholar 

  32. Hicken, J.E., Zingg, D.W.: Superconvergent functional estimates from summation-by-parts finite-difference discretizations. SIAM J. Sci. Comput. 33(2), 893–922 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  33. Hicken, J.E., Zingg, D.W.: Dual consistency and functional accuracy: a finite-difference perspective. J. Comput. Phys. 256, 161–182 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  34. Antonietti, P.F., Buffa, A., Perugia, I.: Discontinuous Galerkin approximation of the Laplace eigenproblem. Comput. Methods Appl. Mech. Eng. 195(25), 3483–3503 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  35. Shahbazi, K., Mavriplis, D.J., Burgess, N.K.: Multigrid algorithms for high-order discontinuous Galerkin discretizations of the compressible Navier–Stokes equations. J. Comput. Phys. 228(21), 7917–7940 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  36. Peraire, J., Persson, P.-O.: The compact discontinuous Galerkin (CDG) method for elliptic problems. SIAM J. Sci. Comput. 30(4), 1806–1824 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  37. Shahbazi, K.: An explicit expression for the penalty parameter of the interior penalty method. J. Comput. Phys. 205(2), 401–407 (2005)

    Article  MATH  Google Scholar 

  38. Hesthaven, J.S., Warburton, T.: Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. Springer, New York (2008)

    Book  MATH  Google Scholar 

  39. Kirby, R.M., Karniadakis, G.E.: Selecting the numerical flux in discontinuous Galerkin methods for diffusion problems. J. Sci. Comput. 22–23(1–3), 385–411 (2005)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Funding was provided by National Science Foundation (Grant No. 1554253) and Air Force Office of Scientific Research (Grant No.FA9550-15-1-0242)

Author information

Authors and Affiliations

  1. Rensselaer Polytechnic Institute, Troy, NY, USA

    Jianfeng Yan, Jared Crean & Jason E. Hicken

Authors
  1. Jianfeng Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jared Crean
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jason E. Hicken
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianfeng Yan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yan, J., Crean, J. & Hicken, J.E. Interior Penalties for Summation-by-Parts Discretizations of Linear Second-Order Differential Equations. J Sci Comput 75, 1385–1414 (2018). https://doi.org/10.1007/s10915-017-0591-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-017-0591-8

Keywords

Search

Navigation