A Finite Element Method for High-Contrast Interface Problems with Error Estimates Independent of Contrast

Abstract

We define a new finite element method for a steady state elliptic problem with discontinuous diffusion coefficients where the meshes are not aligned with the interface. We prove optimal error estimates in the $L^2$ norm and $H^1$ weighted semi-norm independent of the contrast between the coefficients. Numerical experiments validating our theoretical findings are provided.

Appendices

Appendix 1: Technical Lemmas

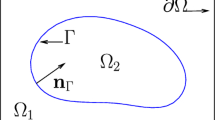
In this section we prove two technical lemmas involving geometrical estimates on elements intersected by the interface $\Gamma$. We remind the reader that we assume that $\Gamma$ is a simple ${\mathcal {C}}^2$ curve with an arc-length parameterization $\varvec{X}:[0,|\Gamma |)\rightarrow \Gamma$, and assumption (1)–(3) in Sect. 2.1.

We assume that r is the radius of our tubular neighborhood given in Lemma 1. Equivalently, for any $0< {\tau }\le r$ we have

$$\begin{aligned} Tub({\tau })=\{x: \text {dist}(x, \Gamma ) \le {\tau }\}. \end{aligned}$$

Moreover, for any $x \in Tub(r)$ there exists a unique $x_\Gamma \in \Gamma$ such that $\text {dist}(x,x_\Gamma )=\text {dist}(x, \Gamma )$ and $x-x_\Gamma$ is perpendicular to $\Gamma$ at $x_\Gamma$.

Lemma 13

Consider the $\Gamma _{s}$ a segment of the curve $\Gamma$ and $\ell$ the straight segment connecting the two end points of $\Gamma _{s}$. Assume that $|\ell | \le r$, where r is the radius of the r-tubular neighborhood. Then, it holds

$$\begin{aligned} |\Gamma _{s}| \le 2 |\ell |. \end{aligned}$$

Proof

Let $x_1, x_2$ be the endpoints of the line segment $\ell$. For $i=1,2$, let $N_{i}$ be the line that is normal to $\Gamma$ at $x_i$. Let ${\tilde{S}}$ be the infinite region enclosed by $N_{1}$ and $N_{2}$, then let $S= Tub(r/2) \cap {\tilde{S}}$ be the tubular section of $\Gamma _s$. We see that the area of S is given by $|S|= r|\Gamma _{s}|$. Let $M_{i}$ $i=1,2$ be the two lines that are parallel to $\ell$ and distance r from $\ell$. Consider the trapezoid, R, enclosed by $N_{i}, M_{i}, i=1,2$. We note that the area of R is given by $|R|=2 r |\ell |$. The result will follow if we show that $S \subset R$ since this will imply that $r|\Gamma _{s}| \le 2r|\ell |$.

To this end, we first note that the line segment $\ell \subset Tub(r/2)$ since the distance of any point in $\ell$ to $\Gamma$ is less than $|\ell /2|$ which we are assuming is less than r / 2. Let $x \in S$, then we know there exists a unique point $x_\Gamma \in \Gamma _s$ where the distance from x to $x_\Gamma$ is less than r / 2 and the line, which we denote by $L_x$, that passes through x and $x_\Gamma$ is perpendicular to $\Gamma$ at $x_\Gamma$. We know that $L_x$ intersects $\ell$ and we call this point y. We also know that distance between y and $x_\Gamma$ is less than r / 2 since $y \in \ell \subset Tub(r/2)$. Hence, we have shown that $\text {dist}(y,x) \le r$. This, of course implies that the distance of x to the infinite line $\ell _{\text {ext}}$ (which is the line that contains the line segment $\ell$) is at most r. In other words, x is in between the two lines $M_1$ and $M_2$. Since x was in the tubular section S it was in between the two lines $N_1$ and $N_2$ and hence x belongs to the trapezoid R. (Fig. 4) $\square$

Fig. 4

Illustration of a curve segment $\Gamma _{s}$, straight line segment $\ell$ connecting the end points of $\Gamma _{s}$, the tubular section of radius S, and the trapezoid R

1.1 Proof of Lemma 6

Let $e=\mathrm {Int}(\partial T_1\cap \partial T_2)\in {\mathcal {E}}_h^\Gamma$, with $T_1, T_2\in {\mathcal {T}}^h$, and the previous definitions of $e^\pm = e\cap \Omega ^\pm$. We analyze the case in $\Omega ^-$. The same analysis is valid in $\Omega ^+$. We proceed analyzing two cases depending on the intersection of the edge e with $\Gamma$:

• (i) If $e\cap \Gamma = \emptyset$, ($e=e^-$). If either $T_1$ or $T_2$ does not belong to ${\mathcal {T}}_h^\Gamma$ the results is trivial. Consider the case where $T_1$ and $T_2$ belong to ${\mathcal {T}}_h^\Gamma$, the interface sections $T_{1,\Gamma }$ and $T_{2,\Gamma }$ are nonempty. We consider the midpoint $m_e$ the segment e and the ball $B_{|e|/2}(m_e)$ of radius |e| / 2 and centered at $m_e$. If the interface does not cross the ball $B_{|e|/ 2}(m_e)$ then we have

  $$\begin{aligned} |T_1^{-}|\ge |B_{|e|/ 2}(m_e) \cap T_1|. \end{aligned}$$

  Denote by ${\underline{\alpha }}$ the minimum angle of the triangulation (given by shape regularity), and let ${\tilde{\alpha }}=\min \{{\underline{\alpha }}, \pi /4\}$. Now consider the isosceles triangle ${\tilde{T}}_1$ with base edge e and base angles ${\tilde{\alpha }}$. Then, clearly ${\tilde{T}}_1 \subset B_{|e|/ 2}(m_e) \cap T_1$ and $|{\tilde{T}}_1 |=(|e^-|/2)^2\tan \{{\tilde{\alpha }}\}$. Therefore, $|T_1^{-}| \ge (|e^-|/2)^2\tan \{{\tilde{\alpha }}\}$. Assume then that the interface crosses the ball $B_{|e|/2}(m_e)$ in $T_1$. Observe that this implies that there exists a point in $T_{1,\Gamma }$ who’s normal passes through $m_e$ with distance less than |e| / 2. Now, if $T_{2,\Gamma }$ crosses the ball then we will have two points on $\Gamma$ at a distance less than |e| / 2 whose normal passes through $m_e$ which contradicts the tubular neighborhood assumption. Therefore

  $$\begin{aligned} \max _{i=\{1,2\}}|T_{i}^{-}|\ge \Big (\frac{|e|}{2}\Big )^2\tan \{{\tilde{\alpha }}\}. \end{aligned}$$

• (ii) If $e\cap \Gamma \ne \emptyset$. Similarly as in the previous case, consider $m_e$ the midpoint of $e^{-}$ and the ball of radius $|e^{-}|/2$ centered at $m_e$. We observe that this ball can not cross both $T_{1,\Gamma }$ and $T_{2,\Gamma }$. Therefore

  $$\begin{aligned} \max _{i=\{1,2\}}|T_{i}^{-}|\ge \Big (\frac{|e^-|}{2}\Big )^2\tan \{{\tilde{\alpha }}\}. \end{aligned}$$

1.2 Proof of Lemma 11

We analyze the case in $\Omega ^-$. We first observe that, by triangle inequality we have

$$\begin{aligned} |l_T|\,\,\le \sum _{i=1}^3 |e^{-}_i|\,\,\le \,\,3\,\max _{i=\{1,2,3\}} |e^-|. \end{aligned}$$

Therefore, using Lemma 13

$$\begin{aligned} |T_\Gamma |\,\,\le \,\, 6\max _{i=1,2,3} |e_i^-|. \end{aligned}$$

Same analysis is valid to prove the statement in $\Omega ^+$.

Appendix 2: Construction of Basis Functions of $S^{1}(T)$

In this section we define basis functions $\{w_1,w_2,w_3\}$ of the space $S^{1}(T)$, for $T\in {\mathcal {T}}_h^{\Gamma }$. Consider $\{x_1,x_2,x_3\}$ nodes of the element T. Let $\{\lambda _1,\lambda _2,\lambda _3\}$ be the barycentric coordinates of a point $x\in T$ with respect to $\{x_1,x_2,x_3\}$. Consider the following representation

$$\begin{aligned} w_i(x) = \left\{ \begin{array}{ll} w_i^-(x), &{} \hbox {if }x\in T^-; \\ w_i^+(x), &{} \hbox {if }x\in T^+. \end{array} \right. w_i^{\pm }(x) = \sum _{j = 1}^{3} a_{i,j}^{\pm } \lambda _{j}(x). \end{aligned}$$

We construct $\{w_1,w_2,w_3\}$, a set of basis functions of the space $S^1(T)$, by satisfying the following conditions: for $i =1,2,3$

$$\begin{aligned} \left\{ \begin{array}{ll} w_{i}(x_j) = \delta _{i,j}&{} \hbox { for } j=1,2,3; \\ {[ w_i(x_0) ]}= 0 &{} x_0\in T_\Gamma ;\\ {[D_{\varvec{t}_0}w_i]} = 0&{} \varvec{t}_0 = \varvec{t}(x_0);\\ {[D_{\varvec{n}_0}w_i = 0]}&{} \varvec{n}_0 = \varvec{n}(x_0); \end{array} \right. \quad \hbox {where}\quad \delta _{i,j} = \left\{ \begin{array}{ll} 1, &{} \hbox {if } i=j \\ 0, &{} \hbox {if } i\ne j. \end{array} \right. \end{aligned}$$

These conditions are written in a system of size $6\times 6$ using the barycentric coordinates representation of $w_i^{\pm }$, i.e., we find the unknowns coefficients $\{a_{i,j}^{\pm }\}_{j=1}^{3}$ of $w_i$ for $i=1,2,3$, solutions of:

$$\begin{aligned} \left( \begin{array}{cccccc} {\tilde{\delta }}_{1,+} &{} 0 &{} 0 &{} {\tilde{\delta }}_{1,-} &{} 0 &{} 0 \\ 0 &{} {\tilde{\delta }}_{2,+} &{} 0 &{} 0 &{} {\tilde{\delta }}_{2,-} &{} 0 \\ 0 &{} 0 &{} {\tilde{\delta }}_{3,+} &{} 0 &{} 0 &{} {\tilde{\delta }}_{3,-} \\ \lambda _1(x_0) &{} \lambda _2(x_0) &{} \lambda _3(x_0) &{} -\lambda _1(x_0) &{} -\lambda _2(x_0) &{} -\lambda _3(x_0) \\ -D_{\varvec{t}_0} \lambda _1 &{} -D_{\varvec{t}_0} \lambda _2 &{} -D_{\varvec{t}_0} \lambda _3&{} D_{\varvec{t}_0} \lambda _1 &{} D_{\varvec{t}_0} \lambda _2 &{}D_{\varvec{t}_0} \lambda _3 \\ -\rho ^{+} D_{\varvec{n}_0} \lambda _1 &{} -\rho ^{+}D_{\varvec{n}_0} \lambda _2 &{} \rho ^{+}D_{\varvec{n}_0} \lambda _3&{} \rho ^{-}D_{\varvec{n}_0} \lambda _1 &{} \rho ^{-}D_{\varvec{n}_0} \lambda _2 &{}\rho ^{-}D_{\varvec{n}_0} \lambda _3 \\ \end{array} \right) \left( \begin{array}{c} a_{i,1}^+ \\ a_{i,2}^+ \\ a_{i,3}^+ \\ a_{i,1}^- \\ a_{i,2}^- \\ a_{i,3}^- \\ \end{array} \right) = \left( \begin{array}{c} \delta _{i,1} \\ \delta _{i,2} \\ \delta _{i,3} \\ 0 \\ 0 \\ 0\\ \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} {\tilde{\delta }}_{j,\pm } = \left\{ \begin{array}{ll} 1, &{} \hbox {if } x_{j}\in T^{\pm } \\ 0, &{} \hbox {if } x_{j}\in T^{\mp }. \end{array} \right. \end{aligned}$$