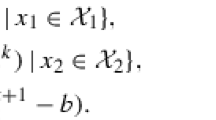Skip to main content
SpringerLink
Log in

A Flexible ADMM Algorithm for Big Data Applications

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

We present a Flexible Alternating Direction Method of Multipliers (F-ADMM) algorithm for solving optimization problems involving a strongly convex objective function that is separable into \(n \ge 2\) blocks, subject to (non-separable) linear equality constraints. The F-ADMM algorithm uses a Gauss–Seidel scheme to update blocks of variables, and a regularization term is added to each of the subproblems. We prove, under common assumptions, that F-ADMM is globally convergent and that the iterates converge linearly. We also present a special case of F-ADMM that is partially parallelizable, which makes it attractive in a big data setting. In particular, we partition the data into groups, so that each group consists of multiple blocks of variables. By applying F-ADMM to this partitioning of the data, and using a specific regularization matrix, we obtain a hybrid ADMM (H-ADMM) algorithm: the grouped data is updated in a Gauss–Seidel fashion, and the blocks within each group are updated in a Jacobi (parallel) manner. Convergence of H-ADMM follows directly from the convergence properties of F-ADMM. Also, we describe a special case of H-ADMM that may be applied to functions that are convex, rather than strongly convex. Numerical experiments demonstrate the practical advantages of these new algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The Gaussian back substitution step involves a vector of size \(N+m - N_1\) and a square upper triangular matrix of the same size. Recall that \(x_i \in {{\mathbf {R}}}^{N_i}\), so \(N_1\) is the dimension of \(x_1\).

  2. The precise constant depends on the ‘reduceall’ implementation of MPI.

  3. Indeed, the theory in [8] holds under weaker assumptions, but the condition \(P_1,P_2 \succ 0\) is sufficient for the discussion here.

  4. To the best of our knowledge, the \(P_j\) matrices defined in [19, 20] and the general \(P_j\) matrices considered in this paper are the only regularizers in the current literature that relate to this special case of ‘general n split into \(\ell =2\) groups’ setup.

References

  1. Bertsekas, D.P.: Extended monotropic programming and duality. J. Optim. Theory Appl. 139(2), 209–225 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bertsekas, D.P.: Incremental aggregated proximal and augmented Lagrangian algorithms. Technical Report LIDS-3176. Cambridge (2015)

  3. Boley, D.: Local linear convergence of the alternating direction method of multipliers on quadratic or linear programs. SIAM J. Optim. 23(4), 2183–2207 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  4. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2010)

    Article  MATH  Google Scholar 

  5. Caia, X., Han, D., Yuan, X.: The direct extension of ADMM for three-block separable convex minimization models is convergent when one function is strongly convex. Technical Report (2014)

  6. Chen, C., He, B., Ye, Y., Yuan, X.: The direct extension of ADMM for multi-block convex minimization problems is not necessarily convergent. Math. Program. 155(1), 57–79 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. Deng, W., Lai, M.J., Peng, Z., Yin, W.: Parallel multi-block ADMM with \(o(1/k)\) convergence. Technical Report. Department of Mathematics, UCLA, Los Angeles. (2014)

  8. Deng, W., Yin, W.: On the global and linear convergence of the generalized alternating direction method of multipliers. J. Sci. Comput. 66(3), 889–916 (2016)

    Article  MathSciNet  Google Scholar 

  9. Dong, Q., Liu, X., Wen, W., Yuan, Y.: A parallel line search subspace correction method for composite convex optimization. J. Oper. Res. Soc. China 3(2), 163–187 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Eckstein, J.: Some saddle-function splitting methods for convex programming. Optim. Methods Softw. 4(1), 75–83 (1994)

    Article  MathSciNet  Google Scholar 

  11. Eckstein, J., Bertsekas, D.P.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55, 293–318 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  12. Eckstein, J., Yao, W.: Understanding the convergence of the alternating direction method of multipliers: theoretical and computational perspectives. Technical Report. Rutgers University, (2015)

  13. Fortin, M., Glowinksi, R.: Chapter 3: on decomposition-coordination methods using an augmented Lagrangian. In: Fortin, M., Glowinksi, R. (eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary-Value Problems, pp. 97–144. Elsevier, Amsterdam (1983)

    Chapter  Google Scholar 

  14. Fu, X., He, B., Wang, X., Yuan, X.: Block-wise alternating direction method of multipliers with Gaussian back substitution for multiple-block convex programming. Technical Report. (2014)

  15. Gabay, D.: Chapter 9: applications of the method of multipliers to variational inequalities. In: Fortin, M., Glowinksi, R. (eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary-Value Problems, pp. 299–331. Elsevier, Amsterdam (1983)

    Chapter  Google Scholar 

  16. Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximations. Comput. Math. Appl. 2(1), 17–40 (1976)

    Article  MATH  Google Scholar 

  17. Glowinski, R., Marroco, A.: Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de dirichlet non linéaires. ESAIM Modélisation Mathématique et Analyse Numérique 9(R2), 41–76 (1975)

    MATH  Google Scholar 

  18. Han, D., Yuan, X.: A note on the alternating direction method of multipliers. J. Optim. Theory Appl. 155(1), 227–238 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. He, B., Xu, M., Yuan, X.: Block-wise ADMM with a relaxation factor for multiple-block convex programming. Technical Report. (2014)

  20. He, B., Yuan, X.: Block-wise alternating direction method of multipliers for multiple-block convex programming and beyond. Technical Report. (2014)

  21. Hong, M., Luo, Z.Q.: On the linear convergence of the alternating direction method of multipliers. Technical Report. (2012)

  22. Hong, M., Luo, Z.Q., Razaviyayn, M.: Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. Technical Report. (2014)

  23. Lai, M.J., Yin, W.: Augmented \(\ell _1\) and nuclear-norm models with a globally linearly convergent algorithm. SIAM J. Imaging Sci. 6(2), 1059–1091 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  24. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  25. Peng, Z., Yan, M., Yin, W.: Parallel and distributed sparse optimization. In: IEEE Asilomar Conference on Signals, Systems and Computers, pp. 659–646. (2013)

  26. Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)

    Book  MATH  Google Scholar 

  27. Rockafellar, R.T., Wets, R.J.B.: Variational Analysis, 3rd edn. Springer, Berlin (2009)

    MATH  Google Scholar 

  28. Lin, T., Ma, S., Zhang, S.: On the global linear convergence of the ADMM with multi-block variables. SIAM J. Optim. 25(3), 1478–1497 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  29. Thakur, R., Gropp, W.D.: Improving the Performance of Collective Operations in MPICH. Springer, Berlin (2003)

    Book  Google Scholar 

  30. Wang, H., Banerjee, A., Luo, Z.Q.: Parallel direction method of multipliers. Technical Report. (2014)

  31. Yang, J., Zhang, Y.: Alternating direction algorithms for \(\ell _1\)-problems in compressive sensing. SIAM J. Sci. Comput. 33(1), 250–278 (2011)

    Article  MathSciNet  Google Scholar 

  32. Yuan, X., Yang, J.: Sparse and low-rank matrix decomposition via alternating direction methods. Technical Report. (2009)

  33. Zavala, V.: Stochastic optimal control model for natural gas network operations. Technical Report. Mathematics and Computer Science Division, Argonne National Laboratory (2013)

Download references

Acknowledgments

The authors would like to thank Professor Wotao Yin and Mr Damek Davis for their helpful discussion and feedback on an earlier version of this work. We would also like to thank the anonymous reviewers, whose comments greatly improved the presentation of this paper.

Author information

Authors and Affiliations

  1. Applied Mathematics and Statistics, Johns Hopkins University, Baltimore, MD, 21218, USA

    Daniel P. Robinson & Rachael Tappenden

Authors
  1. Daniel P. Robinson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rachael Tappenden
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rachael Tappenden.

Additional information

Daniel P. Robinson has received support from the U.S. National Science Foundation under Grant No. DMS–1217153.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Robinson, D.P., Tappenden, R. A Flexible ADMM Algorithm for Big Data Applications. J Sci Comput 71, 435–467 (2017). https://doi.org/10.1007/s10915-016-0306-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-016-0306-6

Keywords

Mathematics Subject Classification

Search

Navigation