Abstract
Tikhonov regularization is a popular method to approximate solutions of linear discrete ill-posed problems when the observed or measured data is contaminated by noise. Multiparameter Tikhonov regularization may improve the quality of the computed approximate solutions. We propose a new iterative method for large-scale multiparameter Tikhonov regularization with general regularization operators based on a multidirectional subspace expansion. The multidirectional subspace expansion may be combined with subspace truncation to avoid excessive growth of the search space. Furthermore, we introduce a simple and effective parameter selection strategy based on the discrepancy principle and related to perturbation results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider one-parameter and multiparameter Tikhonov regularization problems of the form
where \(\Vert \cdot \Vert \) denotes the 2-norm and the superscript i is used as an index. We focus on large-scale discrete ill-posed problems such as the discretization of Fredholm integral equations of the first kind. More precisely, assume A is an ill-conditioned or even singular \(m \times n\) matrix with \(m \ge n\), \({L^{i}}\) are \(p^{i} \times n\) matrices such that the nullspaces of A and \({L^{i}}\) intersect trivially, and \({\mu ^{i}}\) are nonnegative regularization parameters. Furthermore, assume \({\varvec{b}}\) is contaminated by an error \({\varvec{e}}\) and satisfies \(\varvec{b} = A {\varvec{x}}_\star + {\varvec{e}}\), where \({\varvec{x}}_\star \) is the exact solution. Finally, we assume that a bound \(\Vert {\varvec{e}}\Vert \le \varepsilon \) is available, so that the discrepancy principle can be used.
In one-parameter Tikhonov regularization (\(\ell = 1\)), the choice of the regularization operator is typically significant, since frequencies in the nullspace of the operator remain unpenalized. Multiparameter Tikhonov can be used when a satisfactory choice of the regularization operator is unknown in advance, or can be seen as an attempt to combine the strengths of different regularization operators. In some applications, using more than one regularization operator and parameter allows for more accurate solutions [1, 2, 17, 20].
Solving (1) for large-scale problems may be challenging. In case the \({\mu ^{i}}\) are fixed a priori, methods such as LSQR [21] or LSMR [4] may be used. However, the problem becomes more complicated when the regularization parameters are not fixed in advance [12, 15, 17]. In this paper, we present a new subspace method consisting of three phases; a new expansion phase, a new extraction phase, and a new truncation phase. To be more specific, let  be a subspace of dimension \(k \ll n\), and let the columns of \(X_k\) form an orthonormal basis for
be a subspace of dimension \(k \ll n\), and let the columns of \(X_k\) form an orthonormal basis for  . Then we can compute matrix decompositions
. Then we can compute matrix decompositions
where \(U_{k+1}\) and \({V_k^{i}}\) are have orthonormal columns, \(\beta {\varvec{u}}_1 = \varvec{b}\), \(\beta = \Vert {\varvec{b}}\Vert \), \({\underline{H}}_k\) is a \((k+1) \times k\) Hessenberg matrix, and \({K_k^{i}}\) is upper triangular. Denote \(\varvec{\mu } = ({\mu ^{1}}, \dots , {\mu ^{\ell }})\) for convenience. Now restrict the solution space to  so that \({\varvec{x}}_k(\varvec{\mu }) = X_k {\varvec{c}}_k(\varvec{\mu })\), where
so that \({\varvec{x}}_k(\varvec{\mu }) = X_k {\varvec{c}}_k(\varvec{\mu })\), where
The vector \({\varvec{e}}_1\) is the first standard basis vector of appropriate dimension. Our paper has three contributions. First, a new expansion phase where we add multiple search directions to  . Second, a new truncation phase which removes unwanted new search directions. Third, a new method for selecting the regularization parameters \({\mu _k^{i}}\) in the extraction phase. The three phases work alongside each other: the intermediate solution obtained in the extraction phase is preserved in the truncation phase, whereas the remaining perpendicular component(s) from the expansion phase are removed.
. Second, a new truncation phase which removes unwanted new search directions. Third, a new method for selecting the regularization parameters \({\mu _k^{i}}\) in the extraction phase. The three phases work alongside each other: the intermediate solution obtained in the extraction phase is preserved in the truncation phase, whereas the remaining perpendicular component(s) from the expansion phase are removed.
The paper is organized as follows. In Sect. 2 an existing nonlinear subspace method is discussed, whereafter we propose the new multidirectional subspace expansion of the expansion phase. Discussion of the truncation phase follows immediately. Section 3 is focused on discrepancy principle based parameter selection for one-parameter regularization. New lower and upper bounds on the regularization parameter are provided. Sections 4 and 5 describe the extraction phase. In the former, a straightforward parameter selection strategy for multiparameter regularization is given, in the latter, a justification using perturbation analysis. Numerical experiments are performed in Sect. 6 and demonstrate the competitiveness of our new method. We end with concluding remarks in Sect. 7.
2 Subspace Expansion for Multiparameter Tikhonov
Let us first consider one-parameter Tikhonov regularization with a general regularization operator. Then \(\ell = 1\) and we write \(\mu = {\mu ^{1}}\), \(L = {L^{1}}\), and \(K_k = {K_k^{1}}\), such that (1) simplifies to
When \(L=I\) we use the Golub–Kahan–Lanczos bidiagonalization procedure to generate the Krylov subspace

In this case \({\underline{H}}_k\) is lower bidiagonal and \(K_k\) is the identity and
If \(L\ne I\) one can still try to use the above Krylov subspace [12], however, it may be more natural to consider a shift-independent generalized Krylov subspace of the form

spanned by the first k vectors in
This generalized Krylov subspace was first studied by Li and Ye [18] and later by Reichel et al. [23]. An orthonormal basis can be created with a generalization of Golub–Kahan–Lanczos bidiagonalization [13]. However, while the search space grows linearly as a function of the number of matrix-vector products, the dimension of the generalized Krylov subspace grows exponentially as a function of the total degree of a bivariate matrix polynomial. As a result, if we take any vector  and write it as \(p(A^*A, L^*L)A^* {\varvec{b}}\), where p is a bivariate polynomial, then p has at most degree \(\lfloor \log _2 k \rfloor \). This low degree may be undesirable especially for small regularization parameters \(\mu \). Reichel and Yu [24, 25] solve this in part with algorithms that can prioritize one operator over the other. For instance, if \({\varvec{w}}\) is a vector in a group j and B has priority over A, then group \(j+1\) contains \((A^*A){\varvec{w}}\), \((B^*B){\varvec{w}}\), \((B^*B)^2{\varvec{w}}\), ..., \((B^*B)^\rho {\varvec{w}}\). The downside is that \(\rho \) is a user defined constant, and that the expansion vectors are not necessarily optimal.
and write it as \(p(A^*A, L^*L)A^* {\varvec{b}}\), where p is a bivariate polynomial, then p has at most degree \(\lfloor \log _2 k \rfloor \). This low degree may be undesirable especially for small regularization parameters \(\mu \). Reichel and Yu [24, 25] solve this in part with algorithms that can prioritize one operator over the other. For instance, if \({\varvec{w}}\) is a vector in a group j and B has priority over A, then group \(j+1\) contains \((A^*A){\varvec{w}}\), \((B^*B){\varvec{w}}\), \((B^*B)^2{\varvec{w}}\), ..., \((B^*B)^\rho {\varvec{w}}\). The downside is that \(\rho \) is a user defined constant, and that the expansion vectors are not necessarily optimal.
An alternative approach is a greedy nonlinear method described by Lampe et al. [17]. We briefly review their method and state a straightforward extension to multiparameter Tikhonov regularization. First note that the low-dimensional minimization in (3) simplifies to
in the one-parameter case. Next, compute a value \(\mu = \mu _k\) using, e.g., the discrepancy principle. It is easy to verify that
is perpendicular to  , as well as the gradient of the cost function
, as well as the gradient of the cost function
in the point \({\varvec{x}}_k(\mu _k)\). Therefore, this vector is used to expand the search space. As usual, expansion and extraction are repeated until suitable stopping criteria are met.
As previously stated, Lampe et al. [17] consider only one-parameter Tikhonov regularization, however, their method readily extends to multiparameter Tikhonov regularization. Again, the first step is to decide on regularization parameters \(\varvec{\mu }_k\). Next, use the residual of the normal equations
to expand the search space. Note that the residual is again orthogonal to  as well as the gradient of the cost function
as well as the gradient of the cost function
We summarize this multiparameter method in Algorithm 1, but remark that in practice we initially use Golub–Kahan–Lanczos bidiagonalization until a \(\varvec{\mu }_k\) can be found that satisfies the discrepancy principle.
Algorithm 1
(Generalized Krylov subspace Tikhonov regularization; extension of [17])
Input: Measurement matrix A, regularization operators \({L^{1}}\), ..., \({L^{\ell }}\), and data \({\varvec{b}}\).
Output: Approximate solution \({\varvec{x}}_k \approx {\varvec{x}}_\star \).
-
1.
Initialize \(\beta = \Vert {\varvec{b}}\Vert \), \(U_1 = {\varvec{b}} / \beta \), \(X_0 = []\), \({\varvec{x}}_0 = \mathbf{0 }\), and \(\varvec{\mu }_0 = \mathbf{0 }\). for \(k = 1, 2, \dots \) d o
-
2.
Expand \(X_{k-1}\) with \(A^* {\varvec{b}} - ( A^* A + \sum _{i=1}^\ell {\mu _{k-1}^{i}} {L^{i}}^* {L^{i}}) {\varvec{x}}_{k-1}\).
-
3.
Update \(A X_k = U_{k+1} {\underline{H}}_k\) and \({L^{i}} X_k = {V_k^{i}} {K_k^{i}}\).
- 4.
-
5.
 .
. -
6.
\( {\varvec{x}}_k = X_k {\varvec{c}}_k\).
-
7.
i f \(\Vert {\varvec{x}}_k - {\varvec{x}}_{k-1}\Vert /\Vert {\varvec{x}}_k\Vert \) is sufficiently small then break
Suitable regularization operators often depend on the problem and its solution. Multiparameter regularization may be used when a priori information is lacking. In this case, it is not obvious that the residual vector above is a “good” expansion vector, in particular if the intermediate regularization parameters \({\varvec{\mu }}_k\) are not necessarily accurate. Hence, we propose to remove the dependence on the parameters to some extent by expanding the search space with the vectors
separately. Here, we omit \(A^* {\varvec{b}}\) as it is already contained in \(X_k\). Since we expand the search space in multiple directions, we refer to this expansion as a “multidirectional” subspace expansion. Observe that the previous residual expansion vector is in the span of the multidirectional expansion vectors.
It is unappealing for the search space to grow with \(\ell +1\) basis vectors per iteration, because the cost of orthogonalization and the cost of solving the projected problems depend on the dimension of the search space. Therefore, we wish to condense the best portions of the multiple directions in a single vector, and use the following approach. First we expand \(X_k\) with the vectors in (4) and obtain \({\widetilde{X}}_{k+\ell +1}\). Then we compute the decompositions
analogously to (2) and determine parameters \({\varvec{\mu }}_{k+1}\) and the approximate solution \(\widetilde{\varvec{c}}_{k+\ell +1}\). Next, we compute
where Z, P, and \(Q^i\) orthonormal matrices of the form
Here \(I_k\) is the \(k\times k\) identity matrix and \(Z_{\ell +1}\) is an orthonormal matrix so that \(Z_{\ell +1} \widetilde{\varvec{c}}_{k+1:k+\ell +1} = \gamma {\varvec{e}}_1\) for some scalar \(\gamma \). The matrices \(P_{\ell +1}\) and \(Q^i_{\ell +1}\) are computed to make \(\widetilde{{\underline{H}}}_{k+\ell +1} Z^*\) and \({{\widetilde{K}}_{k+\ell +1}^{i}} Z^*\) respectively upper-Hessenberg and upper-triangular again. At this point we can truncate (5) to obtain
and truncate \(Z\widetilde{\varvec{c}}_{k+\ell +1}\) to obtain \({\varvec{c}}_{k+1}\) so that \({\widetilde{X}}_{k+\ell +1} \widetilde{\varvec{c}}_{k+\ell +1} = X_{k+1}\varvec{c}_{k+1}\). The truncation is expected to keep important components, since the directions removed from \(X_{k+\ell +1}\) are perpendicular to the current best approximation \({\varvec{x}}_{k+1}\), and also to the previous best approximations \({\varvec{x}}_{k}\), \({\varvec{x}}_{k-1}\), ..., \({\varvec{x}}_1\). If the rotation and truncation are combined in one step, then the computational cost of the method is  , which quickly becomes smaller than the (re)orthogonalization cost as k grows.
, which quickly becomes smaller than the (re)orthogonalization cost as k grows.
To illustrate our approach, let us consider a one-parameter Tikhonov example where \(\ell = 1\). First we expand \(X_1 = {\varvec{x}}_1\) with vectors \(A^*A{\varvec{x}}_1\) and \(L^*L {\varvec{x}}_1\). Let \(A {\widetilde{X}}_{1+2} = {\widetilde{U}}_{2+2} \widetilde{{\underline{H}}}_{1+2}\) and \(L {\widetilde{X}}_{1+2} = {\widetilde{V}}_{1+2} {\widetilde{K}}_{1+2}\), and use \(\widetilde{{\underline{H}}}_{1+2}\) and \({\widetilde{K}}_{1+2}\) to compute \(\widetilde{\varvec{c}}_{1+2}\). We then compute a rotation matrix \(Z_2\) so that \(Z_2 \widetilde{\varvec{c}}_{2:3} = \pm \Vert \widetilde{\varvec{c}}_{2:3}\Vert {\varvec{e}}_1\), and let Z be defined as in (6). The matrices \(\widetilde{{\underline{H}}}_{1+2} Z^*\) and \({\widetilde{K}}_{1+2} Z^*\) are no longer have their original structure, hence, we need to compute orthonormal P and Q such that \(P \widetilde{{\underline{H}}}_{1+2} Z^*\) is again upper-Hessenberg and \(Q {\widetilde{K}}_{1+2} Z^*\) is upper-triangular. Schematically we have
accompanied by the decompositions
At this point we truncate the subspaces by removing the last columns from \({\widetilde{X}}_{1+2} Z^*\), \({\widetilde{U}}_{2+2} P^*\), \(P \widetilde{{\underline{H}}}_{1+2} Z^*\), \({\widetilde{V}}_{1+2} Q^*\), and \(Q {\widetilde{K}}_{1+2} Z^*\), and the bottom rows of \(P \widetilde{{\underline{H}}}_{1+2} Z^*\) and \(Q {\widetilde{K}}_{1+2} Z^*\), to obtain
Below we summarize the steps of the new algorithm for solving problem (1). In our implementation we take care to use full reorthogonalization and avoid extending \(X_{k}\), \(U_{k+1}\), and \({V_k^{i}}\) with numerically linearly dependent vectors. We omit these steps from the pseudocode for brevity. In addition, we initially expand the search space solely with \(A^*{\varvec{u}}_{k+1}\) until the discrepancy principle can be satisfied conform Proposition 1 in Sect. 3.
Algorithm 2
(Multidirectional Tikhonov regularization)
Input: Measurement matrix A, regularization operators. \({L^{1}}\), ..., \({L^{\ell }}\), and data \({\varvec{b}}\).
Output: Approximate solution \({\varvec{x}}_k \approx {\varvec{x}}_\star \).
-
1.
Initialize \(\beta = \Vert {\varvec{b}}\Vert \), \(U_1 = {\varvec{b}} / \beta \), \(X_0 = []\), \({\varvec{x}}_0 = \mathbf{0 }\), and \(\varvec{\mu }_0 = \mathbf{0 }\).
for \(k=0\), 1, ..., d o
-
2.
Expand \(X_k\) with \(A^* A {\varvec{x}}_{k}\), \({L^{1}}^* {L^{1}} {\varvec{x}}_{k}\), ..., \({L^{\ell }}^* {L^{\ell }} {\varvec{x}}_{k}\).
-
3.
Update \(A{\widetilde{X}}_{k+\ell +1} = {\widetilde{U}}_{k+\ell +2} \widetilde{{\underline{H}}}_{k+\ell +1}\) and \({L^{i}} {\widetilde{X}}_{k+\ell +1} = {{\widetilde{V}}_{k+\ell +1}^{i}} {{\widetilde{K}}_{k+\ell +1}^{i}}\).
- 4.
-
5.
 .
. -
6.
Compute P, Q, and Z (see text).
-
7.
Truncate \(A ({\widetilde{X}}_{k+\ell +1} Z^*) = ({\widetilde{U}} _{k+\ell +2} P^*) (P \widetilde{{\underline{H}}}_{k+\ell +1} Z^*)\) to \(A X_{k+1} = U_{k+2} {\underline{H}}_{k+1}\).
Truncate \({L^{i}} ({\widetilde{X}}_{k+\ell +1} Z^*) = ({{\widetilde{V}}_{k+\ell +1}^{i}} Q^{i*}) (Q^i {{\widetilde{K}}_{k+\ell +1}^{i}} Z^*)\) to \({L^{i}} X_{k+1} = {V_{k+1}^{i}} {K_{k+1}^{i}}\).
-
8.
Truncate \(Z\widetilde{\varvec{c}}_{k+\ell +1}\) to obtain \({\varvec{c}}_{k+1}\) and set \({\varvec{x}}_{k+1} = X_{k+1} {\varvec{c}}_{k+1}\).
-
9.
\(\quad {\mathbf{i }}{\mathbf{f }} \Vert {\varvec{x}}_{k+1} - {\varvec{x}}_k\Vert /\Vert {\varvec{x}}_k\Vert \) is sufficiently small then break
We have completed our discussion of the expansion and truncation phase of our algorithm. In the following section we discuss the extraction phase for one-parameter Tikhonov regularization and discuss the multiparameter case in later sections.
3 Parameter Selection in Standard Tikhonov
In this section we investigate parameter selection for general form one-parameter Tikhonov, where \(\ell = 1\), \(\mu = {\mu ^{1}}\), and \(L = {L^{1}}\). Multiple methods exist in the one-parameter case to determine particular \(\mu _k\), including the discrepancy principle, the L-curve criterion and generalized cross validation; see, for example, Hansen [11, Ch. 7]. We focus on the discrepancy principle which states that \(\mu _k\) must satisfy
where \(\Vert {\varvec{e}}\Vert \le \varepsilon \) and \(\eta >1\) is a user supplied constant independent of \(\varepsilon \).
Define the residual vector \({\varvec{r}}_k(\mu ) = A{\varvec{x}}_k(\mu ) - {\varvec{b}}\) and the function \(\varphi (\mu ) = \Vert {\varvec{r}}_k(\mu )\Vert ^2\). A nonnegative \(\mu _k\) satisfies the discrepancy principle if \(\varphi (\mu _k) = \eta ^2 \varepsilon ^2\). It is known that root finding methods can find solutions, for example, Lampe et al. [17] compare four of them. We prefer bisection for its reliability and straightforward analysis and implementation. The performance difference is not an issue because root finding requires a fraction of the total computation time and is no bottleneck. A unique solution \(\mu _k\) exists under mild conditions, see for instance [3]. Below we give a proof using our own notation.
Assume \({\underline{H}}_k\) and \(K_k\) are full rank and let \(P_k {\varSigma }_k Q_k^*\) be the singular value decomposition of \({\underline{H}}_k K_k^{-1}\). Let the singular values be denoted by
Now we can express \({\varvec{c}}_k(\mu )\) and \(\varphi \) as
and
Or alternatively,
Observe that \(P_k\) is a basis for the range of \({\underline{H}}_k\) and \(I - P_k P_k^*\) is the orthogonal projection onto the nullspace  and is sometimes denoted by
and is sometimes denoted by  . Furthermore, it can be verified that \({\underline{H}}_k\beta {\varvec{e}}_1 \ne \varvec{0}\) if \(A^*{\varvec{b}} \ne \mathbf{0 }\), that is,
. Furthermore, it can be verified that \({\underline{H}}_k\beta {\varvec{e}}_1 \ne \varvec{0}\) if \(A^*{\varvec{b}} \ne \mathbf{0 }\), that is,  .
.
Proposition 1
If \(\beta ^2 \Vert (I - P_k P_k^*) {\varvec{e}}_1\Vert ^2 \le \eta ^2 \varepsilon ^2 < \Vert {\varvec{b}}\Vert ^2\), then there exists a unique \(\mu _k\ge 0\) such that \(\varphi (\mu _k) = \eta ^2 \varepsilon ^2\).
Proof
(See also [3] and references therein). From (9) it follows that \(\varphi \) is a rational function with poles \(\mu =-\sigma _j^2\) for all \(\sigma _j>0\), therefore, \(\varphi \) is \(C^\infty \) on the interval \([0,\infty )\). Additionally, \(\varphi \) is a strictly increasing and bounded function on the same interval, since
implies \(\varphi ^\prime (\mu ) > 0\) and
Consequently, there exists a unique \(\mu _k \in [0,\infty )\) such that \(\varphi (\mu _k) = \eta ^2 \varepsilon ^2\). \(\square \)
Beyond nonnegativity, the proposition above provides little insight on the location of \(\mu _k\) on the real axis, and we would like to have lower and upper bounds. We determine bounds in Proposition 2 and believe the results to be new. Both in practice and for the proof of the subsequent proposition, it is useful to remove nonessential parts of \(\varphi (\mu )\) and instead work with the function
and the quantity
Then \(0\le {\widetilde{\varphi }}(\mu ) \le \rho \), where \(\rho = \Vert P_k^* \varvec{e}_1\Vert \le 1\), and \(\eta ^2\varepsilon ^2\) satisfies the bounds in Proposition 1 if and only if \(0 \le {\widetilde{\varepsilon }} < \rho \), and \(\varphi (\mu _k) = \eta ^2\varepsilon ^2\) if and only if \({\widetilde{\varphi }}(\mu _k) = {\widetilde{\varepsilon }}^2\).
Proposition 2
If \(0 \le {\widetilde{\varepsilon }} < \rho \), and \(\mu _k\) is such that \({\widetilde{\varphi }}(\mu _k) = {\widetilde{\varepsilon }}^2\), then
where \(\sigma _{\min }\) and \(\sigma _{\max }\) are as in (8).
Proof
The key of the proof observe that
for all \(j = 1\), ..., k. Combining this observation with the definition of \({\widetilde{\varphi }}\) yields
Since \(\sum _{j=1}^k |P_k|_{1j}^2 = \Vert P_k^* {\varvec{e}}_1\Vert ^2 = \rho ^2\) and \({\widetilde{\varphi }}(\mu _k) = {\widetilde{\varepsilon }}^2\), it follows that
Hence, if \({\widetilde{\varepsilon }} = 0\), then \(\mu _k = 0\) and we are done. Otherwise \(\mu _k \ne 0\) and we can divide by \(\rho \), take the reciprocals, and subtract 1 to arrive at
So that
and the proposition follows. \(\square \)
It is undesirable to work with the inverse of \(K_k\) when it becomes ill-conditioned. Instead it may be preferred to use the generalized singular value decomposition (GSVD)
where \(P_k\) and \(Q_k\) have orthogonal columns and \(Z_k\) is nonsingular. The matrices \(C_k\) and \(S_k\) are diagonal with entries \(0 \le c_1 \le c_2 \le \dots \le c_k\) and respectively \(s_1 \ge \dots \ge s_k \ge 0\), such that \(c_i^2 + s_i^2 = 1\). The generalized singular values are given by \(c_i / s_i\) and are understood to be infinite when \(s_i = 0\). If \(K_k\) is nonsingular, then the generalized singular values coincide with the singular values of \({\underline{H}}_k K_k^{-1}\). See Golub and Van Loan [8, Section 8.7.3] for more information.
Using a similar derivation as before, we can show that
and that the new bounds are given by
Here \(\mu _k\) is unbounded from above if \(s_k = 0\), that is, if \(K_k\) becomes singular.
The bounds in this section can be readily computed and used to implement bisection and the secant method. We consider parameter selection for multiparameter regularization in the following section.
4 A Multiparameter Selection Strategy
Choosing satisfactory \({\mu _k^{i}}\) in multiparameter regularization is more difficult than the corresponding one-parameter problem. See for example [1, 2, 6, 14, 16, 20, 20]. In particular, there is no obvious multiparameter extension of the discrepancy principle. Nevertheless, methods based on the discrepancy principle exist and we will discuss three of them.
Brezinski et al. [2] had some success with operators splitting. Substituting \({\mu _k^{i}} = {\nu _k^{i}} {\omega _k^{i}}\) in (3) with nonnegative weights \({\omega _k^{i}}\) and \(\sum _{i=1}^\ell {\omega _k^{i}} = 1\) leads to
This form of the minimization problem suggests the approximation of \(X_k^* {\varvec{x}}_\star \) by a linear combination [2, Sect. 3] of \({{\varvec{c}}_k^{i}}({\nu _k^{i}})\), where
and \({\nu _k^{i}}\) is such that \(\Vert {\underline{H}}_k {{\varvec{c}}_k^{i}}({\nu _k^{i}}) - \beta {\varvec{e}}_1\Vert = \eta \varepsilon \). Alternatively, Brezinski et al. [2] consider solving

where \({\nu ^{i}}\) are fixed and obtained from (12). The latter approach provides better results in exchange for an additional QR decomposition. In either case, operator splitting is a straightforward approach, but does not necessarily satisfy the discrepancy principle exactly.
Lu and Pereverzyev [19] and later Fornasier et al. [5] rewrite the constrained minimization problem as a differential equation and approximate
by a model function \(m(\varvec{\mu })\) which admits a straightforward solution to the constructed differential equation. However, it is unclear which \(\varvec{\mu }\) the method finds and its solution may depend on the initial guess. On the other hand, it is possible to keep all but one parameter fixed and compute a value for the free parameter such that the discrepancy principle is satisfied. This allows one to trace discrepancy hypersurfaces to some extent.
Gazzola and Novati [6] describe another interesting method. They start with a one-parameter problem and successively add parameters in a novel way, until each parameter of the full multiparameter problem has a value assigned. Especially in early iterations the discrepancy principle is not satisfied, but the parameters are updated in each iteration so that the norm of the residual is expected to approach \(\eta \varepsilon \). Unfortunately, we observed some issues in our implementation. For example, the quality of the result depends on initial values, as well as the order in which the operators are added (that is, the indexing of the operators). The latter problem is solved by a recently published and improved version of the method [7], which was brought to our attention during the revision of this paper.
We propose a new method that satisfies the discrepancy principle exactly, does not depend on an initial guess, and is independent of the scaling or indexing of the operators. The method uses the operator splitting approach in combination with new weights. Let us omit all k subscripts for the remainder of this section, and suppose \({\mu ^{i}} = \mu {\omega ^{i}}\), where \({\omega ^{i}}\) are nonnegative, but do not necessarily sum to one, and \(\mu \) is such that the discrepancy principle is satisfied. Then (3) can be written as
Since the goal of regularization is to reduce sensitivity of the solution to noise, we use the weights
which bias the regularization parameters in the direction of lower sensitivity with respect to changes in \({\nu ^{i}}\). Here D denotes the (total) derivative with respect to regularization parameter(s), and \({{\varvec{c}}^{i}}\) and \({\nu ^{i}}\) are defined as before, consequently
If for some indices \(D {{\varvec{c}}^{i}}({\nu ^{i}}) = \mathbf{0 }\), then we take a \({{\varvec{c}}^{i}}({\nu ^{i}})\) as the solution, or replace \(\Vert D {{\varvec{c}}^{i}}({\nu ^{i}})\Vert \) by a small positive constant. With this parameter choice, the solution does not depend on the indexing of the operators, nor, up to a constant, on the scaling of A, \(\varvec{b}\), or any of the \({L^{i}}\). The former is easy to see; for the latter, let \(\alpha \), \(\gamma \), and \({\lambda ^{i}}\) be positive constants, and consider the scaled problem
The noisy component of \(\gamma {\varvec{b}}\) is \(\gamma {\varvec{e}}\) and \(\Vert \gamma {\varvec{e}}\Vert \le \gamma \varepsilon \), hence the new discrepancy bound becomes
The bound is satisfied when \({{\widehat{\omega }}^{i}} = \alpha ^2 / (\lambda ^i)^2\; {\omega ^{i}}\), since in this case
and
It may be checked that the weights in (14) are indeed proportional to \(\alpha ^2/(\lambda ^i)^2\), that is
There are additional viable choices for \({\omega ^{i}}\), including two smoothed versions of the above:
which consider the sensitivity of \({{\varvec{c}}^{i}}({\nu ^{i}})\) in the range of \({\underline{H}}\) and \({K^{i}}\) respectively. We summarize the new parameter selection in Algorithm 3 below.
Algorithm 3
(Multiparameter selection)
Input: Projected matrices \({\underline{H}}\), \({K^{1}}\), ..., \({K^{\ell }}\), \(\beta = \Vert {\varvec{b}}\Vert \), noise estimate \(\varepsilon \), uncertainty parameter \(\eta \), and threshold \(\tau \).
Output: Regularization parameters \({\mu ^{1}}\), ..., \({\mu ^{\ell }}\).
-
1.
Use (12) to compute \({{\varvec{c}}^{i}}\) and \({\nu ^{i}}\).
i f \(\Vert D {{\varvec{c}}^{i}}({\nu ^{i}})\Vert \le \tau \Vert {{\varvec{c}}^{i}}({\nu ^{i}})\Vert \) for some i then
-
2.
Set \({\omega ^{i}} = \tau ^{-1}\); or set \({\mu ^{i}} = {\nu ^{i}}\) and \({\mu ^{j}} = 0\) for \(j\ne i\).
else
-
3.
Let \({\omega ^{i}} = \Vert {{\varvec{c}}^{i}}({\nu ^{i}})\Vert /\Vert D {{\varvec{c}}^{i}}({\nu ^{i}})\Vert \).
-
4.
Compute \(\mu \) in (13) such that the discrepancy principle is satisfied.
-
5.
Set \({\mu ^{i}} = \mu {\omega ^{i}}\).
An interesting property of Algorithm 3 is that, under certain conditions, \({\varvec{c}}(\varvec{\mu }({\widetilde{\varepsilon }}))\) converges to the unregularized least squares solution
as the \({\widetilde{\varepsilon }}\) goes to zero. Here \({\underline{H}}^+\) denotes the Moore–Penrose pseudoinverse and \({\varvec{c}}(\mathbf{0 })\) is the minimum norm solution of the unregularized problem. The following proposition formalizes this observation.
Proposition 3
Assume that \({\underline{H}}\) is full rank, \({\underline{H}}^*\beta {\varvec{e}}_1 \ne \mathbf{0 }\), and that \({K^{i}}\) is nonsingular for \(i=1\), ...\(\ell \). Let \({\widetilde{\varepsilon }}\) and \(\rho \) be defined as in Sect. 3, let \(\eta >1\) be fixed, and suppose that \({\nu ^{i}}({\widetilde{\varepsilon }})\) and
are computed according to Algorithm 3 for all \(0\le {\widetilde{\varepsilon }} < \rho \). Then
Proof
First note that \({\underline{H}}^* \beta {\varvec{e}}_1 \ne \mathbf{0 }\) implies that \(\beta > 0\) and \(\rho > 0\). Since \({\underline{H}}\) is full rank, the maps
are continuous for all \(\nu \ge 0\) and \(\varvec{\mu }\ge \mathbf{0 }\), where the latter bound should be interpreted elementwise. Hence
It remains to be shown that
Let \({\widetilde{\varepsilon }}\) be restricted to the interval \([0, \rho /2]\) and define \({\nu _{\max }^{i}} = \sigma _{\max }^2({\underline{H}} ({K^{i}})^{-1})\). By Proposition 2,
which proves the first limit in (15). Furthermore, using the definitions of \({{\varvec{c}}^{i}}({\nu ^{i}}({\widetilde{\varepsilon }}))\) and \(D {{\varvec{c}}^{i}}({\nu ^{i}}({\widetilde{\varepsilon }}))\) we find the bounds
which show that the inequality in (15) is satisfied. Moreover, the bounds show there exist \(\omega _{\min }\) and \(\omega _{\max }\) such that
Now, let \({\mathbf {K}}({\widetilde{\varepsilon }})\) be the nonsingular matrix satisfying
then it can be checked that
Define the right hand side of the equation above as M, then by Proposition 2, each entry of \(\varvec{\mu }({\widetilde{\varepsilon }})\) is bounded from below by 0 and from above by
which goes to 0 as \({\widetilde{\varepsilon }} \downarrow 0\). Therefore, this proves second limit in (15). \(\square \)
Proposition 3 is related to [9, Thm 3.3.3], where it is shown that the solution of a standard form Tikhonov regularization problem converges to a minimum norm least squares solution when the discrepancy principle is used and the noise converges to zero.
In this section we have discussed a new parameter selection method. In the next section we will look at the effect of perturbations in the parameters on the obtained solutions.
5 Perturbation Analysis
The goal of regularization is to make reconstruction robust with respect to noise. By extension, a high sensitivity to the regularization parameters is undesirable. Consider a set of perturbed parameters \(\varvec{\mu }_k + {\varDelta }\varvec{\mu }\); if \(\Vert {\varDelta }\varvec{\mu }\Vert \) is sufficiently small

where M and \({\varDelta } M\) are defined as
Therefore, one might choose \(\varvec{\mu }_k\) to minimize the sensitivity measure
To see the connection with the previous section, suppose that \(\varvec{\mu }_k = {\nu _k^{i}} {\varvec{e}}_i\) and \({\varDelta }\varvec{\mu } = \pm \Vert {\varDelta }\varvec{\mu }\Vert {\varvec{e}}_i\), then
Thus, larger weights \({\omega _k^{i}}\) correspond to smaller lower bounds on \(\Vert M^{-1}{\varDelta } M\Vert \). Having small lower bounds is desirable, since we show in Propositions 4 and 5 that minimizing \(\Vert M^{-1}{\varDelta } M\Vert \) is equivalent to minimizing upper bounds on the forward and backward errors respectively.
Proposition 4
Given regularization parameters \({\mu _k^{i}}\) and perturbations \({\mu _\star ^{i}} = {\mu _k^{i}} + {\varDelta }{\mu _k^{i}}\), let \({\varvec{c}}_k = {\varvec{c}}_k(\varvec{\mu }_k)\), \({\varvec{c}}_\star = {\varvec{c}}_k(\varvec{\mu }_\star )\), \({\varvec{x}}_k = X_k {\varvec{c}}_k\), and \({\varvec{x}}_\star = X_k {\varvec{c}}_\star \). Assume \({\underline{H}}_k\) and all \({K_k^{i}}\) are of full rank and define matrices M and \({\varDelta } M\) as in (16). If M and \(M + {\varDelta } M\) are nonsingular and the \({\varDelta } {\mu _k^{i}}\) are sufficiently small so that \(\Vert M^{-1} {\varDelta } M\Vert < 1\), then
Proof
Observe that \({\varvec{c}}_k = M^{-1} {\underline{H}}_k^* \beta {\varvec{e}}_1\) and \(\varvec{c}_\star = (M + {\varDelta } M)^{-1} {\underline{H}}_k^* \beta {\varvec{e}}_1\). With a little manipulation we obtain
It follows that
Since \(X_k\) has orthonormal columns, the result of the proposition follows. \(\square \)
One may wonder if it is possible to pick a vector \({\varvec{f}}\) close to \(\beta {\varvec{e}}_1\) such that
Or in other words, given perturbed regularization parameters, is there a perturbation of \(\beta {\varvec{e}}_1\) such that the optimal approximation to the exact solution is obtained? The following proposition provides a positive answer.
Proposition 5
Under the assumptions of Proposition 4, there exist vectors \({\varvec{f}}\) and \({\varvec{g}}\) such that \({\varvec{c}}_k = (M + {\varDelta } M)^{-1} {\underline{H}}_k^* {\varvec{f}}\) and \({\varvec{c}}_\star = M^{-1} {\underline{H}}_k^* {\varvec{g}}\). Furthermore, \({\varvec{f}}\) and \({\varvec{g}}\) satisfy
where \(\kappa ({\underline{H}}_k)\) is the condition number of \({\underline{H}}_k\).
Proof
The vector \({\varvec{f}}\) is easy to derive using the ansatz
Let \({\underline{H}}_k = QR\) denote the reduced QR-decomposition of \({\underline{H}}_k\), then
and
for arbitrary \({\varvec{v}}\). Indeed, it is easy to verify that the above vector satisfies
If we choose \({\varvec{v}} = \beta {\varvec{e}}_1\), then
so that
Here \(\Vert R^{-*}\Vert \; \Vert R^*\Vert \) is the condition number \(\kappa ({\underline{H}}_k)\) and \(\Vert {\varDelta } M M^{-1}\Vert = \Vert M^{-1} {\varDelta } M\Vert \), since both M and \({\varDelta } M\) are symmetric. This proves the first part of the proposition.
The second part is analogous. In particular, we use the ansatz
and derive
Again it is easy to verify that \({\varvec{c}}_\star = M^{-1} {\underline{H}}_k^* {\varvec{g}}\). Observe that \({\varvec{g}}\) can be rewritten as
such that
Since \(\Vert {\varDelta } M M^{-1}\Vert = \Vert M^{-1} {\varDelta } M\Vert < 1\), it follows that
which concludes the proof. \(\square \)
We have discussed forward and backward error bounds which help motivate our parameter choice. Now that we have investigated each of the three phases of our method, we are ready to show numerical results.
6 Numerical Experiments
We benchmark our algorithm with problems from Regularization Tools by Hansen [10]. Each problem provides an ill-conditioned \(n \times n\) matrix A, a solution vector \({\varvec{x}}_\star \) of length n and a corresponding measured vector \({\varvec{b}}\). We let \(n = 1024\) and add a noise vector \({\varvec{e}}\) to \({\varvec{b}}\). The entries of \({\varvec{e}}\) are drawn independently from the standard normal distribution. The noise vector is then scaled such that \(\varepsilon = \Vert {\varvec{e}}\Vert \) equals \(0.01 \Vert {\varvec{b}}\Vert \) or \(0.05 \Vert {\varvec{b}}\Vert \) for 1 and 5 % noise respectively. We use \(\eta = 1.01\) for the discrepancy bound in (7). We test the algorithms with 1000 different noise vectors for every triplet A, \({\varvec{x}}_\star \), and \({\varvec{b}}\) and report the median results.
The algorithms terminate when the relative difference between two subsequent approximations is less then 0.01, when \({\varvec{x}}_{k+1}\) is (numerically) linear dependent in \(X_k\), when both \(U_{k+1}\) and none of the \({V_k^{i}}\) can be expanded, or when a maximum number of iterations is reached. For Algorithm 2 we use a maximum of 20 iterations and for Algorithm 1 a maximum of \((\ell +1) \times 20\) iterations. For the sake of a fair comparison, the algorithms return the best obtained approximations and their iteration numbers.
For each test problem, the tables below list the relative error obtained with Algorithm 1, abbreviated by \(E_\text {od}\), and Algorithm 2, abbreviated by \(E_\text {md}\). OD and MD stand for one direction and multidirectional respectively. Also listed are the ratio \(\rho _E\) of \(E_\text {md}\) to \(E_\text {od}\) and the ratio \(\rho _\text {mv}\) of the number of matrix-vector products. That is,
Only matrix-vector multiplications with A, \(A^*\), \({L^{i}}\), and \({L^{i}}^*\) count towards the total number of MVs used by each algorithm. We note, however, that multiplications with \({L^{i}}\) and \({L^{i}}^*\) are often less costly than multiplications with A and \(A^*\).
Table 1 lists the results one-parameter Tikhonov regularization, where we used the following regularization operators. The first derivative operator \(L_1\) with stencil \([1,-1]\) for Gravity-3, Heat-5, Heat, and Phillips. The second derivative operator \(L_2\) with stencil \([1,-2,1]\) for Deriv2-1, Deriv2-2, Foxgood, Gravity-1, and Gravity-2. The third derivative operator \(L_3\) with stencil \([-1,3,-3,1]\) for Baart. The fifth derivative operator \(L_5\) with stencil \([-1,5,-10,10,-5,1]\) and Deriv2-3. The derivative operators \(L_d\) are of size \((n-d) \times n\).
The table shows that multidirectional subspace expansion can obtain small improvements in the relative error at the cost of a small number of extra matrix-vector products, especially for 1 % noise. We stress that in these cases, Algorithm 1 is allowed to perform additional MVs, but converges with a higher relative error. If there is no improvement in the relative error, we see that multidirectional subspace expansion can improve convergence, for example, for the Deriv2 problems as well as Foxgood.
Table 2 lists the results for multiparameter Tikhonov regularization. We used the following regularization operators for each problem: the derivative operator \(L_d\) as listed above, the identity operator I, and the orthogonal projection \((I - N_d N_d^*)\), where the columns of \(N_d\) are an orthonormal basis for the nullspace  .
.
Overall, we observe larger improvements in the relative error for multidirectional subspace expansion, but also a larger number MVs. We no longer see cases where multidirectional subspace expansion terminates with fewer MVs. In fact, the relative error is the same for Heat, although more MVs are required. Finally, Fig. 1 illustrates an example of the improved results which can be obtained by using multidirectional subspace expansion.
baart test matrix with \(n = 1024\) and 1 % noise. The solid line is the exact solution. The dashed line is the solution obtained with multiparameter regularization and the residual subspace expansion (Algorithm 1). The dotted line is the solution obtained with multiparameter regularization and multidirectional subspace expansion (Algorithm 2)
In the next tests we attempt to reconstruct the original image from a blurred and noisy observation. Consider an \(n \times n\) grayscale image with pixel values in the interval [0, 1]. Then \({\varvec{x}}\) is a vector of length \(n^2\) obtained by stacking the columns of the image below each other. The matrix A represents a Gaussian blurring operator, generated with blur from Regularization Tools. The matrix A is block-Toeplitz with half-bandwidth band=11 and the amount of blurring is given by the variance sigma=5. The entries of the noise vector \({\varvec{e}}\) are independently drawn from the standard normal distribution after which the vector is scaled such that \(\varepsilon = {\mathbb {E}}[\Vert {\varvec{e}}\Vert ] = 0.05 \Vert {\varvec{b}}\Vert \). We take \(\eta \) such that \(\Vert {\varvec{e}}\Vert \le \eta \varepsilon \) in 99.9 % of the cases. That is,
For regularization we choose an approximation to the Perona–Malik [22] operator

where \(\rho \) is a small positive constant. Because  is a nonlinear operator, we first perform a small number of iterations with a finite difference approximation \(L_{{\varvec{b}}}\) of
is a nonlinear operator, we first perform a small number of iterations with a finite difference approximation \(L_{{\varvec{b}}}\) of  . The resulting intermediate solution \(\widetilde{\varvec{x}}\) is used for a new approximation \(L_{\tilde{\varvec{x}}}\) of
. The resulting intermediate solution \(\widetilde{\varvec{x}}\) is used for a new approximation \(L_{\tilde{\varvec{x}}}\) of  . Finally, we run the algorithms a second time with \(L_{\widetilde{\varvec{x}}}\) and more iterations; see Reichel et al. [23] for more information regarding the implementation of the Perona–Malik operator.
. Finally, we run the algorithms a second time with \(L_{\widetilde{\varvec{x}}}\) and more iterations; see Reichel et al. [23] for more information regarding the implementation of the Perona–Malik operator.
The first test image is also used in [13, 23, 25], and is shown in Figure 2. We use \(\rho = 0.075\), 20 iterations for the first run, and 100 iterations for the second run. The second image is an image of Saturn, see Figure 3. For this image we use \(\rho = 0.03\), 25 iterations for the first run and 150 iterations for the second run. In both cases we stop the iterations around the point where convergence flattens out, as can be seen from the convergence history in Figure 4. The figure uses the peak signal-to-noise ratio (PSNR) given by
versus the iteration number k. A higher PSNR means a higher quality reconstruction.
We observe that multidirectional subspace expansion may allow convergence to a more accurate solution. Because multidirectional subspace expansion requires extra matrix-vector products, we investigate the performance in Table 3 and when the PSNR of the output of Algorithm 2 achieves parity with the PSNR of the output of Algorithm 1. There is only a small difference in the total number of matrix-vector products when parity is achieved, but a large improvement in wall clock time. This improvement is in large part due to the block operations which can only be used Algorithm 2. For reference, the runtimes were obtained on an Intel Core i7-3770 and with MATLAB R2015b on 64-bit Linux 4.2.5.
7 Conclusions
We have presented a new method for large-scale Tikhonov regularization problems. In accordance with Algorithm 2, the method combines a new multidirectional subspace expansion with optional truncation to produce a higher quality search space. The multidirectional expansion generates a richer search space, whereas the truncation ensures moderate growth. Numerical results illustrate that our method can yield more accurate results or faster convergence. Furthermore, we have presented lower and upper bounds on the regularization parameter when the discrepancy principle is applied to one-parameter regularization. These lower and upper bounds can be used in particular to initiate bisection or the secant method. In addition, we have introduced a straightforward parameter choice for multiparameter regularization, as summarized by Algorithm 3. The parameter selection satisfies the discrepancy principle, and is based on easy to compute derivatives that are related to the perturbation results of Sect. 5.
References
Belge, M., Kilmer, M.E., Miller, E.L.: Efficient determination of multiple regularization parameters in a generalized l-curve framework. Inverse Probl. 18(4), 1161–1183 (2002)
Brezinski, C., Redivo-Zaglia, M., Rodriguez, G., Seatzu, S.: Multi-parameter regularization techniques for ill-conditioned linear systems. Numer. Math. 94(2), 203–228 (2003)
Calvetti, D., Reichel, L.: Tikhonov regularization of large linear problems. BIT 43(2), 263–283 (2003)
Fong, D., Saunders, M.A.: LSMR: an iterative algorithm for sparse least-squares problems. SIAM J. Sci. Comput. 33(5), 2950–2971 (2011)
Fornasier, M., Naumova, V., Pereverzyev, S.V.: Parameter choice strategies for multipenalty regularization. SIAM J. Numer. Anal. 52(4), 1770–1794 (2014)
Gazzola, S., Novati, P.: Multi-parameter Arnoldi–Tikhonov methods. Electron. Trans. Numer. Anal. 40, 452–475 (2013)
Gazzola, S., Reichel, L.: A new framework for multi-parameter regularization. BIT, 1–31 (2015)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. Johns Hopkins University Press, Baltimore (1996)
Groetsch, C.: The Theory of Tikhonov Regularization for Fredholm Equations of the First Kind. Pitman Publishing, Boston (1984)
Hansen, P.C.: Regularization tools: a matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 6, 1–35 (1994)
Hansen, P.C.: Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion. SIAM, Philadelphia (1998)
Hochstenbach, M.E., Reichel, L.: An iterative method for Tikhonov regularization with a general linear regularization operator. J. Integral Equ. Appl. 22(3), 465–482 (2010)
Hochstenbach, M.E., Reichel, L., Yu, X.: A Golub-Kahan-type reduction method for matrix pairs. J. Sci. Comput. 65(2), 767–789 (2015)
Ito, K., Jin, B., Takeuchi, T.: Multi-parameter Tikhonov Regularization. arXiv:1102.1173v2 [math.NA] (2011). Preprint
Kilmer, M.E., Hansen, P., Español, M.: A projection-based approach to general-form Tikhonov regularization. SIAM J. Sci. Comput. 29(1), 315–330 (2007)
Kunisch, K., Pock, T.: A bilevel optimization approach for parameter learning in variational models. SIAM J. Imaging Sci. 6(2), 938–983 (2013)
Lampe, J., Reichel, L., Voss, H.: Large-scale Tikhonov regularization via reduction by orthogonal projection. Linear Algebra Appl. 436(8), 2845–2865 (2012)
Li, R.C., Ye, Q.: A Krylov subspace method for quadratic matrix polynomials with applications to constrained least squares problems. SIAM J. Matrix Anal. Appl. 25(2), 405–528 (2003)
Lu, S., Pereverzyev, S.V.: Multi-parameter regularization and its numerical realization. Numer. Math. 118(1), 1–31 (2011)
Lu, S., Pereverzyev, S.V., Shao, Y., Tautenhahn, U.: Discrepancy curves for multi-parameter regularization. J. Inverse Ill-Posed Probl. 18(6), 655–676 (2010)
Paige, C.C., Saunders, M.A.: LSQR: an algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 8(1), 43–71 (1982)
Perona, P., Malik, J.: Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12(7), 629–639 (1990)
Reichel, L., Sgallari, F., Ye, Q.: Tikhonov regularization based on generalized Krylov subspace methods. Appl. Numer. Math. 62(9), 1215–1228 (2012)
Reichel, L., Yu, X.: Matrix decompositions for Tikhonov regularization. Electron. Trans. Numer. Anal. 43, 223–243 (2015)
Reichel, L., Yu, X.: Tikhonov regularization via flexible Arnoldi reduction. BIT 55(4), 1145–1168 (2015)
Acknowledgments
We would like to thank the editor and the referees for their excellent feedback and helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is part of the research program “Innovative methods for large matrix problems”, which is (partly) financed by the Netherlands Organization for Scientific Research (NWO).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zwaan, I.N., Hochstenbach, M.E. Multidirectional Subspace Expansion for One-Parameter and Multiparameter Tikhonov Regularization. J Sci Comput 70, 990–1009 (2017). https://doi.org/10.1007/s10915-016-0271-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0271-0
Keywords
- Tikhonov
- Multiparameter Tikhonov
- Generalized Krylov
- Multidirectional subspace expansion
- Subspace truncation
- Subspace method
- Linear discrete ill-posed problem
- Regularization
- Regularization parameter



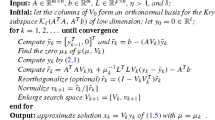
 .
. .
.


