Skip to main content
SpringerLink
Log in

Radial Basis Function ENO and WENO Finite Difference Methods Based on the Optimization of Shape Parameters

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

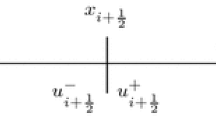
Abstract

We present adaptive finite difference ENO/WENO methods with infinitely smooth radial basis functions (RBFs). These methods slightly perturb the polynomial reconstruction coefficients with RBFs as the reconstruction basis and enhance accuracy in the smooth region by locally optimizing the shape parameters. Compared to the classical ENO/WENO methods, the RBF-ENO/WENO methods provide more accurate reconstructions and sharper solution profiles near the jump discontinuity. Furthermore the RBF-ENO/WENO methods are easy to implement in the existing classical ENO/WENO code. The numerical results in 1D and 2D presented in this paper show that the proposed finite difference RBF-ENO/WENO methods perform better than the classical ENO/WENO methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. The value of \(\varepsilon ^2\) is not necessarily non-negative and \(\varepsilon \) can be either real or complex for the optimization of the error. We note that the raw value of the shape parameter, \(\varepsilon \), is not used for the reconstruction; what we use in the reconstruction is \(\varepsilon ^2\). Thus a complex value of \(\varepsilon \) is still allowed for the RBF-ENO/WENO formulation.

  2. To prevent the case that the denominator of (24) becomes zero, a small positive number \(\gamma \), is added in the denominator. In practice, we use \(\varepsilon ^2 \approx \frac{2}{\varDelta x^2}\cdot \frac{-f_{i-1}+2f_{i}-f_{i+1}}{-f_{i-1}+5f_{i}+2 f_{i+1}+\gamma }\), where \(\gamma \) is a small positive constant, e.g. \(\gamma = 10^{-13}\).

  3. Note that the denominator in (26) could be zero. However, in the implementation of the RBF-ENO/WENO methods, we apply a modified version of (27), which is explained in [8, 9]. In this alternative way of implementation, we check the magnitude of the denominator first. Only when the denominator is larger than some threshold, we compute the critical point as in (26) to check whether it is within the interval of [0, 3]. Otherwise, the stencil is considered to be smooth.

  4. The precise CFL condition is \(\varDelta t = C {\varDelta x}^{{\ell }/{3}}\), where \(\ell \) is the order of the method. Since we are using a simpler form of \(\varDelta t = C \varDelta x\), the convergence is slower than expected for the small values of N. But for the large values of N, we can use the linear relation between the temporal and spatial spacings. This is what we observe in Tables 4 and 5, as well as in Figs. 1 and 3.

References

  1. Aboiyar, T., Georgoulis, E.H., Iske, A.: Adaptive ADER methods using kernel-based polyharmonic spline WENO reconstruction. SIAM J. Sci. Comput. 32, 3251–3277 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  2. Borges, R., Carmona, M., Costa, B., Don, W.-S.: An improved WENO scheme for hyperbolic conservation laws. J. Comput. Phys. 227, 3191–3211 (2008)

    Article  MATH  Google Scholar 

  3. Buhman, M.D.: Radial Basis Functions—Theory and Implementations. Cambridge University Press, Cambridge (2003)

    Book  Google Scholar 

  4. Chen, X., Jung, J.-H.: Matrix stability of multiquadric radial basis function methods for hyperbolic equations with uniform centers. J. Sci Comput. 51, 683–702 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  5. Costa, B., Don, W.-S.: High order hybrid central—WENO finite difference scheme for conservation laws. J. Comput. Appl. Math. 204, 209–218 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Costa, B., Don, W.-S.: Multi-domain hybrid spectral-WENO methods for hyperbolic conservation laws. J. Comput. Phys. 224, 970–991 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Costa, B., Don, W.-S., Gottlieb, D., Sendersky, R.: Two-dimensional multi-domain hybrid spectral-WENO methods for the conservation laws. Commun. Comput. Phys. 1, 1–31 (2006)

    MATH  Google Scholar 

  8. Guo, J., Jung, J.-H.: A RBF-WENO finite volume method for hyperbolic conservation laws with the monotone polynomial interpolation method. Under review (2016)

  9. Guo, J., Jung, J.-H.: A numerical study of the local monotone polynomial edge detection for the hybrid WENO method. Under review (2016)

  10. Ha, Y., Kim, C.H., Lee, Y.J., Yoon, J.: An improved weighted essentially non-oscillatory scheme with a new smoothness indicator. J. Comput. Phys. 232, 68–86 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Harten, A., Engquist, B., Osher, S., Chakravarthy, S.R.: Uniformly high order accurate essentially non-oscillatory schemes III. J. Comput. Phys. 71, 231–303 (1987)

    Article  MATH  Google Scholar 

  12. Henrick, A.K., Aslam, T.D., Powers, J.M.: Mapped weighted-essentially non-oscillatory schemes: achieving optimal order near critical points. J. Comput. Phys. 207, 542–567 (2005)

    Article  MATH  Google Scholar 

  13. Hesthaven, J., Gottlieb, S., Gottlieb, D.: Spectral Methods for Time Dependent Problems. Cambridge University Press, Cambridge (2007)

    Book  MATH  Google Scholar 

  14. Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  15. Larsson, E., Fornberg, B.: Theoretical and computational aspects of multivariate interpolation with increasingly flat radial basis functions. Comput. Math. Appl. 49, 103–130 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lax, P.D.: Weak solutions of nonlinear hyperbolic equations and their numerical computation. Commun. Pure Appl. Math. 7, 159–193 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  17. Lee, Y., Yoon, J., Micchelli, C.: On convergence of flat multivariate interpolation by translation kernels with finite smoothness. Constr. Approx. 40, 37–60 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, P., Gao, Z., Don, W.-S., Xie, S.: Hybrid Fourier-continuation method and weighted essentially non-oscillatory finite difference scheme for Hyperbolic Conservation Laws in a single-domain framework. J. Sci. Comput. 64, 670–695 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Shahbazi, K., Albin, N., Bruno, O.P., Hesthaven, J.S.: Multi-domain Fourier-continuation/WENO hybrid solver for conservation laws. J. Comput. Phys. 230, 8779–8796 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Shu, C.-W.: Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In: Cockburn, B., Shu, C.-W., Johnson, C., Tadmor, E., Quarteroni, A. (eds.) Advanced Numerical Approximation of Nonlinear Hyperbolic Equations, pp. 325–432. Springer, Heidelberg (1998)

    Chapter  Google Scholar 

  21. Shu, C.-W.: High order weighted essentially non-oscillatory schemes for convection dominated problems. SIAM Rev. 51, 82–126 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  22. Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471 (1988)

    Article  MATH  Google Scholar 

  23. Sod, G.A.: Survey of several finite-difference methods for systems of non-linear hyperbolic conservation laws. J. Comput. Phys. 27, 1–31 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  24. Woodward, P., Colella, P.: The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comput. Phys. 54, 115–173 (1984)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors thank W.-S. Don for his useful communication. We also thank the anonymous reviewers for their valuable comments.

Author information

Authors and Affiliations

  1. Department of Mathematics, University at Buffalo, The State University of New York, Buffalo, NY, 14260-2900, USA

    Jingyang Guo & Jae-Hun Jung

Authors
  1. Jingyang Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jae-Hun Jung
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jae-Hun Jung.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, J., Jung, JH. Radial Basis Function ENO and WENO Finite Difference Methods Based on the Optimization of Shape Parameters. J Sci Comput 70, 551–575 (2017). https://doi.org/10.1007/s10915-016-0257-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-016-0257-y

Keywords

Search

Navigation