Skip to main content
SpringerLink
Log in

Finite Element Method and A Priori Error Estimates for Dirichlet Boundary Control Problems Governed by Parabolic PDEs

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

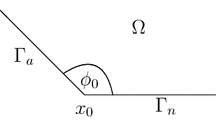
Finite element approximations of Dirichlet boundary control problems governed by parabolic PDEs on convex polygonal domains are studied in this paper. The existence of a unique solution to optimal control problems is guaranteed based on very weak solution of the state equation and \(L^2(0,T;L^2(\varGamma ))\) as control space. For the numerical discretization of the state equation we use standard piecewise linear and continuous finite elements for the space discretization of the state, while a dG(0) scheme is used for time discretization. The Dirichlet boundary control is realized through a space–time \(L^2\)-projection. We consider both piecewise linear, continuous finite element approximation and variational discretization for the controls and derive a priori \(L^2\)-error bounds for controls and states. We finally present numerical examples to support our theoretical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Apel, T., Flaig, T.G.: Crank–Nicolson schemes for optimal control problems with evolution equations. SIAM J. Numer. Anal. 50, 1484–1512 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arada, N., Raymond, J.P.: Dirichlet boundary control of semilinear parabolic equations: part I. Appl. Math. Optim. 45, 125–143 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  3. Belgacem, F.B., Bernardi, C., Fekih, H.E.: Dirichlet boundary control for a parabolic equation with a final observation I: a space–time mixed formulation and penalization. Asymptot Anal. 71, 101–121 (2011)

  4. Berggren, M.: Approximation of very weak solutions to boundary value problems. SIAM J. Numer. Anal. 42, 860–877 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bramble, J.H., Pasciak, J.E., Schatz, A.H.: The construction of preconditioners for elliptic problems by substructing I. Math. Comput. 47, 103–134 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  6. Casas, E., Mateos, M., Raymond, J.P.: Penalization of Dirichlet optimal control problems. ESAIM Control Optim. Calc. Var. 15, 782–809 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Casas, E., Raymond, J.P.: Error estimates for the numerical approximation of Dirichlet boundary control for semilinear elliptic equations. SIAM J. Control Optim. 45, 1586–1611 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  8. Casas, E., Sokolowski, J.: Approximation of boundary control problems on curved domains. SIAM J. Control Optim. 48, 3746–3780 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ciarlet, P.G.: The Finite Element Methods for Elliptic Problems. Elsevier, North-Holland (1978)

    Google Scholar 

  10. Deckelnick, K., Günther, A., Hinze, M.: Finite element approximation of Dirichlet boundary control for elliptic PDEs on two- and three-dimensional curved domains. SIAM J. Control Optim. 48, 2798–2819 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  11. French, D.A., King, J.T.: Approximation of an elliptic control problem by the finite element method. Numer. Funct. Anal. Optim. 12, 299–314 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  12. French, D.A., King, J.T.: Analysis of a robust finite element approximation for a parabolic equation with rough boundary data. Math. Comput. 60, 79–104 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  13. Fursikov, A.V., Gunzburger, M.D., Hou, L.S.: Boundary value problems and optimal boundary control for the Navier-Stokes systems: the two-dimensional case. SIAM J. Control Optim. 36, 852–894 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  14. Geveci, T.: On the approximation of the solution of an optimal control problem governed by an elliptic equation. RAIRO Anal. Numer. 13, 313–328 (1979)

    MathSciNet  MATH  Google Scholar 

  15. Gong, W., Yan, N.N.: A posteriori error estimate for boundary control problems governed by the parabolic partial differential equations. J. Comput. Math. 27, 68–88 (2009)

    MathSciNet  MATH  Google Scholar 

  16. Gong, W., Yan, N.N.: Mixed finite element method for Dirichlet boundary control problem governed by elliptic PDEs. SIAM J. Control Optim. 49, 984–1014 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  17. Grisvard, P.: Singularities in Boundary Value Problems. Springer, Berlin (1992)

    MATH  Google Scholar 

  18. Gunzburger, M.D., Hou, L.S.: Treating inhomogeneous essential boundary conditions in finite element methods and the calculation of boundary stresses. SIAM J. Numer. Anal. 29, 390–424 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  19. Hinze, M.: A variational discretization concept in control constrained optimization: the linear-quadratic case. Comput. Optim. Appl. 30, 45–63 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  20. Hinze, M., Kunisch, K.: Second order methods for boundary control of the instationary Navier–Stokes system. ZAMM Z. Angew. Math. Mech. 84, 171–187 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  21. Hinze, M., Matthes, U.: A note on variational discretization of Neumann boundary control problems. Control Cybern. 38, 577–591 (2009)

    MathSciNet  MATH  Google Scholar 

  22. Hinze, M., Pinnau, R., Ulbrich, M., Ulbrich, S.: Optimization with PDE Constraints, Mathematical Modelling: Theory and Applications, vol. 23. Springer, Berlin (2009)

    Google Scholar 

  23. Kunisch, K., Vexler, B.: Constrained Dirichlet boundary control in \(L^2\) for a class of evolution equations. SIAM J. Control Optim. 46, 1726–1753 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Lions, J.L.: Optimal Control of Systems Governed by Partial Differential Equations. Springer, Berlin (1971)

    Book  MATH  Google Scholar 

  25. Lions, J.L., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications, vol. I, II. Springer, Berlin (1972)

    Book  Google Scholar 

  26. Liu, W.B., Ma, H.P., Tang, T., Yan, N.N.: A posteriori error estimates for discontinuous Galerkin time-stepping method for optimal control problems governed by parabolic equations. SIAM J. Numer. Anal. 42, 1032–1061 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  27. Liu, W.B., Yan, N.N.: A posteriori error estimates for optimal control problems governed by parabolic equations. Numer. Math. 93, 497–521 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  28. Liu, W.B., Yan, N.N.: Adaptive Finite Element Methods for Optimal Control Governed by PDEs. Science press, Beijing (2008)

    Google Scholar 

  29. May, S., Rannacher, R., Vexler, B.: Error analysis fo a finite element approximation of elliptic Dirichlet boundary control problems. SIAM J. Control Optim. 51(3), 2585–2611 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. Meidner, D., Vexler, B.: A priori error estimates for space–time finite element discretization of parabolic optimal control problems. Part I: problems without control constraints. SIAM J. Control Optim. 47(3), 1150–1177 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  31. Meidner, D., Vexler, B.: A priori error estimates for space–time finite element discretization of parabolic optimal control problems. Part II: problems with control constraints. SIAM J. Control Optim. 47(3), 1301–1329 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  32. Meidner, D., Vexler, B.: A priori error analysis of the Petrov-Galerkin Crank–Nicolson scheme for parabolic optimal control problems. SIAM J. Control Optim. 49(5), 2183–2211 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  33. Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer, Berlin (2006)

    MATH  Google Scholar 

  34. Vexler, B.: Finite element approximation of elliptic Dirichlet optimal control problems. Numer. Funct. Anal. Optim. 28, 957–973 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  35. von Daniels, N., Hinze, M., Vierling, M.: Crank-Nicolson time stepping and variational discretization of control-constrained parabolic optimal control problems. SIAM J. Control Optim. 53(3), 1182–1198 (2015)

  36. Winther, R.: Error estimates for a Galerkin approximation of a parabolic control problem. Ann. Math. Pura App. 117(4), 173–206 (1978)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The first author would like to thank the Alexander von Humboldt Foundation for the support during the stay in University of Hamburg, Germany where this work was initialized. This work was supported by the National Basic Research Program of China under Grant 2012CB821204, the National Natural Science Foundation of China under Grant 11201464 and 91330115, and the scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry. The second author gratefully acknowledges the support of the DFG Priority Program 1253 entitled “Optimization with Partial Differential Equations”. The third author was supported by National Natural Science Foundation of China under Grant 11301311. The authors also would like to thank two anonymous referees for their valuable suggestions which lead to an improved paper.

Author information

Authors and Affiliations

  1. LSEC, Institute of Computational Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Wei Gong

  2. Schwerpunkt Optimierung und Approximation, Universität Hamburg, Bundesstrasse 55, 20146, Hamburg, Germany

    Michael Hinze

  3. School of Mathematics Sciences, Shandong Normal University, Jinan, 250014, China

    Zhaojie Zhou

Authors
  1. Wei Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Hinze
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhaojie Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Gong.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gong, W., Hinze, M. & Zhou, Z. Finite Element Method and A Priori Error Estimates for Dirichlet Boundary Control Problems Governed by Parabolic PDEs. J Sci Comput 66, 941–967 (2016). https://doi.org/10.1007/s10915-015-0051-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0051-2

Keywords

Mathematics Subject Classification

Search

Navigation