Skip to main content
SpringerLink
Log in

An integral discretization scheme on a graded mesh for a fractional differential equation with integral boundary conditions

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

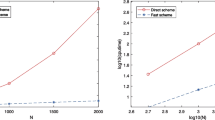
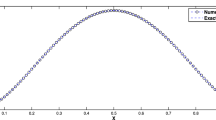
In this paper, a fractional differential equation with integral conditions is studied. The fractional differential equation is transformed into an integral equation with two initial values, where the initial values needs to ensure that the exact solution satisfies the integral boundary conditions. A graded mesh based on a priori information of the exact solution is constructed and the linear interpolation is used to approximate the functions in the fractional integral. The rigorous analysis about the convergence of the discretization scheme is derived by using the truncation error estimate techniques and the generalized Grönwall inequality. A quasi-Newton method is used to determine the initial values so that the numerical solution satisfies two integral boundary conditions within a prescribed precision. It is shown that the scheme is second-order convergent, which improves the results on the uniform mesh.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. A. Seal, S. Natesan, Convergence analysis of a second-order scheme for fractional differential equation with integral boundary conditions. J. Appl. Math. Comput. 69, 465–489 (2023)

    Article  Google Scholar 

  2. K. Diethlm, The Analysis of Fractional Differential Equations, Lecture Notes in Mathematics, vol. 2004. (Springer, Berlin, 2010)

    Book  Google Scholar 

  3. I. Podlubny, Fractional Differential Equations (Academic Press, New York, 1999)

    Google Scholar 

  4. A.A. Kilbas, H.M. Srivastaval, J.J. Trujillo, Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies, vol. 204 (Elsevier, Amsterdam, 2006)

    Google Scholar 

  5. M. Stynes, J.L. Gracia, A finite difference method for a two-point boundary value problem with a Caputo fractional derivative. IMA J. Numer. Anal. 35(2), 689–721 (2015)

    Article  Google Scholar 

  6. J.L. Gracia, M. Stynes, Central difference approximation of convection in Caputo fractional derivative two-point boundary value problems. J. Comput. Appl. Math. 273, 103–115 (2015)

    Article  Google Scholar 

  7. N. Kopteva, M. Stynes, An efficient collocation method for a Caputo two-point boundary value problem. BIT 55(4), 1105–1123 (2015)

    Article  Google Scholar 

  8. H. Liang, M. Stynes, Collocation methods for general Caputo two-point boundary value problems. J. Sci. Comput. 76, 390–425 (2018)

    Article  Google Scholar 

  9. Z. Cen, J. Huang, A. Xu, An efficient numerical method for a two-point boundary value problem with a Caputo fractional derivative. J. Comput. Appl. Math. 336, 1–7 (2018)

    Article  Google Scholar 

  10. Z. Cen, J. Huang, A. Xu, A. Le, A modified integral discretization scheme for a two-point boundary value problem with a Caputo fractional derivative. J. Comput. Appl. Math. 367, 112465 (2020)

    Article  Google Scholar 

  11. M.M. Meerschaert, C. Tadjeran, Finite difference approximations for fractional advection-dispersion flow equation. J. Comput. Appl. Math. 172(1), 65–77 (2004)

    Article  Google Scholar 

  12. N.H. Sweilam, A.A.E. El-Sayed, S. Boulaaras, Fractional-order advection-dispersion problem solution via the spectral collocation method and the non-standard finite difference technique. Chaos Solitons Fractals 144, 110736 (2021)

    Article  Google Scholar 

  13. N.H. Sweilam, M.M. Khader, M. Adel, Chebyshev pseudo-spectral method for solving fractional advection-dispersion equation. Appl. Math. 5(19), 3240–3248 (2014)

    Article  Google Scholar 

  14. V. Saw, S. Kumar, Fourth kind shifted Chebyshev polynomials for solving space fractional order Advection-dispersion equation based on collocation method and finite difference Approximation, Int. J. Appl. Comput. Math., 4 (2018) Article number 82

  15. V. Saw, S. Kumar, Second kind Chebyshev polynomials for solving space fractional advection-dispersion equation using collocation method. Iran. J. Sci. Technol. Trans. Sci. 43(3), 1027–1037 (2019)

    Article  Google Scholar 

  16. M.M. Khader, N.H. Sweilam, Approximate solutions for the fractional advection-dispersion equation using Legendre pseudo-spectral method. Comput. Appl. Math. 33, 739–750 (2014)

    Article  Google Scholar 

  17. J.P. Roop, Numerical approximation of a one-dimensional space fractional advection-dispersion equation with boundary layer. Comput. Math. Appl. 56, 1808–1819 (2008)

    Article  Google Scholar 

  18. M.O. Deville, A. Mojtabi, One-dimensional linear advection-diffusion equation: analytical and finite element solutions. Comput. Fluids 107, 189–195 (2014)

    Google Scholar 

  19. L.K. Gadzova, Nonlocal boundary-value problem for a linear ordinary differential equation with fractional discretely distributed differentiation operator. Math. Notes 106, 904–908 (2019)

    Article  Google Scholar 

  20. S.J.C. Mary, A. Tamilselvan, Numerical method for a non-local boundary value problem with Caputo fractional order. J. Appl. Math. Comput. 67, 1–17 (2021)

    Article  Google Scholar 

  21. N. Kopteva, M. Stynes, Analysis and numerical solution of a Riemann-Liouville fractional derivative two-point boundary value problem. Adv. Comput. Math. 43, 77–99 (2017)

    Article  Google Scholar 

  22. P. Lyu, S. Vong, A high-order method with a temporal nonuniform mesh for a time-fractional Benjamin-Bona-Mahony equation. J. Sci. Comput. 80, 1607–1628 (2019)

    Article  Google Scholar 

  23. C.P. Li, Q. Yi, A. Chen, Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J. Comput. Phys. 316, 614–631 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

We would like to thank the anonymous reviewers for their valuable suggestions and comments for the improvement of this paper.

Funding

The work was supported by Zhejiang Provincial Natural Science Foundation of China (Grant Nos. LGF22H260003, LTGY23H240002), Zhejiang Province Higher Education Teaching Reform Project (Grant Nos. jg20220457, jg20220466), and Ningbo Municipal Natural Science Foundation (Grant No. 2023J302).

Author information

Authors and Affiliations

  1. Institute of Mathematics, Zhejiang Wanli University, Ningbo, 315100, China

    Zhongdi Cen, Jian Huang & Aimin Xu

Authors
  1. Zhongdi Cen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aimin Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The first author carried out the literature review, designed the numerical algorithm, and wrote the main manuscript text. The second author conducted numerical experiments and participated in designing the numerical algorithm, and the third author participated in analyzing the error and designing the numerical algorithm. All authors reviewed and approved the final manuscript.

Corresponding author

Correspondence to Jian Huang.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cen, Z., Huang, J. & Xu, A. An integral discretization scheme on a graded mesh for a fractional differential equation with integral boundary conditions. J Math Chem (2024). https://doi.org/10.1007/s10910-024-01596-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10910-024-01596-7

Keywords

Mathematics Subject Classification

Search

Navigation