1 Introduction

A main objective in synthetic biology is to control living cells [1,2,3,4,5,6]—a challenging problem that requires addressing a number of complicating factors displayed by intracellular networks:

(N):

Nonlinearity. Intracellular networks are nonlinear (bimolecular), i.e. they include reactions involving two reacting molecules.

(D):

Dimensionality. Intracellular networks are higher-dimensional, i.e. they contain a large number of coupled molecular species.

(U):

Uncertainty. The experimental information about the structure, rate coefficients and initial conditions of intracellular networks is uncertain (incomplete).

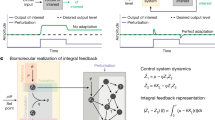
When embedded into an input network satisfying properties (N), (D) and (U), an ideal molecular controller network would ensure that the resulting output network autonomously traces a predefined dynamics in a stable and accurate manner over a desired time-interval. Controllers that maintain accuracy in spite of suitable uncertainties are said to achieve robust adaptation (homeostasis)—a fundamental design principle of living systems [7,8,9,10,11,12]. Control can be sought over deterministic dynamics when all of the molecular species are in higher-abundance [13, 15], or over stochastic dynamics when some species are present at lower copy-numbers [16,17,18]. See also Fig. 1, and Appendices A and B.

Fig. 1
figure 1

Schematic representation of biochemical control. A black-box input network \(\mathcal {R}_{\alpha }\) is displayed, consisting of unknown biochemical interactions shown in grey, where \(X_1 \rightarrow X_2\) (respectively, \(X_1 \dashv X_2\)) indicates that species \(X_1\) influences species \(X_2\) positively (respectively, negatively). The particular input network contains one interfacing species \(X_1\), shown as a green hexagon, that can be interfaced with a controller. The rest of the input species, that cannot be interfaced with a controller, are called residual species; one of the residual species, \(X_2\), is highlighted as a yellow triangle, while some of the other ones are displayed in grey. A controller network \(\mathcal {R}_{\beta , \gamma } = \mathcal {R}_{\beta } \cup \mathcal {R}_{\gamma }\) is also shown, consisting of controlling species \(Y_1\) and \(Y_2\) shown as a red circle and blue square, respectively, whose predefined biochemical interactions are shown in black. The controller consists of the core \(\mathcal {R}_{\beta } = \mathcal {R}_{\beta }(Y_1, Y_2)\), specifying how the controlling species interact among themselves, and the interface \(\mathcal {R}_{\gamma } = \mathcal {R}_{\gamma }(X_1, Y_1, Y_2)\), specifying how the controlling species \(Y_1\) and \(Y_2\) interact with the species \(X_1\). The composite network \(\mathcal {R}_{\alpha ,\beta ,\gamma } = \mathcal {R}_{\alpha } \cup \mathcal {R}_{\beta , \gamma }\) is called an output network. The particular controller \(\mathcal {R}_{\beta , \gamma }\) displayed corresponds to the network (8), with \(i = j = 1\), from Sect. 3 (Color figure online)

Full size image

In context of electro-mechanical systems, accuracy robust to some uncertainties can be achieved via so-called integral-feedback controllers (IFCs) [19]. Loosely speaking, IFCs dynamically calculate a time-integral of a difference (error) between the target and actual values of the controlled variable. The error is then used to decrease (respectively, increase) the controlled variable when it deviates above (respectively, below) its target value via a negative-feedback loop. However, IFCs implementable with electro-mechanical systems are not necessarily implementable with biochemical reactions [20]. Central to this problem is the fact that the error takes both positive and negative values and, therefore, cannot be directly represented as a nonnegative molecular abundance. In this context, a non-biochemical IFC has been mapped to a bimolecular one in [21], which has been adapted in [22] and called the “antithetic integral-feedback controller" (AIFC).

Performance of the AIFC has been largely studied when unimolecular and/or lower-dimensional input networks are controlled [22,23,24,25]; in contrast, intracellular networks are generally bimolecular and higher-dimensional (challenges (N) and (D) stated above). For example, authors from [22] analyze performance of the AIFC in context of controlling average copy-numbers of intracellular species at the stochastic level. In this setting, in [22, Theorem 2], the authors specify a class of unimolecular input networks that can be controlled with the AIFC; in particular, to ensure stability, these input networks have to satisfy an algebraic constraint given as [22, Eq. 7]. This technical condition cannot generally be guaranteed to hold as it not only depends on the rate coefficients of the controller, but also on the uncertain rate coefficients of a given input network. More precisely, affine input networks, i.e. unimolecular input networks that contain one or more basal productions (zero-order reactions), can violate condition [22, Eq. 7]. In contrast, linear input networks, i.e. unimolecular networks with no basal production, always satisfy this condition. To showcase the performance of the AIFC, the authors from [22] put forward a gene-expression system as the input network, given by [22, Eq. 9], and demonstrate that the AIFC can arbitrarily control the average protein copy-number, and mitigate the uncertainties in the input rate coefficients (challenge (U) stated above). However, this unconditional success arises because basal transcription is not included in the linear gene-expression input network [22, Eq. 9], which ensures that condition [22, Eq. 7] always holds. A similar particular choice of an input network without basal production is put forward in [23], where the AIFC is experimentally implemented. The AIFC has also been analyzed in context of controlling species concentrations at the deterministic level in [24, 25]; however, the results are derived only for a restricted class of linear input networks that, due to lacking basal production, unconditionally satisfy [22, Theorem 2].

Questions of critical importance arise in context of controlling unimolecular networks: When the AIFC is applied on affine input networks (unimolecular networks with basal production), how likely is control to fail? Are the consequences of control failures biochemically safe or hazardous [26]? Does there exist a molecular IFC with a better stability performance than the AIFC? In particular, assume that a given intracellular network is modelled as being affine; then, the AIFC is successful provided the stability condition [22, Eq. 7] holds. However, a critical challenge arises because it is not possible to a-priori guarantee that [22, Eq. 7] holds, because the rate coefficients of the intracellular network are uncertain [challenge (U)].

While analyzing control of unimolecular networks in their own right is of some theoretical relevance, the vast majority of intracellular networks are not unimolecular [challenge (N)] and, hence, e.g. condition [22, Eq. 7] does not even apply. Therefore, a far more important question for intracellular control is: How do molecular IFCs perform when applied to bimolecular and higher-dimensional input networks? In particular, the structure of intracellular networks is itself in general uncertain; consequently, only approximate models can be put forward, that neglect a number of coupled molecular species and processes that are “hidden” in the intracellular system. Hence, even if a less-detailed model of an intracellular network happens to be successfully controlled, there is in general no guarantee that this remains true when a more-detailed model is used—a phenomenon we call phantom control.

The main objective of this paper is to address these questions. We show that at the center of these issues are equilibria—stationary solutions of the reaction-rate equations (RREs) that govern the deterministic dynamics of biochemical networks [13, 14]. In particular, molecular concentrations can reach only equilibria that are nonnegative. In this context, we show that IFCs can destroy all nonnegative equilibria of the controlled system and lead to a control failure; furthermore, this failure can be catastrophic, as some of the molecular concentrations can then experience an unbounded increase with time (blow-up). We call this hazardous phenomenon, involving absence of nonnegative equilibria and blow-up of some of the underlying species abundances, a negative-equilibrium catastrophe (NEC), which we outline in Fig. 2. To the best of our knowledge, analyses of NECs and the related challenges in molecular control, which are the focus of this paper, are absent from the literature. For example, the only form of instability presented in [22, 24, 25] are bounded deterministic oscillations, which average out at the stochastic level and do not correspond to violation of condition [22, Eq. 7]; in contrast, we show that this condition is violated when NECs occur.

Fig. 2
figure 2

Caricature representation of a successful and catastrophically failed intracellular control. a Displays a cell successfully controlled with the IFC in the setup shown in Fig. 1. The time-evolution of the underlying species concentrations are shown in b. In particular, the target species \(X_1\) approaches a desired equilibrium, shown as a black dashed line, and the equilibrium for the residual species \(X_2\) is positive. c Displays a cell that has taken lethal damage due to a failure of the IFC. In particular, as shown in d, the target equilibrium for \(X_1\) enforces a negative equilibrium for the residual species \(X_2\). However, since molecular concentrations are nonnegative, this equilibrium cannot be reached and, therefore, control fails. Furthermore, the failure is catastrophic, as concentrations of some of the underlying species (in this example, species \(X_2\) and \(Y_1\)) blow up, placing a lethal burden on the cell. b and d are obtained by solving the reaction-rate equations for the output network (16)\(\cup \)(19) from Sect. 5 with the dimensionless coefficients \((\alpha _0, \alpha _1, \alpha _2, \alpha _3) = (1, 1,1/10, 3/2)\), \((\beta _0, \beta _1, \gamma _1, \gamma _2, \gamma _3) = (100, 1, 10, 10, 1)\), and with \((\alpha _0, \alpha _1, \alpha _2, \alpha _3) = (1, 25,2/5,3/2)\), \((\beta _0, \beta _1, \gamma _1, \gamma _2, \gamma _3) = (100, 1, 10,2/3, 1)\), respectively

Full size image

The paper is organized as follows. In Sects. 2–4, we present some fundamental results regarding control of unimolecular networks; these results are then used to facilitate the analysis of control of bimolecular networks, which we present in Sect. 5. In particular, in Sect. 2, we prove that unimolecular IFCs do not exist due to a NEC. We then derive a class of bimolecular IFCs given by (8) in Sect. 3; as a consequence of demanding in the derivation that the controlling variables are positive, we obtain IFCs that influence the target species both positively and negatively, in contrast to the AIFC that acts only positively. In Sect. 4, we apply different variants of these controllers on a unimolecular gene-expression network (9), and then generalize the results. In particular, we show that the AIFC can lead to a NEC when applied to (9), both deterministically and stochastically; more broadly, we show that the AIFC does not generically operate safely when applied to unimolecular networks. Furthermore, we prove that there exists a two-dimensional (two-species) IFC that eliminates NECs when applied to any (arbitrarily large) stable unimolecular input network. However, in Sect. 5 we demonstrate that, without detailed information about the input systems, NECs generally cannot be prevented when bimolecular networks are controlled. In particular, we show that, in stark contrast to dimension-independent control of unimolecular networks, control of bimolecular networks suffers from the curse of dimensionality - the problem becomes more challenging as the dimension of the input network increases. We conclude the paper by presenting a summary and discussion in Sect. 6. Notation and background theory are introduced as needed in the paper, and are summarized in Appendices A and B. Rigorous proofs of the results presented in Sects. 2, 4 and 5 are provided in Appendices C–D, E and F, respectively.

2 Nonexistence of unimolecular IFCs

In this section, we consider an arbitrary one-dimensional black-box input network \(\mathcal {R}_{\alpha } = \mathcal {R}_{\alpha }(X_1)\), where \(X_1\) is a single interfacing species and there are no residual species, and the goal is to control the dynamics of the target \(X_1\); see also Fig. 1 for a more general setup. In this paper, we assume all reaction networks are under mass-action kinetics [13, 14] with positive dimensionless rate coefficients, which are displayed above or below the reaction arrows; we denote the rate coefficients of \(\mathcal {R}_{\alpha }\) by \(\varvec{\alpha } \in \mathbb {R}_{>}^a\), where \(\mathbb {R}_{>}\) is the space of positive real numbers. In what follows, we say that a reaction network is unimolecular (respectively, bimolecular) if it contains at least one reaction with one (respectively, two) reactants, but no reaction with more reactants.

2.1 Non-biochemical controller

Let us consider an affine controller formally described by the network \(\mathcal {\bar{R}}_{\beta , \gamma } = \mathcal {\bar{R}}_{\beta }(\bar{Y}_1) \cup \mathcal {\bar{R}}_{\gamma }(X_1, \bar{Y}_1)\), given by

$$\begin{aligned}&\mathcal {\bar{R}}_{\beta }: \varnothing \xrightarrow []{\beta _{0}} \bar{Y}_1, \nonumber \\&\mathcal {\bar{R}}_{\gamma }: X_1 \xrightarrow []{\gamma _1} X_1 - \bar{Y}_1, \nonumber \\&\qquad \quad \bar{Y}_1 \xrightarrow []{\gamma _2} \bar{Y}_1 + X_1. \end{aligned}$$
(1)

Here, \(\mathcal {\bar{R}}_{\beta } = \mathcal {\bar{R}}_{\beta }(\bar{Y}_1)\) is the controller core, describing the internal dynamics of the controlling species \(\bar{Y}_1\), where the reactant \(\varnothing \) denotes a source, while \(\mathcal {\bar{R}}_{\gamma } = \mathcal {\bar{R}}_{\gamma }(X_1, \bar{Y}_1)\) is the controller interface, specifying interactions between \(\bar{Y}_1\) and the target species \(X_1\) from the input network, see also Fig. 1. Let us denote abundances of species \(\{X_1, \bar{Y}_1\}\) from the output network \(\mathcal {R}_{\alpha } \cup \mathcal {\bar{R}}_{\beta , \gamma }\) at time \(t \ge 0\) by \((x_1, \bar{y}_1) = (x_1(t), \bar{y}_1(t)) \in \mathbb {R}^2\). At the deterministic level, formal reaction-rate equations (RREs) [13, 14] read

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= f_1(x_1; \, \varvec{\alpha }) + \gamma _2 \bar{y}_1, x_1^* = \frac{\beta _0}{\gamma _1}, \nonumber \\ \frac{\textrm{d} \bar{y}_1}{\textrm{d} t}&= \beta _0 - \gamma _{1} x_1, \quad \qquad \quad \bar{y}_1^*= - \gamma _2^{-1} f_1 \left( \frac{\beta _0}{\gamma _1}; \, \varvec{\alpha }\right) , \end{aligned}$$
(2)

where \(f_1(x_1; \, \varvec{\alpha })\) is an unknown function describing the dynamics of \(\mathcal {R}_{\alpha }\), and \((x_1^*, \bar{y}_1^*) \in \mathbb {R}^2\) is the unique equilibrium of the output network, obtained by solving the RREs with zero left-hand sides. Assuming that \((x_1^*, \bar{y}_1^*)\) is globally stable, network (1) is an IFC; in particular, in this case, \(x_1^* = (\beta _0/\gamma _1)\) is independent of the initial conditions and the input coefficients \(\varvec{\alpha }\). However, controller (1) cannot be interpreted as a biochemical reaction network. In particular, the term \((-\gamma _{1} x_1)\) in (2) induces a process graphically described by \(X_1 \xrightarrow []{\gamma _1} X_1 - \bar{Y}_1\) in (1), which consumes species \(\bar{Y}_1\) even when its abundance is zero. Consequently, variables \((x_1, \bar{y}_1)\) may take negative values and, therefore, cannot be interpreted as molecular concentrations [20].

2.2 Unimolecular controllers

The only unimolecular analogue of the IFC (1), that contains only one controlling species \(Y_1\), is of the form

$$\begin{aligned}&\mathcal {R}_{\beta }: \quad \varnothing \xrightarrow []{\beta _{0}} Y_1, \nonumber \\&\mathcal {R}_{\gamma }: \quad X_1 \xrightarrow []{\gamma _1} X_1 + Y_1, \nonumber \\&\qquad \quad \quad Y_1 \xrightarrow []{\gamma _2} Y_1 + X_1. \end{aligned}$$
(3)

The RREs and the equilibrium for the output network \(\mathcal {R}_{\alpha } \cup \mathcal {R}_{\beta , \gamma }\) are given by

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= f_1(x_1; \, \varvec{\alpha }) + \gamma _2 y_1, \quad x_1^* = -\frac{\beta _0}{\gamma _1}, \nonumber \\ \frac{\textrm{d} y_1}{\textrm{d} t}&= \beta _0 + \gamma _{1} x_1, \quad \quad \quad \qquad y_1^*= - \gamma _2^{-1} f_1 \left( -\frac{\beta _0}{\gamma _1}; \, \varvec{\alpha }\right) . \end{aligned}$$
(4)

Given nonnegative initial conditions, variables \((x_1, y_1)\) from (4) are confined to the nonnegative quadrant \(\mathbb {R}_{\ge }^2\), and represent biochemical concentrations. However, the \(x_1\)-component of the equilibrium from (4) is negative and, therefore, not reachable by the controlled system. Furthermore, \(y_1\) is a monotonically increasing function of time, \(\textrm{d} y_1/\textrm{d} t > 0\), i.e. \(y_1\) blows up. We call this phenomenon a deterministic negative-equilibrium catastrophe (NEC), see also Appendix A. Network (3) not only fails to achieve control, but it introduces an unstable species and is, hence, biochemically hazardous. In Appendix C, we prove that a NEC occurs at both deterministic and stochastic levels for any candidate unimolecular IFC, which we state as the following theorem.

Theorem 2.1

There does not exist a unimolecular integral-feedback controller.

Proof

See Appendix C. \(\square \)

To the best of our knowledge, Theorem 2.1 has not been previously reported in the literature. A related result is presented in [23, Proposition S2.7] and states that a molecular controller \(\mathcal {R}_{\beta } \cup \mathcal {R}_{\gamma }\), satisfying a set of assumptions, including the assumption that the interface \(\mathcal {R}_{\gamma }\) contains only catalytic reactions, is a molecular IFC only if the core \(\mathcal {R}_{\beta }\) contains a bimolecular degradation. No such assumptions have been made in Theorem 2.1, which holds for all unimolecular networks; in particular, we allow interface \(\mathcal {R}_{\gamma }\) to contain non-catalytic reactions, such as \(Y_i \rightarrow X_j\) and \(X_i \rightarrow Y_j\).

3 Design of bimolecular IFCs

Theorem 2.1 implies that only bimolecular (and higher-molecular) biochemical networks may exert integral-feedback control. An approach to finding such networks is to map non-biochemical IFCs into biochemical networks, while preserving the underlying integral-feedback structure. This task can be achieved using special mappings called kinetic transformations [20]. Let us consider the non-biochemical system (2). The first step in bio-transforming (2) is to translate relevant trajectories \((x_1, \bar{y}_1)\) into the nonnegative quadrant. However, since \(\mathcal {R}_{\alpha }(X_1)\) is a black-box network, i.e. \(f_1(x_1; \, \varvec{\alpha })\) is unknown and unalterable, only \(\bar{y}_1\) can be translated; to this end, we define a new variable \(y_1 \equiv (\bar{y}_1 + T)\), with translation \(T > 0\), under which (2) becomes

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= f_1(x_1; \, \varvec{\alpha }) + \gamma _2 y_1 - \gamma _2 T, \quad x_1^* = \frac{\beta _0}{\gamma _1}, \nonumber \\ \frac{\textrm{d} y_1}{\textrm{d} t}&= \beta _0 - \gamma _{1} x_1, \qquad \qquad \qquad \,\,\qquad y_1^*= - \gamma _2^{-1} f_1 \left( \frac{\beta _0}{\gamma _1}; \, \varvec{\alpha }\right) + T. \end{aligned}$$
(5)

Terms \((-\gamma _1 x_1)\) and \((-\gamma _2 T)\), called cross-negative terms [20], do not correspond to biochemical reactions and, therefore, must be eliminated. Let us note that cross-negative terms also play a central role in the questions of existence of other fundamental phenomena in biochemistry, such as oscillations, multistability and chaos [14, 20, 27]. Term \((-\gamma _1 x_1)\) can be eliminated with the so-called hyperbolic kinetic transformation, presented in Appendix D, which involves introducing an additional controlling species \(Y_2\) and extending system (5) into

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= f_1(x_1; \, \varvec{\alpha }) + \gamma _2 y_1 - \gamma _2 T, \quad x_1^* = \frac{\beta _0}{\gamma _1}, \nonumber \\ \frac{\textrm{d} y_1}{\textrm{d} t}&= \beta _0 - \beta _{1} y_1 y_2, \qquad \qquad \qquad \quad \, y_1^*= - \gamma _2^{-1} f_1 \left( \frac{\beta _0}{\gamma _1}; \, \varvec{\alpha }\right) + T, \nonumber \\ \frac{\textrm{d} y_2}{\textrm{d} t}&= \gamma _{1} x_1 - \beta _{1} y_1 y_2, \qquad \qquad \qquad y_2^*= \frac{\beta _0}{\beta _1}(y_1^*)^{-1}. \end{aligned}$$
(6)

Note that (5) and (6) have identical equilibria (time-independent solutions) for the species \(X_1\) and \(Y_1\), and that the equilibria for the species \(Y_1\) and \(Y_2\) have a hyperbolic relationship; furthermore, provided \(\beta _1\) is sufficiently large, time-dependent solutions of (5) and (6) are close as well, see Appendix D. On the other hand, cross-negative term \((-\gamma _2 T)\) can be eliminated via multiplication with \(x_1\) and any other desired factor; such operations do not influence the \(x_1\)-equilibrium, which is determined solely by the RREs for \(y_1\) and \(y_2\), and which we want to preserve. One option is to simply map \((-\gamma _2 T)\) to \((-\gamma _2 T x_1)\), and take T large enough to ensure that the \(y_1^*\)-equilibrium is positive; however, this approach requires the knowledge of \(f_1(x_1; \, \varvec{\alpha })\). A more robust approach is to map \((-\gamma _2 T)\) to \((-\gamma _2 T x_1 y_2)\), under which, defining \(\gamma _3 \equiv \gamma _2 T\), one obtains

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= f_1(x_1; \, \varvec{\alpha }) + \gamma _2 y_1 \qquad x_1^* = \frac{\beta _0}{\gamma _1}, \nonumber \\&\quad - \gamma _3 x_1 y_2,\nonumber \\ \frac{\textrm{d} y_1}{\textrm{d} t}&= \beta _0 - \beta _{1} y_1 y_2, \qquad \qquad 0 = (y_1^*)^2 + \left[ \gamma _2^{-1} f_1 \left( \frac{\beta _0}{\gamma _1}; \, \varvec{\alpha }\right) \right] y_1^* - \left( \frac{\gamma _3}{\gamma _1 \gamma _2} \frac{\beta _0^2}{\beta _1} \right) , \nonumber \\ \frac{\textrm{d} y_2}{\textrm{d} t}&= \gamma _{1} x_1 - \beta _{1} y_1 y_2, \qquad y_2^*= \frac{\beta _0}{\beta _1}(y_1^*)^{-1}. \end{aligned}$$
(7)

The quadratic equation for \(y_1^*\) from (7) always has one positive solution; therefore, there always exists an equilibrium with positive \(y_1\)- and \(y_2\)-components.

In what follows, we largely consider input networks \(\mathcal {R}_{\alpha }(\mathcal {X})\) with at most two interfacing species \(\{X_1, X_2\}\), and focus on controlling the target species \(X_1\) with the bimolecular controllers induced by (7), given by

$$\begin{aligned} \mathcal {R}_{\beta }(Y_1, Y_2): \;{} & {} \varnothing&\xrightarrow []{\beta _0} Y_1, \nonumber \\{} & {} Y_1 + Y_2&\xrightarrow []{\beta _1} \varnothing , \nonumber \\ \mathcal {R}_{\gamma }^{0}(Y_2; \, X_1): \;{} & {} X_1&\xrightarrow []{\gamma _{1}} X_1 + Y_2, \nonumber \\ \mathcal {R}_{\gamma }^{+}(X_i; \, Y_1): \;{} & {} Y_1&\xrightarrow []{\gamma _{2}} X_i + Y_1, \; \; \; \; \; \; \text {for some } i \in \{1, 2\}, \nonumber \\ \mathcal {R}_{\gamma }^{-}(X_j; \, Y_2): \;{} & {} X_j + Y_2&\xrightarrow []{\gamma _{3}} Y_2, \qquad \qquad \quad \text {for some } j \in \{1, 2\}. \end{aligned}$$
(8)

In particular, the controller core \(\mathcal {R}_{\beta }(Y_1, Y_2)\) consists of a production of \(Y_1\) from a source, and a bimolecular degradation of \(Y_1\) and \(Y_2\). On the other hand, the controller interface consists of the unimolecular reactions \(\mathcal {R}_{\gamma }^0(Y_2; \, X_1)\), and \(\mathcal {R}_{\gamma }^{+}(X_i; \, Y_1)\), that produce \(Y_2\) catalytically in \(X_1\), and \(X_i\) catalytically in \(Y_1\), respectively, and the bimolecular reaction \(\mathcal {R}_{\gamma }^{-}(X_j; \, Y_2)\) that degrades an interfacing species \(X_j\) catalytically in \(Y_2\). We call reactions \(\mathcal {R}_{\gamma }^{+}(X_i; \, Y_1)\) and \(\mathcal {R}_{\gamma }^{-}(X_j, Y_2)\) positive and negative interfacing, respectively. Furthermore, we say that positive (respectively, negative) interfacing is direct if \(i = 1\) (respectively, if \(j = 1\)), i.e. if it is applied to the target species \(X_1\); otherwise, the interfacing is said to be indirect. In Fig. 1, we display controller (8) with direct positive and negative interfacing applied to an input network with a single interfacing species \(X_1\).

As shown in this section, positive and negative interfacing arise together naturally when molecular IFCs are designed using the theoretical framework from [20]. In this context, it is interesting to note that the “housekeeping” sigma/anti-sigma system in E. coli, proposed to implement integral control [22], has been experimentally shown to be capable of exhibiting both positive and negative transcriptional control, at least when hijacked by bacteriophage [28]. On the other hand, while the AIFC from [22] is of the form (8), it lacks negative interfacing \(\mathcal {R}_{\gamma }^{-}(X_j; \, Y_2)\). In view of the derivation from this section, the AIFC is missing a key designing step, namely the translation from (5); consequently, NECs may occur due to \(y_1^*\)- and \(y_2^*\)-equilibria being negative. Let us note that the negative interfacing \(\mathcal {R}_{\gamma }^{-}(X_j; \, Y_2)\) has also been considered in [29], where this reaction is shown to be capable of eliminating oscillations at the deterministic level, and reducing variance at the stochastic level, for a particular gene-expression input network. In contrast, in this section, we have systematically derived reaction \(\mathcal {R}_{\gamma }^{-}(X_j; \, Y_2)\) in order to ensure that a positive equilibrium for \(Y_1\) and \(Y_2\) exists. Such matters are not discussed in [29], where basal transcription is set to zero in the gene-expression input network considered, so that negative equilibria are not encountered.

4 Control of unimolecular input networks

In this section, we study performance of the IFCs (8) when applied on unimolecular input networks. To this end, let us consider the input network \(\mathcal {R}_{\alpha }^1 = \mathcal {R}_{\alpha }^1(X_1, X_2)\), given by

(9)

We interpret (9) as a two-dimensional reduced (simplified) model of a higher-dimensional gene-expression network. In this context, \(X_1\) is a degradable protein species that is produced via translation from a degradable mRNA species \(X_2\), which is transcribed from a gene; some of the “hidden" species (dimensions), that are not explicitly modelled, such as genes, transcription factors and waste molecules, are denoted by \(\varnothing \). See also Fig. 3a for a schematic representation of network (9). The RREs of (9) have a unique globally stable equilibrium given by

$$\begin{aligned} x_1^{**}&= \frac{\alpha _0 \alpha _2}{\alpha _1 \alpha _3}, \quad x_2^{**} = \frac{\alpha _0}{\alpha _1}. \end{aligned}$$
(10)

For simplicity, in this section we assume that \(X_1\) is an interfacing species, while \(X_2\) is residual (i.e. \(X_2\) cannot be interfaced with a controller); the goal is to control the equilibrium concentration of the target species \(X_1\) at the deterministic level, and its average copy-number at the stochastic level. To this end, we embed different variants of the controller (8) into (9).

Fig. 3
figure 3

Schematic representation of the gene-expression input network (9). a Displays (9) with basal transcription rate \(\alpha _0\). b Displays network (9) with tripled effective transcription rate, \(3 \alpha _0\), arising when an activating transcription factor binds to the underlying gene promoter

Full size image

4.1 Pure positive interfacing

Let us first consider controller (8) with only positive interfacing, i.e. the AIFC from [22], which is denoted by \(\mathcal {R}_{\beta , \gamma }^{+} \equiv \mathcal {R}_{\beta } \cup \mathcal {R}_{\gamma }^0 \cup \mathcal {R}_{\gamma }^{+}\) and reads

$$\begin{aligned} \mathcal {R}_{\beta }(Y_1, Y_2): \;{} & {} \varnothing&\xrightarrow []{\beta _0} Y_1, \nonumber \\{} & {} Y_1 + Y_2&\xrightarrow []{\beta _1} \varnothing , \nonumber \\ \mathcal {R}_{\gamma }^{0}(Y_2; \, X_1): \;{} & {} X_1&\xrightarrow []{\gamma _{1}} X_1 + Y_2, \nonumber \\ \mathcal {R}_{\gamma }^{+}(X_1; \, Y_1): \;{} & {} Y_1&\xrightarrow []{\gamma _{2}} X_1 + Y_1. \end{aligned}$$
(11)

The RREs for the output network (9)\(\cup \)(11) are given by

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= \left( \alpha _2 x_2 - \alpha _3 x_1 \right) + \gamma _2 y_1, \quad \quad \frac{\textrm{d} x_2}{\textrm{d} t} = \alpha _0 - \alpha _1 x_2, \nonumber \\ \frac{\textrm{d} y_1}{\textrm{d} t}&= \beta _0 - \beta _{1} y_1 y_2, \quad \qquad \quad \qquad \quad \frac{\textrm{d} y_2}{\textrm{d} t} = \gamma _{1} x_1 - \beta _{1} y_1 y_2, \end{aligned}$$
(12)

with the unique equilibrium

$$\begin{aligned} x_1^*&= \frac{\beta _0}{\gamma _1}, \quad x_2^* = \frac{\alpha _0}{\alpha _1}, \quad y_1^* = \frac{\alpha _3}{\gamma _2} \left( \frac{\beta _0}{\gamma _1} - \frac{\alpha _0 \alpha _2}{\alpha _1 \alpha _3}\right) , \quad y_2^* = \frac{\beta _0}{\beta _1} (y_1^*)^{-1}. \end{aligned}$$
(13)

As anticipated in Sect. 3, the AIFC can lead to equilibria with negative \(y_1\)- and \(y_2\)-components. In particular, Eq. (13) implies that the output nonnegative equilibrium is destroyed when \((x_1^* = \beta _0/\gamma _1) < (x_1^{**} = \alpha _0 \alpha _2/(\alpha _1 \alpha _3))\). Hence, using only positive interfacing, it is not possible to achieve an output equilibrium below the input one. To determine the dynamical behavior of (9)\(\cup \)(11) when the nonnegative equilibrium ceases to exist, let us consider the linear combination of species concentration \((\alpha _3^{-1} x_1 + \alpha _1^{-1} \alpha _2 \alpha _3^{-1} x_2 + \gamma _1^{-1} (y_2 - y_1))\) that, using (12), satisfies

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d} t} \left( \frac{1}{\alpha _3} x_1 + \frac{\alpha _2}{\alpha _1 \alpha _3} x_2 + \frac{1}{\gamma _1} (y_2 - y_1) \right) \nonumber \\&\quad = - \left( \frac{\beta _0}{\gamma _1} - \frac{\alpha _0 \alpha _2}{\alpha _1 \alpha _3}\right) + \frac{\gamma _2}{\alpha _3} y_1 \ge - \left( \frac{\beta _0}{\gamma _1} - \frac{\alpha _0 \alpha _2}{\alpha _1 \alpha _3}\right) . \end{aligned}$$
(14)

When \(\beta _0/\gamma _1 < \alpha _0 \alpha _2/(\alpha _1 \alpha _3)\), Eq. (14) implies that a species concentration blows up for all nonnegative initial conditions, i.e. the output network displays a deterministic NEC; by applying identical argument to the first-moment equations, it follows that a stochastic NEC occurs as well. This result is summarized as a bifurcation diagram in Fig. 4a.

Fig. 4
figure 4

Application of the IFCs (8) on the input network (9) with rate coefficients \((\alpha _1, \alpha _2, \alpha _3) = (2/5,2, 4)\), and piecewise constant \(\alpha _0 = \alpha _0(t)\) which changes at \(t = 50\) and leads to a catastrophic bifurcation. a Displays a bifurcation diagram for the output network (9)\(\cup \)(11), while b–d show the underlying deterministic and stochastic trajectories with \(\alpha _0 = 4\) for \(t < 50\) and \(\alpha _0 = 12\) for \(t \ge 50\), leading to a change in the parameter space indicated by the black arrow in a. The control coefficients are fixed to \((\beta _0, \beta _1,\gamma _1, \gamma _2) = (40, 4, 4, 4)\). Analogous plots are shown in e–h for the output network (9)\(\cup \)(15) with \(\alpha _0 = 12\) for \(t < 50\) and \(\alpha _0 = 4\) for \(t \ge 50\), and \((\beta _0, \beta _1,\gamma _1, \gamma _3) = (40, 4, 4, 4)\), and for the output network (9)\(\cup \)(16) in i–l using the same coefficient values as in a–d, and with \(\gamma _3 = 4\)

Full size image

Let us consider network (9) with rate coefficients \(\varvec{\alpha } = (\alpha _0, \alpha _1, \alpha _2, \alpha _3)\) fixed so that the input \(x_1\)-equilibrium from (10) is given by \(x_1^{**} = 5\); then, the output \(x_1\)-equilibrium from (13) must satisfy the constraint \(x_1^* > 5\). Let us stress that, since the input rate coefficients \(\varvec{\alpha }\) (and the structure of the input network itself) are generally uncertain (see property (U) from Sect. 1), condition \(x_1^* > 5\) is not a-priori known. Assume the goal is to steer the output equilibrium to 10, i.e. we fix the control coefficients \(\beta _0\) and \(\gamma _1\) so that \(x_1^* = \beta _0/\gamma _1 = 10\); this setup is shown as a black dot at (5, 10) in Fig. 4a, which happens to lie in the region where the output network displays a nonnegative equilibrium. However, assume that at a future time, as a response to an environmental perturbation, an activating transcription factor binds to the underlying gene promoter, tripling the transcription rate of the input network, which we model by allowing the transcription rate coefficient \(\alpha _0\) to be time-dependent, see Fig. 3b. Such a perturbation would move the system from coordinate (5, 10) to (15, 10), into the unstable region, which we show as a black arrow in Fig. 4a. Put another way, the AIFC would fail at its main objective—maintaining accurate control robustly with respect to uncertainties.

In Fig. 4b–d, we show the deterministic and stochastic trajectories for the species \(X_1\), \(Y_1\) and \(Y_2\), obtained by solving the RREs (12) and applying the Gillespie algorithm [30] on (9)\(\cup \)(11), respectively; also shown as a dashed grey line in Fig. 4b is the target equilibrium \(x_1^* = 10\). For time \(t < 50\), when the input network operates as in Fig. 3a, and the output system is in the configuration (5, 10) from Fig. 4a, the AIFC achieves control. However, for time \(t \ge 50\), when the transcription rate has increased as in Fig. 3b, and the output system is at (15, 10) from Fig. 4a, control fails; even worse, the species \(Y_2\) blows up for all admissible initial conditions. Intuitively, this hazardous phenomenon (NEC) occurs because, when the target equilibrium is below the input one, the best accuracy result that the AIFC can achieve is to minimally increase \(X_1\). Such a task is accomplished with \(y_1 \rightarrow 0\) which, as a consequence of a hyperbolic relationship between \(y_1\) and \(y_2\), enforces \(y_2 \rightarrow \infty \), which is a worst stability result.

4.2 Pure negative interfacing

Consider controller (8) with pure direct negative interfacing, denoted by \(\mathcal {R}_{\beta , \gamma }^{-} \equiv \mathcal {R}_{\beta } \cup \mathcal {R}_{\gamma }^0 \cup \mathcal {R}_{\gamma }^{-}\) and given by

$$\begin{aligned} \mathcal {R}_{\beta }(Y_1, Y_2): \;{} & {} \varnothing&\xrightarrow []{\beta _0} Y_1, \nonumber \\{} & {} Y_1 + Y_2&\xrightarrow []{\beta _1} \varnothing , \nonumber \\ \mathcal {R}_{\gamma }^{0}(Y_2; \, X_1): \;{} & {} X_1&\xrightarrow []{\gamma _{1}} X_1 + Y_2, \nonumber \\ \mathcal {R}_{\gamma }^{-}(X_j; \, Y_2): \;{} & {} X_1 + Y_2&\xrightarrow []{\gamma _{3}} Y_2. \end{aligned}$$
(15)

By analogous arguments as with controller (11), one can prove that deterministic and stochastic NECs occur when \(x_1^* > x_1^{**}\), i.e. controller (15) cannot steer the output equilibrium above the input one; when control above the input equilibrium is attempted, species \(Y_1\) blows up. We display a bifurcation diagram and trajectories for the output network (9)\(\cup \)(15) in Fig. 4e–h.

4.3 Combined positive and negative interfacing

Let us now analyze controller (8) with positive and negative interfacing applied together to the target species \(X_1\), as suggested by the derivation in Sect. 3. This controller is denoted by \(\mathcal {R}_{\beta , \gamma }^{\pm } \equiv \mathcal {R}_{\beta } \cup \mathcal {R}_{\gamma }^0 \cup \mathcal {R}_{\gamma }^{+} \cup \mathcal {R}_{\gamma }^{+}\) and given by

$$\begin{aligned} \mathcal {R}_{\beta }(Y_1, Y_2): \;{} & {} \varnothing&\xrightarrow []{\beta _0} Y_1, \nonumber \\{} & {} Y_1 + Y_2&\xrightarrow []{\beta _1} \varnothing , \nonumber \\ \mathcal {R}_{\gamma }^{0}(Y_2; \, X_1): \;{} & {} X_1&\xrightarrow []{\gamma _{1}} X_1 + Y_2, \nonumber \\ \mathcal {R}_{\gamma }^{+}(X_1; \, Y_1): \;{} & {} Y_1&\xrightarrow []{\gamma _{2}} X_1 + Y_1, \nonumber \\ \mathcal {R}_{\gamma }^{-}(X_j; \, Y_2): \;{} & {} X_1 + Y_2&\xrightarrow []{\gamma _{3}} Y_2. \end{aligned}$$
(16)

The RREs of the output network (9)\(\cup \)(16) have two equilibria, given by

$$\begin{aligned} x_1^*&= \frac{\beta _0}{\gamma _1}, \quad x_2^* = \frac{\alpha _0}{\alpha _1}, \quad y_2^* = \frac{\beta _0}{\beta _1} (y_1^*)^{-1}, \end{aligned}$$
(17)

where \(y_1^*\) satisfies

$$\begin{aligned} (y_1^*)^2 + \frac{\alpha _3}{\gamma _2} \left( \frac{\alpha _0 \alpha _2}{\alpha _1 \alpha _3} - \frac{\beta _0}{\gamma _1} \right) y_1^* - \left( \frac{\gamma _3}{\gamma _1 \gamma _2} \frac{\beta _0^2}{\beta _1} \right)&= 0. \end{aligned}$$
(18)

By design from Sect. 3, quadratic Eq. (18) always has exactly one positive equilibrium, so that no NEC can occur with controller (16); we confirm this fact in Fig. 4i–l.

4.4 Arbitrary unimolecular input networks

Test network (9) demonstrates that controller (8) with only positive, or only negative, interfacing does not generically ensure stability of the output network. In other words, the corresponding output network experiences NECs over a large region in the parameter space, as displayed in Fig. 4a and e. On the other hand, controller (8) with combined positive and negative interfacing, applied directly to the target species, induces no NEC, as shown in Fig. 4i. A special feature of unimolecular networks is that distinct species cannot influence each other negatively. Consequently, to ensure existence of a nonnegative equilibrium, negative interfacing must generally be applied directly to the target species, while positive interfacing can be applied directly or indirectly (i.e. to any suitable interfacing species). We now more formally state this result; for more details, see Appendix E. To aid the statement of the theorem, we say that an input network is degenerate if its \(x_1\)-equilibrium is zero, \(x_1^{**} = 0\); otherwise, the network is said to be nondegenerate. The set of all degenerate networks forms a negligibly small subset of general unimolecular networks.

Theorem 4.1

Consider an arbitrary nondegenerate unimolecular input network \(\mathcal {R}_{\alpha }\) whose RREs have an asymptotically stable equilibrium, the family of controllers \(\mathcal {R}_{\beta ,\gamma }\) given by (8), and the output network \(\mathcal {R}_{\alpha ,\beta ,\gamma } = \mathcal {R}_{\alpha } \cup \mathcal {R}_{\beta ,\gamma }\). Then, controller \(\mathcal {R}_{\beta ,\gamma }^{\pm }\) with both positive and negative interfacing, with negative interfacing being direct, ensures that the output network \(\mathcal {R}_{\alpha ,\beta ,\gamma }\) has a nonnegative equilibrium for all parameter values \((\varvec{\alpha }, \varvec{\beta },\varvec{\gamma }) \in \mathbb {R}_{>}^{a + b + c}\). On the other hand, the other variants of the controller (8) do not generically ensure that the output network \(\mathcal {R}_{\alpha ,\beta ,\gamma }\) has a nonnegative equilibrium; furthermore, when a nonnegative equilibrium does not exist, these controllers induce deterministic and stochastic blow-ups (NECs) for all nonnegative initial conditions.

Proof

See Appendix E. \(\square \)

Note that the only variant of (8) that generically eliminates NECs may be experimentally most challenging to implement: bimolecular reaction \(\mathcal {R}_{\gamma }^{-}\) must be applied directly to the target species.

In the degenerate case, when the equilibrium of the target species from the input network is zero, \(x_1^{**} = 0\), in addition to the positive–negative controller \(\mathcal {R}_{\beta ,\gamma }^{\pm }\), the AIFC \(\mathcal {R}_{\beta ,\gamma }^{+}\) also generically ensures existence of a nonnegative equilibrium. However, the degenerate input networks can describe only a small class of biochemical processes. For example, when there is no basal transcription, i.e. when \(\alpha _0 = 0\), the equilibrium of network (9) is zero and, consequently, the output equilibrium (13) is always nonnegative. In particular, the output equilibrium is then nonnegative independent of the uncertainties in the input coefficients, so that the key challenge (U) highlighted in Sect. 1 is mitigated. This gene-expression input network without basal transcription, \(\alpha _0 = 0\), has been used in [22] to demonstrate a desirable stochastic behavior of the AIFC. However, as we have shown in this section, when a more general gene-expression model is used, with \(\alpha _0 \ne 0\), the AIFC can fail and induce both deterministic and stochastic catastrophes as a consequence of the challenge (U). The results from [24, 25] also focus on similar degenerate input networks.

Let us stress that, while the AIFC is NEC-free when applied to unimolecular input networks with zero basal production, even an arbitrarily small basal production may cause a NEC to occur over a large parameter regime. For example, let us consider network (9) with the following rate coefficients: \(\alpha _0 = \varepsilon \), \(\alpha _2 = 1/\varepsilon ^2\) and \(\alpha _1 = \alpha _3 = 1\), where \(0 < \varepsilon \ll 1\) is sufficiently small, i.e. we are considering a slower-transcription and faster-translation gene-expression network [31]. It then follows from (13) that the AIFC can achieve control only when the target equilibrium is set to a sufficiently large value, \(\beta _0/\gamma _1 > \alpha _0 \alpha _2/(\alpha _1 \alpha _3) = 1/\varepsilon \); in other words, even though the basal transcription is small, nevertheless the AIFC fails catastrophically over a large parameter regime due to a large translation rate.

5 Control of bimolecular input networks: curse of dimensionality

As expressed by challenge (N) in Sect. 1, most intracellular networks are bimolecular, rather than unimolecular, limiting the applicability of Theorem 4.1. For example, in Sect. 4, we have used the unimolecular input network (9) with a time-dependent rate coefficient to model intracellular gene expression with regulated transcription. To obtain a more realistic model, instead of introducing an effective time-dependent rate coefficient, the reduced network (9) must be extended by including other coupled auxiliary species (e.g. transcription factors and genes) and processes (e.g. pre-transciption and post-translation events); the resulting extended input network is then bimolecular, and therefore Theorem 4.1 no longer applies. In particular, a special property of unimolecular networks is that distinct species can influence each other only positively; in contrast, distinct species can influence each other both positively and negatively in bimolecular networks. For this reason, when stable unimolecular input networks are controlled, NECs can be eliminated purely by ensuring that the controlling species equilibrium \(\textbf{y}^*\) is positive; the input species equilibrium \(\textbf{x}^*\) is then necessarily nonnegative. In other words, the problem of controlling unimolecular networks is independent of the challenge (D) from Sect. 1, i.e. the problem does not become more challenging as the dimension of the input network increases. On the other hand, we show in this section that, as a consequence of nonlinearities and positive–negative interactions among distinct species, the problem of controlling bimolecular networks suffers from the curse of dimensionality—the problem becomes more challenging as the dimension of the input network increases.

5.1 Two-species reduced input network: residual NEC

Let us consider a two-dimensional reduced model of an intracellular process, given by the bimolecular input network \(\mathcal {R}_{\alpha }^2(X_1, X_2)\) which reads

$$\begin{aligned} \mathcal {R}_{\alpha }^2(X_1, X_2):{} & {} \varnothing \xrightarrow []{\alpha _{0}}&X_1, \quad X_1 \xrightarrow []{\alpha _{1}} X_2, \quad X_1 + X_2 \xrightarrow []{\alpha _{2}} 2 X_2, \quad X_2 \xrightarrow []{\alpha _{3}} \varnothing , \end{aligned}$$
(19)

where \(X_1\) is produced from a source and converted into a degradable species \(X_2\) via first- and second-order conversion reactions. We assume that \(X_1\) is an interfacing and target species, while \(X_2\) is residual. The RREs of (19) have a unique asymptotically stable equilibrium, given by

$$\begin{aligned} x_1^{**}&= \frac{\alpha _0 \alpha _3}{\alpha _0 \alpha _2 + \alpha _1 \alpha _3}, \quad x_2^{**} = I_2(x_1^{**}; \, \varvec{\alpha }) = \frac{\alpha _0}{\alpha _3}, \end{aligned}$$
(20)

where the function \(I_2 = I_2(x_1; \, \varvec{\alpha })\) is given by

$$\begin{aligned} I_2(x_1; \, \varvec{\alpha }) \equiv \frac{\alpha _1}{\alpha _2} x_1 \left( \frac{\alpha _3}{\alpha _2} - x_1 \right) ^{-1}. \end{aligned}$$
(21)

We call (21) a residual invariant, which is simply the \(x_2\)-equilibrium expressed as a function of the \(x_1\)-equilibrium and the input coefficients \(\varvec{\alpha }\).

Fig. 5
figure 5

Application of the IFC (16) on the input network (19) with rate coefficients \((\alpha _0, \alpha _1, \alpha _3) = (200, 1/7, 5)\), and \(\alpha _2 = 1/3\) for \(t < 50\), which changes to \(\alpha _2 = 1\) for \(t \ge 50\) and leads to a catastrophic bifurcation. a–d Display the deterministic and stochastic trajectories for the output network (16)\(\cup \)(19), with control coefficients \((\beta _0, \beta _1,\gamma _1, \gamma _2, \gamma _3) = (100, 1,10,10,1)\)

Full size image

Let us embed the controller (16) into (19), leading to the RREs of the output network given by

$$\begin{aligned} \frac{\textrm{d} x_1}{\textrm{d} t}&= \left( \alpha _0 - \alpha _1 x_1 - \alpha _2 x_1 x_2 \right) + h(x_1, y_1, y_2; \, \varvec{\gamma }),\nonumber \\&\text {where } h(x_1, y_1, y_2; \, \varvec{\gamma }) = \gamma _2 y_1 - \gamma _3 x_1 y_2,\nonumber \\ \frac{\textrm{d} x_2}{\textrm{d} t}&= \alpha _1 x_1 + \alpha _2 x_1 x_2 - \alpha _3 x_2, \nonumber \\ \frac{\textrm{d} y_1}{\textrm{d} t}&= g_1(x_1, y_1, y_2; \, \varvec{\beta }, \varvec{\gamma }) = \beta _0 - \beta _{1} y_1 y_2, \nonumber \\ \frac{\textrm{d} y_2}{\textrm{d} t}&= g_2(x_1, y_1, y_2; \, \varvec{\beta }, \varvec{\gamma }) = \gamma _{1} x_1 - \beta _{1} y_1 y_2, \end{aligned}$$
(22)

which display two equilibria, one of which is never nonnegative, while the other equilibrium satisfies

$$\begin{aligned} x_1^*&= \frac{\beta _0}{\gamma _1}, \quad x_2^* = I_2 \left( x_1^{*}, \varvec{\alpha } \right) , \quad y_1^*> 0, \; \; y_2^* > 0. \end{aligned}$$
(23)

In particular, the functional form of the residual equilibrium \(x_2^{*}\) from (23) is the same as the form of \(x_2^{**}\) from (20); put another way, the form of the residual species equilibrium is invariant under control, justifying calling the function (21) a residual invariant. To ensure that the output network (16)\(\cup \)(19) displays a nonnegative equilibrium, the residual invariant (21), now evaluated at the target equilibrium \(x_1^* = \beta _0/\gamma _1\), must be nonnegative, giving rise to the condition

$$\begin{aligned} I_2 \left( x_1^{*}, \varvec{\alpha } \right) \ge 0 \iff \frac{\beta _0}{\gamma _1} \le \frac{\alpha _3}{\alpha _2}. \end{aligned}$$
(24)

Therefore, while (16) guarantees existence of a nonnegative equilibrium for stable unimolecular input networks (see Theorem 4.1), the same is generally false for bimolecular networks, as the equilibrium of the residual species, which are not interfaced with the controller, can become negative.

In Fig. 5, we display the deterministic and stochastic trajectories for the output network (16)\(\cup \) (19) over a time-interval such that condition (24) is satisfied for \(t < 50\), and violated for \(t \ge 50\). One can notice that the output network undergoes deterministic and stochastic NECs. Critically, not only does the controlling species \(Y_1\) blow up, but also the residual species \(X_2\). In other words, controller (16) destabilizes the originally asymptotically stable input network (19). We call this hazardous phenomenon a residual NEC, as it arises because a residual species has no nonnegative equilibrium (equivalently, because a residual invariant is not nonnegative). Intuitively, when the concentration of the target species \(X_1\) is increased beyond the upper bound from (24), residual species \(X_2\), which influences \(X_1\) negatively, counteracts the positive action of the controlling species \(Y_1\), resulting in a joint blow-up. We also display this phenomenon in context of intracellular control in Fig. 2.

Let us stress that the condition \(I_2 \left( x_1^{*}, \varvec{\alpha } \right) \ge 0\) from (24) must be obeyed by every molecular controller (e.g. containing integral, proportional and/or derivative actions [19]) that cannot be interfaced with \(X_2\). Put another way, no matter how one chooses the functions \(g_1\), \(g_2\) and h in (22), the inequality \(I_2 \left( x_1^{*}, \varvec{\alpha } \right) \ge 0\) must be satisfied, which imposes an upper bound on the achievable output equilibrium via \(x_1^* < \alpha _3/\alpha _2\). The only way to eliminate this residual invariant condition is to eliminate the residual species \(X_2\), i.e. to design an appropriate controller that can be interfaced with both \(X_1\) and \(X_2\). However, as stated in challenges (D) and (U) in Sect. 1, intracellular networks generally contain a large number of coupled biochemical species with different biophysical properties, some of which may be unknown (hidden) or poorly characterized; therefore, it is generally unfeasible to demand that a controller is designed that can be interfaced with any desired species. In what follows, we further investigate this issue.

5.2 Three-species extended input network: phantom control

The two-dimensional network (19) has been put forward as a reduced model of an intracellular process, obtained by neglecting a number of molecular species that do not influence the dynamics of \(X_1\) and \(X_2\), or by using perturbation theory to eliminate slower or faster auxiliary species from considerations [32]. However, the goal of such model reductions is to capture the dynamics of the species \(X_1\) and \(X_2\) on a desired time-scale, and not necessarily to capture how the underlying higher-dimensional intracellular process responds to control. In this context, let us extend network (19) by including a “hidden” residual species \(X_3\) into consideration, which interacts with \(X_1\) and \(X_2\) according to the three-dimensional input network \(\mathcal {R}_{\alpha , \varepsilon }^3 = \mathcal {R}_{\alpha , \varepsilon }^3(X_1, X_2,X_3)\), given by

$$\begin{aligned}&\mathcal {R}_{\alpha , \varepsilon }^3: \qquad \varnothing \xrightarrow []{\alpha _{0}} \quad X_1, \quad X_1 \xrightarrow []{\alpha _{1}} X_2, \quad X_1 + X_2 \xrightarrow []{\alpha _{2}} 2 X_2, \quad X_2 \xrightarrow []{\alpha _{3}} \varnothing , \nonumber \\&\quad X_3 \xrightarrow []{\varepsilon } \quad X_1 + X_3, \quad \varnothing \xrightarrow []{\alpha _{4}} X_3, \quad X_3 \xrightarrow []{\alpha _{5}} 2 X_3, \quad X_2 + X_3 \xrightarrow []{\alpha _{6}} X_2, \nonumber \\&\quad \text {where } \frac{\alpha _5}{\alpha _6} < \frac{\alpha _0}{\alpha _3}, \; \; 0 \le \varepsilon \ll 1. \end{aligned}$$
(25)

The residual species \(X_3\) influences \(X_1\) and \(X_2\) only weakly via the slower reaction \(X_3 \xrightarrow []{\varepsilon } X_1 + X_3\) in (25), where \(0 \le \varepsilon \ll 1\) is sufficiently small. One can readily show that the dynamics of the species \(X_1\) and \(X_2\) from the input networks (19) and (25) are identical as \(\varepsilon \rightarrow 0\), which we denote by writing \(\lim _{\varepsilon \rightarrow 0} \mathcal {R}_{\alpha , \varepsilon }^3 = \mathcal {R}_{\alpha }^2\). Furthermore, the RREs of the network (25) have a unique asymptotically stable positive equilibrium, given at the leading order by

$$\begin{aligned}&x_1^{**} \approx \frac{\alpha _0 \alpha _3}{\alpha _0 \alpha _2 + \alpha _1 \alpha _3}, \quad x_2^{**} \approx I_2(x_1^{**}; \, \varvec{\alpha }) = \frac{\alpha _0}{\alpha _3}, \nonumber \\&x_3^{**} \approx I_3(x_1^{**}; \, \varvec{\alpha }) = \frac{\alpha _4}{\alpha _6} \left( \frac{\alpha _0}{\alpha _3} - \frac{\alpha _5}{\alpha _6}\right) ^{-1}, \end{aligned}$$
(26)

where the residual invariants \(I_2 = I_2(x_1; \, \varvec{\alpha })\) and \(I_3 = I_3(x_1; \, \varvec{\alpha })\) are given by

$$\begin{aligned}&I_2(x_1; \, \varvec{\alpha }) \equiv \frac{\alpha _1}{\alpha _2} x_1 \left( \frac{\alpha _3}{\alpha _2} - x_1 \right) ^{-1},\nonumber \\&I_3(x_1; \, \varvec{\alpha }) \equiv \frac{\alpha _4}{\alpha _6} \left( I_2(x_1; \, \varvec{\alpha }) - \frac{\alpha _5}{\alpha _6} \right) ^{-1}. \end{aligned}$$
(27)

In what follows, we let \(\varvec{\alpha } = (\alpha _0, \alpha _1, \alpha _2, \alpha _3, \alpha _4, \alpha _5, \alpha _6) = (200, 1/7, 1/3,5,1,4,1)\) and \(\varepsilon = 10^{-2}\); in Fig. 6, we demonstrate that the \((x_1, x_2)\)-dynamics of networks (19) and (25) are then close.

Fig. 6
figure 6

Input network (25) with rate coefficients \(\varvec{\alpha } = (\alpha _0, \alpha _1, \alpha _2, \alpha _3, \alpha _4, \alpha _5, \alpha _6) = (200, 1/7, 1/3,5,1,4,1)\) and different values of \(\varepsilon \). a–b display the deterministic trajectories for the species \(X_1\) and \(X_2\), respectively, from the input network (25) with \(\varepsilon = 0\) (equivalently, the input network (19)) and with \(\varepsilon = 10^{-2}\)

Full size image

Let us now embed the controller (16) into (25); the RREs of the output network (16)\(\cup \)(25) have two equilibria, both of which have identical \((x_1, x_2, x_3)\)-components, given by

$$\begin{aligned} x_1^*&= \frac{\beta _0}{\gamma _1}, \quad x_2^* = I_2(x_1^{*}; \, \varvec{\alpha }), \quad x_3^* = I_3(x_1^{*}; \, \varvec{\alpha }). \end{aligned}$$
(28)

In addition to requiring that \(I_2(x_1^{*}; \, \varvec{\alpha }) \ge 0\), one must now also demand that \(I_3(x_1^{*}; \, \varvec{\alpha }) \ge 0\), to ensure that the (previously neglected) residual species \(X_3\) displays a nonnegative equilibrium, leading to

$$\begin{aligned} I_2 \left( x_1^{*}, \varvec{\alpha } \right) , I_3 \left( x_1^{*}, \varvec{\alpha } \right) \ge 0 \iff \frac{\alpha _3 \alpha _5}{\alpha _1 \alpha _6 + \alpha _2 \alpha _5} \le \frac{\beta _0}{\gamma _1} \le \frac{\alpha _3}{\alpha _2}. \end{aligned}$$
(29)

By accounting for the residual species \(X_3\), a lower bound is imposed on the achievable output equilibrium \(x_1^* = \beta _0/\gamma _1\) in (29), while no such lower bound is imposed in (24). Therefore, while the reduced network (19) is suitable to approximate the dynamics of \(X_1\) and \(X_2\) from the extended network (25), i.e. \(\lim _{\varepsilon \rightarrow 0} \mathcal {R}_{\alpha , \varepsilon }^3 = \mathcal {R}_{\alpha }^2\), network (19) is not suitable to approximate how (25) responds to control, i.e. \(\lim _{\varepsilon \rightarrow 0} (\mathcal {R}_{\alpha , \varepsilon }^3 \cup \mathcal {R}_{\beta , \gamma }^{\pm }) \ne (\mathcal {R}_{\alpha }^2 \cup \mathcal {R}_{\beta , \gamma }^{\pm })\). When a reduced network is successfully controlled under a parameter choice for which a corresponding extended network fails to be controlled, we say that a phantom control, as opposed to genuine control, occurs for the reduced network. Hence, when the lower bound in (29) is violated, network (16)\(\cup \)(19) displays a phantom control.

For the chosen input coefficients \(\varvec{\alpha }\), it follows from (29) that one can achieve the output equilibrium only within the small interval approximately given by \(13.6 \le x_1^* \le 15\); therefore, even small uncertainties in the input coefficients (challenge (U) from Sect. 1) can then move the system outside of this range, where the control fails. In Fig. 7a–c, we display the deterministic trajectories for the species \(X_1\), \(X_3\) and \(Y_2\) when the target equilibrium is given by \(x_1^* = \beta _0/\gamma _1 = 5\), thus violating only the lower bound from (29). One can notice that a deterministic NEC occurs—the target species \(X_1\) fails to reach the desired equilibrium, while the residual species \(X_3\) and the controlling species \(Y_2\) blow-up; one can similarly show that a stochastic NEC occurs. Analogous plots are shown in Fig. 7d–f when \(x_1^* = \beta _0/\gamma _1 = 30\), violating the upper bound from (29); one can notice that the species \(X_2\) and \(Y_1\) blow up, as in Fig. 5.

Fig. 7
figure 7

Application of the IFC (16) on the input network (25) with rate coefficients \((\alpha _0, \alpha _1, \alpha _2, \alpha _3, \alpha _4, \alpha _5, \alpha _6) = (200, 1/7, 1/3,5,1,4,1)\) and \(\varepsilon = 10^{-2}\). a–c Display some of the deterministic trajectories for the output network (16)\(\cup \)(25), when control coefficients are fixed to \((\beta _0, \beta _1,\gamma _1, \gamma _2, \gamma _3) = (50, 1,10,100,10)\). Analogous plots are shown in d–f when \((\beta _0, \beta _1,\gamma _1, \gamma _2, \gamma _3) = (300, 1,10,100,10)\)

Full size image

5.3 Arbitrary bimolecular input networks

One can continue the model-refinement process which led from network (19) to (25) by including more auxiliary species \(X_4, X_5, X_6, \ldots \), each of which generally introduces an additional constraint, \(I_4, I_5, I_6, \ldots \ge 0\), which must be obeyed for an equilibrium to be nonnegative. More generally, let \(\mathcal {R}_{\alpha }\) be an arbitrary N-dimensional input network satisfying properties (N), (D) and (U) from Sect. 1, \(\mathcal {R}_{\beta , \gamma }\) an arbitrary M-dimensional IFC, and \(\mathcal {R}_{\alpha , \beta , \gamma } = \mathcal {R}_{\alpha } \cup \mathcal {R}_{\beta , \gamma }\) the corresponding \((N + M)\)-dimensional output network. In order to ensure that an equilibrium \((\textbf{x}^*, \textbf{y}^*) \in \mathbb {R}^{N + M}\) of \(\mathcal {R}_{\alpha , \beta , \gamma } \) is nonnegative, there are exactly two options.

5.3.1 Fine-tuning the control coefficients

The first option is to choose the control coefficients \(\varvec{\beta }\) and \(\varvec{\gamma }\) so that the equilibria of all of the \((N + M)\) species are nonnegative. However, this approach involves solving a system of \((N + M)\) nonlinear inequalities with uncertain coefficients \(\varvec{\alpha }\), which is an intractable theoretical problem. Furthermore, owing to a large number of inequalities, even when a nonnegative equilibrium does exist, the admissible values for \(\varvec{\beta }\) and \(\varvec{\gamma }\) may be confined to a small set, which can lead to a large parameter regime where IFCs can catastrophically fail. The fact that these issues are of concern when intracellular networks are controlled has been demonstrated already with as low as two-dimensional network (19) containing only one bimolecular reaction, and the three-dimensional network (25) containing two bimolecular reactions. Let us note that these issues are related to the fact that the proportion of the state-space \(\mathbb {R}^{N + M}\) occupied by the nonnegative orthant \(\mathbb {R}_{\ge }^{N + M}\) is given by \(2^{-(N + M)}\), which decreases exponentially as the dimension of the input network N increases—a fact known as the curse of dimensionality.

5.3.2 Interfacing the controller with every input species

A necessary condition to bypass the intractable problem of fine-tuning the control coefficients is to eliminate all of the residual invariant constraints \(I_n, I_{n+1}, \ldots \ge 0\), which can be achieved only by eliminating all of the residual species. Therefore, the second option is to design a suitable controller that can be interfaced with all of the N input species, which is an unfeasible experimental problem. However, for theoretical purposes, assume all the input species are interfacing; does there then exist an IFC that ensures a nonnegative equilibrium exists for every choice of the coefficients \(\varvec{\alpha }\), \(\varvec{\beta }\) and \(\varvec{\gamma }\), thus mitigating challenge (U)?

Theorem 5.1

Assume \(\mathcal {R}_{\alpha }\) is an arbitrary mass-action input network with N input species, all of which are interfacing. Then, there exists a bimolecular integral-feedback controller \(\mathcal {R}_{\beta , \gamma }\), containing 2N controlling species, such that the output network \(\mathcal {R}_{\alpha , \beta , \gamma } = \mathcal {R}_{\alpha } \cup \mathcal {R}_{\beta , \gamma }\) has a positive equilibrium for every choice of the rate coefficients \((\varvec{\alpha }, \varvec{\beta },\varvec{\gamma }) \in \mathbb {R}_{>}^{a + b + c}\).

Proof

See Appendix F for a constructive proof. \(\square \)

In Appendix F, we design a controller that achieves this task by generalizing the approach from Sect. 3, and applying the controller of the form (16) to every input species; therefore, the dimension of the controller scales with the dimension of the input network.

6 Discussion

In this paper, we have demonstrated that molecular IFCs can display severe stability issues when applied to biochemical networks subject to uncertainties. In particular, all nonnegative equilibria of the controlled network can vanish under IFCs, and some of the species abundances can then blow up. We call this hazardous phenomenon a negative-equilibrium catastrophe (NEC). In context of electro-mehanical systems, analogous phenomenon is known as integrator windup [19]—equilibria of the controlled system reach beyond the boundary of physically allowed values. For some electro-mechanical systems, one only requires the equilibria to be real (as opposed to complex); for biochemical systems, one additionally requires that the equilibria are also nonnegative. Let us stress that requiring an equilibrium to be nonnegative is significantly more restrictive than only requiring it is real. For example, while real linear systems of equations generically have a unique real solution, finding parameter regimes where a positive solution exists is non-trivial [33]; for nonlinear systems, determining such parameter regimes is generally even more challenging, see Sect. 5.3. The consequences of these issues, which are unavoidable for biochemical systems, have been under-explored in the molecular control literature to date.

We have shown in Sect. 2 that, due to the nonnegativity constraint, affine (unimolecular) biochemical systems cannot achieve integral control and, even worse, lead to catastrophes (NECs); in contrast, some affine electro-mechanical systems can achieve integral control [19]. In Sect. 3, using the theoretical framework from [20], we have then constructed a family of bimolecular (nonlinear) IFCs (8). In Sect. 4, we have proved in Theorem 4.1 that a particular two-dimensional (two-species) molecular IFC of the form (8) ensures existence of a nonnegative equilibrium when applied to stable input unimolecular networks of arbitrary dimensions; in particular, NECs can be eliminated in a dimension-independent manner when unimolecular networks are controlled. In contrast, in Sect. 5, we have demonstrated that control of bimolecular networks suffers from the curse of dimensionality—every species in the input network can in general introduce a constraint which must be obeyed for a nonnegative equilibrium to exist, leading to an intractable problem. For theoretical purposes, we have proved in Theorem 5.1 that, assuming all of the input species are known and interfacing—a generally experimentally unfeasible assumption, then there exists a higher-dimensional IFC that always eliminates NECs. Let us note that, in all of the biochemical networks studied in this paper, NECs simultaneously occur at both deterministic and stochastic levels. In particular, as opposed to the instability arising from bounded deterministic oscillations [22, 24, 25], which average out at the stochastic level, NECs in general persist in the stochastic setting.

Intracellular networks are in general bimolecular, higher-dimensional and subject to uncertainties, as respectively described by the properties (N), (D) and (U) in Sect. 1. Due to these challenges, generally only reduced (approximate) models of intracellular networks are available, which are obtained by eliminating a number of the underlying auxiliary coupled molecular species and reactions. The objective of these lower-dimensional reduced models is to capture the dynamics of desired intracellular species on a time-scale of interest [32]. However, using reduced models for purpose of control is in general unjustified due to NECs, i.e. reduced models do not necessarily capture how the underlying extended models respond to control. In particular, it takes only one of the many input species to display a negative equilibrium for control to fail and a catastrophic event to unfold; hence, including a previously neglected molecular species into a successfully controlled reduced model can result in an extended model for which control fails—a phenomenon we call phantom control, see Sect. 5. Let us note that, when a reduced model displaying a NEC is extended to include e.g. finite resources or dilution, then some of the underlying species concentrations, instead of growing to infinity, would reach finite, but large, values. Nevertheless, the effects of unwanted large concentrations, such as sequestration of ribosomes and depletion of metabolites, are potentially very harmful; moreover, in such a scenario, the underlying IFCs has failed to deliver control and perfect adaptation. NECs therefore place a fundamental limit to applicability of molecular IFCs in synthetic biology. In particular, if one attempts to address NECs, instead of a systematic approach, an ad-hoc approach is in general necessary, consisting of gathering detailed experimental information about a desired intracellular network and designing suitable higher-dimensional controllers that can be interfaced with appropriate input species.