1 Introduction

In this article, we are concerned with constructing a strategy to obtain an approximate solution to the following first-order IVP:

$$\begin{aligned} u'(t) = w (t, u),\,\quad u (t_{0}) = u_{0},\quad t \in [t_0,t_N],\quad u \in \mathbb {R},\quad w:[t_0,t_N] \times \mathbb {R} \rightarrow \mathbb {R} , \end{aligned}$$
(1)

where \( t_{0} \) and \( t_{N} \) denote the initial and final points of the integration interval, and the function w(t, u) fulfils the Lipchitz’s condition that guarantees the existence and uniqueness theorem given in [2].

Many physical phenomena in which a quantity varies in time and at the same time relies upon its past values could be modelled by (1). For example, equation (1) has been used to model many real-world application problems in different disciplines, including physics, electrical and mechanical engineering, economics, mathematical chemistry, or mathematical biology.

Numerical treatments of a type of problem (1) have received a lot of consideration because most of the differential equations arising from the modelling of physical phenomena do not have known theoretical solutions. Thus, it is of practical interest to consider numerical solutions for such model problems.

We remark that to choose the most efficient and stable numerical technique for computing (1), it is preferable to have qualitative information about the solution. The primary information is the stiffness of the problem. The explicit Runge–Kutta methods (ERKMs) are generally unsuitable for the solution of stiff problems because ERKMs may fail to provide the solution or give wrong results. The instability of ERKM methods motivated researchers in this field to consider implicit Runge–Kutta methods (IRKMs). Several IRKMs have been proposed and applied by different scholars to solve stiff IVPs of the form in (1). Among the various IRKMs you can consult [3,4,5,6,7,8,9,10].

Another numerical strategy for integrating (1) is the implicit multistep-methods (IMMs); IMMs utilize the estimation of the approximation at more than one mesh point to calculate approximate solutions at the next point. The IMMs need another strategy to start them, leading to an increase in the total number of function evaluations and CPU time. Numerous outstanding researchers in Numerical Analysis have used different IMMs for solving (1). Some interesting monographs that have employed IMMs to provide approximate solutions to stiff and non-stiff problems are those in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

Several approximate techniques have been proposed recently for the numerical treatment of (1). Among those techniques, we can mention a higher-order embedded method proposed by Kim et al. [29], the Chebyshev collocation technique by Piao et al. [30], the highly stable implicit–explicit schemes presented by Izzo and Jackiewicz [31], the general linear methods developed by Abdi and Jackiewicz [32], the new hybrid symmetric technique by Kovalnogov et al. [33], a fitted finite difference approach by Chen and Simos [34], or the Numerov-type methods proposed by Medvedeva et al. [35].

This article presents and applies a suitable error estimation and stepsize controller for a newly developed one-step A-stable method (OSASM) for solving (1). Although the development of the method and its theoretical analysis has been carried out for a scalar problem, we must point out that it can also be applied for solving initial-value differential systems, as shown in Sect. 5.

2 Mathematical formulation of the OSASM

Consider a partition \(t_0<t_1<\cdots < t_N\) with \(h= t_{j+1}-t_j\) and suppose that the theoretical solution of the IVP in (1) on a generic subinterval \([t_n, t_{n+1}]\), is approximated by the following polynomial

$$\begin{aligned} u(t)\simeq r(t) = \sum _{j=0}^{5} a_{j}\, t^{j}, \end{aligned}$$
(2)

whose first derivative can be approximated by

$$\begin{aligned} u'(t)\simeq r'(t)=\sum _{j=1}^{5}a_{j}jt^{j-1}, \end{aligned}$$
(3)

where \(a_j\in \mathbb {R}\) are unknown coefficients that would be obtained imposing some collocation and interpolation conditions at specified nodes.

The OSASM is formulated by considering three off-step points \(t_{n+c_1}=t_n+ c_1 h\), \(t_{n+c_2}=t_n+ c_2 h\), and \(t_{n+c_3}=t_n+ c_3 h\) with \(0<c_1<c_2<c_3<1\), on \([t_n, t_{n+1}]\).

Equation (2) is evaluated at \(t_n\), and the one in (3) is also evaluated at \(t_n,t_{n+c_1},t_{n+c_2},t_{n+c_3},t_{n+1}\) to get a system of equations

$$\begin{aligned}{} & {} r(t_n)=u_n\,, \\{} & {} r'(t_{n})=w_{n}, r'(t_{n+c_1})=w_{n+c_1}, r'(t_{n+c_2})=w_{n+c_2}, r'(t_{n+c_3})=w_{n+c_3}, r'(t_{n+1})=w_{n+1}, \end{aligned}$$

with six unknowns \(a_n,n=0(1)5\), where \(u_{n+j}\) and \(w_{n+j}\) denote respectively approximations of \(u(t_{n+j})\) and \(u'(t_{n+j})=w(t_{n+j},u(t_{n+j}))\).

After getting the values of \(a_n,n=0(1)5\), and substituting them into the Eq. (2), and replacing the variable \(t=t_n+xh,\) then, the polynomial in (2) may be written as

$$\begin{aligned} r(t_n+ x h)= & {} \alpha _0(x)u_n+h\left( \beta _0(x) w_n+\beta _{c_1} (x)w_{n+c_1}+\beta _{c_2} (x)w_{n+c_2} \nonumber \right. \\{} & {} \quad \left. +\beta _{c_3} (x)w_{n+c_3}+\beta _1(x)w_{n+1}\right) , \end{aligned}$$
(4)

where \( \alpha _0(x)=1\), and the coefficients \(\left\{ \beta _i(x)\right\} _{i=0,c_1, c_2,c_3,1}\) depend on \(c_1,c_2,c_3\).

Taking \(x=1\) in (4), which corresponds to the point \(t_{n+1}=x_n+h\), after inserting \(c_1=\frac{1}{2}-\frac{2}{\sqrt{21}},\, c_2=\frac{1}{2},\,c_3=\frac{1}{2}+\frac{2}{\sqrt{21}}\), we obtain the following formula, which is the main scheme of the proposed OSASM:

$$\begin{aligned} u_{n+1}= & {} u_n+ \frac{h}{1200} \left( -136 w_n+441 w_{n+c_1}+590 w_{n+c_2}+441 w_{n+c_3}-136 w_{n+1}\right) . \nonumber \\ \end{aligned}$$
(5)

We note that the values of the \(c_i\) are not taken arbitrarily, but after optimizing the local truncation error (LTE) of the formula in (4). In order to provide numerical solutions to problem (1) simultaneously at the points \(t_{n+c_1},t_{n+c_2},t_{n+c_3},t_{n+1}\), we also take \(x=c_1,x=c_2,x=c_3\). Doing this, we obtain a total of four formulas that form the OSASM. The remaining formulas are

$$\begin{aligned}{} & {} u_{n+c_1} \nonumber \\{} & {} \quad =u_n +\frac{h \left( 4 \left( 8192 \sqrt{21}-22113\right) w_n+63 \left( 6174-1091 \sqrt{21}\right) w_{n+c_1}+20 \left( 26019-5696 \sqrt{21}\right) w_{n+c_2}\right) }{2116800} \nonumber \\{} & {} \qquad +\frac{h \left( 567 \left( 686-149 \sqrt{21}\right) w_{n+c_3}+4 \left( 8192 \sqrt{21}-37863\right) w_{n+1}\right) }{2116800},\nonumber \\{} & {} u_{n+c_2}\nonumber \\{} & {} \quad = u_n +\frac{h \left( -932 w_n+63 \left( 5 \sqrt{21}+14\right) w_{n+c_1}+1180 w_{n+c_2}+63 \left( 14-5 \sqrt{21}\right) w_{n+c_3}+388 w_{n+1}\right) }{4800},\nonumber \\{} & {} u_{n+c_3}\nonumber \\{} & {} \quad = u_n +\frac{h \left( -4 \left( 8192 \sqrt{21}+22113\right) w_n+567 \left( 149 \sqrt{21}+686\right) w_{n+c_1}+20 \left( 5696 \sqrt{21}+26019\right) w_{n+c_2}\right) }{2116800}\nonumber \\{} & {} \qquad + \frac{h \left( 63 \left( 1091 \sqrt{21}+6174\right) w_{n+c_3}-4 \left( 8192 \sqrt{21}+37863\right) w_{n+1}\right) }{2116800}. \end{aligned}$$
(6)

3 Theoretical analysis of the OSASM technique

This section gives the theoretical analysis of the OSASM technique, concerning the order of accuracy, convergence and linear stability analysis.

3.1 Order of accuracy, consistency, and convergence of the OSASM

We rewrite the scheme in (5)–(6) as

$$\begin{aligned} \bar{R} \, U_n=h\, \bar{S}\, U'_n, \end{aligned}$$
(7)

where \(\bar{R}, \bar{S}\) denote constant matrices containing the coefficients of the Formulas (5)–(6), and

$$\begin{aligned}{} & {} U_n= \left( u_n,u_{n+c_1}, u_{n+c_2}, u_{n+c_3}, u_{n+1}\right) ^T,\\{} & {} U'_n= \left( u'_n,u'_{n+c_1}, u'_{n+c_2},u'_{n+c_3},u'_{n+1}\right) ^T. \end{aligned}$$

We define the operator \({\gamma }\) related to the OSASM in (5)–(6) as

$$\begin{aligned} {\gamma }[u(t);h]= & {} \sum _{j\in I}\left[ \Theta _{j}u\left( t_{n}+jh\right) -h\Psi _{j}u'\left( t_{n}+jh\right) \right] , \end{aligned}$$
(8)

where \(\Theta _j\) and \(\Psi _j \) are respectively vector columns of \(\bar{R}\) and \(\bar{S}\), and \(I=\{0,c_1,c_2,c_3,1\}\). Expanding \(u\left( t_{n}+jh\right) \) and \(u'\left( t_{n}+jh\right) \) in Taylor series about \(t_n\), we get

$$\begin{aligned} {\gamma }[u(t);h]=\theta _{0}u(t_n)+\theta _{1}h u'(t_n)+\theta _{2}h^2u''(t_n)+\cdots +\theta _{q}h^{q}\omega ^{q}(t_n)+\cdots , \end{aligned}$$
(9)

where

$$\begin{aligned} \theta _{q}= & {} \frac{1}{q!}\left[ \sum _{j\in I}^{k}j^{q}\Theta _{j} - q\sum _{j\in I}^{k}j^{q-1}\Psi _{j}\right] , \end{aligned}$$
(10)

and \(q=0,1,2,\dots \)

Considering the Formulas (5)–(6), we get \(\theta _{0}=0, \theta _{1}=0,\dots , \theta _{5}=0\) and

$$\begin{aligned} \theta _{6} = \left( \frac{25 h^6 u^{(6)}\left( t_n\right) }{17069875},\, -\frac{ h^6 u^{(6)}\left( t_n\right) }{71680},\, \frac{25 h^6 u^{(6)}\left( t_n\right) }{17069875},\, 0 \right) ^T, \end{aligned}$$

which is the vector of LTEs of the OSASM formulas. The method in (5)–(6) may be reformulated as a Runge–Kutta method, and thus the theory for these methods can be applied here. The vector of stage values is given by \(c=\left( 0,c_1,c_2,c_3,1\right) \) and the coefficients of the Butcher array can be obtained readily from the Formulas (5)–(6). It is a routine task to check that the order conditions are verified up to order 6, which ultimately is the order of the method.

It is worth remarking that the scheme is zero-stable since the OSASM is a one-step method. Since the order is greater than one, then OSASM is consistent with the differential problems under consideration. It is also important to note that the OSASM is convergent because OSASM is zero-stable and consistent.

3.2 Linear stability analysis of the OSASM

The concept of linear stability analysis (LSA) plays an essential role in the solution of IVPs in ODEs. This LSA is frequently referred to as absolute stability, and is crucial when solving stiff differential equations. Owing to this, we study the linear stability of the newly developed technique by applying the method in (7) to the following standard test equation

$$\begin{aligned} u'=- \eta u,\quad Re(\eta ) < 0, \end{aligned}$$
(11)

where \(\eta \) stands for a complex parameter and the above equation has a bounded solution that will be zero as t tends to infinity. Applying the scheme in (5)–(6) to (11) to have

$$\begin{aligned} U_{n+1}=S(z)U_n, \quad z= \eta h, \end{aligned}$$
(12)

where \(\eta \) is a complex parameter and S(z) denotes the following stability matrix

$$\begin{aligned} S(z)= \left( C^{0}+zE\right) ^{-1} \left( C^{1}+zD\right) , \end{aligned}$$
(13)

with

$$\begin{aligned}{} & {} C^{0}= \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{}0 \\ 0 &{} 1 &{} 0 &{}0 \\ 0 &{} 0 &{} 1 &{}0\\ 0 &{} 0 &{} 0 &{}1 \end{array} \right] , \quad C^{1}= \left[ \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right] , \\{} & {} E=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 1+ \frac{\left( 8192 \sqrt{21}-22,113\right) z }{529,200}\\ 0 &{} 0 &{} 0 &{} 1-\frac{233 z }{1200} \\ 0 &{} 0 &{} 0 &{} 1-\frac{\left( 8192 \sqrt{21}+22,113\right) z }{529,200} \\ 0 &{} 0 &{} 0 &{} 1-\frac{17z}{150} \\ \end{array} \right) ,\\{} & {} D= \left( \begin{array}{cccc} 1+ \frac{\left( 1091 \sqrt{21}-6174\right) z }{33,600}&{}\left( \frac{356}{315 \sqrt{21}}-\frac{59}{240}\right) z &{} \frac{3 \left( 149 \sqrt{21}-686\right) z }{11,200}&{}\frac{\left( 37,863-8192 \sqrt{21}\right) z }{529,200} \\ -\frac{21 \left( 5 \sqrt{21}+14\right) z }{1600}&{}1-\frac{59 z }{240}&{}\frac{21 \left( 5 \sqrt{21}-14\right) z }{1600}&{}-\frac{97 z }{1200} \\ -\frac{3 \left( 149 \sqrt{21}+686\right) z }{11,200}&{}-\frac{\left( 5696 \sqrt{21}+26,019\right) z }{105,840}&{}1-\frac{\left( 1091 \sqrt{21}+6174\right) z }{33,600}&{}\frac{\left( 8192 \sqrt{21}+37,863\right) z }{529,200} \\ -\frac{1}{400} (147 z )&{}-\frac{1}{120} (59 z )&{}-\frac{1}{400} (147 z )&{}1+\frac{17 z }{150} \\ \end{array} \right) . \end{aligned}$$

The obtained eigenvalues for S(z) are \(\left\{ 0,0,0,\frac{5 z^4+198 z^3+2076 z^2+10,080 z+20,160}{5 z^4-198 z^3+2076 z^2-10,080 z+20,160}\right\} \).

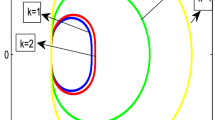
It is observed that the numerical solution relies upon the reported eigenvalues, and the stability properties of the new scheme will be characterized by the spectral radius, \( \rho ( S(z))\). The region of absolute stability \(\mathbb {S}\) for the proposed method is represented as \(\mathbb {S}= \left\{ z\in \mathbb {C}: \left| \rho ( S(z)) \right| < 1 \right\} \) and its domain is displayed in Fig. 1. The proposed OSASM is A-stable because the left half complex plane is contained in \(\mathbb {S}\).

Fig. 1
figure 1

Absolute stability region in the complex z-plane for the OSASM using (11)

Full size image

4 Error estimation and control strategy of the proposed method

In order to obtain an efficient implementation of any numerical technique and solve challenging problems like the stiff differential equations, estimating and controlling some measure of errors by varying the step size is required. The proposed method given in (5)–(6) may be formulated and computed in variable step-size mode (VSS) by using a lower order technique to estimate the local error (LE) at the final point on each iteration. To achieve a robust estimation of the LTE, we adopt a similar approach as in the book by Ascher and Petzold [27]. The following multi-step formula of order \(p =4\)

$$\begin{aligned} u^*_{n+1}= & {} u_n+\frac{h}{32} \left( 7 w_{n+c_1}+18 w_{n+c_2}+7 w_{n+c_3}\right) , \end{aligned}$$
(14)

and local truncation error \((LTE)=-\frac{17 h^5 u^{(5)}\left( t_n\right) }{120,960} +O\left( h^6\right) \) has been used to estimate the LE at the end-point. This error estimate provides the basis for determining the step-size for the next step. The estimation of the LE is obtained through the quotient

$$\begin{aligned} EST=\frac{\Vert u_{n+1}-u^*_{n+1}\Vert }{ \left\| \frac{ATOL}{RTOL}+ u_{n+1}\right\| } \,, \end{aligned}$$

where we have taken \(\Vert \cdot \Vert \) as the maximum norm, and ATOL and RTOL are predefined absolute and relative tolerances, respectively. If \(EST \le \) ATOL, then we accept the results and take the next step as \(h_{new} = 2 \times h_{old}\). If \(EST > \) ATOL, then we reject the obtained results by decreasing the step-size and repeat the calculations with the following new step

$$\begin{aligned} h_{new} = \mu \times h_{old} \left( \dfrac{ATOL}{EST }\right) ^{1/(p+1)}, \end{aligned}$$
(15)

where \(0< \mu < 1\) is a suitable adjustment factor whose purpose is to avoid failed steps during implementation.

5 Implementation details of the OSASM

The proposed A-stable technique is implemented in a step by step mode. We rewrite the system in (5)–(6) as \(\varvec{W(u)=0}\) where the unknowns are

$$\begin{aligned} {\tilde{\textbf{U}}}=(u_{c_1},u_{c_2},u_{c_3},u_1). \end{aligned}$$

Since the OSASM is an implicit scheme, we use modified Newton’s method (MNM) to solve the obtained system of non-linear equations. The MNM is given by

$$\begin{aligned} {\tilde{\textbf{U}}}^{i+1}= \tilde{{\textbf {U}}}^{i}-\left( {\textbf {J}}^{i} \right) ^{-1} {\textbf {W}}^{i}, \end{aligned}$$

where \({\textbf {J}}\) represents the Jacobian matrix of \({\textbf {W}}\). The starting values to use MNM for solving the systems on each iteration are taken as

$$\begin{aligned} u_{n+j}=u_n+(j h) w_n,\quad n=0,1,2,\dots ,N-1,\quad j=c_1, c_2, c_3, 1. \end{aligned}$$

The developed method can also be applied using a componentwise implementation to solve systems of first-order IVPs with m equations of the form:

$$\begin{aligned} {\textbf {u}}'={\textbf {w}}(t,{\textbf {u}}^T), \quad {\textbf {u}}(t_{0}) = {\textbf {u}}_{0}, \quad t_0\le t\le t_N, \end{aligned}$$

where \({\textbf {u}}=(u_1,\dots ,u_m)^T\),

$$\begin{aligned} {\textbf {w}}(t,{\textbf {u}}^T)=(w_1(x,{\textbf {u}}^T),\dots ,w_m(t,{\textbf {u}}^T))^T, \end{aligned}$$

and \({\textbf {u}}_0=(u_{1,0},\dots ,u_{m,0} )^T\). In the case of m-dimensional IVPs, we get on each step an algebraic system of 4m non-linear equations, which we also solve utilizing MNM, as in the scalar one-dimensional IVPs. The stopping criterion and the maximum number of iterations used while executing the MNM are \( \Vert \tilde{{\textbf {U}}}^{i+1}-\tilde{{\textbf {U}}}^{i}\Vert \le 2 \times ATOL\) and 100, respectively.

6 Numerical experiments

Here, we illustrate the numerical performance of the proposed OSASM on some real-life model first-order IVPs. We note that the effectiveness and efficiency of the method in (5)–(6) and the strategy in (14) will rely on the VSS approach given in (15). To measure the accuracy of the proposed OSASM with other existing numerical strategies, the following error formulas have been considered

$$\begin{aligned} MAXAE = \max _{j=0,\dots ,N} \left\| u(t_j) - {u_j}\right\| _{\infty },\quad MAXRE= \max _{j=0,\dots ,N} \left\| \dfrac{u(t_j) - {u_j}}{u(t_j)} \right\| _{\infty }, \end{aligned}$$

where \(u(t_j)\) is the exact solution, and \({u_j}\) is the computed result at each point \(t_j\) of the discrete grid.

The following methods have been considered for comparisons:

  • OSASM: The one-step A-stable method presented in (5)–(6).

  • BBDM: The block backward differentiation method in [36].

  • SDGLM: The second derivative general linear method in [37].

  • ode15s: A multistep solver reported in [37].

  • RADAU-IIA: The implicit Runge–Kutta method of order five in [22].

  • CCM: The Chebyshev Collocation Method of order eight in [30].

  • NDSolve : The built-in package solver in Mathematica.

6.1 Test Problem 1

In the first problem, we solve a scalar stiff problem [36], given by

$$\begin{aligned} u'(t)=&-\frac{u(t)-\cos (2 \pi t)}{\sigma }-2 \pi \sin (2 \pi t), \quad u(0)= 1, \quad 0 \le t \le 10. \end{aligned}$$

The true solution of this problem is

$$\begin{aligned} u(t) =\cos (2 \pi t). \end{aligned}$$
Table 1 Comparison of the numerical results on Problem 1 with \( h_{ini} = 10^{-2},\sigma = 10^{-3}, t \in [0,10] \)
Full size table
Fig. 2
figure 2

Plots of absolute errors (left), exact and OSASM solutions (right) for Problem 1 with \(h_{ini} = 10^{-2}, \sigma = 10^{-6}, t \in [0,20]\)

Full size image

In Table 1, we can observe the data for this problem. Not only the proposed method is the one that provides the best maximum absolute error (MAXAE), but it presents the lowest number of steps (NS), being the most efficient of the methods considered. Figure 2 shows the absolute errors along the integration interval and the exact and the discrete solutions for the proposed method for ATOL = RTOL \( = 10^{-6}, h_{ini} = 10^{-2}\).

6.2 Test Problem 2

Consider a non-linear stiff first-order system of ODEs [37] given by

$$\begin{aligned}&u'_{1}(t)= -10,\!004 u_{1}(t) + 10,\!000 u_{2}(t) ^4, \quad u_{1}(0)= 1,\\&u'_{2}(t)=u_{1}(t)-u_{2}(t) \left( u_{2}(t)^3+1\right) , \quad u_{2}(0)= 1, \quad 0 \le t \le 5. \end{aligned}$$

The exact solution to this system is

$$\begin{aligned} u_{1}(t) =\exp (-4 t),\quad u_{2}(t) =\exp (-t). \end{aligned}$$
Table 2 Comparison of the numerical results on Problem 2 with \( h_{ini} = 10^{-3} \)
Full size table

The results in Table 2 show again the good performance of the proposed method.

6.3 Test Problem 3

We also consider the non-linear well-known Robertson’s chemical problem which has been studied earlier by Mazzia and Iavernaro [38]

$$\begin{aligned}&u'_{1}(t)= 10^4 u_{2}(t) u_{3}(t)-\frac{u_{1}(t)}{25}, \quad u_{1}(0)= 1,\\&u'_{2}(t)= \frac{ u_{1}(t)}{25}-3\times 10^7 u_{2}(t)^2-10^4 u_{2}(t) u_{3}(t), \quad u_{2}(0)= 0, \\&u'_{3}(t)= 3 \times 10^7 u_{2}(t)^2, \quad u_{3}(0)= 0, \quad 0 \le t \le 40. \end{aligned}$$

To compare the maximum absolute errors, the following reference solution at the final point \(t_N = 40\) given in [38] has been used,

$$\begin{aligned}{} & {} u_{1}(t_N) = 0.7158270687194135, \\{} & {} u_{2}(t_N) = 9.185534764558135 \times 10^{-6}, \\{} & {} u_{3}(t_N) =0.28416374574582. \end{aligned}$$
Table 3 Comparison of the numerical results on Problem 3 with \( h_{ini} = 10^{-3} \)
Full size table

The data in Table 3 indicates the outstanding performance of the proposed method for this problem, where the total number of function evaluations (NFEVAL) is considerably reduced compared with the methods used for comparison.

6.4 Test Problem 4

We consider the Chapman model problem that describes how ozone is generated and destroyed with conditions useful for the lower to the middle stratosphere. In this case, the atmosphere consists of the chemistry of \(O_{2}, O\) and \(O_{3}\). In this situation, there are four chemical reactions [39]

$$\begin{aligned}&\textrm{O}+ \textrm{O}_{2}+M \rightarrow \textrm{O}_{3}+M\, k_{1},\\ {}&\textrm{O}+ \textrm{O}_{3} \rightarrow 2 \textrm{O}_{2}\, k_{2},\\ {}&\textrm{O}_{2}+ h \nu \rightarrow 2 \textrm{O} \, k_{3},\\ {}&\textrm{O}_{3}+h\nu \rightarrow \textrm{O}+\textrm{O}_{2}\, k_{4},\\ \end{aligned}$$

where \(k_{1}, k_{2},k_{3},k_{4}\) stand for the reaction rates, M stands for an additional molecule required to carry off excess energy, and hv represents the absorption of light, a photochemical process. The first reaction produces ozone, but the second and third reactions produce ozone destruction. The amount of molecular oxygen, \(\textrm{O}_{2}\), is kept constant for this problem (a reasonable assumption in the atmosphere). The first two reaction rates are constant (only functions of temperature), whereas the subsequent two, which are determined by light absorption, change during the day. The resulting system has the following form if we set \(u_{1}, u_{2}, u_{3} \) to be the concentrations of \(\textrm{O}, \textrm{O}_{2}, \textrm{O}_{3}\), respectively:

$$\begin{aligned}&u'_{1}(t)= -k_{1} u_{1}(t) u_{3}(t) - k_{2} u_{1}(t) u_{2}(t) +2k_{3} u_{3}(t) +k_{4} u_{2}(t) , \quad u_{1}(0)= 10^{6},\\&u'_{2}(t)= k_{1} u_{1}(t) u_{3}(t) - k_{2} u_{1}(t) u_{2}(t) -k_{4} u_{2}(t) , \quad u_{2}(0)= 10^{12}, \\ \end{aligned}$$

with the constant values

$$\begin{aligned} u_{3}(t) = 3.7 \times 10^{16}, \quad k_{1} =1.63 \times 10^{-16}, \quad k_{2} =4.66 \times 10^{-16} , \end{aligned}$$

and

$$\begin{aligned} k_{i} = \left\{ \begin{array}{ll} \exp \left( \dfrac{-a_{i}}{\sin (w t)}\right) ,&{}{} \sin (w t) > 0, ~ i= 3, 4, \\ 0, &{}{} \sin (w t) \le 0, \end{array}\right. \end{aligned}$$

being

$$\begin{aligned} a_{3} = 22.62, \quad a_{4} =7.601, \quad w = \frac{\pi }{43{,}200}. \end{aligned}$$
Fig. 3
figure 3

Chapman atmosphere: numerical solution obtained by the proposed OSASM method

Full size image

Figure 3 shows the numerical results from the OSASM with ATOL = RTOL \( = 10^{-6}, h_{ini} = 10^{-3}\). This figure shows that the solutions provided by the proposed method are in good agreement with the numerical results in [40].

6.5 Test Problem 5

We also consider the Belousov–Zhabotinskii chemical reaction Oregonator problem originated from chemistry, given as follows: [37]

$$\begin{aligned}&u'_{1}(t)= 77.27 \left( u_{2}(t) + u_{1}(t) \left( 1- 8.375 \times 10^{-6} u_{1}(t)- u_{2}(t) \right) \right) , \quad u_{1}(0)= 3,\\&u'_{2}(t)= \dfrac{1}{77.27} \left( u_{3}(t)-(1+u_{1}(t))u_{2}(t) \right) , \quad u_{2}(0)= 2, \\&u'_{3}(t)= 0.161 (u_{1}(t)-u_{3}(t)), \quad u_{3}(0)= 1, \quad 0 \le t \le 360. \end{aligned}$$
Table 4 Comparison of the numerical results on Problem 5 with \( h_{ini} = 10^{-2} \)
Full size table

The numerical results in Table 4 show again the good efficiency of the OSASM method.

6.6 Test Problem 6

Consider the following one-dimensional stiff Burgers’ equation model problem given in [30]

$$\begin{aligned}{} & {} u_t+u u_{x} = \nu u_{xx} ,\quad u(0,x) = - \sin (\pi x) ,\quad u(t,-1) = u(t,1) = 0, \\{} & {} 0 \le t \le 1, \quad -1 \le x \le 1, \end{aligned}$$

whose exact solution is unknown. Burgers’ equation is a mathematical model of the motion of a viscous compressible gas, where u is the speed of the gas, v is the kinematic viscosity, x is the spatial coordinate, and t is the time.

Table 5 Comparison of the numerical results on Problem 6 with \( h_{ini} = 10^{-1}, M = 99 \)
Full size table
Fig. 4
figure 4

NDSolve and OSASM solutions (dot lines) for Problem 6 with ATOL = \(10^{-4}\), RTOL = \(10^{-2}, h_{ini} = 10^{-1}\)

Full size image

Test Problem 4 is solved by discretizing the first-order and second-order spatial derivatives, and then applying the proposed method, following a similar procedure as in the method of lines. The \(u_x\) and \(u_{xx}\) in Problem 4 are discretized by the classical approximations

$$\begin{aligned} u_{x} \simeq \frac{u(x_{i+1},t)-u(x_{i-1},t)}{2 \delta x},\quad u_{xx} \simeq \frac{u(x_{i+1},t)-2u(x_i,t)+u(x_{i-1},t)}{\delta x^2}, \end{aligned}$$
(16)

where \(\delta x = \dfrac{(x_{M+1}-x_{0})}{M+1}\), and M is the internal number of spatial nodes. The data in Table 5 indicates the good performance of the proposed method for the Burgers’ problem. The approximate solutions provided by NDSolve and the OSASM method for Problem 6 are displayed in Fig. 4.

7 Conclusion

This article introduced a VSS formulation of a new OSASM. The proposed OSASM is sixth-order convergent with the favorable characteristic of A-stability. The proposed OSASM has been successfully used to integrate problem (1), and the obtained numerical results confirmed that the OSASM is a suitable solver for solving stiff differential systems. The procedure of controlling the step size using a reasonable error estimation and an adaptive strategy to get better accuracy is also described. The efficiency of the OSASM, when compared with some existing techniques, is remarkable.