1 Introduction

Symmetry is one of the fundamental paradigms through which the universe and that which is contained within it may be examined, understood, and simplified. Symmetry is generally utilised as a method of binary classification into discrete categories through the representations afforded by group theory. However, as demonstrated by Zabrodsky, Peleg, and Avnir, this illuminates only one facet of the utility that symmetry can provide [1]. Continuous symmetry measures offer a framework through which symmetry can be examined and, in accordance with Leibniz’s continuity principle, account for a continuum of infinitesimal changes that underlie a finite or discrete change [1, 2]. Earlier works in continuous symmetry measures have developed robust methodologies for characterising symmetry. Measurement of near-symmetry in the form of syntopy was developed by Mezey and Maruani, who demonstrated that fuzzy-set theory could be utilised to extend point-group symmetry and enable the analysis of quasi-symmetric geometries [3]. The work of Mezey further developed the applications of symmetry analysis through the examination of the symmetries of critical points, deformations, and reaction paths, which demonstrated the utility in understanding symmetry and near symmetry for the purposes of examining reactivity and as a method for characterising change within molecular electronic structure [4,5,6]. Chirality measures, which characterise the degree to which molecular geometries and electronic structures form non-superimposable images when transformed by reflection, were also introduced by the work of Mezey as a method for quantifying the divergence of structures from their reflected image [7,8,9]. The symmetric Scaling-Nested Dissimilarity Measure (SNDSM) further demonstrated that shape comparisons with a well-supported metric could be achieved and relied upon for the analysis of symmetry and chirality even in structures that are approaching achirality [10]. As well as of the work of Mezey and collaborators, the measures introduced by Pinsky and Avnir describe an ingenious methodological approach for evaluating the quality of symmetry operations [11]. However, despite their robustness, these can prove difficult to apply in an automated form to large or highly irregular systems due to the complexity of their evaluation. The available methods for continuous symmetry analysis, although still robust and valuable in their domains of application, show similar limitations when the analysis of large irregular species is required. The Symmetrizer described by Largent, Polik, and Schmidt applies most effectively to nearly symmetric objects, and the methodologies requiring construction of polyhedra also prove difficult to apply to large systems [12,13,14].

The utility of continuous symmetry measures, when applied to quantum mechanical systems, has been particularly well demonstrated in the works of Alemany et al. In these works, the development of continuous symmetry measures and associated techniques of probing the symmetry of molecular orbitals and electronic structure, have been applied to a variety of systems and structures [15, 16]. The application of symmetry to the understanding of nanocrystallites has also been shown to give insight into the role of symmetry in determining the cross-over between molecular and metallic systems in Au clusters [17]. The present study introduces a fully automated approach to measuring symmetry and a new form of continuous symmetry measurement. It also defines three other measures and examination techniques derived from this continuous symmetry measure and demonstrates their application to a variety of systems. This work provides a new theoretical framework with which symmetry can be examined, namely a symmetry vector space that unites group theory and continuous symmetry into a homogeneous description of symmetry.

2 Results

The four analytical tools developed in the Irregular Particle Symmetry Analysis (IPSA) program are two forms of continuous symmetry measure (CSMl and CSMlm), single-atom comparative symmetry (SASl), soft-tolerance point-group assignment (SToPAlm), and symmetry-orientation cross-sections (SOCSl). The following sections show the application of these tools to various types of molecules and metallic nanoparticles, giving clear examples of the utility and robustness of the IPSA methodologies. Further examples are also presented within the supplementary information.

3 Symmetry analysis applied to methanol

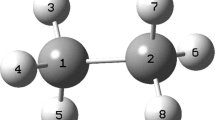
Symmetry analysis of methanol optimised with Density Functional Theory (DFT) indicated it to be in the Cs point group with a mirror plane passing through the oxygen and carbon atoms, Fig. 1. The soft tolerance point group assignment, SToPA5099, found the molecule to be consistent with Cs at a 97.31% limit of confidence [31]. There was also a 2.69% C1, indicating that some atoms were slightly deviated towards asymmetry. To further investigate the nature of this deviation, the symmetry of atoms with respect to the reflection plane was also examined with Single-Atom Symmetry. The SASl indicated that all atoms were highly symmetric with respect to the reflection plane; however, as shown in Table 1, some deviances from perfect symmetry were observed. The hydrogen atom bisected by the reflection plane, H(2), showed some variation, indicating a small positional change relative to the reflection plane that best describes the other atoms. The continuous symmetry for the molecule at CSM0.95 was found to be 0.9895, indicating that a reflectional transformation through the plane would result in near exact equivalence in position. The slight divergence from perfect symmetry (CSM0.95 = 1) is likely due to the limits of numerical precision and energy cut-offs in the DFT calculation.

Fig. 1
figure 1

The Pipek-Mezey localised orbital centroids of methanol (blue spheres) and dihedral reflection plane. Colour scheme: black, red and white spheres indicate C, O, and H respectively

Full size image
Table 1 Single-atom symmetry for methanol (SAS95).
Full size table

The centroids of localised molecular orbitals, which give the weighted centre of the electron densities of each localised orbital, were also examined using the symmetry analysis techniques to gain insight into the symmetry of the bonding orbitals and the lone pairs on the oxygen, Fig. 1. These were also consistent with a Cs point-group at 88.87% confidence and with 11.13% C1 character indicating a greater degree of asymmetry than that of the atomic positions. The reflection plane was again found to be of high quality, with a CSM0.95 of 0.9568, although slightly lower than the symmetry of the nuclear positions. This shared symmetry of the atomic positions and electronic structure is consistent with the predictions of Neumann’s theory [18, 19]. Neumann’s theory also provides a framework for examining other electronic properties that rely upon structural symmetry. For instance, the Cs point-group, indicating a single plane of reflectional symmetry for both the nuclear positions and the orbital centroids, as is shown in Fig. 1, implies that a permanent dipole must exist. By a qualitative application of Neumann’s theorem, it can also be determined that the dipole must lie within the plane of reflection. Indeed, the matrix elements that form the dipole that do not lie in the plane must necessarily either cancel or be zero, which is consistent with the DFT calculated dipole moment for methanol.

4 Sulphur hexafluoride polarizability tensor

SToPA0.970.99 assigned Oh symmetry to sulphur hexafluoride (SF6). Examination of the symmetry indicates that the physical properties must comport with the 9 reflection planes, 13 proper rotation axes, 7 improper rotation axes, and an inversion centre. The set of unique elements in Table S1 in the Supplementary Information shows the vectors necessary to characterise the symmetry of the SF6 molecule.

The centre of inversion, i.e., symmetry vector order O = -2, indicates that no permanent dipole is present. Other electronic properties, such as polarizability, can also be examined even without determining the precise values of the polarizability constants. The polarizability, a 2nd order rank tensor, must comport to a symmetry compatible with the Oh point group. In order to conform with the reflection and two-fold rotation, the polarizability tensor must be symmetric about the diagonal, and all off-diagonal terms must be equal; this ensures that the tensor can be diagonalised to produce isotropic polarizability (α), as expressed in Eq. 1 [19]. This isotropic polarisability also allows the conclusion to be drawn, SF6 is inactive under examination with Rotational-Raman spectroscopy, which demonstrates the agreement of the IPSA algorithm with group theory.

$$\alpha = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&{{\alpha _{xy}}}&{{\alpha _{xz}}}\\{{\alpha _{yx}}}&{{\alpha _{yy}}}&{{\alpha _{yz}}}\\{{\alpha _{zx}}}&{{\alpha _{zy}}}&{{\alpha _{zz}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&{{\alpha _{xy}}}&{{\alpha _{xy}}}\\{{\alpha _{xy}}}&{{\alpha _{xx}}}&{{\alpha _{xy}}}\\{{\alpha _{xy}}}&{{\alpha _{xy}}}&{{\alpha _{xx}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&0&0\\0&{{\alpha _{xx}}}&0\\0&0&{{\alpha _{xx}}}\end{array}} \right]$$
(1)

5 NH3 dipole and polarizability

Symmetry analysis of the nuclear positions and the centroids of ammonia localised molecular orbitals indicates a C3V point group. The symmetry of the centroids demonstrates the degeneracy and equivalence between the nitrogen-hydrogen bonds. This information can be used to determine the dipole orientation, which is known to occur due to the lack of inversion symmetry. For reasons of symmetry, the dipole must appear at the intersection of the mirror planes and the C3 rotation axis, which is consistent with the results from the DFT calculation. In this case, the dipole orientation is restricted to invariance under C3 rotation about the molecular axis and within the plane of molecular symmetry, which coincides with the rotation axis.

The polarizability tensor (α) may be constructed by defining a coordinate frame of reference to conform to two axes of the molecular symmetry. Here the primary axis is aligned with the z-axis, and a hydrogen nitrogen bond is brought into alignment with the y-axis, Eq. 1.

$$\alpha = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&{{\alpha _{xy}}}&{{\alpha _{xz}}}\\{{\alpha _{yx}}}&{{\alpha _{yy}}}&{{\alpha _{yz}}}\\{{\alpha _{zx}}}&{{\alpha _{zy}}}&{{\alpha _{zz}}}\end{array}} \right]$$
(1)

The application of symmetry transformation matrices allows for the relationship between the tensor constants to be examined. Applying a reflection about the y-axis, σ1 as shown in Eq. 2, determines that the terms αxy, αyx, αyz, and αzy are necessarily 0. [19]

$$\begin{array}{l}\alpha = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&{{\alpha _{xy}}}&{{\alpha _{xz}}}\\{{\alpha _{yx}}}&{{\alpha _{yy}}}&{{\alpha _{yz}}}\\{{\alpha _{zx}}}&{{\alpha _{zy}}}&{{\alpha _{zz}}}\end{array}} \right] = {\sigma _1}\left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&{{\alpha _{xy}}}&{{\alpha _{xz}}}\\{{\alpha _{yx}}}&{{\alpha _{yy}}}&{{\alpha _{yz}}}\\{{\alpha _{zx}}}&{{\alpha _{zy}}}&{{\alpha _{zz}}}\end{array}} \right]\sigma _1^T = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&{ - {\alpha _{xy}}}&{{\alpha _{xz}}}\\{ - {\alpha _{yx}}}&{{\alpha _{yy}}}&{ - {\alpha _{yz}}}\\{{\alpha _{zx}}}&{ - {\alpha _{zy}}}&{{\alpha _{zz}}}\end{array}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&0&{{\alpha _{xz}}}\\0&{{\alpha _{yy}}}&0\\{{\alpha _{zx}}}&0&{{\alpha _{zz}}}\end{array}} \right]\end{array}$$
(2)

Application of the rotated reflection transformation, σ2, further demonstrates that the αxx and αyy terms must be equal and that the αzx and αxz must also be equal to zero, Eq. 3.

$$\alpha = {\sigma _2}\left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&0&{{\alpha _{xz}}}\\0&{{\alpha _{yy}}}&0\\{{\alpha _{zx}}}&0&{{\alpha _{zz}}}\end{array}} \right]=\sigma _2^T \alpha = \left[ {\begin{array}{*{20}{c}}{\frac{{3{\alpha _{yy}}}}{4} + \frac{{{\alpha _{xx}}}}{4}}&{\frac{{\sqrt 3 {\alpha _{yy}}}}{4} - \frac{{\sqrt 3 {\alpha _{xx}}}}{4}}&{\frac{{ - {\alpha _{xz}}}}{2}}\\{\frac{{\sqrt 3 {\alpha _{yy}}}}{4} - \frac{{\sqrt 3 {\alpha _{xx}}}}{4}}&{\frac{{{\alpha _{yy}}}}{4} + \frac{{3{\alpha _{xx}}}}{4}}&{\frac{{\sqrt 3 {\alpha _{xy}}}}{2}}\\{\frac{{ - {\alpha _{zx}}}}{2}}&{\frac{{\sqrt 3 {\alpha _{zx}}}}{2}}&{{\alpha _{zz}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{\alpha _{xx}}}&0&0\\0&{{\alpha _{xx}}}&0\\0&0&{{\alpha _{zz}}}\end{array}} \right]$$
(3)

Equation 3 gives the form of the polarizability tensor, α, which is consistent with the diagonal components of the tensor predicted by coupled perturbed self-consistent field, CPSCF, analytic calculation of the diagonalised ammonia tensor, Eq. 4. The IPSA symmetry analysis proved to be consistent with group theory and the symmetry of properties derived from the electronic structure, which can be accessed by examining the symmetries of the component atoms or, more directly, the localised orbital centroids.

$${\alpha _{{\rm{CPSCF}}}}\left( {{\rm{N}}{{\rm{H}}_3}} \right) = \left[ {\begin{array}{*{20}{c}}{12.688}&0&0\\0&{12.689}&0\\0&0&{13.094}\end{array}} \right]$$
(4)

6 Chloromethane and dichloromethane natural vibration modes

SASl provides insight into the vibration modes without requiring the vectors of the vibrational motion to be examined. The initial geometry of the chloromethane conforms to the C3v point group with mean SAS0.95 scores of 5.996 ± 0.004. Analysis of the displacement geometry extrema corresponding to the 3160 cm-1 infrared active vibrational mode gives a mean SAS0.795 score of 0.787 ± 0.220. The lower score, the lower the symmetry; this is consistent with the SToPA0.800.99, which determined the point group to be 100% C1. Examination of the symmetry vectors of the 3160 cm-1 vibrational mode, Table 2, indicates that a reflection plane, assigned with 80% confidence, is the only symmetry element contributing to the SAS score. From this concept, it is possible to determine an asymmetric stretch vibrational mode of the H(0) and H(1) atoms, shown in Fig. 2. The SAS analysis also indicates a small displacement of the carbon atom, which further supports the vibration being an asymmetric stretch. The SAS of the H(2) and Cl atoms indicates that these have much smaller distortions with respect to the reflection plane. It should be noted that in-plane distortions of the Cl and H(2) atoms are not necessarily visible from these scores. A more detailed examination of the lower-lying symmetry elements using looser tolerances for SToPA and SAS would be required to resolve this mode fully. However, this is sufficient to identify the vibrational mode as being primarily an asymmetric stretch of the H(0)—C—H(1) bonds.

Fig. 2
figure 2

Geometries of chloromethane and dichloromethane. Colour scheme: black, green and white spheres indicate C, Cl, and H, respectively

Full size image

The same analysis technique can also be applied to the 3161 cm-1 displacement geometry. The symmetry vector indicates a reflection plane, and H(0) and H(1) display a similar distortion. Combined with the Cs character found by the SToPA0.800.99, this distortion suggests a symmetric stretching mode. The advantage of this form of analysis becomes more apparent if, rather than using extrema in which the displacements are visible upon cursory inspection, a smaller displacement is used; for example, 0.01% of the maxima, as is shown in Table S2. These geometries appear indistinguishable with a root mean square deviation (RMSD) of only 0.0039 Å; however, symmetry analysis allows clear insight into the types of distortion.

Table 2 Single-atom symmetry (SASl) of chloromethane (equilibrium) and the maximum distortion geometry of the 3160 cm− 1 and 3161 cm− 1 vibrational modes
Full size table

Figure 3 shows the reflection symmetry-orientation cross-sections (σ-SOCS) projected on a plane for methane, chloromethane, and dichloromethane. Despite being in significantly different point groups and having distinct substituents, the σ-SOCS of these molecules indicates similar morphologies. Methane shows six unique reflection planes, indicated by maxima in the σ-SOCS projection, i.e., the brightest spots. These maxima are linked by four unique dihedral bands, which indicate planes bisecting atoms but are not true reflections. Given the number of atoms, σ-SOCS demonstrates that the geometry must be a single central carbon atom with four identical substituents (R) arranged such R—C—R. However, these cannot be linearly distributed as a square configuration would cause only two dihedral bands. The periodicity of the maxima, with three occurring on each dihedral band, indicates that the atoms must necessarily be arranged in a trigonal configuration relative to each dihedral, in complete accordance with the known tetrahedral geometry of methane.

Fig. 3
figure 3

σ-SOCS of methane (Top) – point group Td, dichloromethane (Middle) – point group C2v, and chloromethane (Centre) – point group C3v

Full size image

As with methane, chloromethane shows four dihedral bands indicating four atoms arranged around a central one. Examination of the σ-SOCS maxima shows that three of them lie coincident with the dihedral band, which indicates that there are three equivalent atoms located in a trigonal configuration about a fourth distinct atom. This analysis suggests a tetrahedral configuration with one inequivalent atom breaking the tetrahedral symmetry. The overall lower value of the background symmetry and the lower values of the dihedral bands, which do not contain maxima, also indicate that the carbon atom moved away from the geometric centre. σ-SOCS shows that the C—Cl bond length is unique in the molecule, as the dihedral lines for any equivalent bonds would be of equal intensity. For the same reason, the σ-SOCS also indicates equivalence between the C—H bonds due to the common dihedral band intensity.

The σ-SOCS of dichloromethane also has four significant dihedral bands, which indicates four substituents, and two maxima, corresponding to two distinct reflection planes. The meeting dihedral bands to form the maxima can naturally be partitioned into two inequivalent pairs, which each contain a pair of equivalent atoms, with the distinction between the pairs being indicated by the lack of maxima at the crossing points of the dihedral bands. The orthogonality of the reflection planes is apparent due to the angular spacing of the maxima. This symmetry information indicates a doubly substituted tetrahedron by the difference in the height of the dihedral bands, which is caused by two pairs of bond lengths. The fifth dihedral band, which is significantly less symmetric and of lower intensity than those previously discussed, arises due to a significant deviation of the carbon atom from the geometric centre, also indicating the inequivalent character of the pairs of bonds in the structure.

7 Symmetry of nanoparticles

Changes in morphology that deviate from isolated ground-state geometries are often prevalent in real-world systems due to both environmental effects and thermal energetic contributions. Symmetry analysis can also be applied to understand further the changes that occur within these systems. To model these forms of structural deformations, an Au19 nanoparticle with Oh symmetry, Fig. 4, was gradually distorted to C1 symmetry using randomly generated displacements and then analysed using the CSM95 measure; the results of which are summarised in Table 3. This method allows for the characterisation of the qualities of all symmetry elements, which is advantageous over the application of discrete binary measures. Indeed, discrete categorisations would interpret changes above the numerical tolerance to result in the immediate loss of symmetry elements. Furthermore, the SToPA point group categorisation allows for the capture of point group symmetry within the bounds of acceptable fluctuations, such as in systems with thermal noise or slight numerical imprecision. The measures used to categorise the distorted Au19 particles are relatively constrained and narrow, resulting in more noticeable changes in symmetry with distortions. However, IPSA allows for this range to be tuned such that it can even provide analytic utility in the examination of state changes or distortions in low-symmetry structures.

Fig. 4
figure 4

Au19 nanoparticle in ground state Oh morphology

Full size image
Table 3 Continuous symmetry measurement of random distortions of Au19. (*Th symmetry is a coincidence of computer-generated random displacements of magnitude 0.001 Å)
Full size table

The actual symmetry of the 0.1 Å distorted cluster is confirmed by tight tolerance SToPA0.9890.99 to be 100% – C1. However, analysis with SToPA0.600.99 reveals it to have 88.22% – Cs, 6.05% – Ci, and 5.73% – C1 characters. At 0.1 Å distortion, the structure still has a high amount of reflection, and the geometry is near an invertible geometry. In contrast with the analysis of a distorted cluster, a randomly positioned set of 20 atoms measured using SToPA0.600.99 shows only 100.00% – C1 character. This result emphasises the utility of soft tolerance measures in examining symmetries for categorisation and discrimination in automated methodologies for investigating the deviation from point-group symmetry.

The similarities between symmetries can also be examined, for instance, for the Oh point-group geometries Au19 and SF6. Figure 5 shows the σ-SOCS, with nine perfect planes of reflectional symmetry, as indicated by the maxima with a quality > 0.97. The differences in the absolute value of the low symmetry regions are directly related to the size of the structures. The larger moiety has more significant change over a given angle and, thus, a lower average symmetry between axes. This effect can be corrected by the normalisation of the longest distance between the origin and an atom. However, in terms of examining the symmetry comparatively, the similarities between the structures are immediately obvious. The proximity of the Au19 moiety to more complex symmetries is also readily apparent, as shown by the small peaks between the maxima, referred to as the local maxima. They indicate some reflection or improper rotation character at these sites, which does not exist for the SF6. Both structures indicate nine perfect reflection planes divided into six planes that appear as maxima along with dihedral bands, shown as yellow and orange lines in the rightmost plots of Fig. 5, and three that appear at dihedral band intersections. The periodicity of the maxima, π/4 radians, and displacement of the maxima that lie upon the dihedral bands’ intersections show that the set of three reflection planes are distributed orthogonally to each other, with the other six being placed between them. The results immediately suggest the structure to be a member of the Oh point group, as both threefold and fourfold symmetries can be observed. The threefold symmetries appear as rectangles due to the mapping of the sphere onto a 2-dimensional plane and the smearing along the x-axis of the uppermost and lowermost points of the y-axis, labelled as point A2 in the plots shown in Fig. 5.

Fig. 5
figure 5

σ-SOCS of SF6 (upper), σ-SOCS of Au19 (lower). Labelled plots show the maxima, as indicated with green and cyan circles, and the dihedral bands, shown as orange and yellow lines

Full size image

The Au19 map also shows several dihedral bands that are not observed in the σ-SOCS of SF6, e.g., linear arrangements of atoms that do not exist in the sulphur hexafluoride. As the dihedrals of SF6 can be trivially attributed to the linear pairs of fluorine atoms, this indicates that dihedrals in Au19 can be found between the vertex Au atoms and that the edges of the cluster atoms are bisected by perfect mirror planes. From this, it can be known that the Au19 cluster has trigonal facets with three atoms to each edge. The nine dihedral bands also indicate that eighteen atoms form unique dihedrals, with the nineteenth atom placed at the centre.

We further applied σ-SOCS to larger metal structures. The Au38’s nineteen dihedral bands visible in Figure 6 can account for all of the pairs of atoms, which, in combination with the lack of distortion of the bands, suggests that no central atom is present. Both fourfold and threefold rotations are visible within the threefold regions. Some degree of sixfold character is also visible, meaning hexagonal facets with a central atom and threefold rotational symmetry due to either the extended facet or the internal particle structure. Such a result agrees with the fourfold regions, which also lie upon the intersection of dihedral bands, suggesting that the reflection planes must bisect two sets of atoms arranged in line with the reflection plane. Overall, the σ-SOCS suggests a truncated octahedral morphology, with square facets which are bounded by hexagonal ones, combined with an octahedral structure within the trigonal faces and vertices respectively aligned with the hexagonal and square facets of the truncated octahedron, which is consistent with the Oh point group classification.

Fig. 6
figure 6

(Top) σ-SOCS of Au38 (left), and Au79 (right). (Bottom) 3-dimensional representations of the reflection σ-SOCS of SF6, Au19, Au38, and Au79 (left to right)

Full size image

Identifying the dihedral bands in the σ-SOCS of larger structures, such as that of Au79 shown in Fig. 6-top-right, is more challenging due to the complexity. However, it can still be observed that there are threefold and fourfold rotational character regions with the intersection of orthogonal dihedral bands indicating a central atom. It can also be observed that the fourfold area is bounded by three local maxima, with the central-local maximum located more closely to the dihedral of the reflection plane. Such information suggests an octahedral geometry, consistent with Au19, bounded by a larger structure conformant with octahedral symmetry. The relatively low intensity of the dihedral bands linking the centre of the trigonal facets and the fourfold rotational sites, compared to those bands that conform with the edges of the facets, indicates that it is unlikely for the corner atoms to be present on the larger octahedral geometry. Hence, the geometry observed is a cuboctahedron, with an internal octahedron consistent with the structure of Au19. This analysis proves that σ-SOCS provides information of the external and internal structure of the system under scrutiny.

As is shown in Fig. 6-bottom, the representation of σ-SOCS maps as 3-dimensional structures can also provide immediate insight into the similarities between geometries. The comparison of the σ-SOCS geometries for SF6, Au19, Au38, and Au79 shows that the structures share perfect reflectional symmetry, indicated by the position and number of the maximum peaks. This representation also provides a clear visualisation of the spatial relationships between maxima, local maxima, and dihedral bands.

8 Discussion

The previous case studies and further examples in the supplementary information demonstrate the application of IPSA and a variety of purposes to which its continuous symmetry measurement and associated analytical functions can be applied. These methodologies provide unique applications of symmetry as a tool for analysis, categorisation, and improvement of existing unsupervised analysis methodologies. However, it is currently limited to addressing geometry rather than densities, volume data, or orbital structures, apart from the localised orbital centroids. Periodic systems are also explicitly excluded from this methodology, as the current form of the symmetry measure is unable to quantify the periodicity and deviations from tiling or frieze symmetries.

For demanding calculations, such as those in quantum mechanical methods, symmetry analysis applications to tensor reduction imply an increment in code efficiency. The use of soft or lose-tolerance symmetry provides good tensor approximations as an initial guess. Furthermore, tight-tolerance analysis can further reduce the dimensionality of a tensor matrix without the need for approximation. IPSA applications to simplify tensor measurements extend beyond polarizabilities and dipoles to include pyroelectricity, piezoelectricity, elasticity, and any other isotropic and anisotropic tensor properties.

The analysis of distortion and deviation from symmetry using SToPA, SAS, and CSMl techniques allows for examining the nature of structural changes with greater sensitivity than available methods like Root Mean Square Deviation (RMSD) comparison between geometries. These novel symmetry analysis techniques provide greater insight into the form of deformations, as distinctions between minimal structural deviations can be easily determined with a tunable sensitivity. The authors expect this to have significant utility in examining molecular dynamics trajectories. The careful tuning of the tolerances and limits may be used to investigate conformational changes indistinguishable by RMSD. IPSA also aids in the scrutiny of polarised spectra, where anisotropies in experimentally derived data can be compared directly with the symmetry shown in the SOCS maps and 3-dimensional representations.

The symmetry-orientation space, beyond the applications of the IPSA software, also provides a unique space in which systems can be examined and studied. Although developed for application to 3-dimensional point-groups that are particularly relevant to chemical systems, this space potentially has applications in the physical sciences beyond the scope of this particular study. Indeed, IPSA and the symmetry vector space can be expanded upon to represent and examine the symmetry elements of space-groups or Poincaré groups.

9 Methodology

9.1 Density functional theory

Density functional theory was used for geometry optimisation and single point calculations for molecules and metallic clusters. These were performed using the ORCA quantum mechanical code implementation of the B3LYP exchange-correlations functional, the Karlsruhe quadruple zeta with valence and polarisation function basis set (def2-QZVP,) and the auxiliary Weigend basis set (def2/J) [20,21,22,23,24,25,26]. An energy change threshold of 2.72×10− 5 eV with a maximum gradient of 5.14×10− 3 eV Å−1and a maximum displacement of 5.28×10− 4 Å were used as convergence criteria for the calculations. Analytical frequency calculations, as implemented in the ORCA code, were used to characterise the optimised structures. Orbital localisation and centroid analysis were undertaken using the methodology described by Vidossich and Lledós using the Pipek–Mezey orbital localisation technique [27, 28].

9.2 Symmetry analysis software

The Irregular Particle Symmetry Analysis (IPSA) is a parallel code developed in the Rust programming language as both a stand-alone command-line interface analysis tool and Python 3.0 accessible library, enabling the automation of the symmetry analysis techniques and the incorporation into existing unsupervised methodologies and toolchains [29, 30]. The code implements four measures of symmetry using novel methods of analysis for the examination of geometries.

The process applied by the software can be broadly divided into parsing, preparation, analysis, and interpretation. Parsing, preparation, and interpretation are trivial in terms of time-cost, while analysis is a bottleneck that scales approximately with O(N3), where N is the number of atoms. The presence of multiple atomic species decreases the number of pairwise comparisons required for each atom. Hence, a molecule of 30 atoms but three chemical elements would require fewer resources for analysis than a structure with 20 atoms of the same element. Furthermore, higher symmetry structures tend to have fewer potential axes and, whilst smaller geometries require analysis for fewer rotation orders, an artificial cap of rotational order, Omax= 15, is introduced by default for geometries with more than fifteen atoms. Pre-calculating values for pairs of atoms relative to the axis being tested and reusing order-independent components also increases IPSA performance. These measures ensure that calculations are relatively efficient despite their potential for complexity. Small structures have an analysis period of milliseconds, while larger geometries of around 20 atoms of 2 — 3 elements have been found to take seconds on a standard desktop computer. Details and run-times for various sample systems are provided within the supplementary information, Table S3. This efficiency makes IPSA a practical tool for analysing simulated structures at a relatively low time-cost addition to existing computational calculations. The methodologies also have applications to interpret spectra, property prediction, and structure elucidation from experimentally resolved geometries. Detailed description of the symmetry measure derivation, continuous symmetry measurement, the vector space representation and the multiple components forming IPSA are included in the Supplementary Information.