1 Introduction

Many important phenomena and dynamic processes can be described by nonlinear partial differential equations [2, 3, 5]. PDEs arising in many physical and chemical fields like fluid dynamics, condensed matter, biophysics, plasma physics, biogenetics, optical fibers, biology and other areas of engineering. A wealth of methods have been developed to find these exact physically significant solutions of a PDE though it is rather difficult [5, 6]. These methods include the sine-cosine method [19], the extended tanh method [13], the simplest equation method [9], non-classical method, the Lie symmetry method [14], the homogeneous balance method [22], sub-equation method [4], multiple exp-function method [12] and others methods [7, 8, 10].

One of the most efficient methods of studying differential equations is the Lie group method or symmetry analysis [6, 11, 14,15,16,17]. A symmetry group of a system of differential equations transforms solutions of the system to other solutions. Once one has determined the symmetry group of a system of differential equations, a number of applications become available.

In this paper, based on the Lie group method, we will investigate a modification and generalization of an important equation to find an optimal system of one-dimensional subalgebras and we used them to perform symmetry reductions and determine new group-invariant solutions of this equation. We consider a modified generalized multidimensional Kadomtsev–Petviashvili equation given by

$$\begin{aligned} \left( u_t+\lambda _1 u^n u_x+\lambda _2 u_{xxx}\right) _x+\lambda _3 u_{yy} + \lambda _4 u_{zz}=0, \end{aligned}$$
(1)

where n and \(\lambda _i\) for \(i=1,\ldots ,4\) are constants. This equation characterizes the dynamics of solitons and the nonlinear waves in plasma physics and fluid dynamics. The physics of dusty plasmas has been an important topic of rapidly interest from academic point of view and the view of its new applications in space and modern astrophysics because of its huge existence in different areas such as magnetosphere, plasma crystals, cometary tails and atmosphere of lower part of the earth, with potential applications in modern technology, such as metallic and semiconductor nanostructures or microelectronics, quantum dots and carbon nanotubes. During the last decade, the researchers found a great interest to study the propagation of linear and nonlinear characteristics of electrostatic and electromagnetic modes based on the quantum hydrodynamic models.

Several authors have studied some special cases of KP equation, which can be written in normalized form as follows:

$$\begin{aligned} \left( u_t+6 u u_x+ u_{xxx}\right) _x+3\sigma ^2 u_{yy}=0, \end{aligned}$$
(2)

where u(t, x, y) is a scalar function, t is the time coordinate and x and y are respectively the longitudinal and transverse spatial coordinates. The case \(\sigma =1\) is known as the KPII equation, and models, for instance, water waves with small surface tension. The case \(\sigma =i\) is known as the KPI equation, and may be used to model waves in thin films with high surface tension. Several authors [1, 18, 23] have studied Eq. (2), using bifurcation analysis, an extended homogeneous balance method and the multiple rogue wave solutions technique respectively. In [20] Wazwaz proposed the modification of KP equation as the below form

$$\begin{aligned} 4u_t-6u^2u_x+u_{xxx}+6u_x\partial ^{-1}u_y+3\partial ^{-1}u_{yy}=0, \end{aligned}$$
(3)

in which the propagation of the ion-acoustic waves in a plasma with non-isothermal electrons has been utilized, and in [21] Wazwaz and El-Tantawy proposed the generalized KP equation given as

$$\begin{aligned} u_{xxxy}+3\left( u_x u_y\right) _x+u_{tx}+u_{ty}+u_{tz}-u_{zz}=0, \end{aligned}$$
(4)

Equation (1) characterizes the dynamics of solitons and the nonlinear waves in plasma physics and fluid dynamics and in [4] the authors employ the sub-equation method to obtain exact solutions to the proposed strongly nonlinear time-fractional differential equations of conformable type.

The outline of this paper is as follows: In the following section we perform a study of Lie symmetries of the modified generalized multidimensional Kadomtsev–Petviashvili equation (1) and we establish our main results about it. We deal the point symmetries classification, commutators table of Lie algebra, Lie symmetry groups and new solutions that we obtain using these groups. Also we study the symmetry reductions that we can obtain by using the generators calculated previously. In Sect. 2, we employ the similarity variable and similarity solution to obtain symmetry reductions to ODE’s for the modified generalized multidimensional KP equation (1). In Sect. 3 we derive low-order local conservation laws admitted by (1) on the whole solution space, by employing the multiplier method. Finally, concluding remarks are presented in Sect. 4.

2 Lie symmetries

In this section, we will perform Lie symmetry analysis for (1) firstly. The main task of the classical Lie method is to seek some symmetries and look for exact solutions of a given partial differential equation. According to the Lie theory, to obtain Lie symmetries of the modified generalized multidimensional KP equation (1), we consider a one-parameter Lie group of infinitesimal transformations acting on independent and dependent variables

$$\begin{aligned} {\hat{t}}= & {} t+\varepsilon \tau (t,x,y,z,u)+O(\varepsilon ^2),\nonumber \\ {\hat{x}}= & {} x+\varepsilon \xi _1(t,x,y,z,u)+O(\varepsilon ^2),\nonumber \\ {\hat{y}}= & {} y+\varepsilon \xi _2(t,x,y,z,u)+O(\varepsilon ^2),\nonumber \\ {\hat{z}}= & {} z+\varepsilon \xi _3(t,x,y,z,u)+O(\varepsilon ^2),\nonumber \\ {\hat{u}}= & {} u+\varepsilon \eta (t,x,y,z,u)+O(\varepsilon ^2). \end{aligned}$$
(5)

where \(\varepsilon\) is the group parameter and \(\tau ,\) \(\xi _1\), \(\xi _2\), \(\xi _3\) and \(\eta\) are the infinitesimal of the transformations for the independent and dependent variables respectively. The vector field associated with the above group of transformations can be written as

$$\begin{aligned} V= & {} \tau (t,x,y,z,u)\frac{\partial }{\partial t}+\xi _1(t,x,y,z,u) \frac{\partial }{\partial x}+\xi _2(t,x,y,z,u) \frac{\partial }{\partial y}\nonumber \\&+\,\xi _3(t,x,y,z,u) \frac{\partial }{\partial z}+\eta (t,x,y,z,u)\frac{\partial }{\partial u}, \end{aligned}$$
(6)

where

$$\begin{aligned} \frac{d{\hat{t}}}{d\varepsilon }= & {} \tau (t,x,y,z,u),\qquad \frac{d{\hat{x}}}{d\varepsilon }=\xi _1(t,x,y,z,u),\qquad \frac{d{\hat{y}}}{d\varepsilon }= \xi _2(t,x,y,z,u),\\ \frac{d{\hat{z}}}{d\varepsilon }= & {} \xi _3(t,x,y,z,u),\qquad \frac{d{\hat{u}}}{d\varepsilon }= \eta (t,x,y,z,u). \end{aligned}$$

with the initial conditions \(({\hat{t}},{\hat{x}},{\hat{y}},{\hat{z}},{\hat{u}})\mid _{\varepsilon =0}=(t,x,y,z,u).\)

Applying the fourth prolongation \(pr^{(4)}V\) to Eq.(1), we obtain the invariance condition,

$$\begin{aligned} pr^{(4)}V(\Delta )\mid _{\varepsilon =0}=0. \end{aligned}$$
(7)

as the solutions space of (1) is invariant under the point transformation group (5), where

$$\begin{aligned}\Delta =\left( u_t+\lambda _1 u^n u_x+\lambda _2 u_{xxx}\right) _x+\lambda _3 u_{yy} + \lambda _4 u_{zz}=0.\end{aligned}$$

The fourth prolongation is given by

$$\begin{aligned} pr^{(4)}V=V+\sum _{J}\phi ^J(t,x,y,z,u^{(4)})\frac{\partial }{\partial u_J}, \end{aligned}$$
(8)

where

$$\begin{aligned} \phi ^J(t,x,y,z,u^{(4)})= & {} \partial _J(\eta -\tau u_t-\xi _1 u_x+\xi _2 u_y+\xi _3 u_z)\nonumber \\&+ \tau u_{J,t}+\xi _1 u_{J,x}+\xi _2 u_{J,y}+\xi _3 u_{J,z}, \end{aligned}$$
(9)

with \(J=(j_1,\ldots ,j_k), 1\le j_k\le 4\), \(1\le k\le 4\), \(u_{J,x^i}=\frac{\partial ^{k+1}u}{\partial x^i\partial x^{j1}\ldots \partial x^{j_k}}\) and \(\partial _J=\frac{\partial ^k}{\partial x^{j_1}\partial x^{j_2}...\partial x^{j_k}}\).

Specifically the fourth prolongation can be given as

$$\begin{aligned} pr^{(4)}V= & {} V+\phi ^{x}\frac{\partial }{\partial u_x}+\phi ^{xx}\frac{\partial }{\partial u_{xx}}+\phi ^{tx}\frac{\partial }{\partial u_{tx}}\nonumber \\&+\phi ^{yy}\frac{\partial }{\partial u_{yy}}+\phi ^{zz}\frac{\partial }{\partial u_{zz}}+\phi ^{xxxx}\frac{\partial }{\partial u_{xxxx}}. \end{aligned}$$
(10)

where \(\phi ^x,\, \phi ^{xx},\, \phi ^{tx},\, \phi ^{yy},\, \phi ^{zz},\, \phi ^{xxxx}\) are given explicitly in terms of \(\tau ,\) \(\xi _1\), \(\xi _2\), \(\xi _3\), \(\eta\) and the derivatives of \(\eta\). By using (10) we find the coefficient functions \(\tau (t,x,y,z,u)\), \(\xi _1(t,x,y,z,u)\), \(\xi _2(t,x,y,z,u)\), \(\xi _3(t,x,y,z,u)\) and \(\eta (t,x,y,z,u)\). From (7) and (10), the invariance condition reads as

$$\begin{aligned}&\phi ^{tx} +\lambda _1 n (u^{n-1}u_{xx}+(n-1)u^{n-2}u_x^2)\eta +2\lambda _1 n u^{n-1}u_x\phi ^{x}\nonumber \\&\qquad +\lambda _1 u^n \phi ^{xx} +\lambda _3\phi ^{yy} +\lambda _4\phi ^{zz} +\lambda _2\phi ^{xxxx}=0. \end{aligned}$$
(11)

where

$$\begin{aligned} \phi ^x= & {} D_x\eta -u_tD_x\tau -u_x D_x\xi _1-u_yD_x\xi _2-u_z D_x\xi _3\nonumber \\ \phi ^{tx}= & {} D_x\phi ^t-u_{tt}D_x\tau -u_{tx} D_x\xi _1-u_{ty}D_x\xi _2-u_{tz} D_x\xi _3\nonumber \\ \phi ^{xx}= & {} D_x\phi ^x-u_{tx}D_x\tau -u_{xx} D_x\xi _1-u_{xy}D_x\xi _2-u_{xz} D_x\xi _3\nonumber \\ \phi ^{yy}= & {} D_y\phi ^y-u_{ty}D_y\tau -u_{xy} D_y\xi _1-u_{yy}D_y\xi _2-u_{zy} D_y\xi _3\nonumber \\ \phi ^{zz}= & {} D_z\phi ^z-u_{tz}D_z\tau -u_{xz} D_z\xi _1-u_{yz}D_z\xi _2-u_{zz} D_z\xi _3\nonumber \\ \phi ^{xxxx}= & {} D_x\phi ^x-u_{txxx}D_x\tau -u_{xxxx} D_x\xi _1-u_{xxxy}D_x\xi _2-u_{xxxz} D_x\xi _3 \end{aligned}$$
(12)

and \(D_t\), \(D_x\), \(D_y\) and \(D_z\) t denote the total differential operators with respect to t, x, y and z

$$\begin{aligned} D_{x^i}=\frac{\partial }{\partial x^i}+u_{x^i}\frac{\partial }{\partial u}+u_{x^ix^j}\frac{\partial }{\partial u_{x^j}}+ \ldots \end{aligned}$$

where \(i=1,2,3,4\) and \((x^1,x^2,x^3,x^4)=(t,x,y,z)\).

2.1 Classification of Lie point symmetries

In this section we calculate the Lie point symmetries admitted by the modified generalized multidimensional Kadomtsev–Petviashvili equation (1). A point symmetry of (1) is a one-parameter Lie group of transformations on (t, x, y, z, u) generated by a vector field of the form (6), whose prolongation leaves invariant equation (1). The condition for a vector field (6) to generate a point symmetry of Eq. (1) is given by (11), that splits with respect to the x, y, z and t derivatives of u giving an overdetermined linear system of equations for the infinitesimals \(\tau (t,x,y,z,u),\,\) \(\xi _1(t,x,y,z,u),\,\) \(\xi _2(t,x,y,z,u)\), \(\xi _3(t,x,y,z,u)\) and \(\eta (t,x,y,z,u)\) and the parameters a, b. Solving this system we obtain the next theorem:

Theorem 1

The point symmetries admitted by Eq. (1) are generated by:

  1. 1.

    For \(\lambda _3\ne 0\) and \(\lambda _4\ne 0\):

    $$\begin{aligned} V_1= & {} \partial _t,\quad V_2=\partial _x, \quad V_3=\partial _y,\quad V_4=\partial _z ,\nonumber \\ V_5= & {} t\partial _t+\frac{1}{3}x\partial _x+\frac{2}{3}y\partial _y+\frac{2}{3}z\partial _z-\frac{2}{3n}u\partial _u,\nonumber \\ V_6= & {} z\partial _x-2\lambda _4 t\partial _z ,\quad V_7=\lambda _3 z\partial _y-\lambda _4 y\partial _z , \quad V_8=y\partial _x-2\lambda _3 t\partial _y \end{aligned}$$
    (13)
  2. 2.

    For \(\lambda _3=0\) and \(\lambda _4\ne 0\):

    $$\begin{aligned}&V_1,\, V_3,\, V_5,\, V_{f_1}=f_1(y)\partial _x,\, \nonumber \\&V_{g_1}=z g_1(y)\partial _x-2\lambda _4 t g_1(y)\partial _z,\, V_{h_1}=h_1(y)\partial _z \end{aligned}$$
    (14)
  3. 3.

    For \(\lambda _3\ne 0\) and \(\lambda _4=0\):

    $$\begin{aligned}&V_1,\, V_4,\, V_5,\, V_{f_2}=f_2(z)\partial _x, \nonumber \\&V_{g_2}=y g_2(z)\partial _x-2\lambda _4 t g_2(z)\partial _y,\, V_{h_2}=h_2(z)\partial _y \end{aligned}$$
    (15)
  4. 4.

    For \(\lambda _3\ne 0\) and \(\lambda _4\ne 0\):

    $$\begin{aligned} V_1,\, V_5,\, V_{f}=F(y,z)\partial _x,\, V_{G_1}= G_1(z)\partial _y,\, V_{G_2}=G_2(y)\partial _z \end{aligned}$$
    (16)

Proof

By using (11), letting the coefficients \(\tau (t,x,y,z,u),\,\) \(\xi _1(t,x,y,z,u),\,\) \(\xi _2(t,x,y,z,u)\), \(\xi _3(t,x,y,z,u)\) and \(\eta (t,x,y,z,u)\) of the polynomial be zero yields a set of differential equations of the functions. By simplifying the system, we obtain

$$\begin{aligned}&\xi _{3_u}=0,\,\xi _{3_x}=0,\,\xi _{2_u}=0,\,\xi _{2_x}=0,\,\xi _{1_u}=0,\,\tau _u=0,\nonumber \\&\tau _x=0,\,\eta _{uu}=0,\,\tau _z=0,\,\tau _y=0,\,\eta _{ux}=0,\,\xi _{1_{xx}}=0,\nonumber \\&\lambda _3(\xi _{3_y})+\lambda _4(\xi _{2_z})=0,\,\xi _{3_t}+2\lambda _4(\xi _{1_z})=0,\, \xi _{3_z}-2(\xi _{1_x})=0,\,\xi _{2_t}+2\lambda _3(\xi _{1_y})=0,\nonumber \\&\xi _{2_y}-2(\xi _{1_x})=0,\,3(\xi _{1_x})-\tau _t=0,\,2\lambda _4(\eta _{uz})-\lambda _4(\xi _{3_{zz}})-\lambda _3(\xi _{3_{yy}})=0,\nonumber \\&2\lambda _3(\eta _{uy})-\lambda _4(\xi _{2_{zz}})-\lambda _3(\xi _{2_{yy}})=0,\, 2\lambda _1(\xi _{1_x})u^{n+1}+\lambda _1 n \eta u^n-(\xi _{1_t})u=0,\nonumber \\&(\eta _u)u+2(\xi _{1_x})u+n\eta -\eta =0,\nonumber \\&\lambda _1(\eta _{xx})u^n+\lambda _4(\eta _{zz})+\lambda _3(\eta _{yy})+\lambda _2(\eta _{xxxx})+\eta _{tx}=0\nonumber \\&2\lambda _1 n(\eta _x)u^n+(\eta _{tu})u-\lambda _4(\xi _{1_{zz}})u-\lambda _3(\xi _{1_{yy}})u-(\xi _{1_{tx}})u=0,\nonumber \\ \end{aligned}$$
(17)

Solving system (17) on can arrive at the previous generators. \(\square\)

The previous vector fields are closed under the Lie bracket. Thus the symmetry generators form a closed Lie algebra. The commutation relationships of Lie algebras determined by the symmetry generators (13) are shown in Table 1, where \([V_i,V_j]\) is the commutator for the Lie algebra defined by

$$\begin{aligned} {}[V_i,V_j]=V_iV_j-V_jV_i. \end{aligned}$$
Table 1 Commutator table of Lie algebra of (13)
Full size table

Then we build the adjoint table for each pair of elements \(V_i\) and \(V_j\), with \(i,j = 1,\ldots ,7\), where

$$\begin{aligned}\begin{array}{rl}\text{ Ad }(\text{ exp }(\varepsilon V))W_0&{}=\sum _{n=0}^\infty \frac{\varepsilon ^n}{n!}(\text{ com }V)^n(W_0)\\ &{}=W_0-\varepsilon [V,W_0]+\frac{\varepsilon ^2}{2}[V,[V,W_0]]-\cdots \end{array} \end{aligned}$$

The adjoint relationship of the Lie algebra is shown in Table 2. We will use the adjoint representation to decompose all the subalgebras of the Lie algebra in equivalence classes of conjugated subalgebras. From the action attached infinitesimal of a Lie algebra over itself, we can rebuild the adjoint representation to the underlying Lie group adding the Lie series.

Table 2 Adjoint table of the Lie algebra
Full size table

To calculate the reductions of Eq. (1) we use elements of the optimal system of subalgebras. An optimal system of subalgebras is a list of subalgebras that are not equivalent or conjugated. Also, any other subalgebra of the Lie algebra is conjugated or equivalent with it. For calculate the optimal system, we first calculate the adjoint transformation matrix of the modified generalized multidimensional Kadomtsev–Petviashvili equation (1). We consider a linear combination of \(V_i\)

$$\begin{aligned} V=\alpha _1 V_1+\alpha _2 V_2+\alpha _3 V_3+\alpha _4 V_4+\alpha _5 V_5+\alpha _6 V_6+\alpha _7 V_7+\alpha _8 V_8 \end{aligned}$$
(18)

and we define

$$\begin{aligned} \begin{array}{rl} &{}f_i^\epsilon :G\rightarrow G\\ &{} V\rightarrow Ad(exp(\epsilon _i V_i))V \end{array} \end{aligned}$$
(19)

The function \(f_i^\epsilon\) is a linear maps for \(i=1,2,\ldots ,8\), also we define the matrix \(A_i^\epsilon\) with respect to basis \(\{V_1,V_2,V_3,V_4,V_5,V_6,V_7,V_8\}\), for \(i=1,2,\ldots ,8\) as follows:

$$\begin{aligned}&Ad(exp(\epsilon _i V_i))V\nonumber \\&\quad =(\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5,\alpha _6,\alpha _7,\alpha _8) A_i (V_1,V_2,V_3,V_4,V_5,V_6,V_7,V_8)^t \end{aligned}$$
(20)

with

$$\begin{aligned} A_1= & {} \left( \begin{array}{cccccccc} 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \\ -\epsilon _1&{}0&{}0&{}0&{}1&{}0&{}0&{}0 \\ 0&{}0&{}0&{}2\lambda _4\epsilon _1&{}0&{}1&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0 \\ 0&{}0&{}2\lambda _3\epsilon _1&{}0&{}0&{}0&{}0&{}1 \end{array} \right) , \qquad A_2= \left( \begin{array}{cccccccc} 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \\ 0&{}-\frac{1}{3}\epsilon _2&{}0&{}0&{}1&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array} \right) \\ A_3= & {} \left( \begin{array}{cccccccc} 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \\ 0&{}0&{}-\frac{2}{3}\epsilon _3&{}0&{}1&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0 \\ 0&{}0&{}0&{}\lambda _4\epsilon _3&{}0&{}0&{}1&{}0 \\ 0&{}-\epsilon _3&{}0&{}0&{}0&{}0&{}0&{}1 \end{array} \right) , \qquad A_4= \left( \begin{array}{cccccccc} 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \\ 0&{}-\frac{2}{3}\epsilon _4&{}0&{}0&{}1&{}0&{}0&{}0 \\ 0&{}0&{}0&{}-\epsilon _4&{}0&{}1&{}0&{}0 \\ 0&{}0&{}-\lambda _3\epsilon _4&{}0&{}0&{}0&{}1&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array} \right) \\ A_5= & {} \left( \begin{array}{cccccccc} e^{\epsilon _5}&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}e^{\frac{\epsilon _5}{3}}&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}e^{\frac{2\epsilon _5}{3}}&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}e^{\frac{2\epsilon _5}{3}}&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}e^{-\frac{\epsilon _5}{3}}&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}e^{-\frac{\epsilon _5}{3}} \end{array} \right) , A_6= \left( \begin{array}{cccccccc} 1&{}0&{}0&{}-2\lambda _4\epsilon _6&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}1&{}0&{}0&{}0&{}0&{}0 \\ 0&{}\epsilon _6&{}0&{}1&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}1&{}\frac{1}{3}\epsilon _6&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}-\lambda _4\epsilon _6 \\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array} \right) \\ A_7= & {} \left( \begin{array}{cccccccc} 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}1&{}-\lambda _4\epsilon _7&{}0&{}0&{}0&{}0 \\ 0&{}0&{}\lambda _3\epsilon _7&{}1&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}\lambda _4\epsilon _7 \\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0 \\ 0&{}0&{}0&{}0&{}0&{}\lambda _3\epsilon _7&{}0&{}1 \end{array} \right) , A_8= \left( \begin{array}{cccccccc} 1&{}0&{}-2\lambda _3\epsilon _8&{}0&{}0&{}0&{}0&{}0 \\ 0&{}1&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}\epsilon _8&{}1&{}0&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}\frac{1}{3}\epsilon _8 \\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}\lambda _3\epsilon _8&{}1&{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array} \right) \end{aligned}$$

Finally the general adjoint matrix A, calculated using the previous matrix, is given by

$$\begin{aligned} A=\left( \begin{array}{cccccccc} e^{\epsilon _5}&{}2 \epsilon _6\epsilon _7\epsilon _8\lambda _3\lambda _4e^{\frac{1}{3}\epsilon _5}&{}-2\epsilon _8\lambda _3 e^{\frac{2}{3}\epsilon _5}&{} A_{14}&{}0&{}0&{}0&{}0 \\ 0&{}e^{\frac{1}{3}\epsilon _5}&{}0&{}0&{}0&{}0&{}0&{}0 \\ 0&{}A_{32}&{}e^{\frac{2}{3}\epsilon _5}&{}-\epsilon _7\lambda _4e^{\frac{2}{3}\epsilon _5}&{}0&{}0&{}0&{}0 \\ 0&{}\epsilon _6e^{\frac{1}{3}\epsilon _5}&{} \epsilon _7\lambda _3e^{\frac{2}{3}\epsilon _5}&{} e^{\frac{2}{3}\epsilon _5}&{}0&{}0&{}0&{}0 \\ -\epsilon _1&{}A_{52}&{}A_{53}&{}A_{54}&{}1&{}A_{56}&{}0&{}\frac{1}{3}\epsilon _8 e^{-\frac{1}{3}\epsilon _5}\\ 0&{}-\epsilon _3\epsilon _7\lambda _4 e^{-\frac{1}{3}\epsilon _5}&{} 2 \epsilon _1\epsilon _7\lambda _3\lambda _4 e^{-\frac{1}{3}\epsilon _5}&{}A_{64}&{}0&{} e^{-\frac{1}{3}\epsilon _5}&{}0&{}\epsilon _7\lambda _4 e^{-\frac{1}{3}\epsilon _5} \\ 0&{}A_{72}&{}A_{73}&{}A_{74}&{}0&{} \epsilon _8\lambda _3 e^{-\frac{1}{3}\epsilon _5}&{}1&{}A_{78} \\ 0&{}-\epsilon _3 e^{-\frac{1}{3}\epsilon _5}&{} 2\epsilon _1\lambda _3 e^{-\frac{1}{3}\epsilon _5}&{} A_{84}&{}0&{}\epsilon _7\lambda _3 e^{-\frac{1}{3}\epsilon _5}&{}0&{} e^{-\frac{1}{3}\epsilon _5} \end{array} \right) \nonumber \\ \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{array}{l} A_{14}=2(\epsilon _7\epsilon _8\lambda _3\lambda _4- \epsilon _6\lambda _4)e^{\frac{2}{3}\epsilon _5},\\ A_{32}=-(\epsilon _6\epsilon _7 \lambda _4-\epsilon _8)e^{\frac{1}{3}\epsilon _5}\\ A_{52}=-\frac{1}{3}\epsilon _3\epsilon _8 e^{-\frac{1}{3}\epsilon _5}-\frac{1}{3}\epsilon _2-\frac{2}{3}\epsilon _4\\ A_{53}=\frac{2}{3}\epsilon _1\epsilon _7\lambda _3\lambda _4 e^{-\frac{1}{3}\epsilon _5}-\frac{2}{3}\epsilon _3\\ A_{54}=\frac{2}{3}(\epsilon _7\epsilon _8\lambda _3+\epsilon _6)\epsilon _1\lambda _4 e^{-\frac{1}{3}\epsilon _5}-\frac{1}{3}(\epsilon _7\epsilon _8\lambda _3+\epsilon _6)\epsilon _4 e^{-\frac{1}{3}\epsilon _5}\\ A_{56}=\frac{1}{3}(\epsilon _7\epsilon _8\lambda _3+\epsilon _6) e^{-\frac{1}{3}\epsilon _5}\\ A_{64}=2\epsilon _1\lambda _4 e^{-\frac{1}{3}\epsilon _5}-\epsilon _4 e^{-\frac{1}{3}\epsilon _5}\\ A_{72}=-(\epsilon _7\epsilon _8\lambda _3\lambda _4-\epsilon _6\lambda _4)\epsilon _3 e^{-\frac{1}{3}\epsilon _5}\\ A_{73}=2(\epsilon _7\epsilon _6\lambda _3\lambda _4-\epsilon _6\lambda _4)\epsilon _1\lambda _3 e^{-\frac{1}{3}\epsilon _5}-\epsilon _4\lambda _3 \\ A_{74}=2\epsilon _1\epsilon _8\lambda _3\lambda _4 e^{-\frac{1}{3}\epsilon _5}-\epsilon _4\epsilon _8\lambda _3 e^{-\frac{1}{3}\epsilon _5}+\epsilon _3\lambda _4 \\ A_{78}=(\epsilon _7\epsilon _8\lambda _3\lambda _4-\epsilon _6\lambda _4) e^{-\frac{1}{3}\epsilon _5}\\ A_{84}=2\epsilon _1\epsilon _7\lambda _3\lambda _4 e^{-\frac{1}{3}\epsilon _5}-\epsilon _4\epsilon _7\lambda _3 e^{-\frac{1}{3}\epsilon _5} \end{array} \end{aligned}$$

By using (21) the adjoint transformation equation to (1) is

$$\begin{aligned} (\beta _1,\beta _2,\beta _3,\beta _4,\beta _5,\beta _6,\beta _7,\beta _8)=(\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5,\alpha _6,\alpha _7,\alpha _8) A.\end{aligned}$$

Then we have the equation system

$$\begin{aligned} \beta _1= & {} \alpha _1 e^{\epsilon _5}-\alpha _5\epsilon _1\nonumber \\ \beta _2= & {} \alpha _1 2 \epsilon _6\epsilon _7\epsilon _8\lambda _3\lambda _4e^{\frac{1}{3}\epsilon _5}+\alpha _3 e^{\frac{1}{3}\epsilon _5} +\alpha _3 A_{32} + \alpha _4 \epsilon _6e^{\frac{1}{3}\epsilon _5}\nonumber \\&+\alpha _5 A_{52} + \alpha _6 -\epsilon _3\epsilon _7\lambda _4 e^{-\frac{1}{3}\epsilon _5}+\alpha _7 A_{72}+\alpha _8 -\epsilon _3 e^{-\frac{1}{3}\epsilon _5}\nonumber \\ \beta _3= & {} \alpha _1 2\epsilon _8\lambda _3 e^{\frac{2}{3}\epsilon _5}+\alpha _3 e^{\frac{2}{3}\epsilon _5}+\alpha _4 \epsilon _7\lambda _3e^{\frac{2}{3}\epsilon _5} +\alpha _5 A_{54} \nonumber \\&+ \alpha _6 2 \epsilon _1\epsilon _7\lambda _3\lambda _4 e^{-\frac{1}{3}\epsilon _5} +\alpha _7 A_{73}+\alpha _8 2\epsilon _1\lambda _3 e^{-\frac{1}{3}\epsilon _5}\nonumber \\ \beta _4= & {} \alpha _1 A_{14}-\alpha _3 \epsilon _7\lambda _4e^{\frac{2}{3}\epsilon _5} + \alpha _4 e^{\frac{2}{3}\epsilon _5} +\alpha _5 A_{54}+\alpha _6 A_{64}+\alpha _7 A{74}+\alpha _8 A_{84}\nonumber \\ \beta _5= & {} \alpha _5\nonumber \\ \beta _6= & {} \alpha _5 A_{56}+\alpha _6 e^{-\frac{1}{3}\epsilon _5}+\alpha _7 \epsilon _8\lambda _3 e^{-\frac{1}{3}\epsilon _5}+\alpha _8 \epsilon _7\lambda _3 e^{-\frac{1}{3}\epsilon _5}\nonumber \\ \beta _7= & {} \alpha _7\nonumber \\ \beta _8= & {} \alpha _5 \frac{1}{3}\epsilon _8 e^{-\frac{1}{3}\epsilon _5}+\alpha _6 \epsilon _7\lambda _4 e^{-\frac{1}{3}\epsilon _5} +\alpha _7 A_{78}+\alpha _8 e^{-\frac{1}{3}\epsilon _5} \end{aligned}$$
(22)

and it must have solutions for \(\epsilon _i\) for \(i=1,2,\ldots ,8\), for certain values of \(\alpha _i\) and \(\beta _i\), \(i=1,2,\ldots ,8\). Then we can obtain the generators of the optimal one-dimensional system: \(\alpha _1V_1+\alpha _2V_2+\alpha _3V_3+\alpha _4V_4, \, V_5,\, V_6+\alpha V_1+\beta V_3,\, V_7+\alpha V_1+\beta V_2, \,V_8+\alpha V_1+\beta V_4\).

2.2 Lie symmetry groups and new solutions

In this part, by solving the following initial problems, we can get the Lie symmetry group from the related symmetries to get some new exact solutions from the known ones. To calculate the one-parameter Lie symmetry group g(t, x, y, z, u) generated through the general vector field (6), we consider

$$\begin{aligned} g(t,x,y,z,u)= ({\hat{t}}, {\hat{x}}, {\hat{y}}, {\hat{z}}, {\hat{u}}) \end{aligned}$$
(23)

and we solve the following initial problems

$$\begin{aligned} \frac{\partial {\hat{t}}}{\partial \epsilon }= & {} \tau (t,x,y,z,u), {\hat{t}}\mid _{\epsilon =0}=t\nonumber \\ \frac{\partial {\hat{x}}}{\partial \epsilon }= & {} \xi _1(t,x,y,z,u), {\hat{x}}\mid _{\epsilon =0}=x\nonumber \\ \frac{\partial {\hat{y}}}{\partial \epsilon }= & {} \xi _2(t,x,y,z,u), {\hat{y}}\mid _{\epsilon =0}=y\nonumber \\ \frac{\partial {\hat{z}}}{\partial \epsilon }= & {} \xi _3(t,x,y,z,u), {\hat{z}}\mid _{\epsilon =0}=z\nonumber \\ \frac{\partial {\hat{u}}}{\partial \epsilon }= & {} \eta (t,x,y,z,u), {\hat{u}}\mid _{\epsilon =0}=u \end{aligned}$$
(24)

Therefore, from (24) we can obtain the corresponding Lie symmetry group, that is to say the one-parameter Lie symmetry groups \(g_i\), \(i = 1,\ldots ,8,\) which are generated through \(V_i\), \(i = 1,\ldots ,8\), respectively are given by

$$\begin{aligned} \begin{array}{l} g_1 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}}, {\hat{z}}, {\hat{u}})=(t+\epsilon , x, y, z, u) \\ \textit{ time translation}\\ g_2 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}},{\hat{z}}, {\hat{u}})=(t, x+\epsilon , y,z,u) \\ \textit{ space-translations along the x-axis} \\ g_3 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}}, {\hat{z}},{\hat{u}})=(t, x, y+\epsilon ,z, u) \\ \textit{ space-translations along the y-axis} \\ g_4 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}}, {\hat{z}},{\hat{u}})=(t, x, y, z+\epsilon , u) \\ \textit{ space-translations along the z-axis} \\ g_5 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}}, {\hat{z}},{\hat{u}})=(t e^{\epsilon }, x e^{\frac{\epsilon }{3}}, y e^{\frac{2\epsilon }{3}}, z e^{\frac{2\epsilon }{3}}, u e^{-\frac{2\epsilon }{3n}} \\ \textit{ nonhomogeneous scaling group} \\ g_6 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}},{\hat{z}},{\hat{u}})=(t, -\lambda _4\epsilon ^2t+\epsilon z+x, y ,-2\lambda _4\epsilon t+z. u ) \\ \textit{ time and space dependent shift} \\ g_7 : (t, x,y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}},{\hat{z}}, {\hat{u}})=(t, x, \frac{y+\lambda _3\epsilon z}{1+\lambda _3\lambda _4\epsilon ^2},\frac{z-\lambda _4\epsilon y}{1+\lambda _3\lambda _4\epsilon ^2}, u) \\ \textit{ space-dependent shift} \\ g_8 : (t, x, y, z,u) \rightarrow ({\hat{t}}, {\hat{x}}, {\hat{y}}, {\hat{z}},{\hat{u}})=(t, -\lambda _3 t\epsilon ^2+\epsilon y+x, y-2\lambda _3\epsilon t, z, u) \\ \textit{ time and space dependent shift} \\ \end{array} \end{aligned}$$
(25)

where \(\epsilon\) is the group parameter. The theory of Lie assures that a group of symmetry transforms solution into solutions, then we can conclude that if \(u=f(t, x, y,z)\) represents a known solution of the differential equation (1), by applying the different groups of symmetry \(g_i\), \(i=1,\ldots 8,\) we can calculate the new solutions of (1).

Based on (25), the corresponding new solutions of (1) can be given by:

$$\begin{aligned}&{\hat{u}}_1 =f(t-\epsilon , x, y,z) \end{aligned}$$
(26)
$$\begin{aligned}&{\hat{u}}_2 =f(t, x-\epsilon , y,z) \end{aligned}$$
(27)
$$\begin{aligned}&{\hat{u}}_3 =f(t, x, y-\epsilon , z) \end{aligned}$$
(28)
$$\begin{aligned}&{\hat{u}}_4 =f(t,x,y,z-\epsilon ) \end{aligned}$$
(29)
$$\begin{aligned}&{\hat{u}}_5 =f(te^{-\epsilon }, x e^\frac{-\epsilon }{3}, y e^\frac{-2\epsilon }{3}, z e^\frac{-2\epsilon }{3})e^\frac{-2\epsilon }{3n} \end{aligned}$$
(30)
$$\begin{aligned}&{\hat{u}}_6 =f(t, x-\epsilon z-\lambda _4\epsilon ^2 t, y, z+2\lambda _4\epsilon t) \end{aligned}$$
(31)
$$\begin{aligned}&{\hat{u}}_7 =f(t,x, y-\lambda _3\epsilon z, z+\lambda _4\epsilon y) \end{aligned}$$
(32)
$$\begin{aligned}&{\hat{u}}_8 =f(t, x-\epsilon y-\lambda _3\epsilon ^2 t, y+2\lambda _3\epsilon t, z) \end{aligned}$$
(33)

3 Symmetry reductions

In this section we mainly consider the one-dimensional subalgebras computed in the previous subsection and obtain symmetry reductions of modified generalized multidimensional Kadomtsev–Petviashvili equation. Similarity variables and similarity solutions associated with any vector field \(V=\tau \partial _t+\xi _1\partial _x+\xi _2\partial _y+\xi _3\partial _z+\eta \partial _u\) can be accomplished by its Lagrange’s system

$$\begin{aligned} \frac{dt}{\tau }=\frac{dx}{\xi _1}=\frac{dy}{\xi _2}=\frac{dz}{\xi _3}=\frac{du}{\eta } \end{aligned}$$
(34)

(i) We first consider the Lie point symmetry \(\alpha _1 V_1+\alpha _2 V_2+\alpha _3 V_3+\alpha _4 V_4\). Equation (34) becomes

$$\begin{aligned} \frac{dt}{\alpha _1}=\frac{dx}{\alpha _2}=\frac{dy}{\alpha _3}=\frac{dz}{\alpha _4}=\frac{du}{u} \end{aligned}$$

and we obtain the similarity variables and similarity solution

$$\begin{aligned} w_{1}= & {} \alpha _1 x-\alpha _2 t,\quad w_{2}=\alpha _1 y-\alpha _3 t,\nonumber \\ w_3= & {} \alpha _1 z-\alpha _4 t \quad u=h(w_1,w_2,w_3).\end{aligned}$$
(35)

Substituting (35) into (1) we obtain a new reduction equation with the independent variables \(w_1\), \(w_2\) and \(w_3\) as follows

$$\begin{aligned}&\lambda _1\alpha _1^2 n h^{n-1}(h_{w_1})^2+\lambda _4\alpha _1^2 h_{w_3 w_3}+\lambda _3\alpha _1^2 h_{w_2 w_2}+\lambda _2\alpha _1^4 h_{w_1w_1w_1w_1}\nonumber \\&\quad +\lambda _1\alpha _1^2 h^n h_{w_1w_1}-\alpha _1\alpha _2 h_{w_1w_1}-\alpha _1\alpha _4 h_{w_1w_3}-\alpha _1\alpha _3 h_{w_1w_2}=0. \end{aligned}$$
(36)

Again, utilizing the Lie symmetry method on Eq. (36), we obtain the following similarity variables and similarity solution

$$\begin{aligned} \begin{array}{ccc} s_1=w_1-w_2,\quad s_2=w_1-w_3,\quad h=g(s_1,s_2)\end{array}\end{aligned}$$
(37)

and the following reduction equation with the independent variables \(s_1\) and \(s_2\)

$$\begin{aligned}&4\alpha _1^2\lambda _1 n g^{n-1} g_{s_2}+4\lambda _1\alpha _1^2 g^{n-1} g_{w_1}n+\lambda _1\alpha _1^2 n g^{n-1} g_{s_1}^2+16\lambda _2\alpha _1^2 g_{s_2s_2s_2s_2} \nonumber \\&\quad +\,4\lambda _1\alpha _1^2 g^n g_{s_1s_2} -4\alpha _1\alpha _2 g_{s_2s_2}+\lambda _4 \alpha _1^2 g_{s_2s_2}+\lambda _2\alpha _1^4 g_{s_1s_1s_1s_1}+8\lambda _2\alpha _1^2 g_{s_1s_1s_1s_2}\nonumber \\&\quad +\,24\lambda _2\alpha _1^4 g_{s_1s_1s_2s_2}+\lambda _1\alpha _1^2 g^n g_{s_1s_1}-\alpha _1\alpha _3 g_{s_1s_1}+\lambda _3\alpha _1^2 g_{s_1s_1}\nonumber \\&\quad +\,32\lambda _2\alpha _1^4 g_{s_1s_2s_2s_2}+4\lambda _1\alpha _1^2 g^n g_{s_1s_2}-2\alpha _1\alpha _3 g_{s_1s_2}-2\alpha _1\alpha _2 g_{s_1s_2}=0. \end{aligned}$$
(38)

(ii) We now consider the Lie point symmetry \(V_5\) and Eq. (34) becomes

$$\begin{aligned}\frac{dt}{t}=\frac{dx}{\frac{1}{3}}=\frac{dy}{\frac{2}{3}y}=\frac{dz}{\frac{2}{3}z}=\frac{du}{-\frac{2}{3n}u}.\end{aligned}$$

We obtain the similarity variables and similarity solution

$$\begin{aligned} \begin{array}{ccc} w_{1}=\alpha 1 x t^{-\frac{1}{3}},\quad w_{2}=y t^{-\frac{2}{3}},\quad w_3=z t^{-\frac{2}{3}} \quad&u=h(w_1,w_2,w_3)t^{-\frac{2}{3n}}.\end{array}\end{aligned}$$
(39)

and the new reduction equation with the independent variables \(w_1\), \(w_2\) and \(w_3\)

$$\begin{aligned}&-\frac{2}{3}h_{w_1w_3}w_3-\frac{2}{3} h_{w_1w_2}w_2-\frac{1}{3} h_{w_1w_1}w_1+\lambda _1 h_{w_1w_1} h^n+\lambda _1 (h_{w_1})^2 n h^{n-1}\nonumber \\&\quad -\frac{2}{3n}h_{w_1}+\lambda _4 h_{w_3w_3}+\lambda _3 h_{w_2w_2}+\lambda _2 h_{w_1w_1w_1w_1}-\frac{1}{3}h_{w_1}=0. \end{aligned}$$
(40)

By using the following similarity variables and similarity solution with (40)

$$\begin{aligned} \begin{array}{ccc} s_1=w_1,\quad s_2=\lambda _4 w_2^2+\lambda _3 w_3^2,\quad h=g(s_1,s_2)\end{array}\end{aligned}$$
(41)

we obtain the following reduction equation with the independent variables \(s_1\) and \(s_2\)

$$\begin{aligned}&4\lambda _3\lambda _4 g_{s_2s_2}s_2-\frac{4}{3}g_{s_1s_2}s_2-\frac{1}{3}g_{s_1s_1}s_1+\lambda _1 g^{n-1}g_{s_1}^2n \nonumber \\&\quad -\frac{2}{3n}g_{s_1}+4 \lambda _3\lambda _4 g_{s_2}+\lambda _2 g_{s_1s_1s_1s_1}+\lambda _1 g^n g_{s_1s_1}-\frac{1}{3}g_{s_1}=0. \end{aligned}$$
(42)

One more time we apply the Lie symmetry method, to equation (42) this time. We obtain the point symmetries for this equation. By using the similarity variable and similarity solution \(r=s_2 s_1^{-4}\) and \(g=f(r)s_1^{-\frac{2}{n}}\) we obtain the following reduction EDO with the independent variable r and dependent variable f,

$$\begin{aligned}&256\lambda _2r^4f^{iv)}+2176\lambda _2r^3f''' +16\lambda _1r^2f^2f''\nonumber \\&\quad +4272\lambda _2 r^2f''+32\lambda _1 r^2 f f'' 4\lambda _3\lambda _4 r f''+44\lambda _1 r f^2 f' \nonumber \\&\quad +1656 \lambda _2 r f' +4\lambda _3\lambda _4 f'+4\lambda _1 f^3+24\lambda _2 f=0. \end{aligned}$$
(43)

with solution when \(\lambda _1=0\) given by

$$\begin{aligned} \begin{array}{rl} f(r)=&{}c_1 BesselJ\left( \frac{1}{4}, \gamma _1\right) ^2+c_2 hypergeom\left( [1,1],\left[ \frac{5}{4},\frac{3}{2},\frac{7}{4}\right] ,-\gamma _1^2\right) \\ \\ &{}+ c_3 BesselJ\left( \frac{1}{4}, \gamma _1\right) \left( 12\sqrt{r\lambda _2} BesselJ\left( \frac{3}{4}, \gamma _1\right) -\sqrt{\lambda _3\lambda _4}BesselJ\left( \frac{7}{4}, \gamma _1\right) \right) \\ \\ &{} +24 c_4 \lambda _2\sqrt{\lambda _3\lambda _4} BesselJ\left( \frac{3}{4}, \gamma _1\right) BesselJ\left( \frac{7}{4}, \gamma _1\right) \\ \\ &{}-\frac{c_4}{\sqrt{r}}\left( 144 r \lambda _2^{3/2} BesselJ\left( \frac{3}{4}, \gamma _1\right) ^2 +\lambda _3\lambda _4\sqrt{\lambda _2} BesselJ\left( \frac{7}{4}, \gamma _1\right) ^2\right) . \end{array}\nonumber \\ \end{aligned}$$
(44)

where \(\gamma _1= \frac{\sqrt{\lambda _3\lambda _4}}{8\sqrt{r\lambda _2}}\) and it give us the following solution for (1)

$$\begin{aligned} u(t,x,y,z)= & {} c_1 BesselJ\left( \frac{1}{4}, \gamma _1\right) ^2+c_2 hypergeom\left( [1,1],\left[ \frac{5}{4},\frac{3}{2},\frac{7}{4}\right] ,-\gamma _1^2\right) \nonumber \\&+ c_3 BesselJ\left( \frac{1}{4}, \gamma _1\right) \left( 12\sqrt{(x^{-4-\frac{2}{n}}(\lambda _4 y^2 +\lambda _3 z^2))\lambda _2} BesselJ\left( \frac{3}{4}, \gamma _1\right) \right) \nonumber \\&- c_3 BesselJ\left( \frac{1}{4}, \gamma _1\right) \left( \sqrt{\lambda _3\lambda _4}BesselJ\left( \frac{7}{4}, \gamma _1\right) \right) \nonumber \\&+24 c_4 \lambda _2\sqrt{\lambda _3\lambda _4} BesselJ\left( \frac{3}{4}, \gamma _1\right) BesselJ\left( \frac{7}{4}, \gamma _1\right) \nonumber \\&-\frac{c_4}{\sqrt{x^{-4-\frac{2}{n}}(\lambda _4 y^2 +\lambda _3 z^2)}}\left( 144 (x^{-4-\frac{2}{n}}(\lambda _4 y^2 +\lambda _3 z^2)) \lambda _2^{3/2} BesselJ\left( \frac{3}{4}, \gamma _1\right) ^2 \right) \nonumber \\&-\frac{c_4}{\sqrt{x^{-4-\frac{2}{n}}(\lambda _4 y^2 +\lambda _3 z^2)}} \left( \lambda _3\lambda _4\sqrt{\lambda _2} BesselJ\left( \frac{7}{4}, \gamma _1\right) ^2\right) , \end{aligned}$$
(45)

and \(\gamma _1= \frac{\sqrt{\lambda _3\lambda _4}}{8\sqrt{\lambda _2 x^{-4-\frac{2}{n}}(\lambda _4 y^2 +\lambda _3 z^2) }}\).

In Fig. 1 we considere (45) in the cases \(z=1\), \(x=1\) and \(y=1\) respectively and \(\lambda _1=0,5, \lambda _2=2, \lambda _3=1\), \(\lambda _4=1\), \(c_1=-1, c_2=0,4, c_3=1, c_4=2\).

Fig. 1
figure 1

Exact solution of (1) given by (45)

Full size image

(iii) We first consider the Lie point symmetry \(V_6+\alpha _1 V_1+\alpha _3 V_3\) and we obtain the similarity variables and similarity solution

$$\begin{aligned} \begin{array}{ccc} w_{1}=\alpha _1 x-t z,\quad&w_{2}=\alpha _1 y-\alpha _2 t,\quad w_3=z \quad&u=h(w_1,w_2,w_3).\end{array}\end{aligned}$$
(46)

and the following reduction equation, for \(\lambda _4=0\), with the independent variables \(w_1\), \(w_2\) and \(w_3\)

$$\begin{aligned}&-\alpha _1 h_{w_1 w_1} w_3-\lambda _1 \alpha _1^2 h^{n-1} h_{w_1}^2n+\lambda _3\alpha _1^2 h_{w_2w_2}\nonumber \\&\quad +\lambda _2\alpha _1^4 h_{w_1w_1w_1w_1}+\lambda _1\alpha _1^2 h^n h_{w_1w_1}-\alpha _1\alpha _2 h_{w_1w_2}=0. \end{aligned}$$
(47)

Applying the Lie symmetry method on Eq. (47), we obtain the following similarity variables and similarity solution

$$\begin{aligned} \begin{array}{ccc} s_1=f_1(w_3)w_2-f_2(w_3)w_1,\quad s_2=w_3,\quad h=g(s_1,s_2)\end{array}\end{aligned}$$
(48)

and the following reduction equation with the independent variables \(s_1\) and \(s_2\)

$$\begin{aligned}&\lambda _2 g_{s_1s_1s_1s_1}f_2(s_2)^4-g_{s_1s_1}s_2 f_2(s_2)^2-\lambda _1 g^{n-1}g_{s_1}^2 n f_2(s_2)^2\nonumber \\&\quad -\lambda _1 g^n g_{s_1s_1}f_2(s_2)^2+\alpha _2 g_{s_1s_1}f_1(s_2)f_2(s_2)+\lambda _3 g_{s_1s_1} f_1(s_2)^2=0. \end{aligned}$$
(49)

When \(f_1(w_2)=f_2(w_2)=1\) Eq. (49) give us

$$\begin{aligned}&\lambda _2 g_{s_1s_1}-\frac{\lambda _1}{n+1} g^{n+1}-g (s_2-\alpha _2-\lambda _3)=0 \end{aligned}$$
(50)

with solution when \(n=0\) and \((\lambda _2+s_2)(\lambda _1-\alpha _2-\lambda _3)>0\)

$$\begin{aligned}&g=c_1 e^{s_1\sqrt{\frac{\lambda _2+s_2}{\lambda _1-\alpha _2-\lambda _3}}}+ c_2 e^{-s_1\sqrt{\frac{\lambda _2+s_2}{\lambda _1-\alpha _2-\lambda _3}}}, \end{aligned}$$
(51)

and the following solution in the case \(n=0\) and \((\lambda _2+s_2)(\lambda _1-\alpha _2-\lambda _3)<0\),

$$\begin{aligned}&g=c_1 \sinh \left( {s_1\sqrt{\frac{\lambda _2+s_2}{\lambda _3+\alpha _2-\lambda _1}}}\right) + c_2 \cosh \left( {s_1\sqrt{\frac{\lambda _2+s_2}{\lambda _3+\alpha _2-\lambda _1}}}\right) . \end{aligned}$$
(52)

This give us the following solutions of (1) respectively

$$\begin{aligned} u(t,x,y,z)= & {} c_1 e^{(-\alpha _1 x+\alpha _1 y -\alpha _2 t +tz)\sqrt{\frac{\lambda _2+z}{\lambda _1-\alpha _2-\lambda _3}}}+ \nonumber \\&c_2 e^{-(-\alpha _1 x+\alpha _1 y -\alpha _2 t +tz)\sqrt{\frac{\lambda _2+z}{\lambda _1-\alpha _2-\lambda _3}}}, \end{aligned}$$
(53)

and

$$\begin{aligned} u(t,x,y,z)= & {} c_1 \sinh \left( {(-\alpha _1 x+\alpha _1 y -\alpha _2 t +tz)\sqrt{\frac{\lambda _2+z}{\lambda _3+\alpha _2-\lambda _1}}}\right) \nonumber \\&+ c_2 \cosh \left( {(-\alpha _1 x+\alpha _1 y -\alpha _2 t +tz)\sqrt{\frac{\lambda _2+z}{\lambda _3+\alpha _2-\lambda _1}}}\right) . \end{aligned}$$
(54)

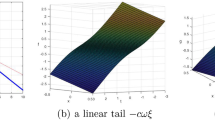
In Fig. 2 we considere (53) in the cases \(z=0\), \(t=1\) and \(z=1\), \(y=1\) respectively with \(\alpha _2=-1\), \(\lambda _1=2, \lambda _2=0,5, \lambda _3=1\), \(c_1=1, c_2=1, c_3=1, c_4=1\). In Fig.  3 we considere (54) in the cases \(z=0\), \(t=1\) and \(z=1\), \(y=1\) respectively with \(\alpha _2=1\), \(\lambda _1=2, \lambda _2=0,5, \lambda _3=1\), \(c_1=1, c_2=1, c_3=1, c_4=1\).

Fig. 2
figure 2

Exact solution of (1) given by (53)

Full size image
Fig. 3
figure 3

Exact solution of (1) given by (54)

Full size image

(iv) When we consider the Lie point symmetry \(V_7+\alpha _1 V_1+\alpha _2 V_2\) we obtain for \(\lambda _4=0\) the similarity variables and similarity solution

$$\begin{aligned} \begin{array}{ccc} w_{1}=\alpha 1 x-\alpha _2 t,\quad&w_{2}=\alpha _1 y-\lambda _3 z t ,\quad w_3=z \quad&u=h(w_1,w_2,w_3).\end{array}\end{aligned}$$
(55)

and the reduction equation with the independent variables \(w_1\), \(w_2\) and \(w_3\) as follows

$$\begin{aligned}&-\lambda _3\alpha _1 h_{w_1w_1}w_3+\lambda _1\alpha _1^2 h^{n-1} h_{w_1}^2 n +\lambda _3\alpha _1^2 h_{w_2w_2}\nonumber \\&\quad +\lambda _2\alpha _1^4 h_{w_1w_1w_1w_1}+\lambda _1\alpha _1^2 h^n h_{w_1w_1}-\alpha _1\alpha _2 h_{w_1w_1}=0. \end{aligned}$$
(56)

(v) When we use the generator \(V_8+\alpha _1 V_1+\alpha _4 V_4\) we obtain the similarity variables and similarity solution

$$\begin{aligned} \begin{array}{ccc} w_{1}=\alpha 1 x-\frac{1}{2}ty,\quad&w_{2}=\alpha _1 y-\frac{1}{2}t^2,\quad w_3=\alpha _1 z-\alpha _4 t \quad&u=h(w_1,w_2,w_3).\end{array}\end{aligned}$$
(57)

Substituting (35) into (1) and the following reduction equation

$$\begin{aligned}&\frac{1}{2}\alpha _1 w_2 h_{w_1w_1}+\lambda _1\alpha _1^2 h^{n-1} h_{w_1}^2 n+\lambda _4\alpha _1^2 h_{w_2w_3}\nonumber \\&\quad -\alpha _1\alpha _4 h_{w_1w_3}+\lambda _1\alpha _1^2 h^n h_{w_1w_1}\lambda _4\alpha _1^4 h_{w_1w_1w_1w_1}=0 \end{aligned}$$
(58)

4 Conservation laws

Conservations laws are very important in the study of differential equations. They have also been used in the development of numerical methods and in obtaining exact solutions for some partial differential equations. They describe chemical and physical conserved quantities such as energy, electric charge, mass, etc. A local conservation law for the modified generalized multidimensional Kadomtsev–Petviashvili equation (1) is a divergence expression holding on the whole solution space \(\varepsilon\) of equation (1)

$$\begin{aligned} \begin{array}{l} \left( D_tT+D_xX+D_yY +D_zZ\right) \mid _\varepsilon =0\end{array}\end{aligned}$$
(59)

The conserved density T and the spatial fluxes X, Y and Z are functions of t, x, y, z, u and derivatives of u. Here \(D_t\), \(D_x\), \(D_y\) and \(D_z\) denote the total derivative operators with respect t, x, y and z respectively. This method makes use of the concept of multiplier, that is, a function

$$\begin{aligned}Q(t,x,y,z,u,u_t,u_x, \,\ldots )\end{aligned}$$

which satisfies that

$$\begin{aligned} \left( \left( u_t+\lambda _1 u^n u_x+\lambda _2 u_{xxx}\right) _x+\lambda _3 u_{yy} + \lambda _4 u_{zz}\right) Q\end{aligned}$$

is a divergence expression for solutions of (1) and for any function u(t, x, y, z). There is a one-to-one correspondence between non-trivial multipliers and non-trivial conservation laws in characteristic form.

All non-trivial conservation laws arise from multipliers. When we move off of the set of solutions of Eq. (1), every non-trivial local conservation law (59) is equivalent to one that can be expressed in the characteristic form

$$\begin{aligned}&\left( D_t{\widehat{T}}+D_x{\widehat{X}}+D_y{\widehat{Y}} +D_z{\widehat{Z}} \right) \nonumber \\&\quad =\left( \left( u_t+\lambda _1 u^n u_x+\lambda _2 u_{xxx}\right) _x+\lambda _3 u_{yy} + \lambda _4 u_{zz}\right) Q\end{aligned}$$
(60)

that vanishes on the set of solutions of Eq. (1) where \(({\widehat{T}},{\widehat{X}},{\widehat{Y}}, {\widehat{Z}})\) differs from (T, X, Y, Z) by a trivial conserved current. We find all multipliers by solving the determining equation

$$\begin{aligned} \frac{\delta }{\delta u}\left( \left( u_t+\lambda _1 u^n u_x+\lambda _2 u_{xxx}\right) _x+\lambda _3 u_{yy} + \lambda _4 u_{zz}\right) Q=0 \end{aligned}$$
(61)

where \(\frac{\delta }{\delta u}\) is the Euler–Lagrange operator \({\hat{E}}[u]\) given by

$$\begin{aligned} {\hat{E}}[u]:= & {} \frac{\partial }{\partial u}+ \sum _{s\ge 1}(-1)^sD_{i_1}\cdots D_{i_s}\frac{\partial }{\partial u_{i_1 i_2 \ldots i_s}} \nonumber \\= & {} \frac{\partial }{\partial u}-D_t\frac{\partial }{\partial u_t} -D_x\frac{\partial }{\partial u_x}-D_y\frac{\partial }{\partial u_y}-D_z\frac{\partial }{\partial u_z}+D_x^2\frac{\partial }{\partial u_{xx}}+ \ldots \end{aligned}$$
(62)

and the general form for a low-order multiplier for the generalized (2+1)-dimensional nonlinear evolution equation (1) is given by \(Q(t, x, y, u, u_t, u_x, u_y, u_z, u_{xx}, u_{xxx}).\) The determining equation (61) yields a linear determining system for the multipliers Q(t, x, y, z, u).

$$\begin{aligned} \begin{array}{l} Q_t(t,x,y,z,u)=0, Q_{u_{xx}}(t,x,y,z,u)=0, \\ Q_x(t,x,y,z, u)=0, Q_{u_{xxx}}(t,x,y,z,u)=0,\\ Q_y(t,x,y,z,u)=0, Q_{z}(t,x,y,z,u)=0, Q_{u}(t,x,y,z,u)=0, \\ Q_{u_{xyy}}(t,x,y,z,u)+\frac{\lambda _4}{\lambda _2} Q_{u_{xzz}}(t,x,y,z,u)=0, \\ Q_{u_{tx}}(t,x,y,z,u)+\lambda _4 Q_{u_{zz}}(t,x,y,z,u)+\lambda _3 Q_{u_{yy}}(t,x,y,z,u)=0. \\ \lambda _3^2 Q_{u_{yyyy}}(t,x,y,z,u)+\lambda _4^2 Q_{u_{zzzz}}(t,x,y,z,u)+2\lambda _4\lambda _3 Q_{u_{yyzz}}(t,x,y,z,u)=0. \end{array} \end{aligned}$$
(63)

We solve this determining system and we get the multiplier \(Q=1\). For each of the conserved currents obtained, Eq. (59) is satisfied when the modified generalized multidimensional KP equation holds. By solving the determining equation (61), the solution multiplier Q give us these conserved densities and fluxes of Eq. (1). The low-order local conservation laws admitted on the whole solution space \(\varepsilon _{+}\) by the modified generalized multidimensional KP equation (1) are given by

$$\begin{aligned} \begin{array}{l} T_1= u_x,\quad X_1= \lambda _1 u u_x+\lambda _2 u_{xxx}, \quad Y_1= \lambda _3 u_y\quad Z_1= \lambda _4 u_z.\end{array} \end{aligned}$$
(64)

5 Concluding remarks

In this paper, by using the Lie symmetry analysis method we studied the modified generalized multidimensional Kadomtsev–Petviashvili equation (1). For the first time, the classical Lie point symmetries were used to construct an optimal system of one-dimensional subalgebras. This system was then used to obtain symmetry reductions and new group-invariant solutions of (1). Also we have calculated the Lie symmetry group from the related symmetries to get some new exact solutions from the known ones. Again for the first time, we have derived the conservation laws for (1) by employing the multiplier method.