1 Introduction

In the field of computer aided geometric design (CAGD), offset curves and surfaces have got considerable attention since they are widely used in various practical applications such as tolerance analysis, geometric optics and robot path-planning.

This work can be considered as a continuation or a note of our recently published work [2]. Then, for some applications of this kind of problem in the domain of chemical sciences, one can consult such applications in [2], for example the authors in [1] investigate the electrocoagulation/flotation (ECF) treatment efficiency for the removal of copper, turbidity and organic substances from the waste offset printing developer (WOPD). Meanwhile, the authors in [17] show the ability to recover the subsurface of surface-enhanced Raman scattering (SERS) signal. In [19], the authors reviews the interplay of weak non-covalent interactions involved in the formation of self-assembled mono-layers of organic molecules and the strong chemical binding in directed-assembly of organic molecules on solid surfaces.

The authors in [4] have elucidated the relationship between the coverage of cadmium carboxylate on CdSe surfaces and the trapping dynamics. Reducing the metal enrichment increases the rate of hole trapping and reduces the PLQY. In [16] the authors have employed transient absorption spectroscopy and transient photocurrent measurements to characterize the dynamics of photogenerated holes in CoPi-modified BiVO\(_4\) photoanodes. The competition between water oxidation and electron/hole recombination was quantified using a simple kinetic model. In [6] transient absorption spectroscopy was used to analyse the trapping of electrons and holes generated by band gap excitation of NiO nanoparticle films. The analysis revealed that after a fs pulse the hole is trapped on a sub-picosecond time scale in a “Ni\(^{4+}\)” state. Meanwhile in [13] the authors have presented direct time-resolved spectroscopic evidence for quasi-type-II band alignment in graded alloy CdS\(_x\)Se\(_{1-x}\) NCs through analysis of the ultrafast charge carrier dynamics as a function of chemical composition. The fast \(\thicksim 3\) ps hole-trapping process disappears as sulfur composition increases to form a graded CdS-rich shell with VB offset such that excited holes are confined to the CdSe-rich core. The authors in [12] demonstrate that measuring the sub-30-pm displacements of atoms from high-symmetry positions in the atomically resolved scanning tunnelling microscopy allows the physical order parameter fields to be visualized in real space on the single-atom level. This local crystallographic analysis is applied to the in-situ-grown manganite surfaces. In particular, using direct bond-angle mapping the authors report direct observation of structural domains on manganite surfaces, and trace their origin to surface-chemistry-induced stabilization of ordered Jahn-Teller displacements. In recent decades, the alkali metals have been measured by X-ray photoelectron spectroscopy (XPS), which is a powerful technique to detect elemental compositions of the surface of the material and determine the related chemical states. In [21] the XPS profiles of the alkali metals are analyzed via the ZPS analysis method, the BOLS notation, tight-binding (TB) theory, and density functional theory (DFT) method, which not only facilitates the reproduction of thermal and size trend of energy changes, but also clarifies the physical origin of their core-electron BE shifts in alkali metals.

Offset curves and surfaces are defined as locus of the points which distance along the normal direction from the original ones.

The parametric representation of the offset of a given parametric surface \(\varvec{s}(u,v)\) is another parametric surface given by

$$\begin{aligned} \varvec{s}_d(u,v)=\varvec{s}(u,v)+d\; \varvec{n}(u,v), \end{aligned}$$
(1)

where d is the signed offset distance and \(\varvec{n}(u,v)\) is the unit normal vector at the point \(\varvec{s}(u,v)\).

Except a very surfaces as planes, spheres, cones, torus or cylinders, offset surfaces cannot be expressed in the same forms as their original ones. Therefore, approximation methods are needed.

In some of the engendering applications, we need to extend the concept of the standard offset surface, such as geodesic offset, where the constant distance is replaced by geodesic distance, or generalized offset, where the offset distance is not necessarily along the normal direction.

Generalized offset curves and surfaces were first introduced by Bréchner[3] and have been extended further, from the differential geometric as well as algebraic point of view by Pottman[18].

For a regular parametric surface \(\varvec{r}(u,v)=(x(u,v),y(u,v),z(u,v))\), its two unit tangent vectors in the directions of u and v and its normal vector are given by

$$\begin{aligned} \varvec{e}_1=\frac{\varvec{r}_u(u,v)}{\langle \varvec{r}_u(u,v)\rangle _3},\quad \varvec{e}_2=\frac{\varvec{r}_v(u,v)}{\langle \varvec{r}_v(u,v)\rangle _3},\quad \varvec{n}(u,v)=\frac{\varvec{r}_u(u,v)\times \varvec{r}_v(u,v)}{\langle \varvec{r}_u(u,v)\times \varvec{r}_v(u,v)\rangle _3}, \end{aligned}$$
(2)

respectively, where \(\langle \,\cdot \rangle _3\) is the usual Euclidean norm in \(\mathbb {R}^3\).

In this situation, the generalized surface \(\varvec{r}^0(u,v)\) with the variable offset distance and direction determined by the vectors \(d_1(u,v)\varvec{e}_1(u,v)\), \(d_2(u,v)\varvec{e}_2(u,v)\) and \(d_3(u,v)\varvec{n}(u,v)\) is defined by

$$\begin{aligned} \varvec{r}^0(u,v)=\varvec{r}(u,v)+d_1(u,v)\varvec{e}_1(u,v)+d_2(u,v)\varvec{e}_2(u,v)+d_3(u,v)\varvec{n}(u,v). \end{aligned}$$
(3)

Hole-filling techniques appear in many different real applications, like surface reconstruction in engineering [20], 3D human body scanning, dental reconstruction, reverse engineering, etc. In 3D scanning applications for example, data can be missing due to accessibility limitations, occlusion, reflecting spaces or surfaces perpendicular to camera/scanner.

In [11] the procedure considered presents a surface reconstruction and hole-filling scheme, based on a network of parallel and/or orthogonal curves, called also wireframes, where previously some specific one-dimensional curve reconstructions have been accomplished inside the hole that they want to fill. Under this perspective, the authors face the problem of filling surface by mixing the models presented in some of their references in an efficient way. Instead of addressing the problem as a whole, which yields a very complicated computational frame, the authors generate the reconstructed filling surface through one-dimensional filling curves subsequently used to generate the global filling smooth surface. The method proposed is developed just for explicit surface.

In [10] the methods and the procedures studied manage to find a smooth bivariate spline function that minimizes certain functional, and that properly takes into account all the features that the authors want this approximate spline to fulfill, this means technique of minimizing functionals in order to obtain splines verifying certain required conditions has been used in the literature in the last years. Among these possible conditions, there are the volume restrictions, that can be included as an interpolation condition inside the corresponding finite element space constructed, or a just as another approximation term to be included in the associated quadratic functional. Also, the authors has included some other approximation or interpolation conditions at some specific points outside the holes.

In [9] the authors propose to generalize the filling method previously developed in other works in order to fill holes with some shape conditions, i.e. in such a way that the filling path “inherits” as much as possible the shape of the original surface where it is known. In other words, in real single-variable calculus, there are definitions for increasing, decreasing, concave and convex functions. These definitions involve derivatives and make reference to shape characteristics of the functions. Following this idea, given a data function f with a hole, the method proposed in their paper consists of estimating the shape of f inside the hole by constructing functions that estimate the unknown derivatives of f whose derivatives inside the hole be as close as possible to the estimates ones of f, pretending in this way that the shapes of the function f and its filing path be close.

In [8] the authors treat the problem of adequately filling the holes of 3D-surfaces, not necessarily explicit, and even closed in parametric form, as spheroid type ones: that is, such obtained by a radial function of the spherical coordinates.

In [7] the authors develop two different approaches of a method to fill polygonal holes in a given surfaces by using smoothing variational splines: discontinuous filling and regular filling. In the discontinuous case, they fill the holes with spline functions in a finite element space that minimizes an energy functional. Such filling are chosen to be smooth and as close as possible to the original surface in the neighborhoods of the hole. In this approach the global reconstructed surface will not be continuous. On the contrary, in the regular case, they do not only fill the holes, but also they replace the known surface with another very similar in such a way that the global reconstructed surface will have the desired regularity.

In some practical cases we also know some specific geometrical constrains, of industrial and design type, as the special case of a specified volume inside each on of this sub-domains. The studied method in this work manages to find a function of a biquadratic spline space that minimizes certain quadratic functional that includes the usual semi-norm of order two in a Sobolev space. This minimizing functional technique has proven to be effective on some approximation methods in different functional spaces (see [14, 15] and the references therein).

We study here the problem in which we have surface points (e.g. from a given function, or from some data acquisition procedure) where there is a lack of information inside some sub-domains. As we said this work is a continuation of [2] let’s give a very clear observation between the two works, in fact first this work it is about filling holes and second the approximation is made with the biquadratic splines functions that are of class 1, while in [2] it is done with the bi-cubic splines that are of class 2. This clearly shows that the degree of approximation in this work has been significantly reduced.

The remainder of the manuscript is organized as follows. In sect. 2 we give some necessary formulations and preliminaries. In sect. 3 we present an approximation method of the generalized offset surface with the hole, in the first step we formulate the problem, in the second step we show how to compute such surface and in the last step we prove a convergence result. Section 4 is devoted to study an approximation method of the filling hole, in the first step we formulate the problem, in the second step we show a computation result. In sect. 5 we define the smoothing parametric biquadratic spline filling the hole. Finally, we present some numeric and graphical examples in order to prove the effectiveness and the useful of our method.

2 Notations and preliminaries

We denote by \(\langle \,\cdot \,\rangle _k\) and \(\langle \, , \, \rangle _k\) respectively, the Euclidean norm and the inner product in \(\mathbb {R}^r\).

For any interval (a, b) ((c, d)) with \(a<b\) (\(c<d\)) we consider the rectangle \(R=(a,b)\times (c,d)\).

For any set \(\omega \subset \mathbb {R}^2\) let \(H^3(\omega ;\mathbb {R}^3)\) be the usual Sobolev space of (classes of) functions \(\varvec{u}\) belong to \(L^2(\omega ;\mathbb {R}^3)\), together with their partial derivatives \(D^{\varvec{\beta }}\varvec{u}\), with \(\varvec{\beta }=(\beta _1,\beta _2)\), in the distribution sense, of order \(\vert \varvec{\beta }\vert =\beta _1+\beta _2\le 3\). This space is equipped with the inner products

$$\begin{aligned} (\varvec{u},\varvec{v})_{\ell .\omega }=\sum _{\vert \varvec{\beta }\vert =\ell }\int _\omega \langle D^{\varvec{\beta }}\varvec{u} (\varvec{p})D^{\varvec{\beta }}\varvec{v}(\varvec{p})\rangle _3 d\varvec{p},\quad 0\le \ell \le 3, \end{aligned}$$

the semi-norms \(\displaystyle \vert \varvec{u}\vert _{\ell ,\omega }=(\varvec{u},\varvec{u})_\ell ^\frac{1}{2}\), for \(0\le \ell \le 3\), and the norm \(\displaystyle \Vert \varvec{u}\Vert _\omega =\left( \sum _{\ell =0}^3 \vert \varvec{u}\vert _{\ell ,\omega }^2\right) ^\frac{1}{2}\).

Let \(T_n=\{a=x_0<x_1<\cdots <x_n=b\}\) and \(T_m=\{c=y_0<y_1<\cdots <y_m=d\}\) be two partitions of [a, b] and [c, d] respectively, and \(S_2(T_n)\), \(S_2(T_m)\) the spaces of quadratic spline functions of class \(C^1\) constructed from \(T_n\) and \(T_m\) respectively. It is verified that \(\dim (T_n)=n+2\) and \(\dim (T_m)=m+2\)

Let \(\{\phi _1(x),\ldots ,\phi _{n+2}(x)\}\) and \(\{\psi _1(y),\ldots ,\psi _{m+2}(y)\}\) be respectively the quadratic B-spline bases functions of \(S_2(T_n)\) and \(S_2(T_m)\), we consider the space of biquadratic functions

$$\begin{aligned} S_2(T_n,T_m)= span\{\phi _1(x),\ldots ,\phi _{n+2}(x)\}\otimes span\{\psi _1(y),\ldots ,\psi _{m+2}(y)\}. \end{aligned}$$

Let \(M=\dim S_2(T_n,T_m)=(n+2)(m+2)\).

For \(i=1,\ldots ,n+2\), \(j=1,\ldots ,m+2\) and for any \((x,y)\in R\), we define \(B_{(m+2)(i-1)+j}(x,y)=\phi _i(x)\psi _j(y)\). Then \(\{B_1,\ldots ,B_M\}\) is the biquadratic B-spline basis functions of \(S_2(T_n,T_m)\).

Being \(\displaystyle h=\max \{\frac{b-a}{n}, \frac{d-c}{m}\}\), let \(V_h=(S_2(T_n,T_m))^3\) be the parametric space of biquadratic splines functions. It is verified that \(V_h\subset H^2(R;\mathbb {R}^3)\cap C^1(\bar{R};\mathbb {R}^3)\).

Let \(\mathbb {R}^{k,3}\) be the space of real matrices of k rows and 3 columns equipped with the inner product \(\displaystyle \langle A,B\rangle _{k,3}=\sum _{i=1}^k\sum _{j=1}^3 a_{ij} b_{ij}\), with \(A=\mathop {(a_{ij})}\nolimits _{\begin{array}{c} 1\le i\le k\\ 1\le j\le 3 \end{array}}\), \(B=\mathop {(b_{ij})}\nolimits _{\begin{array}{c} 1\le i\le k\\ 1\le j\le 3 \end{array}}\) and the corresponding norm \(\displaystyle \langle A\rangle _{k,3}=\langle A,A\rangle _{k,3}^{\frac{1}{2}}\).

Let \(\mathcal {T}_h\) be the set of partition rectangles \(T_n\times T_m\) of R, we consider a closed set \(H\subset R\) (the hole) and let \(\displaystyle H_h=\mathop {\bigcup }\limits _{\begin{array}{c} K\in \mathcal {T}_h\\ K\cap H\ne \emptyset \end{array}} K.\)

Now, given a surface \(\mathcal {S}\) parameterized by the function \(\varvec{f}:\; R\rightarrow \mathbb {R}^3\) and its generalized offset surface \(\mathcal {O}\) parameterized by the function

$$\begin{aligned} \varvec{s}_{\varvec{f}}(x,y)=\varvec{f} (x,y)+d_1(u,v)\varvec{e}_1(u,v)+d_2(u,v)\varvec{e}_2(u,v)+d_3(u,v)\varvec{n}(u,v), \end{aligned}$$

for all \((x,y)\in R.\) Suppose we can know the points of \(\mathcal {S}\) by the parametrization \(\varvec{f}\) only over \(R-H\).

We wish to approximate the surface \(\mathcal {O}\) parameterized by \(\varvec{s}_f\) from a finite set of points of \(\varvec{f} (R-H)\) and filling the holes by a constructed function of type

$$\begin{aligned} \varvec{\sigma }^h (x,y)=\left\{ \begin{array}{ll} \varvec{\sigma }_1^h(x,y),\quad &{} (x,y)\in R-H_h,\\ \varvec{\sigma }_2^h(x,y),\quad &{} (x,y)\in H_h,\end{array}\right. \end{aligned}$$

such that \(\varvec{\sigma }^h\in V_h\).

3 Approximating \(\varvec{s}_f\vert _{R-H_h}\)

3.1 Formulating of the problem

For each \(N\in \mathbb {N}^\star\), let \(A_N=\{\varvec{a}_1,\ldots ,\varvec{a}_k\}\) be a finite set of \(k=k(N)\) points of \(R-H\) such that

$$\mathop {\sup }\limits_{{p \in R - H}} \min _{{a \in A^{N} }} \langle {\text{ }}p - a\rangle _{2} = O\left( {\frac{1}{N}} \right),\quad N \to + \infty .{\text{ }}$$
(4)

Hence, we can obtain, for N sufficiently large, that \(k(N)>N\).

Now, let \(d_1(u,v)\varvec{e}_1(u,v)\), \(d_2(u,v)\varvec{e}_2(u,v)\) and \(d_3(u,v)\varvec{n}(u,v)\) be some given offset variables distances and directions.

Let \(\rho :\, H^2(R;\mathbb {R}^3)\rightarrow \mathbb {R}^{k,3}\) be the Lagrangian operator defined by \(\rho \varvec{v}=(v(\varvec{a}_i))_{1\le i\le k}\) and suppose that

$$\begin{aligned} \ker \rho \cap \mathbb {P}_2(R;\mathbb {R}^3)=\emptyset , \end{aligned}$$
(5)

where \(\mathbb {P}_2(R;\mathbb {R}^3)\) is the linear space of the restrictions to R of the bivariate polynomials of degree less than or equal to 2 with vectorial coefficients in \(\mathbb {R}^3\).

For any real number \(\varepsilon >0\), let \(J_1:\, H^2(R;\mathbb {R}^3)\rightarrow \mathbb {R}\) be the functional given by

$$\begin{aligned} J_1^h(\varvec{v})=\langle \rho (\varvec{v})-\rho (\varvec{s}_f)\rangle _{k,3}+\varepsilon \vert \varvec{v}\vert ^2_{2,R}. \end{aligned}$$

Problem 1 We consider the following minimization problem: Find \(\varvec{\sigma }_1^h\in V_h\) such that

$$\begin{aligned} \forall \varvec{v}\in V_h,\quad J_1^h(\varvec{\sigma }_1^h)\le J_1^h(\varvec{v}). \end{aligned}$$
(6)

Proposition 1

Problem (6) has a unique solution, called the generalized offset biquadratic spline in \(V_h\) relative to N, \(A_N\), \(\rho (\varvec{s}_{\varvec{f}})\), \(d_1\), \(d_2, d_3\) and \(\varepsilon\), that is characterized as the unique solution of the following variational problem: Find \(\varvec{\sigma }_1^h\in V_h\) such that

$$\begin{aligned} \forall \varvec{v} \in V_h,\quad \langle \rho (\varvec{v}), \rho (\varvec{\sigma }_1^h)\rangle _{k,3}+\varepsilon (\varvec{v},\varvec{\sigma }_1^h)_{2,R}=\langle \rho (\varvec{v}), \rho (\varvec{s}_{\varvec{f}})\rangle _{k,3}. \end{aligned}$$
(7)

Proof

Let define the following application

$$\begin{aligned} \varvec{v}\longmapsto [[\,\varvec{v} \,]]=\left( \langle \rho \varvec{v} \rangle ^2_{k,3}+\varepsilon \vert \varvec{v} \vert ^2_{2,R}\right) ^{\frac{1}{2}}. \end{aligned}$$

Using (4) we obtain that the application \(\, [[\,\,\cdot \,\,]]\,\) defines a norm in \(V_h\) which is equivalent to the usual norm \(\Vert \,\cdot \,\Vert _R\). Meanwhile, it is easily to prove that the symmetric bilinear form \(\tilde{a}:\, V_h\times V_h \rightarrow \mathbb {R}\) defined by

$$\begin{aligned} \tilde{a} (\varvec{u}, \varvec{v})=\langle \rho (\varvec{u}), \rho (\varvec{v})\rangle _{k,3}+\varepsilon (\varvec{u}, \varvec{v})_{2,R} \end{aligned}$$

is continuous and \(V_h\)-elliptic.

Then, the result is obtained applying Lax-Milgram Lemma (see [5]) taking into account that the linear application \(\Phi : H^2(R;\mathbb {R}^3) \rightarrow \mathbb {R}\) defined by

$$\begin{aligned} \Phi (\varvec{v})= \langle \rho (\varvec{v}), \rho (\varvec{s}_{\varvec{f}})\rangle _{k,3} \end{aligned}$$

is continuous. \(\square\)

3.2 Computing the solution \(\varvec{\sigma }_1^h\)

Now, we are going to see how to compute in practice the generalized offset biquadratic spline \(\varvec{\sigma }_1^h\in V_h\) relative to N, \(A_N\), \(\rho (\varvec{s}_{\varvec{f}})\), \(d_1\), \(d_2\), \(d_3\) and \(\varepsilon\). Let \(\{\omega _1,\ldots ,\omega _M\}\) be the biquadratic B-spline basis functions of \(S_2(T_n,T_m)\) and \(\{\varvec{j}_1,\varvec{j}_2,\varvec{j}_3\}\) the canonical one of \(\mathbb {R}^3\). We define

$$\begin{aligned} \forall \, i=1,\ldots ,M,\ \forall \, \ell =1,2,3,\ j=3(i-1)+\ell ,\ \varvec{v}_j=\omega _i \varvec{j}_\ell . \end{aligned}$$

Then \(\{\varvec{v}_1,\ldots ,\varvec{v}_{3M}\}\) is a basis of \(V_h\).

Thus \(\displaystyle \varvec{\sigma }_1^h=\sum _{i=1}^{3M} \alpha _i \varvec{v}_i\), with \(\alpha _1,\ldots .\alpha _{3M}\in \mathbb {R}\) are the solution of the linear system

$$\begin{aligned} \left( \mathcal {A} \mathcal {A}^T+\varepsilon \mathcal {R}\right) \varvec{\alpha }=\varvec{b}, \end{aligned}$$
(8)

where

$$\begin{aligned} \begin{array}{l} \displaystyle \mathcal {A}=\mathop {\left( \varvec{v}_i(\varvec{a}_j)\right) }\nolimits _{\begin{array}{c} 1\le i\le 3M,\\ 1\le j\le k \end{array}},\\ \displaystyle \mathcal {R}=\left( (\varvec{v}_i,\varvec{v}_j)_{2,R}\right) _{1\le i,j\le 3M},\\ \varvec{\alpha }=(\alpha _1,\ldots ,\alpha _{3M})^T,\\ \varvec{b}=\left( \langle \rho (\varvec{s}_{\varvec{f}}),\rho (\varvec{v}_i)\rangle _{k,3}\right) _{1\le i\le 3M}. \end{array} \end{aligned}$$

Remark 1

We can observe that for computing the solution of the linear system (8) only certain values of \(\varvec{s}_{\varvec{f}}\) on \(R-H\) are necessary.

3.3 Convergence result

The objective of this subsection is to prove, under adequate conditions, that the generalized offset biquadratic spline in \(V_h\) relative to N, \(A_N\), \(\rho (\varvec{s}_{\varvec{f}})\), \(d_1\), \(d_2\), \(d_3\) and \(\varepsilon\) converges to \(\varvec{s}_{\varvec{f}}\) locally in \(R-H\) as N tends to \(+\infty\) and h tends to 0.

For this, we can reason as [2, sect. 5] by using the unique parametric biquadratic spline function \(\varvec{S}_M\in V_h\) which solves the interpolation problem

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{S}_M(x_i,y_j)=\varvec{s}_{\varvec{f}}(x_i,y_j),\ i=0,\ldots ,n,\ j=0,\ldots ,m.\\ \displaystyle \frac{\partial \varvec{S}_M}{\partial x}(x_0,y_j)=\frac{\partial \varvec{s}_{\varvec{f}}}{\partial x}(x_0,y_j),\ j=0,\ldots ,m,\\ \displaystyle \frac{\varvec{S}_M}{\partial y}(x_i,y_0)=\frac{\partial \varvec{s}_{\varvec{f}}}{\partial y}(x_i,y_0),\ i=0,\ldots ,n,\\ \displaystyle \frac{\partial ^2\varvec{S}_M}{\partial x\partial y}(x_0,y_0)=\frac{\partial ^2\varvec{s}_{\varvec{f}}}{\partial x\partial y}(x_0,y_0), \end{array} \end{aligned}$$

and considering its restriction \(\left. \varvec{S}_M\right| _{R-H}\).

The interpolation function \(\varvec{S}_M\) verifies that there exist a positive real constant C such that

$$\begin{aligned} \vert \varvec{S}_M-\varvec{s}_{\varvec{f}}\vert _{\ell ,R-H}\le C h^{3-\ell },\ \ell =0,1,2. \end{aligned}$$

Hence, reasoning as in [2, Theorem 7] we can prove the following result.

Theorem 1

Suppose the hypotheses (4) and the following ones

$$\begin{aligned} \varepsilon =O(N^2),\ N\rightarrow +\infty , \end{aligned}$$
(9)

and

$$\begin{aligned} \frac{h N^2}{\varepsilon }=O(1),\ N\rightarrow +\infty \end{aligned}$$
(10)

hold. Then, for any \(\varvec{x}\in R-H\) there exists an open subset \(\omega _{\varvec{x}}\subset R-H\) such that \(\varvec{x}\in \omega _{\varvec{x}}\) and

$$\begin{aligned} \lim _{N\rightarrow +\infty } \Vert \varvec{\sigma }_1^h-\varvec{s}_{\varvec{f}}\Vert _{2,\omega _{\varvec{x}}}=0. \end{aligned}$$

Proof

From (9), (10) one has that \(h\rightarrow 0\) as \(N\rightarrow +\infty\). Then, given \(\varvec{x}\in R-H\), there exists \(h_1>0\) such that, for \(h\le h_1\), \(\varvec{x}\in R-H_h\) and thus there exists an open subset \(\omega _{\varvec{x}} \subset R-H\) such that \(\varvec{x}\in \omega _{\varvec{x}}\) and \(\omega _{\varvec{x}}\subset R-H_h\), for all \(h\le h_1\).

From here, and reasoning as in [2, Theorem 7] we can obtained the result.\(\square\)

4 Filling holes

4.1 Formulating the problem

We denote by \(B_h=A_N\cap H_h=\{\varvec{b}_1,\ldots ,\varvec{b}_{M_1}\}\), \(C_h^N=\{\varvec{c}_1,\ldots , \varvec{c}_{M_2} \}\) the set of all the knots of \(T_n\times T_m\) that they are on some side of the boundary of \(H_h\) and \(D_h^N=\{ \varvec{d}_1,\ldots ,\varvec{d}_{M_3}\}\) the set of all knots of \(C_h^N\) that are not vertices.

For \(i=1,2,3\) we consider the operators \(\rho _i^h: H^2(R;\mathbb {R}^3)\rightarrow \mathbb {R}\) given by

$$\begin{aligned} \begin{array}{l} \displaystyle \rho _1^h(\varvec{v})=\left( \varvec{v}(\varvec{b}_i)\right) _{1\le i\le M_1},\\ \displaystyle \rho _2^h(\varvec{v})=\left( \varvec{v}(\varvec{c}_i)\right) _{1\le i\le M_2},\\ \displaystyle \rho _3^h(\varvec{v})=\left( \frac{\partial \varvec{v}}{\partial \varvec{n}}(\varvec{d}_i)\right) _{1\le i\le M_3}, \end{array} \end{aligned}$$

where \(\displaystyle \frac{\partial \varvec{v}}{\partial \varvec{n}}\) indicates the normal derivative of the restriction of \(\varvec{v}\) to \(H_h\).

Let \(V_h^*\) be the restriction set of the functions of \(V_h\) to \(H_h\) and let consider the subsets

$$\begin{aligned}&X_h=\{\varvec{v}\in V_h^*\ \vert \, \rho _i^h(\varvec{v})=\rho _i^h(\varvec{\sigma }_1^h),\, i=2,3\},\\&X_h^0=\{\varvec{v}\in V_h^*\ \vert \, \rho _i^h(\varvec{v})=\varvec{0},\, i=2,3\}. \end{aligned}$$

Now, let \(J_2^h: X_h\rightarrow \mathbb {R}\) be the functional given by

$$J_{2}^{h} (v) = \left\langle {\rho _{1}^{h} \left( v \right) - \rho _{1}^{h} \left( {\sigma _{1}^{h} } \right)} \right\rangle _{{M_{1} ,3}}^{1} + \varepsilon \left| v \right|_{{2,H_{h} }}^{2}$$

Problem 2 We consider the following minimization problem: Find \(\varvec{\sigma }_2^h\in X_h\) such that

$$\begin{aligned} \forall \,\varvec{v}\in X_h,\ J_2^h(\varvec{\sigma }_2^h) \le J_2^h(\varvec{v}). \end{aligned}$$
(11)

Proposition 2

Problem (11) has a unique solution that is characterized as the unique solution of the following variational problem: Find \(\varvec{\sigma }_2^h\in X_h\) such that

$$\begin{aligned} \forall \, \varvec{v}\in X_h^0,\ \langle \rho _1^h(\varvec{v}),\rho _1^h(\varvec{\sigma }_2^h)\rangle _{M_1,3}+\varepsilon (\varvec{v},\varvec{\sigma }_2^h)_{2,H_h}=\langle \rho _1^h(\varvec{v}),\rho _1^h(\varvec{\sigma }_1^h)\rangle _{M_1,3}. \end{aligned}$$
(12)

Proof

We consider the application \(\tilde{a}: X_h\times X_h\rightarrow \mathbb {R}\) given by

$$\begin{aligned} \tilde{a}(\varvec{u},\varvec{v})=2\left( \langle \rho _1^h(\varvec{u}),\rho _1^h(\varvec{v})\rangle _{M_1,3}+\varepsilon (\varvec{u},\varvec{v})_{2,H_h}\right) . \end{aligned}$$

Obviously this is a bilinear and symmetric form in \(X_h\). It is easily to prove that \(\tilde{a}\) is continuous and \(X_h\)-coercive taking into account that the application

$$\begin{aligned} \varvec{v}\rightarrow [[\varvec{v}]]=\left( \langle \rho _1^h(\varvec{v})\rangle ^2_{M_1,3}+\varepsilon \vert \varvec{v}\vert _{2,H_h}^2\rangle )\right) ^{\frac{1}{2}} \end{aligned}$$

defines a norm in \(X_h\) which is equivalent to the usual norm \(\Vert \,\cdot \,\Vert _{H_h}\).

Let \(\varphi (\varvec{v})=2\left( \langle \rho _1^h(\varvec{v}),\rho _1^h(\varvec{\sigma }_1^h)\rangle _{M_1,3}\right)\), which is clearly a continuous and linear application.

So, by applying Stampacchia Theorem (see [5]), we conclude that there exists a unique \(\varvec{\sigma }_2^h\in X_h\) such that \(\tilde{a}(\varvec{\sigma }_2^h,\varvec{\omega }-\varvec{\sigma }_2^h)\ge \varphi (\varvec{\omega }-\varvec{\sigma }_2^h)\), for all \(\varvec{\omega }\in X_h\), which implies that \(\tilde{a}(\varvec{\sigma }_2^h,\varvec{v})\ge \varphi (\varvec{v})\), for all \(\varvec{v}\in X_h^0\),

Taking into account that \(X_h^0\) is a linear subspace, if \(\varvec{v}\in X_0^h\) then \(-\varvec{v}\in X_0^h\) and thus \(\tilde{a}(\varvec{\sigma }_2^h,-\varvec{v})\ge \varphi (-\varvec{v})\). From this we obtain that \(\tilde{a}(\varvec{\sigma }_2^h,\varvec{v})=\varphi (\varvec{v})\), for any \(\varvec{v}\in X_h^0\).

Furthermore, \(\varvec{\sigma }_2^h\) is the minimum in \(X_h\) of the functional \(\displaystyle \Phi (\varvec{v})=\frac{1}{2} \tilde{a}(\varvec{v},\varvec{v})-\varphi (\varvec{v})\), which is the minimum of \(J_2\) in \(X_h\) since \(\Phi (\varvec{v})=J_2(\varvec{v})-\langle \rho _1^h(\varvec{\sigma }_1^h)\rangle _{M_1,3}\).

Hence, we conclude the result. \(\square\)

Proposition 3

There exists \((\varvec{\sigma }_2^h,\varvec{\lambda }_1,\varvec{\lambda }_2)\in X_h\times \mathbb {R}^{M_2,3} \times \mathbb {R}^{M_3,3}\) such that

$$\begin{aligned} \begin{array}{l} \displaystyle \langle \rho _1^h(\varvec{\sigma }_2^h),\rho _1^h (\varvec{v})\rangle _{M_1,3}+\varepsilon (\varvec{\sigma }_2^h,\varvec{v})_{2,X_h}+\langle \rho _2^h(\varvec{v}),\varvec{\lambda }_1\rangle _{M_2,3}+\\ \displaystyle \langle \rho _3^h(\varvec{v}),\varvec{\lambda }_2\rangle _{M_3,3}=\langle \rho _1^h(\varvec{\sigma }_1^h),\rho _1^h(\varvec{v})\rangle _{M_1,3} \end{array} \end{aligned}$$
(13)

Proof

Let us denote by \(\{\varvec{\omega }_1^h,\ldots ,\varvec{\omega }_{M_2}^h\}\) the basis functions of \(X_h\) associate to the degrees of freedom \(\{v(\varvec{c}_i)\, \vert \, i=1,\ldots , M_2\}\) and by \(\{\varvec{\omega }_{M_2+1}^h,\ldots ,\varvec{\omega }_{M_2+M_3}^h\}\) the basis functions of \(X_h\) associate to the degrees of freedom \(\displaystyle \{\frac{\partial \varvec{v}}{\partial \varvec{n}}(\varvec{d}_{j})\,\vert \, j=1,\ldots ,M_3\}\).

For each \(\varvec{v}\in X_h\), let \(\displaystyle \varvec{\omega }=\varvec{v}-\sum _{j=1}^{M_2} \varvec{v}(\varvec{c}_j) \varvec{\omega }_j^h-\sum _{j=1}^{M_3} \frac{\partial \varvec{v}}{\partial \varvec{n}}(\varvec{d}_j)\varvec{\omega }_{M_2+j}^h\). Then \(\omega \in X_h\). Moreover, for any \(k=1,\ldots ,M_2\),

$$\begin{aligned} \varvec{\omega }(\varvec{c}_k)=\varvec{v} (\varvec{c}_k)-\sum _{j=1}^{M_2} \varvec{v}(\varvec{c}_j) \varvec{\omega }_j^h(\varvec{c}_k)-\sum _{j=1}^{M_3} \frac{\partial \varvec{v}}{\partial \varvec{n}}(d_j)\varvec{\omega }_{M_2+j}^h (\varvec{c}_k)=0, \end{aligned}$$

and, for \(k=1,\ldots M_3\), one has

$$\begin{aligned} \frac{\partial \varvec{\omega }}{\partial \varvec{n}}(\varvec{d}_k)=\frac{\partial \varvec{v}}{\partial \varvec{n}} (\varvec{d}_k)-\sum _{j=1}^{M_2} \varvec{v}(\varvec{c}_j)\frac{\partial \varvec{\omega }_j^h}{\partial \varvec{n}} (\varvec{d}_k)-\sum _{j=1}^{M_3} \frac{\partial \varvec{v}}{\partial \varvec{n}}(\varvec{d}_j) \frac{\partial \varvec{\omega }_{M_2+j}^h}{\partial \varvec{n}} (\varvec{d}_k)=0. \end{aligned}$$

So \(\rho _2^h(\varvec{\omega })=\rho _3^h(\varvec{\omega })=0\) and consequently \(\varvec{\omega }\in X_h^0\).

Let \(\varvec{\sigma }_2^h\) the solution of (12). Then we have \(\varvec{\sigma }_2^h \in X_h\) and

$$\begin{aligned} \langle \rho _1^h(\varvec{\sigma }_2^h),\rho _1^h(\varvec{\omega })\rangle _{M_1,3}+\varepsilon (\varvec{\sigma }_2^h,\varvec{\omega })_{2,H_h}=\langle \rho _1^h(\varvec{\omega }),\rho _1^h(\varvec{\sigma }_1^h)\rangle _{M_1,3}. \end{aligned}$$

By linearity we obtain

$$\begin{aligned} \begin{array}{l} \displaystyle \langle \rho _1^h(\varvec{\sigma }_2^h),\rho _1^h(\varvec{v})\rangle _{M_1,3}+\sum _{j=1}^{M_2}\left( \langle \rho _1^h(\varvec{\sigma }_1^h)-\rho _1^h(\varvec{\sigma }_2^h),\rho _1^h(\varvec{\omega }_j\rangle _{M_1,3}+\right. \\ \displaystyle \left. +\varepsilon (\varvec{\sigma }_2^h,\varvec{\omega }_j^h)_{2,H_h}\right) \varvec{v}(\varvec{c}_j)+\sum _{j=1}^{M_3}\left( \langle \rho _1^h(\varvec{\sigma }_1^h)-\rho _1^h(\varvec{\sigma }_2^h),\rho _1^h(\varvec{\omega }_{M_2+j}\rangle _{M_1,3}+\right. \\ \displaystyle \left. +\varepsilon (\varvec{\sigma }_2^h,\varvec{\omega }_{M_2+j}^h)_{2,H_h}\right) \frac{\partial \varvec{v}}{\partial \varvec{n}}(\varvec{d}_j)=\langle \rho _1^h(\varvec{\sigma }_1^h),\rho _1^h(\varvec{v})\rangle _{M_1,3}. \end{array} \end{aligned}$$

If we denote by

$$\begin{aligned} \begin{array}{l} \displaystyle \varvec{\lambda }_1=\left( \langle \rho _1^h(\varvec{\sigma }_1^h)-\rho _1^h(\varvec{\sigma }_2^h)\rangle _{M_1,3}+\varepsilon (\varvec{\sigma }_2^h,\varvec{\omega }_j^h)_{2,H_h}\right) _{1\le j\le M_2},\\ \displaystyle \varvec{\lambda }_2=\left( \langle \rho _1^h(\varvec{\sigma }_1^h)-\rho _1^h(\varvec{\sigma }_2^h)\rangle _{M_1,3}+\varepsilon (\varvec{\sigma }_2^h,\varvec{\omega }_j^h)_{2,H_h}\right) _{M_2\le j\le M_2+M_3}, \end{array} \end{aligned}$$

then we conclude that (12) holds.

The uniqueness of \(\varvec{\lambda }_1\) and \(\varvec{\lambda }_2\) is immediate. \(\square\)

4.2 Computing the solution \(\varvec{\sigma }_2^h\)

From the basis \(\{\omega _1,\ldots ,\omega _M\}\) of \(S_2(T_n,T_m)\), let \(\{\omega _1^h,\ldots ,\omega _\mu ^h\}\) be the set of the functions of this basis such that

$$\begin{aligned} \sup (\omega _i^h)\cap H_h\ne \emptyset ,\ i=1,\ldots ,\mu , \end{aligned}$$

and we define

$$\begin{aligned} \forall \, i=1,\ldots ,\mu ,\ \forall \,\ell =1,2,3,\ j=3(i-1)+\ell ,\ \varvec{v}_j^h=\omega _i^h\varvec{j}_\ell . \end{aligned}$$

Then \(\{\varvec{v}_1^h,\ldots ,\varvec{v}_\mu ^h\}\) is a basis of \(V_h^*\).

Thus \(\displaystyle \varvec{\sigma }_2^h=\sum _{i=1}^{\mu } \beta _i \varvec{v}_i^h\), where \(\beta _1,\ldots ,\beta _{\mu }\in \mathbb {R}\) are de coefficients of \(\varvec{\sigma }_2^h\).

Applying Proposition 3, by linearity, this coefficients can be obtained from the unique solution of the linear system

$$\left( {\begin{array}{*{20}c} {\mathcal{A}_{h} \mathcal{A}_{h}^{T} + \varepsilon \mathcal{R};} & {\mathcal{B}_{h} ;} & {\mathcal{D}_{h} } \\ {\mathcal{B}_{h}^{T} ;} & {{\mathbf{0}};} & {\mathbf{0}} \\ {\mathcal{D}_{h}^{T} ;} & {{\mathbf{0}};} & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \beta \\ {\lambda _{1} } \\ {\lambda _{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ {d_{3} } \\ \end{array} } \right),{\text{ }}$$
(14)

where

$$\begin{aligned} \begin{array}{l} \mathcal {A}_h=\mathop {\left( \varvec{v}_i^h(\varvec{b}_j)\right) }\nolimits _ {\begin{array}{c} 1\le i\le \mu \\ 1\le j\le M_1 \end{array}},\\ \mathcal {R} = \left( (\varvec{v}_i^h,\varvec{v}_j^h)_{2,H_h}\right) _{1\le i,j\le \mu },\\ \mathcal {B}_h=\mathop {\left( \varvec{v}_i^h(\varvec{c}_j)\right) }\nolimits _ {\begin{array}{c} 1\le i\le \mu \\ 1\le j\le M_2 \end{array}},\\ \displaystyle \mathcal {D}_h=\mathop {\left( \frac{\partial \varvec{v}_i^h}{\partial \varvec{n}}(\varvec{d}_j)\right) }\nolimits _{\begin{array}{c} 1\le i\le \mu \\ 1 \le j \le M_3 \end{array}},\\ \varvec{\beta }=(\beta _1,\ldots ,\beta _{\mu })^T,\\ \varvec{d}_1=\left( \langle \rho _1^h(\varvec{v}_i^h),\rho _1^h(\varvec{\sigma }_1^h)\rangle _{M_1,3}\right) _{1\le i\le \mu },\\ \varvec{d}_2=\left( \varvec{\sigma }_1^h(\varvec{c}_i)\right) _{1\le i\le M_2},\\ \displaystyle \varvec{d}_3=\left( \frac{\partial \varvec{\sigma }_1^h}{\partial \varvec{n}}(\varvec{d}_i)\right) _{1\le i\le M_3}. \end{array} \end{aligned}$$

Remark 2

Observe that for computing the solution of (14) only the values of \(\varvec{\sigma }_1^h\) on \(H_h\) and its normal derivative on the boundary of \(H_h\) are neccesary.

5 The solution of the problem

Definition 1

We define the smoothing parametric biquadratic spline function filling holes of \({\varvec{f}}\vert _{R-H_h}\) in \(V_h\) associated with \(A_N\) and \(\varepsilon\) as the function

$$\begin{aligned} \varvec{\sigma }^h(\varvec{x})=\left\{ \begin{array}{l} \varvec{\sigma }_1^h(\varvec{x}),\ \varvec{x}\in R-H_h,\\ \varvec{\sigma }_2^h(\varvec{x}),\ \varvec{x}\in H_h. \end{array} \right. \end{aligned}$$

By construction it is verified that \(\varvec{\sigma }\in V_h\).

6 Numerical and graphical examples

To test the effectiveness of our method we suppose that the initial surface parameterized by the function \(\varvec{f}:\; R=(0,1)\times (0,1)\rightarrow \mathbb {R}^3\) is given by

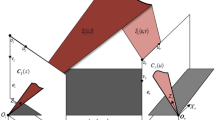
$$\begin{aligned} {\varvec{f}}(x,y)=\left( y\cos \left( \frac{1}{2}(2\pi x-3\pi )\right) , y\sin \left( \frac{1}{2}(2\pi x-3\pi )\right) ,x\right) . \end{aligned}$$

We consider a hole H that is the close of the interior of the ellipses \(25(x-0.35)^2+150(y-0.75)^2=1\) and \(150(x-0.75)^2+35(y-0.3)^2=1\) and the surface with these holes parameterized by \({\varvec{f}}\vert _{R-H}\) (see Fig. 1 left side).

Given the variable distances defined by \(d_1(x,y)=0.2\sin (0.5(x-y)^2+0.3)\), \(d_2(x,y)=0.2(\sin (0.5(x-y)^2+0.3)\) and \(d_3(x,y)=-0.2\cos (0.2\cos (0.5(x-y)^2+0.3)\), we consider the corresponding generalized offset surface with holes \(\displaystyle \varvec{s}_{\varvec{f}}\vert _{R-H}\) (see Fig. 1 right side).

Fig. 1
figure 1

Graph of the initial surface parameterized by \(\varvec{f}\) and the generalized offset surface parameterized by \(\varvec{s}_{\varvec{f}}\), on the left side, and both with holes, on the right side)

Full size image

First, we start with a graphical example. For this, from a partition \(\mathcal {T}_h\) of \(8\times 8\) equal squares, i.e. \(9\times 9\) knots, we construct the approximated hole \(H_h\) (see Fig. 2 left side) and we take a set \(A_N\) of \(k(N)=500\) random points in the closed set of \(R-H\) (see Fig. 2 right side).

Fig. 2
figure 2

Hole H and the approximated hole \(H_h\) (thick black) from a partition of the domain in \(8\times 8\) equal squares, on the left, and \(N=500\) random approximation points in \(\bar{R-H}\), on the right

Full size image

Second, we compute the smoothing parametric biquadratic spline in \(V_h\) associated with \(A_N\), \(\rho ({\varvec{s}}_{\varvec{f}})\) and \(\varepsilon =10^{-9}\), called \(\varvec{\sigma }_1^h\), and an estimation of the relative \(L^2\)-error given by the number

$${\text{Error}}_{1} = \sqrt {\frac{{\sum\limits_{{i = 1}}^{{5000}} {\left( {\sigma _{1}^{h} \left( {\xi _{i} - s_{f} (\xi _{i} )} \right)} \right)^{2} } }}{{\sum\limits_{{i = 1}}^{{5000}} {\left( {s_{f} \left( {\xi _{i} } \right)} \right)^{2} } }}} ,{\text{ }}$$

where \(\{\xi _1,\ldots ,\xi _{5000}\}\) is a set of 5000 random points of the closed set of \(R-H_h\).

Fig. 3 shows the original surfaces parameterized by the functions \(\varvec{f}\vert _{R-H_h}\) and \(\varvec{s}_{\varvec{f}}\vert _{R-H_h}\), on the left side, and the approximated generalized offset surfaces parameterized by \(\varvec{\sigma }_1^h\), on the right side, from bottom to top in both cases. The obtained estimated relative error is \(Error_1=2.7695\times 10^{-4}\).

Fig. 3
figure 3

Original surface with the approximated hole (\(\varvec{f}\vert _{R-H_h}\)) and its generalized offset surface (\(\varvec{s}_{\varvec{f}}\vert _{R-H_h}\)), left side, and its approximated generalized offset surfaces parameterized by (\(\varvec{\sigma }_1^h\)) for \(\varepsilon =10^{-9}\), right side, from bottom to top in both cases. \(Error_1=2.7695\times 10^{-4}\)

Full size image

Third, we compute the smoothing parametric biquadratic spline function in \(V_h\vert _H\) associated with \(H_h\), \(\rho _i\varvec{\sigma }_1^h\), for \(i=1,2,3\), and \(\varepsilon =10^{-9}\), denoted by \(\varvec{\sigma }_2^h\).

Fourth, we compute the smoothing parametric biquadratic spline function filling holes of \(\varvec{f}\) in \(V_h\) associated with \(A_N\) and \(\varepsilon =10^{-9}\), denoted by \(\varvec{\sigma }^h\) and an estimation of the relative \(L^2\)-error given by the number

$${\text{Error}} = \sqrt {\frac{{\sum\limits_{{i = 1}}^{{5000}} {\left( {\sigma ^{h} \left( {\xi _{i} } \right) - s_{f} \left( {\xi _{i} } \right)} \right)^{2} } }}{{\sum\limits_{{i = 1}}^{{5000}} {\left( {s_{f} \left( {\xi _{i} } \right)} \right)^{2} } }}} ,{\text{ }}$$

where \(\{\xi _1,\ldots ,\xi _{5000}\}\) is a set of 5000 random points of R.

Fig. 4 shows the original surface with the approximated hole parameterized by \(\varvec{f}\vert _{R-H}\) and its approximated generalized offset surface filling hole, parameterized by the smoothing parametric biquadratic spline filling hole function \(\varvec{\sigma }^h\), from bottom to top. The obtained estimated relative error is \(Error=2.7216\times 10^{-4}\).

Fig. 4
figure 4

Original surface with the approximated hole, parameterized by \(\varvec{f}\vert _{R-H}\) and its approximated generalized offset filling hole, parameterized by the smoothing parametric biquadratic spline filling hole function \(\varvec{\sigma }^h\), from bottom to top. \(Error=2.7216\times 10^{-4}\)

Full size image

Finally, Table 1 shows the estimated relative errors \(Error_1\) and Error from the different values of the parameters of the problem \(n=m\), k(N) and \(\varepsilon\).

Table 1 Function f(x, y). The estimated relative errors \(Error_1\) and Error from different values of the parameters of the problem \(n=m\), k(N) and \(\varepsilon\)
Full size table

Reflection and conclusion.

In the introduction we have cited and talked a bit about various references in the literature that have dealt with the problem of holes with various methods and extended techniques to fill these holes, our idea here was to present a comparison with these works, but due to the originality of our work we believe that such a comparison cannot be made. In fact, no paper presents the offset problem, even our extended method for filling holes is different. The complexity of our work translates into mixing two approximation methods, the first is offset and the second is filling holes. Studying these criteria together is not so easy.

It should be noted that approach approximation method of this paper is made with the biquadratic splines functions that are of class 1, while for example in [2] it is done with the bi-cubic splines that are of class 2. This clearly shows that the degree of approximation in this work has been significantly reduced. Moreover, from Table 1, one can observe that as the data points increases the estimation of the error decreases, and also when the value of the parameter \(\varepsilon\) decreases the estimation of the error decreases, hence we can conclude the compatibility between the theory of the convergence result and the numerical ones. In short, we can conclude form the study of the table, where several data of the problem appear, and figures the effectiveness of our algorithm as an approximation method.

As an open research for the future is the possibility of extending the manuscript to find some numerical application directly or indirectly with chemistry.