Solving linear unbranched pathways with Michaelis–Menten kinetics using the Lambert W-function

Abstract

In this paper, an n-step, linear and unbranched pathway with Michaelis–Menten kinetics is solved in a quasi-analytical way. The method, based on the optimal control theory, calculates the optimal enzyme concentrations while minimizing the operation time. In the computation of the solution, the Lambert W-function plays a fundamental role, due to the presence of a non-linear kinetic model. Our method allows us to obtain the generalized solution and to perform the sensitivity analysis of the catalytic parameters.

Appendices

Appendix 1: Proof of Theorem 2.

We now prove that the solution obtained using Pontryagin’s Minimum Principle is effectively a solution of our problem. In (22), we have $F=1$, $B=1$ and the Hamiltonian H is:

$$\begin{aligned} H= & {} 1+\lambda _{1}\left[ -\dfrac{k_{1}x_{1}}{K_{m1} + x_{1}} u_{1}\right] +\lambda _{2}\left[ \dfrac{k_{1}x_{1}}{K_{m1}+x_{1}} u_{1}-\dfrac{k_{2}x_{2}}{K_{m2}+x_{2}}u_{2}\right] \nonumber \\&+\cdots +\lambda _{n}\left[ \dfrac{k_{n-1}x_{n-1}}{K_{mn-1}+x_{n-1}} u_{n-1}-\dfrac{k_{n}x_{n}}{K_{mn}+x_{n}}u_{n}\right] \end{aligned}$$

(32)

which is autonomous, so that $H_{t}\equiv 0\Rightarrow H(t)=ct$. This condition together with (iv) implies that $H(t)=0$. Now the optimality condition (ii) leads to:

$$\begin{aligned} \underset{\mathbf {u}\in U}{\min }H=\underset{\mathbf {u}\in U}{\min }\left\{ -\sum _{i=1}^{n}\frac{k_{i}(\lambda _{i}-\lambda _{i+1})x_{i}}{K_{mi}+x_{i}} u_{i}\right\} =\underset{\mathbf {u}\in U}{\min }\left\{ -\sum _{i=1}^{n} \mu _{i}u_{i}\right\} \end{aligned}$$

(33)

with $\lambda _{n+1}=0$. According to the optimality condition (i), we have:

$$\begin{aligned} \overset{\cdot }{\lambda }_{i}=k_{i}K_{mi}(\lambda _{i}-\lambda _{i+1})\frac{u_{i}}{(K_{mi}+x_{i})^{2}}; \quad (i=1,\ldots ,n) \end{aligned}$$

(34)

It is known from (33) that the control $u_{i}$ is activated when the switching function $\mu _{i}$ reaches its maximum. Moreover, when this happens, the coefficient $\mu _{i}$ must be positive, because otherwise $u_{i}=0$. Hence, it follows that $\lambda _{i}$ is decreasing. From (33):

$$\begin{aligned} \mu _{i}=\frac{k_{i}(\lambda _{i}-\lambda _{i+1})x_{i}}{K_{mi}+x_{i}} \ge 0\Rightarrow \lambda _{i}\ge \lambda _{i+1} \end{aligned}$$

(35)

We obtain the optimal solution constructively by intervals, starting at $t=0$ and concatenating the results. This procedure will prove essential in order to obtain a simple solution to the problem. We shall also see that using the following condition in (22):

$$\begin{aligned} U(t)=\{\mathbf {u}\in {\mathbb {R}}^{n} \vert u_{1}\ge 0,\ldots , u_{n}\ge 0; \quad u_{1}+\cdots +u_{n}\le 1\} \end{aligned}$$

(36)

we are not going to require either the final condition (i) $\lambda _{i}^{*}(t_{f}^{*})=0$ for the costate variables, or the transversality condition (iv) $H(t)=0$. As a matter of fact, we shall see that it will not be necessary to compute $\lambda _{i}^{*}$, so that we shall not compute H(t) either.

(1) Interval: $\left[ 0,t_{1}\right]$.

We reason by contradiction. Assume that $u_{1}=0$. From (19):

$$\begin{aligned} \left. \begin{array}{l} \dot{x}_{1}=-\dfrac{k_{1}x_{1}}{K_{m1}+x_{1}}u_{1}=0\\ x_{1}(0)=1 \end{array} \right\} \Rightarrow x_{1}(t)=1, \quad \forall t \end{aligned}$$

(37)

and the product would not be produced. Hence, we have $u_{1}=1$ and from condition (36) we get:

$$\begin{aligned} u_{i}=0, \quad i=2,\ldots ,n \end{aligned}$$

(38)

Once the optimal values for the enzymes are computed, we can solve now (19):

(39)

In Appendix 2 we give the details of the solution. In order to generalize the formula, it is interesting to use the following notation: we denote by $x_{ji}(t)$ the concentration of j-metabolite in the i-interval $[t_{i-1},t_{i}],$ $i=1,\ldots ,n$, with $x_{10}(t_{0})=1$. So, we have:

$$\begin{aligned} \begin{array}{l} x_{11}(t)=K_{m1}W\left( \frac{x_{10}(t_{0})}{K_{m1}} e^{\frac{x_{10}(t_{0})}{K_{m1}}}e^{-\frac{k1}{K_{m1}}(t-t_{0})}\right) \\ x_{21}(t)=1-x_{11}(t)\\ x_{i1}(t)=0; \quad i=3,\ldots ,n \end{array} \end{aligned}$$

(40)

From (34), the following holds:

$$\begin{aligned} \overset{\cdot }{\lambda }_{1}=\frac{k_{1}K_{m1}(\lambda _{1}-\lambda _{2} )}{(K_{m1}+x_{1})^{2}}; \quad \overset{\cdot }{\lambda }_{i}=0, \quad i=2,\ldots ,n \end{aligned}$$

(41)

From (33) and (19), after some elementary computations and substituting $\dot{\lambda }_{1}$ and $\dot{x}_{1}$ by their values, we get

$$\begin{aligned} \mu _{1}=\frac{k_{1}(\lambda _{1}-\lambda _{2})x_{1}}{K_{m1}+x_{1}} \Rightarrow \overset{\cdot }{\mu }_{1}=\frac{k_{1}(\dot{\lambda }_{1}-\dot{\lambda }_{2})x_{1}}{K_{m1}+x_{1}}+\frac{k_{1}(\lambda _{1}-\lambda _{2})\dot{x}_{1}}{\left( K_{m1}+x_{1}\right) ^{2}}=0 \end{aligned}$$

(42)

On the other hand:

$$\begin{aligned} \mu _{2}=\frac{k_{2}(\lambda _{2}-\lambda _{3})x_{2}}{K_{m2}+x_{2}} \Rightarrow \dot{\mu }_{2}=\frac{k_{2}(\lambda _{2}-\lambda _{3})K_{m2}}{\left( K_{m2}+x_{2}\right) ^{2}}\frac{k_{1}}{K_{m1}+x_{1}}x_{1}\ge 0 \end{aligned}$$

(43)

So that

$$\begin{aligned} \begin{array}{lll} \overset{\cdot }{\mu }_{1}=0 &{} \Rightarrow &{} \mu _{1}=ct\\ \overset{\cdot }{\mu }_{2}\ge 0 &{} \Rightarrow &{} \mu _{2}=\text {increasing}\\ \mu _{i}=0 &{} \Rightarrow &{} \mu _{i}=0; \quad i=3,\ldots ,n \end{array} \end{aligned}$$

(44)

(2) Interval: $\left[ t_{1},t_{2}\right] .$

With a reasoning analogue to the one used for the first interval:

$$\begin{aligned} u_{1}=0, \quad u_{2}=1; \quad u_{i}=0, \quad (i=3,\ldots ,n) \end{aligned}$$

(45)

and:

(46)

which gives:

$$\begin{aligned} \overset{\cdot }{\lambda }_{1}=0; \quad \overset{\cdot }{\lambda }_{2} =\frac{k_{2}K_{m2}(\lambda _{2}-\lambda _{3})}{(K_{m2}+x_{2})^{2}}; \quad \overset{\cdot }{\lambda }_{i}=0, \quad i=3,\ldots ,n \end{aligned}$$

(47)

and performing the adequate substitutions, one proves that:

$$\begin{aligned} \begin{array}{lll} \overset{\cdot }{\mu }_{1}\le 0 &{} \Rightarrow &{} \mu _{1}=\text {decreasing} \\ \overset{\cdot }{\mu }_{2}=0 &{} \Rightarrow &{} \mu _{2}=ct\\ \overset{\cdot }{\mu }_{3}\ge 0 &{} \Rightarrow &{} \mu _{3}=\text {increasing} \\ \mu _{i}=0 &{} \Rightarrow &{} \mu _{i}=0; \quad i=4,\ldots ,n \end{array} \end{aligned}$$

(48)

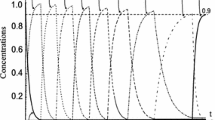
In Fig. 7, the behavior of the switching functions is shown.

Fig. 7

Illustration of the behavior of the switching functions

The values for each successive interval are similarly obtained, by concatenating the solutions. For the sake of simplicity, we present only the solution for the last one.

(n) Interval: $[t_{n-1},t_{f}]$.

In this case:

$$\begin{aligned} u_{i}=0, \quad (i=1,\ldots ,n-1); \quad u_{n}=1 \end{aligned}$$

(49)

$$\begin{aligned} \begin{array}{lll} \left. \begin{array}{l} \dot{x}_{i}=0\\ x_{i}(t_{n-1})=x_{ii}(t_{i}) \end{array} \right\}\Rightarrow & {} x_{in}(t)=x_{ii}(t_{i}); \quad i=1,\ldots ,n-1 \end{array} \end{aligned}$$

(50)

and

$$\begin{aligned}&\left. \begin{array}{l} \dot{x}_{n}=-\dfrac{k_{n}x_{n}}{K_{mn}+x_{n}}\\ x_{n}(t_{n-1})=x_{nn-1}(t_{n-1}) \end{array} \right\} \Rightarrow \nonumber \\&\quad \Rightarrow x_{nn}(t)=K_{mn}W\left( \frac{x_{nn-1}(t_{n-1})}{K_{mn}} e^{\frac{x_{nn-1}(t_{n-1})}{K_{mn}}}e^{-\frac{k_{n}}{K_{mn}}(t-t_{n-1} )}\right) \end{aligned}$$

(51)

$$\begin{aligned} \begin{array}{lll} \overset{\cdot }{\mu }_{i}=0 &{} \Rightarrow &{} \mu _{2}=ct; \quad i=1,\ldots ,n-2\\ \overset{\cdot }{\mu }_{n-1}\le 0 &{} \Rightarrow &{} \mu _{n-1} =\text {decreasing}\\ \mu _{n}=0 &{} \Rightarrow &{} \mu _{n}=ct \end{array} \end{aligned}$$

(52)

Once the optimum values for $x_{i}^{*}$ and $u_{i}^{*}$ have been obtained, it is still required to compute the values of the following unknowns: the switching times $t_{1},t_{2},\dots ,t_{n-1}$ and the operation time $t_{f}$. In order to do so, we use the restriction (21) which we have not used yet. The simplest way is to apply the Lagrange multipliers to the augmented functional:

$$\begin{aligned} L(t_{1},t_{2},\ldots ,t_{n-1},t_{f},\beta )=t_{f}+\beta (x_{1n}(t_{f} )+x_{2n}(t_{f})+\cdots +x_{nn}(t_{f})-C_{f}) \end{aligned}$$

(53)

where the values of the concentrations $x_{1n}(t_{f}),x_{2n}(t_{f} ),\ldots ,x_{nn}(t_{f})$ are given by (24), (25) and (26), and in which one sees that the unknowns $t_{1},t_{2},\dots ,t_{n-1}$ appear. We need to solve the non-linear system:

$$\begin{aligned} \frac{\partial L}{\partial t_{1}}=0;\frac{\partial L}{\partial t_{2}} =0;\ldots ;\frac{\partial L}{\partial t_{n-1}}=0;\frac{\partial L}{\partial t_{f}}=0;\frac{\partial L}{\partial \beta }=0 \end{aligned}$$

(54)

which can be done with any computer algebra software. This is the only part of the solution which is not carried out analytically, whence our calling it “quasi-analytical.” Now the problem is completely solved.

Appendix 2: Solution of the state equations

In order to shed some light on the solution of the state equations, we carry it out completely for the case of the interval $[0,t_{1}]$. First, we solve the differential equation for $x_{1}(t)$:

$$\begin{aligned} \frac{dx_{1}}{dt}=-\dfrac{k_{1}x_{1}}{K_{m1}+x_{1}}\Rightarrow \left( \frac{K_{m1}}{x_{1}}+1\right) dx_{1}=-k_{1}dt \end{aligned}$$

(55)

Integrating:

$$\begin{aligned} K_{m1}\ln x_{1}+x_{1}=-k_{1}t+C \end{aligned}$$

(56)

Imposing the initial condition $x_{1}(0)=1$, we get $C=1$, so that

$$\begin{aligned} K_{m1}\ln x_{1}+x_{1}=-k_{1}t+1\Rightarrow \ln x_{1}+\frac{x_{1}}{K_{m1} }=-\frac{k_{1}}{K_{m1}}t+\frac{1}{K_{m1}} \end{aligned}$$

(57)

By exponentiation:

$$\begin{aligned} e^{\ln x_{1} + \frac{x_{1}}{K_{m1}}} = e^{\frac{1}{K_{m1}} - \frac{k_{1}}{K_{m1}} t}\Rightarrow x_{1} e^{\frac{x_{1}}{K_{m1}}} = e^{\frac{1}{K_{m1}}-\frac{k_{1} }{K_{m1}}t} \end{aligned}$$

(58)

Dividing by $K_{m1}$:

$$\begin{aligned} \frac{x_{1}}{K_{m1}}e^{\frac{x_{1}}{K_{m1}}}=\frac{1}{K_{m1}}e^{\frac{1}{K_{m1}}-\frac{k_{1}}{K_{m1}}t} \end{aligned}$$

(59)

And from the definition of the Lambert W-function

$$\begin{aligned} x=W(x)e^{W(x)} \end{aligned}$$

(60)

we get:

$$\begin{aligned} x_{1}(t)=K_{m1}W\left( \frac{1}{K_{m1}}e^{\frac{1}{K_{m1}}}e^{-\frac{k1}{K_{m1}}t}\right) \end{aligned}$$

(61)

In order to obtain the closed form expression for $x_{2}(t)$, instead of integrating

$$\begin{aligned} \dot{x}_{2}=\dfrac{k_{1}x_{1}}{K_{m1}+x_{1}}; \quad x_{2}(0)=0 \end{aligned}$$

(62)

it is much easier to realize that

$$\begin{aligned} \dot{x}_{1}+\dot{x}_{2}=0 \end{aligned}$$

(63)

from which follows, immediately, that

$$\begin{aligned} x_{1}(t)+x_{2}(t)=c\Rightarrow x_{1}(0)+x_{2}(0)=c\Rightarrow c=1 \end{aligned}$$

(64)

so that we get the recurrence relation:

$$\begin{aligned} x_{1}(t)+x_{2}(t)=1\Rightarrow x_{2}(t)=1-x_{1}(t) \end{aligned}$$

(65)

And one proceeds similarly for the remaining intervals.