Kirchhoff index of periodic linear chains

Abstract

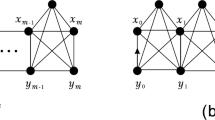
A periodic linear chain consists of a weighted $2n$-path where new edges have been added following a certain periodicity. In this paper, we obtain the effective resistance and the Kirchhoff index of a periodic linear chain as non trivial functions of the corresponding expressions for the path. We compute the expression of the Kirchhoff index of any homogeneous and periodic linear chain which generalizes the previously known results for ladder-like and hexagonal chains, that correspond to periods one and two respectively.

Appendix

If for any $k\in \mathbb {Z},\, T_k$ and $U_k$ are the $k$th Chebyshev polynomials of first and second kind respectively, see [4], it is well-known that for any sequence of Chebyshev polynomials $\{P_k\}_{k\in \mathbb {Z}}$; that is, polynomials satisfying the recurrence relation $P_{k+2}(z)=2zP_{k+1}(z)-P_k(z),\, k\in \mathbb {Z}$, there exist $A,B\in \mathbb {R}$ such that $P_k=AT_k+BU_{k-1}$ for any $k\in \mathbb {Z}$. Moreover, as $q=1+c^{-1}ap>1$, since the values

$$\begin{aligned} \alpha&= q+\sqrt{q^2-1}=c^{-1}\big (ap+c+\sqrt{ap(ap+2c}\,\big ) \nonumber \\ \beta&= q-\sqrt{q^2-1}=c^{-1}\big (ap+c-\sqrt{ap(ap+2c}\,\big ) \end{aligned}$$

(5)

are the roots of the polynomial $x^2-2qx+1$, each Chebyshev sequence can be expressed as a linear combination of the sequences $\{\alpha ^k\}_{k\in \mathbb {Z}}$ and $\{\beta ^k\}_{k\in \mathbb {Z}}$. Specifically, it is also well-known, see newly [4], that

$$\begin{aligned} T_k(q)=\dfrac{1}{2}\big (\alpha ^k+\beta ^k\big )\quad \hbox {and}\quad U_{k}(q)=\dfrac{1}{\alpha -\beta }\big (\alpha ^{k+1}-\beta ^{k+1}\big ),\quad k\in \mathbb {Z}, \end{aligned}$$

(6)

which in particular implies that $T_k(q)>0$ for any $k\in \mathbb {Z}$ and $U_k(q)>0$ for any $k\in \mathbb {N}$, since $0<\beta <1<\alpha$ (and $\alpha \beta =1$).

Lemma 1

For any $k\in \mathbb {Z}$ the following identities hold:

$$\begin{aligned} T_{k\pm 1}(q)=qT_k(q)\pm (q^2-1)U_{k-1}(q)\qquad \hbox {and}\qquad U_k(q)=T_k(q)+qU_{k-1}(q). \end{aligned}$$

Moreover

$$\begin{aligned} U_k(q)U_m(q)=\dfrac{1}{2(q^2-1)}\big [T_{k+m+2}(q)-T_{k-m}(q)\Big ],\quad k,m\in \mathbb {Z}\end{aligned}$$

and given $m\ge 1$,

$$\begin{aligned} \sum \limits _{k=1}^mT_{m-2k}(q)&= \sum \limits _{k=1}^mT_{m+2-2k}(q) = qU_{m-1}(q),\\ \sum \limits _{k=1}^mT_{m+1-2k}(q)&= U_{m-1}(q)\\ \sum \limits _{k=1}^mT_{m-1-2k}(q)&= \big (2(q^2-1)+1\big )U_{m-1}(q). \end{aligned}$$

Lemma 2

If $\{P_k(q)\}_{k\in \mathbb {Z}}$ is a Chebyshev sequence, then for any $A,B\in \mathbb {R}$, and $r,t\in \mathbb {N}^*$ such that $t\le r$

$$\begin{aligned} \displaystyle \sum \limits _{k=t}^r(A k+B)P_{k}(q)&= \dfrac{c}{2pa}(A r+B)\big (P_{r+1}(q)-P_r(q)\big ) \\&\quad -\, \dfrac{c}{2pa}(A t+B)\big (P_{t}(q)-P_{t-1}(q)\big )+ \dfrac{cA}{2pa}\big (P_{t}(q)-P_r(q)\big ). \end{aligned}$$

The following relations between the polynomials defined in (4), are very useful throughout the paper. All of them are consequence of Lemma 1.

Lemma 3

For any $m\in \mathbb {Z}$ we have

$$\begin{aligned} cT_{h}(q)+a(p+1)U_{h-1}(q)&= aQ_{h-m}(q)U_{m-1}(q) \\&\quad +\, \dfrac{c}{2p}V_{m-1}(q)\Big [Q_{h-m}(q)-Q_{h-m-1}(q)\Big ]. \end{aligned}$$

In addition,

$$\begin{aligned} \displaystyle \sum \limits _{\ell =1}^h U_{\ell -1}(q)Q_{h-\ell }(q)&= \dfrac{1}{2a(ap+2c)}\big [p_1T_{h}(q)+p_2U_{h-1}(q)\big ],\\ \sum \limits _{\ell =1}^h U_{\ell -1}(q)Q_{h-\ell -1}(q)&= \dfrac{1}{2a(ap+2c)}\big [p_3T_{h}(q)+p_4U_{h-1}(q)\big ]\\ \sum \limits _{\ell =1}^h V_{\ell -1}(q)Q_{h-\ell }(q)&= \dfrac{1}{(ap+2c)}\big [p_5T_h(q)+p_6U_{h-1}(q)\big ],\\ \sum \limits _{\ell =1}^h V_{\ell -1}(q)Q_{h-\ell -1}(q)&= \dfrac{1}{c(ap+2c)}\big [p_7T_{h}(q)+p_8U_{h-1}(q)\big ] \end{aligned}$$

where,