1 Introduction

The decay energy spectrometry (DES) project at NIST is intended to provide a direct, absolute, and complete assay of small quantities of radionuclides, with applications in security, environment monitoring, medicine, and electronics [1]. By using a superconducting transition edge sensor (TES) to measure the thermal energy of individual decay events with high energy resolution (resolving power ≥ 1000 at 5 MeV), DES provides a unique fingerprint to identify each radionuclide in a sample. Here, a deep-etched silicon structure is used to form the thermal link between the TES-island sensing element and the TES-frame connected to the thermal bath. Compared to a thin membrane construction, this approach makes the chip easier to fabricate and more robust for handling [2]. The TES characterization is motivated by radiation sensing applications that require high stopping power. For decay energy measurements, we use an approximately 0.5 mm3 gold foil absorber containing embedded radionuclides. This foil is attached to the TES absorber pad, with an indium microsphere that is compressed to achieve thermal contact. The decay times of pulses from Am-241 sources collected with this system were longer than expected, suggesting low electro-thermal feedback, which may be caused by insufficient thermal link between TES-frame and bath. We believe that the high energy of DES pulses (≈ 1 pJ) compared to x-ray applications (< 0.02 pJ) contributes to the challenge. Achieving pulses faster than 50 ms with the higher energy absorbed in each pulse requires a higher thermal conductance from island to frame and a correspondingly higher TES bias power of a few hundred pW. If the thermal link between frame and bath is insufficient, the entire chip will heat up, and pulse height will be reduced in a similar manner as running a well-linked configuration at high bath temperature Tbath.

We use a TES-island heater and a secondary TES located on the TES-frame to measure the thermal resistance from the TES-island to the TES-frame, and from the TES-frame to the bath. We fit a heat flow model to our results, and from this we calculate the TES-frame temperature during device operation and the heat capacity of the TES-island. This characterization method may also be of interest for experiments that use arrays of lower particle energy TESs where the total bias power exceeds 100 pW.

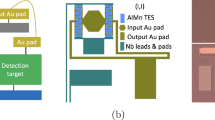
2 Experimental Details

The TES has a Mo-Cu bilayer with Cu normal-metal bars, normal state resistance Rn ≈ 12 mΩ, and transition temperature Tc ≈ 100 mK. The TES is located on an island which is thermally linked to the bath via silicon deep-etched meander structures. The same silicon etch separated the wafer into individual 4.9 mm by 4.9 mm chips. On the TES-island there is an Au-coated Cu pad used for mounting samples, linked thermally to the TES with a trapezoidal shape Cu feature. In the characterization measurements presented below, a “blank” sample, of similar mechanical properties as our DES samples but without radioactive material, is attached. The chip is mounted on an Au-plated Cu surface in a solid Cu enclosure. Small BeCu spring clips placed on the TES-frame provide physical clamping, and gold wire bonds between TES-frame and Cu surface provide thermal connection. The TES-island contains a resistive heater (Cu) with resistance Rheat ≈ 70 mΩ. The TES-frame contains a TES of similar composition to the island TES, Rn ≈ 12 mΩ, and Tc ≈ 100 mK. Two TES chips were installed in a dilution refrigerator with base temperature of \(20\) mK.

As depicted in Fig. 1, TES1 has a higher thermal link conductivity from TES-island to TES-frame (Gif) compared to TES2. Conversely, the frame of TES2 has a higher thermal conductivity link to the bath compared to TES1. Therefore, we expect TES1 to operate at a higher TES-frame temperature Tframe than TES2.

Fig. 1
figure 1

Two TES chips with dissimilar thermal configurations for testing the frame temperature. Gif refers to the thermal conductivity between TES-island and TES-frame, set by the length of the silicon etched meander structure. (Color figure online)

Full size image

We use a four-wire technique to measure Rheat and confirm it does not change (within 2 mΩ) over the temperature range of this experiment. Subsequently, we apply a constant current measured with a multimeter, and the heater power is calculated by \({P}_{{\text{heat}}}={I}_{{\text{heat}}}^{2}{R}_{{\text{heat}}}\).

A very low bias current (0.2 µA) is applied to either the island TES or frame TES, which is sufficient to measure the difference between the superconducting and normal state using our DC SQUID readout, without substantially affecting Tc by magnetic or self-heating effects [3]. Iheat is then raised until the transition is observed (sudden decrease in TES current). For a given bath temperature, Iheat to initiate the superconducting to normal transition is repeatable to under 0.5%, and the TES acts as a point thermometer indicating TTES = Tc. Because the TES is not generating heat while superconducting, it is assumed to be in equilibrium with the phonon temperature of the underlying silicon. This measurement is carried out at multiple Tbath. The points (Tbath, Pheat) are plotted and fit by a thermal conduction law (Eq. 1), with (n, k, Tc) being the fit parameters for each TES [4].

$$P_{{{\text{heat}}}} = k\left( {T_{{\text{c}}}^{n} - T_{{{\text{bath}}}}^{n} } \right)$$
(1)

Tbath is varied from 35 to 92 mK, and Pheat to reach Tc is plotted in Fig. 2, along with the results of fitting Eq. (1) to the data. Next, we apply thermal power conservation Eq. (2) to solve for Tframe when the central TES is at Tc, with subscripts i and f referring to the (n, k, Tc) fits for the island and frame TESs, respectively. The results are shown in Fig. 3.

$$k_{{\text{i}}} \left( {T_{{\text{c}}}^{{n_{{\text{i}}} }} - T_{{{\text{bath}}}}^{{n_{{\text{i}}} }} } \right) = k_{{\text{f}}} \left( {T_{{{\text{frame}}}}^{{n_{{\text{f}}} }} - T_{{{\text{bath}}}}^{{n_{{\text{f}}} }} } \right)$$
(2)
Fig. 2
figure 2

Thermal parameter fits. Markers represent measured values, and solid lines represent the power law fit to the data points, with fit parameters indicated in the figure. (Color figure online)

Full size image
Fig. 3
figure 3

Calculated Tframe at varying Tbath, when the island TES is biased in the transition region. Dashed line indicates Tframe = Tbath. (Color figure online)

Full size image

It is also possible to use the heater to determine C, the heat capacity of the TES-island and attached absorber. In this procedure, the (n, k, Tc) values are found as described above, the entire TES is cooled down to Tbath, then a constant Pheat is applied, and tf—the time required to reach Tc—is recorded. The experimental measurement point is (Pheat, tf) for each trial. The system of equations Eq. (3) to Eq. (8) is solved numerically to obtain a best fit for the electron and lattice heat capacity parameters \(\gamma\) and \(\alpha\) (\(\alpha\) is assumed to be zero in our temperature range). With a correct solution, the equations match the observed tf at various Pheat as illustrated in Fig. 4.

$$P_{{{\text{net}}}} \left( t \right) = P_{{{\text{heat}}}} - P_{{{\text{out}}}} \left( t \right)$$
(3)
$$P_{{{\text{out}}}} \left( t \right) = k \cdot \left( {T_{{\text{i}}} \left( t \right)^{n} - T_{{{\text{bath}}}}^{n} } \right)$$
(4)
$$\frac{{dT_{{\text{i}}} \left( t \right)}}{dt} = \frac{{P_{{{\text{net}}}} \left( t \right)}}{{C\left( {T_{{\text{i}}} \left( t \right)} \right)}}$$
(5)
$$C\left( T \right) = \gamma T + \alpha T^{3}$$
(6)
$$\mathop \smallint \limits_{0}^{{t_{f} }} \frac{{{\text{d}}T_{{\text{i}}} \left( t \right)}}{{{\text{d}}t}} \cdot {\text{d}}t = T_{{\text{c}}} - T_{{{\text{bath}}}}$$
(7)
Fig. 4
figure 4

Calculated TES-island temperature with constant Pheat of 377 and 188 pW, matching Tc (dashed line) at the experimentally measured tf (filled circles). (Color figure online)

Full size image

3 Discussion

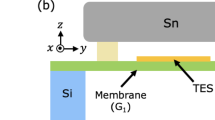
It is observed that even with a nominally good thermal link (40 Au wire bonds at the TES-frame in addition to two BeCu clamps), Tframe may be significantly above Tbath. This suggests that the thermal conductance from TES-frame to bath needs to be considered when modeling TES response. From the TES-frame, thermal energy exits the chip through electron–phonon coupling to a gold pad on the TES-frame and then through electron-mediated conduction in gold wire bonds to the surrounding metal structure at Tbath (Fig. 5).

Fig. 5
figure 5

Path of heat flow from TES-island to thermal bath. (Color figure online)

Full size image

For the gold wire bonds, assuming the temperature of a 1 mm long, 25.4 µm diameter wire is 20 mK, gold resistivity at room temperature \({\rho }_{{\text{rt}}}=0.022\) m·µΩ, and residual resistance ratio (RRR)  of  10, the Wiedemann–Franz law gives a thermal conductivity of \(1/{R}_{{\text{t}}}=\) 108 nW/K. With the sub-nW powers involved, even a single wire bond should remain within 2 mK of \({T}_{{\text{bath}}}\) (in turn supporting the assumption of a single temperature for the wire). The observed \({G}_{{\text{fb}}}\) from frame to bath at Tframe ≈ 100 mK was 90 nW/K and 200 nW/K for TES1 and TES2 respectively.

For the gold pads on the TES-frame, to which the gold wire bonds are attached, the electron–phonon coupling is given theoretically by Eq. (8), where \({\Sigma }_{{\text{Au}}}\) is the strength of electron–phonon thermal coupling in gold, \({T}_{{\text{f}}}\) is the phonon temperature of the silicon frame, and \({T}_{{\text{epad}}}\) is the electron temperature of the gold pad. For our TES chips, the deposited gold volume is \(V=5.67\times {10}^{5}\) µm3. For a constant power, the deviation of \({T}_{{\text{f}}}\) from \({T}_{{\text{epad}}}\approx {T}_{{\text{bath}}}\) is increased substantially at lower \({T}_{{\text{bath}}}\), due to the \({T}^{5}\) dependence.

$$P = {\Sigma }_{{{\text{Au}}}} \cdot V \cdot \left( {T_{{{\text{frame}}}}^{5} - T_{{{\text{epad}}}}^{5} } \right)$$
(8)

We may expect \(T_{{{\text{epad}}}} \approx T_{{{\text{bath}}}}\) due to the high conductivity of the gold wires, and \({T}_{{\text{frame}}}\) has been calculated as illustrated in Fig. 3. Since \(P\) and \(V\) are also known, Eq. (8) is used to estimate \({\Sigma }_{{\text{Au}}}\) in our chips under the assumption that the entire temperature drop \({T}_{{\text{f}}}-{T}_{{\text{bath}}}\) occurs in the electron–phonon coupling. For TES1, \({\Sigma }_{{\text{Au}}}\approx 0.45\) nW·µm−3·K−5. For TES2, \({\Sigma }_{{\text{Au}}}\approx 1.1\) nW·µm−3·K−5. We do not expect large variations in \({\Sigma }_{{\text{Au}}}\) between chips, and the difference between the above two estimates may be attributed to the 40 wire bonds in TES2 contributing to the \(V\) term, increasing it beyond the nominal deposited volume. From the literature we may expect \({\Sigma }_{{\text{Au}}}\approx\) (1.4 to 3.8) nW·µm−3·K−5 [5, 6], which is higher than the estimated values for our chips. Two sources of thermal resistance that may contribute to this difference are conduction through the Si chip frame and acoustic mismatch. With 4 wire bonds in TES1, the thermal energy travels through up to 2.4 mm along the length of each gold pad (0.91 nW/K at 35 mK) and underlying Si (11.6 nW/K at 35 mK), since the gold bonds are in the corners of the frame; this effect is reduced when wire bonds are evenly spaced along the pad. The acoustic mismatch [7] between the Si substrate and Au pad adds another 99 nW/K at 35 mK. Other possible causes for the high frame temperature, such as inadequate thermal links further up the chain towards the dilution refrigerator mixing chamber, are being investigated.